A First Exploration of the Ts/VI “Analytical Triangle” Technique with UAV Imagery for Deriving Key Surface Energy Balance Parameters at Very High Spatial Resolution
Abstract
1. Introduction
2. Experimental Set Up
2.1. Study Site and Ground Instrumentation
2.2. UAV Data: Acquisition
3. Methods
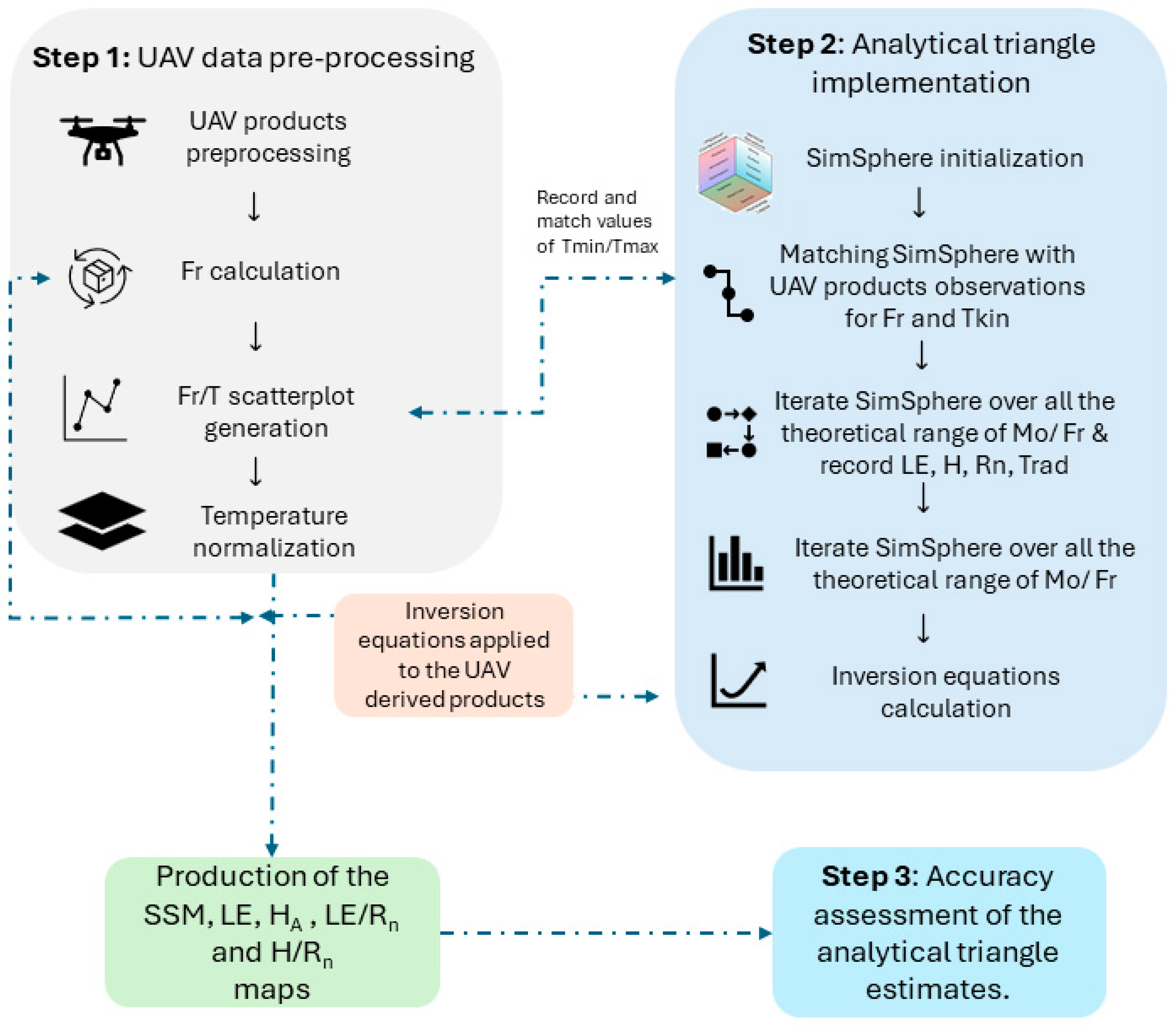
3.1. UAV Data Pre-Processing
3.2. Analytical Triangle Implementation
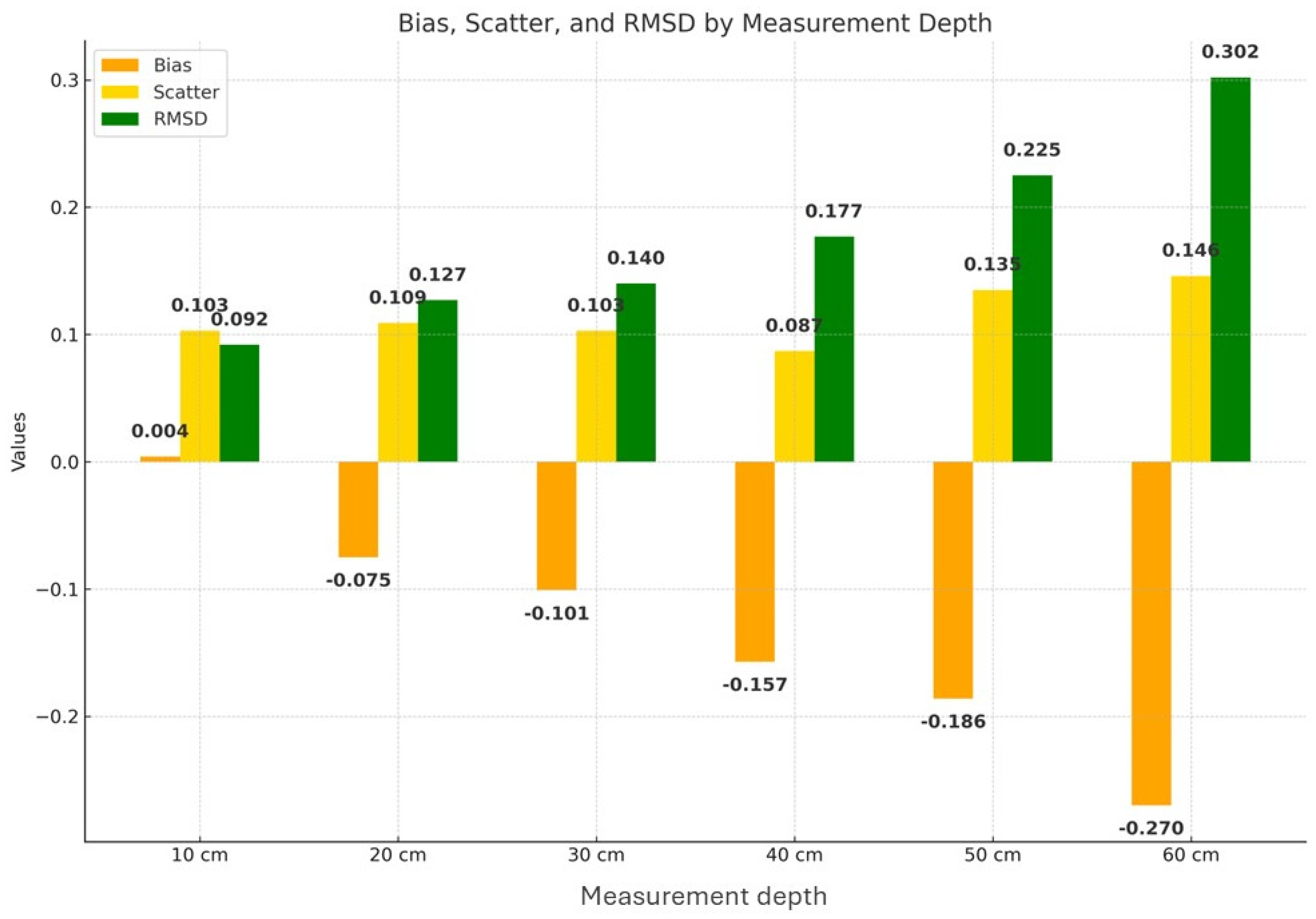
3.3. Accuracy Assessment
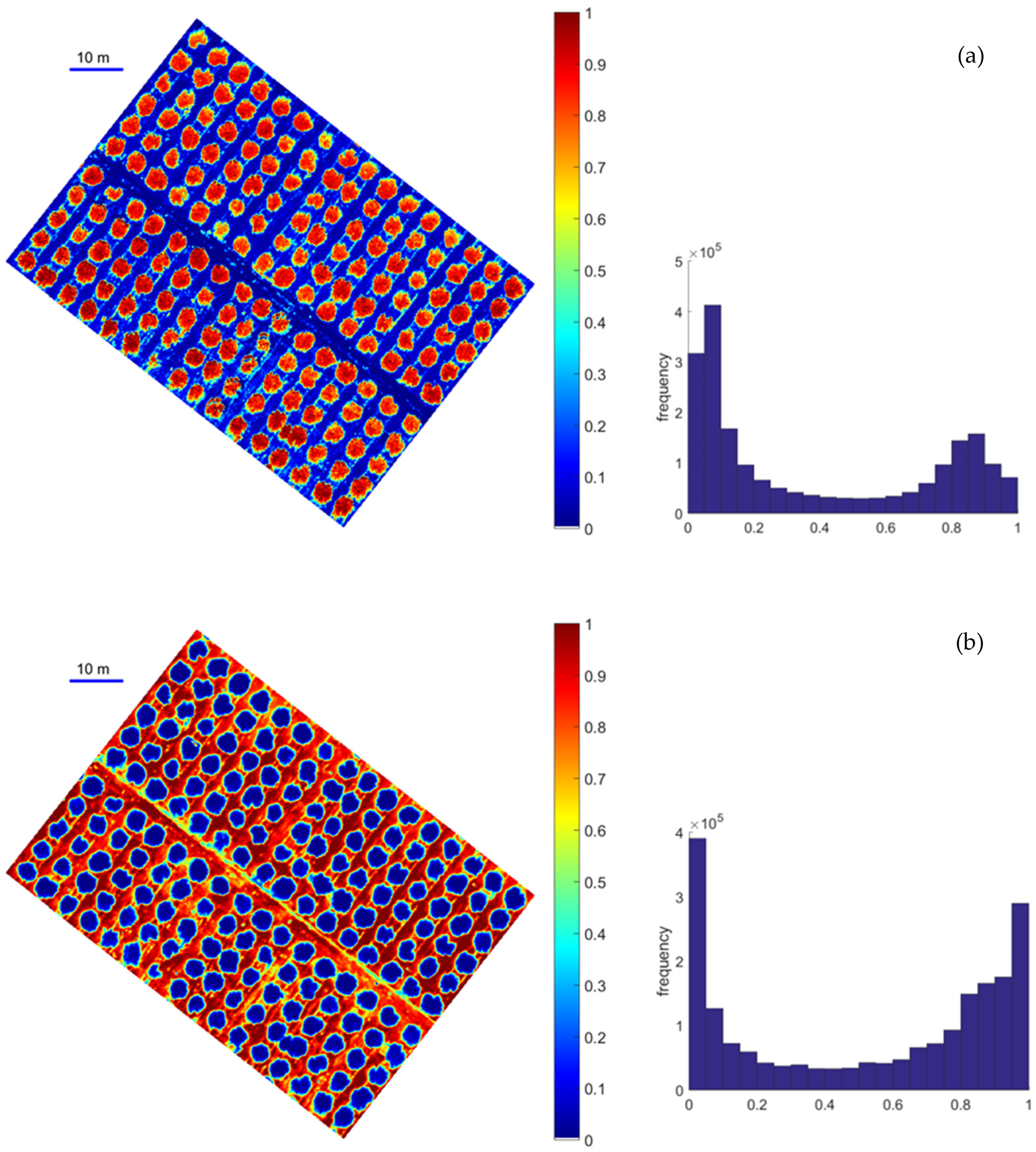
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bao, Y.; Lin, L.; Wu, S.; Kwal Deng, K.A.; Petropoulos, G.P. Surface Soil Moisture Retrievals over Partially Vegetated Areas from the Synergy of Sentinel-1 and Landsat 8 Data Using a Modified Water-Cloud Model. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 76–85. [Google Scholar] [CrossRef]
- Tran, B.N.; Van Der Kwast, J.; Seyoum, S.; Uijlenhoet, R.; Jewitt, G.; Mul, M. Uncertainty Assessment of Satellite Remote-Sensing-Based Evapotranspiration Estimates: A Systematic Review of Methods and Gaps. Hydrol. Earth Syst. Sci. 2023, 27, 4505–4528. [Google Scholar] [CrossRef]
- Suni, T.; Guenther, A.; Hansson, H.C.; Kulmala, M.; Andreae, M.O.; Arneth, A.; Artaxo, P.; Blyth, E.; Brus, M.; Ganzeveld, L.; et al. The Significance of Land-Atmosphere Interactions in the Earth System—iLEAPS Achievements and Perspectives. Anthropocene 2015, 12, 69–84. [Google Scholar] [CrossRef]
- Avissar, R. Conceptual Aspects of a Statistical-dynamical Approach to Represent Landscape Subgrid-scale Heterogeneities in Atmospheric Models. J. Geophys. Res. 1992, 97, 2729–2742. [Google Scholar] [CrossRef]
- Tsesmelis, D.E.; Karavitis, C.A.; Kalogeropoulos, K.; Tsatsaris, A.; Zervas, E.; Vasilakou, C.G.; Stathopoulos, N.; Skondras, N.A.; Alexandris, S.G.; Chalkias, C.; et al. Development and Application of Water and Land Resources Degradation Index (WLDI). Earth 2021, 2, 515–531. [Google Scholar] [CrossRef]
- Tsesmelis, D.E.; Karavitis, C.A.; Kalogeropoulos, K.; Zervas, E.; Vasilakou, C.G.; Skondras, N.A.; Oikonomou, P.D.; Stathopoulos, N.; Alexandris, S.G.; Tsatsaris, A.; et al. Evaluating the Degradation of Natural Resources in the Mediterranean Environment Using the Water and Land Resources Degradation Index, the Case of Crete Island. Atmosphere 2022, 13, 135. [Google Scholar] [CrossRef]
- Shen, C.; Niu, J.; Phanikumar, M.S. Evaluating Controls on Coupled Hydrologic and Vegetation Dynamics in a Humid Continental Climate Watershed Using a Subsurface-land Surface Processes Model. Water Resour. Res. 2013, 49, 2552–2572. [Google Scholar] [CrossRef]
- FAO. The State of the World’s Land and Water Resources for Food and Agriculture 2021—Systems at Breaking Point; FAO: Rome, Italy, 2022; ISBN 978-92-5-136127-6. [Google Scholar]
- Bai, L.; Long, D.; Yan, L. Estimation of Surface Soil Moisture with Downscaled Land Surface Temperatures Using a Data Fusion Approach for Heterogeneous Agricultural Land. Water Resour. Res. 2019, 55, 1105–1128. [Google Scholar] [CrossRef]
- Alexandridis, T.; Cherif, I.; Bilas, G.; Almeida, W.; Hartanto, I.; Van Andel, S.; Araujo, A. Spatial and Temporal Distribution of Soil Moisture at the Catchment Scale Using Remotely-Sensed Energy Fluxes. Water 2016, 8, 32. [Google Scholar] [CrossRef]
- Srivastava, P.K.; Pandey, P.C.; Petropoulos, G.P.; Kourgialas, N.N.; Pandey, V.; Singh, U. GIS and Remote Sensing Aided Information for Soil Moisture Estimation: A Comparative Study of Interpolation Techniques. Resources 2019, 8, 70. [Google Scholar] [CrossRef]
- Loew, A.; Stacke, T.; Dorigo, W.; De Jeu, R.; Hagemann, S. Potential and Limitations of Multidecadal Satellite Soil Moisture Observations for Selected Climate Model Evaluation Studies. Hydrol. Earth Syst. Sci. 2013, 17, 3523–3542. [Google Scholar] [CrossRef]
- Shi, Q.; Liang, S. Surface-Sensible and Latent Heat Fluxes over the Tibetan Plateau from Ground Measurements, Reanalysis, and Satellite Data. Atmos. Chem. Phys. 2014, 14, 5659–5677. [Google Scholar] [CrossRef]
- Chrysafi, A.; Virkki, V.; Jalava, M.; Sandström, V.; Piipponen, J.; Porkka, M.; Lade, S.J.; La Mere, K.; Wang-Erlandsson, L.; Scherer, L.; et al. Quantifying Earth System Interactions for Sustainable Food Production via Expert Elicitation. Nat. Sustain. 2022, 5, 830–842. [Google Scholar] [CrossRef]
- Liu, J.-G.; Xie, Z.-H. Improving Simulation of Soil Moisture in China Using a Multiple Meteorological Forcing Ensemble Approach. Hydrol. Earth Syst. Sci. 2013, 17, 3355–3369. [Google Scholar] [CrossRef]
- Xu, K.; Wang, X.; Jiang, C.; Sun, O.J. Assessing the Vulnerability of Ecosystems to Climate Change Based on Climate Exposure, Vegetation Stability and Productivity. For. Ecosyst. 2020, 7, 23. [Google Scholar] [CrossRef]
- Liu, Y.; Jing, W.; Wang, Q.; Xia, X. Generating High-Resolution Daily Soil Moisture by Using Spatial Downscaling Techniques: A Comparison of Six Machine Learning Algorithms. Adv. Water Resour. 2020, 141, 103601. [Google Scholar] [CrossRef]
- Tian, G.; Ma, B.; Xu, X.; Liu, X.; Xu, L.; Liu, X.; Xiao, L.; Kong, L. Simulation of Urban Expansion and Encroachment Using Cellular Automata and Multi-Agent System Model—A Case Study of Tianjin Metropolitan Region, China. Ecol. Indic. 2016, 70, 439–450. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Ireland, G.; Barrett, B. Surface Soil Moisture Retrievals from Remote Sensing: Current Status, Products & Future Trends. Phys. Chem. Earth Parts A/B/C 2015, 83–84, 36–56. [Google Scholar] [CrossRef]
- Gonzalez-Dugo, V.; Goldhamer, D.; Zarco-Tejada, P.J.; Fereres, E. Improving the Precision of Irrigation in a Pistachio Farm Using an Unmanned Airborne Thermal System. Irrig. Sci. 2015, 33, 43–52. [Google Scholar] [CrossRef]
- Chandel, A.K.; Khot, L.R.; Molaei, B.; Peters, R.T.; Stöckle, C.O.; Jacoby, P.W. High-Resolution Spatiotemporal Water Use Mapping of Surface and Direct-Root-Zone Drip-Irrigated Grapevines Using UAS-Based Thermal and Multispectral Remote Sensing. Remote Sens. 2021, 13, 954. [Google Scholar] [CrossRef]
- Chen, Q.; Tang, X.; Li, B.; Tang, Z.; Miao, F.; Song, G.; Yang, L.; Wang, H.; Zeng, Q. Spatial Downscaling of Soil Moisture Based on Fusion Methods in Complex Terrains. Remote Sens. 2023, 15, 4451. [Google Scholar] [CrossRef]
- Nieto, H.; Kustas, W.P.; Torres-Rúa, A.; Alfieri, J.G.; Gao, F.; Anderson, M.C.; White, W.A.; Song, L.; Alsina, M.D.M.; Prueger, J.H.; et al. Evaluation of TSEB Turbulent Fluxes Using Different Methods for the Retrieval of Soil and Canopy Component Temperatures from UAV Thermal and Multispectral Imagery. Irrig. Sci. 2019, 37, 389–406. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Sude, B.; Geng, B.; Ma, J.; Lin, X.; Hao, Z.; Jing, W.; Chen, Q.; Quan, Z. Observation of the Winter Regional Evaporative Fraction Using a UAV-Based Eddy Covariance System over Wetland Area. Agric. For. Meteorol. 2021, 310, 108619. [Google Scholar] [CrossRef]
- Sun, Y.; Ma, J.; Sude, B.; Lin, X.; Shang, H.; Geng, B.; Diao, Z.; Du, J.; Quan, Z. A UAV-Based Eddy Covariance System for Measurement of Mass and Energy Exchange of the Ecosystem: Preliminary Results. Sensors 2021, 21, 403. [Google Scholar] [CrossRef] [PubMed]
- Ge, X.; Wang, J.; Ding, J.; Cao, X.; Zhang, Z.; Liu, J.; Li, X. Combining UAV-Based Hyperspectral Imagery and Machine Learning Algorithms for Soil Moisture Content Monitoring. PeerJ 2019, 7, e6926. [Google Scholar] [CrossRef] [PubMed]
- Niu, H.; Hollenbeck, D.; Zhao, T.; Wang, D.; Chen, Y. Evapotranspiration Estimation with Small UAVs in Precision Agriculture. Sensors 2020, 20, 6427. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Nieto, H.; Neumann Andersen, M.; Kørup, K.; Larsen, R.; Morel, J.; Parsons, D.; Zhou, Z.; Manevski, K. Accurate Estimates of Land Surface Energy Fluxes and Irrigation Requirements from UAV-Based Thermal and Multispectral Sensors. ISPRS J. Photogramm. Remote Sens. 2023, 198, 238–254. [Google Scholar] [CrossRef]
- Ruwaimana, M.; Satyanarayana, B.; Otero, V.; Muslim, A.M.; Syafiq, A.M.; Ibrahim, S.; Raymaekers, D.; Koedam, N.; Dahdouh-Guebas, F. The Advantages of Using Drones over Space-Borne Imagery in the Mapping of Mangrove Forests. PLoS ONE 2018, 13, e0200288. [Google Scholar] [CrossRef] [PubMed]
- Petropoulos, G.P.; Srivastava, P.K.; Ferentinos, K.P.; Hristopoulos, D. Evaluating the Capabilities of Optical/TIR Imaging Sensing Systems for Quantifying Soil Water Content. Geocarto Int. 2020, 35, 494–511. [Google Scholar] [CrossRef]
- Zhang, D.; Tang, R.; Zhao, W.; Tang, B.; Wu, H.; Shao, K.; Li, Z.-L. Surface Soil Water Content Estimation from Thermal Remote Sensing Based on the Temporal Variation of Land Surface Temperature. Remote Sens. 2014, 6, 3170–3187. [Google Scholar] [CrossRef]
- Capodici, F.; Cammalleri, C.; Francipane, A.; Ciraolo, G.; La Loggia, G.; Maltese, A. Soil Water Content Diachronic Mapping: An FFT Frequency Analysis of a Temperature–Vegetation Index. Geosciences 2020, 10, 23. [Google Scholar] [CrossRef]
- Anagnostopoulos, V.; Petropoulos, G.P.; Ireland, G.; Carlson, T.N. A Modernized Version of a 1D Soil Vegetation Atmosphere Transfer Model for Improving Its Future Use in Land Surface Interactions Studies. Environ. Model. Softw. 2017, 90, 147–156. [Google Scholar] [CrossRef]
- Carlson, T. An Overview of the “Triangle Method” for Estimating Surface Evapotranspiration and Soil Moisture from Satellite Imagery. Sensors 2007, 7, 1612–1629. [Google Scholar] [CrossRef]
- Maltese, A.; Capodici, F.; Ciraolo, G.; Loggia, G. Soil Water Content Assessment: Critical Issues Concerning the Operational Application of the Triangle Method. Sensors 2015, 15, 6699–6718. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Sandric, I.; Hristopulos, D.; Nahum Carlson, T. Evaporative Fluxes and Surface Soil Moisture Retrievals in a Mediterranean Setting from Sentinel-3 and the “Simplified Triangle”. Remote Sens. 2020, 12, 3192. [Google Scholar] [CrossRef]
- Carlson, T.N.; Petropoulos, G.P. A New Method for Estimating of Evapotranspiration and Surface Soil Moisture from Optical and Thermal Infrared Measurements: The Simplified Triangle. Int. J. Remote Sens. 2019, 40, 7716–7729. [Google Scholar] [CrossRef]
- Piles, M.; Petropoulos, G.P.; Sánchez, N.; González-Zamora, Á.; Ireland, G. Towards Improved Spatio-Temporal Resolution Soil Moisture Retrievals from the Synergy of SMOS and MSG SEVIRI Spaceborne Observations. Remote Sens. Environ. 2016, 180, 403–417. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Maltese, A.; Carlson, T.N.; Provenzano, G.; Pavlides, A.; Ciraolo, G.; Hristopulos, D.; Capodici, F.; Chalkias, C.; Dardanelli, G.; et al. Exploring the Use of Unmanned Aerial Vehicles (UAVs) with the Simplified ‘Triangle’ Technique for Soil Water Content and Evaporative Fraction Retrievals in a Mediterranean Setting. Int. J. Remote Sens. 2021, 42, 1623–1642. [Google Scholar] [CrossRef]
- Petropoulos, G.; Carlson, T.N.; Wooster, M.J.; Islam, S. A Review of Ts/VI Remote Sensing Based Methods for the Retrieval of Land Surface Energy Fluxes and Soil Surface Moisture. Prog. Phys. Geogr. Earth Environ. 2009, 33, 224–250. [Google Scholar] [CrossRef]
- Gillies, R.R.; Kustas, W.P.; Humes, K.S. A Verification of the “triangle” Method for Obtaining Surface Soil Water Content and Energy Fluxes from Remote Measurements of the Normalized Difference Vegetation Index (NDVI) and Surface e. Int. J. Remote Sens. 1997, 18, 3145–3166. [Google Scholar] [CrossRef]
- Capehart, W.J.; Carlson, T.N. Decoupling of Surface and Near-surface Soil Water Content: A Remote Sensing Perspective. Water Resour. Res. 1997, 33, 1383–1395. [Google Scholar] [CrossRef]
- Karpouzli, E.; Malthus, T. The Empirical Line Method for the Atmospheric Correction of IKONOS Imagery. Int. J. Remote Sens. 2003, 24, 1143–1150. [Google Scholar] [CrossRef]
- Negm, A.; Capodici, F.; Ciraolo, G.; Maltese, A.; Provenzano, G.; Rallo, G. Assessing the Performance of Thermal Inertia and Hydrus Models to Estimate Surface Soil Water Content. Appl. Sci. 2017, 7, 975. [Google Scholar] [CrossRef]
- Valor, E. Mapping Land Surface Emissivity from NDVI: Application to European, African, and South American Areas. Remote Sens. Environ. 1996, 57, 167–184. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Paolini, L. Land Surface Temperature Retrieval from LANDSAT TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Petropoulos, G.; Carlson, T.; Wooster, M. An Overview of the Use of the SimSphere Soil Vegetation Atmosphere Transfer (SVAT) Model for the Study of Land-Atmosphere Interactions. Sensors 2009, 9, 4286–4308. [Google Scholar] [CrossRef]
- Carlson, T.N.; Person, A.A.; Canich, T.J.; Petropoulos, G.P. Simsphere: A Downloadable Soil–Vegetation–Atmosphere–Transfer (SVAT) Model for Teaching and Research. Bull. Am. Meteorol. Soc. 2021, 102, E2198–E2206. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Lekka, C. Recent Developments to the SimSphere Land Surface Modelling Tool for the Study of Land-Atmosphere Interactions. Sensors 2024, 24, 3024. [Google Scholar] [CrossRef]
- Carlson, T.N.; Gillies, R.R.; Schmugge, T.J. An Interpretation of Methodologies for Indirect Measurement of Soil Water Content. Agric. For. Meteorol. 1995, 77, 191–205. [Google Scholar] [CrossRef]
- Deng, K.A.K.; Lamine, S.; Pavlides, A.; Petropoulos, G.P.; Bao, Y.; Srivastava, P.K.; Guan, Y. Large Scale Operational Soil Moisture Mapping from Passive MW Radiometry: SMOS Product Evaluation in Europe & USA. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 206–217. [Google Scholar] [CrossRef]

| Name | Description | Mathematical Definition |
|---|---|---|
| Bias | Bias (accuracy) | |
| Scatter | Scatter (precision) | |
| RMSD | Root Mean Square Difference |
| Flux Comparisons | Predicted (P) | Observed (O) | Difference (P-O) |
|---|---|---|---|
| LE flux (Wm−2) | 193.62 | 198.62 | −5.00 |
| H flux (Wm−2) | 271.67 | 336.69 | −65.02 |
| LE/Rn | 0.325 | 0.313 | 0.012 |
| H/Rn | 0.456 | 0.295 | 0.161 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petropoulos, G.P.; Detsikas, S.E.; Kalogeropoulos, K.; Pavlides, A. A First Exploration of the Ts/VI “Analytical Triangle” Technique with UAV Imagery for Deriving Key Surface Energy Balance Parameters at Very High Spatial Resolution. Drones 2024, 8, 290. https://doi.org/10.3390/drones8070290
Petropoulos GP, Detsikas SE, Kalogeropoulos K, Pavlides A. A First Exploration of the Ts/VI “Analytical Triangle” Technique with UAV Imagery for Deriving Key Surface Energy Balance Parameters at Very High Spatial Resolution. Drones. 2024; 8(7):290. https://doi.org/10.3390/drones8070290
Chicago/Turabian StylePetropoulos, George P., Spyridon E. Detsikas, Kleomenis Kalogeropoulos, and Andrew Pavlides. 2024. "A First Exploration of the Ts/VI “Analytical Triangle” Technique with UAV Imagery for Deriving Key Surface Energy Balance Parameters at Very High Spatial Resolution" Drones 8, no. 7: 290. https://doi.org/10.3390/drones8070290
APA StylePetropoulos, G. P., Detsikas, S. E., Kalogeropoulos, K., & Pavlides, A. (2024). A First Exploration of the Ts/VI “Analytical Triangle” Technique with UAV Imagery for Deriving Key Surface Energy Balance Parameters at Very High Spatial Resolution. Drones, 8(7), 290. https://doi.org/10.3390/drones8070290








