Abstract
This paper integrates intelligent reflecting surfaces (IRS) with unmanned aerial vehicles (UAV) to enhance the transmission performance of the Internet of Vehicles (IoV) through non-orthogonal multiple access (NOMA). It focuses on strengthening the signals from cell edge vehicles (CEVs) to the base station by optimizing the wireless propagation environment via an IRS-equipped UAV. The primary goal is to maximize the sum data rate of CEVs while satisfying the constraint of the successive interference cancellation (SIC) decoding threshold. The challenge lies in the non-convex nature of jointly considering the power control, subcarrier allocation, and phase shift design, making the problem difficult to optimally solve. To address this, the problem is decomposed into two independent subproblems, which are then solved iteratively. Specifically, the optimal phase shift design is achieved using the deep deterministic policy gradient (DDPG) algorithm. Furthermore, the graph theory is applied to determine the subcarrier allocation policy and derive a closed-form solution for optimal power control. Finally, the simulation results show that the proposed joint phase shift and resource management scheme significantly enhances the sum data rate compared to the state-of-the-art schemes, thereby demonstrating the benefits of integrating the IRS-equipped UAV into NOMA-enhanced IoV.
1. Introduction
As a key enabler of intelligent transportation systems (ITS), unmanned aerial vehicles (UAVs) can be used to improve the transmission performance of the Internet of Vehicle (IoV) in rural highways [1]. Generally, the UAV is regarded as an active component of the IoV (e.g., the aerial relay) that can enhance the flexibility, robustness, and throughput [2]. By seamlessly integrating UAVs into IoV, several advantages come to the forefront, fundamentally transforming how transportation networks operate [3,4,5]. On the one hand, UAVs offer unparalleled mobility and coverage, overcoming the geographical limitations that often hinder the deployment of conventional infrastructure in rural areas. With the ability to traverse vast expanses swiftly, UAVs ensure continuous connectivity for vehicles, regardless of terrain obstacles or distance. This inherent mobility not only extends the reach of IoV networks but also enables real-time data transmission, which is essential for dynamic traffic management and remote monitoring in remote regions [6,7]. On the other hand, UAVs introduce a layer of resilience and redundancy to IoV systems, mitigating the risks associated with single points of failure or infrastructure damage. In scenarios where ground-based communication infrastructure may be compromised due to natural disasters or accidents, UAVs serve as agile alternatives, ensuring uninterrupted communication and operational continuity. This redundancy enhances the reliability of IoV networks, fostering safer and more efficient transportation ecosystems even in the face of unforeseen disruptions [8,9,10]. In essence, by harnessing the capabilities of UAVs as active components within IoV, rural highways stand to benefit from enhanced connectivity, resilience, and efficiency, paving the way for smarter and more sustainable transportation solutions.
However, as an active aerial relay, the application of UAVs in fifth generation (5G)- and beyond 5G (B5G)-enabled IoV is questionable. The reason for this is that 5G/B5G-enabled IoV adopts a quasi-optic millimeter wave (mmWave) and visible light for communications [11,12,13]. In this situation, although the UAVs can facilitate line-of-sight (LoS) transmissions, the higher path loss attenuates the propagation signals between the UAV and cell edge vehicles (CEVs) and between the UAV and base station (BS) [14]. First, the higher path loss inherent in mmWave and visible-light communication systems presents a formidable obstacle for UAVs operating as relay nodes. Unlike traditional frequency bands, mmWave signals are highly susceptible to attenuation from environmental factors such as foliage, atmospheric conditions, and even building materials. Consequently, the effectiveness of UAVs in establishing robust connections with CEVs and the BS is diminished, compromising the reliability and throughput of IoV [15,16,17]. Moreover, the dynamic nature of UAV deployment exacerbates the challenges associated with maintaining stable connectivity in 5G and B5G environments. As UAVs navigate through airspace, they encounter varying degrees of interference and signal degradation, further impeding their ability to sustain seamless communication links with vehicles and infrastructure components [18,19,20]. Therefore, while UAVs offer inherent advantages when used as aerial relays in traditional communication frameworks, their integration into 5G- and B5G-enabled IoV necessitates innovative approaches to address the unique propagation characteristics and operational dynamics associated with advanced wireless technologies. Efforts to mitigate path loss, enhance spectral efficiency, and optimize UAV mobility are paramount to unlocking the full potential of UAVs in shaping the future of intelligent transportation systems.
Facing the above challenges, the authors [21,22] adopted an intelligent reflecting surface (IRS)-equipped UAV to create ITS-related services for vehicle platooning in obstructed rural highways covered by 5G/B5G. First, the IRS technique can enhance 5G/B5G signal coverage in rural areas, especially in situations with a complex terrain or buildings that block signals [23,24]. By using UAVs carrying IRSs, dynamic signal reflection and adjustment are achievable, optimizing signal quality and thus enhancing communication efficiency and reliability [25]. Second, UAVs are highly mobile and flexible, and are able to quickly adjust their positions and flight paths according to actual needs and environmental changes, providing optimal signal reflection and coverage to the areas in need in real-time [26,27]. Third, compared to the construction of fixed BSs or communication towers, using an IRS-equipped UAV significantly reduces the cost of infrastructure construction and maintenance, making it particularly suitable for remote or economically disadvantaged rural areas. Finally, on rural roads where communication is obstructed, the stable communication service provided by UAVs can effectively support the operation of an ITS, such as automatic vehicle queuing, traffic flow management, and emergency response, improving road utilization efficiency, reducing traffic congestion, and enhancing driving safety [28,29]. To maximize the energy efficiency of IRS-equipped UAVs, a scheme for the joint optimization of resource allocation, phase shift, and trajectory was proposed in [30]. Additionally, the non-orthogonal multiple access (NOMA) technique has been emerging as a potential solution in UAV-assisted networks, which can achieve timely, reliable, and seamless data exchange [31]. Therefore, some recent efforts in [32,33] combined IRS-equipped UAVs with the NOMA technique to obtain the benefits of both. The sum data rate maximization schemes used to fully exploit the advantages of NOMA-enhanced, IRS-equipped UAVs, are presented in [34,35,36].
However, it is challenging to integrate the IRS-equipped UAV and NOMA technique into IoV while optimizing the resource management and phase shift design. First, the works in [21,22,30] make an implicit assumption that spectrum-efficient resource management can be achieved. Actually, in dynamic IoV, the subcarrier allocation and power control policies need to be delicately designed to improve the communication performance. Second, although the introduction of IRS can enhance signal strengths, the constraint of the successive interference cancellation (SIC) decoding threshold cannot be ignored. This practical factor has not been fully considered in [32,34,36]. Third, compared with the hover mode, the mobile IRS-equipped UAV can further maintain aerial LoS links. Unfortunately, this issue has been overlooked in [33,35]. Finally, due to the highly complex coupling among optimization variables (e.g., the power, subcarrier, and phase shift) and mixed combinatorial features, it is difficult to solve the sum data rate maximization problem in the context of the considered scenarios. Especially, considering the limitations on the computing ability of CEVs, we need to design a low-complexity scheme to jointly optimize the resource management and phase shift with an acceptable running time.
This paper is motivated by several key considerations, as mentioned above, and proposes a NOMA-enhanced communication framework in IoV to enhance uplink performance, utilizing an IRS-equipped UAV to assist in the data transmissions of CEVs. Then, we explore the challenge of maximizing the sum data rate by considering power control, subcarrier allocation, and phase shift design. This complex problem is constrained by the SIC decoding threshold. An iterative optimization (IO) algorithm, employing coordinate polling, is introduced to address the non-convex nature of the problem, where the power, subcarrier, and phase shift are solved in turn. Finally, the simulation results demonstrate that our proposed scheme outperforms current state-of-the-art schemes [2,21,31,35] in terms of sum data rate. Additionally, the number of supported CEVs, and the influence of network parameters, convergence, and complexity are fully shown and discussed.
The remainder of this paper is organized as follows. Section 2 presents the system model and problem formulation, establishing the foundational concepts and objectives of our study. Section 3 introduces the proposed scheme to maximize the sum data rate. Section 4 is dedicated to the simulation results, validating the effectiveness of our proposed scheme through extensive simulations. Finally, Section 5 concludes the paper by summarizing the key findings and suggesting directions for future research.
2. System Model and Problem Formulation
As shown in Figure 1, we consider an uplink of NOMA-enhanced IoV, where V single-antenna CEVs (denoted as ) transmit the signals to the BS with the assistance of an IRS-equipped UAV. The IRS has Y elements, denoted as . To increase the road capacity, vehicle platooning adopts vehicle-to-everything (V2X) techniques to let a group of CEVs travel closely in a train-like manner [37]. To simplify the problem, we consider vehicular communication on a straight rural highway. In CEV-UAV-BS links, there are K subcarriers, denoted as . Additionally, the direct CEV-BS links are assumed to be blocked by obstacles [38]. We define the subcarrier allocation policy as , where is the subcarrier allocation indicator. If the v-th CEV occupies the k-th subcarrier, ; otherwise, . Due to the high mobility of the IRS-equipped UAV and CEVs, the transmission channels vary rapidly. Therefore, we use the outdated channel estimation method proposed in [22] to reduce the pilot overhead.
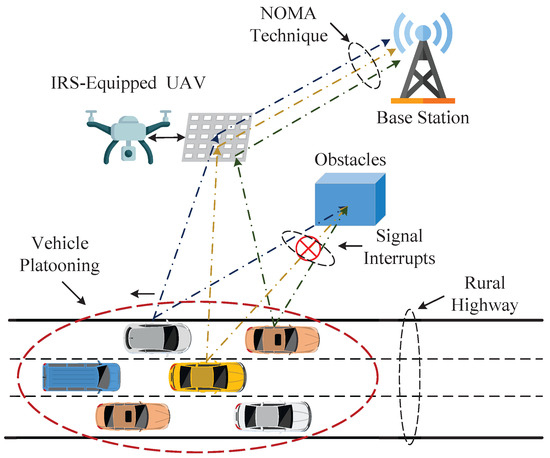
Figure 1.
NOMA-enhanced IoV assisted by an IRS-equipped UAV.
The signal-to-interference-plus-noise ratio (SINR) of the v-th CEV is
where is the transmitted power of v-th CEV, denoted as ; is the channel between the IRS-equipped UAV and BS on the k-th subcarrier, ; is the channel between the v-th CEV and IRS-equipped UAV on the k-th subcarrier, ; is the phase shift matrix, , , where is the phase shift of y-th reflection unit; is the noise power; is the co-channel interference, and we have , where i is the i-th CEV that also occupies the k-th subcarrier; is the channel between the i-th CEV and IRS-equipped UAV on the k-th subcarrier, ; is the subcarrier allocation policy of i-th CEV, ; is the transmitted power of i-th CEV, .
To successfully implement the NOMA technique, the SIC decoding threshold needs to be considered. We define the decoding indicator as , which is expressed as follows:
where . According to (1) and (2), the uplink data rate of the v-th CEV is
where is the channel bandwidth.
By optimizing the subcarrier allocation , power control , and phase shift , we aim to maximize the sum data rate of CEVs. The sum data rate maximization problem is mathematically formulated as P1, which is constrained by the SIC decoding threshold and phase resolution.
where is the maximum transmitted power. In P1, (4b) ensures that each CEV is assigned to a subcarrier; (4c) and (4d) together define that each subcarrier can only accommodate a maximum of two CEVs [39]; (4e) limits the range of transmitted power for each CEVs; (4f) constrains the phase shift of IRS. It should be noted that the phase shift of each reflection unit is continuous and the modulus is always 1 [30].
Remark: Our paper explicitly addresses the mobility aspect of UAVs within the context of IoV, rather than merely focusing on stationary systems. However, it is important to note that we did not undertake trajectory optimization for the UAVs in this study. Instead, we emphasize the advantages of preset trajectories over trajectory optimization within UAV-assisted IoV, particularly highlighting the real-time nature of information transmission. While trajectory optimization undoubtedly offers benefits, such as enhanced efficiency and adaptability, preset trajectories excel in scenarios where timely data exchange is paramount. Moving forward, our future work will indeed delve into optimizing UAV trajectories, aiming to strike a balance between efficiency and real-time communication demands within the IoV.
3. Sum Data Rate Maximization Scheme
In Section 3, an IO algorithm based on coordinate polling is presented to deal with P1, as shown in Figure 2. Specifically, P1 is decoupled into the phase shift optimization problem P2 and resource management problem P3. The DDPG algorithm is used to optimize the phase shift. Then, the subcarrier allocation problem is reformulated as a maximum weighted independent set (MWIS) issue using the graph theory, and the closed-form expression of optimal power control is derived theoretically. In the designed IO algorithm, the selection of initial inputs is recognized as a pivotal factor influencing both the convergence and the ultimate outputs of the process. To address this, initial inputs are randomly selected within the feasible domain of the problem, providing the algorithm with the opportunity to reach the global optimum. Furthermore, given the significant impact that the initial input selection can have on the results, the Monte Carlo method is incorporated into our algorithm. This approach involves conducting multiple runs with varied initial inputs and subsequently analyzing the results. Through this comparative analysis, we can effectively evaluate the performance of the algorithm under different conditions, thereby enabling the identification and selection of the most optimal result as the final solution. This method enhances the robustness and reliability of the algorithm’s outputs.
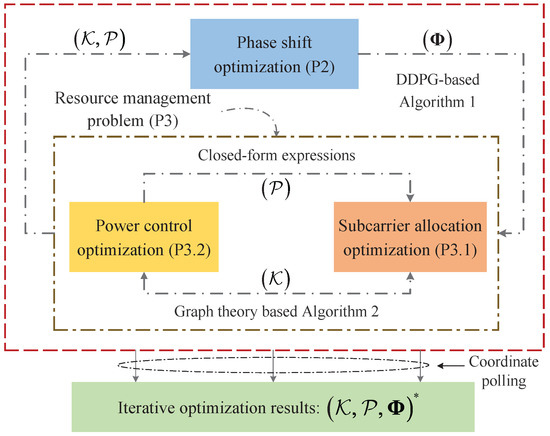
Figure 2.
Overall algorithmic framework.
3.1. Phase Shift Design
Given and , the phase shift design problem is simplified into:
The DDPG algorithm based on the Actor–Critic structure is used to solve P2. This is because the use of DDPG presents significant advantages in solving the IRS phase shift design problem. First, DDPG integrates deep learning with deterministic policy gradient techniques, adeptly managing high-dimensional and continuous action spaces, and thus enabling the IRS to achieve more precise and complex phase shift adjustments. Second, DDPG utilizes an experience replay mechanism that more effectively harnesses past experiences to boost learning efficiency and stability. Moreover, the adoption of DDPG can circumvent local optima in the phase shift design problem, enhancing system robustness and adaptability. In conclusion, the application of DDPG in solving P2 endows the IRS-equipped UAV with increased flexibility and intelligence. Specifically, the action vector, state vector, and reward function are designed as follows.
(A) Action Vector: Let denote the action vector. Since the inputs of the neural network are real numbers, needs to be decomposed into real and imaginary parts. We define the total training steps as T, denoted as . The action vector of the t-th step is given by
where and are real and imaginary parts, respectively.
(B) State Vector: In the t-th step, the state vector is
(C) Reward Function: Since this paper aims to maximize , the reward of the t-th step is set to , i.e., . In the Actor network, the normalization layer and the second hidden layer adopt the rectified linear activation (ReLU) function and the hyperbolic tangent (Tanh) function, respectively. In the Critic network, and are separately fed to two individual hidden layers and then connected to two normalization layers. The results of two normalization layers are concatenated and subsequently linked to one hidden layer. As discussed in [32], the Adam optimizer is used to update the neural network parameters. Additionally, the learning rates of Actor and Critic are 0.001 and 0.002, respectively.
The action vector composed of is the output of the Actor network. Meanwhile, the value of each element in is constrained by the Tanh function, and its range is . Due to the range restriction, cannot be used directly to calculate . In this situation, needs to be normalized, and we have the following:
where .
The steps used to solve P2 are summarized in Algorithm 1. In the proposed scheme using the DDPG algorithm to solve the phase shift design problem, the complexity burden during simulation and the accuracy of the algorithm play critical roles. The DDPG algorithm, being a model-free, off-policy Actor–Critic method based on deep reinforcement learning, allows for continuous action spaces, making it suitable for the phase shift design problem, where the phase shifts can have a continuum of values. However, the complexity of implementing DDPG is relatively high because it requires the maintenance of two neural networks: the actor network that proposes actions and the critic network that evaluates these actions. Furthermore, training these networks involves numerous forward and backward propagations, which are computationally intensive, especially when handling complex environments and large state spaces, as in IRS-enabled vehicular scenarios.
| Algorithm 1 DDPG-based phase shift design |
|
Accuracy-wise, DDPG can offer high precision in determining optimal phase shifts due to its ability to continuously learn and adapt its policy. The algorithm benefits from experience replay and target networks, which help to stabilize the learning process and improve convergence to the optimal policy. Nevertheless, the accuracy of DDPG is highly dependent on adequate hyperparameter tuning, network architecture choices, and sufficient exploration of the action space during training. Therefore, while DDPG holds potential for efficiently resolving the phase shift design problem with high accuracy, it does so at the cost of increased computational complexity. Ensuring the successful deployment of DDPG involves a careful balance between complexity, computational resources, and the precision requirements of IRS-enabled vehicular scenarios.
3.2. Optimization of Resource Management
Given , the resource management problem is simplified into:
For P3, since and are highly coupled in the objective function and constraints, P3 is further decoupled and iteratively solved.
3.2.1. Subcarrier Allocation
In this stage, it is assumed that and have been determined. Then, the subcarrier allocation problem is transformed into:
We define a weighted undirected graph (WUG) as . The definitions of the WUG, maximum weighted independent set (MWIS), and independent set (IS) can be found in [40]. In , , , and are the set of vertices, the set of edges, and the weight, respectively. A combination is constructed, where , , , and . We define the vertex f corresponding to the combination , and the weight of vertex f is expressed as follows:
where . Let denote the neighborhood of vertex f in , and we have . In addition, let denote the number of neighbors of vertex f in . As discussed in [40], P3.1 can be viewed as an MWIS problem, and can be solved by using Algorithm 2.
| Algorithm 2 Graph-theory-based subcarrier allocation |
|
3.2.2. Power Control
Similarly, we assume that and were given in advance, and the power control problem is expressed as follows:
A combination is introduced to represent the v-th and i-th CEVs that share the k-th subcarrier. As introduced above, we have . For combination , there are three cases.
Case (A): Both the v-th and i-th CEVs can satisfy the constraint of concurrently. We have
and
To satisfy , we can obtain
and
Case (B): Only the v-th or i-th CEV can satisfy the constraint of . We have
where (17a) indicates that only the v-th CEV can satisfy the constraint of , and (17b) indicates that only the i-th CEV can satisfy the constraint of .
Case (C): None of them can satisfy the constraint of , and we have .
Lemma 1.
The closed-form expression of optimal power control is shown in (18), where . It is noted that due to , we have .
Proof.
Through a comprehensive analysis of Cases (A)–(C), (19) can be derived. In (19), the first line and second line represent Case (A), the third line represents Case (B), and the fourth line represents Case (C). Lemma 1 is proved. □
3.3. Performance Analysis
In this paper, is obtained through the iterative optimization of . Thus, we need to analyze the convergence. First, we consider a simple scenario consisting of a BS, an IRS-equipped UAV, and a CEV. Since there is only one CEV, we have according to (18). Then, using the enumeration method, we can obtain and . As only one vehicle is present, there is no need to account for co-channel interference and spectrum reuse. In this paper, we consider an application scenario consisting of V CEVs, and the upper bound is
where can be obtained by iterative optimization, as shown in Figure 2. Finally, due to the existence of an upper bound , the convergence can be proven.
This IO algorithm, based on coordinate polling, effectively addresses the complexity of optimizing communication systems, especially in the context of IoV. Decoupling the problem P1 into phase shift optimization P2 and resource management P3 simplifies the overall optimization process. Specifically, the DDPG algorithm is leveraged to optimize the phase shifts of the IRS, which dynamically adjusts the propagation environment to enhance signal quality. This is crucial for ensuring reliable communication in scenarios with high mobility and variable environmental conditions, such as IoV. For resource management, reformulating the subcarrier allocation problem as an MWIS problem allows for an efficient and theoretically grounded approach to optimizing resource allocation. This graph-theory-based method enables a more structured and simplified problem-solving process. Furthermore, deriving a closed-form expression for optimal power control directly supports the effective management of transmission power, thereby maximizing the efficiency and reliability of the communication system. The principal advantages of this approach include enhanced computational efficiency, scalability, and the ability to provide high-quality solutions for complex optimization problems. Its application in IoV is particularly beneficial due to the high mobility of vehicles and the dynamic nature of their communication environment. By optimizing phase shifts and resource management intelligently, it is possible to significantly improve the performance of vehicular communication systems, leading to more a reliable, efficient, and safe IoV.
Unfortunately, while the employed IO algorithm effectively provides solutions for the sum data rate maximization problem P1, it cannot ensure that the global optimal solution is attained. This limitation stems from various factors. Firstly, the IO algorithm, utilizing coordinate polling, might converge to local optima rather than the global optimum. Although capable of simplifying the optimization process by decomposing P1 into phase shift optimization P2 and resource management P3, assurance is not provided that the locally optimal solutions discovered for these sub-problems collectively lead to the global optimum for the primary problem. Secondly, although the IO algorithm offers improved computational efficiency, scalability, and the ability to deliver high-quality solutions, it still depends on heuristics and approximations. However, these approximations may not consistently result in the globally optimal solution, especially in complex optimizations involving non-convexities or discontinuities. Therefore, although the IO algorithm substantially enhances the efficiency of addressing the sum data rate maximization problem P1 in UAV-assisted IoV, it may not ensure the achievement of the global optimal solution due to the inherent algorithmic limitations and complexities associated with modeling the communication environment.
4. Simulation Results
The performance of the proposed sum data rate maximization scheme is evaluated via simulation. We compare it with four state-of-the-art works, namely Scheme 1 [21], Scheme 2 [35], Scheme 3 [31], and Scheme 4 [2]. Specifically, Scheme 1 involves the deployment of an IRS-equipped UAV that dynamically tracks and follows the CEVs, while simultaneously optimizing the phase shift design and subcarrier allocation. In Scheme 2, the IRS is statically installed on buildings, and the NOMA technique is employed to improve spectrum efficiency. Scheme 3 combines UAV-assisted relaying with NOMA, where the UAV employs the decode-and-forward protocol. Finally, Scheme 4 focuses on optimizing resource management within the CEVs, where the NOMA technique is directly employed for communication between CEVs and the BS. According to [2,32], the major simulation parameters set in this paper are as follows: , dBm, dB, KHz, dBm/Hz, , and . Additionally, as discussed in [41], the air-to-ground path loss model is , the multipath fading model follows the Rayleigh fading with 1 variance, the carrier frequency is 2.1 GHz, the speed of the IRS-equipped UAV and CEVs is 50 km/h, and the number of simulation runs is .
Figure 3 plots the sum data rate versus the number of CEVs. It is observed that the proposed scheme outperforms the state-of-the-art works in terms of the sum data rate. Specifically, compared to Schemes 1, 2, 3, and 4, the sum data rate can be increased by 11.8%, 18.4%, 4.2%, and 39.5%. The reasons for the improved performance are as follows. First, in Scheme 1, the IRS-equipped UAV moves with the CEVs, based on which the subcarrier and phase shift are optimized. However, by contrast, the proposed scheme enables NOMA to support more CEVs simultaneously transmitting data under the same spectrum resources, leading to an overall increase in data rates. Second, in Scheme 2, the IRS is fixed to the building and uses NOMA. In this situation, the channel gain brought about by the IRS is weakened, thus reducing the transmission performance. Third, in Scheme 3, the UAV following the CEVs adopts the decode and forward (DF) relay protocol with NOMA, under which the resource management is optimized. However, the transmission bottleneck will limit the data rate of the DF protocol. Finally, in Scheme 4, the CEVs communicate directly with the BS. In this situation, the signal propagation paths cannot be optimized, thereby increasing the path loss and reducing the data rate.
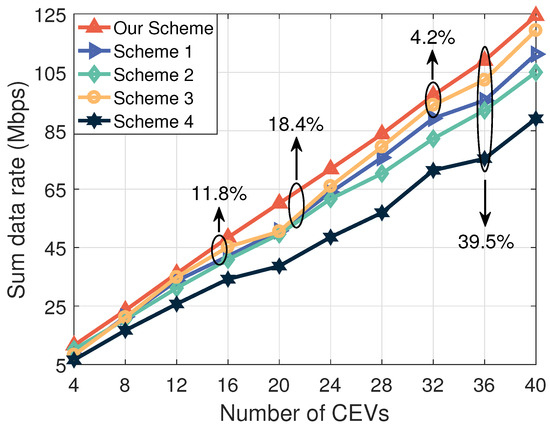
Figure 3.
The sum data rate versus the number of CEVs ( dB and ).
Figure 4 shows the sum data rate versus the decoding threshold. With the increment of , the decoding constraint of NOMA-enhanced IoV becomes harder to satisfy. Therefore, except for Scheme 1 using orthogonal frequency division multiple access (OFDMA), the sum data rate of all schemes is reduced. In particular, for Scheme 4, the performance degradation is most pronounced due to the use of direct communications. In addition, Figure 4 demonstrates that the proposed sum data rate maximization scheme has a stable performance even when is high, which is a good feature for its application in practical ITS-oriented services.
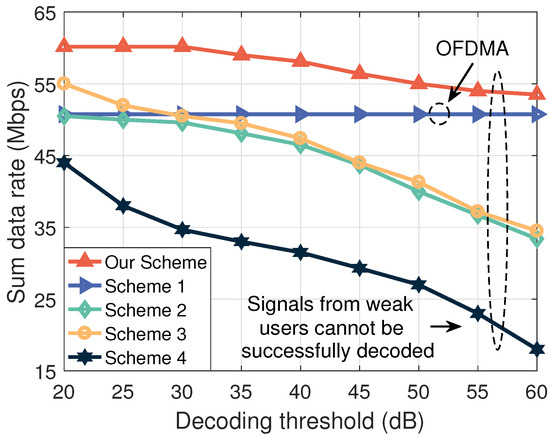
Figure 4.
The sum data rate versus the decoding threshold ( and ).
Figure 5 illustrates the effect of the decoding threshold on the number of supported CEVs. It is observed that the number of supported CEVs in all schemes (except for Scheme 1 using OFDMA) always decreases with the increase in . This is because co-channel interference exists in these NOMA-enabled schemes. The decoding error of v-th CEV (strong user) will affect the decoding of i-th CEV (weak user). In addition, we can observe that even if is high, the proposed scheme can support a large number of CEVs, making it superior to Schemes 2, 3, and 4. The reason for this is that the proposed scheme appropriately pairs the CEVs and adjusts the transmitted power to reduce the co-channel interference. In contrast, Scheme 1 is not affected by . However, the number of supported CEVs for Scheme 1 is very limited.
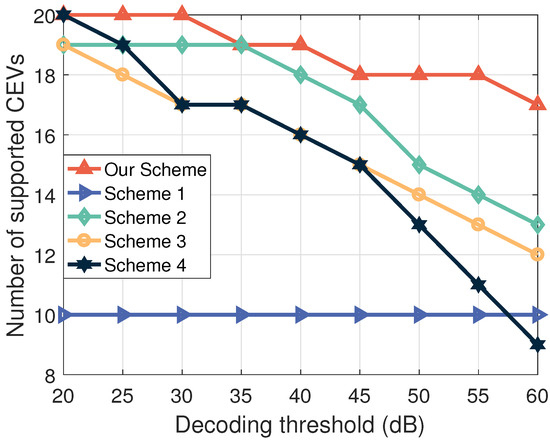
Figure 5.
The effect of decoding threshold on the number of supported CEVs ( and ).
Figure 6 depicts the effect of the number of elements on the sum data rate. We can find that, regardless of the number of elements, the proposed scheme always outperforms Scheme 1, which shows the superiority of the NOMA technique. In addition, the sum data rate increases as the number of elements increases. However, introducing additional elements to IRS increases the complexity, which, in turn, restricts performance improvements and renders it impractical for sustained enhancements in IRS-assisted IoV. Therefore, there is a tradeoff between the sum data rate and the number of elements in terms of the complexity. The low-complexity optimization scheme design, jointly considering the sum data rate and the number of elements, is an important issue for future research.
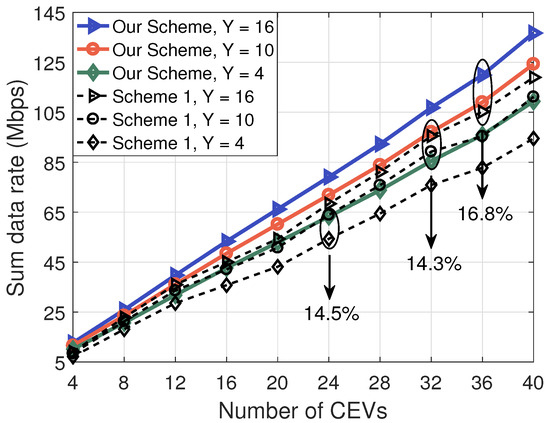
Figure 6.
The effect of the number of elements on the sum data rate ( dB).
Figure 7 plots the convergence characteristics of the designed IO algorithm. We can find that, through repeated iterations, the system gradually adjusts parameters towards the optimal solution, causing the objective function (i.e., the sum data rate) to approach a maximum. When the gradient of the objective function approaches zero, the system reaches a converged state, indicating the discovery of a solution that satisfies the optimization conditions. This process ensures the effectiveness of the designed IO algorithm in finding suitable solutions in the search space. As can be seen from Figure 7, convergence can be achieved after about 50 iterations.
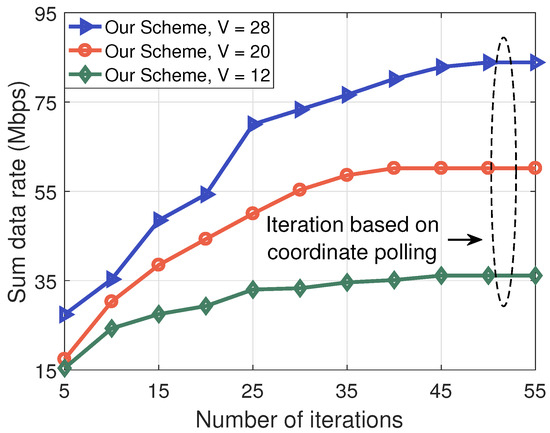
Figure 7.
Convergence comparison ( dB and ).
Figure 8 shows a comparison of the complexity with respect to the number of simulation runs under the different sum data rate optimization schemes. The reason the running time was used as a metric to compare the complexity is that it reflects the computational resources and efficiency required for the practical execution of the scheme. We can see that the complexity of the proposed scheme is close to that of the state-of-the-art works. The average running time needed to perform an optimization scheme is 1.67 s. Note that the running time depends on the hardware parameters. The proposed scheme was simulated in an environment consisting of a 12th Gen Intel Core i7-1260P 2.10 GHz processor, 32.0 GB of RAM, 1.5 TB of ROM, a 64-bit operating system based on x64 architecture, and Windows 11 Professional edition. Specifically, through gradual refinement, the designed IO algorithm can more effectively approximate the global optimum, addressing the challenge of conducting a comprehensive search in large-scale problems. Therefore, the proposed scheme exhibits better execution advantages in IoV, which can alleviate the computational burden, improving the execution efficiency in resource-constrained vehicular environments.
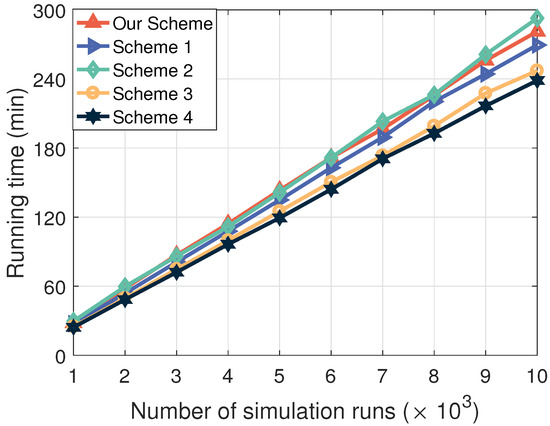
Figure 8.
Complexity comparison ( dB, , and ).
5. Conclusions
This paper investigated the incorporation of an IRS-equipped UAV and the NOMA technique to improve the sum data rate of CEVs in IoV. First, we focused on the uplink of NOMA-enhanced IoV, where the IRS-equipped UAV assisted single-antenna CEVs in transmitting data to the BS. Next, we formulated the sum data rate maximization problem by jointly considering the power control, subcarrier allocation, phase shift design, and SIC decoding threshold. Then, we designed an IO algorithm to deal with this non-convex problem, where three optimization variables were solved in turn. More precisely, the DDPG algorithm was used to obtain the optimal phase shift design. Based on this, we reformulated the subcarrier allocation problem as an MWIS problem, and employed the graph theory to solve it. In addition, according to the decoding constraint, we derived the closed-form expression of optimal power control. Finally, the simulation results showed that, compared with the state-of-the-art works, the sum data rate of CEVs was significantly improved by enabling the IRS-equipped UAV and the NOMA technique. Additionally, the influence of network parameters, convergence, and complexity were analyzed and discussed.
In addition to the above, there are some other directions that are worth further study. First, we can explore the use of real-time control algorithms to dynamically adjust the IRS configuration and adapt to real-time changes in IoV. Second, we can further study the collaborative work of IRS-equipped UAVs in IoV for improved efficiency in information dissemination, monitoring, and emergency response. Finally, we can optimize the energy consumption management for IRS-equipped UAVs while considering the network security and privacy protection.
Author Contributions
L.W.: conceptualization, methodology, software, and writing—original draft preparation. Y.H.: conceptualization, resources, writing—review and editing, supervision, and funding acquisition. B.C.: conceptualization, resources, writing—review and editing, and funding acquisition. A.H.: conceptualization, methodology, formal analysis and writing—review and editing. D.W.: conceptualization, resources, and writing—review and editing. L.Y.: formal analysis and writing—review and editing. F.H.: resources, funding acquisition, and writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Zhejiang Provincial Natural Science Foundation of China under Grant LQ24F010003, in part by the National Natural Science Foundation of China under Grant 62271399, in part by the University-Industry Collaborative Education Program under Grant 231000287070509, in part by the Science and Technology Planning Project of Jiaxing under Grant 2022AY10021, and in part by the Student Research Training Program of Jiaxing University under Grant 8517231248.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Andreou, A.; Mavromoustakis, C.X.; Batalla, J.M.; Markakis, E.K.; Mastorakis, G. UAV-assisted RSUs for V2X connectivity using Voronoi diagrams in 6G+ infrastructures. IEEE Trans. Intell. Transp. Syst. 2023, 24, 15855–15865. [Google Scholar] [CrossRef]
- He, Y.; Wang, D.; Huang, F.; Zhang, R. An MEC-enabled framework for task offloading and power allocation in NOMA enhanced ABS-assisted VANETs. IEEE Commun. Lett. 2022, 26, 1353–1357. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Zhang, L.; Zhang, Y.; Li, Q.; Chen, K.-C. Reliable transmission for NOMA systems with randomly deployed receivers. IEEE Trans. Commun. 2023, 71, 1179–1192. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.; He, X.; Sun, Y. Bandwidth allocation and trajectory control in UAV-assisted IOV edge computing using multiagent reinforcement learning. IEEE Trans. Rel. 2023, 72, 599–608. [Google Scholar] [CrossRef]
- Wang, D.; Wu, M.; Wei, Z.; Yu, K.; Min, L.; Mumtaz, S. Uplink secrecy performance of RIS-based RF/FSO three-dimension heterogeneous networks. IEEE Trans. Wireless Commun. 2024, 23, 1798–1809. [Google Scholar] [CrossRef]
- Ning, B.; Han, Q.-L.; Ge, X.; Sanjayan, J. A zeroing neural network-based approach to parameter-varying platooning control of connected automated vehicles. IEEE Trans. Intell. Veh. 2024, 9, 1977–1988. [Google Scholar] [CrossRef]
- Chauhan, A.; Jaiswal, A. Multidimensional signal space non-orthogonal multiple access with imperfect SIC: A novel SIC reduction technique. IEEE Trans. Veh. Technol. 2024, 73, 2374–2389. [Google Scholar] [CrossRef]
- He, Y.; Huang, F.; Wang, D.; Zhang, R.; Gu, X.; Pan, J. NOMA- and MRC-enabled framework in drone-relayed vehicular networks: Height/trajectory optimization and performance analysis. IEEE Internet Things J. 2023, 10, 22305–22319. [Google Scholar] [CrossRef]
- Wang, D.; Wu, M.; Chakraborty, C.; Min, L.; He, Y.; Guduri, M. Covert communications in air-ground integrated urban sensing networks enhanced by federated learning. IEEE Sens. J. 2023, 24, 5636–5643. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, W.; Wang, J.; Quek, T.Q.S. Hybrid satellite-UAV-terrestrial networks for 6G ubiquitous coverage: A maritime communications perspective. IEEE J. Sel. Areas Commun. 2021, 39, 3475–3490. [Google Scholar] [CrossRef]
- Liu, T.; Zhou, H.; Li, J.; Shu, F.; Han, Z. Uplink and downlink decoupled 5G/B5G vehicular networks: A federated learning assisted client selection method. IEEE Trans. Veh. Technol. 2023, 72, 2280–2292. [Google Scholar] [CrossRef]
- Alsamhi, S.H.; Shvetsov, A.V.; Kumar, S.; Hassan, J.; Alhartomi, M.A.; Shvetsova, S.V.; Sahal, R.; Hawbani, A. Computing in the sky: A survey on intelligent ubiquitous computing for UAV-assisted 6G networks and industry 4.0/5.0. Drones 2022, 6, 177. [Google Scholar] [CrossRef]
- Zhao, D.; Yan, Z.; Wang, M.; Zhang, P.; Song, B. Is 5G handover secure and private? A survey. IEEE Internet Things J. 2021, 8, 12855–12879. [Google Scholar] [CrossRef]
- Bai, Y.; Zhao, H.; Zhang, X.; Chang, Z.; Jäntti, R.; Yang, K. Toward autonomous multi-UAV wireless network: A survey of reinforcement learning-based approaches. IEEE Commun. Surv. Tut. 2023, 25, 3038–3067. [Google Scholar] [CrossRef]
- Ni, Y.; Lin, C.; He, J.; Vinel, A.; Li, Y.; Mosavat-Jahromi, H.; Pan, J. Toward reliable and scalable Internet of Vehicles: Performance analysis and resource management. Proc. IEEE 2020, 108, 324–340. [Google Scholar] [CrossRef]
- Oubbati, O.S.; Chaib, N.; Lakas, A.; Lorenz, P.; Rachedi, A. UAV-assisted supporting services connectivity in urban VANETs. IEEE Trans. Veh. Technol. 2019, 68, 3944–3951. [Google Scholar] [CrossRef]
- Noor-A-Rahim, M.; Liu, Z.; Lee, H.; Khyam, M.O.; He, J.; Pesch, D.; Moessner, K.; Saad, W.; Poor, H.V. 6G for vehicle-to-everything (V2X) communications: Enabling technologies, challenges, and opportunities. Proc. IEEE 2022, 110, 712–734. [Google Scholar] [CrossRef]
- Eskandari, M.; Huang, H.; Savkin, A.V.; Ni, W. Model predictive control-based 3D navigation of a RIS-equipped UAV for LoS wireless communication with a ground intelligent vehicle. IEEE Trans. Intell. Veh. 2023, 8, 2371–2384. [Google Scholar] [CrossRef]
- Javed, A.R.; Hassan, M.A.; Shahzad, F.; Ahmed, W.; Singh, S.; Baker, T.; Gadekallu, T.R. Integration of blockchain technology and federated learning in vehicular (IoT) networks: A comprehensive survey. Sensors 2022, 22, 4394. [Google Scholar] [CrossRef]
- Farooq, S.M.; Hussain, S.M.S.; Ustun, T.S. A survey of authentication techniques in vehicular ad-hoc network. IEEE Intell. Transp. Syst. Mag. 2021, 13, 39–52. [Google Scholar] [CrossRef]
- Eskandari, M.; Savkin, A.V. Deep-reinforcement-learning-based joint 3-D navigation and phase-shift control for mobile Internet of Vehicles assisted by RIS-equipped UAVs. IEEE Internet Things J. 2023, 10, 18054–18066. [Google Scholar] [CrossRef]
- Bansal, A.; Agrawal, N.; Singh, K.; Li, C.-P.; Mumtaz, S. RIS selection scheme for UAV-based multi-RIS-aided multiuser downlink network with imperfect and outdated CSI. IEEE Trans. Commun. 2023, 71, 4650–4664. [Google Scholar] [CrossRef]
- Lai, H.; Li, D.; Xu, F.; Wang, X.; Ning, J.; Hu, Y.; Duo, B. Optimization of full-duplex UAV secure communication with the aid of RIS. Drones 2023, 7, 591. [Google Scholar] [CrossRef]
- Wang, Y.; Lian, Z.; Wang, Y.; Su, Y.; Jin, B.; Zhang, Z. Geometry-based UAV-MIMO channel model for intelligent reflecting surface-assisted communication systems. IEEE Trans. Veh. Technol. 2024, 73, 14–27. [Google Scholar] [CrossRef]
- Ye, R.; Peng, Y.; Al-Hazemi, F.; Boutaba, R. A robust cooperative jamming scheme for secure UAV communication via intelligent reflecting surface. IEEE Trans. Commun. 2024, 72, 1005–1019. [Google Scholar] [CrossRef]
- Lin, Y.; Shu, F.; Zheng, Y.; Liu, J.; Dong, R.; Chen, X.; Wu, Y.; Yan, S.; Wang, J. Two low-complexity efficient beamformers for an IRS- and UAV-aided directional modulation network. Drones 2023, 7, 489. [Google Scholar] [CrossRef]
- Ding, Q.; Yang, J.; Luo, Y.; Luo, C. Intelligent reflecting surfaces vs. full-duplex relays: A comparison in the air. IEEE Commun. Lett. 2024, 28, 397–401. [Google Scholar] [CrossRef]
- Wang, J.; Xu, S.; Han, S.; Xiao, L. UAV-powered multi-user intelligent reflecting surface backscatter communication. IEEE Trans. Veh. Technol. 2023, 72, 10251–10262. [Google Scholar] [CrossRef]
- Shi, B.; Wang, Y.; Li, D.; Cai, W.; Lin, J.; Zhang, S.; Shi, W.; Yan, S.; Shu, F. STAR-RIS-UAV-aided coordinated multipoint cellular system for multi-user networks. Drones 2023, 7, 403. [Google Scholar] [CrossRef]
- Qin, X.; Song, Z.; Hou, T.; Yu, W.; Wang, J.; Sun, X. Joint optimization of resource allocation, phase shift, and UAV trajectory for energy-efficient RIS-assisted UAV-enabled MEC systems. IEEE Trans. Green Commun. Netw. 2023, 7, 1778–1792. [Google Scholar] [CrossRef]
- Vu, T.-H.; Nguyen, T.-T.; Pham, Q.-V.; da Costa, D.B.; Kim, S. A novel partial decode-and-amplify NOMA-inspired relaying protocol for uplink short-packet communications. IEEE Wireless Commun. Lett. 2023, 12, 1244–1248. [Google Scholar] [CrossRef]
- Guo, Y.; Fang, F.; Cai, D.; Ding, Z. Energy-efficient design for a NOMA assisted STAR-RIS network with deep reinforcement learning. IEEE Trans. Veh. Technol. 2023, 72, 5424–5428. [Google Scholar] [CrossRef]
- Chauhan, A.; Ghosh, S.; Jaiswal, A. RIS partition-assisted non-orthogonal multiple access (NOMA) and quadrature-NOMA with imperfect SIC. IEEE Trans. Wireless Commun. 2023, 22, 4371–4386. [Google Scholar] [CrossRef]
- Li, X.; Xie, Z.; Huang, G.; Zhang, J.; Zeng, M.; Chu, Z. Sum rate maximization for RIS-aided NOMA with direct links. IEEE Netw. Lett. 2022, 4, 55–58. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, H.; Shi, Z.; Fu, Y. RIS-level SIC for uplink cascaded-RIS assisted NOMA system. IEEE Commun. Lett. 2023, 27, 1884–1888. [Google Scholar] [CrossRef]
- Zhong, R.; Liu, Y.; Mu, X.; Chen, Y.; Song, L. AI empowered RIS-assisted NOMA networks: Deep learning or reinforcement learning? IEEE J. Sel. Areas Commun. 2022, 40, 182–196. [Google Scholar] [CrossRef]
- Hu, M.; Li, C.; Bian, Y.; Zhang, H.; Qin, Z.; Xu, B. Fuel economy-oriented vehicle platoon control using economic model predictive control. IEEE Trans. Intell. Transp. Syst. 2023, 23, 20836–20849. [Google Scholar] [CrossRef]
- Cao, Y.; Lv, T.; Ni, W. Intelligent reflecting surface aided multi-user mmWave communications for coverage enhancement. In Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), London, UK, 31 August–3 September 2020; pp. 1–6. [Google Scholar]
- Maraqa, O.; Rajasekaran, A.S.; Al-Ahmadi, S.; Yanikomeroglu, H.; Sait, S.M. A survey of rate-optimal power domain NOMA with enabling technologies of future wireless networks. IEEE Commun. Surv. Tut. 2020, 22, 2192–2235. [Google Scholar] [CrossRef]
- Bondy, J.; Murty, U. Graph Theory; Springer: Berlin, Germany, 2008. [Google Scholar]
- He, Y.; Wang, D.; Huang, F.; Zhang, R.; Gu, X.; Pan, J. A V2I and V2V collaboration framework to support emergency communications in ABS-aided Internet of Vehicles. IEEE Trans. Green Commun. Netw. 2023, 7, 2038–2051. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).