Vision-Guided Tracking and Emergency Landing for UAVs on Moving Targets
Abstract
1. Introduction
- Implementation of modified adaptive pure pursuit guidance technique with an extra adaptation parameter to compensate for reduced maneuverability, thus ensuring safe tracking of moving objects.
- Adaptive landing strategy that adapts to tracking deviations and minimizes off-target landings caused by lateral tracking errors and delayed responses, using a lateral offset-dependent vertical velocity control.
- Implementation of the proposed system in a mid-mission emergency landing scenario (Bring Back Home mission), which includes actuator health monitoring to trigger emergency landing and estimate resulting limitations in the system dynamics.
2. UAV and UGV System
2.1. Multirotor UAV System
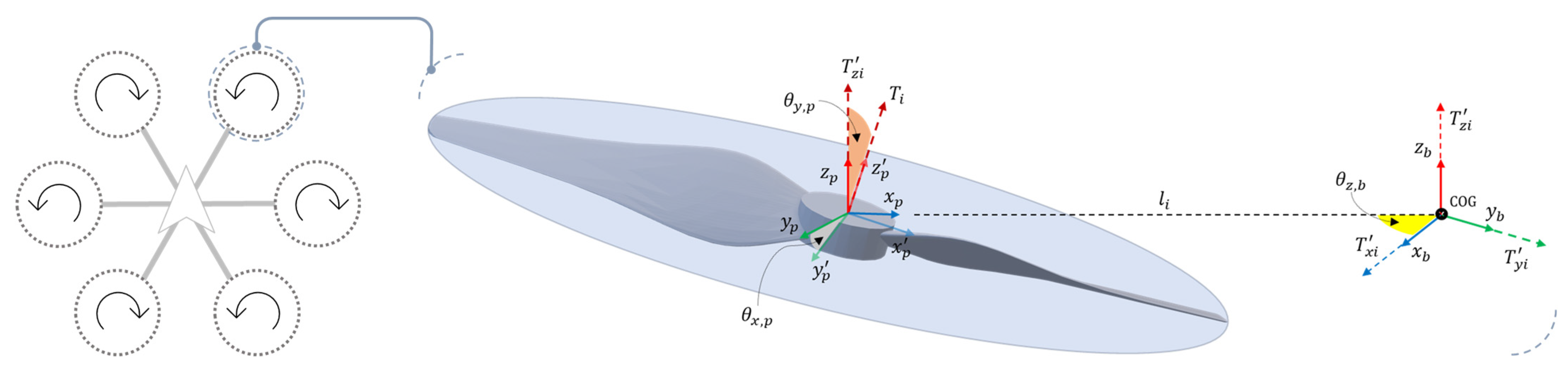
2.1.1. Dynamics of UAV System
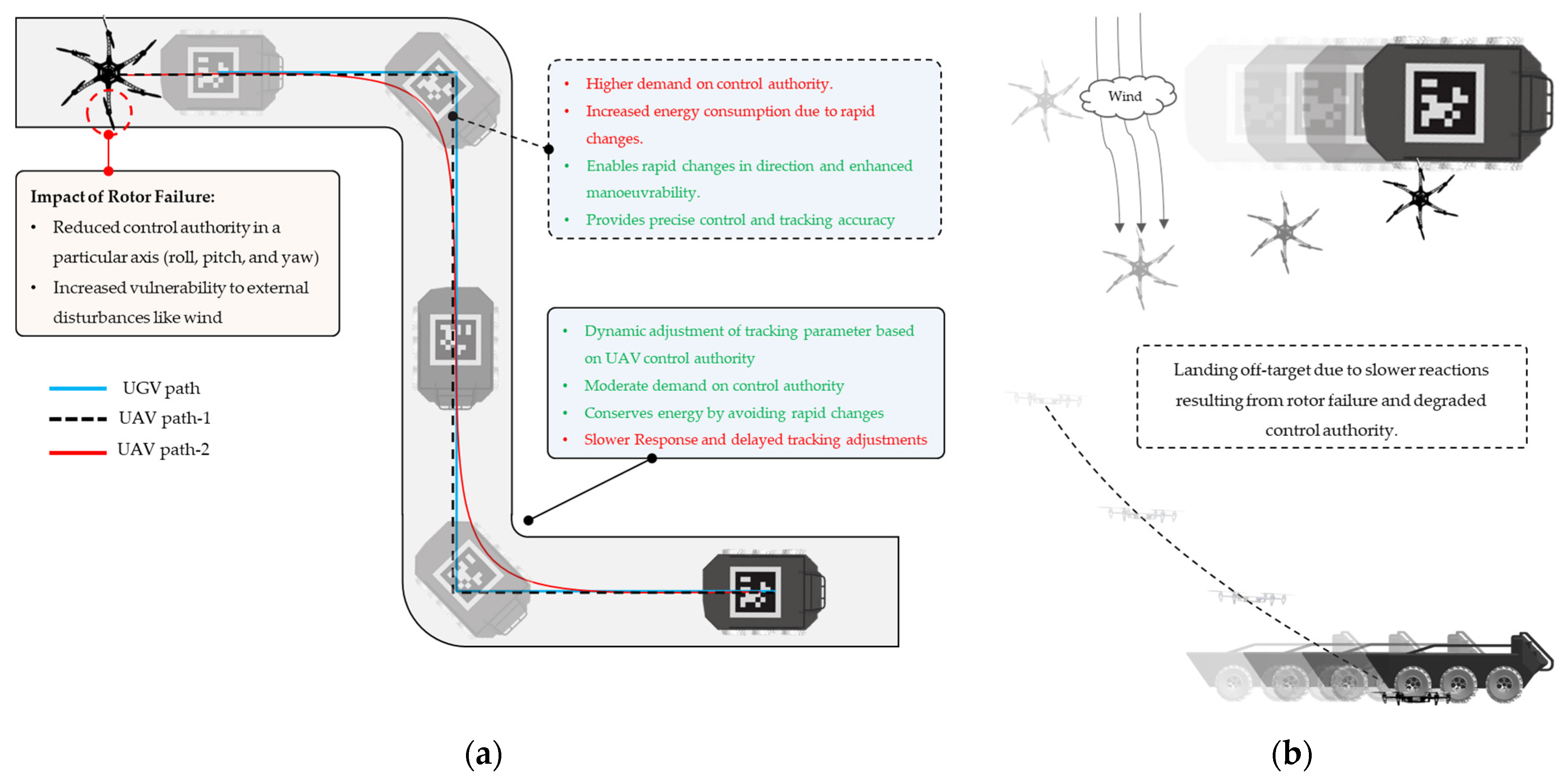
2.1.2. Actuator Failure and Control Degradation
2.1.3. Control Degradation Assessment
2.2. UGV System
2.2.1. UGV Kinematics
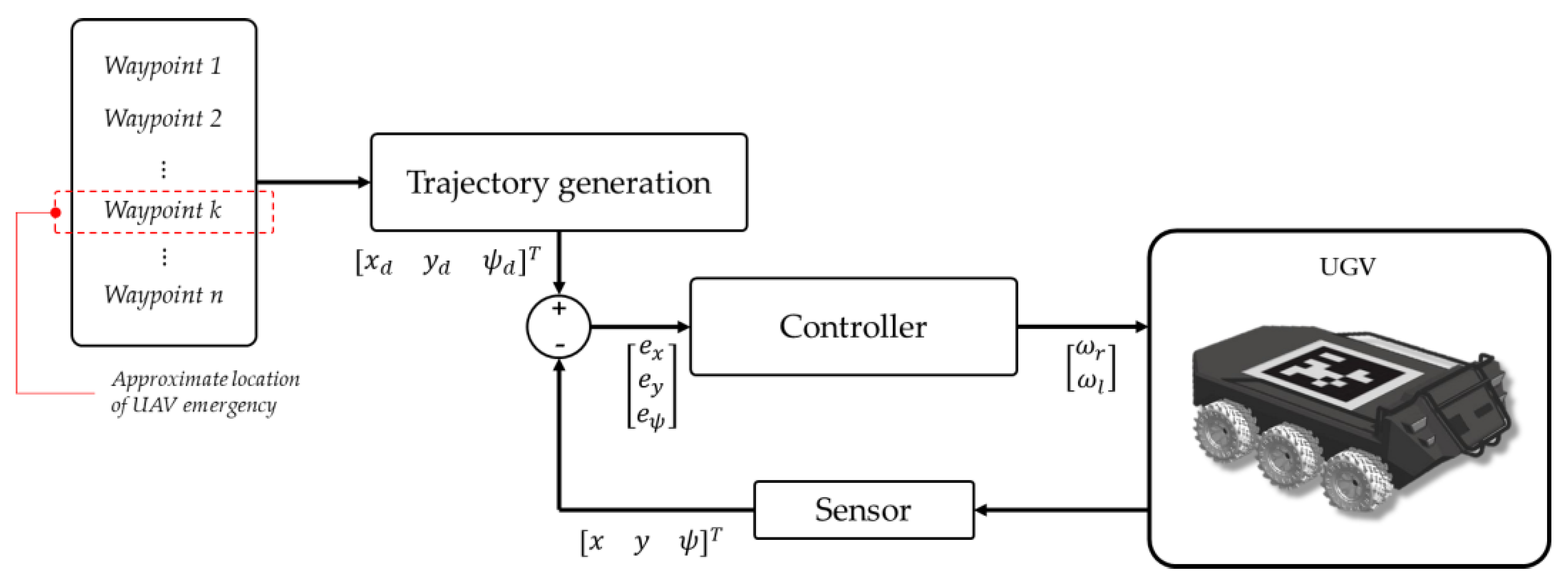
2.2.2. UGV System Guidance Navigation and Control (GNC)
3. Tracking and Emergency Landing Scenario on Moving Object
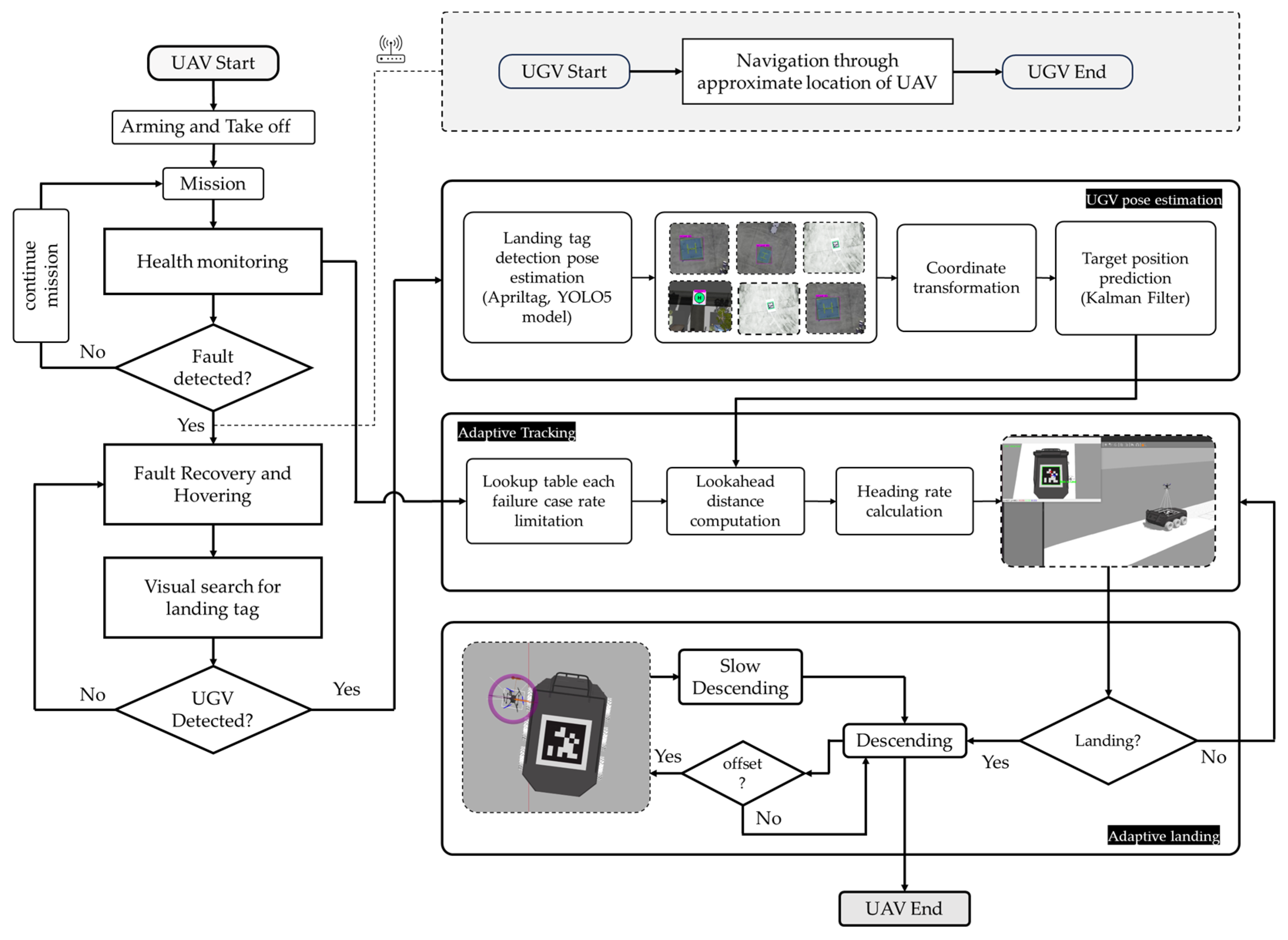
3.1. Emergency Landing Scenario
3.2. UGV Pose Estimation
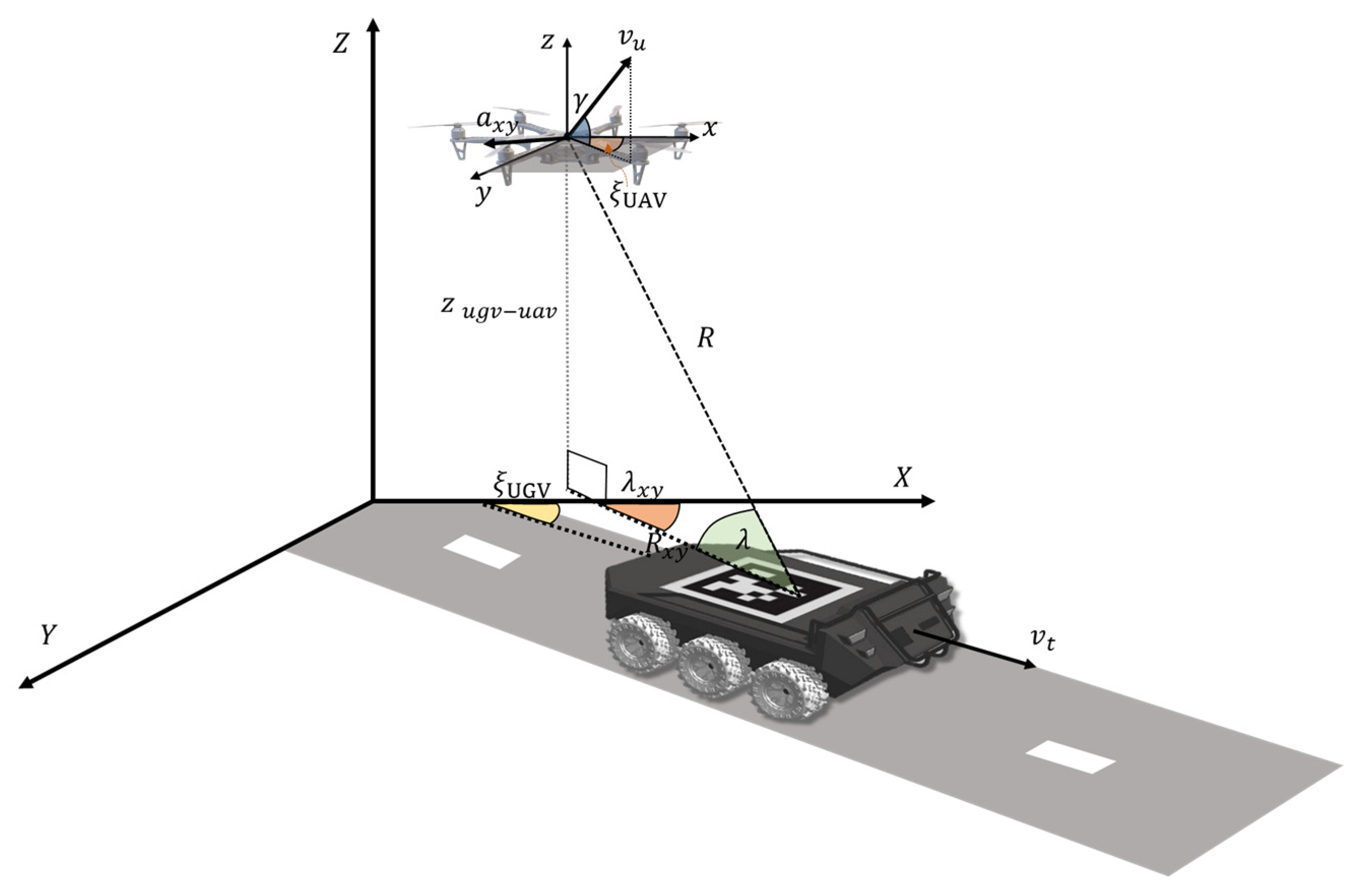
3.3. Target Tracking Using Adaptive Pure Pursuit Guidance
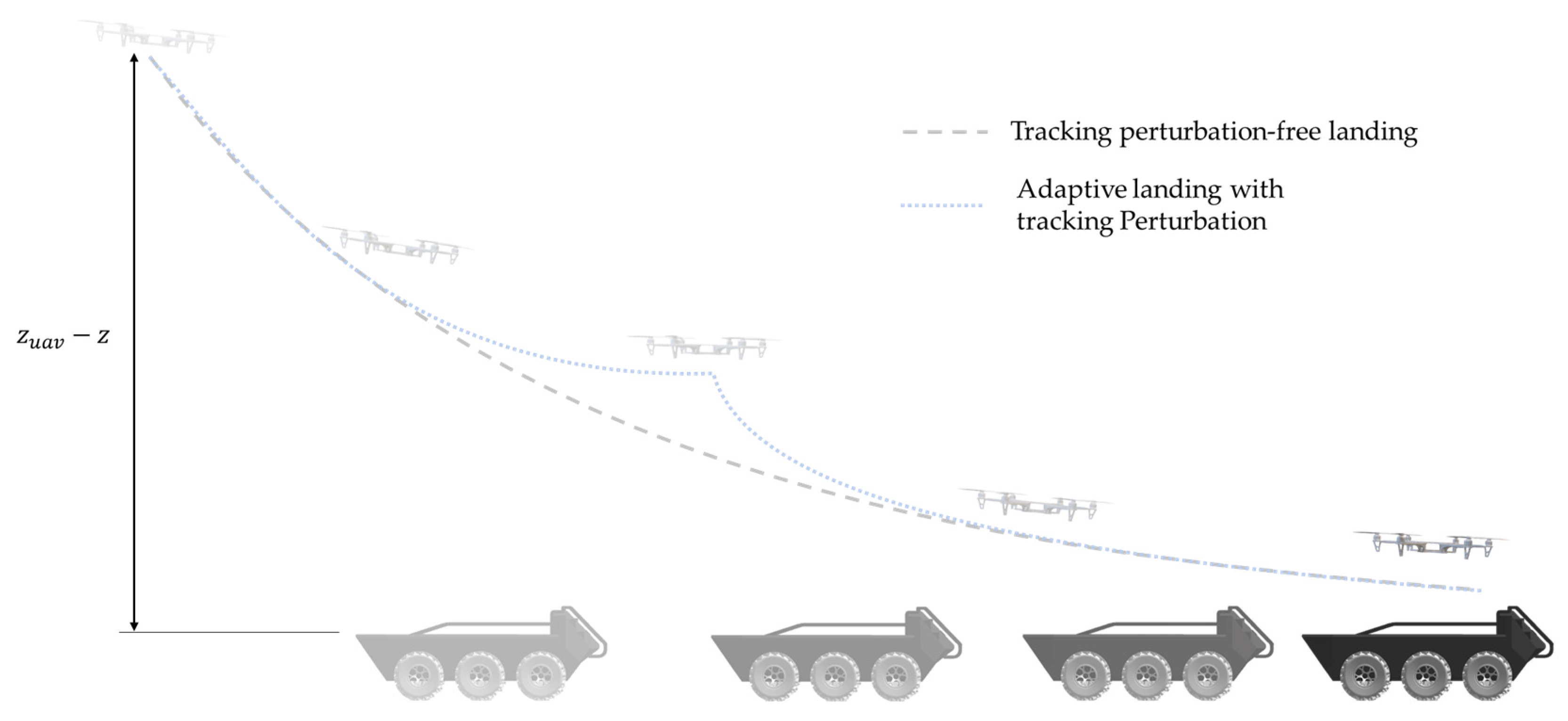
3.4. Adaptive Autonoumus Landing on a Moving Target
| Algorithm 1: Adaptive landing algorithm | |
| Input: UGV position offset relative to UAV position | |
| Output: Velocity and heading rate command | |
| 1 | Initialize: Landing Mode |
| 2 | While True do |
| 3 | If UGV_detected then |
| 4 | controller_lateral )) |
| 5 | If then |
| 6 | |
| 7 | else |
| 8 | controller_vertical |
| 9 | end |
| 10 | end |
| 11 | else If UGV_not_detected then |
| 12 | Increase altitude: |
| 13 | end |
| 14 | end |
4. Results and Discussion
4.1. Test Environment Setup Preparation
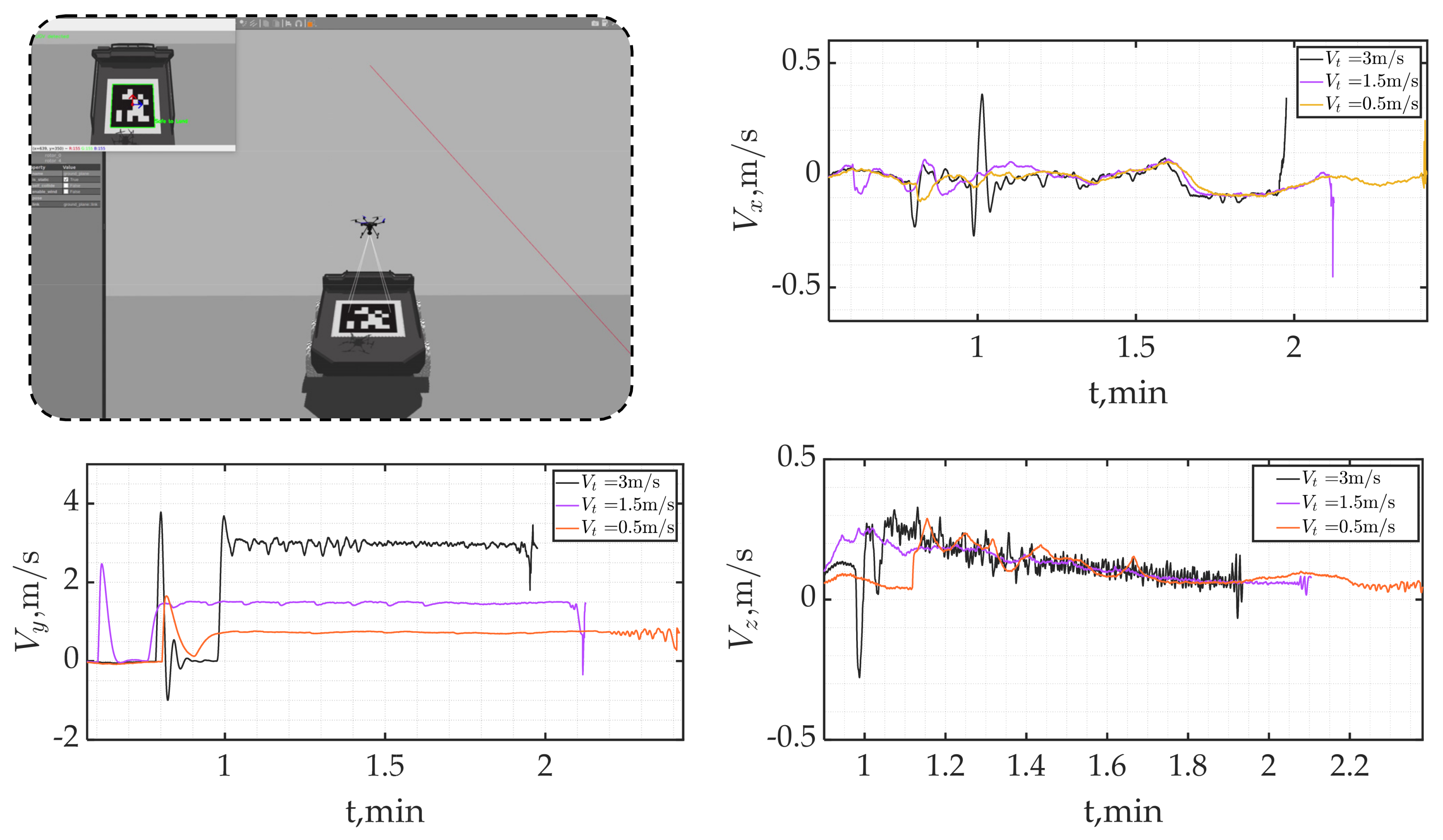
4.2. Tracking and Landing Simulation Result
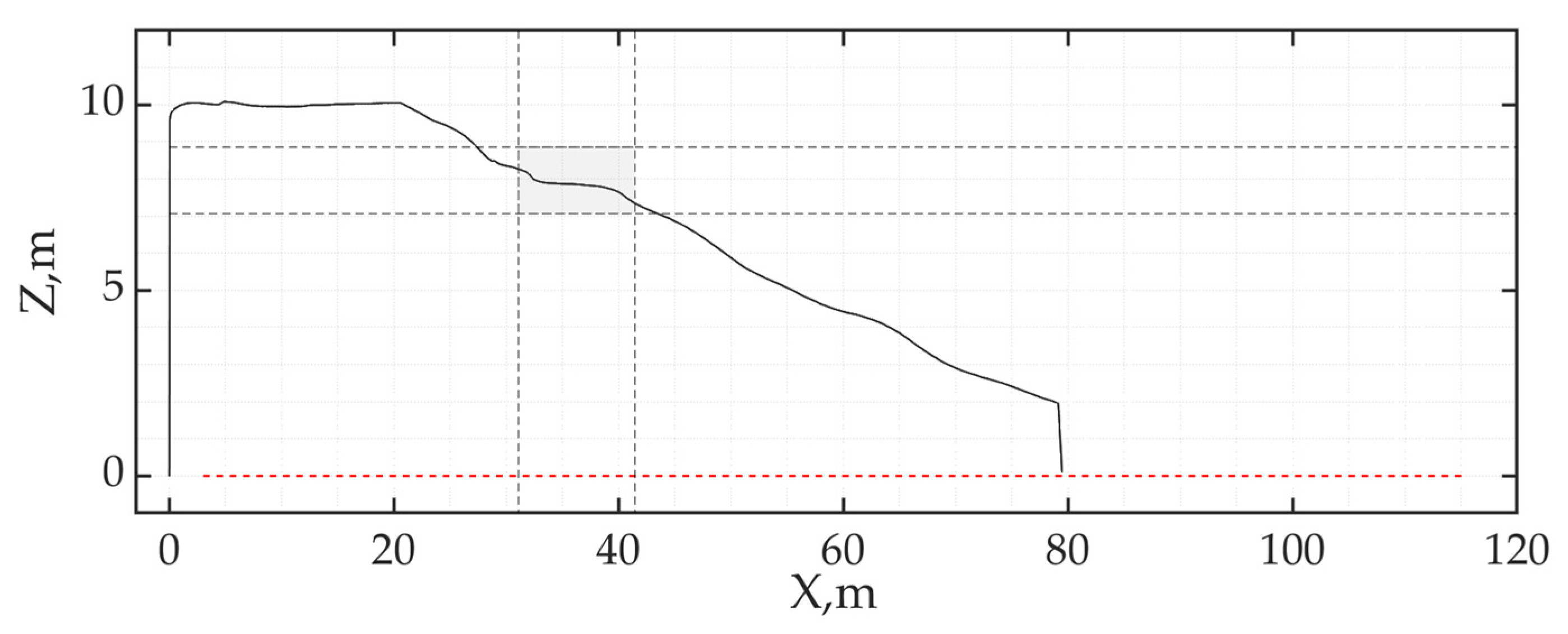
4.2.1. Straight Line Profile Landing
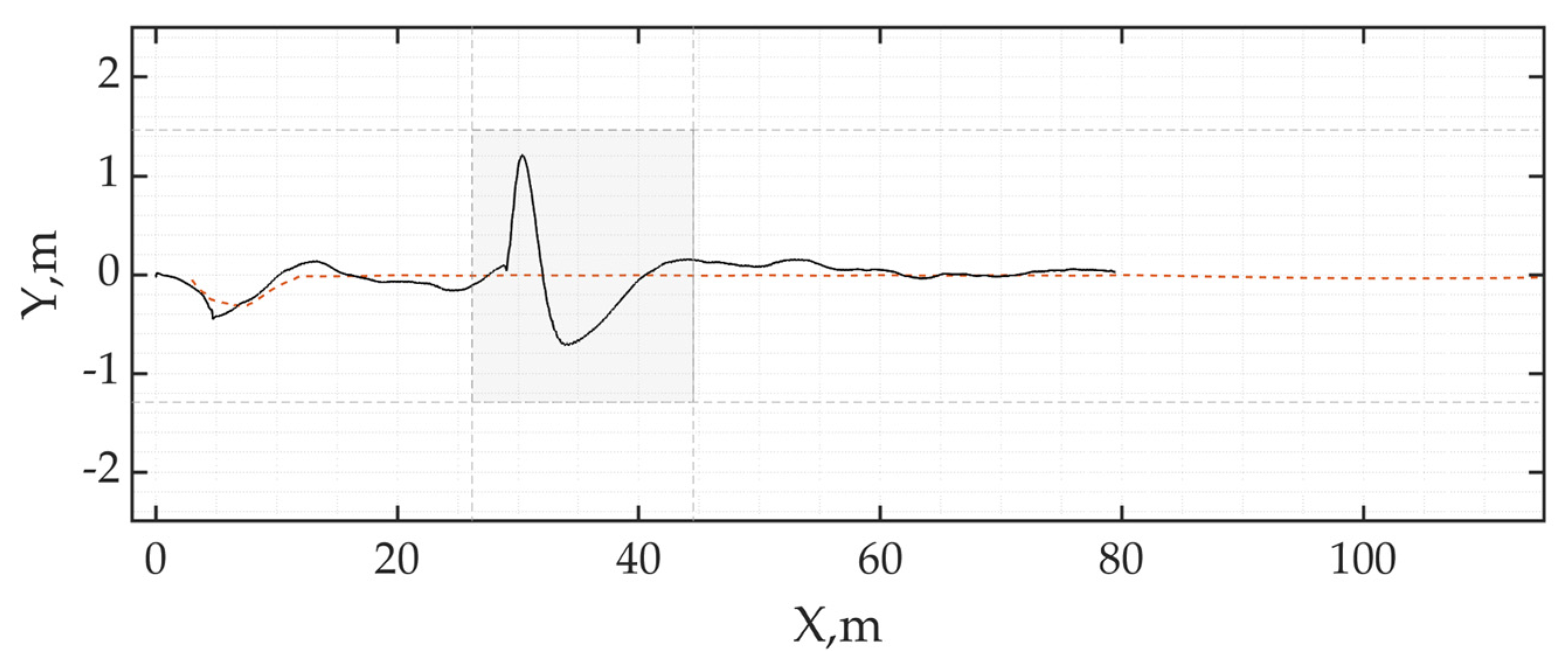
4.2.2. Addressing Tracking Errors, , with Adaptive Landing
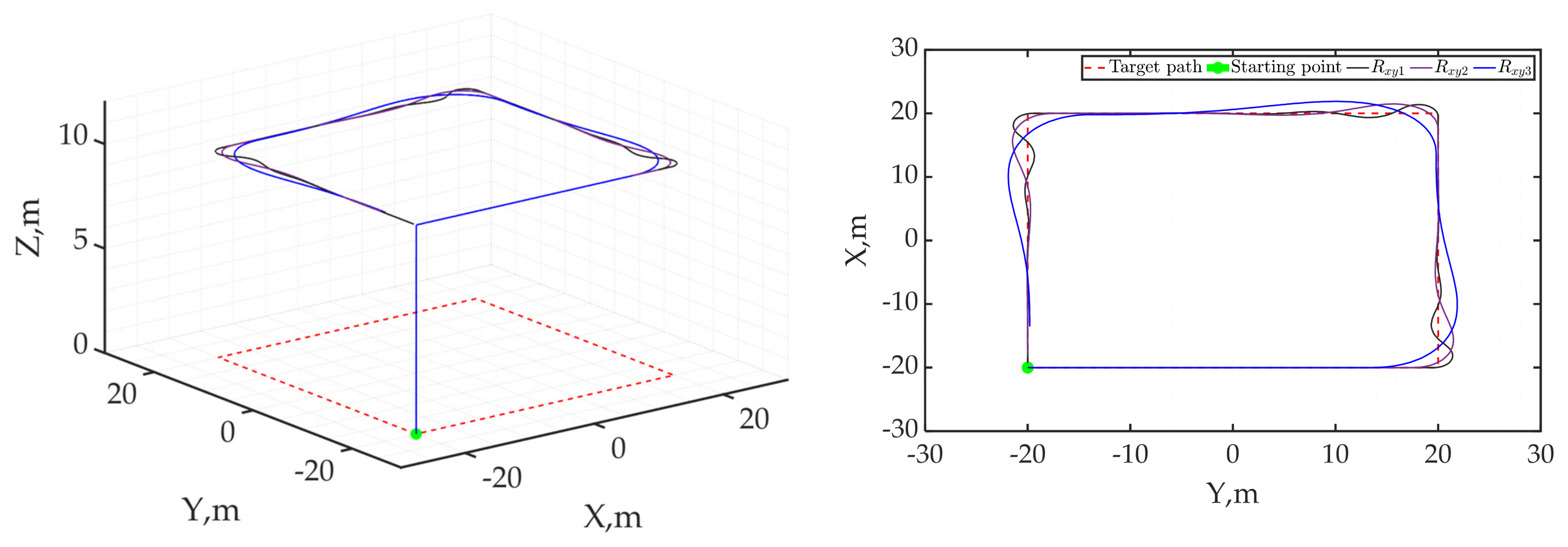
4.2.3. Adaptive Tracking in Circular and Rectangular Profile
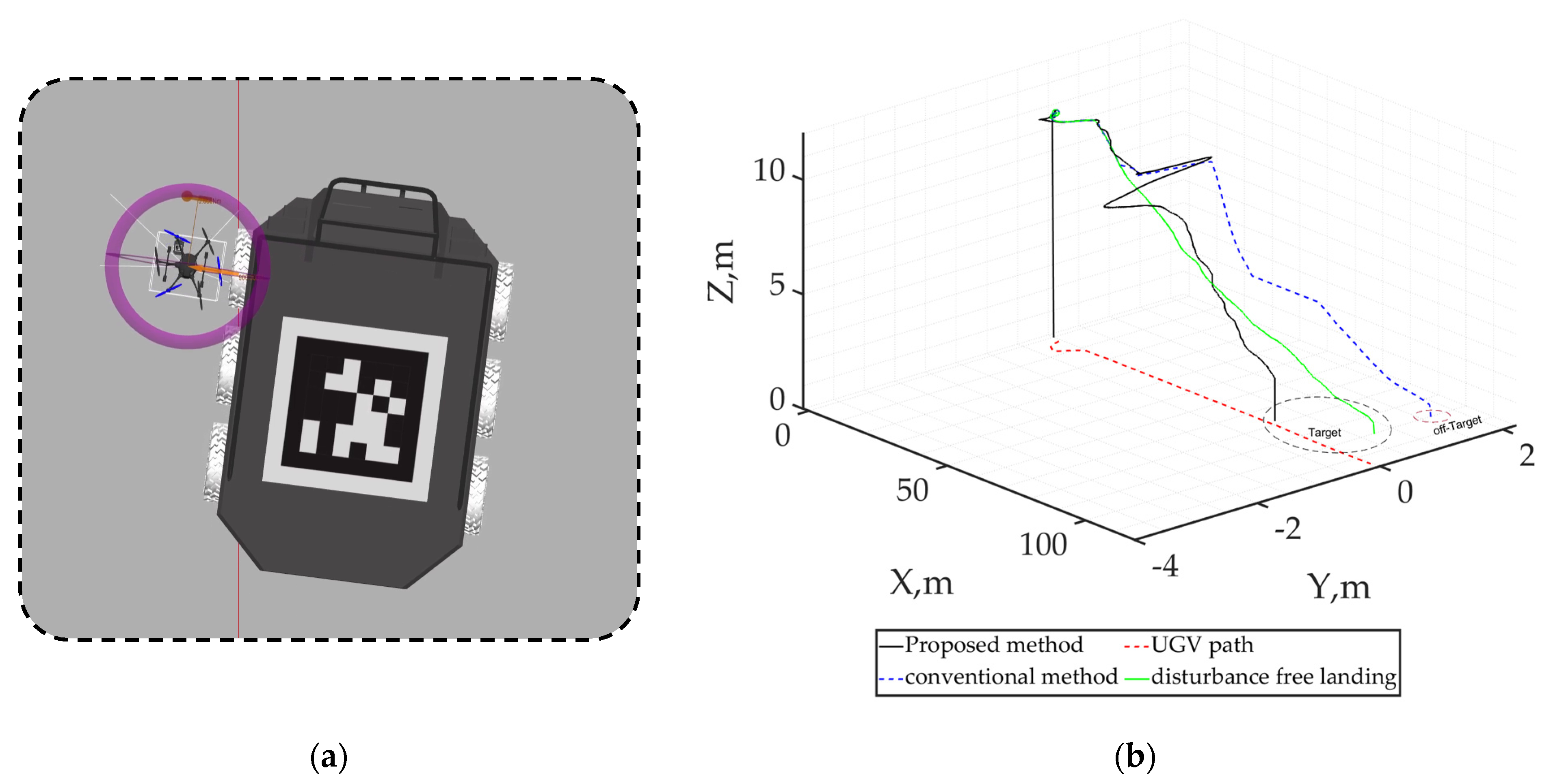
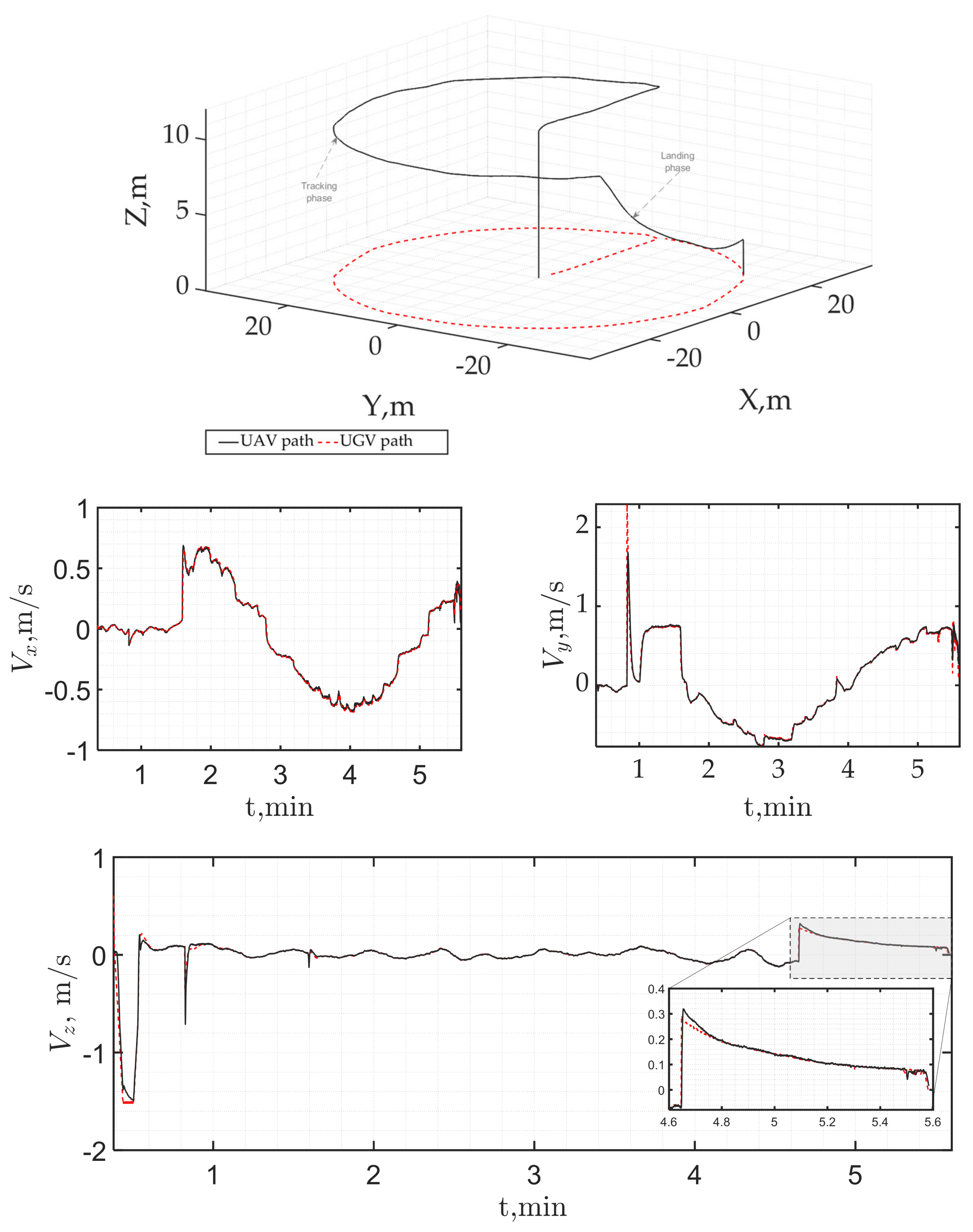
4.2.4. Emergency Landing Scenario in the Event of Actuator Failure: “Bring Back Home” Mission
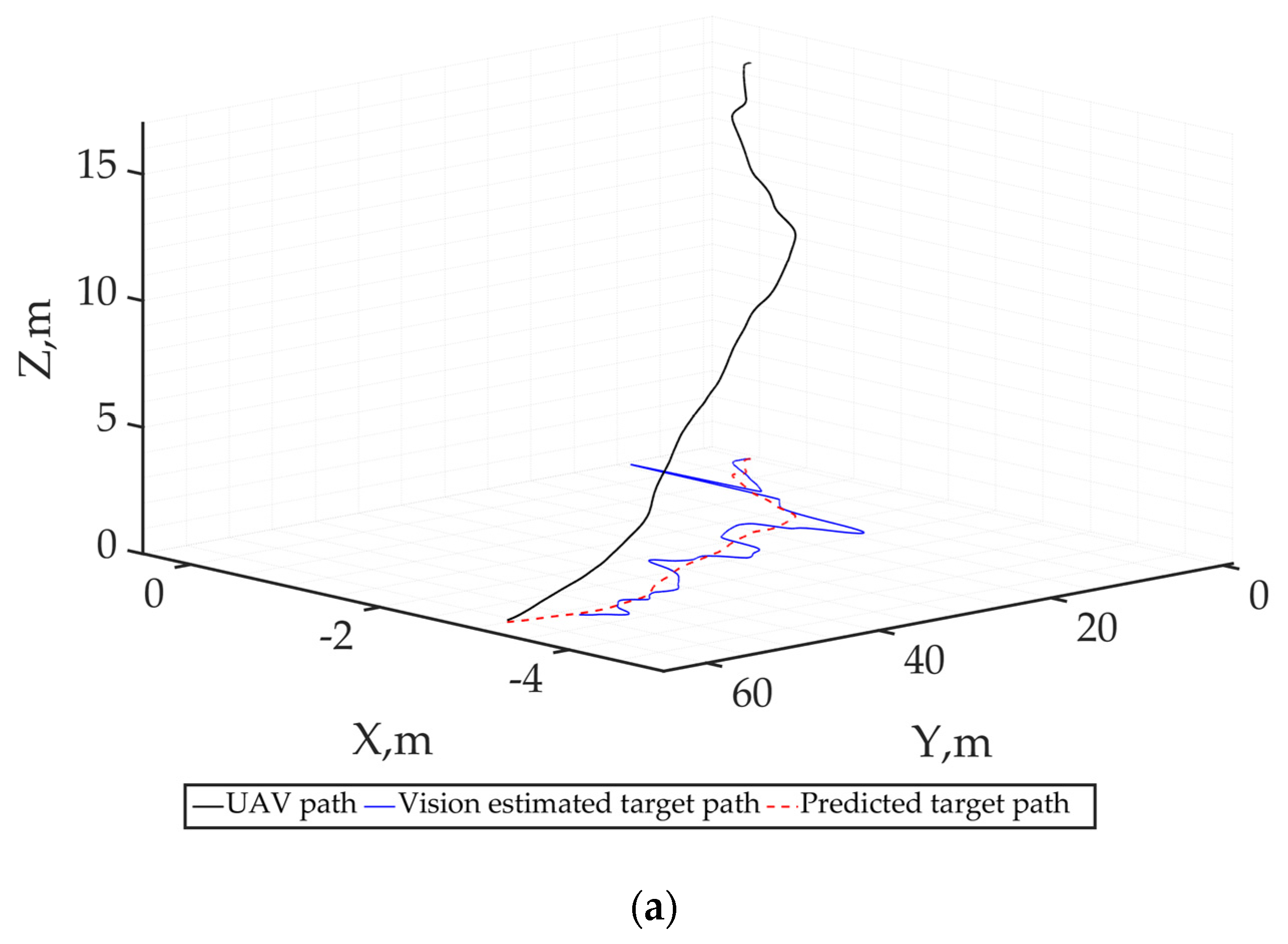
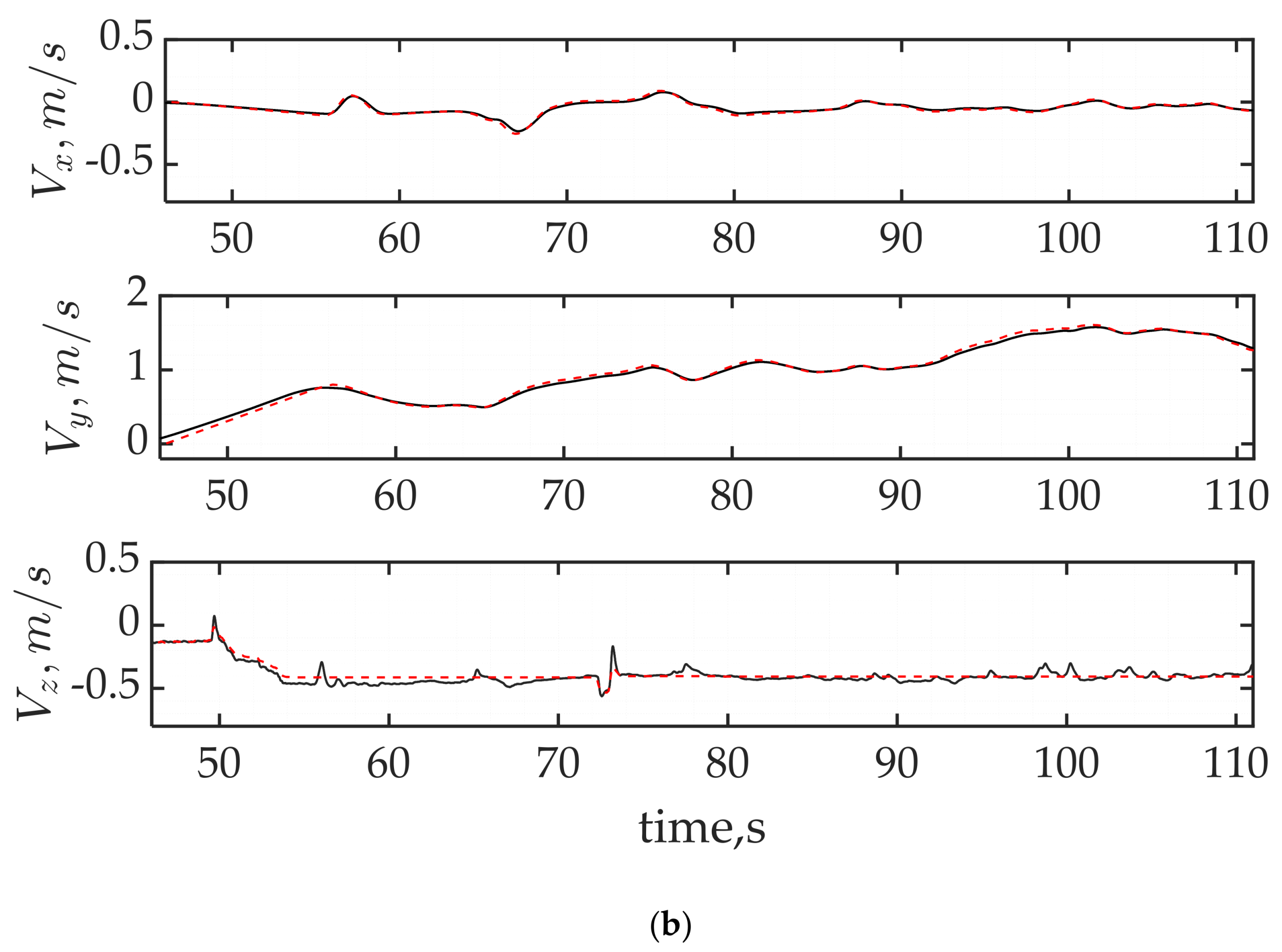
4.2.5. Experimental Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mohsan, S.A.H.; Othman, N.Q.H.; Li, Y.; Alsharif, M.H.; Khan, M.A. Unmanned Aerial Vehicles (UAVs): Practical Aspects, Applications, Open Challenges, Security Issues, and Future Trends. Intell. Serv. Robot. 2023, 16, 109–137. [Google Scholar] [CrossRef]
- Ding, Y.; Xin, B.; Chen, J. A Review of Recent Advances in Coordination Between Unmanned Aerial and Ground Vehicles. Unmanned Syst. 2021, 9, 97–117. [Google Scholar] [CrossRef]
- Sanchez-lopez, J.; Jesus, P.; Srikanth, S.; Pascual, C. An approach toward visual autonomous shipboard landing of a VTOL UAV. J. Intell. Robot. Syst. 2014, 74, 113–127. [Google Scholar] [CrossRef]
- Palafox, P.R.; Garzón, M.; Valente, J.; Roldán, J.J.; Barrientos, A. Robust Visual-Aided Autonomous Takeoff, Tracking, and Landing of a Small UAV on a Moving Landing Platform for Life-Long Operation. Appl. Sci. 2019, 9, 2661. [Google Scholar] [CrossRef]
- He, Z.; Xu, J.-X. Moving Target Tracking by Uavs in an Urban Area. In Proceedings of the 2013 10th IEEE International Conference on Control and Automation (ICCA), Hangzhou, China, 28 April 2013. [Google Scholar] [CrossRef]
- Bie, T.; Fan, K.; Tang, Y. UAV Recognition and Tracking Method Based on Yolov5. In Proceedings of the 2022 IEEE 17th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 28 April 2022. [Google Scholar] [CrossRef]
- Zhigui, Y.; ChuanJun, L. Review on Vision-based Pose Estimation of UAV Based on Landmark. In Proceedings of the 2017 2nd International Conference on Frontiers of Sensors Technologies (ICFST), Shenzhen, China, 28 April 2017. [Google Scholar] [CrossRef]
- Gautam, A.; Singh, M.; Sujit, P.B.; Saripalli, S. Autonomous Quadcopter Landing on a Moving Target. Sensors 2022, 22, 1116. [Google Scholar] [CrossRef]
- Ghommam, J.; Saad, M. Autonomous Landing of a Quadrotor on a Moving Platform. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1504–1519. [Google Scholar] [CrossRef]
- Morales, J.; Castelo, I.; Serra, R.; Lima, P.U.; Basiri, M. Vision-Based Autonomous Following of a Moving Platform and Landing for an Unmanned Aerial Vehicle. Sensors 2023, 23, 829. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.; Wan, N.; Jafarnejadsani, H.; Sun, D.; Holzapfel, F.; Hovakimyan, N. Emergency Landing Trajectory Optimization for Fixed-wing UAV under Engine Failure. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Lippiello, V.; Ruggiero, F.; Serra, D. Emergency Landing for a Quadrotor in Case of a Propeller Failure: A PID Based Approach. In Proceedings of the 2014 IEEE International Symposium on Safety, Security, and Rescue Robotics, Toyako, Japan, 28 April 2014. [Google Scholar]
- Debele, Y.; Shi, H.-Y.; Wondosen, A.; Kim, J.-H.; Kang, B.-S. Multirotor Unmanned Aerial Vehicle Configuration Optimization Approach for Development of Actuator Fault-tolerant Structure. Appl. Sci. 2022, 12, 6781. [Google Scholar] [CrossRef]
- Saied, M.; Shraim, H.; Lussier, B.; Fantoni, I.; Francis, C. Local Controllability and Attitude Stabilization of Multirotor Uavs: Validation on a Coaxial Octorotor. Robot. Auton. Syst. 2017, 91, 128–138. [Google Scholar] [CrossRef]
- Du, G.; Quan, Q.; Yang, B.; Cai, K.-Y. Controllability Analysis for a Class of Multirotors Subject to Rotor Failure/wear. arXiv 2014, arXiv:1403.5986. [Google Scholar] [CrossRef]
- Du, G.-X.; Quan, Q.; Yang, B.; Cai, K.-Y. Controllability Analysis for Multirotor Helicopter Rotor Degradation and Failure. J. Guid. Control Dyn. 2015, 38, 978–985. [Google Scholar] [CrossRef]
- Vey, D.; Lunze, J. Experimental Evaluation of an Active Fault-tolerant Control Scheme for Multirotor Uavs. In Proceedings of the 2016 3rd Conference on Control and Fault-Tolerant Systems (SysTol), Barcelona, Spain, 28 April 2016. [Google Scholar] [CrossRef]
- Xia, K.; Shin, M.; Chung, W.; Kim, M.; Lee, S.; Son, H. Landing a Quadrotor UAV on a Moving Platform with Sway Motion Using Robust Control. Control Eng. Pract. 2022, 128, 105288. [Google Scholar] [CrossRef]
- Bogdan, S.; Orsag, M.; Oh, P. Multi-Rotor Systems, Kinematics, Dynamics, and Control of; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Zhang, J.; Söpper, M.; Holzapfel, F. Attainable Moment Set Optimization to Support Configuration Design: A Required Moment Set Based Approach. Appl. Sci. 2021, 11, 3685. [Google Scholar] [CrossRef]
- Zhao, Y.; BeMent, S.L. Kinematics, Dynamics and Control of Wheeled Mobile Robots. In Proceedings of the 1992 IEEE International Conference on Robotics and Automation, Nice, France, 28 April 1992. [Google Scholar] [CrossRef]
- Suzuki, S. Autonomous Navigation, Guidance and Control of Small 4-wheel Electric Vehicle. J. Asian Electr. Veh. 2012, 10, 1575–1582. [Google Scholar] [CrossRef]
- Lian, J.; Yu, W.; Xiao, K.; Liu, W. Cubic Spline Interpolation-based Robot Path Planning Using a Chaotic Adaptive Particle Swarm Optimization Algorithm. Math. Probl. Eng. 2020, 2020, 20. [Google Scholar] [CrossRef]
- Park, J.; Jung, Y.; Kim, J. Multiclass Classification Fault Diagnosis of Multirotor Uavs Utilizing a Deep Neural Net-work. Int. J. Control Autom. Syst. 2022, 20, 1316–1326. [Google Scholar] [CrossRef]
- Abbas, S.M.; Aslam, S.; Berns, K.; Muhammad, A. Analysis and Improvements in AprilTag Based State Estimation. Sensors 2019, 19, 5480. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Jia, Y.; Shen, W.; Qian, X. A Pose Estimation Method in Dynamic Scene with Yolov5, Mask R-CNN and ORB-SLAM2. In Proceedings of the 2022 7th International Conference on Signal and Image Processing (ICSIP), Suzhou, China, 28 April 2022. [Google Scholar] [CrossRef]
- Subramanian, J.; Asirvadam, V.; Zulkifli, S.; Singh, N.; Shanthi, N.; Lagisetty, R.; Kadir, K. Integrating Computer Vision and Photogrammetry for Autonomous Aerial Vehicle Landing in Static Environment. IEEE Access 2024, 12, 4532–4543. [Google Scholar] [CrossRef]
- Goshtasby, A.; Gruver, W.A. Design of a Single-Lens Stereo Camera System. Pattern Recognit. 1993, 26, 923–937. [Google Scholar] [CrossRef]
- Ma, M.; Shen, S.; Huang, Y. Enhancing UAV Visual Landing Recognition with Yolo’s Object Detection by Onboard Edge Computing. Sensors 2023, 23, 8999. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, X.; Wan, Y.; Wang, J.; Lyu, H. An Improved Yolov5 Method for Small Object Detection in UAV Capture Scenes. IEEE Access 2023, 11, 14365–14374. [Google Scholar] [CrossRef]
- Nepal, U.; Eslamiat, H. Comparing YOLOv3, YOLOv4 and YOLOv5 for Autonomous Landing Spot Detection in Faulty UAVs. Sensors 2022, 22, 464. [Google Scholar] [CrossRef]
- Jung, J.; Yoon, I.; Lee, S.; Paik, J. Object Detection and Tracking-based Camera Calibration for Normalized Human Height Estimation. J. Sens. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Ahn, J.; Shin, S.; Kim, M.; Park, J. Accurate Path Tracking by Adjusting Look-Ahead Point in Pure Pursuit Method. Int. J. Automot. Technol. 2021, 22, 119–129. [Google Scholar] [CrossRef]
- Zhang, M.; Tian, F.; He, Y.; Li, D. Adaptive Path Tracking for Unmanned Ground Vehicle. In Proceedings of the 2017 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 28 April 2017. [Google Scholar] [CrossRef]
- Giesbrecht, J.; Mackay, D.; Collier, J.; Verret, S. Path Tracking for Unmanned Ground Vehicle Navigation: Implementation and Adaptation of the Pure Pursuit Algorithm. DRDC Suffield TM 2005, 224, 2005. [Google Scholar]
- Chuang, H.-M.; He, D.; Namiki, A. Autonomous Target Tracking of UAV Using High-Speed Visual Feedback. Appl. Sci. 2019, 9, 4552. [Google Scholar] [CrossRef]
- Teuliere, C.; Eck, L.; Marchand, E. Chasing a Moving Target from a Flying UAV. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25 September 2011. [Google Scholar] [CrossRef]













Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Debele, Y.; Shi, H.-Y.; Wondosen, A.; Warku, H.; Ku, T.-W.; Kang, B.-S. Vision-Guided Tracking and Emergency Landing for UAVs on Moving Targets. Drones 2024, 8, 182. https://doi.org/10.3390/drones8050182
Debele Y, Shi H-Y, Wondosen A, Warku H, Ku T-W, Kang B-S. Vision-Guided Tracking and Emergency Landing for UAVs on Moving Targets. Drones. 2024; 8(5):182. https://doi.org/10.3390/drones8050182
Chicago/Turabian StyleDebele, Yisak, Ha-Young Shi, Assefinew Wondosen, Henok Warku, Tae-Wan Ku, and Beom-Soo Kang. 2024. "Vision-Guided Tracking and Emergency Landing for UAVs on Moving Targets" Drones 8, no. 5: 182. https://doi.org/10.3390/drones8050182
APA StyleDebele, Y., Shi, H.-Y., Wondosen, A., Warku, H., Ku, T.-W., & Kang, B.-S. (2024). Vision-Guided Tracking and Emergency Landing for UAVs on Moving Targets. Drones, 8(5), 182. https://doi.org/10.3390/drones8050182





