Surrogate Optimal Fractional Control for Constrained Operational Service of UAV Systems
Abstract
1. Motivation and Introduction
1.1. Key Contributions
- This work investigates and evaluates the applicability and the inherent flexibility of FOC for UAV systems. The obtained findings should support the seamless integration of surrogate FOC design within UAV controllers for transport applications.
- A FOPID is more time-consuming and computationally intensive than integer-order PID. Therefore, this work studies and analyzes surrogate modeling and optimization for such an expensive function.
- The investigated surrogate-based FOPID was verified in a simulation with a benchmark waypoint navigation quadrotor model. In addition, it was verified for a real-time twin-rotor copter system, to investigate its real-time performance.
1.2. Outline
2. Literature Review
2.1. Modeling and Control of UAVs
2.2. Optimization Techniques
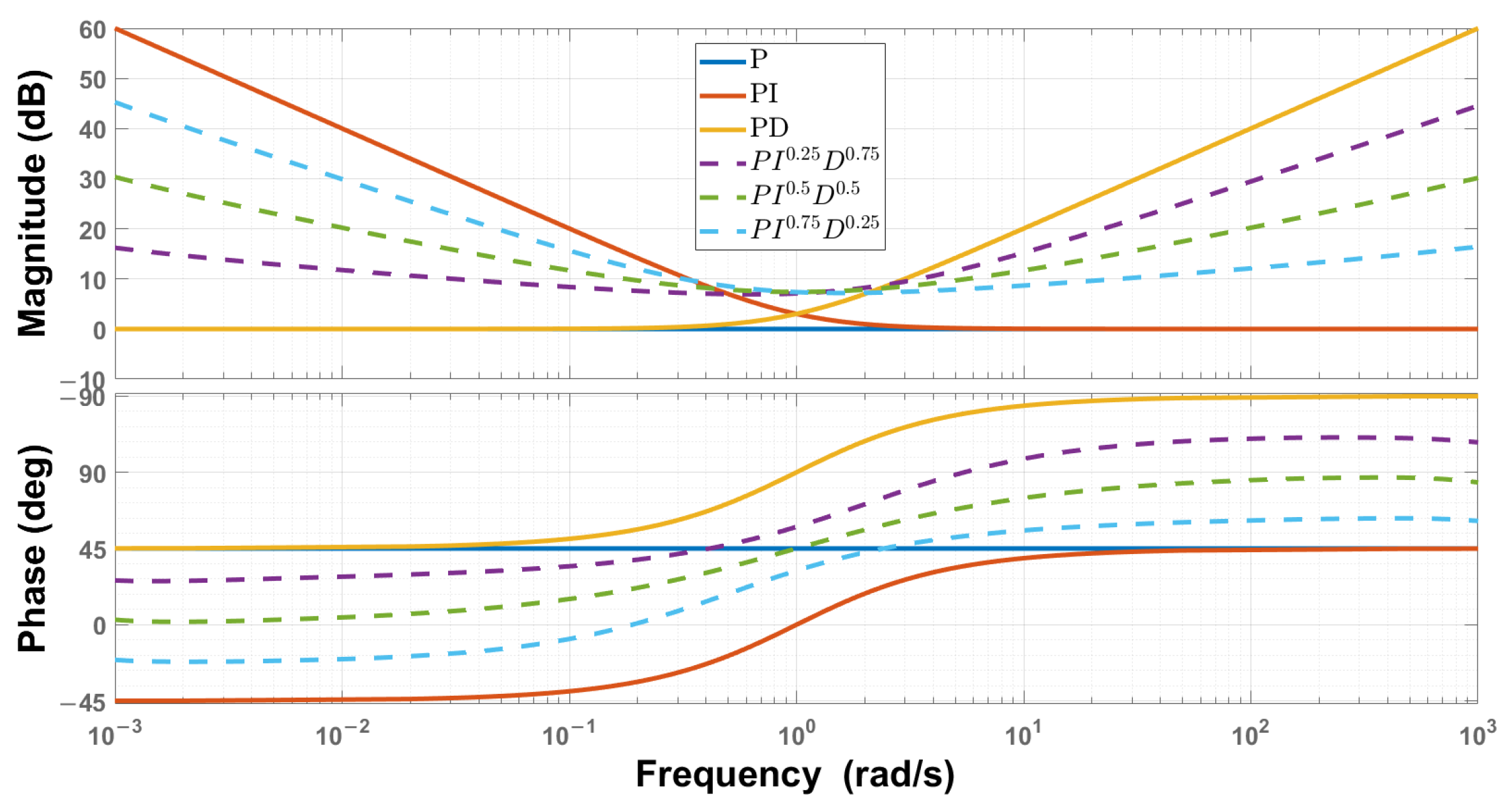
3. Fractional-Order Controllers
3.1. Realization of Fractional-Order Controllers
- Offline computational effort: The optimization objective function is computationally intensive. This problem is targeted through surrogate-based optimization, to obtain a surrogate model of the objective function for more efficient evaluations.
- Real-time implementation of the FOPID controller: The controller is approximated with the Oustaloup technique for suitable orders and frequency bands. Then, the obtained integer-order controller transfer function is discretized and emulated for digital control implementation. The approximation order can be selected as a trade-off between accuracy and real-time performance. The resulting integer order can be further reduced using a balanced reduction method. However, the available hardware was able to handle the calculated integer-order approximation without reduction.
3.2. Fractional-Order PID Controller
4. Mathematical Models for UAV Case Studies
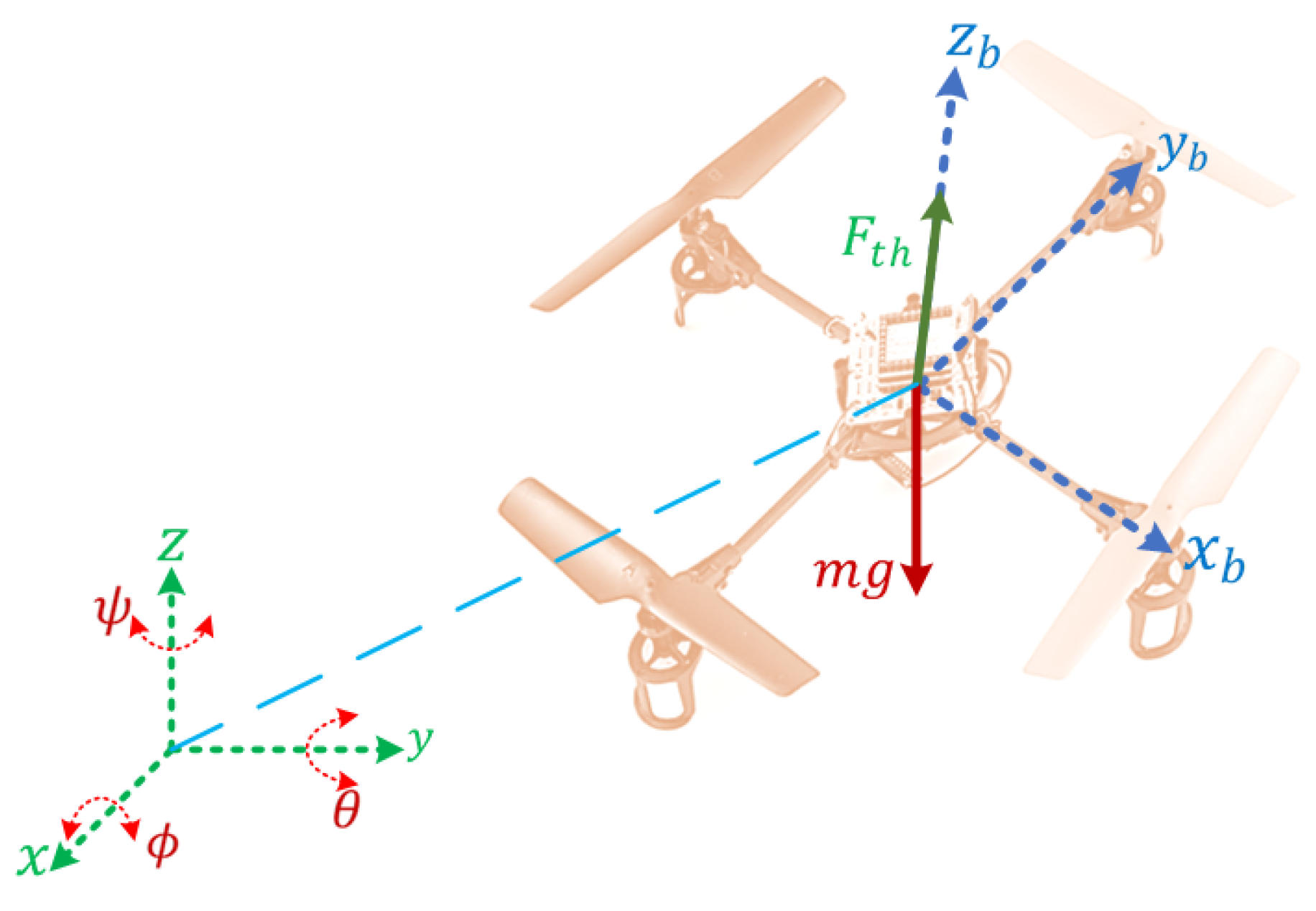
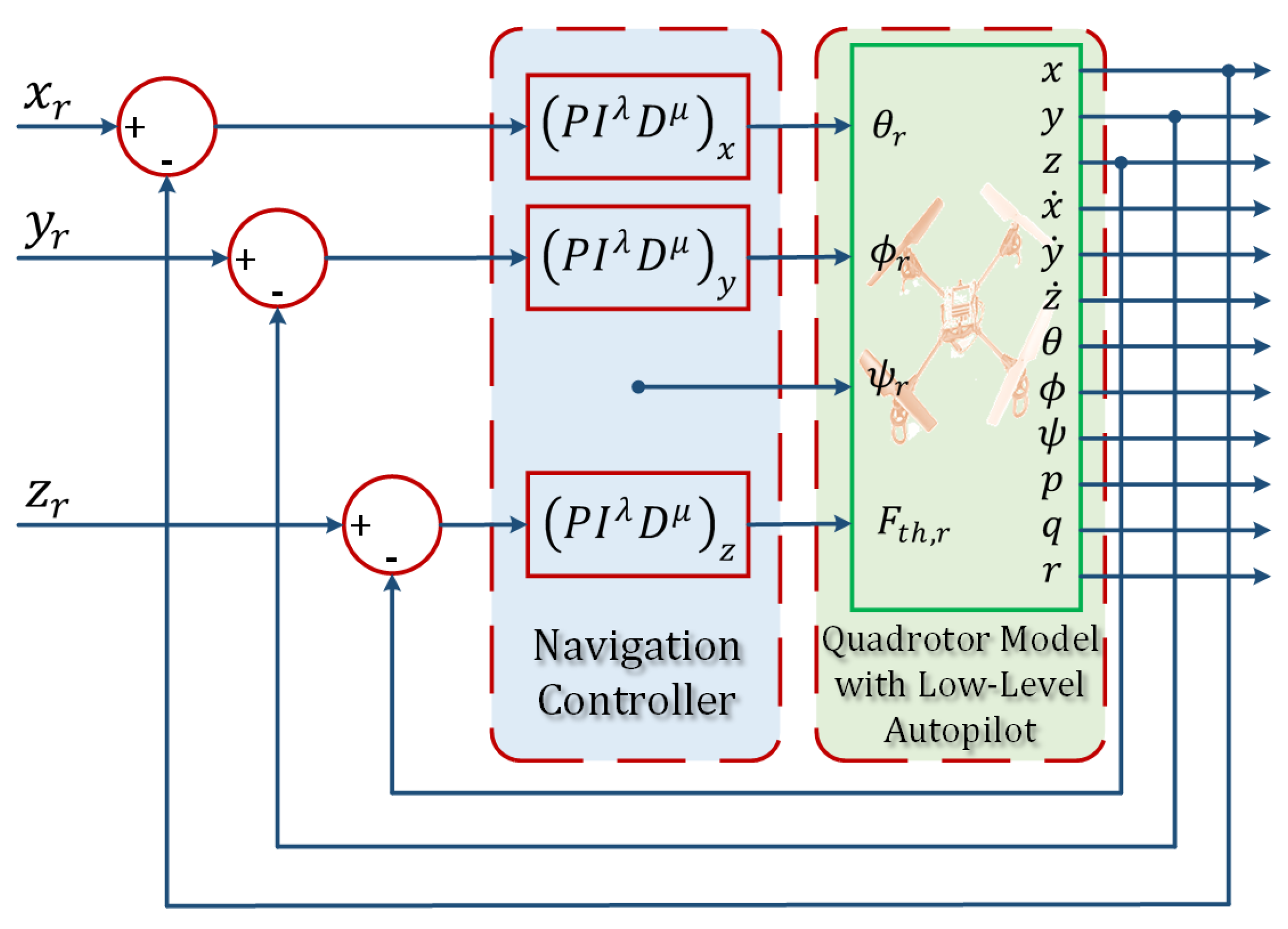
4.1. Quadrotor Benchmark Model
4.2. FOPID Waypoint Navigation Controller for the Quadrotor Benchmark
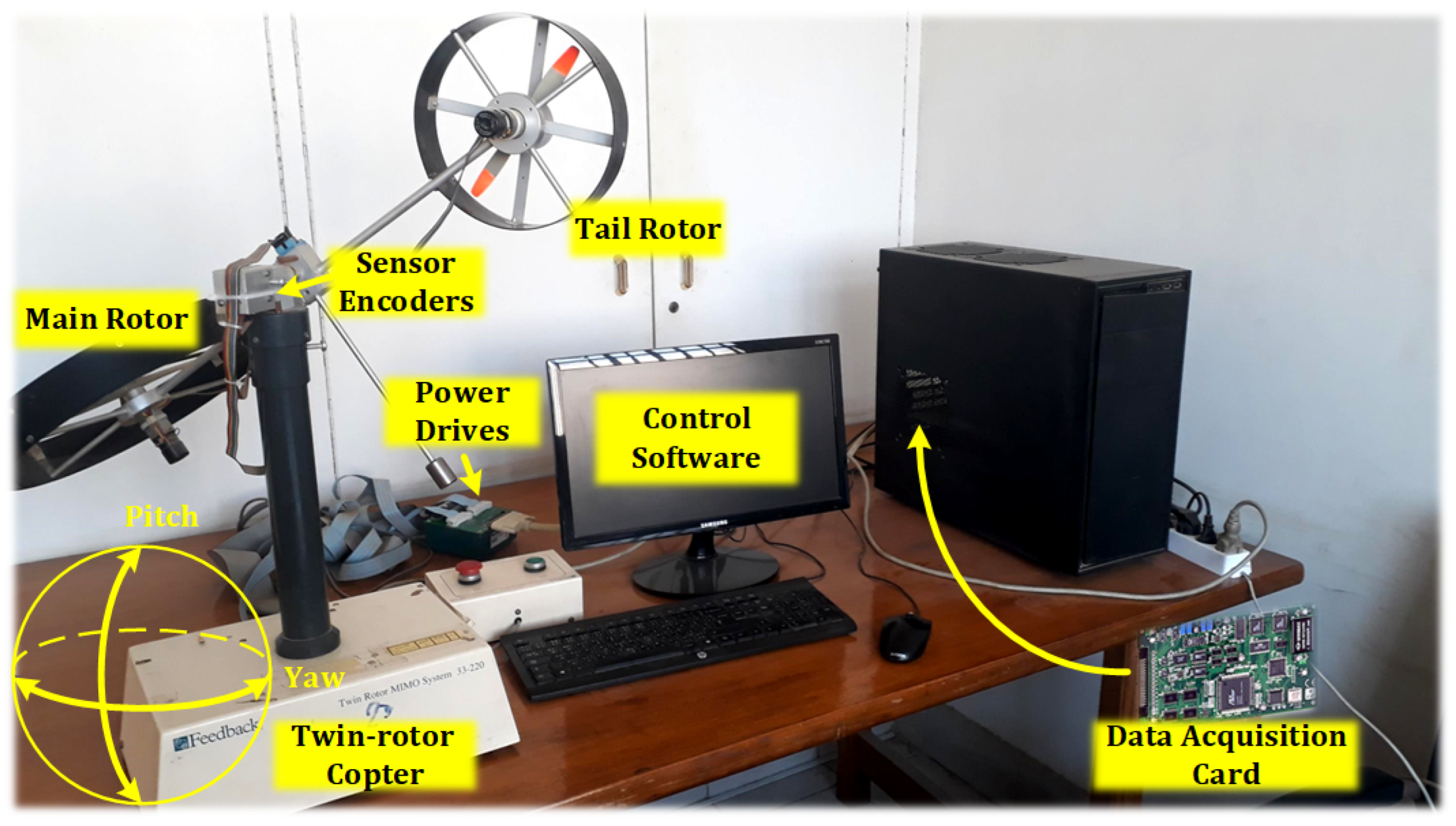
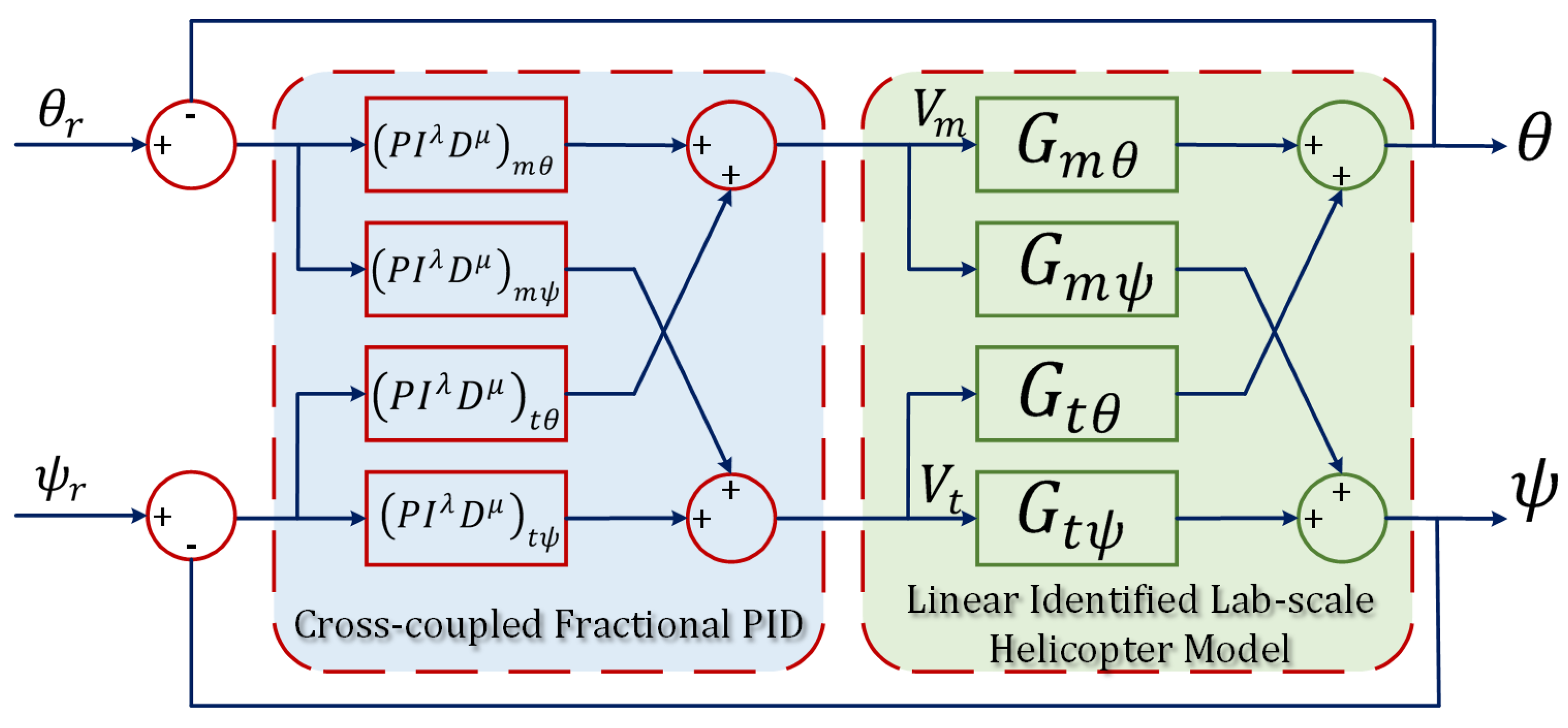
4.3. Twin-Rotor Copter System Model
4.4. Twin-Rotor Copter Real-Time Control Configuration
4.5. Problem Formulation of the FOPID Controller Parameter Optimization
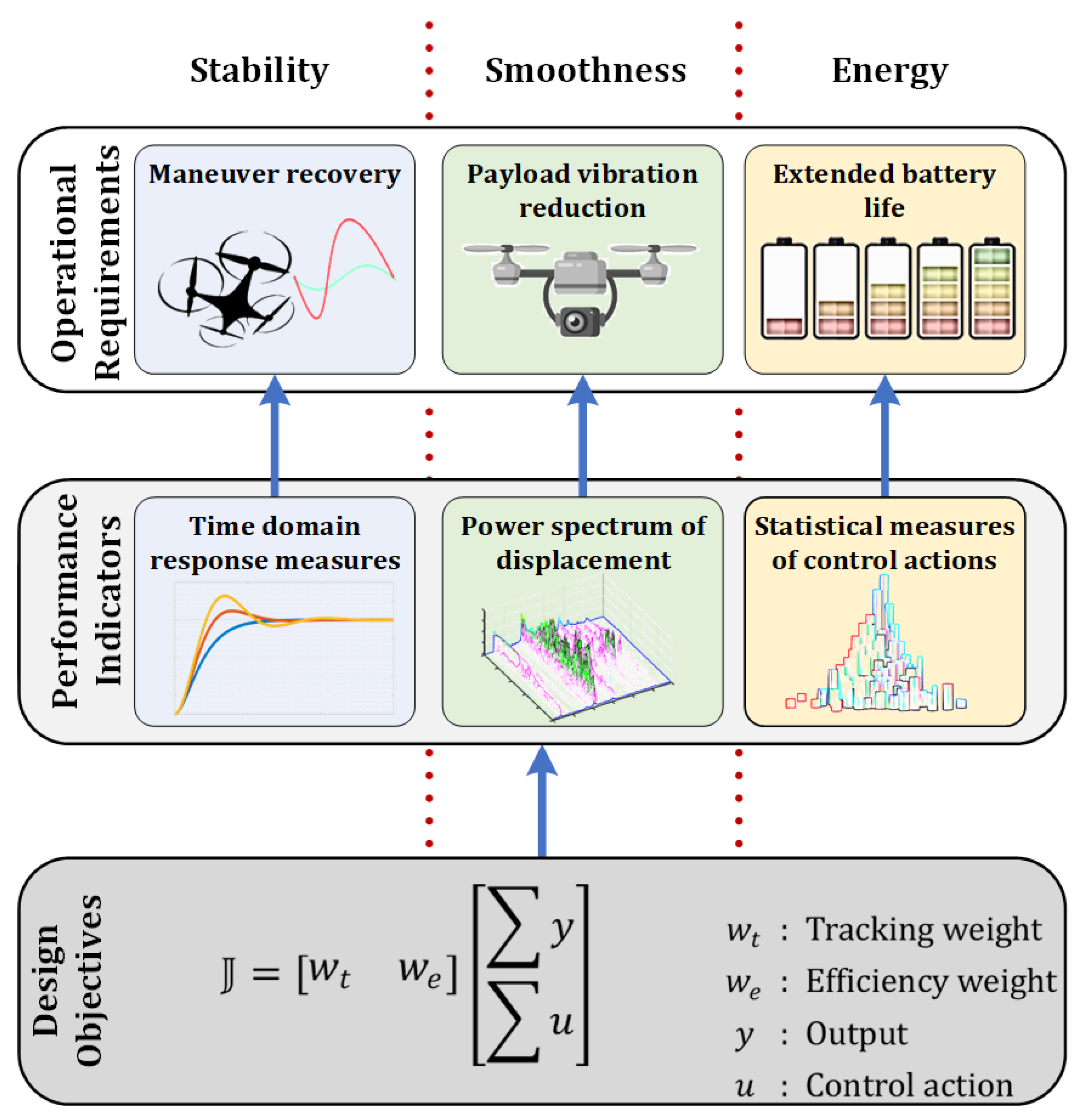
- The trajectory tracking: This requirement was incorporated into the objective function as an integral squared error.
- Energy utilization was inserted as a squared normalized control action to penalize large actions.
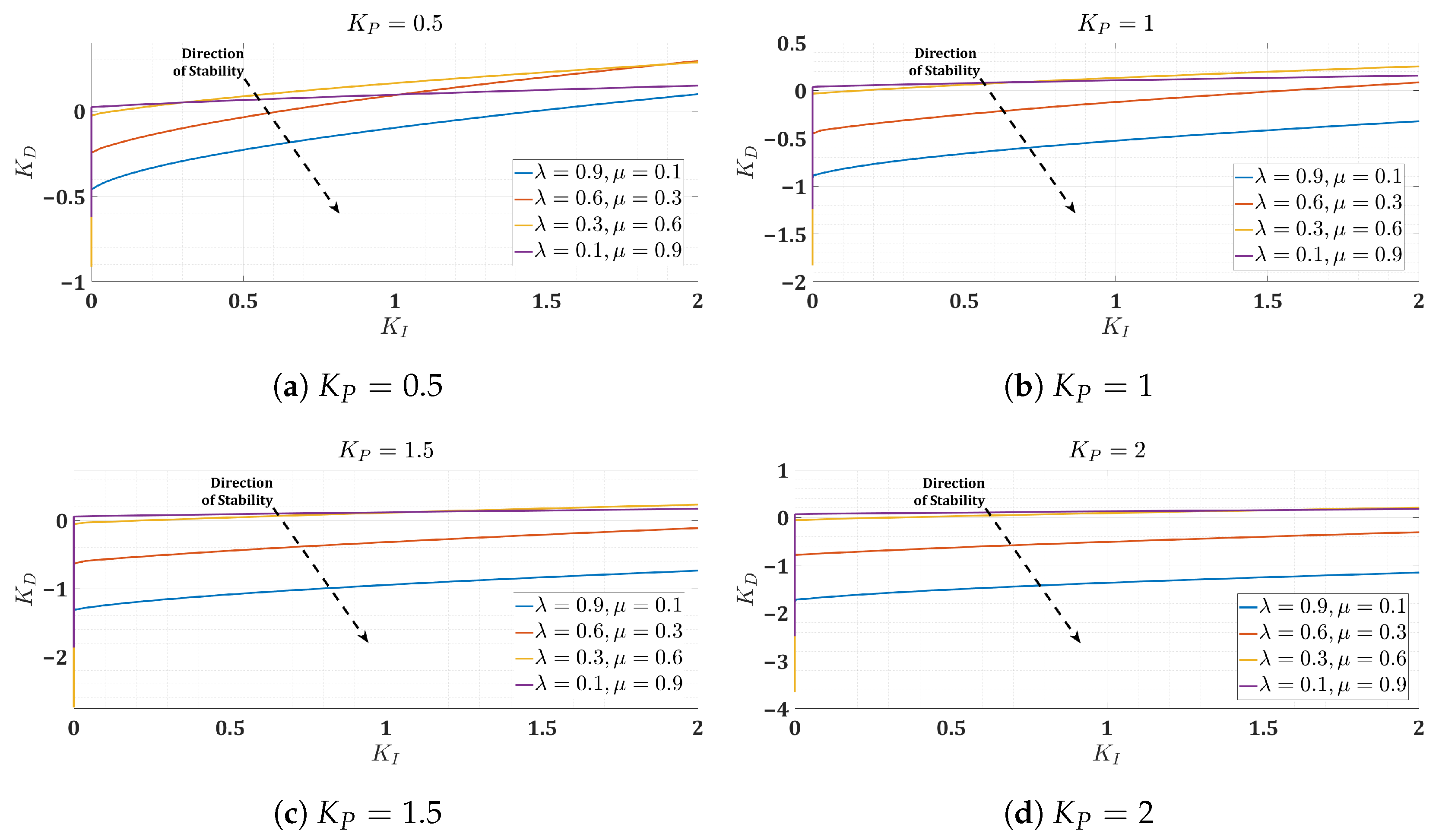
4.6. Stability Analysis of the FOPID Controller
- Real root boundary (RRB) represents the case where the real root crosses the imaginary axis at the origin. For the closed-loop system defined in (15), the RRB is .
- Infinite root boundary (IRB) defines the crossing of the real root of the imaginary axis at infinity.
- Complex root boundary (CRB) is characterized by the crossing of the real parts of a complex pair over the imaginary axis. The CRB curves were obtained using the following system of equations:
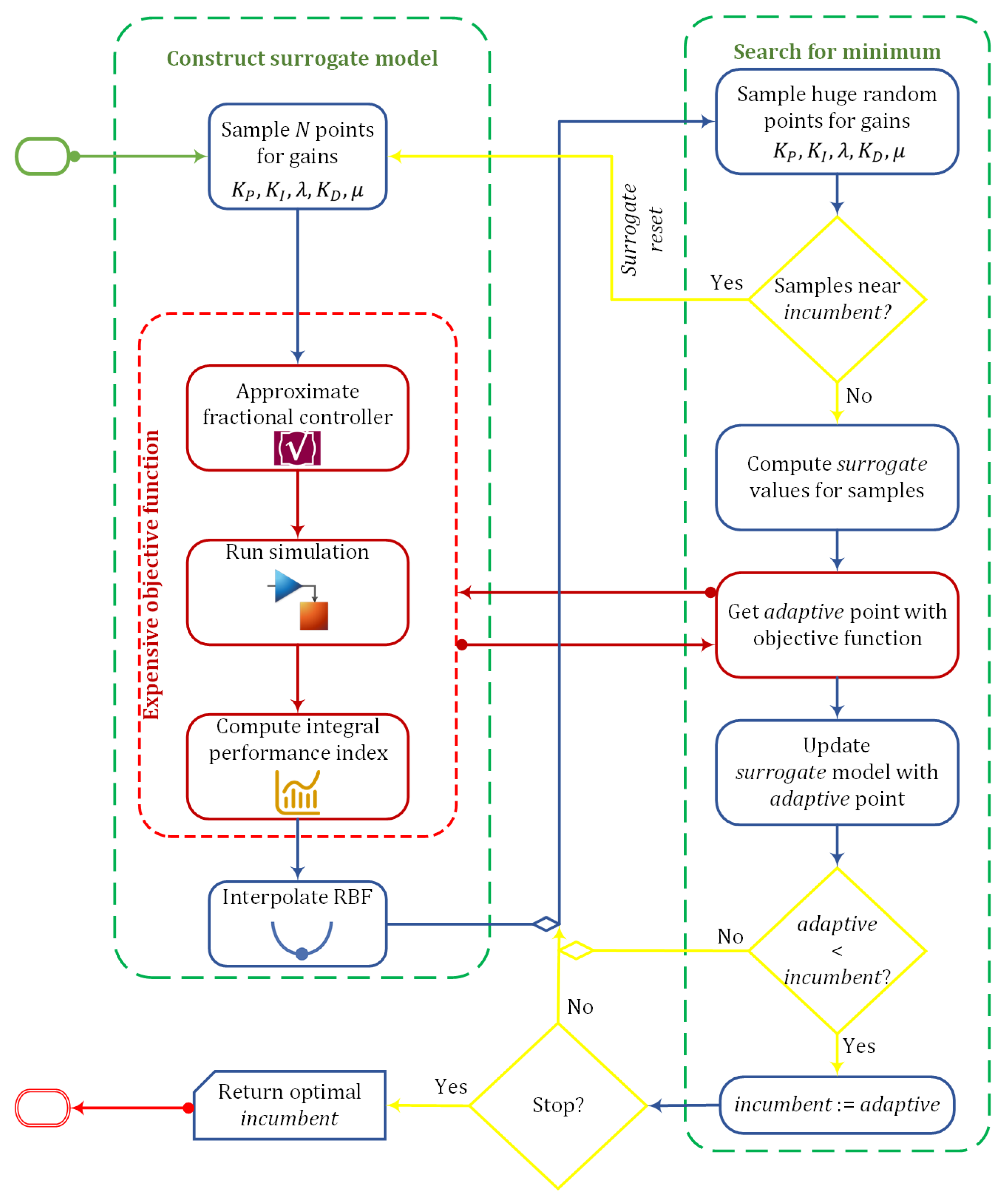
5. Surrogate Optimization
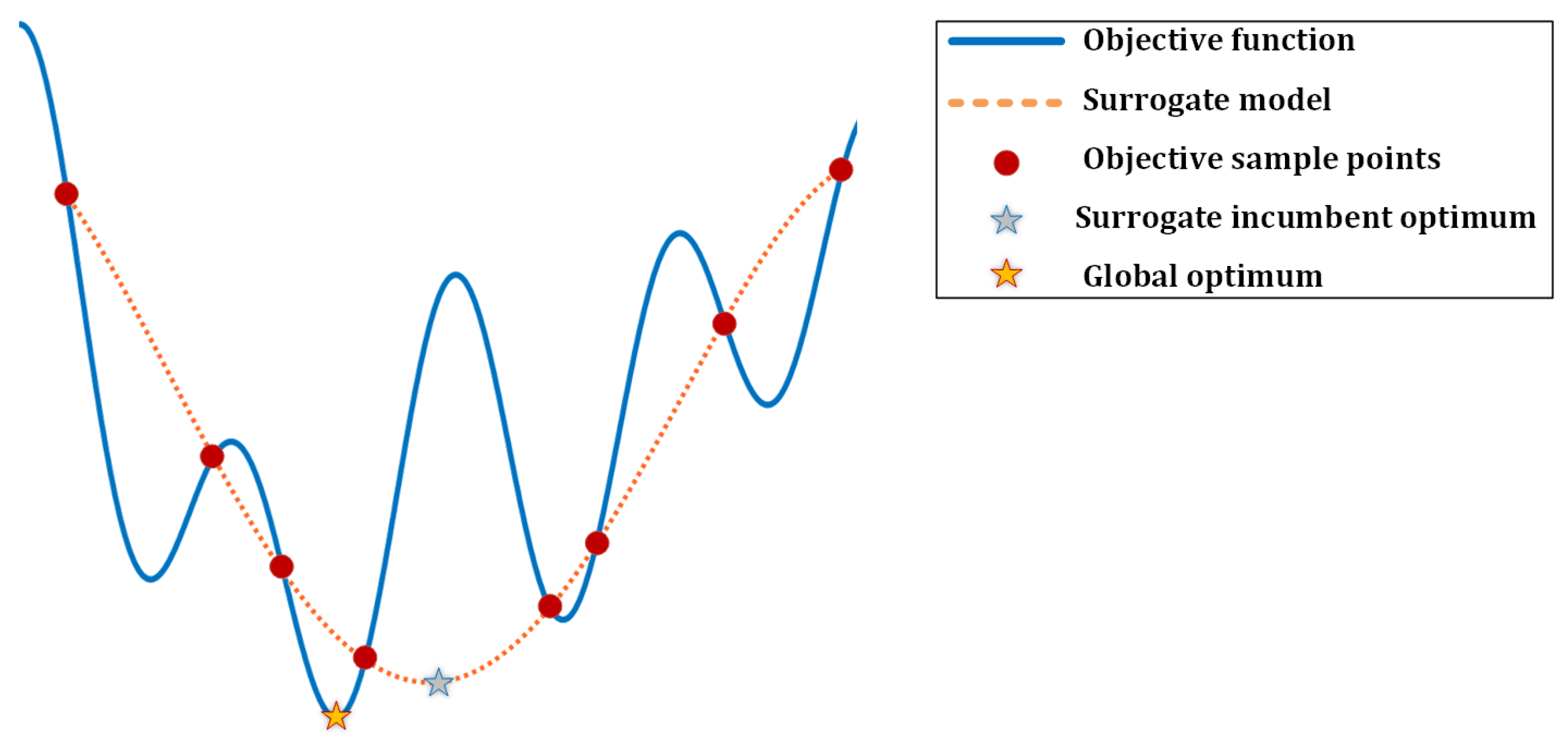
5.1. Surrogate Modeling
5.2. Optimization of the Surrogate Model
6. Results and Discussion
6.1. Quadrotor Optimization Results
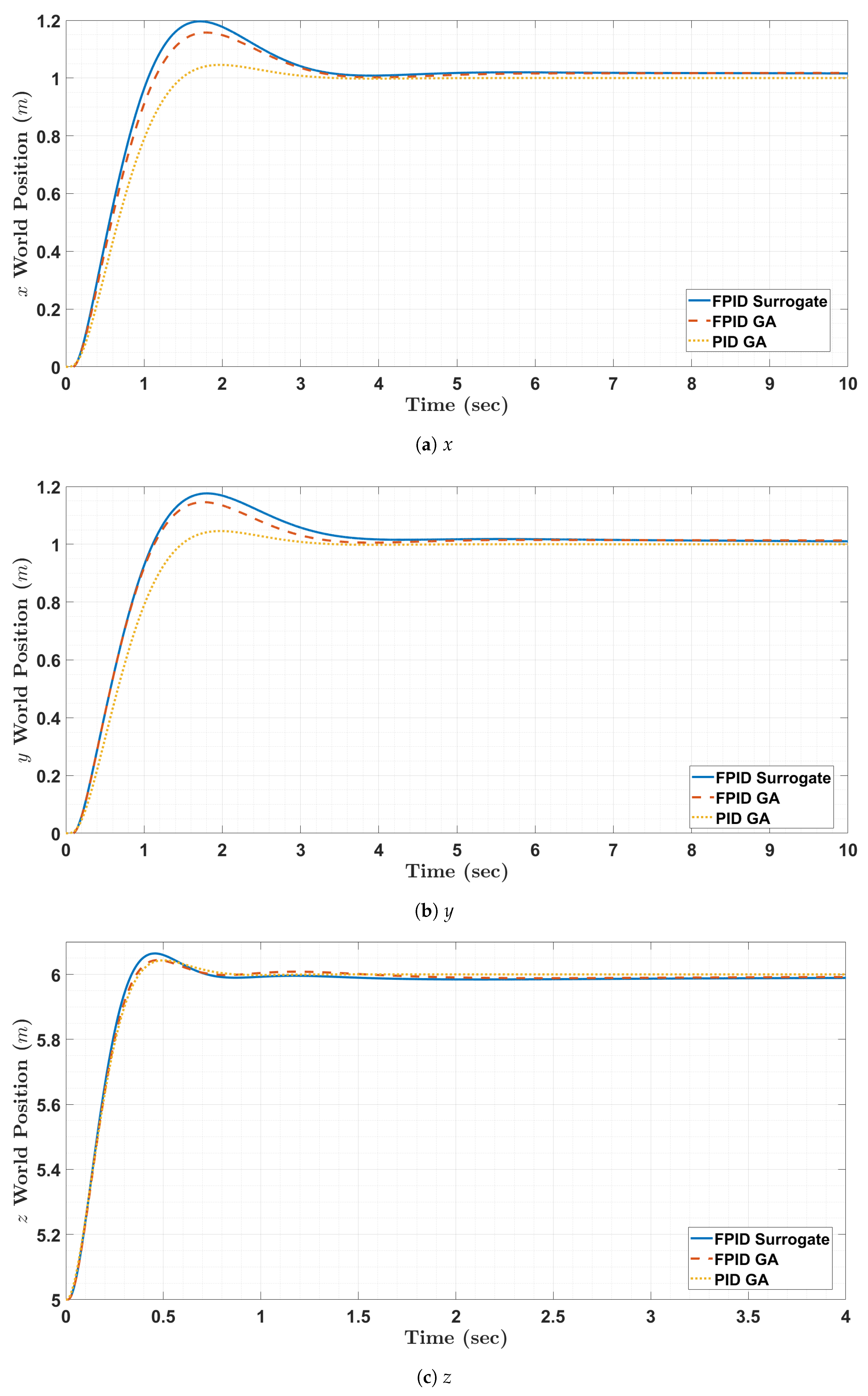
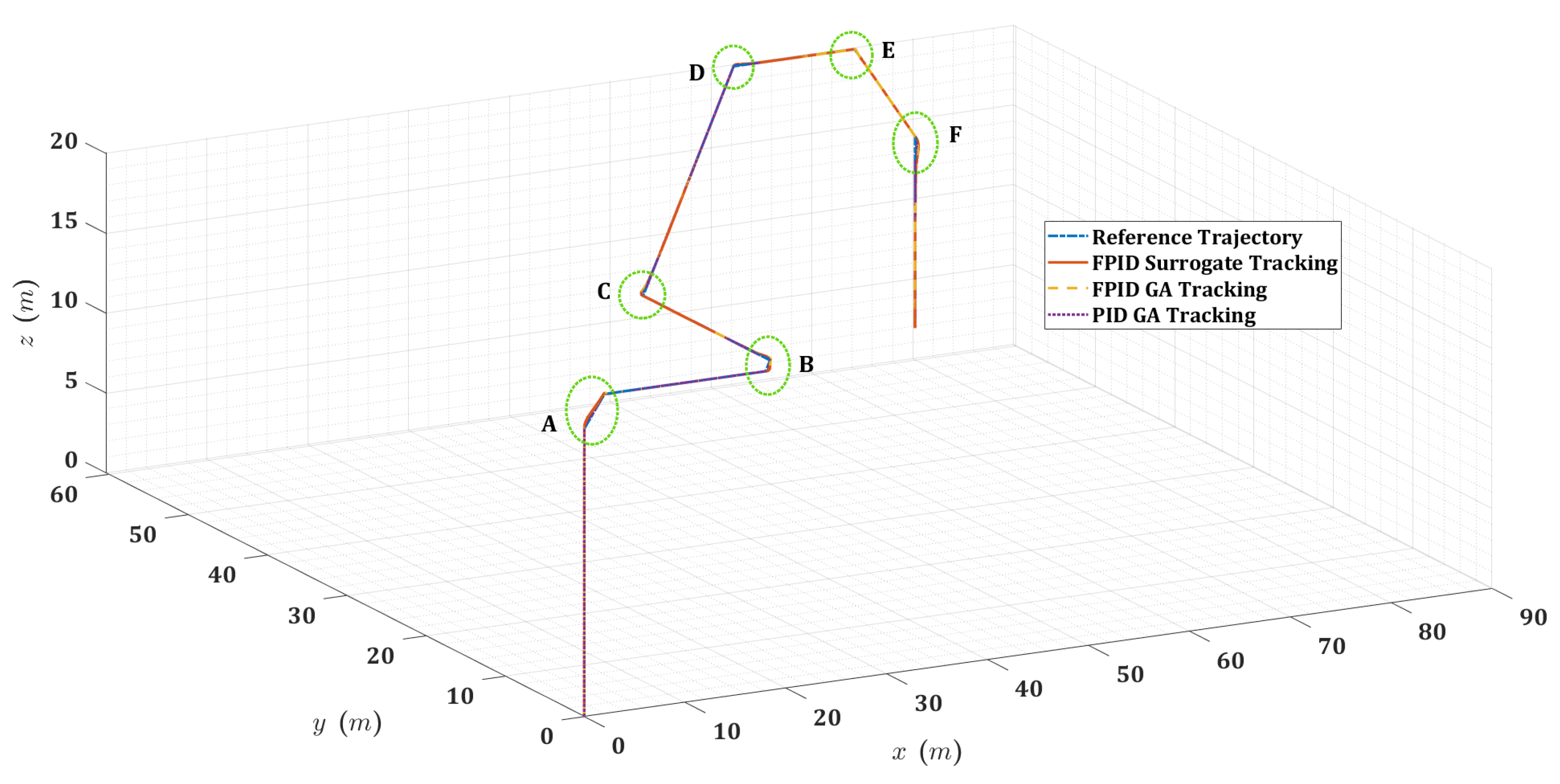
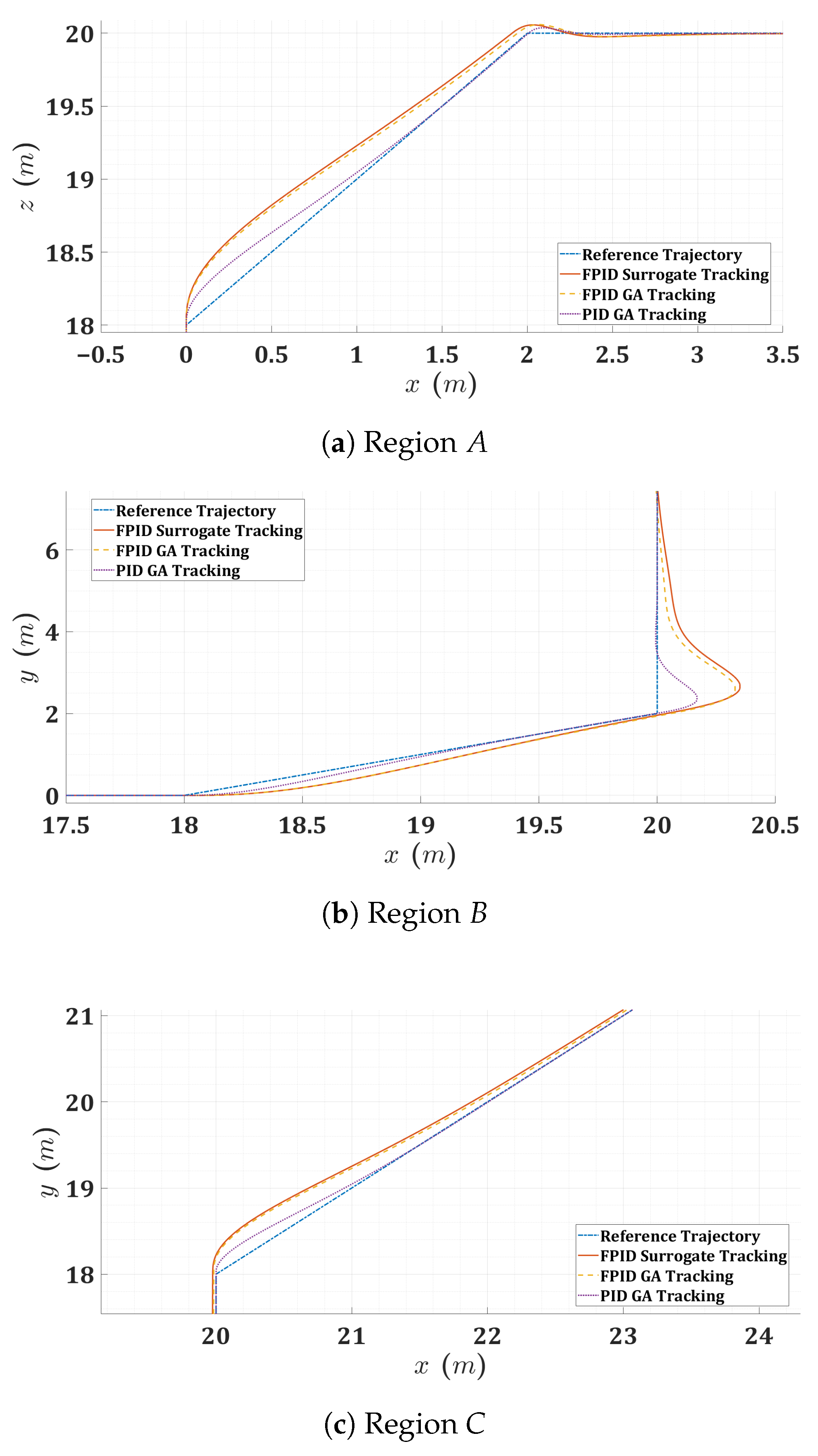
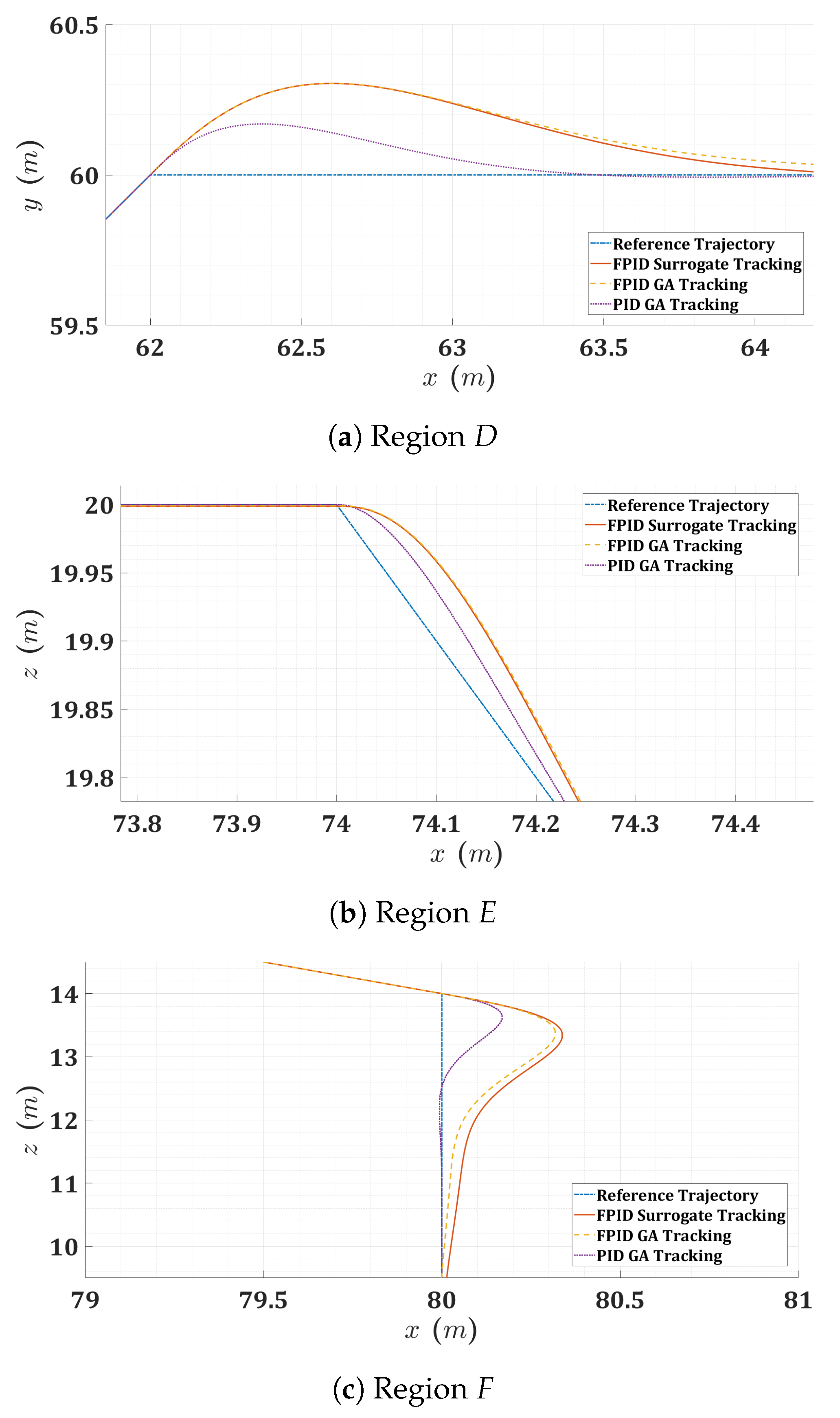
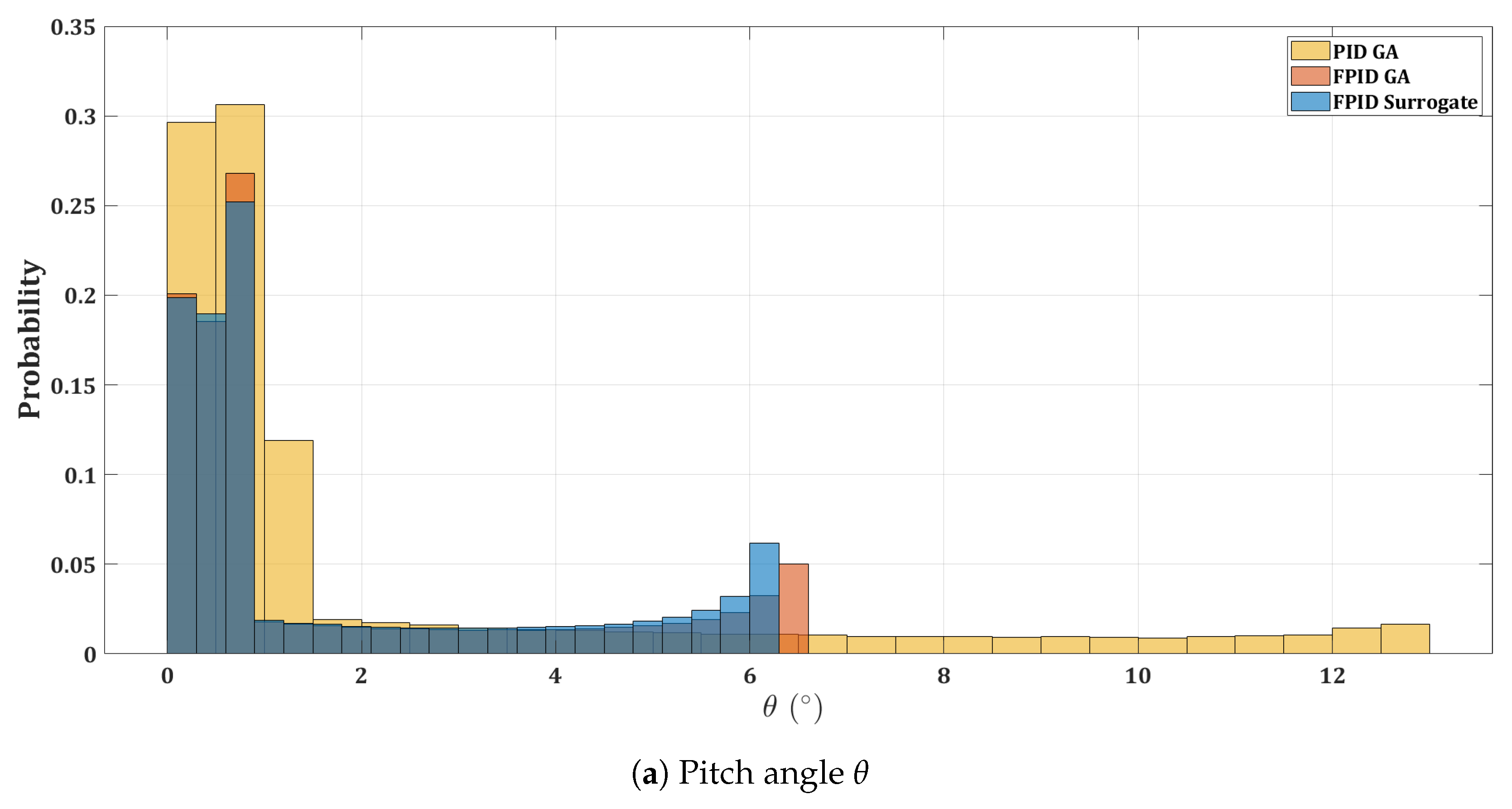
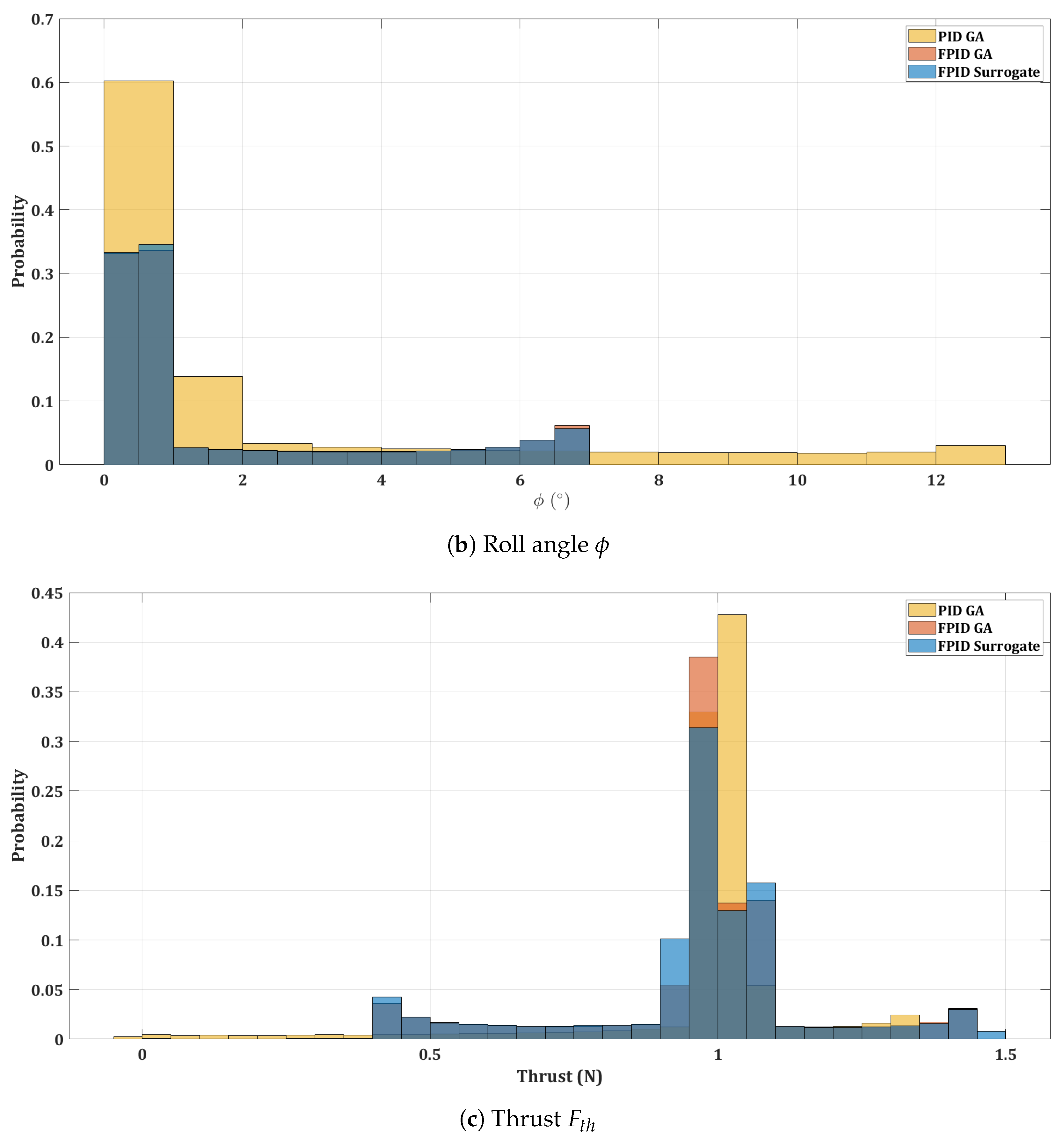
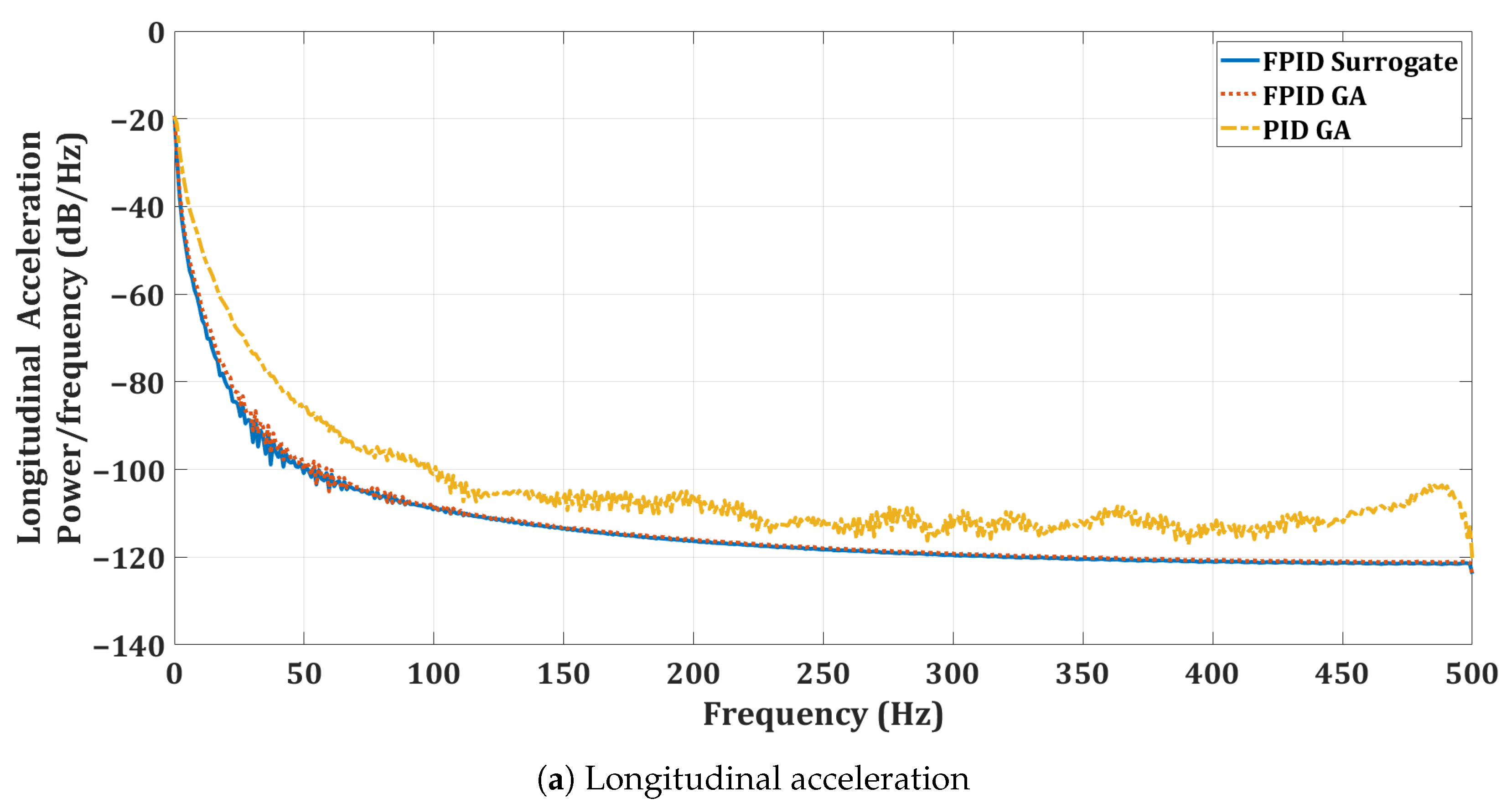
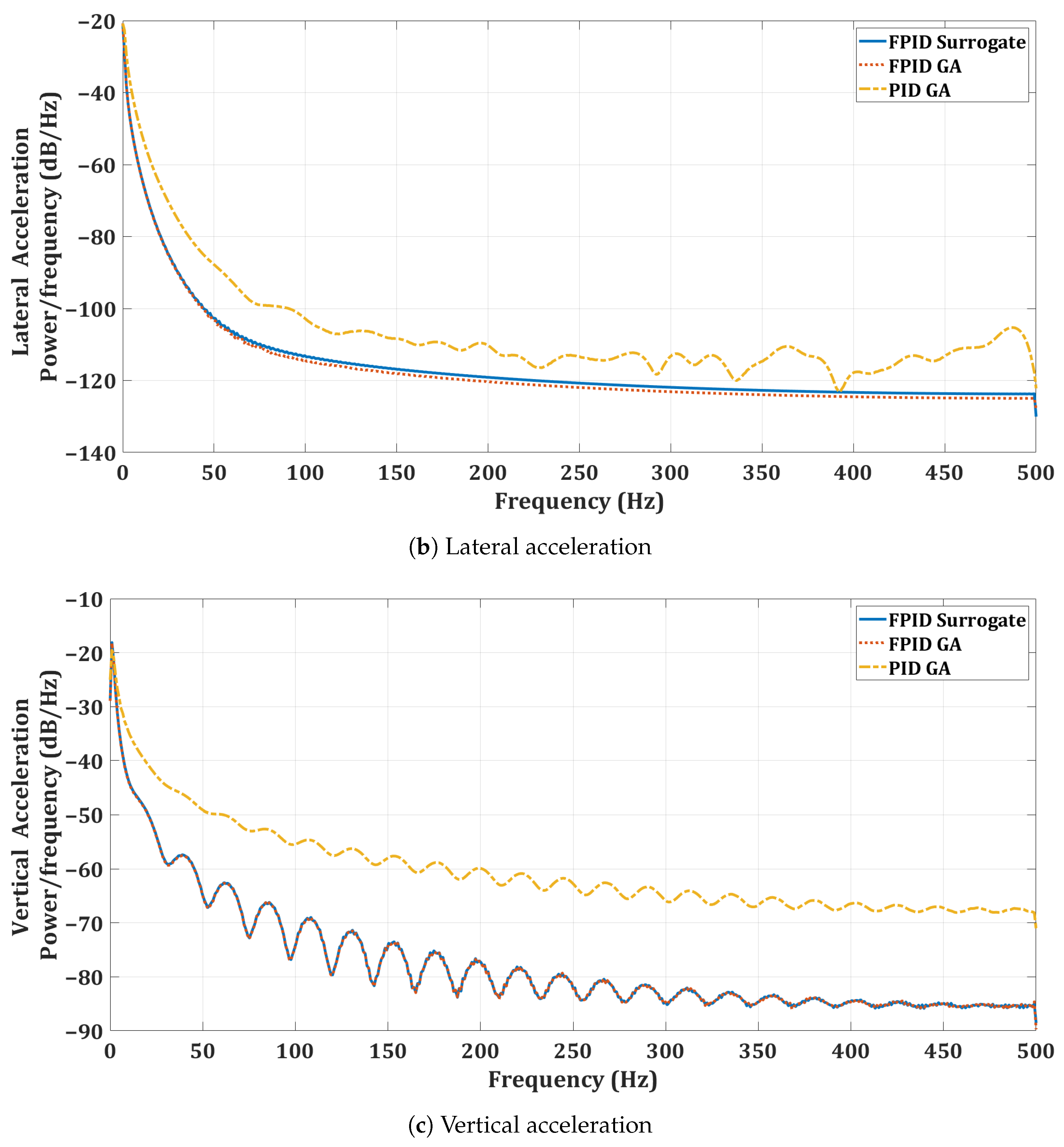
6.2. Simulation of Quadrotor Controllers
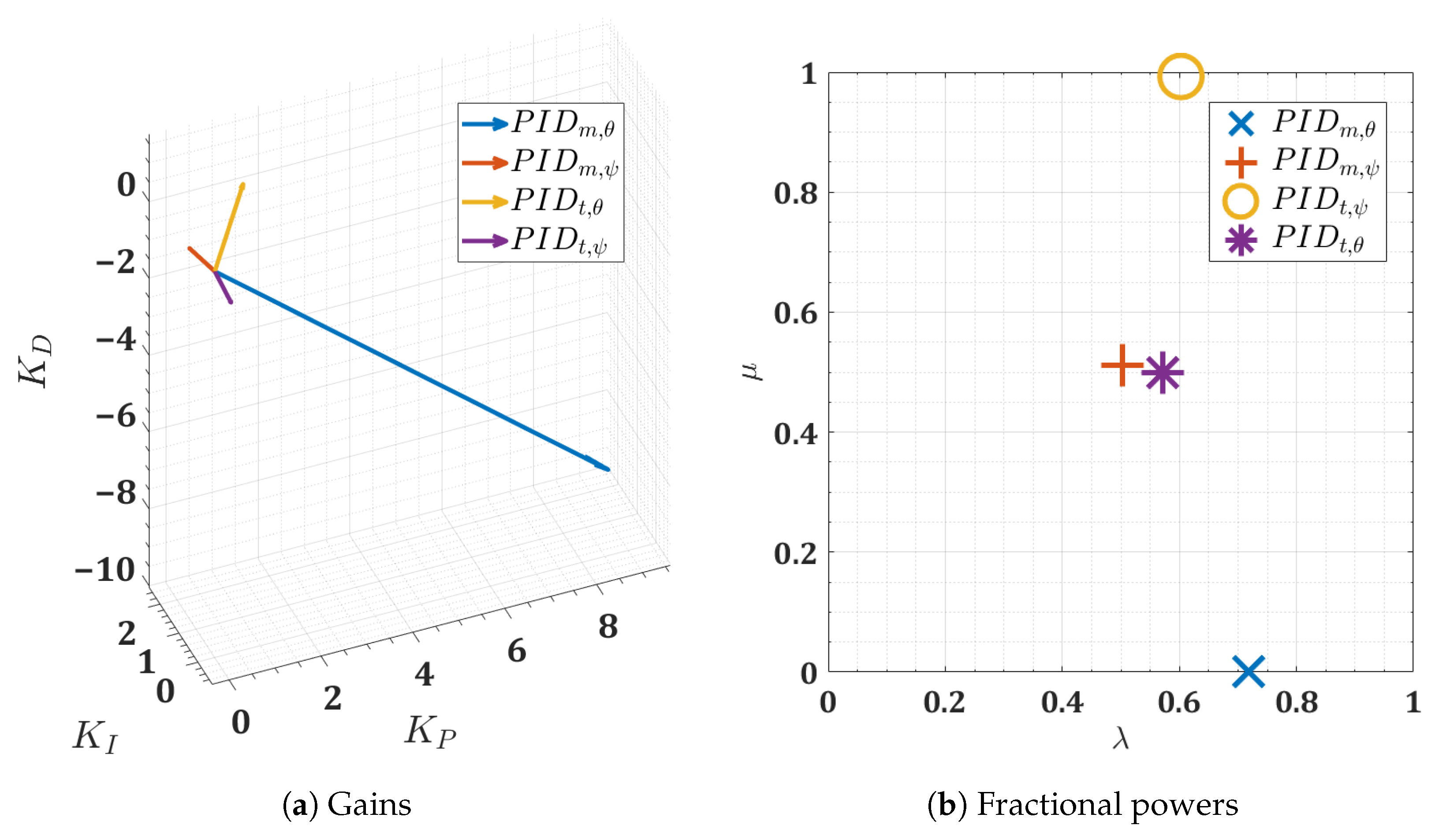
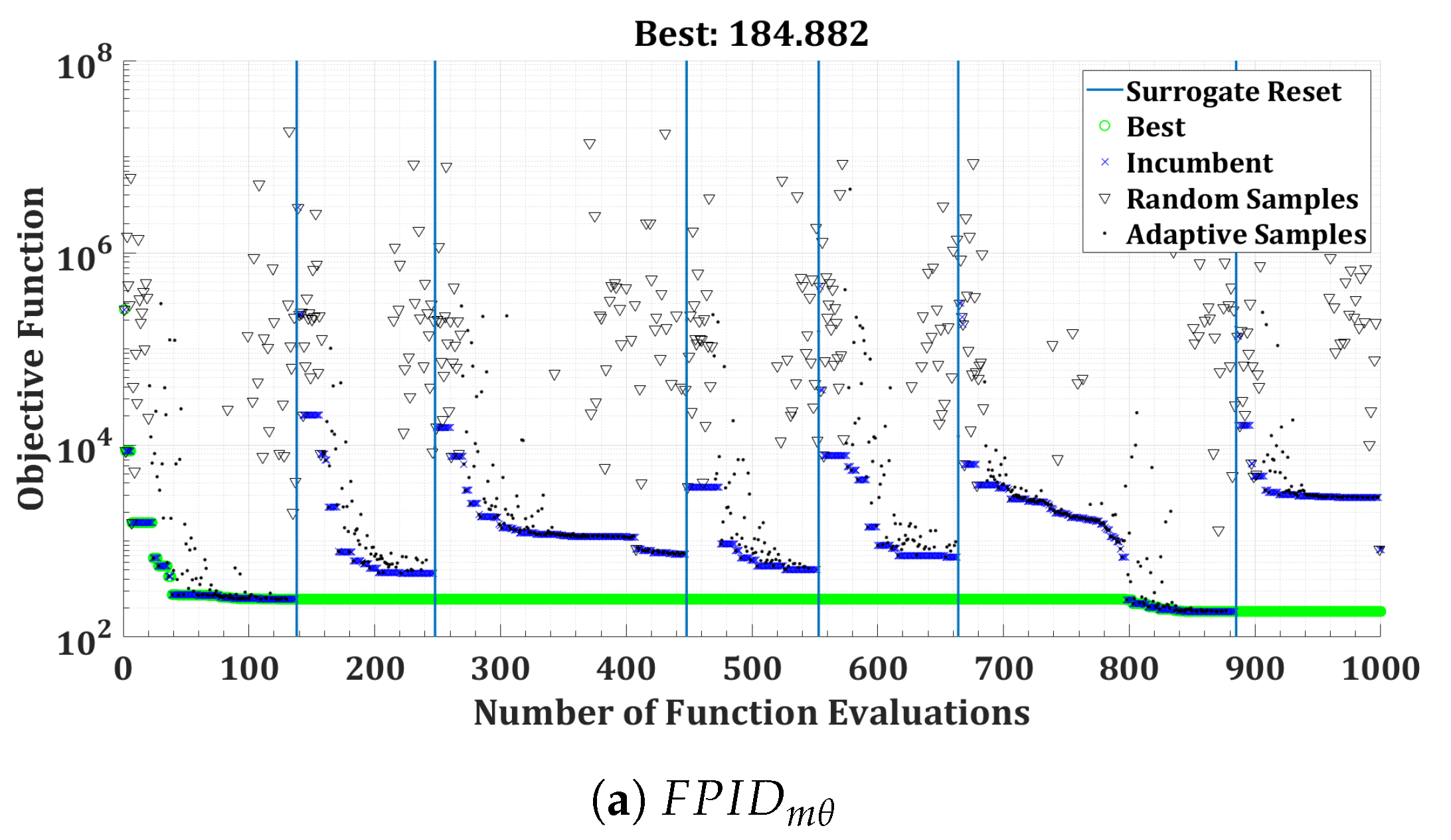
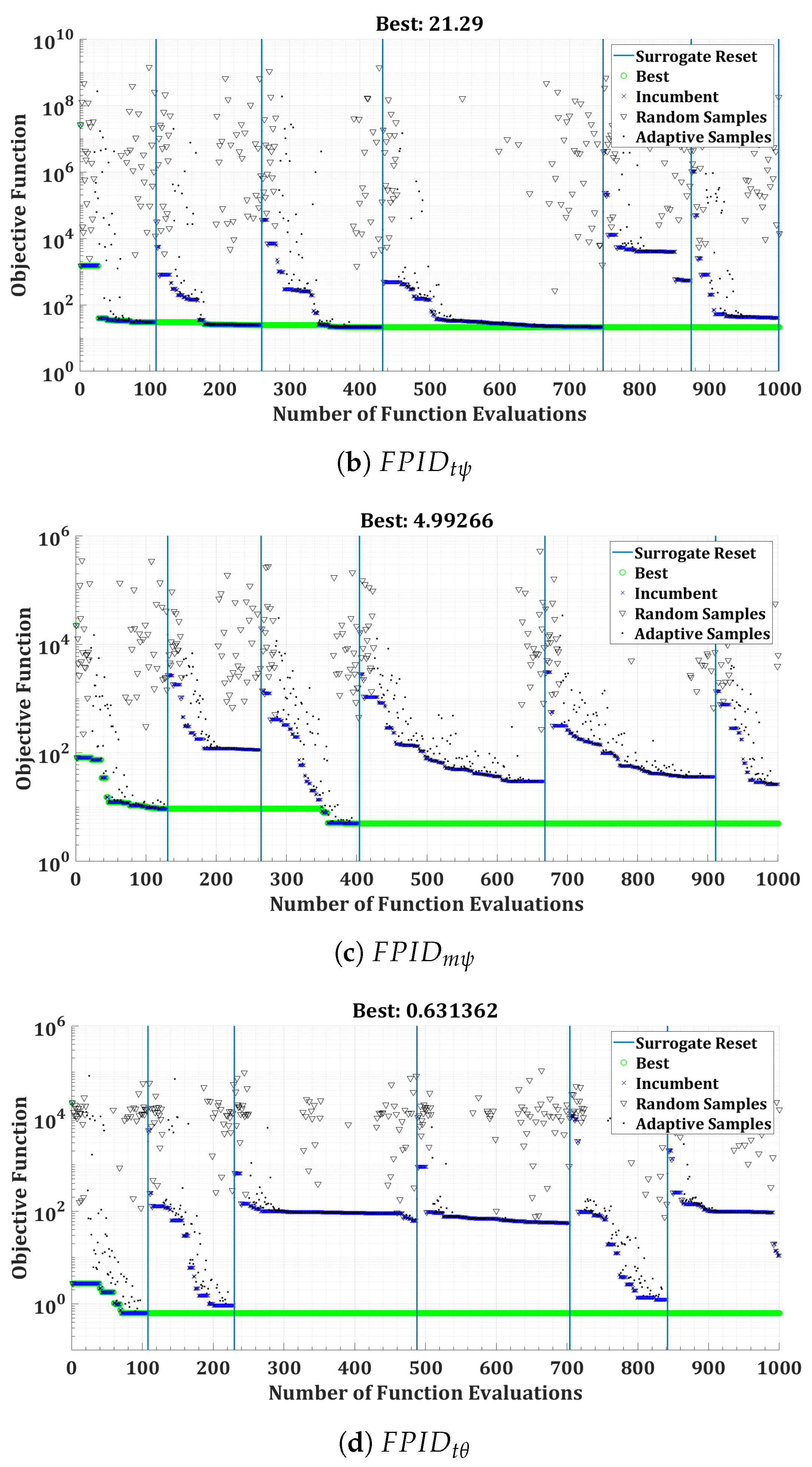
6.3. Twin-Rotor Copter Optimization Results
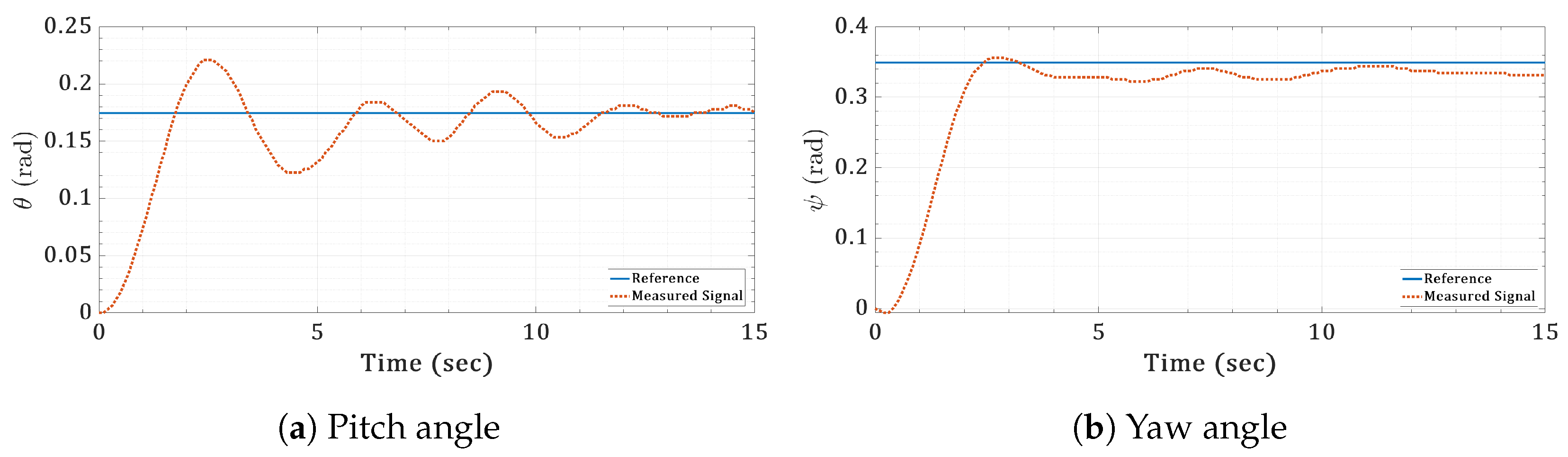
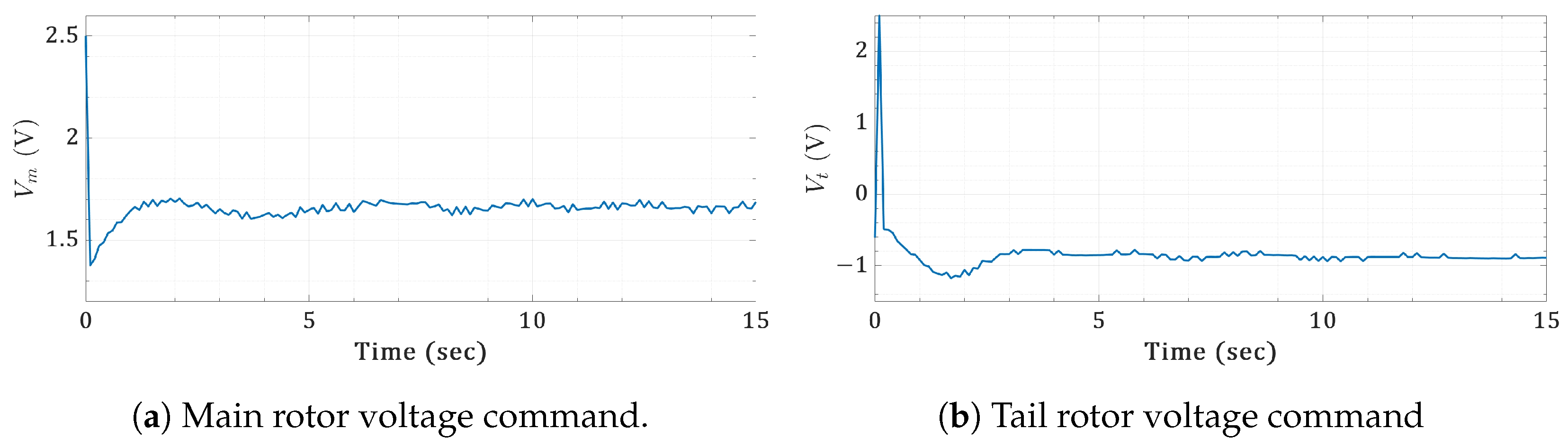
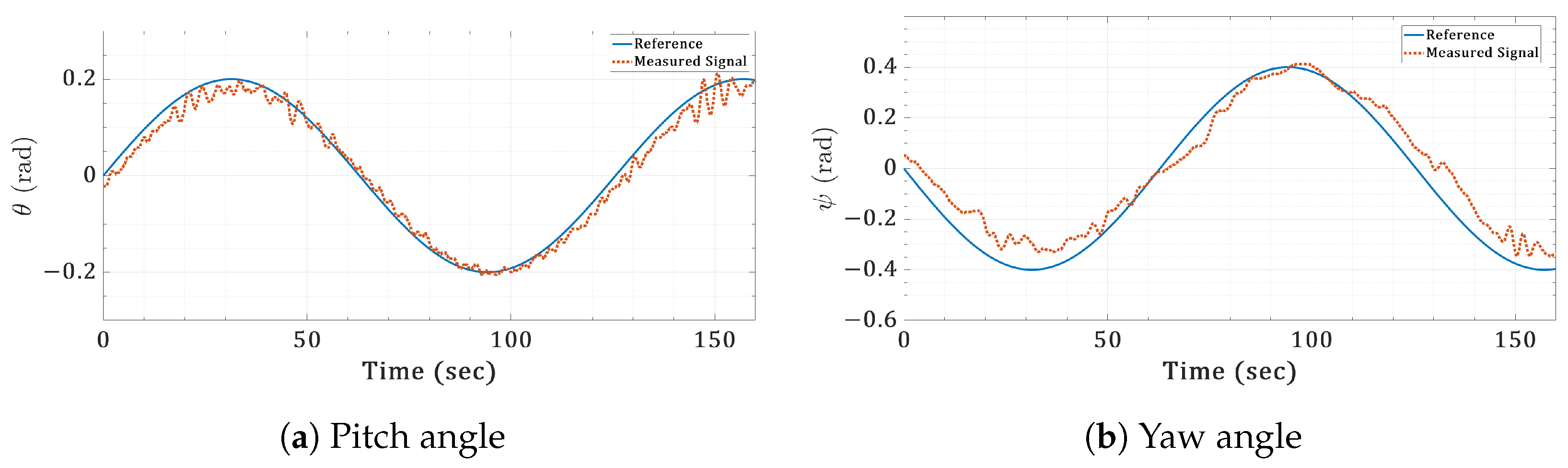
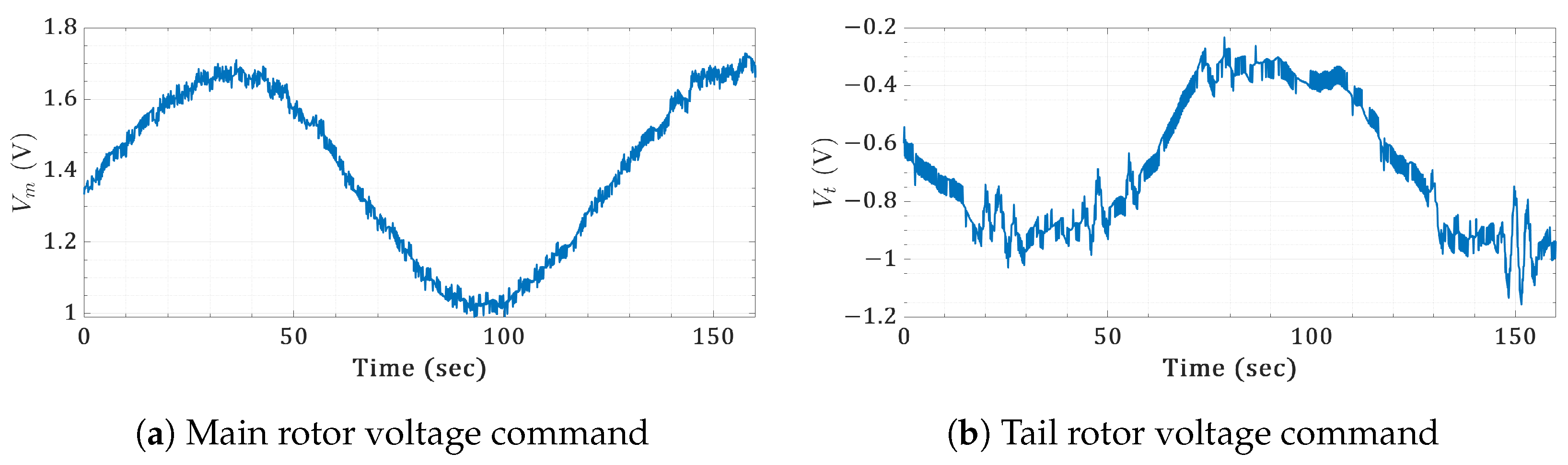
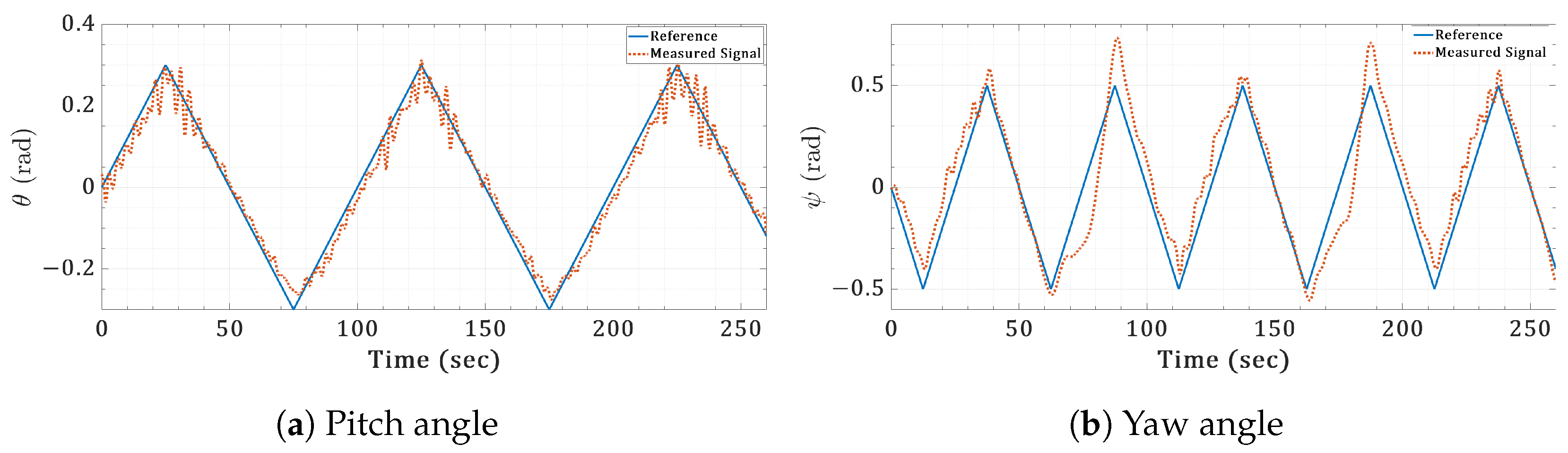
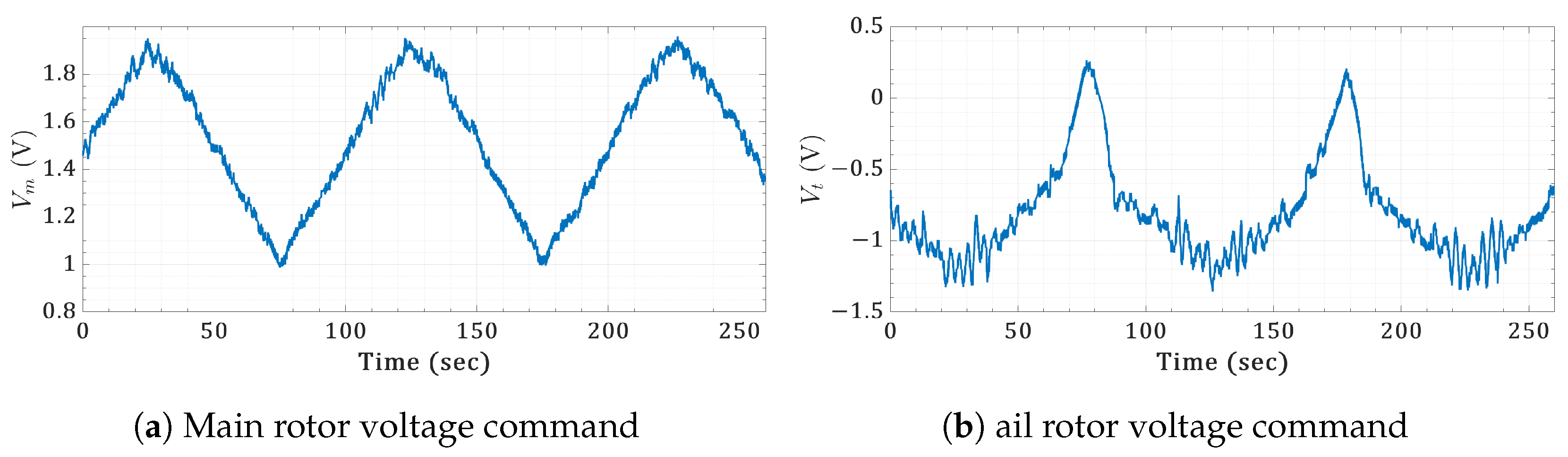
6.4. Real-Time Validation
7. Conclusions and Future Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moustafa, A.M.; Abdelghany, M.B.; Younis, A.S.A.; Moness, M.; Al-Durra, A.; Guerrero, J.M. Software-defined control of an emulated hydrogen energy storage for energy internet ecosystems. Int. J. Hydrogen Energy 2024, 50, 893–909. [Google Scholar] [CrossRef]
- IEA. Implementing Clean Energy Transitions Focus on Road Transport in Emerging Economies; Technical Report; International Energy Agency: Paris, France, 2023. [Google Scholar]
- Kellermann, R.; Biehle, T.; Fischer, L. Drones for parcel and passenger transportation: A literature review. Transp. Res. Interdiscip. Perspect. 2020, 4, 100088. [Google Scholar] [CrossRef]
- Shavarani, S.M.; Nejad, M.G.; Rismanchian, F.; Izbirak, G. Application of hierarchical facility location problem for optimization of a drone delivery system: A case study of Amazon prime air in the city of San Francisco. Int. J. Adv. Manuf. Technol. 2018, 95, 3141–3153. [Google Scholar] [CrossRef]
- Abdelghany, M.B.; Moustafa, A.M.; Moness, M. Benchmarking Tracking Autopilots for Quadrotor Aerial Robotic System Using Heuristic Nonlinear Controllers. Drones 2022, 6, 379. [Google Scholar] [CrossRef]
- Moness, M.; Mostafa, A.M. An algorithm for parameter estimation of twin-rotor multi-input multi-output system using trust region optimization methods. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2013, 227, 435–450. [Google Scholar] [CrossRef]
- Moness, M.; Moustafa, A.M. Tuning a digital multivariable controller for a lab-scale helicopter system via simulated annealing and evolutionary algorithms. Trans. Inst. Meas. Control 2015, 37, 1254–1273. [Google Scholar] [CrossRef]
- ElSayed, M.; Foda, A.; Mohamed, M. The impact of civil airspace policies on the viability of adopting autonomous unmanned aerial vehicles in last-mile applications. Transp. Policy 2024, 145, 37–54. [Google Scholar] [CrossRef]
- Somefun, O.A.; Akingbade, K.; Dahunsi, F. The dilemma of PID tuning. Annu. Rev. Control 2021, 52, 65–74. [Google Scholar] [CrossRef]
- Joseph, S.B.; Dada, E.G.; Abidemi, A.; Oyewola, D.O.; Khammas, B.M. Metaheuristic algorithms for PID controller parameters tuning: Review, approaches and open problems. Heliyon 2022, 8, e09399. [Google Scholar] [CrossRef] [PubMed]
- Bouabdallah, S. Design and Control of Quadrotors with Application to Autonomous Flying. Ph.D. Thesis, Swiss Federal Institute of Technology Lausanne, Lausanne, Switzerland, 2007. [Google Scholar]
- Ozbek, N.S.; Onkol, M.; Efe, M.O. Feedback control strategies for quadrotor-type aerial robots: A survey. Trans. Inst. Meas. Control 2016, 38, 529–554. [Google Scholar] [CrossRef]
- Lopez-Sanchez, I.; Moreno-Valenzuela, J. PID control of quadrotor UAVs: A survey. Annu. Rev. Control 2023, 56, 100900. [Google Scholar] [CrossRef]
- Pounds, P.E.I. Design, Construction and Control of a Large Quadrotor Micro Air Vehicle. Ph.D. Thesis, Australian National University, Canberra, Australia, 2007. [Google Scholar]
- Goel, R.; Shah, S.M.; Gupta, N.K.; Ananthkrishnan, N. Modeling, simulation and flight testing of an autonomous quadrotor. In Proceedings of the ICEAE, Bangalore, India, 18–22 May 2009; pp. 1–7. [Google Scholar]
- Li, J.; Li, Y. Dynamic analysis and PID control for a quadrotor. In Proceedings of the 2011 IEEE International Conference on Mechatronics and Automation, Beijing, China, 7–10 August 2011; pp. 573–578. [Google Scholar]
- Gautam, D.; Ha, C. Control of a Quadrotor Using a Smart Self-Tuning Fuzzy PID Controller. Int. J. Adv. Robot. Syst. 2013, 10, 380. [Google Scholar] [CrossRef]
- Yang, R.; Gao, Y.; Wang, H.; Ni, X. Fuzzy Neural Network PID Control Used in Individual Blade Control. Aerospace 2023, 10, 623. [Google Scholar] [CrossRef]
- Sengupta, S.; Dey, C. Optimal Auto-Tuned PID Controller for Twin Rotor MIMO System. In Advanced Engineering Optimization through Intelligent Techniques; Venkata Rao, R., Taler, J., Eds.; Springer: Singapore, 2023; pp. 591–601. [Google Scholar]
- Marie, M.J.; AL-Suhail, G.A.; Latif, W.A. PSO-based optimal PID controller for twin rotor MIMO system. Int. J. Comput. Technol. 2015, 14, 5719–5730. [Google Scholar] [CrossRef]
- Sivadasan, J.; Shiney, J.R.J. Performance evaluation of a non linear PID controller using chaotic gravitational search algorithm for a twin rotor system. Adv. Control Appl. 2023, 5, e162. [Google Scholar] [CrossRef]
- Su, H.; Ye, Y.; Chen, X.; He, H. Necessary and Sufficient Conditions for Consensus in Fractional-Order Multiagent Systems via Sampled Data Over Directed Graph. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2501–2511. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, H.; Cao, J. Group Consensus in Finite Time for Fractional Multiagent Systems With Discontinuous Inherent Dynamics Subject to Hölder Growth. IEEE Trans. Cybern. 2022, 52, 4161–4172. [Google Scholar] [CrossRef] [PubMed]
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Pham, V.T.; Vaidyanathan, S.; Volos, C.K.; Azar, A.T.; Hoang, T.M.; Van Yem, V. A Three-Dimensional No-Equilibrium Chaotic System: Analysis, Synchronization and Its Fractional Order Form. In Fractional Order Control and Synchronization of Chaotic Systems; Azar, A.T., Vaidyanathan, S., Ouannas, A., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 449–470. [Google Scholar]
- Alsaade, F.W.; Jahanshahi, H.; Yao, Q.; Al-zahrani, M.S.; Alzahrani, A.S. On the Development of a Data-Driven-Based Fractional-Order Controller for Unmanned Aerial Vehicles. Fractal Fract. 2023, 7, 236. [Google Scholar] [CrossRef]
- Hasan, A.F.; Humaidi, A.J.; Al-Obaidi, A.S.M.; Azar, A.T.; Ibraheem, I.K.; Al-Dujaili, A.Q.; Al-Mhdawi, A.K.; Abdulmajeed, F.A. Fractional Order Extended State Observer Enhances the Performance of Controlled Tri-copter UAV Based on Active Disturbance Rejection Control. In Mobile Robot: Motion Control and Path Planning; Azar, A.T., Kasim Ibraheem, I., Jaleel Humaidi, A., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 439–487. [Google Scholar]
- Wang, H.; Li, N.; Luo, Q. Adaptive fractional-order nonsingular fast terminal sliding mode formation control of multiple quadrotor UAVs-based distributed estimator. Asian J. Control 2023, 25, 3671–3686. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, D.; Li, S.; Zhang, W.; Lu, H. Adaptive Robust Control of the UAV-USV Heterogeneous System with Unknown Fractional-Order Dynamics under Multiple Disturbances. In Proceedings of the 2023 42nd Chinese Control Conference (CCC), Tianjin, China, 24–26 July 2023; pp. 5872–5877. [Google Scholar] [CrossRef]
- Yu, Z.; Yang, Z.; Sun, P.; Zhang, Y.; Jiang, B.; Su, C.Y. Refined fault tolerant tracking control of fixed-wing UAVs via fractional calculus and interval type-2 fuzzy neural network under event-triggered communication. Inf. Sci. 2023, 644, 119276. [Google Scholar] [CrossRef]
- Shao, S.; Chen, M. Robust discrete-time fractional-order control for an unmanned aerial vehicle based on disturbance observer. Int. J. Robust Nonlinear Control 2022, 32, 4665–4682. [Google Scholar] [CrossRef]
- Pouzesh, M.; Mobayen, S. Event-triggered fractional-order sliding mode control technique for stabilization of disturbed quadrotor unmanned aerial vehicles. Aerosp. Sci. Technol. 2022, 121, 107337. [Google Scholar] [CrossRef]
- Dong, R. Differential Evolution Versus Particle Swarm Optimization for PIλDμ Controller Design. In Proceedings of the 2009 Fifth International Conference on Natural Computation, Tianjian, China, 14–16 August 2009; Volume 3, pp. 236–240. [Google Scholar]
- Cajo, R.; Thi, T.M.; Copot, C.; Plaza, D.; Keyser, R.D.; Ionescu, C. Multiple UAVs Formation for Emergency Equipment and Medicines Delivery Based on Optimal Fractional Order Controllers. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 318–323. [Google Scholar] [CrossRef]
- Stolfi, D.H.; Danoy, G. Evaluating Surrogate Models for Robot Swarm Simulations. In Optimization and Learning; Dorronsoro, B., Chicano, F., Danoy, G., Talbi, E.G., Eds.; Springer: Cham, Switzerland, 2023; pp. 224–235. [Google Scholar]
- Wu, Z.; Zeng, J.; Hu, Z.; Todd, M.D. Optimization of unmanned aerial vehicle inspection strategy for infrastructure based on model-enabled diagnostics and prognostics. Mech. Syst. Signal Process. 2023, 204, 110841. [Google Scholar] [CrossRef]
- Tang, Q.; Li, Y.; Deng, Z.; Chen, D.; Guo, R.; Huang, H. Optimal shape design of an autonomous underwater vehicle based on multi-objective particle swarm optimization. Nat. Comput. 2020, 19, 733–742. [Google Scholar] [CrossRef]
- Yue, H.; Medromi, H.; Ding, H.; Bassir, D. A novel hybrid drone for multi-propose aerial transportation and its conceptual optimization based on surrogate approach. J. Phys. Conf. Ser. 2021, 1972, 012103. [Google Scholar] [CrossRef]
- Regis, R.G.; Shoemaker, C.A. A Stochastic Radial Basis Function Method for the Global Optimization of Expensive Functions. INFORMS J. Comput. 2007, 19, 497–509. [Google Scholar] [CrossRef]
- Palar, P.S.; Liem, R.P.; Zuhal, L.R.; Shimoyama, K. On the use of surrogate models in engineering design optimization and exploration. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Prague, Czech Republic, 13–17 July 2019; pp. 1592–1602. [Google Scholar] [CrossRef]
- Forrester, A.I.J.; Sóbester, A.; Keane, A.J. Constructing a Surrogate. In Engineering Design via Surrogate Modelling; Wiley Online Books; Wiley: Hoboken, NJ, USA, 2008; pp. 33–76. [Google Scholar] [CrossRef]
- Rosales-Asensio, E.; Rosales, A.E.; Colmenar-Santos, A. Surrogate optimization of coupled energy sources in a desalination microgrid based on solar PV and wind energy. Desalination 2021, 500, 114882. [Google Scholar] [CrossRef]
- Bahlawan, H.; Morini, M.; Pinelli, M.; Spina, P.R.; Venturini, M. Simultaneous optimization of the design and operation of multi-generation energy systems based on life cycle energy and economic assessment. Energy Convers. Manag. 2021, 249, 114883. [Google Scholar] [CrossRef]
- Farhadi, F.; Golestani, S.J.; Teneketzis, D. A Surrogate Optimization-Based Mechanism for Resource Allocation and Routing in Networks With Strategic Agents. IEEE Trans. Autom. Control 2019, 64, 464–479. [Google Scholar] [CrossRef]
- Li, Y.; Xiao, S.; Rotaru, M.; Sykulski, J.K. A Dual Kriging Approach with Improved Points Selection Algorithm for Memory Efficient Surrogate Optimization in Electromagnetics. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Liu, X.; Qu, X.; Ma, X. Optimizing electric bus charging infrastructure considering power matching and seasonality. Transp. Res. Part D Transp. Environ. 2021, 100, 103057. [Google Scholar] [CrossRef]
- Ziółkowski, J.; Lęgas, A.; Szymczyk, E.; Małachowski, J.; Oszczypała, M.; Szkutnik-Rogoż, J. Optimization of the Delivery Time within the Distribution Network, Taking into Account Fuel Consumption and the Level of Carbon Dioxide Emissions into the Atmosphere. Energies 2022, 15, 5198. [Google Scholar] [CrossRef]
- Idrissi, M.; Salami, M.; Annaz, F. A Review of Quadrotor Unmanned Aerial Vehicles: Applications, Architectural Design and Control Algorithms. J. Intell. Robot. Syst. 2022, 104, 22. [Google Scholar] [CrossRef]
- Shaaban, M.; Merzban, M.H.; Khalaf, A.A.M.; Hamed, H.F. Comparison of Various Control Techniques Applied to a Quadcopter. J. Adv. Eng. Trends 2023, 42, 233–244. [Google Scholar] [CrossRef]
- Sabatier, J. Fractional Order Models Are Doubly Infinite Dimensional Models and thus of Infinite Memory: Consequences on Initialization and Some Solutions. Symmetry 2021, 13, 1099. [Google Scholar] [CrossRef]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer Science & Business Media: London, UK, 2010. [Google Scholar]
- Matsuda, K.; Fujii, H. H(infinity) optimized wave-absorbing control—Analytical and experimental results. J. Guid. Control Dyn. 1993, 16, 1146–1153. [Google Scholar] [CrossRef]
- Maamri, N.; Trigeassou, J.C. A Plea for the Integration of Fractional Differential Systems: The Initial Value Problem. Fractal Fract. 2022, 6, 550. [Google Scholar] [CrossRef]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-band complex noninteger differentiator: Characterization and synthesis. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 25–39. [Google Scholar] [CrossRef]
- Tepljakov, A. Fractional-Order Modeling and Control of Dynamic Systems; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Gude, J.J.; García Bringas, P. A Novel Control Hardware Architecture for Implementation of Fractional-Order Identification and Control Algorithms Applied to a Temperature Prototype. Mathematics 2022, 11, 143. [Google Scholar] [CrossRef]
- Tepljakov, A.; Petlenkov, E.; Belikov, J. Embedded system implementation of digital fractional filter approximations for control applications. In Proceedings of the 2014 21st International Conference Mixed Design of Integrated Circuits and Systems (MIXDES), Lublin, Poland, 19–21 June 2014; pp. 441–445. [Google Scholar] [CrossRef]
- Matusiak, M.; Bakala, M.; Wojciechowski, R. Optimal Digital Implementation of Fractional-Order Models in a Microcontroller. Entropy 2020, 22, 366. [Google Scholar] [CrossRef] [PubMed]
- Tepljakov, A.; Alagoz, B.B.; Yeroglu, C.; Gonzalez, E.; HosseinNia, S.H.; Petlenkov, E. FOPID Controllers and Their Industrial Applications: A Survey of Recent Results. IFAC-PapersOnLine 2018, 51, 25–30. [Google Scholar] [CrossRef]
- Coopmans, C.; Podhradsky, M.; Hoffer, N.V. An open-source real-time UAS flight control prototyping and testing platform with fractional-order horizontal controller example. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 949–956. [Google Scholar] [CrossRef]
- Oustaloup, A.; Mathieu, B.; Lanusse, P. The CRONE Control of Resonant Plants: Application to a Flexible Transmission. Eur. J. Control 1995, 1, 113–121. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and PIλDμ controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Chevalier, A.; Francis, C.; Copot, C.; Ionescu, C.M.; De Keyser, R. Fractional-order PID design: Towards transition from state-of-art to state-of-use. ISA Trans. 2019, 84, 178–186. [Google Scholar] [CrossRef] [PubMed]
- Shah, P.; Agashe, S. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
- Dastjerdi, A.A.; Saikumar, N.; HosseinNia, S.H. Tuning guidelines for fractional order PID controllers: Rules of thumb. Mechatronics 2018, 56, 26–36. [Google Scholar] [CrossRef]
- Mellinger, D.; Michael, N.; Kumar, V. Trajectory generation and control for precise aggressive maneuvers with quadrotors. Int. J. Robot. Res. 2012, 31, 664–674. [Google Scholar] [CrossRef]
- The MathWorks, Inc. UAV Toolbox; The MathWorks, Inc.: Natick, MA, USA, 2023. [Google Scholar]
- Feedback Instruments Ltd. Twin Rotor MIMO System Control Experiments; Report 33-949S; Feedback Instruments Ltd.: Crowborough, UK, 2006. [Google Scholar]
- Moness, M.; Diaa-Eldeen, T. Experimental nonlinear identification of a lab-scale helicopter system using MLP neural network. In Proceedings of the 2017 13th International Computer Engineering Conference (ICENCO), Cairo, Egypt, 27–28 December 2017; pp. 166–171. [Google Scholar] [CrossRef]
- Moness, M.; Diaa-Eldeen, T. Experimental black-box dynamic modelling of a Flexible Manoeuvring System. In Proceedings of the 2017 12th International Conference on Computer Engineering and Systems (ICCES), Cairo, Egypt, 19–20 December 2017; pp. 259–265. [Google Scholar] [CrossRef]
- Hamamci, S.E. Stabilization using fractional-order PI and PID controllers. Nonlinear Dyn. 2008, 51, 329–343. [Google Scholar] [CrossRef]
- Powell, M.J.D. The theory of radial basis function approximation in 1990. Adv. Numer. Anal. 1992, 2, 105–210. [Google Scholar]
- Gutmann, H.M. A Radial Basis Function Method for Global Optimization. J. Glob. Optim. 2001, 19, 201–227. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| (s−2) | 3402.97 |
| (s−1) | 116.67 |
| (s−2) | 3402.97 |
| (s−1) | 116.67 |
| (s−1) | 1950 |
| (s−1) | 3900 |
| m (kg) | 0.1 |
| Axis | Controller | Objective Function | Computation Time (min) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min. Value | Mean | Median | Standard Deviation | Average Simulations Count | Mean | Median | Standard Deviation | ||
| x | PID-GA | 664.2483 | 665.0124 | 664.3411 | 1.1576 | 2450 | 14.0791 | 14.0254 | 1.4368 |
| FOPID-GA | 672.5661 | 679.6325 | 678.4195 | 6.8963 | 2517 | 26.3810 | 26.3464 | 3.1829 | |
| FOPID-Surrogate | 672.0003 | 683.4908 | 680.4865 | 8.3657 | 1000 | 11.1183 | 10.9377 | 0.5672 | |
| y | PID-GA | 664.2483 | 665.0124 | 664.3411 | 1.1576 | 2450 | 7.0880 | 7.0214 | 0.9581 |
| FOPID-GA | 673.3710 | 680.4129 | 676.7823 | 8.0841 | 2497 | 21.9964 | 20.4116 | 4.2519 | |
| FOPID-Surrogate | 677.0695 | 682.9058 | 681.5786 | 5.5742 | 1000 | 10.4262 | 10.0240 | 0.7907 | |
| z | PID-GA | 274.7040 | 274.7089 | 274.7041 | 0.0125 | 2450 | 9.5922 | 9.3179 | 1.4732 |
| FOPID-GA | 286.9981 | 289.5838 | 288.8558 | 3.1095 | 2450 | 25.4097 | 23.9121 | 5.1696 | |
| FOPID-Surrogate | 287.9273 | 289.4379 | 289.1571 | 1.2448 | 1000 | 19.3086 | 19.3221 | 1.0178 | |
| Axis | Controller | |||||
|---|---|---|---|---|---|---|
| x | PID-GA | 0.4598 | 0 | 1 | 0.3061 | 1 |
| FOPID-GA | 0.0696 | 0.0089 | 0.9053 | 0.2196 | 0.7202 | |
| FOPID-Surrogate | 0 | 0.0205 | 0.6440 | 0.2480 | 0.6292 | |
| y | PID-GA | 0.4598 | 0 | 1 | 0.3061 | 1 |
| FOPID-GA | 0.0574 | 0.0244 | 0.5658 | 0.2389 | 0.7197 | |
| FOPID-Surrogate | 0.0376 | 0.0544 | 0.4275 | 0.2375 | 0.7272 | |
| z | PID-GA | 8.6983 | 5.8476 | 1 | 1.3159 | 1 |
| FOPID-GA | 0.7844 | 7.6204 | 0.8063 | 2.1821 | 0.6411 | |
| FOPID-Surrogate | 0.6607 | 7.9986 | 0.7507 | 2.2529 | 0.6387 |
| Axis | Controller | Rise Time (s) | Overshoot | Settling Time (s) | Settling Error |
|---|---|---|---|---|---|
| x | PID-GA | 0.9164 | 4.5587 | 2.6726 | 1.5332 |
| FOPID-GA | 0.7591 | 13.7547 | 2.9700 | 0.0177 | |
| FOPID-Surrogate | 0.6958 | 17.7479 | 3.0561 | 0.0161 | |
| y | PID-GA | 0.9164 | 4.5587 | 2.6726 | 1.5332 |
| FOPID-GA | 0.7444 | 13.0912 | 2.9666 | 0.0131 | |
| FOPID-Surrogate | 0.7329 | 16.4277 | 3.4230 | 0.0101 | |
| z | PID-GA | 0.2402 | 4.3196 | 0.6700 | 3.1186 |
| FOPID-GA | 0.2283 | 4.3987 | 0.6157 | 0.0042 | |
| FOPID-Surrogate | 0.2163 | 6.4502 | 0.6352 | 0.0059 |
| Controller | Objective Function | Computation Time (min) | |||
|---|---|---|---|---|---|
| Minimum Value | Mean | Standard Deviation | Mean | Standard Deviation | |
| 184.8821 | 207.2058 | 26.6892 | 9.8651 | 0.2540 | |
| 4.9927 | 5.4286 | 0.3315 | 14.2360 | 0.6657 | |
| 0.6314 | 0.7114 | 0.0508 | 15.1317 | 0.3795 | |
| 21.2900 | 23.3846 | 1.5300 | 10.2655 | 1.1018 | |
| Controller | |||||
|---|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moness, M.; Abdelghany, M.B.; Mohammed, K.M.; Mohamed, M.; Moustafa, A.M. Surrogate Optimal Fractional Control for Constrained Operational Service of UAV Systems. Drones 2024, 8, 141. https://doi.org/10.3390/drones8040141
Moness M, Abdelghany MB, Mohammed KM, Mohamed M, Moustafa AM. Surrogate Optimal Fractional Control for Constrained Operational Service of UAV Systems. Drones. 2024; 8(4):141. https://doi.org/10.3390/drones8040141
Chicago/Turabian StyleMoness, Mohammed, Muhammad Bakr Abdelghany, Khloud Mostafa Mohammed, Moataz Mohamed, and Ahmed M. Moustafa. 2024. "Surrogate Optimal Fractional Control for Constrained Operational Service of UAV Systems" Drones 8, no. 4: 141. https://doi.org/10.3390/drones8040141
APA StyleMoness, M., Abdelghany, M. B., Mohammed, K. M., Mohamed, M., & Moustafa, A. M. (2024). Surrogate Optimal Fractional Control for Constrained Operational Service of UAV Systems. Drones, 8(4), 141. https://doi.org/10.3390/drones8040141







