Comparing Machine Learning Algorithms for Estimating the Maize Crop Water Stress Index (CWSI) Using UAV-Acquired Remotely Sensed Data in Smallholder Croplands
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Maize Canopy Temperature Measurement
2.3. Meteorological Data Collection
2.4. Crop Water Stress Index (CWSI) Calculation
2.5. UAV Multispectral–Thermal System
2.6. Image Acquisition and Processing
2.7. Vegetation Index Selection
2.8. Statistical Analysis
2.9. Accuracy Assessment
3. Results
3.1. Determining Baselines for the Crop Water Stress Index
3.2. Exploring the Relationship between the CWSI and Spectral Variables
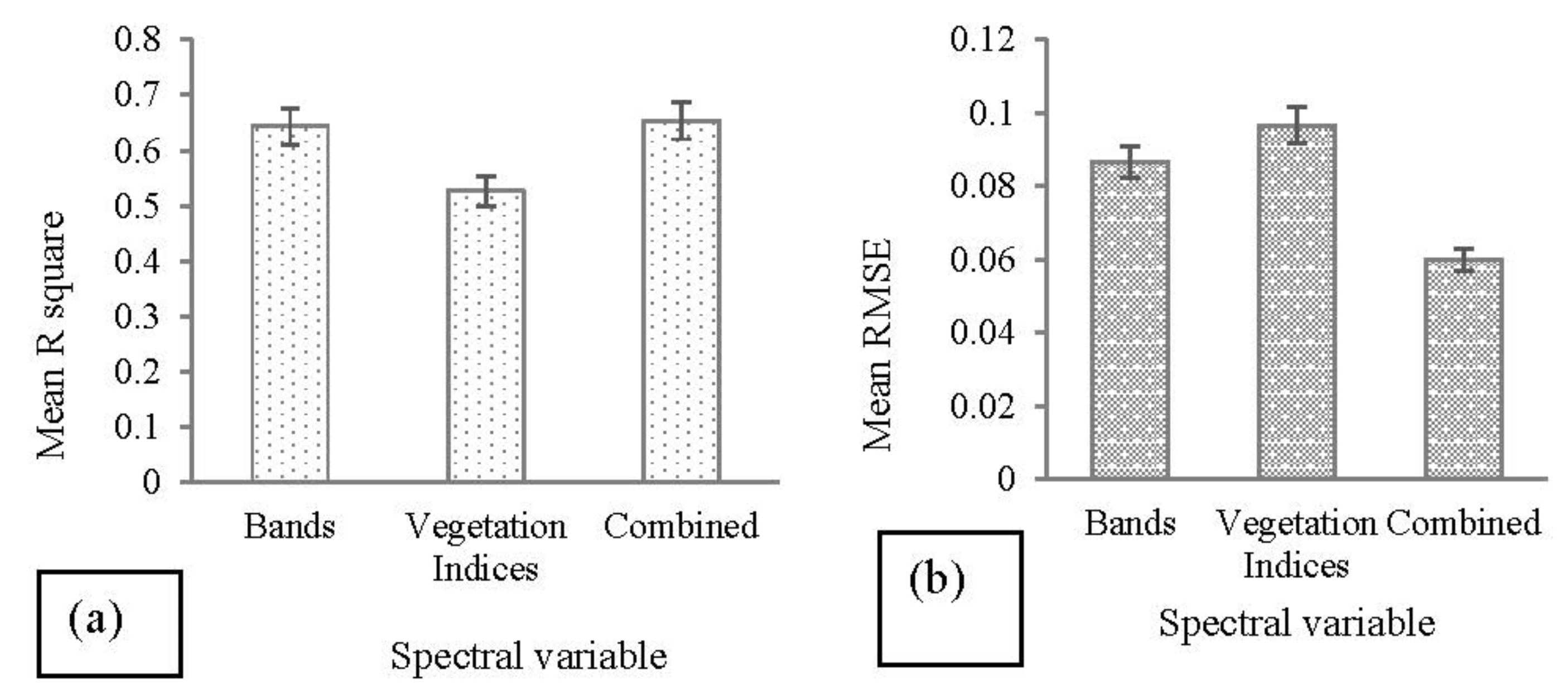
3.3. Comparing the Performance of Spectral Features in Estimating the Maize Crop Water Stress Index across All Algorithms
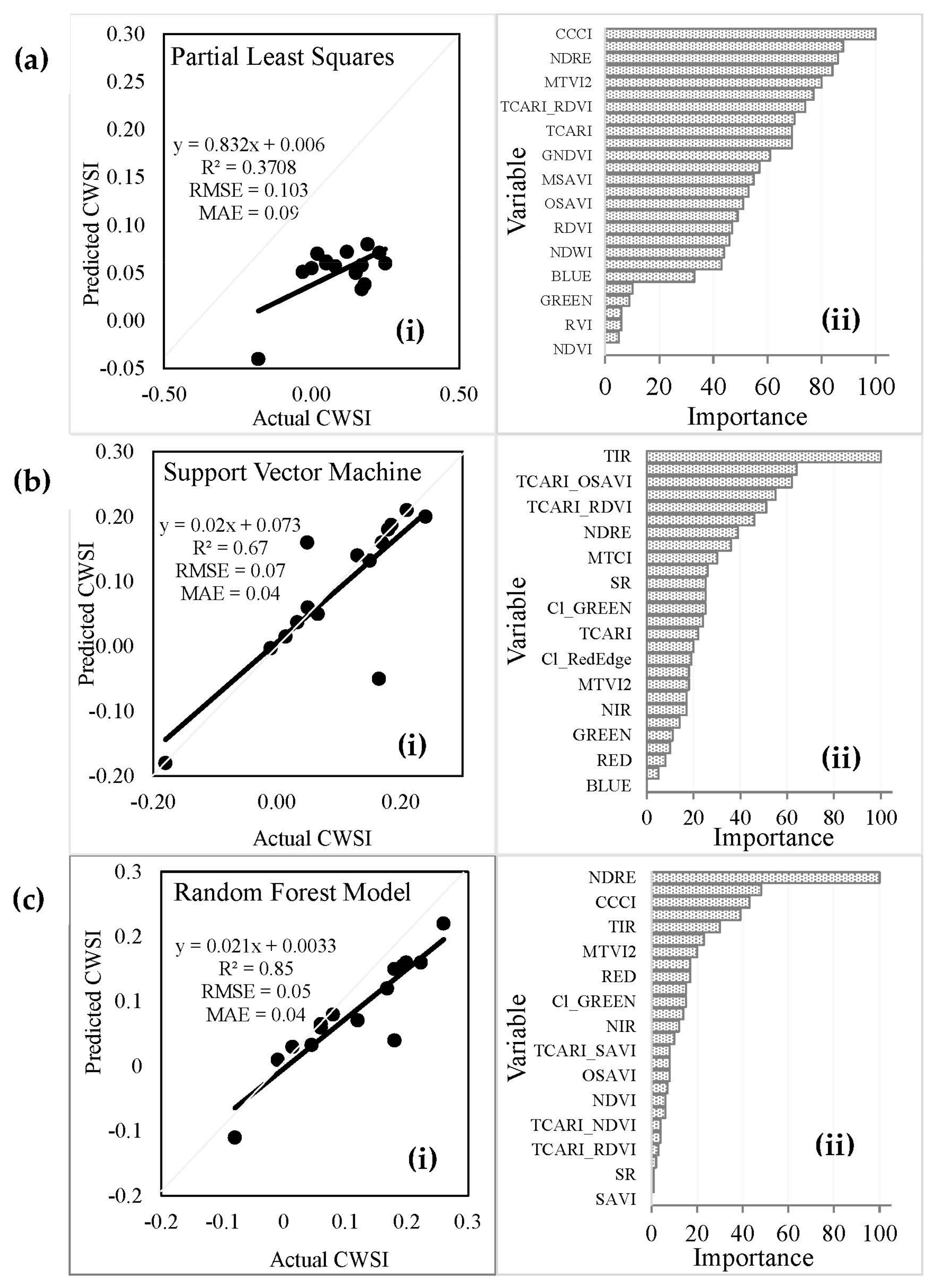
3.4. Comparing the Performance of Machine Learning Algorithms in Estimating Maize Crop Water Stress
3.5. Optimal Models for Estimating the Maize Crop Water Stress Index
3.6. Mapping the Spatial Distribution of Maize Crop Water Stress
4. Discussion
4.1. Estimating the Crop Water Stress Index
4.2. Mapping of the Maize CWSI Using the Optimal Model
4.3. Comparative Performance of Bands, Vegetation Indices, and Combined Datasets
4.4. The Performance of Machine Learning Algorithms in Predicting the Maize Crop Water Stress Index (CWSI)
5. Conclusions
- RF proved to be the most suitable algorithm for predicting the maize CWSI in smallholder croplands, utilising NDRE, MTCI, CCCI, GNDVI, and TIR, as important predictor variables, listed in order of importance. Specifically, RF was optimal compared to PLS and SVM, resulting in the highest R2 (0.79) and the lowest MAE (0.06) and RMSE (0.05) on average in three different data groups (bands only, VI only, and combined data).
- Combining bands and vegetation indices resulted in the best prediction of the maize CWSI compared to using these variables separately. Specifically, the two models, SVM and RF, improved when the analysis was performed with the combined data compared to when performed with bands only or indices only, resulting in the lowest RMSE of 0.07 and 0.05 for SVM and RF, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Simanjuntak, C.; Gaiser, T.; Ahrends, H.E.; Ceglar, A.; Singh, M.; Ewert, F.; Srivastava, A. Impact of climate extreme events and their causality on maize yield in South Africa. Sci. Rep. 2023, 13, 12462. [Google Scholar] [CrossRef] [PubMed]
- Grote, U.; Fasse, A.; Nguyen, T.; Erenstein, O. Food security and the dy-namics of wheat and maize value chains in Africa and Asia. Front. Sustain. Food Syst. 2021, 4, 617009. [Google Scholar] [CrossRef]
- Gerhards, M.; Schlerf, M.; Rascher, U.; Udelhoven, T.; Juszczak, R.; Alberti, G.; Miglietta, F.; Inoue, Y. Analysis of airborne optical and thermal imagery for detection of water stress symptoms. Remote Sens. 2018, 10, 1139. [Google Scholar] [CrossRef]
- Bradshaw, C.D.; Pope, E.; Kay, G.; Davie, J.C.; Cottrell, A.; Bacon, J.; Cosse, A.; Dunstone, N.; Jennings, S.; Challinor, A.; et al. Unprecedented climate extremes in South Africa and implications for maize production. Environ. Res. Lett. 2022, 17, 084028. [Google Scholar] [CrossRef]
- Ferreira, N.C.R.; Rötter, R.P.; Bracho-Mujica, G.; Nelson, W.C.D.; Lam, Q.D.; Recktenwald, C.; Abdulai, I.; Odhiambo, J.; Foord, S. Drought patterns: Their spatiotemporal variability and impacts on maize production in Limpopo province, South Africa. Int. J. Biometeorol. 2023, 67, 133–148. [Google Scholar] [CrossRef]
- Pradawet, C.; Khongdee, N.; Pansak, W.; Spreer, W.; Hilger, T.; Cadisch, G. Thermal imaging for assessment of maize water stress and yield prediction under drought conditions. J. Agron. Crop Sci. 2023, 209, 56–70. [Google Scholar] [CrossRef]
- Ahmad, U.; Alvino, A.; Marino, S. A review of crop water stress assessment using remote sensing. Remote Sens. 2021, 13, 4155. [Google Scholar] [CrossRef]
- Berni, J.A.J.; Zarco-Tejada, P.J.; Sepulcre-Cantó, G.; Fereres, E.; Villalobos, F. Mapping canopy conductance and CWSI in olive orchards using high resolution thermal remote sensing imagery. Remote Sens. Environ. 2009, 113, 2380–2388. [Google Scholar] [CrossRef]
- Buckley, T.N. How do stomata respond to water status? New Phytol. 2019, 224, 21–36. [Google Scholar] [CrossRef] [PubMed]
- Kögler, F.; Söffker, D. Explorative frequency analysis of leaf temperature behavior of maize (Zea mays subsp. mays) at water deficit. Plants 2019, 8, 105. [Google Scholar] [CrossRef] [PubMed]
- Ramírez-Cuesta, J.M.; Ortuño, M.F.; Gonzalez-Dugo, V.; Zarco-Tejada, P.J.; Parra, M.; Rubio-Asensio, J.S.; Intrigliolo, D.S. Assessment of peach trees water status and leaf gas exchange using on-the-ground versus airborne-based thermal imagery. Agric. Water Manag. 2022, 267, 107628. [Google Scholar] [CrossRef]
- Idso, S.B.; Jackson, R.D.; Pinter, P.J.; Reginato, R.J.; Hatfield, J.L. Normalizing the stress-degree-day parameter for environmental variability. Agric. Meteorol. 1981, 24, 45–55. [Google Scholar] [CrossRef]
- Jackson, R.D.; Idso, S.B.; Reginato, R.J.; Pinter, P.J. Canopy temperature as a crop water stress indicator. Water Resour. Res. 1981, 17, 1133–1138. [Google Scholar] [CrossRef]
- Poblete-Echeverría, C.; Espinace, D.; Sepúlveda-Reyes, D.; Zuniga, M.; Sanchez, M. Analysis of crop water stress index (CWSI) for estimating stem water potential in grapevines: Comparison between natural reference and baseline approaches. Acta Hortic. 2018. [Google Scholar] [CrossRef]
- Ru, C.; Hu, X.; Wang, W.; Ran, H.; Song, T.; Guo, Y. Evaluation of the Crop Water Stress Index as an Indicator for the Diagnosis of Grapevine Water Deficiency in Greenhouses. Horticulturae 2020, 6, 86. [Google Scholar] [CrossRef]
- Egea, G.; Padilla-Díaz, C.M.; Martinez-Guanter, J.; Fernández, J.E.; Pérez-Ruiz, M. Assessing a crop water stress index derived from aerial thermal imaging and infrared thermometry in super-high density olive orchards. Agric. Water Manag. 2017, 187, 210–221. [Google Scholar] [CrossRef]
- Park, S.; Ryu, D.; Fuentes, S.; Chung, H.; O’connell, M.; Kim, J. Dependence of cwsi-based plant water stress estimation with diurnal acquisition times in a nectarine orchard. Remote Sens. 2021, 13, 2775. [Google Scholar] [CrossRef]
- Gonzalez-Dugo, V.; Zarco-Tejada, P.J.; Intrigliolo, D.S.; Ramírez-Cuesta, J.M. Normalization of the crop water stress index to assess the within-field spatial variability of water stress sensitivity. Precis. Agric. 2021, 22, 964–983. [Google Scholar] [CrossRef]
- Rud, R.; Cohen, Y.; Alchanatis, V.; Levi, A.; Brikman, R.; Shenderey, C.; Heuer, B.; Markovitch, T.; Dar, Z.; Rosen, C.; et al. Crop water stress index derived from multi-year ground and aerial thermal images as an indicator of potato water status. Precis. Agric. 2014, 15, 273–289. [Google Scholar] [CrossRef]
- Ekinzog, E.K.; Schlerf, M.; Kraft, M.; Werner, F.; Riedel, A.; Rock, G.; Mallick, K. Revisiting crop water stress index based on potato field experiments in Northern Germany. Agric. Water Manag. 2022, 269, 107664. [Google Scholar] [CrossRef]
- Nouraki, A.; Akhavan, S.; Rezaei, Y.; Fuentes, S. Assessment of sunflower water stress using infrared thermometry and computer vision analysis. Water Sci. Technol. Water Supply 2021, 21, 1228–1242. [Google Scholar] [CrossRef]
- Orta, A.H.; Erdem, T.; Erdem, Y. Determination of water stress index in sunflower. Helia 2002, 25, 27–38. [Google Scholar] [CrossRef][Green Version]
- Mwinuka, P.R.; Mbilinyi, B.P.; Mbungu, W.B.; Mourice, S.K.; Mahoo, H.F.; Schmitter, P. The feasibility of hand-held thermal and UAV-based multispectral imaging for canopy water status assessment and yield prediction of irrigated African eggplant (Solanum aethopicum L). Agric. Water Manag. 2021, 245, 106584. [Google Scholar] [CrossRef]
- Qin, A.; Ning, D.; Liu, Z.; Li, S.; Zhao, B.; Duan, A. Determining threshold values for a crop water stress index-based center pivot irrigation with optimum grain yield. Agriculture 2021, 11, 958. [Google Scholar] [CrossRef]
- Zhang, T.X.; Su, J.Y.; Liu, C.J.; Chen, W.H. Potential Bands of Sentinel-2A Satellite for Classification Problems in Precision Agriculture. Int. J. Autom. Comput. 2019, 16, 16–26. [Google Scholar] [CrossRef]
- Gu, S.J.; Liao, Q.; Gao, S.Y.; Kang, S.Z.; Du, T.S.; Ding, R.S. Crop Water Stress Index as a Proxy of Phenotyping Maize Performance under Combined Water and Salt Stress. Remote Sens. 2021, 13, 4710. [Google Scholar] [CrossRef]
- Carroll, D.A.; Hansen, N.C.; Hopkins, B.G.; DeJonge, K.C. Leaf temperature of maize and Crop Water Stress Index with variable irrigation and nitrogen supply. Irrig. Sci. 2017, 35, 549–560. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Zhu, Q.; Niu, Y. Further investigating the performance of crop water stress index for maize from baseline fluctuation, effects of environmental factors, and variation of critical value. Agric. Water Manag. 2023, 285, 108349. [Google Scholar] [CrossRef]
- Pipatsitee, P.; Tisarum, R.; Taota, K.; Samphumphuang, T.; Eiumnoh, A.; Singh, H.P.; Cha-um, S. Effectiveness of vegetation indices and UAV-multispectral imageries in assessing the response of hybrid maize (Zea mays L.) to water deficit stress under field environment. Environ. Monit. Assess. 2023, 195, 128. [Google Scholar] [CrossRef] [PubMed]
- Tandzi, L.N.; Mutengwa, C.S. Estimation of Maize (Zea mays L.) Yield Per Harvest Area: Appropriate methods. Agronomy 2020, 10, 29. [Google Scholar] [CrossRef]
- Zhang, F.; Zhou, G. Estimation of vegetation water content using hyperspectral vegetation indices: A comparison of crop water indicators in response to water stress treatments for summer maize. BMC Ecol. 2019, 19, 18. [Google Scholar] [CrossRef]
- Jin, N.; He, J.Q.; Fang, Q.X.; Chen, C.; Ren, Q.F.; He, L.; Yao, N.; Song, L.B.; Yu, Q. The Responses of Maize Yield and Water Use to Growth Stage-Based Irrigation on the Loess Plateau in China. Int. J. Plant Prod. 2020, 14, 621–633. [Google Scholar] [CrossRef]
- Mulla, D.J. Twenty five years of remote sensing in precision agriculture: Key advances and remaining knowledge gaps. Biosyst. Eng. 2013, 4, 358–371. [Google Scholar] [CrossRef]
- Bian, J.; Zhang, Z.; Chen, J.; Chen, H.; Cui, C.; Li, X.; Chen, S.; Fu, Q. Simplified evaluation of cotton water stress using high resolution unmanned aerial vehicle thermal imagery. Remote Sens. 2019, 11, 267. [Google Scholar] [CrossRef]
- Zhang, L.; Niu, Y.; Zhang, H.; Han, W.; Li, G.; Tang, J.; Peng, X. Maize Canopy Temperature Extracted From UAV Thermal and RGB Imagery and Its Application in Water Stress Monitoring. Front. Plant Sci. 2019, 10, 1270. [Google Scholar] [CrossRef]
- Aldubai, A.A.; Alsadon, A.A.; Al-Gaadi, K.A.; Tola, E.K.; Ibrahim, A.A. Utilizing spectral vegetation indices for yield assessment of tomato genotypes grown in arid conditions. Saudi J. Biol. Sci. 2022, 29, 2506–2513. [Google Scholar] [CrossRef]
- Lee, H.; Wang, J.; Leblon, B. Using linear regression, random forests, and support vector machine with unmanned aerial vehicle multispectral images to predict canopy nitrogen weight in corn. Remote Sens. 2020, 12, 2071. [Google Scholar] [CrossRef]
- Giovos, R.; Tassopoulos, D.; Kalivas, D.; Lougkos, N.; Priovolou, A. Remote sensing vegetation indices in viticulture: A critical review. Agriculture 2021, 11, 457. [Google Scholar] [CrossRef]
- Baluja, J.; Diago, M.P.; Balda, P.; Zorer, R.; Meggio, F.; Morales, F.; Tardaguila, J. Assessment of vineyard water status variability by thermal and multispectral imagery using an unmanned aerial vehicle (UAV). Irrig. Sci. 2012, 30, 511–522. [Google Scholar] [CrossRef]
- Gago, J.; Douthe, C.; Coopman, R.E.; Gallego, P.P.; Ribas-Carbo, M.; Flexas, J.; Escalona, J.; Medrano, H. Uavs challenge to assess water stress for sustainable agriculture. Agric. Water Manag. 2015, 153, 9–19. [Google Scholar] [CrossRef]
- Espinoza, C.Z.; Khot, L.R.; Sankaran, S.; Jacoby, P.W. High Resolution Multispectral and Thermal Remote Sensing-Based Water Stress Assessment in Subsurface Irrigated Grapevines. Remote Sens. 2017, 9, 961. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Gonzalez-Dugo, V.; Williams, L.E.; Suarez, L.; Berni, J.A.J.; Goldhamer, D.; Fereres, E. A PRI-based water stress index combining structural and chlorophyll effects: Assessment using diurnal narrow-band airborne imagery and the CWSI thermal index. Remote Sens. Environ. 2013, 138, 38–50. [Google Scholar] [CrossRef]
- Raczko, E.; Zagajewski, B. Comparison of support vector machine, random forest and neural network classifiers for tree species classification on airborne hyperspectral APEX images. Eur. J. Remote Sens. 2017, 50, 144–154. [Google Scholar] [CrossRef]
- Cai, J.; Lou, J.; Wang, S.; Yang, S. Feature selection in machine learning: A new perspective. Neurocomputing 2018, 300, 70–79. [Google Scholar] [CrossRef]
- Mochida, K.; Koda, S.; Inoue, K.; Hirayama, T.; Tanaka, S.; Nishii, R.; Melgani, F. Computer vision-based phenotyping for improvement of plant productivity: A machine learning perspective. Gigascience 2019, 8, giy153. [Google Scholar] [CrossRef] [PubMed]
- Singhal, G.; Bansod, B.; Mathew, L.; Goswami, J.; Choudhury, B.U.; Raju, P.L.N. Chlorophyll estimation using multi-spectral unmanned aerial system based on machine learning techniques. Remote Sens. Appl. Soc. Environ. 2019, 15, 100235. [Google Scholar] [CrossRef]
- Alabi, T.R.; Abebe, A.T.; Chigeza, G.; Fowobaje, K.R. Estimation of soybean grain yield from multispectral high-resolution UAV data with machine learning models in West Africa. Remote Sens. Appl. Soc. Environ. 2022, 27, 100782. [Google Scholar] [CrossRef]
- Ndlovu, H.S.; Odindi, J.; Sibanda, M.; Mutanga, O.; Clulow, A.; Chimonyo, V.G.P.; Mabhaudhi, T. A comparative estimation of maize leaf water content using machine learning techniques and unmanned aerial vehicle (Uav)-based proximal and remotely sensed data. Remote Sens. 2021, 13, 4091. [Google Scholar] [CrossRef]
- Ma, D.; Rehman, T.U.; Zhang, L.; Maki, H.; Tuinstra, M.R.; Jin, J. Modeling of diurnal changing patterns in airborne crop remote sensing images. Remote Sens. 2021, 13, 1719. [Google Scholar] [CrossRef]
- Guo, Y.; Yin, G.; Sun, H.; Wang, H.; Chen, S.; Senthilnath, J.; Wang, J.; Fu, Y. Scaling effects on chlorophyll content estimations with RGB camera mounted on a UAV platform using machine-learning methods. Sensors 2020, 20, 5130. [Google Scholar] [CrossRef]
- Yang, M.; Gao, P.; Chen, W.; Zhou, P.; Sun, D.; Xie, J.; Lu, J.; Wang, W. Research of Brassica chinensis var. parachinensis under water stress based on machine learning. J. South China Agric. Univ. 2021, 42, 117–126. [Google Scholar] [CrossRef]
- Adam, E.M.I.; Ismail, R.; Mutanga, O. A comparison of selected machine learning classifiers in mapping a South African heterogeneous coastal zone: Testing the utility of an object-based classification with WorldView-2 imagery. Int. J. Remote Sens. 2012, 8538, 177–186. [Google Scholar]
- Masenyama, A.; Mutanga, O.; Dube, T.; Sibanda, M.; Odebiri, O.; Mabhaudhi, T. Inter-Seasonal Estimation of Grass Water Content Indicators Using Multisource Remotely Sensed Data Metrics and the Cloud-Computing Google Earth Engine Platform. Appl. Sci. 2023, 13, 3117. [Google Scholar] [CrossRef]
- Brewer, K.; Clulow, A.D.; Sibanda, M.; Gokool, S.; Naiken, V.; Mabhaudhi, T.T. Predicting the chlorophyll content of maize over phrnotyping as aproxy for crop health in smallholder farming systems. Remote Sens. 2022, 3, 518. [Google Scholar] [CrossRef]
- Costa, C.; Dwyer, L.; Dutilleul, P.; Stewart, D.; Ma, B.; Smith, D. Sample size determination for chlorophyll meter readings on maize hybrids with a broad range of canopy types. J. Plant Nutr. 2003, 8, 1173–1194. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO Irrigation and Drainage Paper No. 56—Crop Evapotranspiration; Food and Agriculture Organisation of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Taghvaeian, S.; Chávez, J.L.; Hansen, N.C. Infrared thermometry to estimate crop water stress index and water use of irrigated maize in northeastern colorado. Remote Sens. 2012, 4, 3619–3637. [Google Scholar] [CrossRef]
- Yue, J.; Feng, H.; Yang, G.; Li, Z. A comparison of regression techniques for estimation of above-ground winter wheat biomass using near-surface spectroscopy. Remote Sens. 2018, 10, 66. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 1, 309. [Google Scholar]
- Gileston, A.; Kaufman, Y.; Merzlyak, M. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Envron. 1996, 3, 289–298. [Google Scholar]
- Fitzgerald, G.; Rodriguez, D.; O’leary, G. Measuring and predicting canopy nitrogen nutrition in wheat using a spectral index—The canopy chlorophyll content index (CCCI). Field crops Res. 2010, 3, 318–324. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant remote sensing vegetation indices: A review of developments and applications. J. Sens. 2017, 1, 1–17. [Google Scholar] [CrossRef]
- Zhang, F.; Zhou, G. Estimation of canopy water content by means of hyperspectral indices based on drought stress gradient experiments of maize in the north plain China. Remote Sens. 2015, 7, 15203–15223. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M. Quantitative estimation of chlorophyll-a using reflectance spectra: Experiments with autumn chestnut and maple leaves. J. Photochem. Photobiol. B Biol. 1994, 3, 247–252. [Google Scholar] [CrossRef]
- Bannari, A.; Morin, D.; Bonn, F.; Huete, A.R. A review of vegetation indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Liu, J.; Pattey, E.; Miller, J.R.; McNairn, H.; Smith, A.; Hu, B. Estimating crop stresses, aboveground dry biomass and yield of corn using multi-temporal optical data combined with a radiation use efficiency model. Remote Sens. Environ. 2010, 114, 1167–1177. [Google Scholar] [CrossRef]
- Varco, J.J.; Fox, A.A.; Raper, T.B.; Hubbard, K.J. Development of sensor based detection of crop nitrogen status for utilization in variable rate nitrogen fertilization. In Precision Agriculture’13; Wageningen Academic Publishers: Wageningen, The Netherlands, 2013. [Google Scholar]
- Dash, J.; Curran, P.J. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Özelkan, E. Water body detection analysis using NDWI indices derived from landsat-8 OLI. Polish J. Environ. Stud. 2020, 29, 1759–1769. [Google Scholar] [CrossRef] [PubMed]
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 3, 337–352. [Google Scholar] [CrossRef]
- Haaland, D.M.; Thomas, E. Partial least-squares methods for spectral analyses. 1. Relation to other quantitative calibration methods and the extraction of qualitative information. Anal. Chem. 1988, 60, 1193–1202. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalshi, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Martens, H.; Naes, T. Multivariate Calibration; John Wiley & Sons: Hoboken, NJ, USA, 1992. [Google Scholar]
- Wold, S.; Sjostrom, M.; Eriksson, L. Pls_regression: A basic tool of chemomrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Krishna, G.; Sahoo, R.N.; Singh, P.; Bajpai, V.; Patra, H.; Kumar, S.; Dandapani, R.; Gupta, V.K.; Viswanathan, C.; Ahmad, T.; et al. Comparison of various modelling approaches for water deficit stress monitoring in rice crop through hyperspectral remote sensing. Agric. Water Manag. 2019, 213, 231–244. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013; ISBN 9781461468493. [Google Scholar]
- Mashiane, K.; Adelabu, S.; Ramoelo, A. Comperative Analysis of Single Bands, Vegetation Indices, and Their Combination in Predicting Grass Species Nitrogen in a Protected Mountainous Area. Appl. Sci. 2023, 13, 7960. [Google Scholar] [CrossRef]
- Eugenio, F.C.; Grohs, M.; Venancio, L.P.; Schuh, M.; Bottega, E.L.; Ruoso, R.; Schons, C.; Mallmann, C.L.; Badin, T.L.; Fernandes, P. Estimation of soybean yield from machine learning techniques and multispectral RPAS imagery. Remote Sens. Appl. Soc. Environ. 2020, 20, 100397. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Ly, H.B.; Ho, L.S.; Al-Ansari, N.; Van Le, H.; Tran, V.Q.; Prakash, I.; Pham, B.T. Influence of data splitting on performance of machine learning models in prediction of shear strength of soil. Math. Probl. Eng. 2021, 2021, 4832864. [Google Scholar] [CrossRef]
- Jamshidi, S.; Zand-Parsa, S.; Kamgar-Haghighi, A.A.; Shahsavar, A.R.; Niyogi, D. Evapotranspiration, Crop Coefficients, and Physiological Responses of Citrus Trees in Semi-arid Climatic Conditions. Agric. Water Manag. 2020, 227, 105838. [Google Scholar] [CrossRef]
- Kacira, M.; Ling, P.P.; Short, T.H. Establishing Crop Water Stress Index (CWSI) Threshold Values for Early, Non–contact Detection of Plant Water Stress. Trans. ASAE 2002, 3, 775. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiaowei, D.; Chen, Z.; Hou, G. A study on the physiological parameters of corn during the jointing stage of growth under soil water stress based on the PSII light quantum yield (QY). HydroResearch 2023, 6, 177–183. [Google Scholar] [CrossRef]
- Zhang, L.; Yan, M.; Ren, Y.; Chen, Y.; Zhang, S. Zinc regulates the hydraulic response of maize root under water stress conditions. Plant Physiol. Biochem. 2021, 159, 123–134. [Google Scholar] [CrossRef]
- Cai, F.; Zhang, Y.; Mi, N.; Ming, H.; Zhang, S.; Zhang, H.; Zhao, X. Maize (Zea mays L.) physiological responses to drought and rewatering, and the associations with water stress degree. Agric. Water Manag. 2020, 241, 106379. [Google Scholar] [CrossRef]
- Ustin, S.; Jacqueemoud, S. How the optical properties of leaves modify the absorption and scattering of energy and enhance leaf functionality. Remote Sens. Plant Biodivers. 2020, 349–384. [Google Scholar]
- Zhu, W.; Sun, Z.; Yang, T.; Li, J.; Peng, J.; Zhu, K.; Li, S.; Gong, H.; Lyu, Y.; Li, B.; et al. Estimating leaf chlorophyll content of crops via optimal unmanned aerial vehicle hyperspectral data at multi-scales. Comput. Electron. Agric. 2020, 178, 105786. [Google Scholar] [CrossRef]
- Nandibewoor, A.; Hebbal, S.M.B.; Hegadi, R. Remote monitoring of Maize crop through satellite multispectral imagery. In Proceedings of the Procedia Computer Science; Elsevier Masson SAS: Amsterdam, The Netherlands, 2015; Volume 45, pp. 344–353. [Google Scholar]
- Naidoo, L.; Main, R.; Cho, M.A.; Madonsela, S.; Majozi, N. Machine learning modelling of crop structure within the Maize Triangle of South Africa. Int. J. Remote Sens. 2022, 43, 27–51. [Google Scholar] [CrossRef]
- Sun, Y.; Qin, Q.; Ren, H.; Zhang, T.; Chen, S. Red-edge Band Vegetation Indices for Leaf Area Index Estimation from Sentinel-2/MSI Imagery. IEEE Trans. Geosci. Remote Sens. 2020, 2, 826–840. [Google Scholar] [CrossRef]
- Xie, X.; Wu, T.; Zhu, M.; Jiang, G.; Xu, Y.; Wang, X.; Pu, L. Comparison of random forest and multiple linear regression models for estimation of soil extracellular enzyme activities in agricultural reclaimed coastal saline land. Ecol. Indic. 2021, 120, 106925. [Google Scholar] [CrossRef]
- Wang, S.; Guan, K.; Wang, Z.; Ainsworth, E.A.; Zheng, T.; Townsend, P.A.; Liu, N.; Nafziger, E.; Masters, M.D.; Li, K.; et al. Airborne hyperspectral imaging of nitrogen deficiency on crop traits and yield of maize by machine learning and radiative transfer modeling. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102617. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, J.; Zhang, X.; Zhang, J.; Cao, Q.; Tian, Y.; Zhu, Y.; Cao, W.; Liu, X. Combining machine learning algorithm and multi-temporal temperature indices to estimate the water status of rice. Agric. Water Manag. 2023, 289, 108521. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, T.; Zhu, Y.; Tian, Y.; Cao, W.; Yao, X.; Wang, N. Comparative analysis of vegetation indices, non-parametric and physical retrieval methods for monitoring nitrogen in wheat using UAV-based multispectral imagery. In Proceedings of the IEEE Internacional Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 7362–7365. [Google Scholar]
- Liang, L.; Di, L.; Huang, T.; Wang, J.; Lin, L.; Wang, L.; Yang, M. Estimation of leaf nitrogen content in wheat using new hyperspectral indices and a random forest regression algorithm. Remote Sens. 2018, 10, 1940. [Google Scholar] [CrossRef]
- Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving soybean leaf area index from unmanned aerial vehicle hyperspectral remote sensing: Analysis of RF, ANN, and SVM regression models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 3, 247–259. [Google Scholar] [CrossRef]
- Atzberger, C.; Guérif, M.; Baret, F.; Werner, W. Comparative analysis of three chemometric techniques for the spectroradiometric assessment of canopy chlorophyll content in winter wheat. Comput. Electron. Agric. 2010, 73, 165–173. [Google Scholar] [CrossRef]
- Wang, R.; Cherkauer, K.; Bowling, L. Corn response to climate stress detected with satellite-based NDVI time series. Remote Sens. 2016, 8, 269. [Google Scholar] [CrossRef]
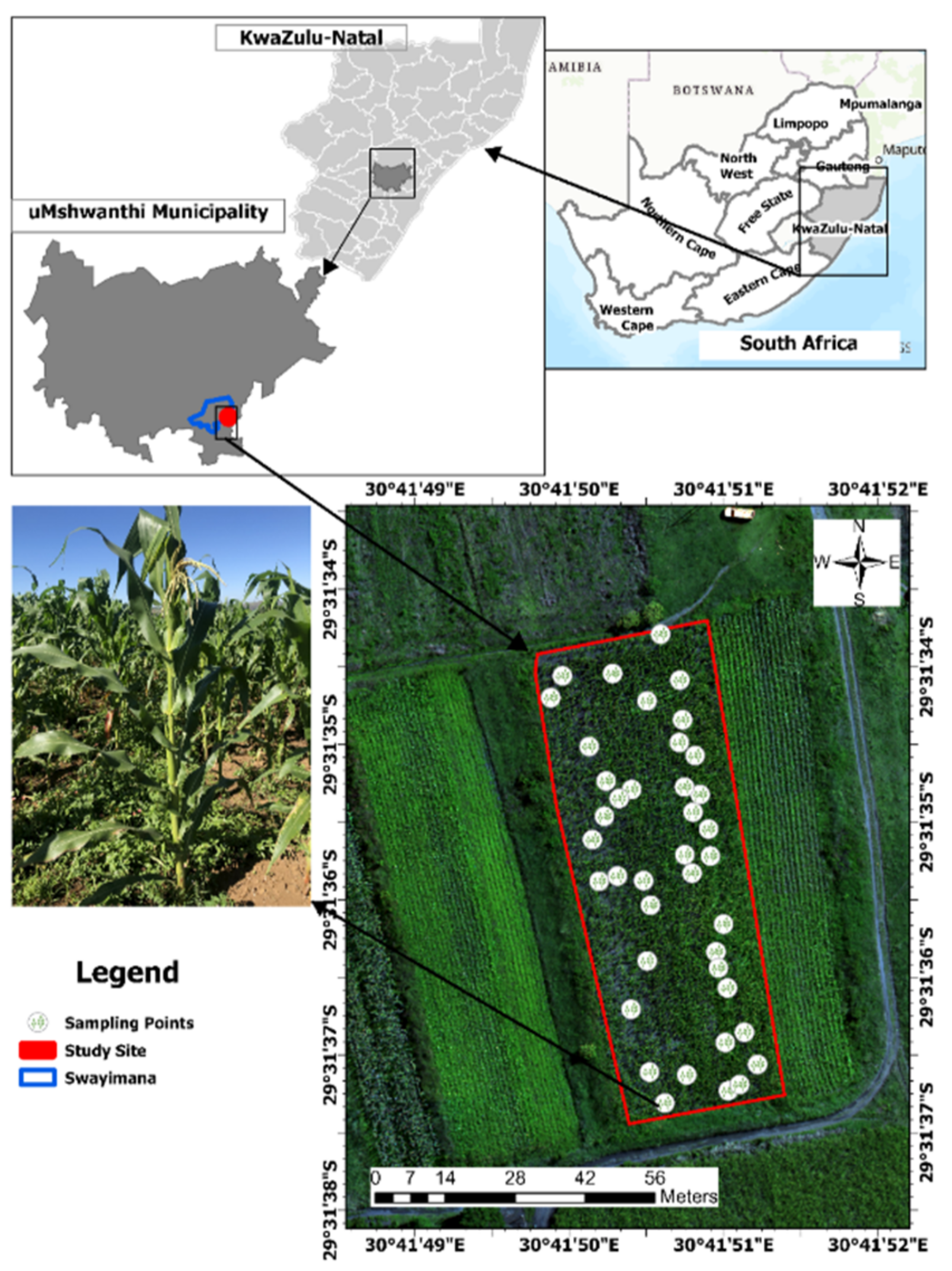






| Spectral Colour | Band Range | Ground Sampling Distance at a Flying Height of 120 m |
|---|---|---|
| Blue | 475 nm | 5.2 cm per pixel |
| Green | 560 nm | 5.2 cm per pixel |
| Red | 668 nm | 5.2 cm per pixel |
| Red Edge | 717 nm | 5.2 cm per pixel |
| Near-Infrared | 842 nm | 5.2 cm per pixel |
| Thermal Infrared | 8000–14,000 nm | 81 cm per pixel |
| Vegetation Index | Equation | Reference |
|---|---|---|
| Normalised Difference Vegetation Index (NDVI) | [59] | |
| Green Normalised Difference Vegetation Index (GNDVI). | [60] | |
| Normalised Difference Red Edge Index (NDRE) | [61] | |
| Soil-Adjusted Vegetation Index (SAVI) | L is a constant between 0 and 1. | [62] |
| Optimized Soil-Adjusted Vegetation Index (OSAVI) | [62] | |
| Green Chlorophyll Index (Cl_green) | [63] | |
| Red Edge Chlorophyll Index (Cl_RED_EDGE) | [63] | |
| Red Edge NDVI (RENDVI) | [64] | |
| Modified Soil-Adjusted Vegetation Index (MSAVI) | (1/2) × (2 × (NIR + 1)-sqrt ((2 × NIR + 1)2 − 8(NIR - RED))) | [65] |
| Simple Ratio (SR) | [66] | |
| Modified Triangular Vegetation Index (MTVI2) | (1.8(NIR − GREEN) − 3.75(RED − GREEN))/(√((2NIR + 1)2) − 6(NIR − 5√RED) − 0.5) | [67] |
| Canopy Chlorophyll Content Index (CCCI) | NDRE/NDVI | [68] |
| MERIS Terrestrial Chlorophyll Index (MTCI) | [69] | |
| Normalised Difference Water Index (NDWI) | (GREN/NIR)/(GREEN/NIR) | [70] |
| Ration Vegetation Index (RVI) | [71] | |
| Transformed Chlorophyll Absorption in Reflectance Index (TCARI) | 3[REDEDGE − RED − 0.2(REDEDGE/GREEN) (REDEDGE/RED)]/OSAVI | [72] |
| No. | Bands | r | No. | Vegetation Index | r | No. | Vegetation Index | r |
|---|---|---|---|---|---|---|---|---|
| 1 | BLUE | −0.41 | 1 | MSAVI | −0.51 | 12 | TCARI_OSAVI | 0.19 |
| 2 | GREEN | −0.51 | 2 | SR | −0.19 | 13 | TCARI_RDVI | −0.55 |
| 3 | RED | −0.54 | 3 | MTVI2 | −0.52 | 14 | CCCI | −0.43 |
| 4 | RED_EDGE | −0.52 | 4 | Cl_RED_EDGE | −0.55 | 15 | MTCI | −0.50 |
| 5 | NIR | −0.53 | 5 | Cl_GREEN | −0.41 | 16 | RVI | −0.19 |
| 6 | TIR | 0.59 | 6 | RDVI | −0.48 | 17 | NDWI | 0.35 |
| 7 | TCARI | −0.53 | 18 | NDVI | −0.14 | |||
| 8 | NDRE | −0.45 | 19 | GNDVI | −0.54 | |||
| 9 | OSAVI | −0.62 | 20 | RENDVI | −0.33 | |||
| 10 | TCARI_NDVI | −0.55 | 21 | SAVI | −0.50 | |||
| 11 | TCARI_SAVI | −0.54 |
| Bands | Vegetation Indices | Combined | |||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | |
| PLSR | 0.5 | 0.1 | 0.078 | 0.45 | 0.11 | 0.088 | 0.44 | 0.1 | 0. 09 |
| SVM | 0.55 | 0.1 | 0.073 | 0.5 | 0.1 | 0.065 | 0.67 | 0.07 | 0.04 |
| RF | 0.88 | 0.06 | 0.049 | 0.63 | 0.08 | 0.054 | 0.85 | 0.05 | 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapari, M.; Sibanda, M.; Magidi, J.; Mabhaudhi, T.; Nhamo, L.; Mpandeli, S. Comparing Machine Learning Algorithms for Estimating the Maize Crop Water Stress Index (CWSI) Using UAV-Acquired Remotely Sensed Data in Smallholder Croplands. Drones 2024, 8, 61. https://doi.org/10.3390/drones8020061
Kapari M, Sibanda M, Magidi J, Mabhaudhi T, Nhamo L, Mpandeli S. Comparing Machine Learning Algorithms for Estimating the Maize Crop Water Stress Index (CWSI) Using UAV-Acquired Remotely Sensed Data in Smallholder Croplands. Drones. 2024; 8(2):61. https://doi.org/10.3390/drones8020061
Chicago/Turabian StyleKapari, Mpho, Mbulisi Sibanda, James Magidi, Tafadzwanashe Mabhaudhi, Luxon Nhamo, and Sylvester Mpandeli. 2024. "Comparing Machine Learning Algorithms for Estimating the Maize Crop Water Stress Index (CWSI) Using UAV-Acquired Remotely Sensed Data in Smallholder Croplands" Drones 8, no. 2: 61. https://doi.org/10.3390/drones8020061
APA StyleKapari, M., Sibanda, M., Magidi, J., Mabhaudhi, T., Nhamo, L., & Mpandeli, S. (2024). Comparing Machine Learning Algorithms for Estimating the Maize Crop Water Stress Index (CWSI) Using UAV-Acquired Remotely Sensed Data in Smallholder Croplands. Drones, 8(2), 61. https://doi.org/10.3390/drones8020061








