High-Altitude Precision Landing by Smartphone Video Guidance Sensor and Sensor Fusion
Abstract
1. Introduction
Literature Review
2. Materials and Methods
2.1. The Smartphone Video Guidance Sensor (SVGS)
- (1)
- Apply the pinhole camera model to map and project a tetrahedron-shaped target of known dimensions (4 LEDs) from the world frame to the image plane and linearize the resultant expression of the target’s 6-DOF vector in the camera frame (two equations for each LED), , about a fixed, small enough, 6-DOF vector initial guess, , up to the first linearization error, :.
- (2)
- Extract the blob location of each LED in the image plane:.
- (3)
- Minimize the residuals in a least squares sense to obtain the optimal 6-DOF vector of the target’s position and attitude in the camera frame, :.
2.1.1. SVGS Collinearity Approximation
2.1.2. Blob Detection
- (a)
- Statistic filtering using blob properties, such as mass and area (SVGS-HAL).
- (b)
- Geometric alignment check.
| Algorithm 1 Blob Selection per color |
|
2.2. High-Altitude Precision Landing: Mission Objectives and Concept of Operations
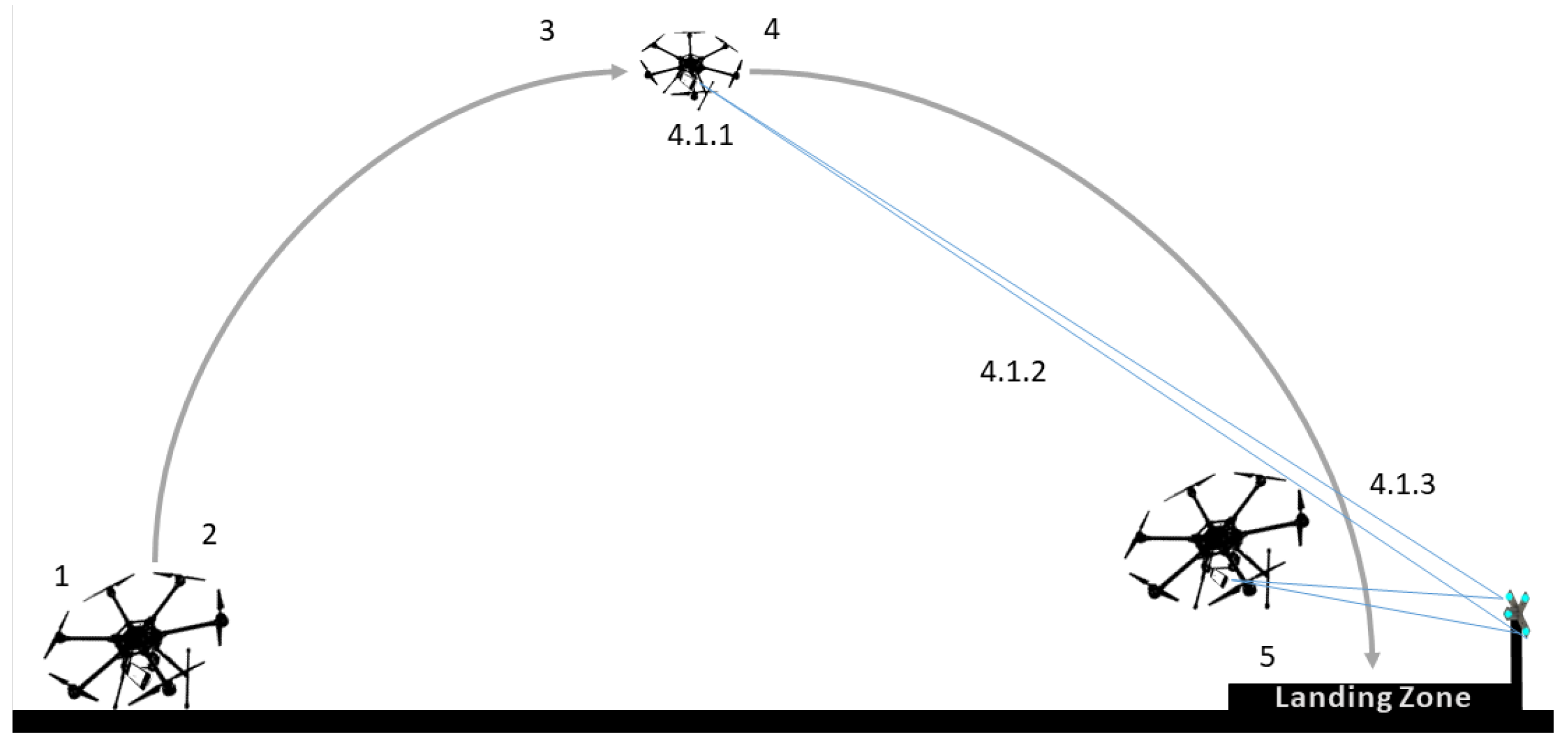
- Precise landing from a high altitude (100 m) to a static target on ground using SVGS, IMU, and barometer measurements in sensor fusion, following the concept of operation shown in Figure 2. GPS-based corrections are limited to reject wind disturbances.
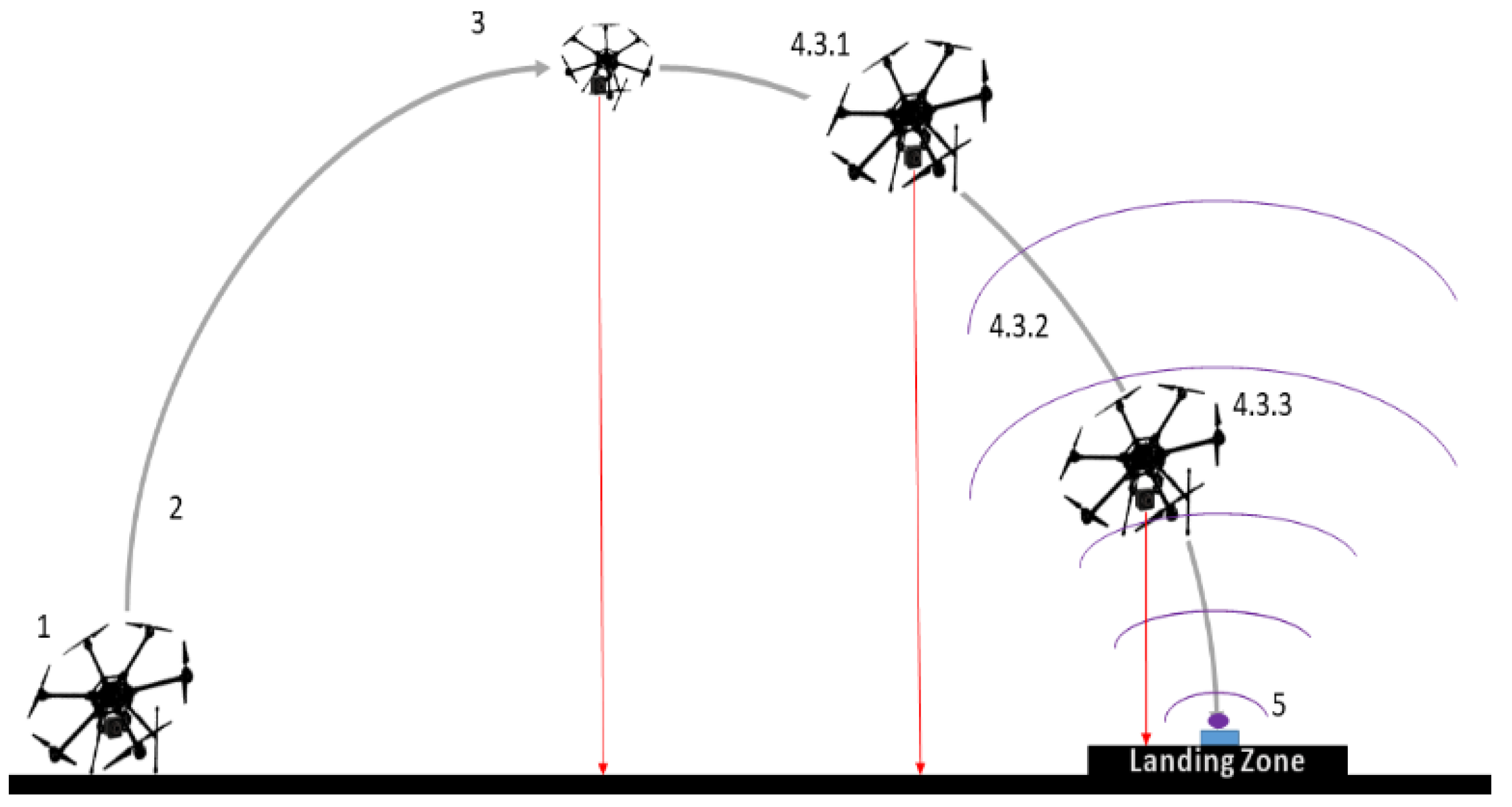
- Precise landing from 40 m to a static infrared beacon on ground, using IMU, a barometer, a 2D infrared sensor, and range sensor measurements in sensor fusion, following the concept of operation shown in Figure 3. GPS-based corrections are limited to reject wind disturbances. This provides a baseline for comparing landing performance, against state of the art commercially available technology.
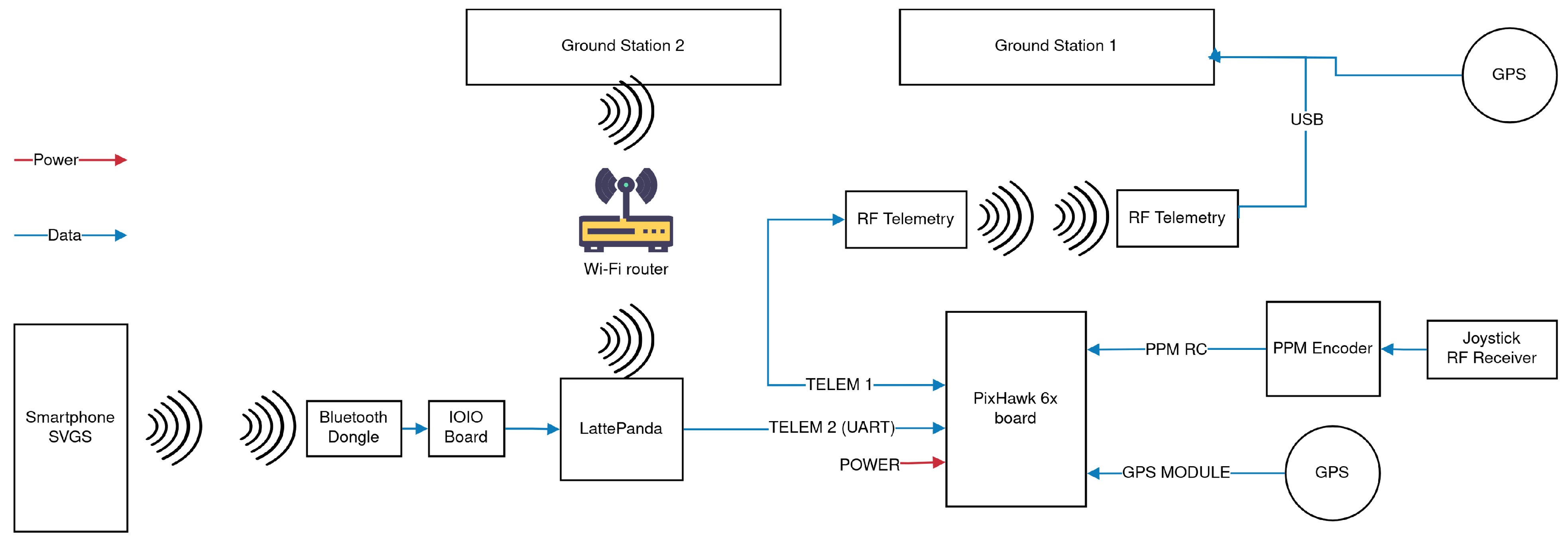
2.3. UAV Hardware Description
- Avionics: PX4 flight control unit (FMU-V6X), LattePanda Delta3 companion computer, UBLOX F9P GNSS module, Futaba T6K 8-Channel 2.4 GHz RC System, and Holybro SiK V2 915 MHz 100 MW Telemetry Module.
- Motors and frame: Tarot X8-II Frame, Tarot 4114/320KV Motors, OPTO 40A 3-6S electronic speed controllers, Tarot 1655 folding electric motor propellers (16 in), 4S-5000 mAh Li-Po battery, and 6S-22000 mAh Li-Po battery.
- Navigation Sensors: for SVGS: Samsung Galaxy S8 smartphone (host platform), IOIO Bluetooth to USB link (communication bridge); and for Infrared Beacon Landing: IR-LOCK PixyCam, TFmini Plus LiDAR Rangefinder.
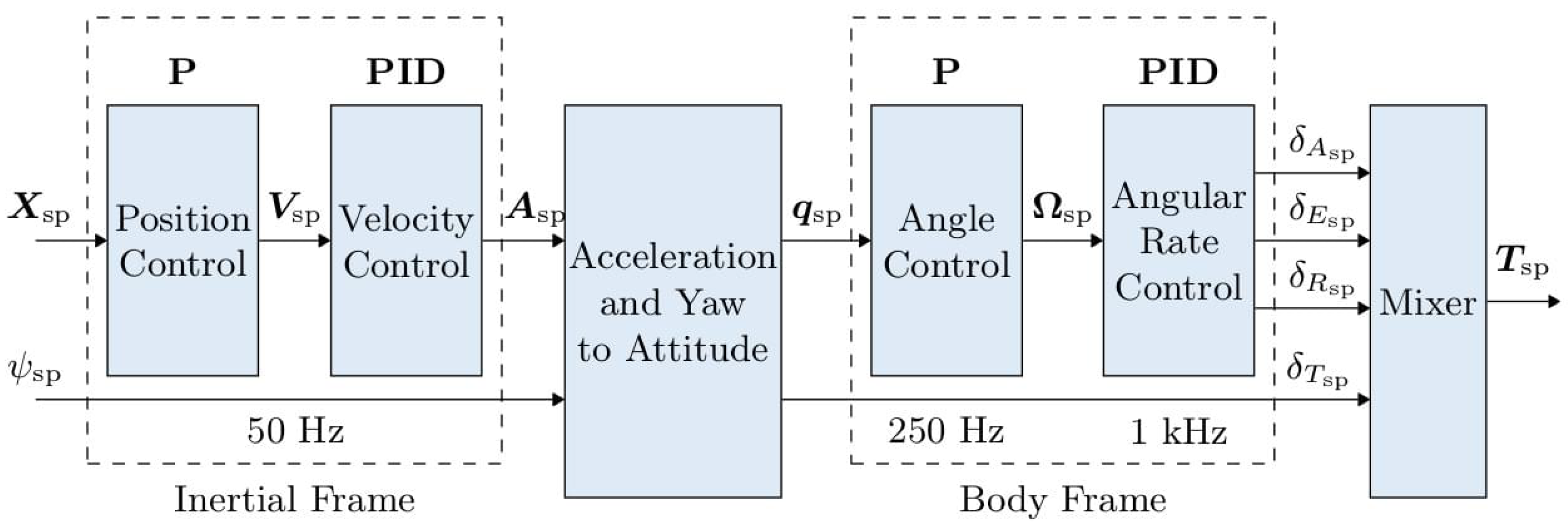
2.4. State Estimation and Sensor Fusion
Sensor Fusion of SVGS Non-Deterministic Intermittent Measurements
- (a)
- A Kalman Filter in the companion computer corrects SVGS sampling frequency values before fusion at the flight controller EKF2. A solution similar to the one described in [1,2] is used, while in this investigation error messages are omitted from being parsed by the companion computer’s Kalman Filter and consequently sent to the flight controller’s EKF2: when SVGS cannot calculate using the selected blobs, it outputs a packet containing a numerical error code to the companion computer.
- (b)
- EKF2 parameters are tuned to avoid unnecessary resets: if state estimates diverge at , the state estimate is removed and the estimation is reinitialized. This explains the gate size parameters used for the magnetometer and barometer in Table 1.
2.5. Motion Controller and Hardware-Software Implementation
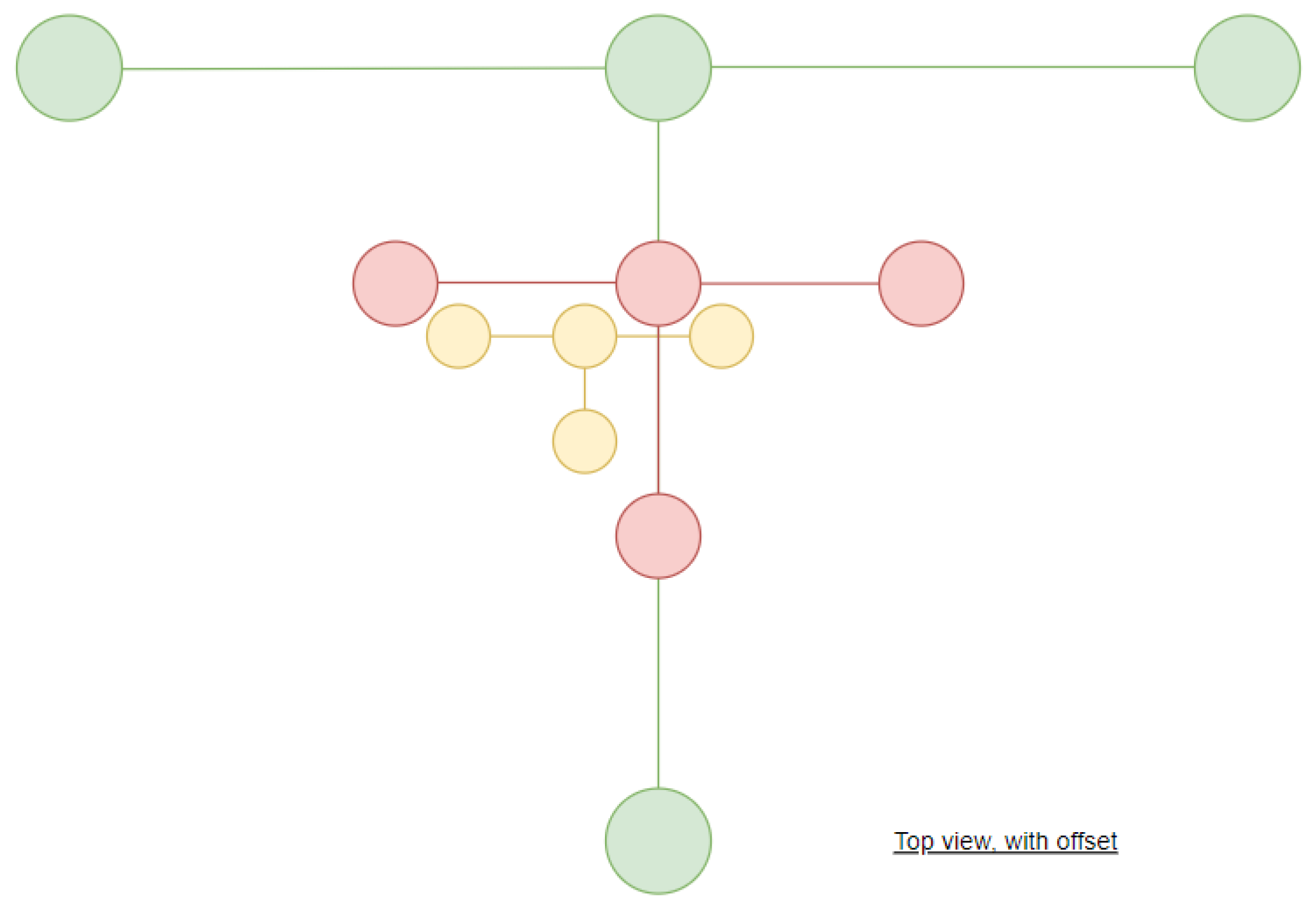
2.5.1. SVGS Landing Beacons for High-Altitude Landing
2.5.2. Avoiding Spurious x and y Position Estimates
- Achieve sufficient target alignment.
- Reset EKF2 to include SVGS or IR-LOCK target position measurements in the local UAV frame.
2.5.3. SVGS Frame Transformations
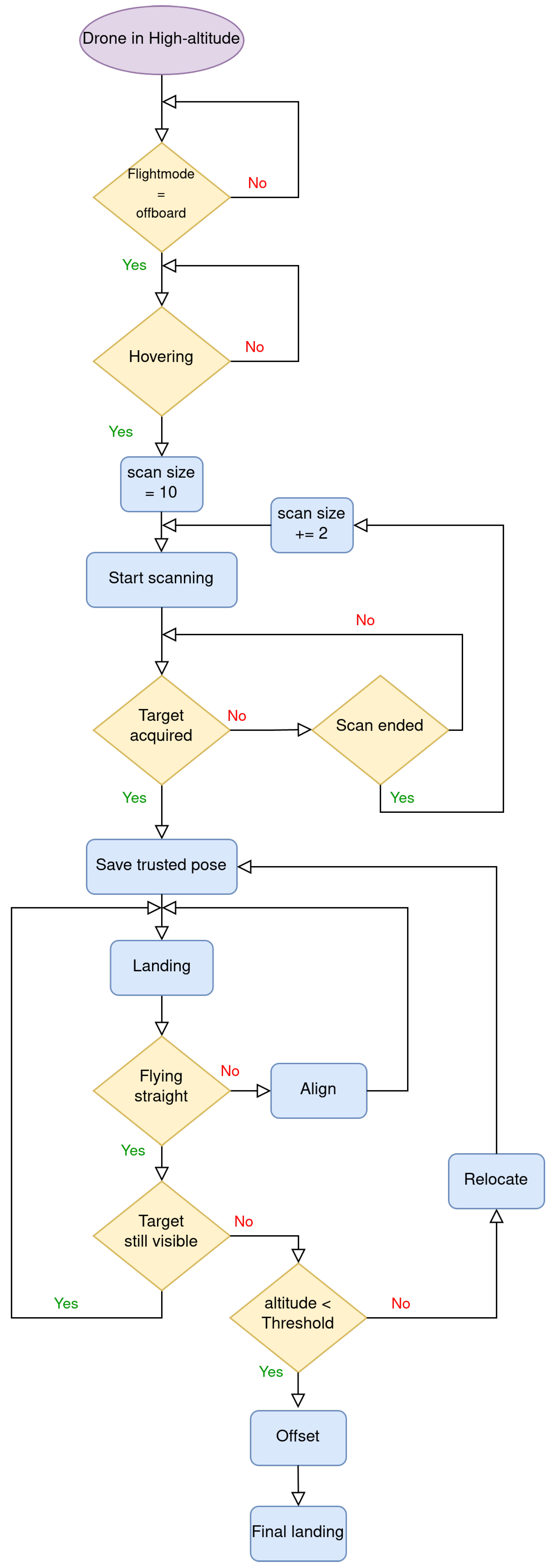
2.5.4. Autonomous Landing Routine
- Go to a predetermined position where the IR beacon should be visible.
- If the beacon is visible, align with it in a horizontal plane. If not, search for the beacon for a predefined number of times. The maximum number of search attempts was set to 20.
- If beacon sight is locked, start descending on top of the beacon. If not, and maximum search attempts have been reached, land.
- If beacon sight is lost during descent but UAV is near ground, land.
- The UAV scans, searching for the landing target, increasing the search radius until the target confirmation is achieved.
- The UAV aligns with the target center and starts descending.
- If the target line of sight is lost during descent, relocate to the last position at which the target sight was confirmed on the -Plane (Local coordinate -Plane). If the target sight cannot be recovered, attempt to relocate using the x, y, z coordinates (f, l, u). Complete relocation often triggers an EKF2 reset.
- At 20 m altitude, the UAV offsets and aligns with the Short-Range Target (SRT), beginning the final approach.
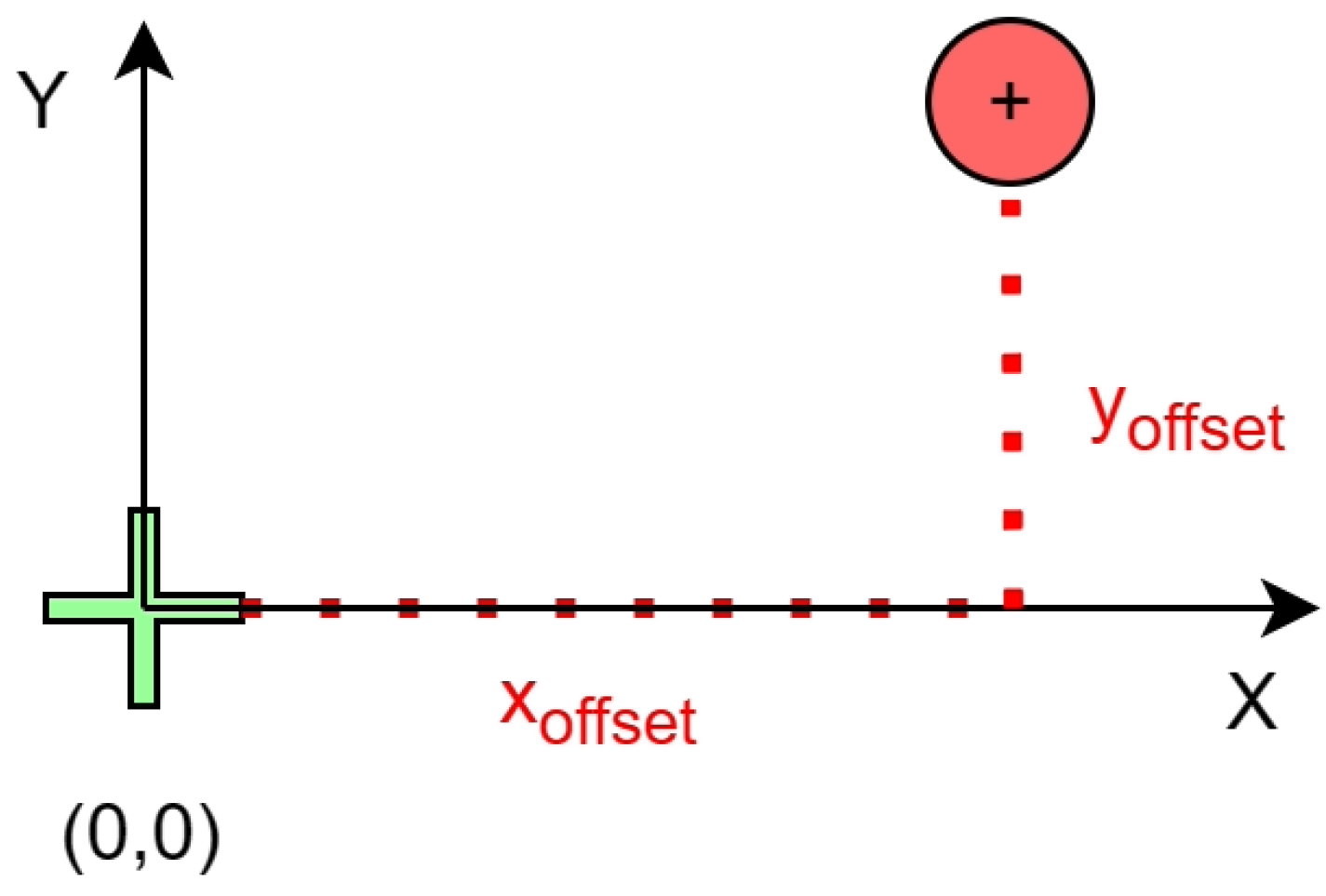
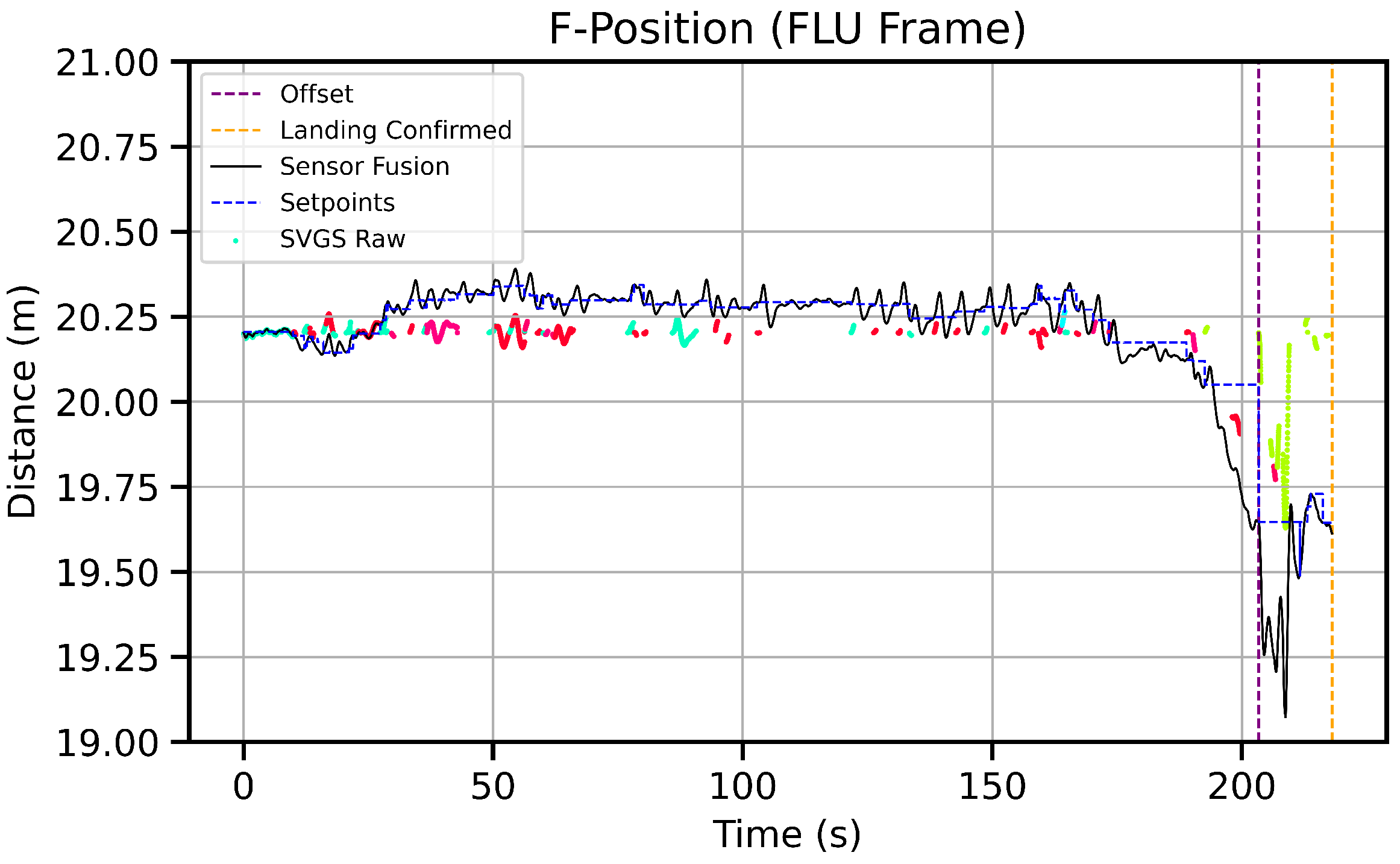
- At ≈3 m altitude, the UAV performs a final offset maneuver. Offset values are selected to improve target sight during final landing approach; transmitted values to EKF2 are corrected to avoid landing on top of the target. The offset maneuver is depicted on Figure 12.
- Complete landing.
2.5.5. Autonomous Landing Framework
- CA1
- Ground Operations and MonitoringThis investigation used the open-source QGroundControl software (Version 3.5) (Ground Station 1 in Figure 6) to monitor telemetry packets from the FCU and to visualize the approximate UAV trajectory. The companion computer running the autonomous routines in the UAV was monitored via remote access by the long-range WiFi network (Ground Station 2, in Figure 6).
- CA2
- ROS Noetic pipeline and Data Acquisition NodeThe autonomous landing routine was developed as custom ROS Noetic nodes bridged by the MAVlink drone communication protocol using the standard wrapper MAVROS [33,34,35]. The communication pipeline is similar to the approach presented in [1,2]; however, functionalities and the information pipelined greatly differ. These changes will be discussed in the next subsections.A central part of the software stack for both landing methods is the ROS data acquisition node, whose primary function is to log information from the FCU sensors, SVGS measurements (from the host platform), and locally calculated setpoints. This approach complements the standard FCU data acquisition, allowing data verification on both communication ends. The ROS nodes defined in the SVGS automated landing package are:
- motion_control_drspider: Implements logic for UAV motion control during the autonomous landing phase. It is also responsible for sending position or velocities setpoints to the “px4_control” node.
- routine_commander_drspider: Coordinates which phase and/or portion of the motion routine must be active if certain conditions are met.
- transformations_drspider: Applies rotations to collected sensor data as needed. Used mainly to convert SVGS values before and after topic remapping (sensor fusion).
- svgs_deserializer_drspider: Converts serial data packets from SVGS and publishes output as a stamped pose message on the topic “target” with the data type of posestamped, a data structure used by ROS that includes a timestamped x, y, z positions, covariance, and orientations. It also applies a Kalman filter to SVGS raw values.
- px4_control_drspider: Obtains setpoints and processed sensor data from motion control nodes and sends them to the flight computer at 30 Hz.
- data_recording_drspider: Subscribes to several variables and records them to a CSV file at 25Hz for data and error analysis.
- Accuracy. In UAVs autonomous routines, commanding a set point in a loop with an abrupt exit condition may lead to getting caught in an endless loop. For instance, let denote a 3-dimensional array with a set point in the FLU coordinate system, and let denote the UAV’s current position in the same frame. If the condition , ) is imposed, the drone may hover for an undetermined amount of time, depending on position estimate quality. Commanding two set points that are close to each other is essentially commanding the same set point: a minimum difference between two set points is required to guarantee actual UAV motion.
- Coding Interface (ROS-MAVROS-PX4). If one commands a new set point and during that the UAV gains momentary sight of the target, one would have to command the UAV back to the sight position for a large instead of having the UAV stop exactly at the target sight position. Thus, a large is not desirable. This is also due to the communication latency within ROS nodes, aggravated by the fact that ROS Noetic uses a central node to communicate with the other nodes [30,33,34].
- UAV System. The value selected for needs to consider the UAV dimensions (Table 2). Two set points that are too similar could create destabilizing UAV behavior (chatter), which can be aggravated by the size and weight of the aerial vessel.
| Algorithm 2 Scan Maneuver |
|
| Algorithm 3 Align Maneuver |
|
| Algorithm 4 Relocation XYZ |
|
| Algorithm 5 Offset Maneuver |
|
| Algorithm 6 Landing Maneuver |
|
3. Results
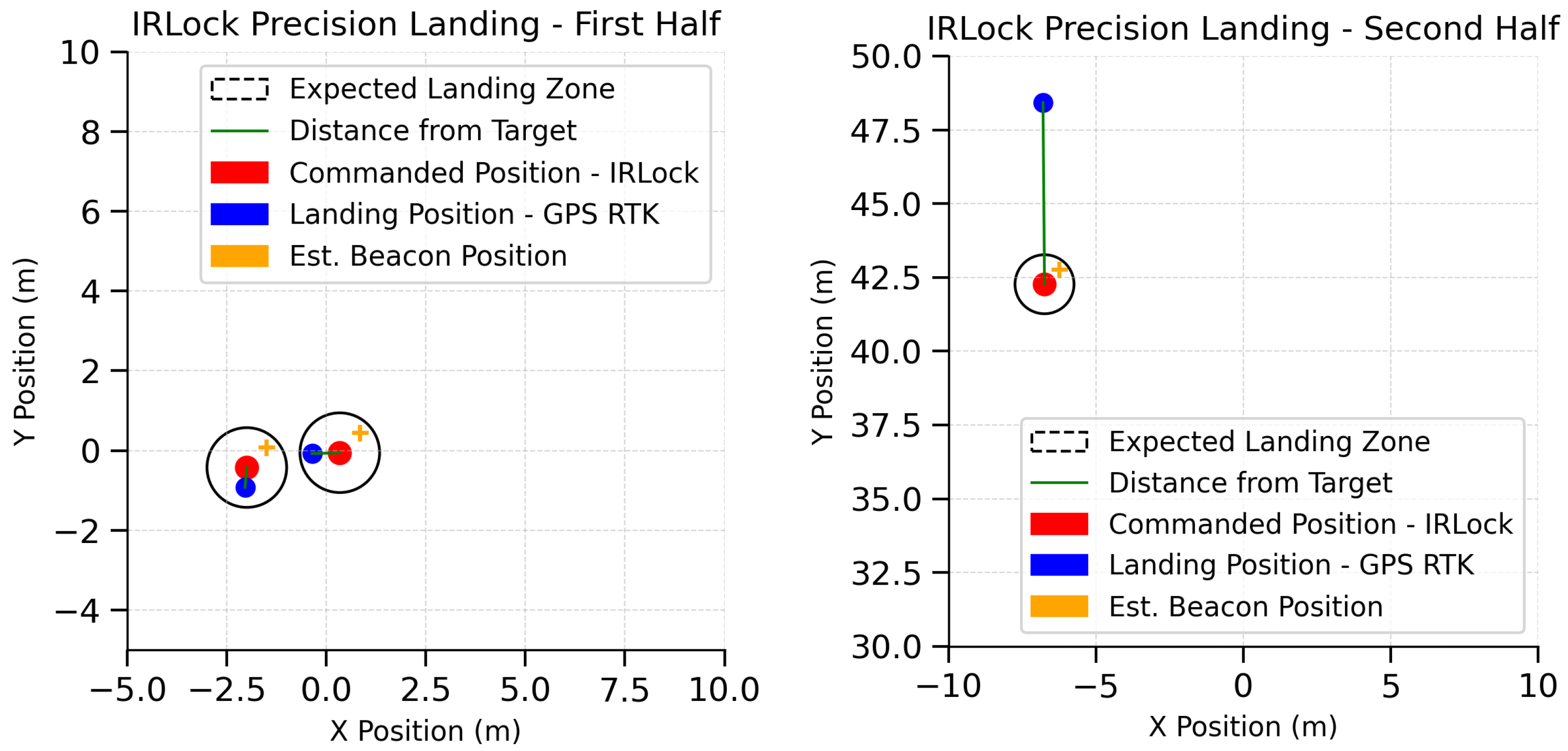
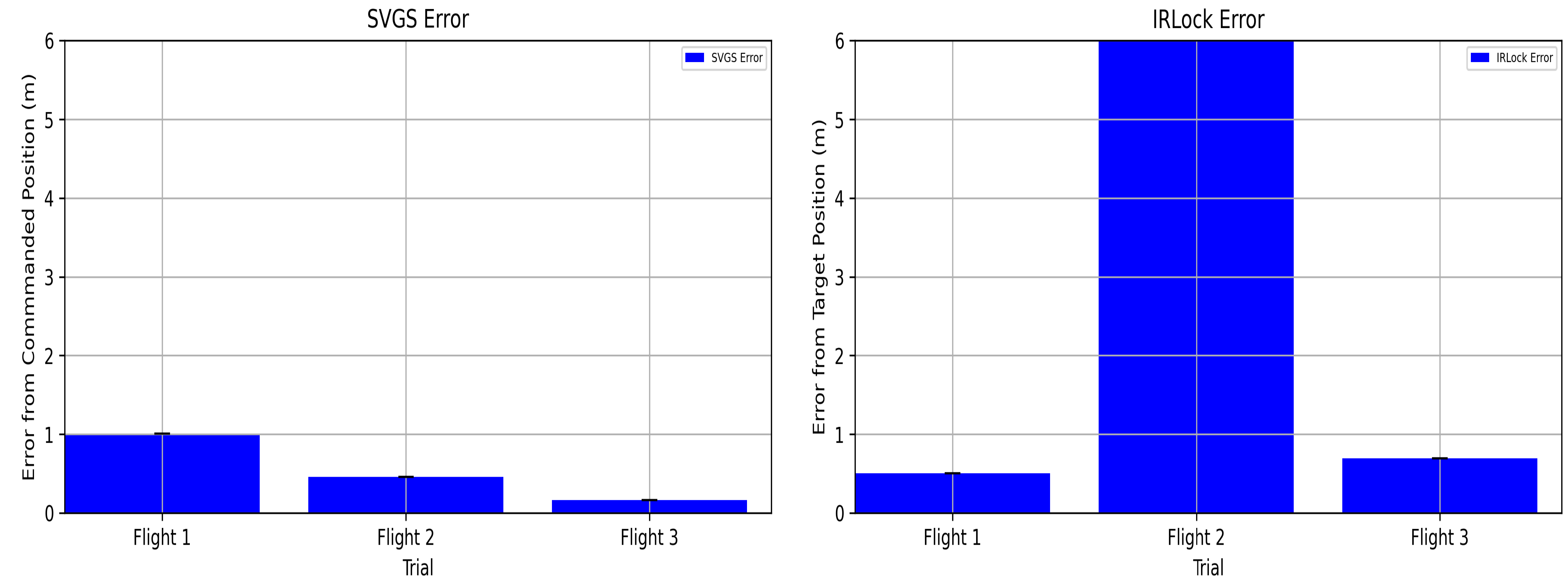
Comparison of Precision Landing Performance
4. Discussion
4.1. SVGS Navigation and Sensor Fusion
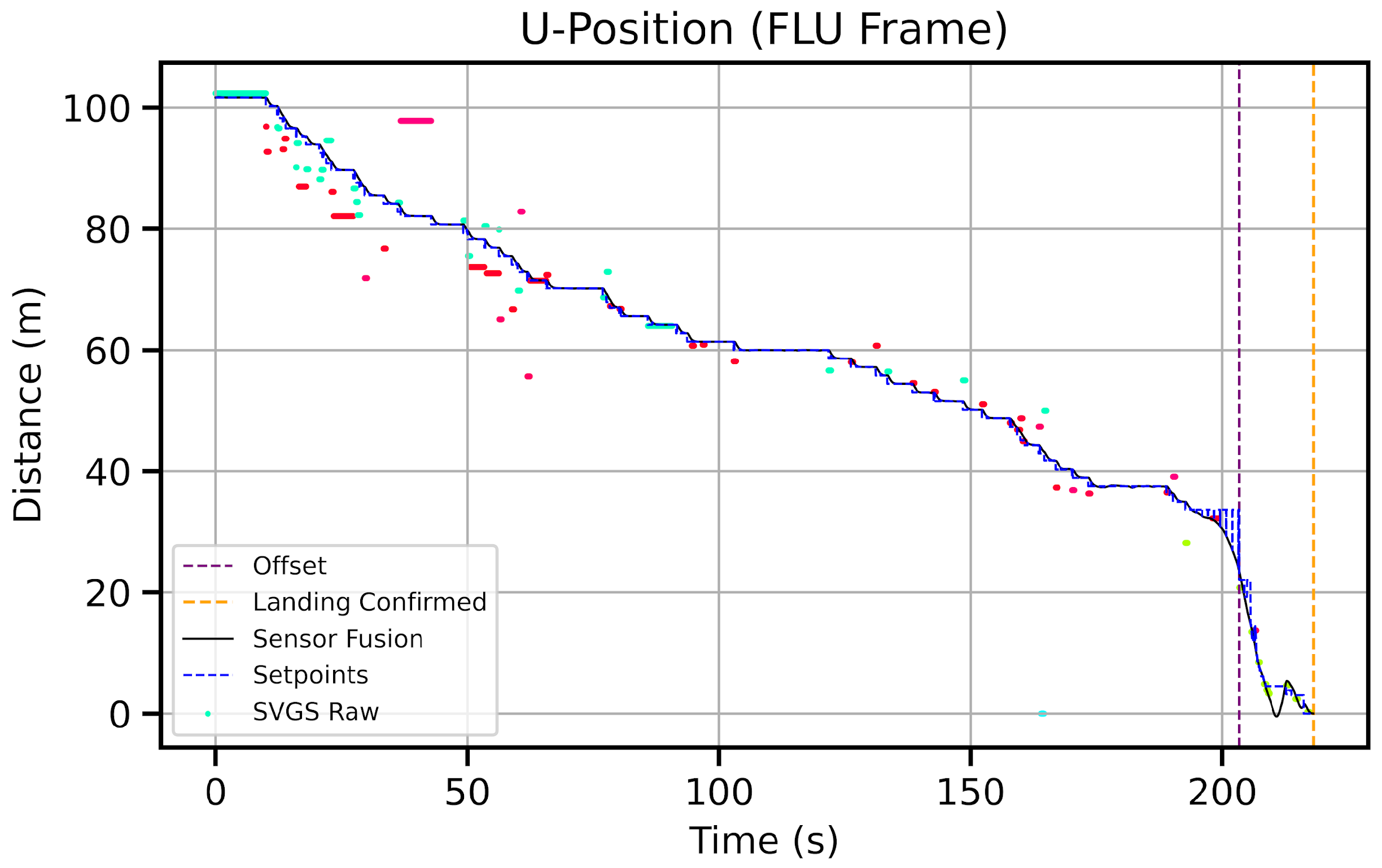
4.1.1. EKF2 Resets and Instability
4.1.2. EKF2 Drift Correction with SVGS
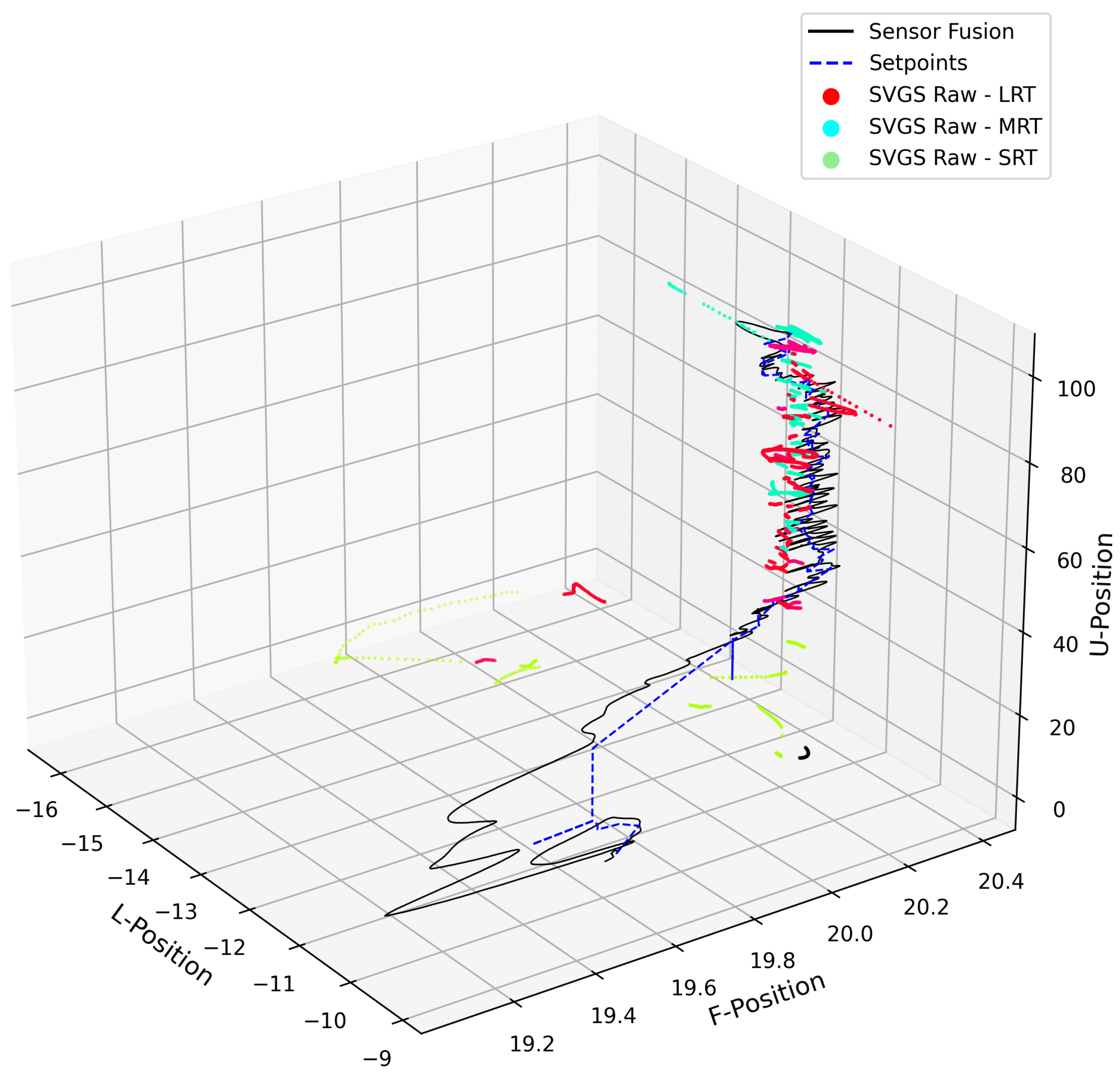
4.2. SVGS Beacon Transition
4.3. SVGS Beacons and IR Beacon
4.4. Influence of GPS RTK in Sensor Fusion
4.5. GPS RTK Latency and SVGS Latency
4.6. Future of SVGS for Guidance and Navigation of UAVs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EKF2 | Extended Kalman Filter 2 |
| SRT | Short-Range Target |
| MRT | Medium-Range Target |
| LRT | Long-Range Target |
| SVGS | Smartphone Video Guidance Sensor |
| HAL | High-Altitude Landing |
| CONOPS | Concept of Operations |
| COTS | Commercial-Off-The-Shelf |
References
- Silva Cotta, J.L.; Rakoczy, J.; Gutierrez, H. Precision landing comparison between Smartphone Video Guidance Sensor and IRLock by hardware-in-the-loop emulation. Ceas Space J. 2023. [Google Scholar] [CrossRef]
- Bautista, N.; Gutierrez, H.; Inness, J.; Rakoczy, J. Precision Landing of a Quadcopter Drone by Smartphone Video Guidance Sensor in a GPS-Denied Environment. Sensors 2023, 23, 1934. [Google Scholar] [CrossRef] [PubMed]
- Bo, C.; Li, X.Y.; Jung, T.; Mao, X.; Tao, Y.; Yao, L. SmartLoc: Push the Limit of the Inertial Sensor Based Metropolitan Localization Using Smartphone. In Proceedings of the 19th Annual International Conference on Mobile Computing & Networking, MobiCom ’13, Miami, FL, USA, 30 September–4 October 2013; pp. 195–198. [Google Scholar] [CrossRef]
- Zhao, B.; Chen, X.; Zhao, X.; Jiang, J.; Wei, J. Real-Time UAV Autonomous Localization Based on Smartphone Sensors. Sensors 2018, 18, 4161. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Xu, Y.; Di, L.; Chen, Y.Q. Low-cost Multi-UAV Technologies for Contour Mapping of Nuclear Radiation Field. J. Intell. Robot. Syst. 2013, 70, 401–410. [Google Scholar] [CrossRef]
- Xin, L.; Tang, Z.; Gai, W.; Liu, H. Vision-Based Autonomous Landing for the UAV: A Review. Aerospace 2022, 9, 634. [Google Scholar] [CrossRef]
- Kong, W.; Zhou, D.; Zhang, D.; Zhang, J. Vision-based autonomous landing system for unmanned aerial vehicle: A survey. In Proceedings of the 2014 International Conference on Multisensor Fusion and Information Integration for Intelligent Systems (MFI), Beijing, China, 28–29 September 2014; pp. 1–8. [Google Scholar] [CrossRef]
- Coopmans, C.; Slack, S.; Robinson, D.J.; Schwemmer, N. A 55-pound Vertical-Takeoff-and-Landing Fixed-Wing sUAS for Science: Systems, Payload, Safety Authorization, and High-Altitude Flight Performance. In Proceedings of the 2022 International Conference on Unmanned Aircraft Systems (ICUAS), Dubrovnik, Croatia, 21–24 June 2022; pp. 1256–1263. [Google Scholar] [CrossRef]
- Pluckter, K.; Scherer, S. Precision UAV Landing in Unstructured Environments. In Proceedings of the 2018 International Symposium on Experimental Robotics, Buenos Aires, Argentina, 5–8 November 2018; pp. 177–187. [Google Scholar]
- Chen, L.; Xiao, Y.; Yuan, X.; Zhang, Y.; Zhu, J. Robust autonomous landing of UAVs in non-cooperative environments based on comprehensive terrain understanding. Sci. China Inf. Sci. 2022, 65, 212202. [Google Scholar] [CrossRef]
- Kalinov, I.; Safronov, E.; Agishev, R.; Kurenkov, M.; Tsetserukou, D. High-Precision UAV Localization System for Landing on a Mobile Collaborative Robot Based on an IR Marker Pattern Recognition. In Proceedings of the 2019 IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 28 April–1 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Arafat, M.Y.; Alam, M.M.; Moh, S. Vision-Based Navigation Techniques for Unmanned Aerial Vehicles: Review and Challenges. Drones 2023, 7, 89. [Google Scholar] [CrossRef]
- Respall, V.; Sellami, S.; Afanasyev, I. Implementation of Autonomous Visual Detection, Tracking and Landing for AR Drone 2.0 Quadcopter. In Proceedings of the 2019 12th International Conference on Developments in Systems Engineering, Kazan, Russia, 7–10 October 2019. [Google Scholar]
- Sani, M.F.; Karimian, G. Automatic navigation and landing of an indoor AR. drone quadrotor using ArUco marker and inertial sensors. In Proceedings of the 2017 International Conference on Computer and Drone Applications (IConDA), Kuching, Malaysia, 9–11 November 2017; pp. 102–107. [Google Scholar] [CrossRef]
- Tanaka, H.; Matsumoto, Y. Autonomous Drone Guidance and Landing System Using AR/high-accuracy Hybrid Markers. In Proceedings of the 2019 IEEE 8th Global Conference on Consumer Electronics (GCCE), Osaka, Japan, 15–18 October 2019; pp. 598–599. [Google Scholar] [CrossRef]
- Neveu, D.; Bilodeau, V.; Alger, M.; Moffat, B.; Hamel, J.F.; de Lafontaine, J. Simulation Infrastructure for Autonomous Vision-Based Navigation Technologies. IFAC Proc. Vol. 2010, 43, 279–286. [Google Scholar] [CrossRef]
- Conte, G.; Doherty, P. An Integrated UAV Navigation System Based on Aerial Image Matching. In Proceedings of the 2008 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008; pp. 1–10. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y.; Lu, H.; Wu, H.; Cheng, L. UAV Autonomous Landing Technology Based on AprilTags Vision Positioning Algorithm. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 8148–8153. [Google Scholar] [CrossRef]
- Wang, J.; Olson, E. AprilTag 2: Efficient and robust fiducial detection. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016. [Google Scholar]
- ArduPilot. Precision Landing and Loiter Using IR Lock. 2023. Available online: https://ardupilot.org/copter/docs/precision-landing-with-irlock.html (accessed on 2 January 2023).
- Andrade Perdigão, J.A. Integration of a Precision Landing System on a Multirotor Vehicle: Initial Stages of Implementation. Master’s Thesis, Universidade da Beira Interior, Covilhã, Portugal, 2018. [Google Scholar]
- Haukanes, N.A. Redundant System for Precision Landing of VTOL UAVs. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2018. [Google Scholar]
- Jitoko, P.; Kama, E.; Mehta, U.; Chand, A.A. Vision Based Self-Guided Quadcopter Landing on Moving Platform During Fault Detection. Int. J. Intell. Commun. Comput. Netw. 2021, 2, 116–128. Available online: https://repository.usp.ac.fj/12939/1/Vision-Based-Self-Guided-Quadcopter-Landing-on-Moving-Platform-During-Fault-Detection.pdf (accessed on 2 January 2024).
- Garlow, A.; Kemp, S.; Skinner, K.A.; Kamienski, E.; Debate, A.; Fernandez, J.; Dotterweich, J.; Mazumdar, A.; Rogers, J.D. Robust Autonomous Landing of a Quadcopter on a Mobile Vehicle Using Infrared Beacons. In Proceedings of the VFS Autonomous VTOL Technical Meeting, Mesa, AZ, USA, 24–26 January 2023. [Google Scholar]
- Badakis, G. Precision Landing for Drones Combining Infrared and Visible Light Sensors. Master’s Thesis, University of Thessaly, Volos, Greece, 2020. [Google Scholar]
- Rakoczy, J. Application of the Photogrammetric Collinearity Equations to the Orbital Express Advanced Video Guidance Sensor Six Degree-of-Freedom Solution; Technical Report; Marshall Space Flight Center: Huntsville, AL, USA, 2003. [Google Scholar]
- Becker, C.; Howard, R.; Rakoczy, J. Smartphone Video Guidance Sensor for Small Satellites. In Proceedings of the 27th Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 10–15 August 2013. [Google Scholar]
- Howard, R.T.; Johnston, A.S.; Bryan, T.C.; Book, M.L. Advanced Video Guidance Sensor (AVGS) Development Testing; Technical Report; NASA-Marshall Space Flight Center: Huntsville, AL, USA, 2003. [Google Scholar]
- Hariri, N.; Gutierrez, H.; Rakoczy, J.; Howard, R.; Bertaska, I. Performance characterization of the Smartphone Video Guidance Sensor as Vision-based Positioning System. Sensors 2020, 20, 5299. [Google Scholar] [CrossRef] [PubMed]
- PX4 Autopilot Software. 2023. Available online: https://github.com/PX4/PX4-Autopilot (accessed on 4 January 2023).
- Lynen, S.; Achtelik, M.W.; Weiss, S.; Chli, M.; Siegwart, R. A robust and modular multi-sensor fusion approach applied to MAV navigation. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3923–3929. [Google Scholar] [CrossRef]
- Hariri, N.; Gutierrez, H.; Rakoczy, J.; Howard, R.; Bertaska, I. Proximity Operations and Three Degree-of-Freedom Maneuvers Using the Smartphone Video Guidance Sensor. Robotics 2020, 9, 70. [Google Scholar] [CrossRef]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R. ROS: An open-source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 12–17 May 2009. [Google Scholar]
- MAVROS. 2023. Available online: https://github.com/mavlink/mavros (accessed on 6 January 2023).
- MAVLink: Micro Air Vehicle Communication Protocol. 2023. Available online: https://mavlink.io/en/ (accessed on 8 January 2023).
- Makhubela, J.K.; Zuva, T.; Agunbiade, O.Y. A Review on Vision Simultaneous Localization and Mapping (VSLAM). In Proceedings of the 2018 International Conference on Intelligent and Innovative Computing Applications (ICONIC), Mon Tresor, Mauritius, 6–7 December 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Civera, J.; Davison, A.J.; Montiel, J.M.M. Inverse Depth Parametrization for Monocular SLAM. IEEE Trans. Robot. 2008, 24, 932–945. [Google Scholar] [CrossRef]








| Sensor | Gate Size (SD) |
|---|---|
| Magnetometer (heading reference) | 5 |
| Barometer * | 5 |
| Infrared + Range | 10 |
| SVGS | 10 |
| GPS | 2 |
| Specifications | DR. Spider |
|---|---|
| Vehicle Mass | 22 lbm |
| Overall Dimensions | 44.3 in × 44.3 in × 19.3 in |
| Max Autonomous Velocity Norm | 1 MPH |
| Max Operational Altitude | 400 ft AGL |
| Max Telemetry Range | 984 ft |
| Approximate Performance Time | 25 min |
| Max Operational Temperature | 122 °F |
| Max Operational Sustained Wind Speed | 10 kts (17 ft/s) |
| Max Operational Gust Wind Speed | 12 kts (17 ft/s) |
| Max Payload Mass | 5.5 lbm |
| Beacon Type and Operating Range | |||
|---|---|---|---|
| Short-Range Target (SRT): 0–20 m | 0 | 0.545 | 0 |
| 0 | −0.49 | 0 | |
| 0 | 0 | 0.365 | |
| 0.315 | 0 | 0 | |
| Medium-Range Target (MRT): 10 m–85 m | 0 | 0.95 | 0 |
| 0 | −0.97 | 0 | |
| 0 | 0 | 0.91 | |
| 0.801 | 0 | 0 | |
| Long-Range Target (LRT): 55 m–200 m | 0 | 7.68 | 0 |
| 0 | −7.97 | 0 | |
| 0 | 0 | 3.09 | |
| 9.14 | 0 | 0 |
| Experiment Setup | |||
|---|---|---|---|
| SVGS—Flight 1 Start | −11.02 | 20.16 | 106.65 |
| SVGS—Flight 1 Landing Command | −9.39 | 20.35 | 0.02 |
| SVGS—Flight 2 Start | −10.97 | 20.20 | 101.65 |
| SVGS—Flight 2 Landing Command | −6.55 | 22.59 | 0.02 |
| SVGS—Flight 3 Start | 9.48 | 12.82 | 101.93 |
| SVGS—Flight 3 Landing Command | 7.92 | 12.03 | 0.017 |
| IRLock—Flight 1 Start | −2.07 | −0.86 | 54.83 |
| IRLock—Flight 1 Landing Command | −2.04 | −0.93 | 0.01 |
| IRLock—Flight 2 Start | −6.61 | 42.24 | 54.95 |
| IRLock—Flight 2 Landing Command (*) | −6.79 | 48.42 | 0.09 |
| IRLock—Flight 3 Start | −0.09 | 0.44 | 53.11 |
| IRLock—Flight 3 Landing Command | −0.08 | 0.36 | 0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva Cotta, J.L.; Gutierrez, H.; Bertaska, I.R.; Inness, J.P.; Rakoczy, J. High-Altitude Precision Landing by Smartphone Video Guidance Sensor and Sensor Fusion. Drones 2024, 8, 37. https://doi.org/10.3390/drones8020037
Silva Cotta JL, Gutierrez H, Bertaska IR, Inness JP, Rakoczy J. High-Altitude Precision Landing by Smartphone Video Guidance Sensor and Sensor Fusion. Drones. 2024; 8(2):37. https://doi.org/10.3390/drones8020037
Chicago/Turabian StyleSilva Cotta, Joao Leonardo, Hector Gutierrez, Ivan R. Bertaska, John P. Inness, and John Rakoczy. 2024. "High-Altitude Precision Landing by Smartphone Video Guidance Sensor and Sensor Fusion" Drones 8, no. 2: 37. https://doi.org/10.3390/drones8020037
APA StyleSilva Cotta, J. L., Gutierrez, H., Bertaska, I. R., Inness, J. P., & Rakoczy, J. (2024). High-Altitude Precision Landing by Smartphone Video Guidance Sensor and Sensor Fusion. Drones, 8(2), 37. https://doi.org/10.3390/drones8020037







