Radiometric Improvement of Spectral Indices Using Multispectral Lightweight Sensors Onboard UAVs
Abstract
1. Introduction
- Photogrammetric techniques pay special attention to the geometric quality of the final product [11], relegating radiometric quality. Therefore, reflectance orthomosaics, as derived from geomatic products frequently used to generate vegetation indices, can incorporate radiometric errors.
- GSD with centimetre resolution introduces BRDF effects due to the position of the sensor and changes in illumination angles during the flight. The pixel size of most satellite images exceeds one metre and is usually several orders of magnitude coarser in resolution compared to that of a UAV image.
- Ignoring parts of the crop that are hidden in an image due to the geometry of the crop (obtained from a DSM generated as a satellite photogrammetric product) and image orientation.
- Avoiding image areas that may be affected by the hotspot effect [14] and correcting the images by using the directional property of reflectance.
- Only using image pixels acquired from a favourable geometry or optimal perspective with respect to the canopy and the sun position, discriminated using the image orientation and the sun position at the time of image acquisition.
- Utilizing the conventional photogrammetric computer tool AgiSoft Metashape.
- Implementing a novel methodology that addresses the aforementioned problems.
- -
- Introducing corrections for the BDRF effect per ortho-image by precisely computing the external orientation of the images and the relative orientation of the object to the acquisition point and to the sun.
- -
- Using the information derived from individual ortho-images rather than geomatic products obtained through photogrammetric processes, while eliminating the radiometric distortion that these processes may incorporate.
- -
- Determining the optimal pixel values from the best ortho-image considering factors such as lighting, possible occultations, and the relative position within the image.
2. Materials and Methods
2.1. Experimental Setup
2.2. Data Acquisition
2.3. Reference Commercial Multispectral Software (AgiSoft Metashape)
2.4. BRDF Correction
2.4.1. Pre-Processing
2.4.2. Radiometric Processing
2.4.3. Optimized Reflectances from the BRDF Correction Model and Derived NDVI
- Is in a hotspot zone.
- Is hidden using the DSM.
- The normalized difference vegetation Index (NDVI) in the orthoimage from the previous step is outside the chosen range (between 0.2 and 1.0 in this case). Consequently, the vegetation is segmented by the NDVI filter calculated with 3-decimal places.
- The horizontal angle between the plant formed by the direction between the sun and the sensor is outside the established range (from −90 to 90 degrees in this case).
2.5. Statistical Analysis
3. Experimental Results
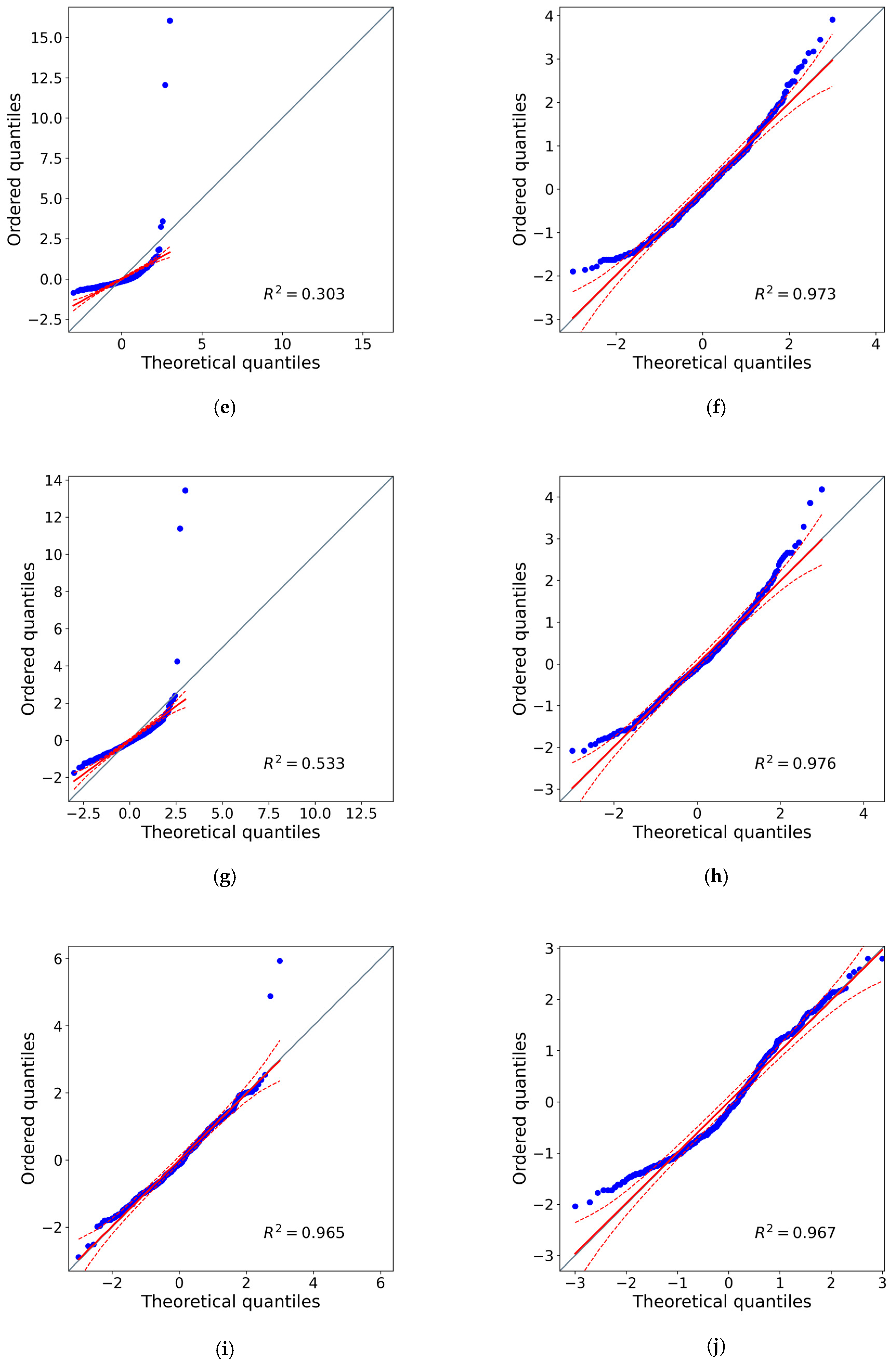
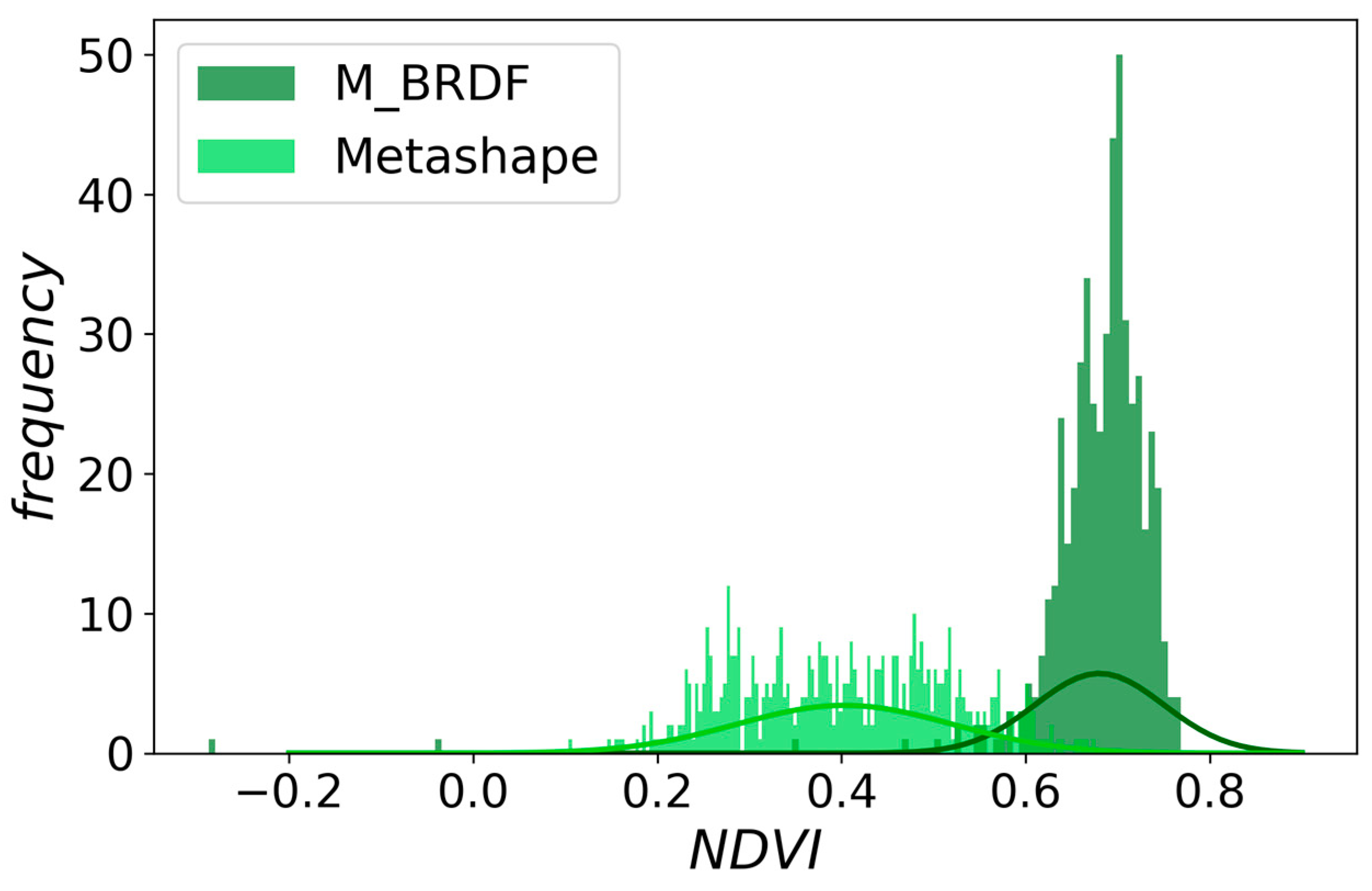
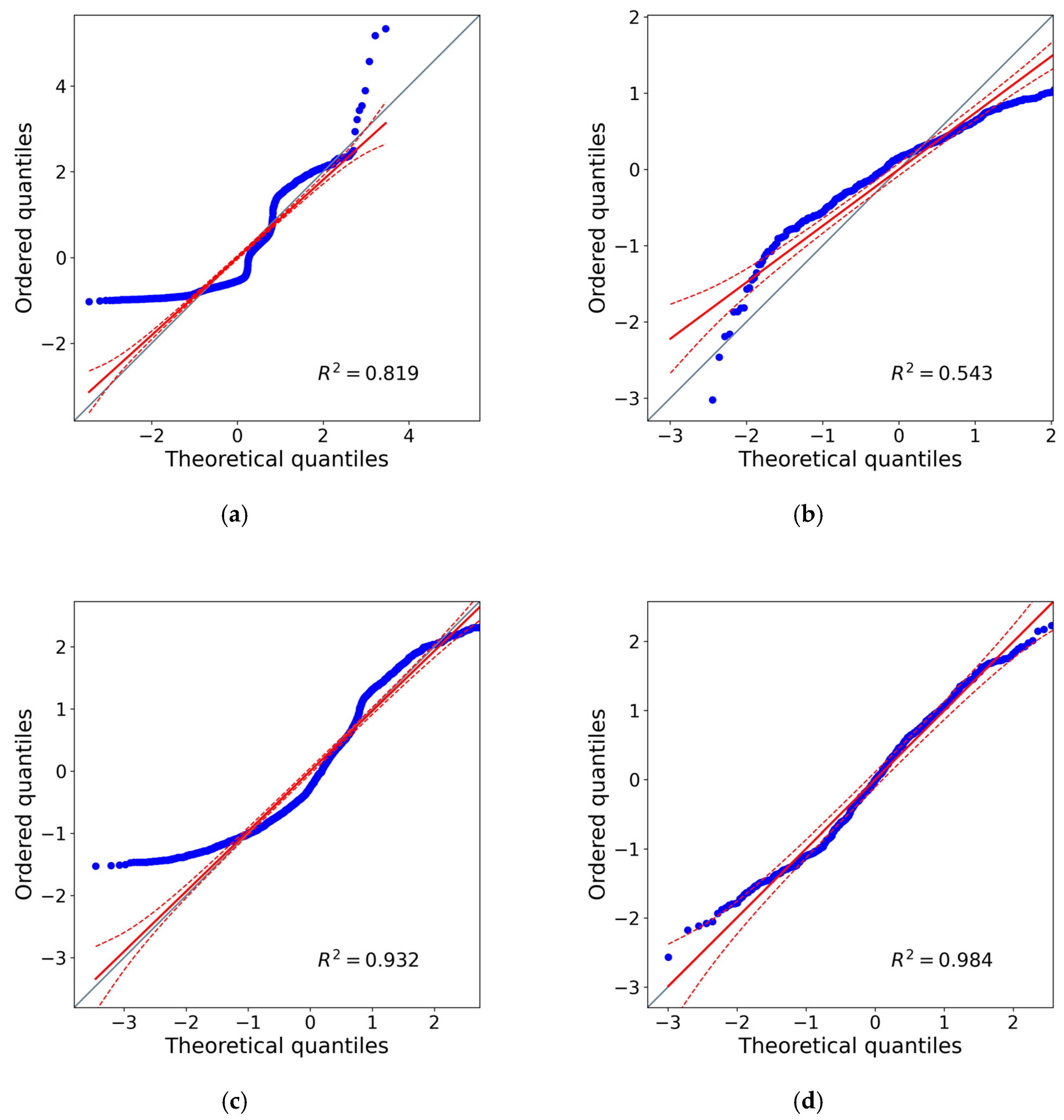
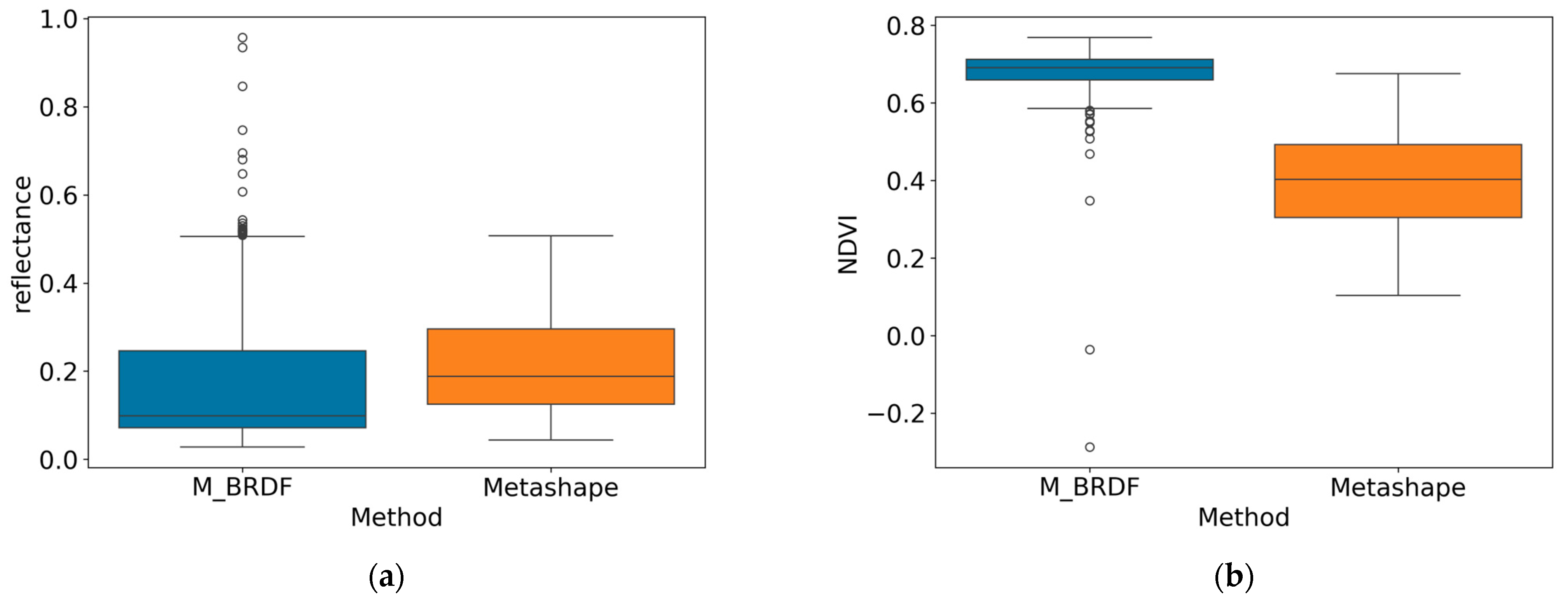
3.1. Reflectance Analysis per Band and NDVI
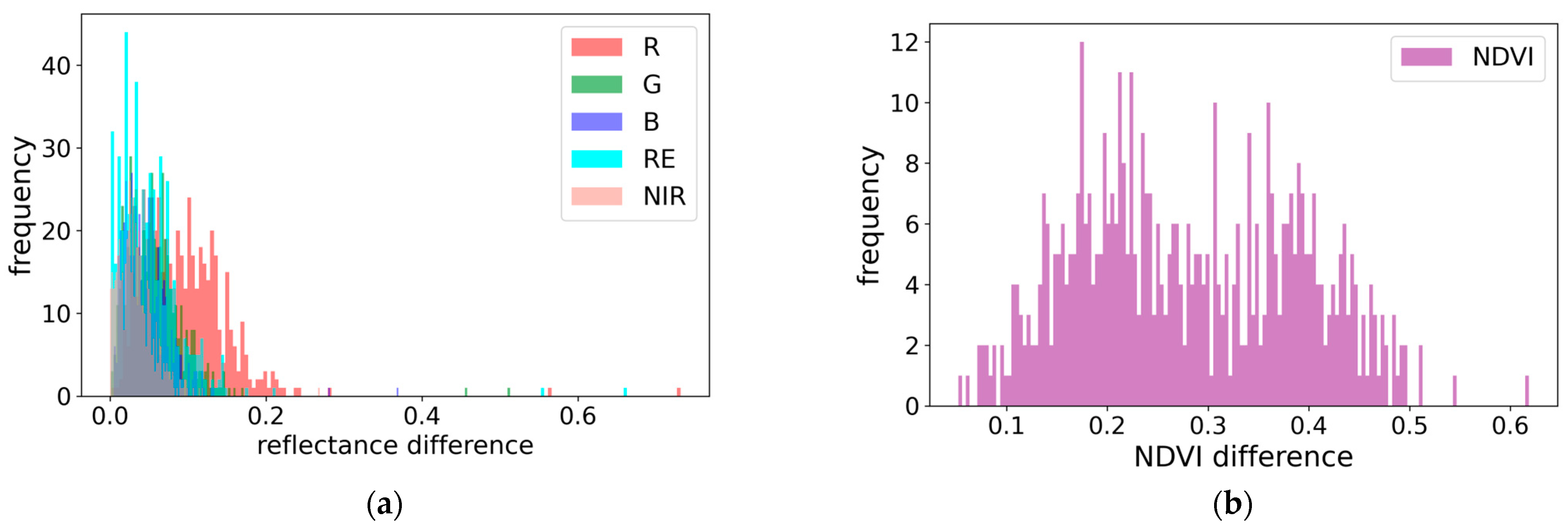
3.2. Spectral Band and NDVI Differences
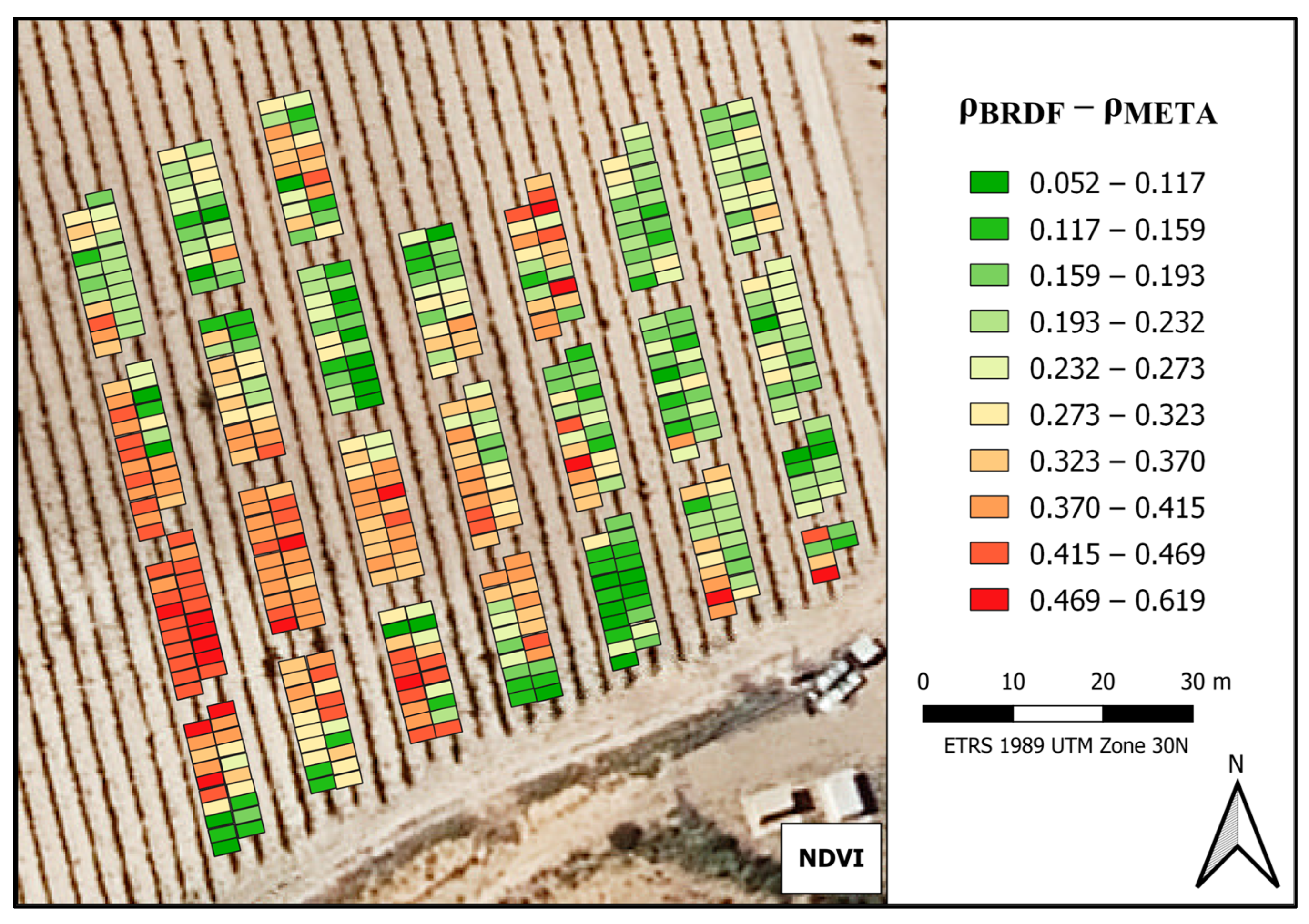
Spatial Analysis of the Differences
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Method | Band | Statistic W | p-Value |
|---|---|---|---|
| M_BRDF | R | 0.208354 | 1.289054 × 10−41 |
| G | 0.316521 | 1.448288 × 10−39 | |
| B | 0.311016 | 1.122708 × 10−39 | |
| RE | 0.541758 | 2.936743 × 10−34 | |
| NIR | 0.968362 | 5.374462 × 10−9 | |
| Metashape | R | 0.979078 | 0.000001 |
| G | 0.970273 | 1.283545 × 10−8 | |
| B | 0.972804 | 4.288144 × 10−8 | |
| RE | 0.97577 | 1.919421 × 10−7 | |
| NIR | 0.965455 | 1.515331 × 10−9 |

| A | B | U-Value | p-Value |
|---|---|---|---|
| M1.1 1 | M12 | 50,988.500 | 0.000 |
| M1.1 | M13 | 246,558.000 | 0.000 |
| M1.1 | M14 | 1060.500 | 0.000 |
| M1.1 | M15 | 1014.000 | 0.000 |
| M1.1 | M21 | 5304.500 | 0.000 |
| M1.1 | M22 | 5050.000 | 0.000 |
| M1.1 | M23 | 89,305.000 | 0.000 |
| M1.1 | M24 | 1014.000 | 0.000 |
| M1.1 | M25 | 1014.000 | 0.000 |
| M1.2 | M1 | 3,253,265.500 | 0.000 |
| M1.2 | M14 | 1513.000 | 0.000 |
| M1.2 | M15 | 1011.000 | 0.000 |
| M1.2 | M21 | 14,433.000 | 0.000 |
| M1.2 | M22 | 14,414.500 | 0.000 |
| M1.2 | M23 | 144,301.000 | 0.032 |
| M1.2 | M24 | 1103.500 | 0.000 |
| M1.2 | M25 | 1014.000 | 0.000 |
| M1.3 | M14 | 1011.000 | 0.000 |
| M1.3 | M15 | 456.500 | 0.000 |
| M1.3 | M21 | 1377.000 | 0.000 |
| M1.3 | M22 | 1439.000 | 0.000 |
| M1.3 | M23 | 11197.500 | 0.000 |
| M1.3 | M24 | 1005.000 | 0.000 |
| M1.3 | M25 | 602.500 | 0.000 |
| M1.4 | M15 | 1459.000 | 0.000 |
| M1.4 | M21 | 212,272.000 | 0.000 |
| M1.4 | M22 | 243,981.000 | 0.000 |
| M1.4 | M23 | 256,848.500 | 0.000 |
| M1.4 | M24 | 43,776.500 | 0.000 |
| M1.4 | M25 | 1624.000 | 0.000 |
| M1.5 | M21 | 256,930.000 | 0.000 |
| M1.5 | M22 | 257,049.000 | 0.000 |
| M1.5 | M23 | 257,049.000 | 0.000 |
| M15 | M24 | 255,821.000 | 0.000 |
| M15 | M25 | 176,590.000 | 0.000 |
| M21 | M22 | 163,985.000 | 0.000 |
| M21 | M23 | 240,322.500 | 0.000 |
| M21 | M24 | 13,782.000 | 0.000 |
| M21 | M25 | 304.000 | 0.000 |
| M22 | M23 | 237,125.000 | 0.000 |
| M22 | M24 | 2411.500 | 0.000 |
| M22 | M25 | 0.000 | 0.000 |
| M23 | M24 | 0.000 | 0.000 |
| M23 | M25 | 0.000 | 0.000 |
| M24 | M25 | 2506.500 | 0.000 |
References
- Jędrejek, A.; Pudełko, R. Exploring the Potential Use of Sentinel-1 and 2 Satellite Imagery for Monitoring Winter Wheat Growth under Agricultural Drought Conditions in North-Western Poland. Agriculture 2023, 13, 1798. [Google Scholar] [CrossRef]
- Radočaj, D.; Šiljeg, A.; Marinović, R.; Jurišić, M. State of Major Vegetation Indices in Precision Agriculture Studies Indexed in Web of Science: A Review. Agriculture 2023, 13, 707. [Google Scholar] [CrossRef]
- Xiong, Y.; Zhang, Z.; Fu, M.; Wang, L.; Li, S.; Wei, C.; Wang, L. Analysis of Vegetation Cover Change in the Geomorphic Zoning of the Han River Basin Based on Sustainable Development. Remote Sens. 2023, 15, 4916. [Google Scholar] [CrossRef]
- Chi, J.; Kim, J.-I.; Lee, S.; Jeong, Y.; Kim, H.-C.; Lee, J.; Chung, C. Geometric and Radiometric Quality Assessments of UAV-Borne Multi-Sensor Systems: Can UAVs Replace Terrestrial Surveys? Drones 2023, 7, 411. [Google Scholar] [CrossRef]
- Stow, D.; Nichol, C.J.; Wade, T.; Assmann, J.J.; Simpson, G.; Helfter, C. Illumination Geometry and Flying Height Influence Surface Reflectance and NDVI Derived from Multispectral UAS Imagery. Drones 2019, 3, 55. [Google Scholar] [CrossRef]
- Osco, L.P.; Junior, J.M.; Ramos, A.P.M.; Jorge, L.A.d.C.; Fatholahi, S.N.; Silva, J.d.A.; Matsubara, E.T.; Pistori, H.; Gonçalves, W.N.; Li, J. A Review on Deep Learning in UAV Remote Sensing. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102456. [Google Scholar] [CrossRef]
- Miyoshi, G.T.; Arruda, M.d.S.; Osco, L.P.; Marcato Junior, J.; Gonçalves, D.N.; Imai, N.N.; Tommaselli, A.M.G.; Honkavaara, E.; Gonçalves, W.N. A Novel Deep Learning Method to Identify Single Tree Species in UAV-Based Hyperspectral Images. Remote Sens. 2020, 12, 1294. [Google Scholar] [CrossRef]
- Bithas, P.S.; Michailidis, E.T.; Nomikos, N.; Vouyioukas, D.; Kanatas, A.G. A Survey on Machine-Learning Techniques for UAV-Based Communications. Sensors 2019, 19, 5170. [Google Scholar] [CrossRef]
- Bouguettaya, A.; Zarzour, H.; Kechida, A.; Taberkit, A.M. Deep Learning Techniques to Classify Agricultural Crops through UAV Imagery: A Review. Neural Comput. Appl. 2022, 34, 9511–9536. [Google Scholar] [CrossRef]
- López-García, P.; Intrigliolo, D.; Moreno, M.A.; Martínez-Moreno, A.; Ortega, J.F.; Pérez-Álvarez, E.P.; Ballesteros, R. Machine Learning-Based Processing of Multispectral and RGB UAV Imagery for the Multitemporal Monitoring of Vineyard Water Status. Agronomy 2022, 12, 2122. [Google Scholar] [CrossRef]
- Agisoft Metashape: Agisoft Metashape. Available online: https://www.agisoft.com/ (accessed on 18 October 2023).
- Herrero-Huerta, M.; Felipe-García, B.; Belmar-Lizarán, S.; Hernández-López, D.; Rodríguez-Gonzálvez, P.; González-Aguilera, D. Dense Canopy Height Model from a Low-Cost Photogrammetric Platform and LiDAR Data. Trees 2016, 30, 1287–1301. [Google Scholar] [CrossRef]
- Tucker, C.J. Spectral estimation of grass canopy variables. Remote Sens. Environ. 1977, 6, 11–26. [Google Scholar] [CrossRef]
- Ortega-Terol, D.; Hernandez-Lopez, D.; Ballesteros, R.; Gonzalez-Aguilera, D. Automatic Hotspot and Sun Glint Detection in UAV Multispectral Images. Sensors 2017, 17, 2352. [Google Scholar] [CrossRef]
- Tu, Y.-H.; Phinn, S.; Johansen, K.; Robson, A. Assessing Radiometric Correction Approaches for Multi-Spectral UAS Imagery for Horticultural Applications. Remote Sens. 2018, 10, 1684. [Google Scholar] [CrossRef]
- Verger i Ten, A.; Camacho-de Coca, F.; Melía, J. Revisión de los modelos paramétricos de BRDF. Rev. Teledetec. Rev. Asoc. Esp. Teledetec. 2005, 23, 65–80. [Google Scholar]
- Kim, M.; Jin, C.; Lee, S.; Kim, K.-M.; Lim, J.; Choi, C. Calibration of BRDF Based on the Field Goniometer System Using a UAV Multispectral Camera. Sensors 2022, 22, 7476. [Google Scholar] [CrossRef]
- Pan, Z.; Zhang, H.; Min, X.; Xu, Z. Vicarious Calibration Correction of Large FOV Sensor Using BRDF Model Based on UAV Angular Spectrum Measurements. J. Appl. Remote Sens. 2020, 14, 027501. [Google Scholar] [CrossRef]
- St»hle, L.; Wold, S. Analysis of Variance (ANOVA). Chemom. Intell. Lab. Syst. 1989, 6, 259–272. [Google Scholar] [CrossRef]
- Pour-Aboughadareh, A.; Mohammadi, R.; Etminan, A.; Shooshtari, L.; Maleki-Tabrizi, N.; Poczai, P. Effects of Drought Stress on Some Agronomic and Morpho-Physiological Traits in Durum Wheat Genotypes. Sustainability 2020, 12, 5610. [Google Scholar] [CrossRef]
- Calamai, A.; Masoni, A.; Marini, L.; Dell’acqua, M.; Ganugi, P.; Boukail, S.; Benedettelli, S.; Palchetti, E. Evaluation of the Agronomic Traits of 80 Accessions of Proso Millet (Panicum miliaceum L.) under Mediterranean Pedoclimatic Conditions. Agriculture 2020, 10, 578. [Google Scholar] [CrossRef]
- Azad, A.K.; Sarker, U.; Ercisli, S.; Assouguem, A.; Ullah, R.; Almeer, R.; Sayed, A.A.; Peluso, I. Evaluation of Combining Ability and Heterosis of Popular Restorer and Male Sterile Lines for the Development of Superior Rice Hybrids. Agronomy 2022, 12, 965. [Google Scholar] [CrossRef]
- Serrano, A.S.; Martínez-Gascueña, J.; Alonso, G.L.; Cebrián-Tarancón, C.; Carmona, M.D.; Mena, A.; Chacón-Vozmediano, J.L. Agronomic Response of 13 Spanish Red Grapevine (Vitis vinifera L.) Cultivars under Drought Conditions in a Semi-Arid Mediterranean Climate. Agronomy 2022, 12, 2399. [Google Scholar] [CrossRef]
- IGN. Atlas Nacional de España. Clima. Available online: http://atlasnacional.ign.es/wane/Clima (accessed on 18 October 2023).
- MicaSense Knowledge Base. Available online: https://support.micasense.com/hc/en-us (accessed on 18 October 2023).
- Taddia, Y.; Russo, P.; Lovo, S.; Pellegrinelli, A. Multispectral UAV Monitoring of Submerged Seaweed in Shallow Water. Appl. Geomat. 2020, 12, 19–34. [Google Scholar] [CrossRef]
- Hernandez-Lopez, D.; Felipe-Garcia, B.; Gonzalez-Aguilera, D.; Arias-Perez, B. An Automatic Approach to UAV Flight Planning and Control for Photogrammetric Applications. Photogramm. Eng. Remote Sens. 2013, 79, 87–98. [Google Scholar] [CrossRef]
- MicaSense RedEdge MX Processing Workflow (Including Reflectance Calibration) in Agisoft Metashape Professional. Available online: https://agisoft.freshdesk.com/support/solutions/articles/31000148780-micasense-rededge-mx-processing-workflow-including-reflectance-calibration-in-agisoft-metashape-pro (accessed on 18 October 2023).
- Walthall, C.L.; Norman, J.M.; Welles, J.M.; Campbell, G.; Blad, B.L. Simple Equation to Approximate the Bidirectional Reflectance from Vegetative Canopies and Bare Soil Surfaces. Appl. Opt. 1985, 24, 383–387. [Google Scholar] [CrossRef] [PubMed]
- Strahler, A.; Lucht, W.; Schaaf, C.; Tsang, T.; Gao, F.; Muller, J. MODIS BRDF/Albedo Product: Algorithm Theoretical Basis Document Version 5.0. MODIS Doc. 1999, 23, 42–47. [Google Scholar]
- MicaSense GitHub. Available online: https://micasense.github.io/imageprocessing/index.html (accessed on 18 October 2023).
- Cardinal, R.N.; Aitken, M.R.F. ANOVA for the Behavioral Sciences Researcher; Psychology Press: London, UK, 2013; ISBN 978-1-134-81410-7. [Google Scholar]
- Strunk, K.K.; Mwavita, M. Design and Analysis in Educational Research: ANOVA Designs in SPSS®; Routledge: London, UK, 2020; ISBN 978-0-429-78006-6. [Google Scholar]
- Rosner, B.; Grove, D. Use of the Mann–Whitney U-Test for Clustered Data. Stat. Med. 1999, 18, 1387–1400. [Google Scholar] [CrossRef]
- McKnight, P.E.; Najab, J. Mann-Whitney U Test. In The Corsini Encyclopedia of Psychology; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010; p. 1. ISBN 978-0-470-47921-6. [Google Scholar]
- Vargha, A.; Delaney, H.D. The Kruskal-Wallis Test and Stochastic Homogeneity. J. Educ. Behav. Stat. 1998, 23, 170–192. [Google Scholar] [CrossRef]
- Ostertagová, E.; Ostertag, O.; Kováč, J. Methodology and Application of the Kruskal-Wallis Test. Appl. Mech. Mater. 2014, 611, 115–120. [Google Scholar] [CrossRef]
- Yuen, K.K. The Two-Sample Trimmed t for Unequal Population Variances. Biometrika 1974, 61, 165–170. [Google Scholar] [CrossRef]
- Luh, W.-M.; Guo, J.-H. A Powerful Transformation Trimmed Mean Method for One-Way Fixed Effects ANOVA Model under Non-Normality and Inequality of Variances. Br. J. Math. Stat. Psychol. 1999, 52, 303–320. [Google Scholar] [CrossRef]
- Cabin, R.J.; Mitchell, R.J. To Bonferroni or Not to Bonferroni: When and How Are the Questions. Bull. Ecol. Soc. Am. 2000, 81, 246–248. [Google Scholar]
- TIDOP-USAL/ANOVA_BRDF: Non-Parametrical ANOVA Analysis for the BRDF. Available online: https://github.com/TIDOP-USAL/ANOVA_BRDF (accessed on 23 October 2023).
- Wen, J.; Liu, Q.; Xiao, Q.; Liu, Q.; You, D.; Hao, D.; Wu, S.; Lin, X. Characterizing Land Surface Anisotropic Reflectance over Rugged Terrain: A Review of Concepts and Recent Developments. Remote Sens. 2018, 10, 370. [Google Scholar] [CrossRef]
- Guo, Y.; Jia, X.; Paull, D. Superpixel-Based Adaptive Kernel Selection for Angular Effect Normalization of Remote Sensing Images With Kernel Learning. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4262–4271. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Li, X.; Strahler, A.H. Topographic Effects on Bidirectional and Hemispherical Reflectances Calculated with a Geometric-Optical Canopy Model. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1186–1193. [Google Scholar] [CrossRef]
- Petach, A.R.; Toomey, M.; Aubrecht, D.M.; Richardson, A.D. Monitoring vegetation phenology using an infrared-enabled security camera. Agric. For. Meteorol. 2014, 195, 143–151. [Google Scholar] [CrossRef]
- Filippa, G.; Cremonese, E.; Migliavacca, M.; Galvagno, M.; Sonnentag, O.; Humphreys, E.; Hufkens, K.; Ryu, Y.; Verfaillie, J.; di Cella, U.M.; et al. NDVI derived from near-infrared-enabled digital cameras: Applicability across different plant functional types. Agric. For. Meteorol. 2018, 249, 275–285. [Google Scholar] [CrossRef]
- Honkavaara, E.; Saari, H.; Kaivosoja, J.; Pölönen, I.; Hakala, T.; Litkey, P.; Mäkynen, J.; Pesonen, L. Processing and Assessment of Spectrometric, Stereoscopic Imagery Collected Using a Lightweight UAV Spectral Camera for Precision Agriculture. Remote Sens. 2013, 5, 5006–5039. [Google Scholar] [CrossRef]







| Weight | 170 g (including DSL) |
| Dimensions | 9.4 cm × 6.3 cm × 4.6 cm |
| External power | 4.2 V–15.8 V, 4 W nominal, 8 W peak |
| GSD | 8.2 cm/pixel at 120 m AGL |
| Blue spectral band | Centre wavelength: 475 nm Bandwidth FWHM: 20 nm |
| Green spectral band | centre wavelength: 560 nm Bandwidth FWHM: 20 nm |
| Red spectral band | Centre wavelength: 668 nm Bandwidth FWHM: 10 nm |
| Red edge spectral band | centre wavelength: 717 nm Bandwidth FWHM: 10 nm |
| NIR spectral band | Centre wavelength: 840 nm Bandwidth FWHM: 40 nm |
| Markers | Easting (m) | Northing (m) | Altitude (m) | Error (m) |
|---|---|---|---|---|
| 2 | 632,939.341 | 4,288,036.966 | 830.224 | 0.0046 |
| 3 | 632,805.756 | 4,288,019.635 | 830.205 | 0.0064 |
| 4 | 632,659.743 | 4,288,040.656 | 835.192 | 0.0007 |
| 5 | 632,741.361 | 4,287,895.546 | 825.769 | 0.0083 |
| 6 | 632,796.057 | 4,287,767.781 | 822.259 | 0.0195 |
| 7 | 632,884.765 | 4,287,736.708 | 821.987 | 0.0173 |
| 8 | 632,973.799 | 4,287,784.585 | 818.104 | 0.0034 |
| 9 | 632,956.238 | 4,287,898.923 | 823.163 | 0.0068 |
| M_BRDF | Metashape | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R | G | B | RE | NIR | R | G | B | RE | NIR | |
| Mean | 0.084 | 0.099 | 0.051 | 0.230 | 0.429 | 0.174 | 0.152 | 0.093 | 0.273 | 0.401 |
| Std. | 0.050 | 0.038 | 0.026 | 0.054 | 0.045 | 0.049 | 0.033 | 0.026 | 0.037 | 0.038 |
| Min. | 0.055 | 0.060 | 0.028 | 0.135 | 0.299 | 0.074 | 0.085 | 0.044 | 0.196 | 0.323 |
| 25% | 0.071 | 0.087 | 0.042 | 0.205 | 0.397 | 0.136 | 0.129 | 0.073 | 0.248 | 0.370 |
| 50% | 0.079 | 0.095 | 0.047 | 0.225 | 0.423 | 0.172 | 0.149 | 0.091 | 0.270 | 0.394 |
| 75% | 0.087 | 0.105 | 0.053 | 0.246 | 0.459 | 0.206 | 0.169 | 0.109 | 0.293 | 0.431 |
| Max. | 0.934 | 0.680 | 0.473 | 0.957 | 0.695 | 0.389 | 0.296 | 0.195 | 0.427 | 0.507 |
| M_BRDF | Metashape | |
|---|---|---|
| Mean | 0.680 | 0.403 |
| Std. | 0.070 | 0.117 |
| Min. | −0.287 | 0.104 |
| 25% | 0.659 | 0.304 |
| 50% | 0.691 | 0.403 |
| 75% | 0.712 | 0.493 |
| Max. | 0.769 | 0.675 |
| Method | Data | Statistic W | p-Value |
|---|---|---|---|
| M_BRDF | Reflectance | 0.818758 | 0.0 |
| NDVI | 0.552042 | 5.717402 × 10−34 | |
| Metashape | Reflectance | 0.931502 | 1.305781 × 10−32 |
| NDVI | 0.98261 | 0.000009 |
| Test | Data | Statistic | p-Value |
|---|---|---|---|
| Mann–Whitney U test | Reflectances | 2,254,515.5 | 0.000 |
| NDVI | 253,900.0 | 0.000 | |
| Kruskal–Wallis H test | Reflectances | 338.385 | 0.000 |
| Band | 4637.855 | 0.000 | |
| NDVI | 722.978 | 0.000 | |
| Yuen t-test | Reflectances | 2291.348 | 0.000 |
| NDVI | 41.920 | 1.6245 × 10−181 |
| ∆R | ∆G | ∆B | ∆RE | ∆NIR | ∆NDVI | |
|---|---|---|---|---|---|---|
| Mean | 0.095 | 0.057 | 0.045 | 0.050 | 0.034 | 0.281 |
| Std. | 0.058 | 0.041 | 0.031 | 0.049 | 0.027 | 0.109 |
| Min. | 0.002 | 0.001 | 0.005 | 0.001 | 0.000 | 0.052 |
| 25% | 0.055 | 0.030 | 0.024 | 0.022 | 0.017 | 0.193 |
| 50% | 0.089 | 0.053 | 0.041 | 0.043 | 0.029 | 0.270 |
| 75% | 0.125 | 0.073 | 0.061 | 0.067 | 0.045 | 0.375 |
| Max. | 0.732 | 0.513 | 0.370 | 0.663 | 0.284 | 0.619 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrés-Anaya, P.; Molada-Tebar, A.; Hernández-López, D.; Moreno, M.Á.; González-Aguilera, D.; Herrero-Huerta, M. Radiometric Improvement of Spectral Indices Using Multispectral Lightweight Sensors Onboard UAVs. Drones 2024, 8, 36. https://doi.org/10.3390/drones8020036
Andrés-Anaya P, Molada-Tebar A, Hernández-López D, Moreno MÁ, González-Aguilera D, Herrero-Huerta M. Radiometric Improvement of Spectral Indices Using Multispectral Lightweight Sensors Onboard UAVs. Drones. 2024; 8(2):36. https://doi.org/10.3390/drones8020036
Chicago/Turabian StyleAndrés-Anaya, Paula, Adolfo Molada-Tebar, David Hernández-López, Miguel Ángel Moreno, Diego González-Aguilera, and Mónica Herrero-Huerta. 2024. "Radiometric Improvement of Spectral Indices Using Multispectral Lightweight Sensors Onboard UAVs" Drones 8, no. 2: 36. https://doi.org/10.3390/drones8020036
APA StyleAndrés-Anaya, P., Molada-Tebar, A., Hernández-López, D., Moreno, M. Á., González-Aguilera, D., & Herrero-Huerta, M. (2024). Radiometric Improvement of Spectral Indices Using Multispectral Lightweight Sensors Onboard UAVs. Drones, 8(2), 36. https://doi.org/10.3390/drones8020036









