A High Performance Nonlinear Longitudinal Controller for Fixed-Wing UAVs Based on Fuzzy-Guaranteed Cost Control
Abstract
1. Introduction
- (1)
- A novel controller structure is proposed to decouple the complex propulsion system from the longitudinal controller using a look-up table approach. This significantly reduces the model’s complexity while maintaining control precision, offering a more efficient solution for UAV control systems.
- (2)
- A new stability criterion based on the T–S fuzzy model for the longitudinal control of fixed-wing UAVs is derived to ensure the global asymptotic stability of the designed nonlinear state-feedback controller, providing a more robust stability framework compared to existing methods.
- (3)
- Comprehensive simulation results, including a detailed comparison with the traditional linear controller and ADRC controller, demonstrate the effectiveness and superiority of the proposed controller, highlighting its potential for advanced UAV control applications.
2. Fixed-Wing UAV Model Description
3. Model of the Propulsion System
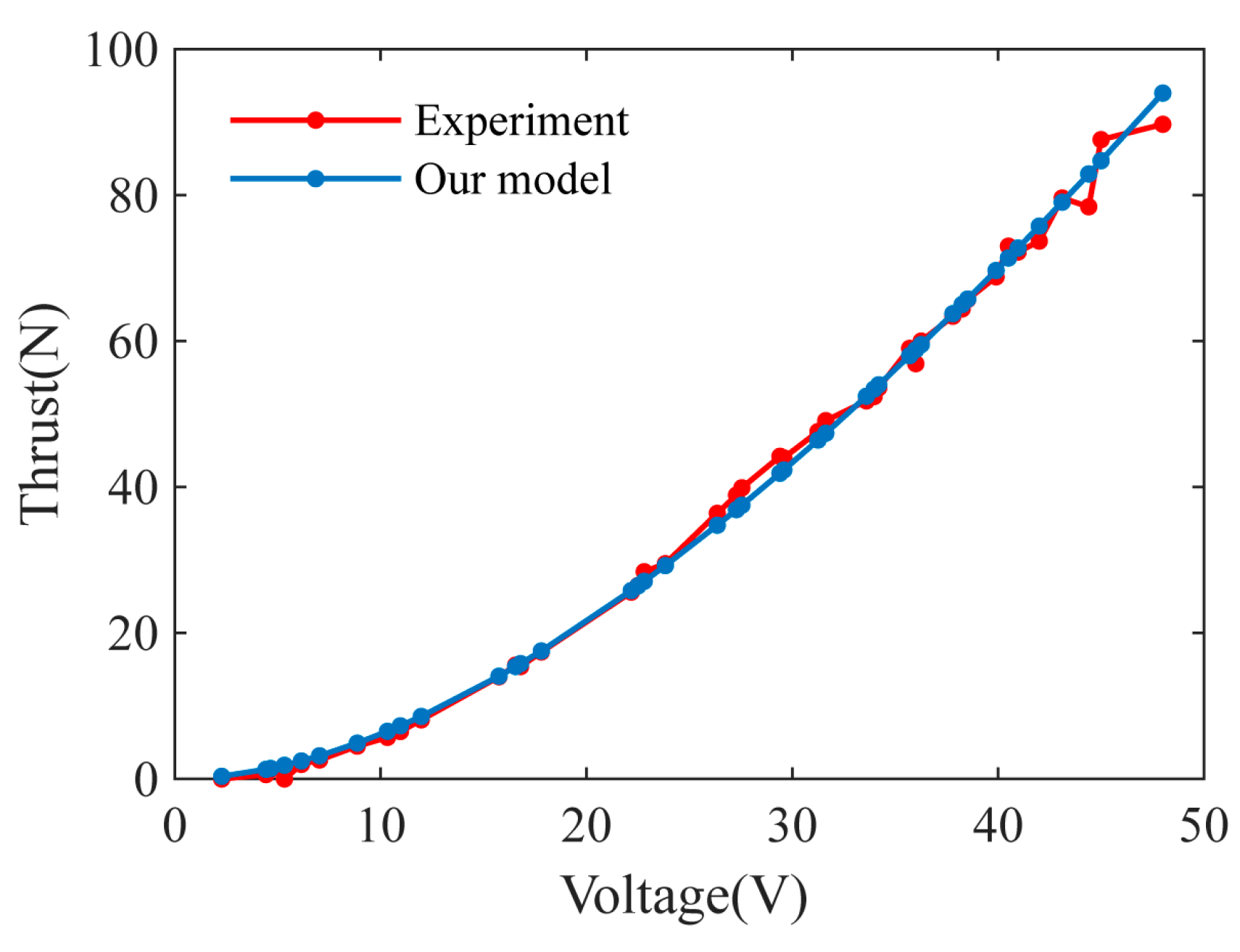
3.1. Motor Model Description
3.2. Propeller Model Description
4. Fuzzy-Guaranteed Cost Controller Design
4.1. T–S Fuzzy Model of the Fixed-Wing System
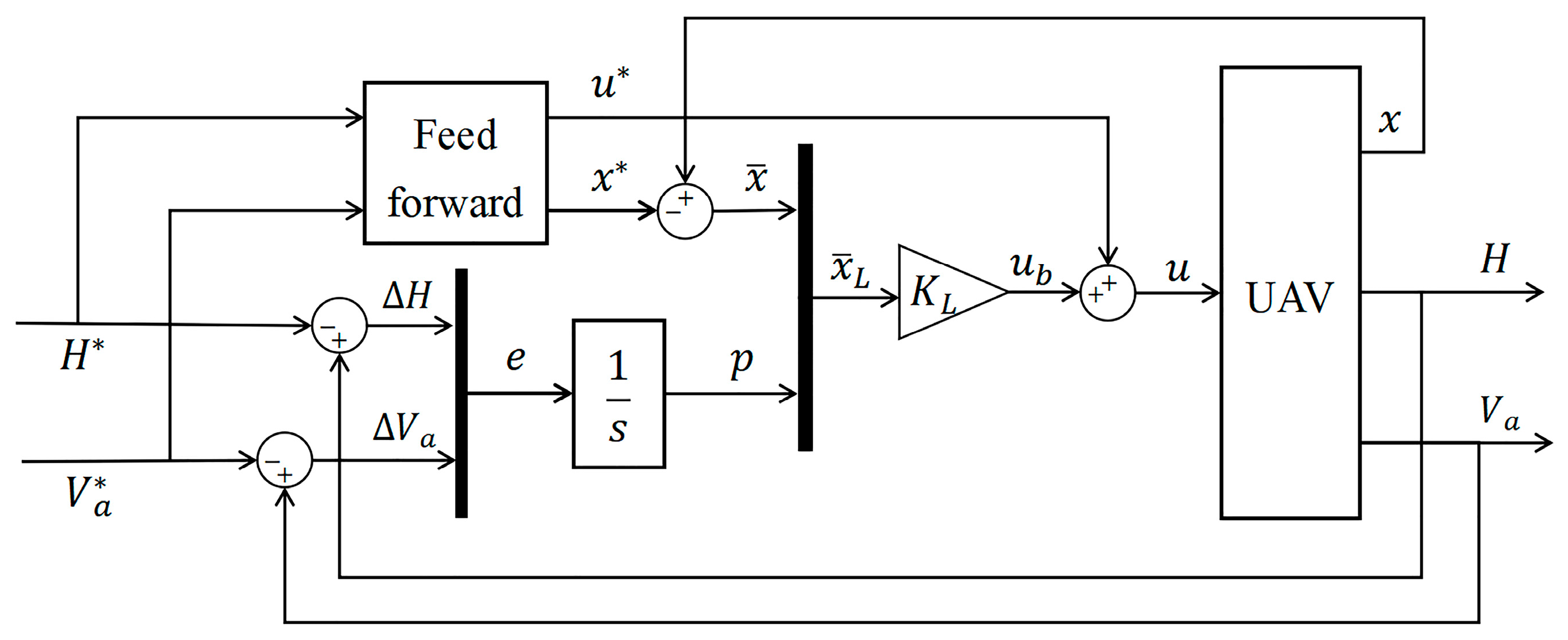
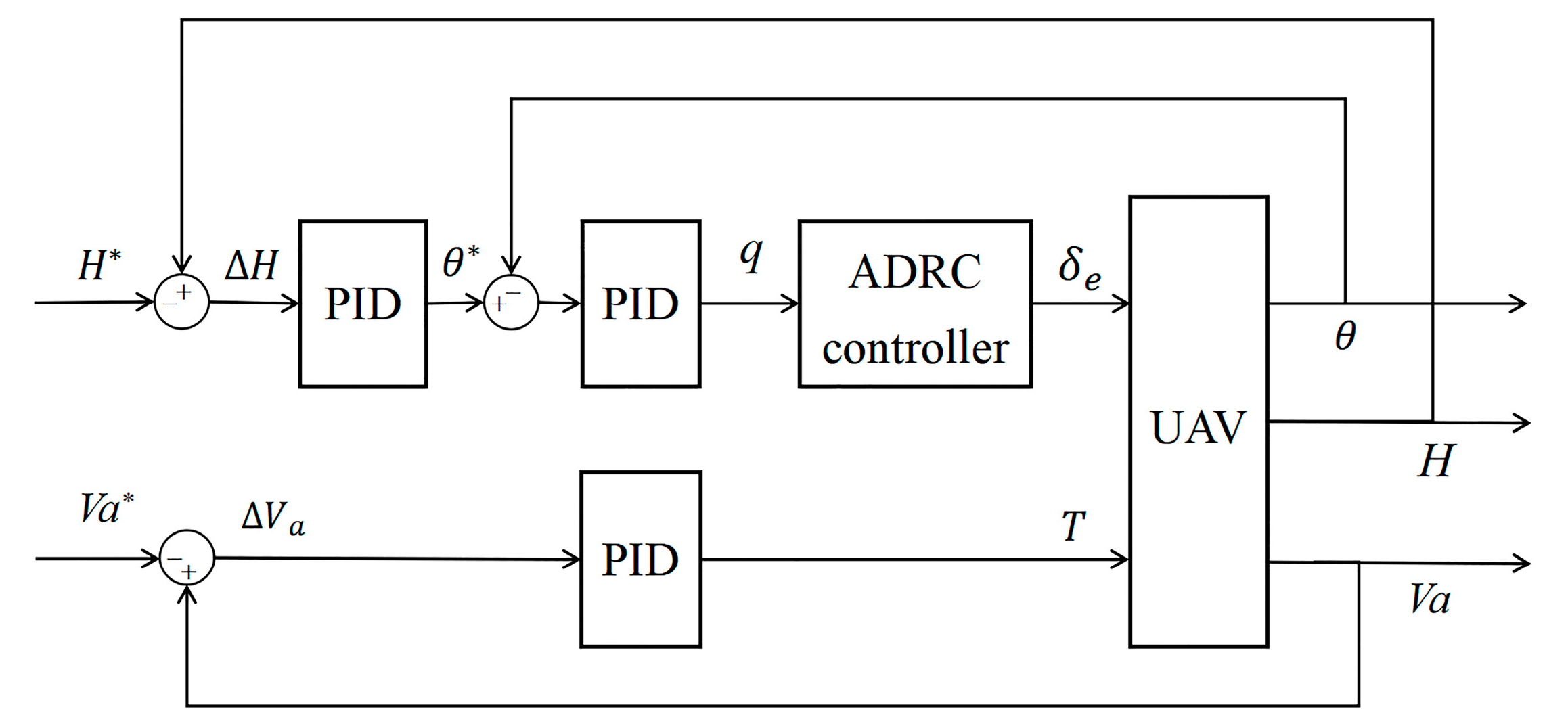
4.2. Controller Structure Design
4.3. T–S Fuzzy-Based Feedback Controller
4.4. The LMI Formulation for Guaranteed Cost Control
5. Results and Discussion
- (1)
- Altitude command.
- (2)
- Lateral motion coupling.
- (3)
- Parameter errors.
- (4)
- Gust wind and turbulence.
5.1. Numerical Experiments of the Propulsion Model
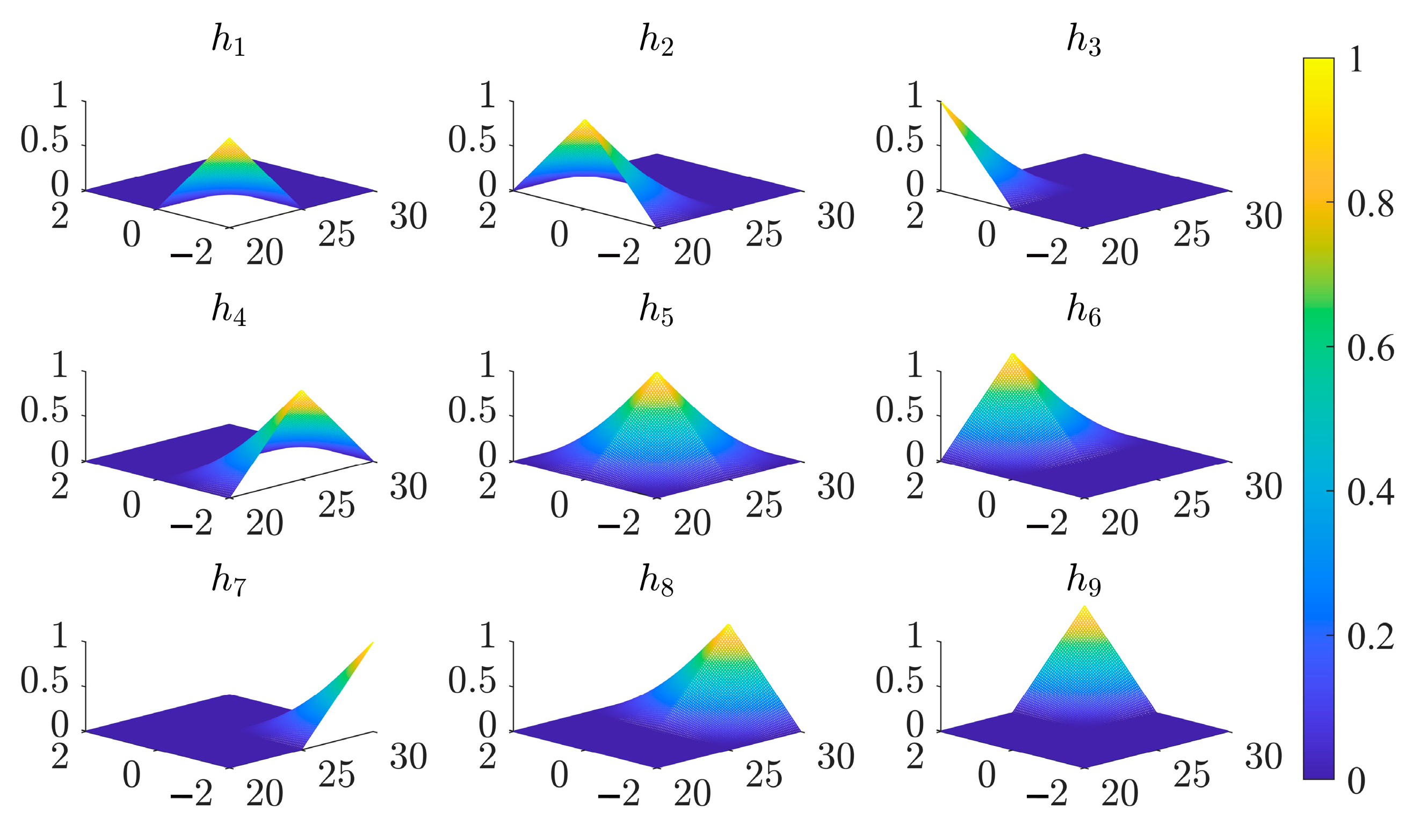
5.2. Definition of the Fuzzy Rules
- (1)
- The sum of all membership degrees equals 1, i.e., ;
- (2)
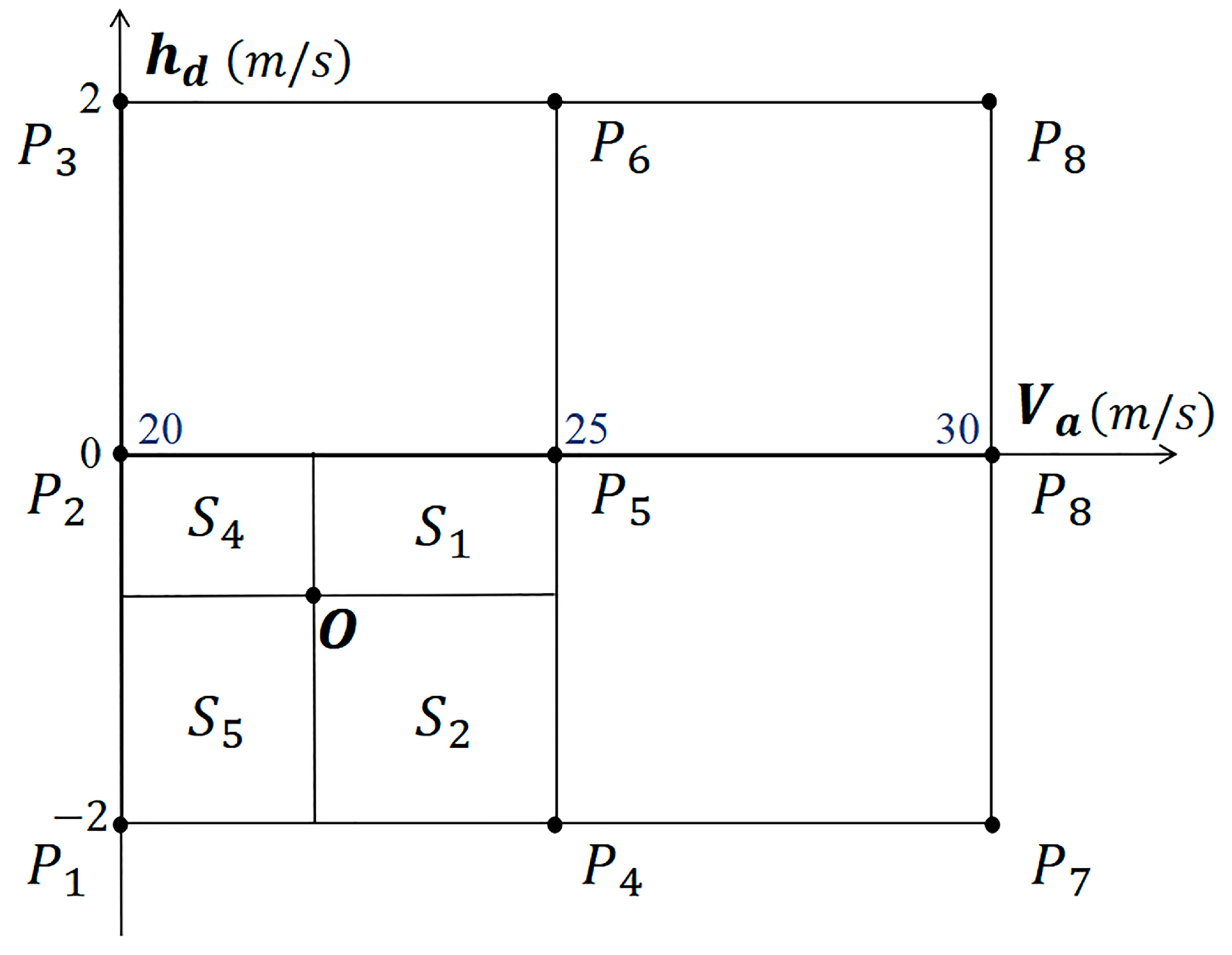
- Only parameters from adjacent operating points are connected by the membership degrees. For example, as shown in Figure 8, in the domain enclosed by , only the parameters of , , , and contribute to the control, rendering ;
- (3)
- Given that the area of the domain enclosed by four adjacent operating points is , when the operating point representing the actual state is inside this area, this area can be divided into four sub-domains with two lines crossing the point O and vertical to the axis. The membership degree of each operating point concerning the actual state is defined as the ratio of its diagonal domain area to the total domain area. Taking Figure 8 as an example, the membership degree function is expressed as
5.3. The Comparative Candidate
5.4. Parameters of the UAV and the F-GCC Controller
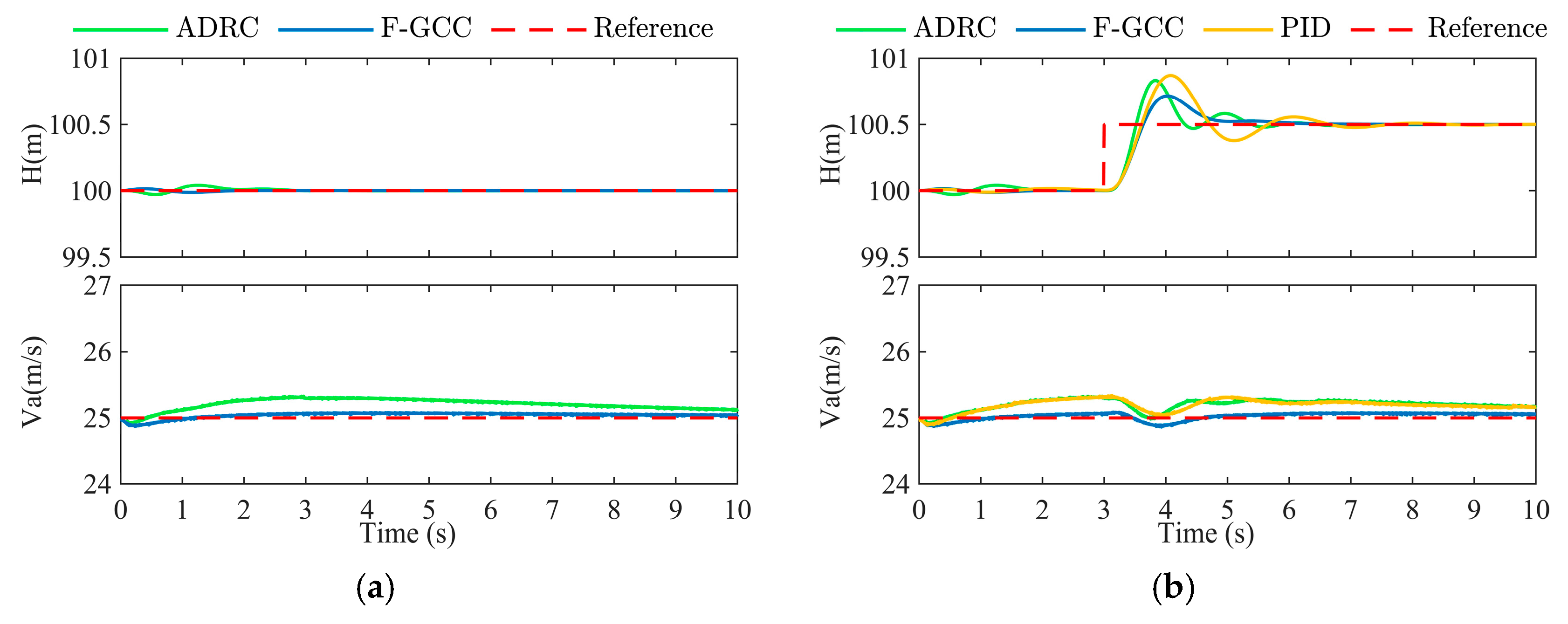
5.5. Experiments of the Altitude Command
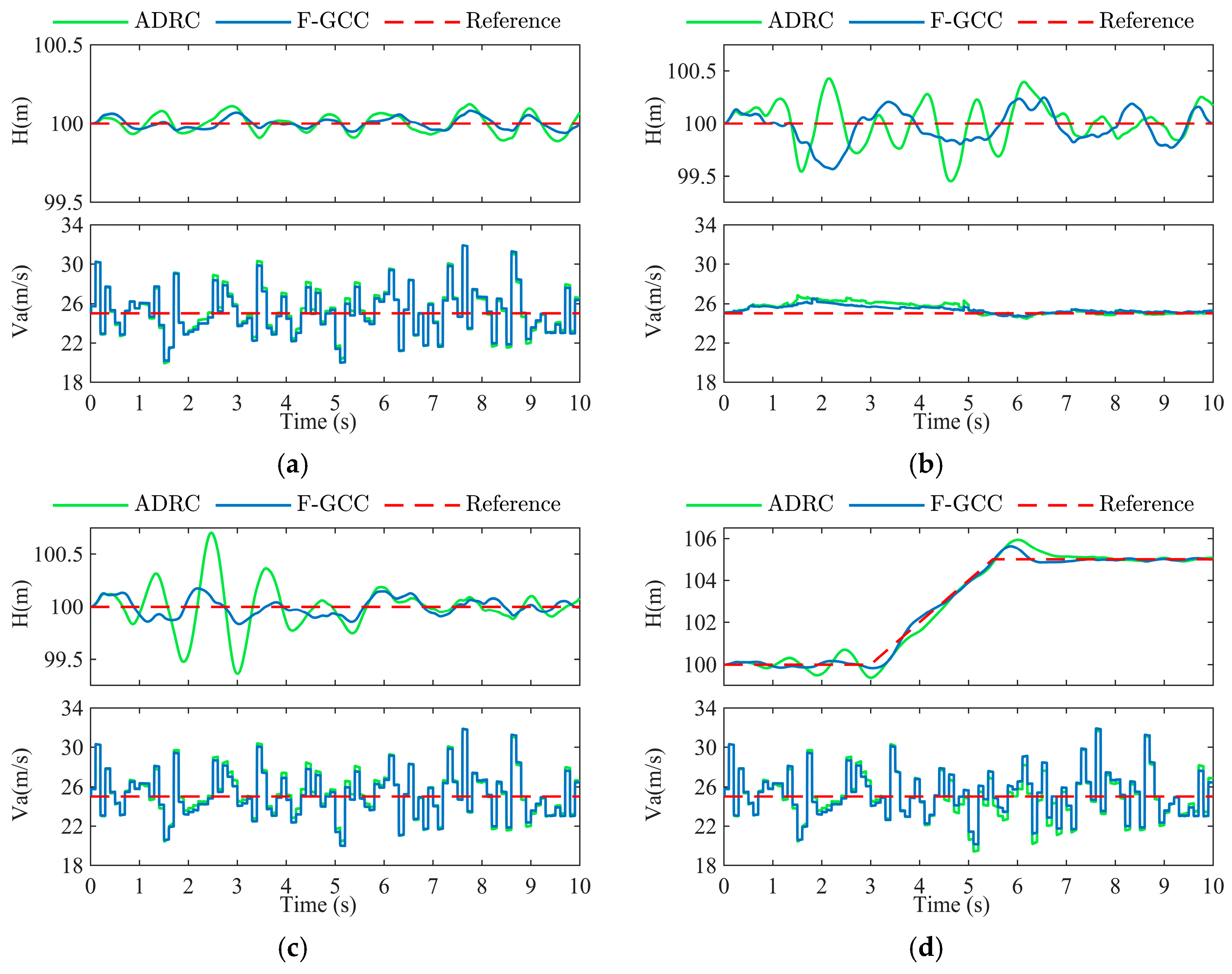
5.6. Experiment with Unknown Disturbances
5.6.1. Lateral Disturbance Experiment (Case 5)
5.6.2. Parameter Variation Experiment (Case 6)
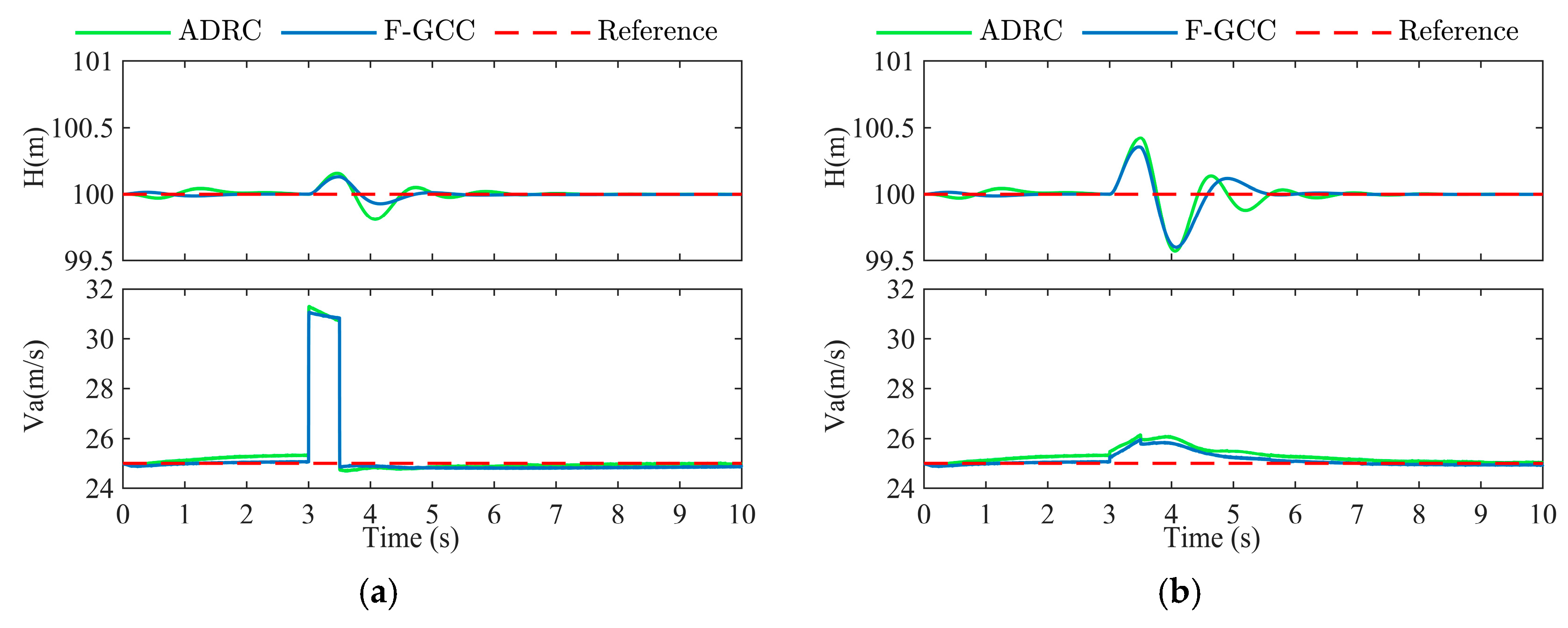
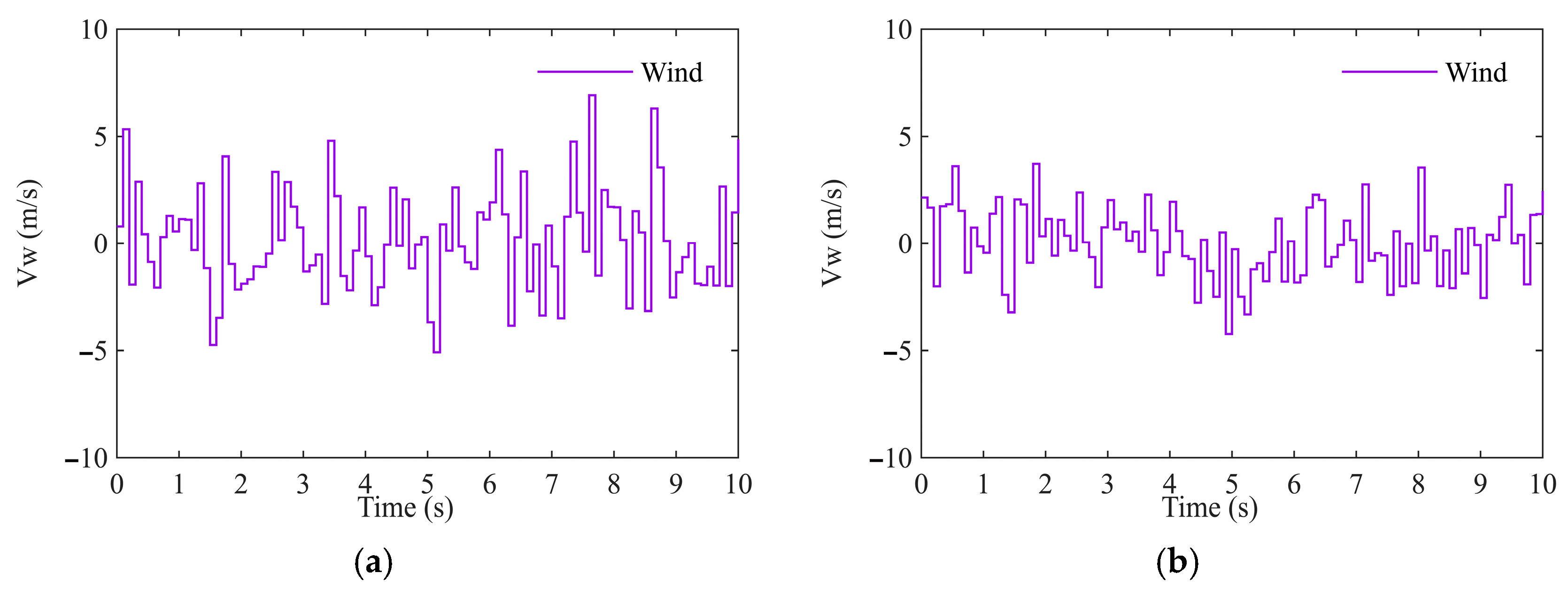
5.6.3. External Disturbance Experiment (Case 7 and Case 8)
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Feedback Gain | Values | ||||||
|---|---|---|---|---|---|---|---|
| 0.617 | 0.482 | −14.136 | −1.884 | −1.294 | −1.327 | 0.086 | |
| −22.556 | 2.719 | −45.448 | −7.083 | −10.765 | −2.056 | −2.677 | |
| 0.747 | 0.487 | −14.226 | −1.916 | −1.249 | −1.328 | 0.101 | |
| −22.070 | 2.961 | −49.634 | −7.985 | −11.208 | −2.424 | −2.685 | |
| 0.827 | 0.493 | −14.313 | −1.942 | −1.221 | −1.329 | 0.111 | |
| −21.689 | 3.109 | −51.591 | −8.385 | −11.371 | −2.507 | −2.703 | |
| 0.005 | 0.411 | −11.350 | −1.547 | −1.220 | −1.041 | 0.010 | |
| −23.360 | −0.284 | 6.418 | 3.587 | −8.122 | 0.341 | −2.761 | |
| 0.024 | 0.412 | −11.369 | −1.552 | −1.212 | −1.038 | 0.012 | |
| −23.101 | −0.243 | 5.989 | 3.414 | −8.100 | 0.395 | −2.770 | |
| 0.033 | 0.412 | −11.387 | −1.557 | −1.205 | −1.034 | 0.014 | |
| −22.784 | −0.251 | 6.692 | 3.487 | −7.936 | 0.561 | −2.773 | |
| −0.201 | 0.350 | −9.529 | −1.265 | −1.024 | −0.786 | −0.017 | |
| −23.100 | −2.059 | 40.739 | 10.083 | −6.150 | 1.827 | −2.713 | |
| −0.180 | 0.348 | −9.510 | −1.263 | −1.013 | −0.784 | −0.015 | |
| −22.788 | −2.035 | 40.635 | 9.942 | −6.106 | 1.864 | −2.709 | |
| −0.168 | 0.347 | −9.496 | −1.261 | −1.006 | −0.782 | −0.013 | |
| −22.437 | −2.055 | 41.406 | 10.033 | −5.994 | 1.965 | −2.707 | |
References
- Van Blyenburgh, P. UAVs: An Overview. Air Space Eur. 1999, 1, 43–47. [Google Scholar] [CrossRef]
- Nex, F.; Armenakis, C.; Cramer, M.; Cucci, D.; Gerke, M.; Honkavaara, E.; Kukko, A.; Persello, C.; Skaloud, J. UAV in the Advent of the Twenties: Where We Stand and What Is Next. ISPRS J. Photogramm. Remote Sens. 2022, 184, 215–242. [Google Scholar] [CrossRef]
- Eckel, L.; Stütz, P. Hyperspectral Sensor Management for UAS: Performance Analysis of Context-Based System Architectures for Camouflage and UXO Anomaly Detection Workflows. Drones 2024, 8, 529. [Google Scholar] [CrossRef]
- Martínez-Carricondo, P.; Agüera-Vega, F.; Carvajal-Ramírez, F.; Mesas-Carrascosa, F.; García-Ferrer, A.; Pérez-Porras, F. Assessment of UAV-Photogrammetric Mapping Accuracy Based on Variation of Ground Control Points. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 1–10. [Google Scholar] [CrossRef]
- Elkhrachy, I. Accuracy Assessment of Low-Cost Unmanned Aerial Vehicle (UAV) Photogrammetry. Alex. Eng. J. 2021, 60, 5579–5590. [Google Scholar] [CrossRef]
- Siddiqi, M.A.; Iwendi, C.; Jaroslava, K.; Anumbe, N. Analysis on Security-Related Concerns of Unmanned Aerial Vehicle: Attacks, Limitations, and Recommendations. Math. Biosci. Eng. 2022, 19, 2641–2670. [Google Scholar] [CrossRef]
- Yaacoub, J.; Noura, H.; Salman, O.; Chehab, A. Security Analysis of Drones Systems: Attacks, Limitations, and Recommendations. Internet Things 2020, 11, 100218. [Google Scholar] [CrossRef] [PubMed]
- Azar, A.T.; Serrano, F.E.; Kamal, N.A.; Koubaa, A. Decoupled Lateral-Longitudinal Dynamic Modeling and Control of Unmanned Aerial Vehicles. In Proceedings of the 2021 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Santa Maria da Feira, Portugal, 28–29 April 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 117–122. [Google Scholar]
- Liu, C.; Chen, W. Disturbance Rejection Flight Control for Small Fixed-Wing Unmanned Aerial Vehicles. J. Guid. Control Dyn. 2016, 39, 2810–2819. [Google Scholar] [CrossRef]
- Susanto, T.; Bayu Setiawan, M.; Jayadi, A.; Rossi, F.; Hamdhi, A.; Persada Sembiring, J. Application of Unmanned Aircraft PID Control System for Roll, Pitch and Yaw Stability on Fixed Wings. In Proceedings of the 2021 International Conference on Computer Science, Information Technology, and Electrical Engineering (ICOMITEE), Banyuwangi, Indonesia, 27–28 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 186–190. [Google Scholar]
- Elsayed, A.; Hafez, A.; Ouda, A.N.; Ahmed, H.E.H.; Abd-Elkader, H.M. Design of Longitudinal Motion Controller of a Small Unmanned Aerial Vehicle. Int. J. Intell. Syst. Appl. 2015, 7, 37–47. [Google Scholar] [CrossRef][Green Version]
- Xu, P.; Wu, Y.; Zuo, J.; Cheng, L. Longitudinal Attitude Control of UAV Based on Fuzzy PID. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Wang, S.; Yao, G.; Chen, F. Cascade PID Attitude Control Based on Adaptive Feedforward Compensation for Fixed-Wing UAV. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 5006–5010. [Google Scholar]
- Sadeghzadeh, I.; Zhang, Y. Actuator Fault-Tolerant Control Based on Gain-Scheduled PID with Application to Fixed-Wing Unmanned Aerial Vehicle. In Proceedings of the 2013 Conference on Control and Fault-Tolerant Systems (SysTol), Nice, France, 9–11 October 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 342–346. [Google Scholar]
- Poksawat, P.; Wang, L.; Mohamed, A. Gain Scheduled Attitude Control of Fixed-Wing UAV with Automatic Controller Tuning. IEEE Trans. Control Syst. Technol. 2018, 26, 1192–1203. [Google Scholar] [CrossRef]
- Melo, A.; Andrade, F.; Guedes, I.; Carvalho, G.; Zachi, A.; Pinto, M. Fuzzy Gain-Scheduling PID for UAV Position and Altitude Controllers. Sensors 2022, 22, 2173. [Google Scholar] [CrossRef] [PubMed]
- Sankaranarayanan, V.; Mahindrakar, A. Control of a Class of Underactuated Mechanical Systems Using Sliding Modes. IEEE Trans. Robot. 2009, 25, 459–467. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, W.; Suzuki, S. UAV Trajectory Tracking under Wind Disturbance Based on Novel Antidisturbance Sliding Mode Control. Aerosp. Sci. Technol. 2024, 149, 109138. [Google Scholar] [CrossRef]
- Irfan, S.; Zhao, L.; Ullah, S.; Javaid, U.; Iqbal, J. Differentiator- and Observer-Based Feedback Linearized Advanced Nonlinear Control Strategies for an Unmanned Aerial Vehicle System. Drones 2024, 8, 527. [Google Scholar] [CrossRef]
- Lungu, M. Auto-Landing of Fixed Wing Unmanned Aerial Vehicles Using the Backstepping Control. ISA Trans. 2019, 95, 194–210. [Google Scholar] [CrossRef]
- Wang, J.; Alattas, K.A.; Bouteraa, Y.; Mofid, O.; Mobayen, S. Adaptive Finite-Time Backstepping Control Tracker for Quadrotor UAV with Model Uncertainty and External Disturbance. Aerosp. Sci. Technol. 2023, 133, 108088. [Google Scholar] [CrossRef]
- Lane, S.; Stengel, R. Flight Control Design Using Nonlinear Inverse Dynamics. In Proceedings of the 1986 American Control Conference, Seattle, WA, USA, 18–20 June 1986; IEEE: Piscataway, NJ, USA, 1986; pp. 587–596. [Google Scholar]
- Pashilkar, A.; Ismail, S.; Ayyagari, R.; Sundararajan, N. Design of a Nonlinear Dynamic Inversion Controller for Trajectory Following and Maneuvering for Fixed Wing Aircraft. In Proceedings of the 2013 IEEE Symposium on Computational Intelligence for Security and Defense Applications (CISDA), Singapore, 16–19 April 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 64–71. [Google Scholar]
- Lungu, M. Auto-Landing of UAVs with Variable Centre of Mass Using the Backstepping and Dynamic Inversion Control. Aerosp. Sci. Technol. 2020, 103, 105912. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, J.; Yuan, X.; Wang, X.; Kuang, M.; Shi, H. Dynamic Characteristics Analysis and Robust Transition Control of Tail-Sitter VTOL UAVs. Aerosp. Sci. Technol. 2024, 145, 108868. [Google Scholar] [CrossRef]
- Putro, I.; Duhri, R. Longitudinal Stability Augmentation Control for Turbojet UAV Based on Linear Quadratic Regulator (LQR) Approach. AIP Conf. Proc. 2020, 2226, 020013. [Google Scholar]
- Niu, T.; Xiong, H.; Zhao, S. Based on ADRC UAV Longitudinal Pitching Angle Control Research. In Proceedings of the 2016 IEEE Information Technology, Networking, Electronic and Automation Control Conference, Chongqing, China, 20–22 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 21–25. [Google Scholar]
- Zhu, G.; Qi, J.; Wu, C. Landing Control of Fixed-Wing UAV Based on ADRC. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 8020–8025. [Google Scholar]
- Bie, G.; Chen, X. UAV Trajectory Tracking Based on ADRC Control Algorithm. ITM Web Conf. 2022, 47, 02017. [Google Scholar] [CrossRef]
- Wang, B.; Yan, Y.; Xiong, X.; Han, Q.; Li, Z. Attitude Control of Small Fixed−Wing UAV Based on Sliding Mode and Linear Active Disturbance Rejection Control. Drones 2024, 8, 318. [Google Scholar] [CrossRef]
- Hervas, J.; Kayacan, E.; Reyhanoglu, M.; Tang, H. Sliding Mode Control of Fixed-Wing UAVs in Windy Environments. In Proceedings of the 2014 13th International Conference on Control Automation Robotics & Vision (ICARCV), Singapore, 10–12 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 986–991. [Google Scholar]
- Lee, H.; Utkin, V. Chattering Suppression Methods in Sliding Mode Control Systems. Annu. Rev. Control 2007, 31, 179–188. [Google Scholar] [CrossRef]
- Putro, I.; Sofyan, S.; Andiarti, R. Incremental Control for LAPAN Turbojet UAV Considering Disturbance and Uncertainties. In Proceedings of the 2019 IEEE International Conference on Aerospace Electronics and Remote Sensing Technology (ICARES), Yogyakarta, Indonesia, 17–18 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–8. [Google Scholar]
- Razmjooei, H.; Palli, G.; Abdi, E.; Strano, S.; Terzo, M. Finite-Time Continuous Extended State Observers: Design and Experimental Validation on Electro-Hydraulic Systems. Mechatronics 2022, 85, 102812. [Google Scholar] [CrossRef]
- Blanchini, F.; Miani, S.; Rinaldi, F. Guaranteed Cost Control for Multi-Inventory Systems with Uncertain Demand. Automatica 2004, 40, 213–223. [Google Scholar] [CrossRef]
- Chang, S.; Peng, T. Adaptive Guaranteed Cost Control of Systems with Uncertain Parameters. IEEE Trans. Autom. Control 1972, 17, 474–483. [Google Scholar] [CrossRef]
- Liu, T.; Liu, Z.; Zhu, F. A Nonlinear Robust Speed Controller for Dual Nonidentical Parallel PMSM System. IEEE Trans. Power Electron. 2022, 37, 10190–10199. [Google Scholar] [CrossRef]
- Tian, X.; Huang, D.; Qin, N.; Gong, Z.; Wang, Q. Guaranteed Cost Optimal Control of High-Speed Train with Time-Delay in Cruise Phase. Int. J. Control Autom. Syst. 2021, 19, 2971–2983. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; Gao, Z.; Li, K. Optimal Guaranteed Cost Cruise Control for High-Speed Train Movement. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2879–2887. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy Identification of Systems and Its Applications to Modeling and Control. IEEE Trans. Syst. Man Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Mao, X.; Zhang, H.; Han, D. T-S Fuzzy Control for a Quad-Rotor UAV. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 3617–3622. [Google Scholar]
- Pedro, J.; Kala, P. Nonlinear Control of Quadrotor UAV Using Takagi-Sugeno Fuzzy Logic Technique. In Proceedings of the 2015 10th Asian Control Conference (ASCC), Kota Kinabalu, Malaysia, 31 May–3 June 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Xu, L.; Ye, Y.; Yi, Y.; Zheng, W. DOB Tracking Control Algorithm for Unmanned Aerial Vehicles with T-S Disturbance Modeling. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 503–508. [Google Scholar]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; Society for Industrial and Applied Mathematics, Ed.; SIAM studies in applied mathematics; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1994; ISBN 978-0-89871-485-2. [Google Scholar]
- Beard, R.; McLain, T. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012; ISBN 978-0-691-14921-9. [Google Scholar]
- Jodeh, N.; Blue, P.; Waldron, A. Development of Small Unmanned Aerial Vehicle Research Platform: Modeling and Simulating with Flight Test Validation. In Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit, Keystone, Colorado, 21–24 August 2006; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006; p. 6261. [Google Scholar]
- Jamnani, J.G. Brushless Direct Current Motor. In Special Electrical Machinery; Desai, J.P., Ed.; Wiley: Hoboken, NJ, USA, 2024; ISBN 978-1-394-19361-5. [Google Scholar]
- Chapman, S.J. Electric Machinery Fundamentals, 5th ed.; McGraw-Hill: New York, NY, USA, 2012; ISBN 978-0-07-352954-7. [Google Scholar]
- Stevens, B.; Lewis, F.; Johnson, E. Aircraft Control and Simulation: Dynamics, Controls Design, and Autonomous Systems: Dynamics, Controls Design, and Autonomous Systems, 1st ed.; Wiley: Hoboken, NJ, USA, 2015; ISBN 978-1-118-87098-3. [Google Scholar]
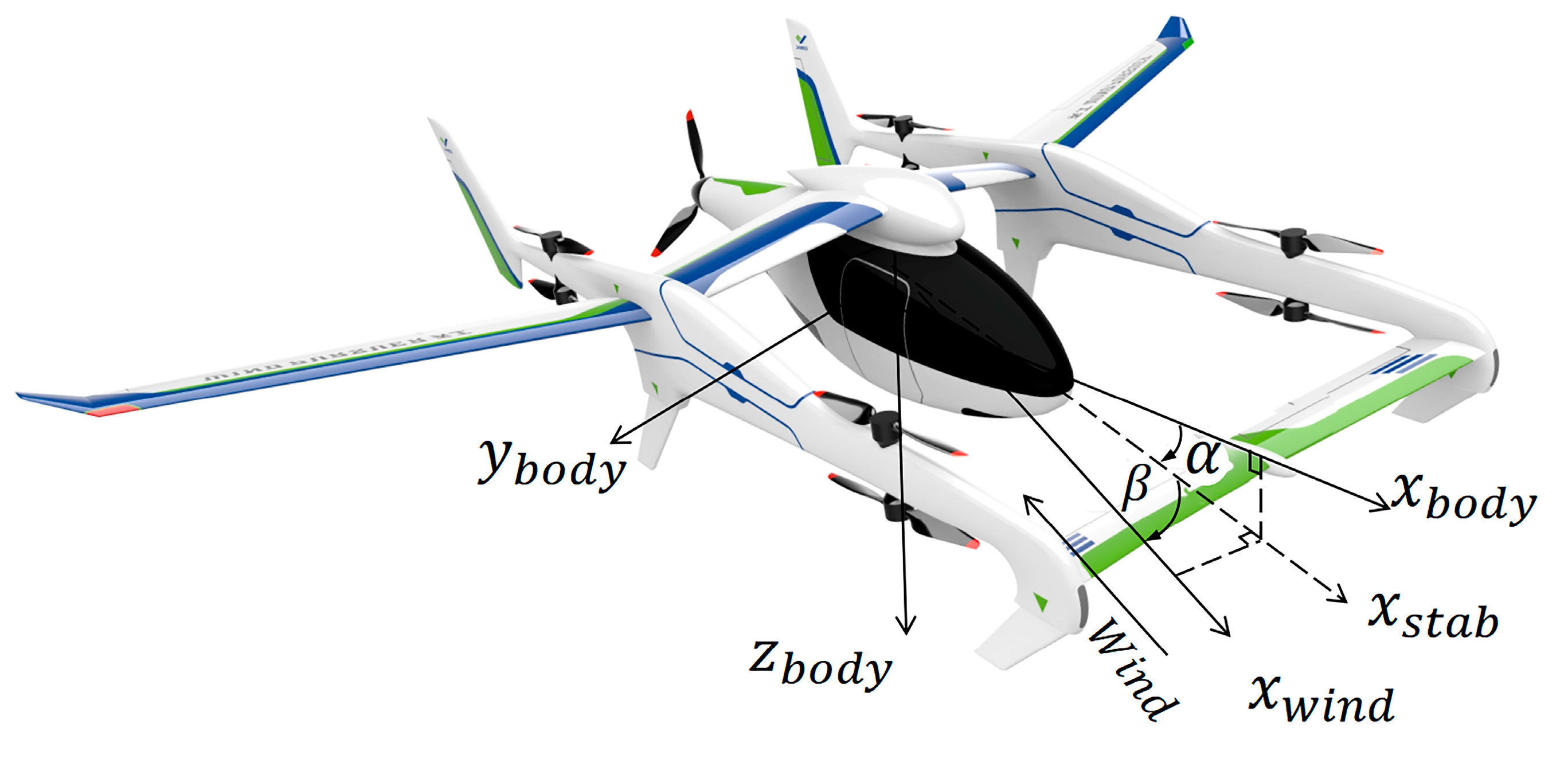


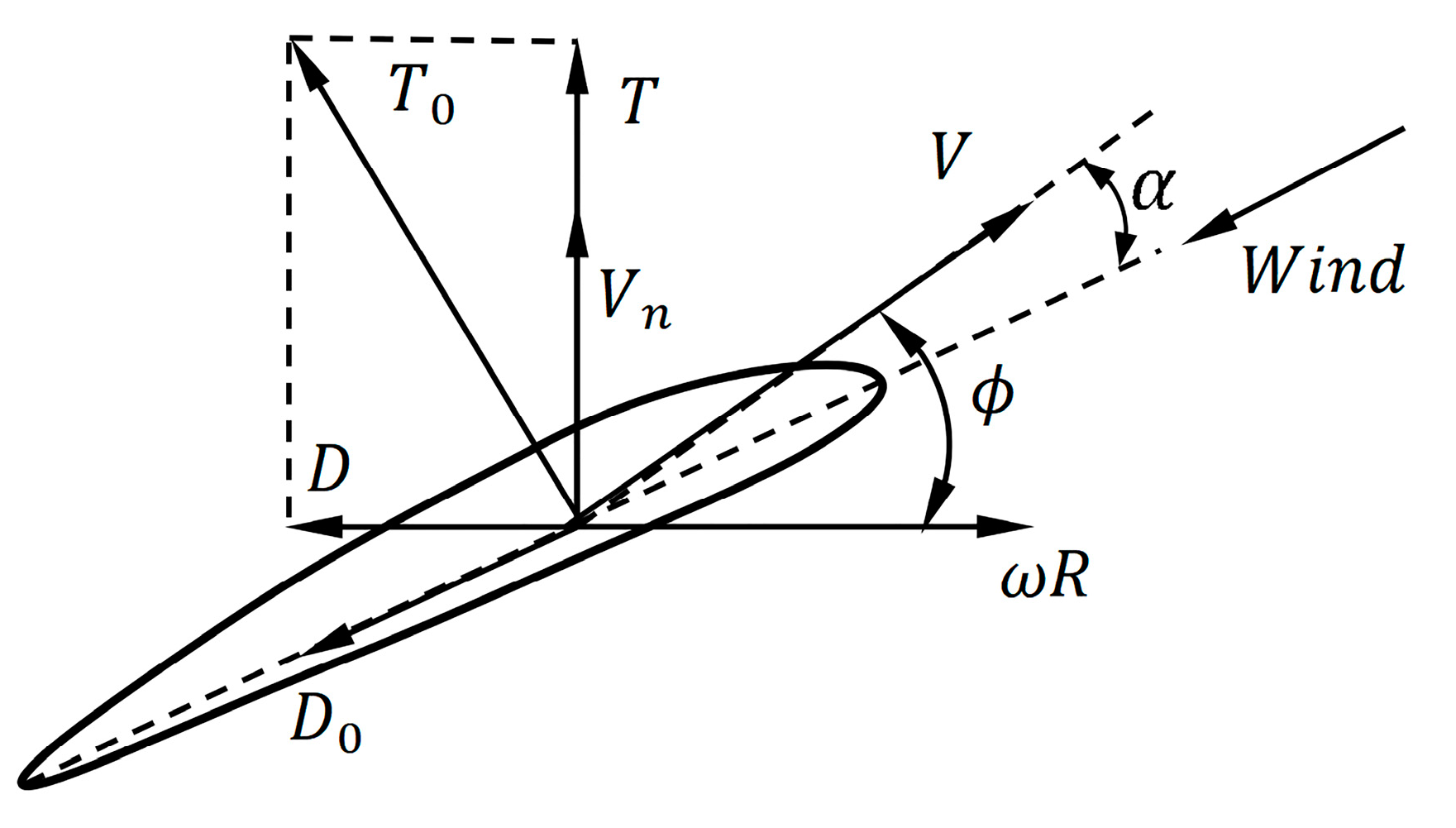

| Name | Description | Name | Description |
|---|---|---|---|
| Components of the UAV velocity | Zero-lift coefficient | ||
| q | Pitch rate | Lift coefficient slope | |
| Pitch angle | Pitch rate lift coefficient | ||
| H | Flight altitude | lift coefficient with respect to elevator deflection | |
| Angle of attack | Zero-lift drag coefficient | ||
| S | Wing area | Induced drag coefficient | |
| Air density | Pitch rate drag coefficient | ||
| m | Mass of the UAV | Drag coefficient with respect to elevator deflection | |
| c | Mean Aerodynamic Chord | pitching moment coefficient when | |
| Airspeed | Pitching moment coefficient with respect to angle of attack | ||
| T | Thrust produced by propeller | Pitch rate pitching moment coefficient | |
| Moment of inertia | Pitching moment coefficient with respect to elevator deflection |
| Name | Description | Name | Description |
|---|---|---|---|
| E | Applied voltage | propeller disk area | |
| Stator resistance | Thrust coefficient | ||
| Motor speed | Drag coefficient | ||
| Characteristic radius of the propeller | Downwash angle | ||
| K | Back electromotive force coefficient | Propeller pitch | |
| Output torque of the motor | Angle of attack of the propeller relative to the air | ||
| Induced speed at the propeller disk | Twist angle at the propeller’s characteristic radius |
| Parameters | Values | |
|---|---|---|
| TD | 0.05 | |
| 300 | ||
| NLSEF | 0.15 | |
| 300 | ||
| c | 0.1 | |
| ESO | 0.05 | |
| 50 | ||
| 500 | ||
| 500 | ||
| 0.5 | ||
| 0.25 | ||
| b | −100 | |
| Parameters | Values | Units | Parameters | Values |
|---|---|---|---|---|
| m | 30 | kg | 0.548 | |
| S | 1.4 | m2 | 0.035 | |
| c | 0.346 | m | 0.028 | |
| b | 4.460 | m | −1.585 | |
| 12.024 | kg·m2 | 0 | ||
| 1.225 | kg/m2 | −0.296 | ||
| 0.5 | None | −4.278 | ||
| 6 | None | −11.24 | ||
| 43.4 | None | −1.484 |
| States | Values | Units |
|---|---|---|
| 100 | m | |
| 25 | m/s | |
| 0 | m/s |
| Parameters | Values |
|---|---|
| Q | |
| R |
| Control Input | Amplitude Limit | Rate Limit | ||
|---|---|---|---|---|
| Values | Units | Values | Units | |
| [−30, 30] | Deg | ±90 | Deg/s | |
| T | [0, 80] | N | None | |
| Cases | Description |
|---|---|
| Case 1 | Constant altitude trajectory—The UAV maintains a flight altitude of 100 m. |
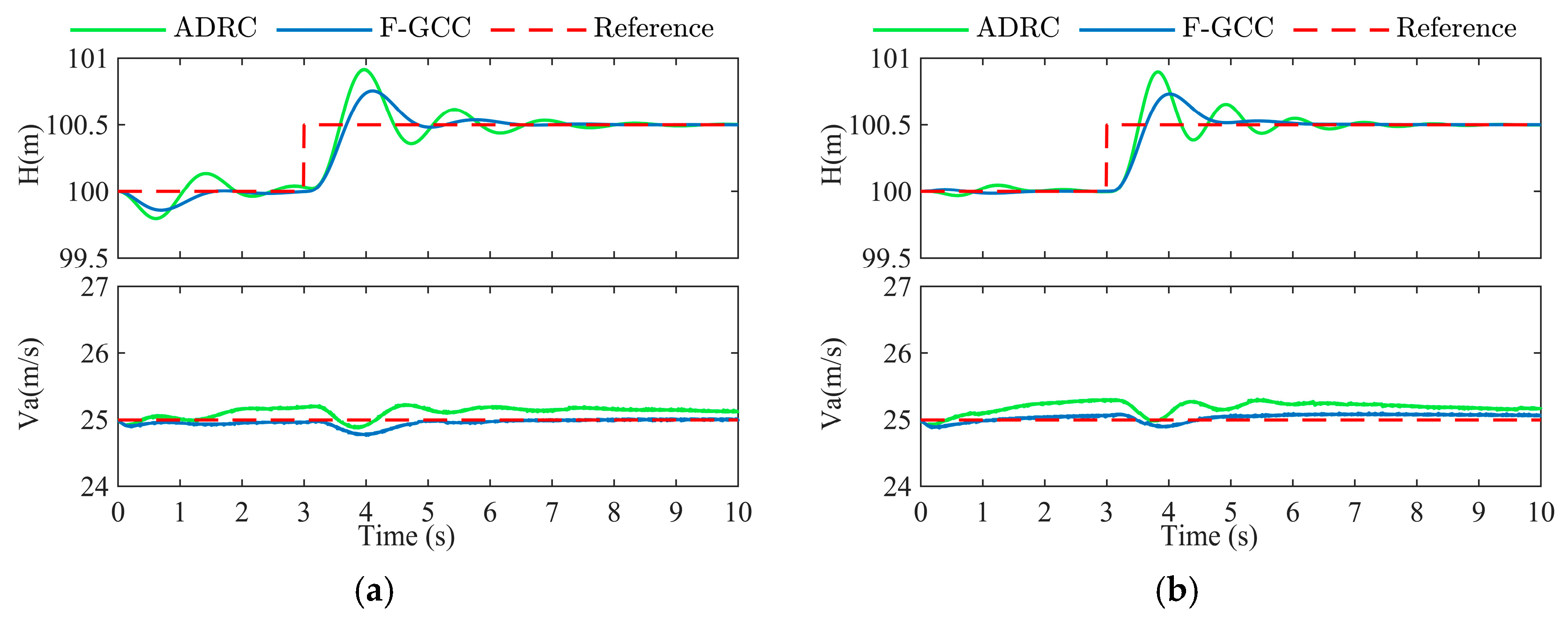
| Case 2 | Small step trajectory—The UAV undergoes a 0.5 m upward step change in altitude. |
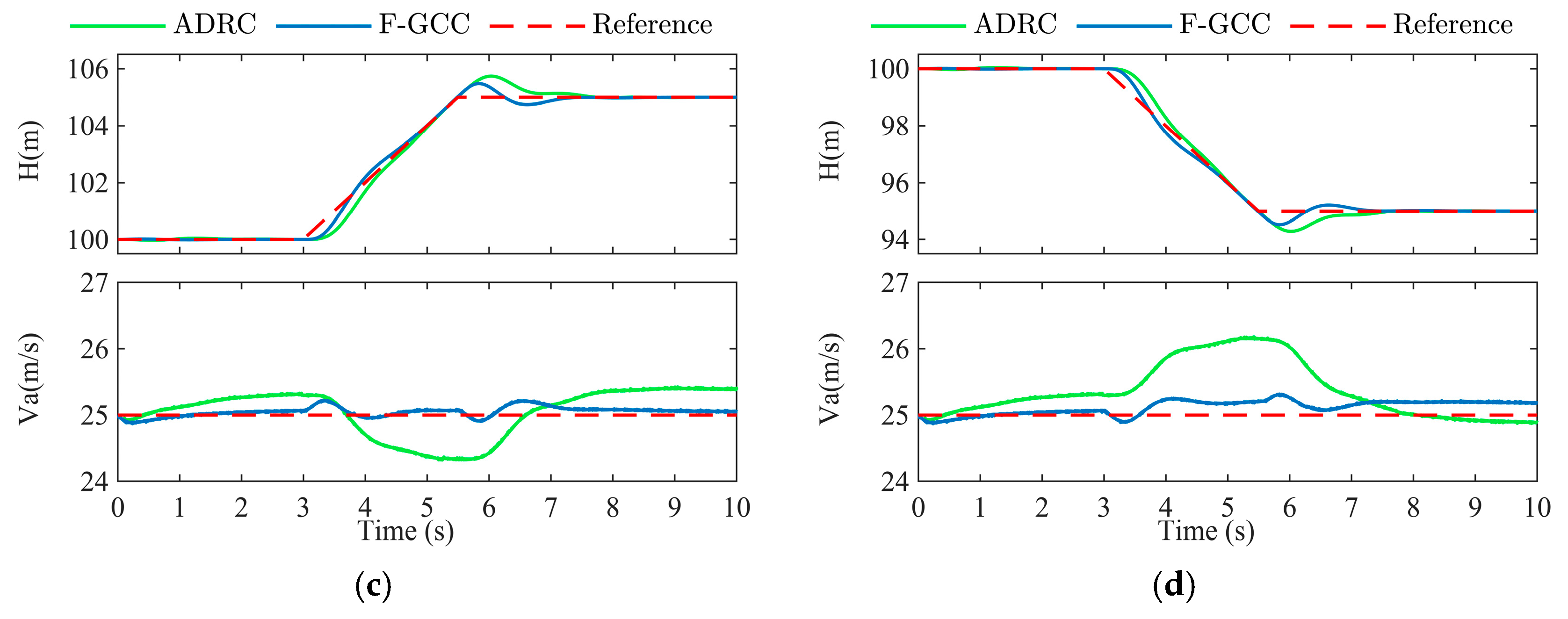
| Case 3 | Climb trajectory—The UAV ascends from 100 m to 105 m with a climb rate of 2 m/s. |
| Case 4 | Descent trajectory—The UAV descends from 100 m to 95 m with a descent rate of −2 m/s. |
| Controller | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| ADRC | 1.065 | 10.580 | 24.710 | 24.090 |
| F-GCC | 0.398 | 10.530 | 14.610 | 14.860 |
| Controller | Rise Time | Settling Time () | Overshoot | Steady-State System Response |
|---|---|---|---|---|
| PID | 0.608 | 4.077 | 74.26% | 100.502 |
| ADRC | 0.518 | 3.268 | 66.600% | 100.500 |
| F-GCC | 0.637 | 2.550 | 43.120% | 100.500 |
| Cases | Description |
|---|---|
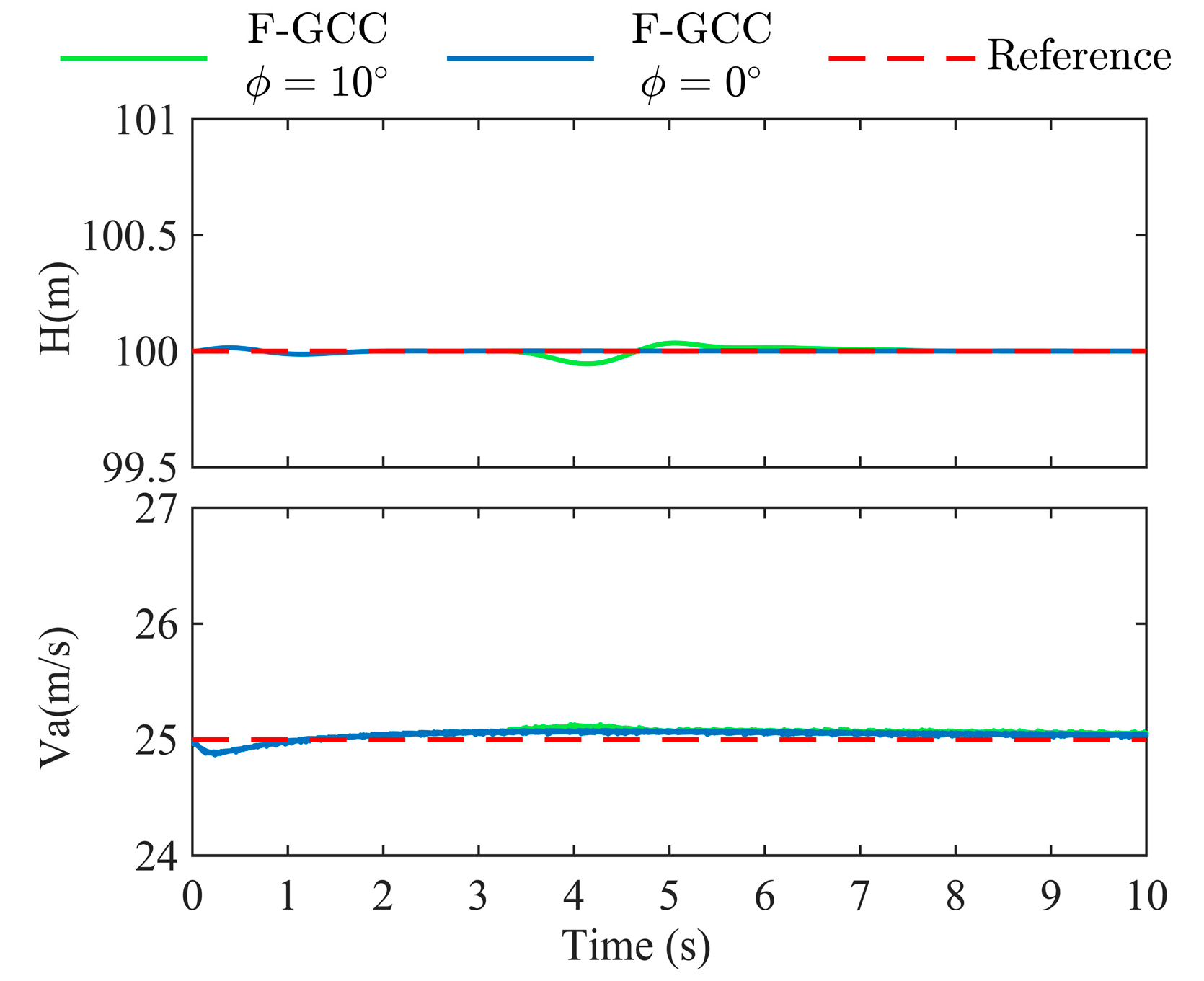
| Case 5 | Lateral control coupling—During level flight at constant altitude, the UAV executes a 10° right roll at the third second, maintains the roll for 2 s, and then returns to level. |
| Case 6 | Inaccurate aerodynamic parameters. Case 6.1 A step ascent experiment when the lift coefficient decreases by 30%, equating to 0.7 times the normal lift coefficient. Case 6.2 A step ascent experiment when the pitch moment coefficient decreases by 30%, corresponding to 0.7 times its usual value. |
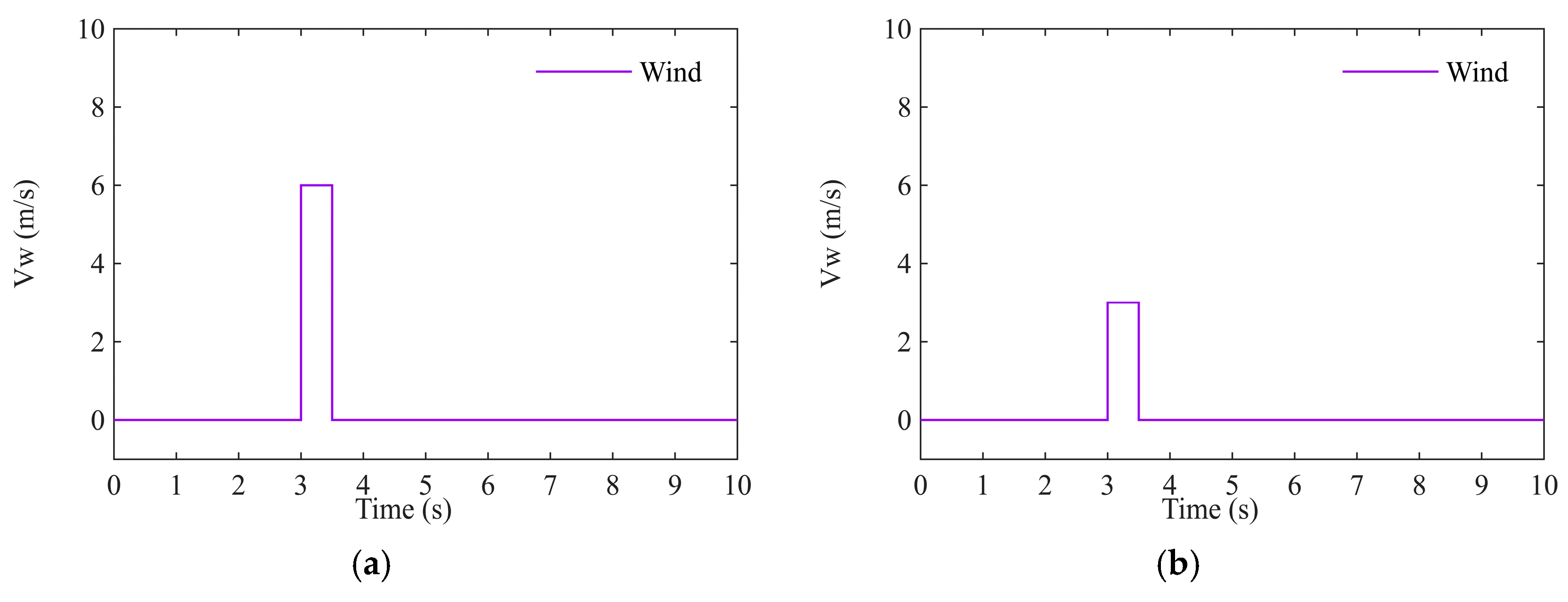
| Case 7 | Gust wind. Case 7.1 A pulse with an amplitude of 6 m/s and a duration of 0.5 s is applied during level flight, in the N-direction (in NED coordinate). Case 7.2 A pulse with an amplitude of 3 m/s and a duration of 0.5 s is applied during level flight, in the D-direction (in NED coordinate). |
| Case 8 | Turbulence. Case 8.1 Random disturbances in the range of [−5.078, 6.914] m/s are applied in the N-direction at level flight. Case 8.2 Random disturbances in the range of [−4.235, 3.711] m/s are applied in the D-direction at level flight. Case 8.3 During level flight, the combined random wind disturbances are applied in the N- and D-directions, with the N-direction in the range of [−5.078, 6.914] m/s and the D-direction in the range of [−1.412, 1.237] m/s. Case 8.4 During climb flight, the combined random wind disturbances are applied in N- and D-directions, with the N-direction in the range of [−5.078, 6.914] m/s and the D-direction in the range of [−1.4117, 1.237] m/s. |
| States | Case 5 |
|---|---|
| 0.398 | |
| 1.609 |
| Controller | Case 6.1 | Case 6.2 | Case 7.1 | Case 7.2 | Case 8.1 | Case 8.2 | Case 8.3 | Case 8.4 |
|---|---|---|---|---|---|---|---|---|
| ADRC | 13.520 | 11.620 | 4.569 | 10.630 | 5.791 | 20.150 | 21.200 | 33.230 |
| F-GCC | 11.360 | 10.640 | 2.884 | 10.280 | 3.387 | 15.920 | 8.470 | 18.100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Liu, X.; Wu, D.; Pi, Z.; Liu, T. A High Performance Nonlinear Longitudinal Controller for Fixed-Wing UAVs Based on Fuzzy-Guaranteed Cost Control. Drones 2024, 8, 661. https://doi.org/10.3390/drones8110661
Li J, Liu X, Wu D, Pi Z, Liu T. A High Performance Nonlinear Longitudinal Controller for Fixed-Wing UAVs Based on Fuzzy-Guaranteed Cost Control. Drones. 2024; 8(11):661. https://doi.org/10.3390/drones8110661
Chicago/Turabian StyleLi, Jun, Xiaobao Liu, Dawei Wu, Zhengyang Pi, and Tianyi Liu. 2024. "A High Performance Nonlinear Longitudinal Controller for Fixed-Wing UAVs Based on Fuzzy-Guaranteed Cost Control" Drones 8, no. 11: 661. https://doi.org/10.3390/drones8110661
APA StyleLi, J., Liu, X., Wu, D., Pi, Z., & Liu, T. (2024). A High Performance Nonlinear Longitudinal Controller for Fixed-Wing UAVs Based on Fuzzy-Guaranteed Cost Control. Drones, 8(11), 661. https://doi.org/10.3390/drones8110661






