Abstract
Unmanned aerial vehicles (UAVs) are widely used to improve the coverage and communication quality of wireless networks and assist mobile edge computing (MEC) due to their flexible deployments. However, the UAV-assisted MEC systems also face challenges in terms of computation offloading and trajectory planning in the dynamic environment. This paper employs deep reinforcement learning to jointly optimize the computation offloading and trajectory planning for UAV-assisted MEC system. Specifically, this paper investigates a general scenario where multiple pieces of user equipment (UE) offload tasks to a UAV equipped with a MEC server to collaborate on a complex job. By fully considering UAV and UE movement, computation offloading ratio, and blocked relations, a joint computation offloading and trajectory optimization problem is formulated to minimize the maximum computational delay. Due to the non-convex nature of the problem, it is converted into a Markov decision process, and solved by the deep deterministic policy gradient (DDPG) algorithm. To enhance the exploration capability and stability of DDPG, the K-nearest neighbor (KNN) algorithm is employed, namely KNN-DDPG. Moreover, the prioritized experience replay algorithm, where the constant learning rate is replaced by the decaying learning rate, is utilized to enhance the converge. To validate the effectiveness and superiority of the proposed algorithm, KNN-DDPG is compared with the benchmark DDPG algorithm. Simulation results demonstrate that KNN-DDPG can converge and achieve 3.23% delay reduction compared to DDPG.
1. Introduction
The rapid growth of Industry 4.0 has fueled the revolution in Industrial Internet of Things (IIoT) services, such as cloud robots in innovative manufacturing environments [1,2]. With the growing demand for computation-intensive and latency-sensitive workloads, IIoT user equipment (UE) such as mobile robots struggle to meet the stringent quality of service requirements. Traditional cloud computing concentrates computation and storage resources in data centers far away from UE, imposing extensive delay and bandwidth consumption during data transmission [3]. Mobile edge computing (MEC) focuses on moving computing resources to the edge of the network to provide high-performance, low-latency services to UE. Therefore, it efficiently handles computation-intensive and latency-sensitive tasks [4].
Previous works mainly focus on fixed base stations (BSs) to provide computing services. For example, Zhao et al. maximized the system utility through offloading computation and resource allocation optimization in cloud-assisted MEC systems [5]. However, in some practical applications (e.g., communication disruption due to natural disasters), deploying traditional terrestrial BSs cannot provide sufficient service range. Thus, the mobility and autonomy of unmanned aerial vehicles (UAVs) become one of the best ways. Currently, UAVs are expected to play a critical role in future wireless communication systems [6]. Indeed, UAVs can serve as relay BSs or aerial BSs in situations where communications are obstructed, thereby enhancing the network coverage in areas that are otherwise inaccessible or experiencing high traffic [7].
UAV-assisted MEC systems have great potential in providing IIoT services, e.g., industry, military, logistics, aerial photography, and smart cities [8,9]. Currently, UAVs can be used as MEC servers in scenarios where UAVs have large battery and computation power, or in scenarios where there is no area of terrestrial MEC systems due to natural disasters. Moreover, UAVs can be used as repeaters to connect two pieces of UE whose communication channels are blocked. This new setup can help UE with limited local resources to access computation resources [10]. With the development of MEC systems, an increasing number of researchers employ deep reinforcement learning (DRL) algorithms to optimize computation offloading and/or trajectory planning for UAV-assisted MEC systems [11,12,13,14,15,16]. Although deep deterministic policy gradient (DDPG) is suitable for continuous control scenarios, it suffers from inefficient exploration, which may lead to limited state space utilization and thus tends to converge to locally optimal solutions [17].
Motivated by the above deficiencies, this paper improves on the DDPG algorithm by utilizing the K-nearest neighbor (KNN) algorithm and priority experience replay (PER) for computation offloading and trajectory optimization UAV-assisted MEC systems. Specifically, KNN searches for high-dimensional data quickly and approximately, and when combined with the K-dimension tree, it reduces the computational complexity. Based on KNN, the states in reinforcement learning (RL) are categorized, and the reward function is incorporated according to the number of different classifications, thus exploring low-frequency states. In addition to this, this paper prioritizes the sampling of important samples in the empirical playback phase of RL, i.e., the PER algorithm, which enhances the ability of DDPG algorithm to explore effectively with a small number of samples. Instead of the traditional constant learning rate during training, the learning rate decay is utilized for training to improve the stability of the algorithm.
The contributions of this paper can be summarized as follows:
- Considering the UAV-assisted MEC system in the presence of obstacle blocked, the joint computation offloading and trajectory optimization (JCOT) problem under a dynamic channel is modeled. Under energy constraints, the JCOT problem is solved by jointly optimizing UE scheduling, computation offloading ratio of UE, UAV trajectory to minimize the maximum computational delay.
- For the JCOT problem, the corresponding Markov decision process (MDP) is designed and formulated, and the KNN-DDPG algorithm is proposed based on the constructed problem. The developed program improves the exploration capabilities of the DDPG in two ways. It enhances the exploration breadth of algorithm by utilizing categorical counting based on the KNN algorithm. Additionally, it improves the algorithm depth of exploration for important data by utilizing sampling based on the PER algorithm.
- Extensive simulations validate that the proposed algorithm improves DDPG under different parameters and communication conditions, and is more stable than other baseline algorithms.
The rest of the paper is organized as follows. Section 2 introduces the recent works on UAV-assisted MEC system. Section 3 presents the system model of UAV-assisted MEC system and the optimization problem. Section 4 introduces the KNN-DDPG algorithm. Section 5 illustrates the simulation results, and makes comparisons with current baseline algorithm. Finally, Section 6 concludes this work. For easy reading, all abbreviations throughout the paper are listed in Table 1.

Table 1.
Summary of abbreviations.
2. Related Work
2.1. Literature Summary
Existing works on UAV-assisted MEC systems can be classified as the following three types, according to their optimization objectives and the proposed algorithms.
- Minimize energy consumption for the entire system or mobile UE. Wang et al. proposed a collaborative resource optimization problem to minimize the total energy consumption of the system by jointly optimizing computation offloading, UAV flight trajectory and edge computing resource allocation [18]. However, this strategy does not effectively exploit the advantages of UAVs in terms of flexibility, mobility and ease of deployment. Wang et al. minimized the total UAV energy consumption through joint partitioning and UAV trajectory scheduling to extend UAV flight time and network lifetime [19].
- Minimize task completion time. Nath et al. studied a multi-user cache-assisted MEC system with stochastic task arrivals and proposed a DDPG-based dynamic scheduling strategy to jointly optimize dynamic caching, computation offloading, and resource allocation in the system [20]. Gao et al. developed a deep reinforcement learning-based approach for trajectory optimization and resource allocation, which intelligently manages the time allocation of TDs to maximize safe computation capacity using Deep Q-Learning. This method considers constraints such as time, UAV motion, minimum computation capacity, and data stability [21]. However, obstacle blocking in practical applications was not considered.
- Balancing energy consumption and latency. Zeng et al. employed method of Lyapunov to transform the long-term optimization problem into two deterministic online optimization subproblems, which were solved iteratively to balance the trade-off between energy consumption and queue stability for users with heterogeneous demands [22]. Their approach minimized both the energy consumption and completion time of UAVs. Zhang et al. considered random UE data arrivals to minimize the long-term average weighted system energy while ensuring queue stability and adhering to UAV trajectory constraints [23,24]. However, their method does not take into account the movement of UE and the entire trajectory of the UAV from the initial position to the destination is recomputed for each time slot, which increases the computational complexity.
The above works are summarized in Table 2.

Table 2.
Summary of related works.
2.2. Motivation and Contribution
Most existing UAV-on-ground channel models rely on deterministic line-of-sight connections to depict free-space path loss, yet this approach often falls short in urban or suburban settings [25]. Furthermore, the communication dynamics in UAV-assisted systems can change rapidly, and many mission offloading challenges are non-convex, making it difficult for conventional optimization methods to handle them effectively. Additionally, while machine learning techniques are often used to address various challenges in UAV-assisted MEC systems, the complexity of data processing and analysis rises as the size of the data increases, which can lead to delays in decision making. On the other hand, DRL tackles these decision-making hurdles by leveraging its capacity to learn and adapt through real-time environmental data. This paper explore a UAV-assisted MEC system, while considering constraints such as UAV energy limitations, UE and UAV movement, UE task size, and blocked conditions. The JCOT problem is modeled as an MDP since the action space in this system is mostly high-dimensional continuous and the problem in this paper is non-convex. Finally, the KNN-DDPG algorithm jointly optimizes UE scheduling, the UAV trajectory, and the computation offloading ratio in order to enhance the realism of the decision problem. The JCOT problem aims to minimize the maximum computational delay.
3. System Model and Problem Formulation
As depicted in Figure 1, a UAV-assisted MEC system comprises N UE and a UAV equipped with a MEC server. The local computing power of UE is limited, but with low-latency computation tasks. In contrast, UAVs with MEC server have strong computation power, and are in proximity to UE to provide MEC services. Thus, UE offloads part of the computation tasks to UAVs for edge computing via 5G ultra reliable ultra latency communication (URLLC).
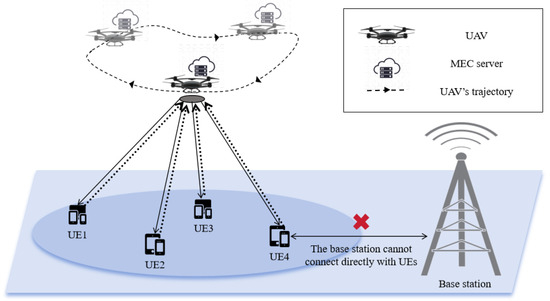
Figure 1.
UAV-assisted model.
3.1. Communication Model
The entire communication period T of the system is divided into time slots of equal size [26]. In each time slot, the UAV can only provide communication and computation services to a single UE [27].
The set of UE in time slot t is denoted as . The coordinates of at time slot t are . The UAV transmits data for in this time slot, and the position of the UAV flight at a fixed altitude H in the horizontal plane is defined as , where the UAV is flying at a fixed altitude H. The coordinates are updated after the UAV has flown to a new hovering position of . The UAV hovers over the location and communicates with one of the UE. In a time slot, the horizontal coordinates of the UAV motion can be expressed as
The new hovering position of the UAV is expressed as
where denotes the flight time of the UAV, is the flight speed of the UAV, is the angle of flight of the UAV in the horizontal plane projection with respect to the x-axis in the horizontal direction. At the time slot t, the distance between the UE and the UAV can be expressed as [28]
UAVs are commonly airborne, and carry communications equipment. Additionally, they have the advantage of a higher altitude position, which helps establish line-of-sight (LoS) communication links, resulting in more stable and efficient communications. Due to the fact that UAVs are much higher than ground UE, the LoS channel of the UAV communication link is more prominent than other channel losses [29]. The LoS communication links channel gain between the UAV and can be expressed as
where denotes the channel gain of 1m and is the distance between the UAV and the UE at the time slot t. Due to the severe impact of obstruction by environmental obstacles present in the system environment (e.g., trees or buildings), the wireless transmission rate can be expressed as
where B denotes the communication bandwidth, denotes the uplink transmit power, indicates the presence or absence of obstacles at time slot t (0 means no blocked and 1 means blocked), and is the transmission loss.
3.2. Computation Model
Unlike the edge computing of terrestrial MEC system, the edge computing of UAV-assisted MEC system involves three processes: computation offloading, local computing, and UAV flight. The proposed UAV includes partial offloading of UE tasks within each time slot. Let indicate the computation offloading ratio from n-th UE to UAV, while the remaining computation tasks are calculated locally. In time slot t, the local computational delay and energy consumption can be expressed as
where denotes the computation size of the n-th UE, is the CPU cycles required to process each unit byte, is the impact factor of chip architecture on CPU processing, and denotes the computing capability of the UE [30]. Due to the small delay in returning results from the MEC server in the UAV, this paper ignores its effect. The computational delay of edge computing is expressed as
The energy consumption for the UAV flight can be expressed as
where is related to the payload of the UAV, denotes the flight time of UAV [12].
The computational delay and energy can be expressed as
where denotes the computing capability of UAV.
3.3. Problem Formulation
To optimize the computation offloading and trajectory planning, we formulate the JCOT problem as follows:
such that
where indicates whether UE is scheduled. Constraints (14) and (15) ensure that the UAV can only communicate with one UE in each time slot. Constraints (16) and (17) denote the constraint ranges of the UAV and the UE. Constraint (18) denotes the blocked situation when the UAV and the UE communicate in time slot t. Constraint (19) constrains the range of values for the computation offloading ratio. Constraint (20) ensures that the energy consumed by the UAV throughout the system does not exceed the maximum battery capacity. Constraint (21) indicates that all tasks need to be due in the entire time period.
4. The Proposed KNN-DDPG Algorithm
The above optimization problem is mixed-integer non-linear programming. Thus, solving this problem by relying on traditional optimization methods is challenging. Therefore, a DRL-based approach is used to solve the problem.
4.1. MDP Modeling
4.1.1. State
The state space at the time slot t is expressed as
where denotes the remaining energy of the UAV battery in the current time slot, is the location of UE, which a UAV selects in the t-th time slot, denotes the location information of UAV, and is the size of remaining tasks the system must complete in the whole period. is the size of the randomly generated task in the current time slot, and is the blocking relationship between UE. For , , .
4.1.2. Action
An agent optimizes the flight angle of the UAV in the continuous motion space by selecting UE to be serviced based on the observed environment and the current system state, including the UE to be served , flight speed , and the computation offloading ratio . At the time slot t, the action space is represented as
It should be noted that the agent selects a variable action if it needs to be decentralized, i.e., if , then . If , , where is an upward rounding symbol.
4.1.3. Reward
The total system reward is the sum of the rewards corresponding to the number of steps the UAV flight. The UAV can obtain an action for each step during the flight while flying to a new position and a UE for data transfer. The maximum delay of edge computing and local computing is minimized under the constraint of UAV energy consumption. The target delay function, as well as the reward function, is expressed as
when , = 1. Otherwise, = 0. When action is performed, the smaller the computational delay, the larger the reward.
4.2. KNN-DDPG Solution
Figure 2 depicts the KNN-DDPG framework.
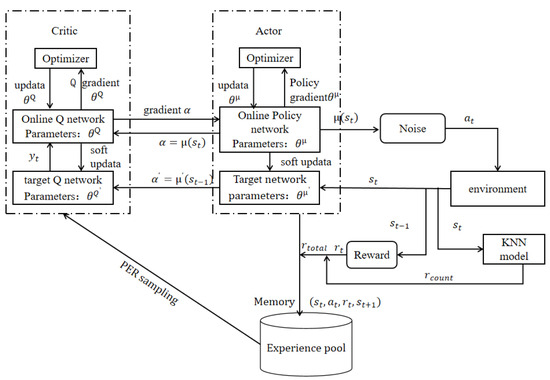
Figure 2.
KNN-DDPG algorithm framework.
The KNN algorithm searches for similar states to speed up the training process of the DDPG algorithm. This approach can utilize the existing empirical data to guide the exploration of the intelligent body by finding similar states in the state space. This guidance improves training efficiency and allows the intelligent body to learn good strategies faster. This modification optimizes the training efficiency and speed. Indeed, accelerating training by searching for similar states reduces the sample complexity of DDPG algorithm, leading to more efficient use of the training data, faster convergence, and improved strategy stability. The main idea is that after classifying the state space according to KNN, counts are counted for different classifications during the training process and count rewards are formed. Combining this reward with the training reward motivates the exploration of historical states. After completing the counting process, the counting results are used for the count reward function of KNN-DDPG, expressed as
where m is the total number of currently categorized states, and a weighted decay factor that decays with the number of iterations is added in order to explore states with a low number of historical samples. is defined as:
where is the set of weights, is the decay factor, and n is the number of iterations. This process prevents the divergence caused by the increasing as the number of iterations increases, thus ensuring the final convergence of the algorithm. Finally, the final total reward is obtained by adding up using custom weights .
In DDPG, the strategy function acts as an “actor”, generating actions based on the current state of the continuous space. The Q-value function acts as a “critic”, evaluating the performance of the actor by estimating the value of the actions taken, thus guiding the actor to improve its subsequent actions. Figure 2 highlights that DDPG uses two different DNNs to approximate the actor network , i.e., the Q-value function, and the critic function , i.e., the Q-value function. The first is learned and improved for final use, and the other is used to calculate the temporal difference (TD) error. In addition, both the actor and the critic networks include a target network with the same structure as the respective primary networks, improving clarity and maintaining consistency in the description of the target networks. The actor network involves the parameter and the critic target network , parameter . The parameters of the critic network are updated by minimizing the loss value (mean square error loss), and the loss function when the Critic network is updated as
where
The maximum discount incentive for DDPG is
where is the discount factor, and is the immediate reward at the i-th time slot.
In traditional DDPG, samples can be randomly extracted in the experience pool M during training. However, this overlooks the significance of individual experiences, meaning that some may hold more learning potential than others. To tackle this shortcoming, PER comes into play, assigning priorities to experiences by evaluating their TD error—essentially gauging the disparity between predicted and target Q-values within DDPG (Equation (32)).
In this paper, rank based prioritization PER is used for prioritization as it has better stability as compared to proportional prioritization. Calculate the sampling probability according to the ranking of the TD errors :
After executing the algorithm, the agent observes the next state and the immediate reward and stores it in M, which at this point has the highest priority . After K transitions in M, the actor target network outputs the action to the critic target network , and the critic network calculates the target value based on Equation (30). The TD-error is calculated, and the transition priority is updated as .
Then, minimize the loss function by updating the critic network Q. The actor network provides the gradient of the small batch of actions to the critic network for the gradient of action . The optimizer can be exported through its optimizer . The actor network can be updated based on Equation (34).
Finally, the DDPG agent soft updates the commenter target network and the actor target network using a small constant , which can be expressed as:
The pseudo-code of the KNN-DDPG algorithm is shown in Algorithm 1.
| Algorithm 1: The proposed KNN-DDPG algorithm |
 |
5. Simulations
In this section, the effectiveness and superiority of the proposed KNN-DDPG algorithm is validated through numerical simulations. First, the simulation parameter settings are presented. The performance of the KNN-DDPG algorithm is then validated under different parameters and conditions, and compared with the benchmark DDPG algorithm.
5.1. Simulation Setting
The simulations is executed based on Python 3.7 and the TensorFlow 2 framework on the Anaconda platform. We consider a square region that has UE randomly placed in a 100 m × 100 m area to simulate the system environment on the Anaconda platform. The remaining parameters are listed in Table 3 [31].

Table 3.
Simulation parameters.
5.2. Result Analysis
Figure 3 demonstrates the delay variation with the number of training episodes for different algorithms. KNN-DDPG demonstrates the best convergence, as it converges quickly, reaches the lowest delay in the early stage of training (within 200 rounds), and shows excellent stability in subsequent training. In contrast, DDPG also shows some convergence, but is slower and more volatile, demonstrating inferior final convergence than KNN-DDPG.
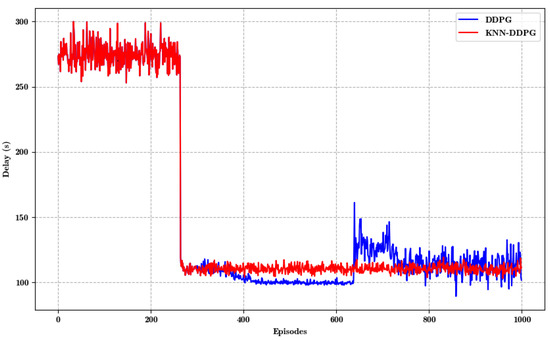
Figure 3.
Convergence of KNN-DDPG and DDPG.
Figure 4 compares the algorithms with different task sizes. Obviously, the length of the box (i.e., the size of the interquartile range) is usually shorter, which validates the stability of KNN-DDPG, as shorter interquartile range imply less fluctuation in the delay values and more consistent performance. At small task sizes, such as medium quality video streaming, real-time conferencing (60 Mbits and 80 Mbits), the median delay of KNN-DDPG is below or close to DDPG, and its delay variation range is small. At medium task sizes, such as high-quality video streaming, basic virtual reality experiences (100 Mbits), the median delay of KNN-DDPG, while slightly higher, is still below or close to DDPG, and its range of data fluctuations is small. At larger task sizes, such as ultra-high-definition video streaming, and high-speed real-time data analysis tasks (120 Mbits and 140 MBits), although the median delay of KNN-DDPG increases, its delay is more tightly distributed, and it exhibits higher stability compared to the DDPG algorithm. KNN-DDPG has less performance fluctuation at all task sizes, especially at small-to-medium task sizes. This stability makes KNN-DDPG more suitable for application scenarios that require stable performance. The delay performance of KNN-DDPG remains stable when the task size increases. Although the performance decreases slightly, it has no significant signs of performance degradation, demonstrating strong robustness.
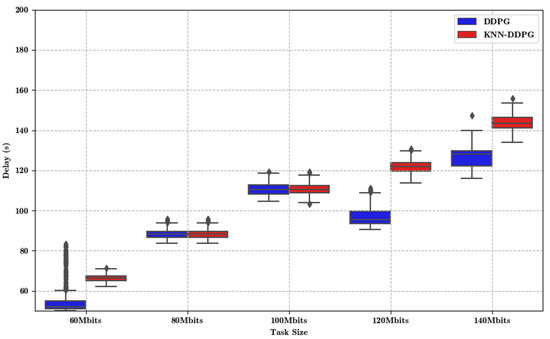
Figure 4.
Delay with different task size.
In summary, KNN-DDPG shows more stability and superiority under most task sizes, especially in scenarios that require low delay and high stability, making KNN-DDPG more competitive. Even under larger task loads, it still maintains a certain performance advantage and stability, making it a preferred solution to cope with various loads in edge computing environments.
To demonstrate the improvement of the algorithm in terms of exploration capability, the following experiment compares the DDPG and KNN-DDPG algorithms during training. The corresponding results are presented in Figure 5, where the color of each point reflects how often the intelligent agent samples the state quantity. Specifically, DDPG utilizes existing strategies in high-power and short-range areas with limited exploration in other areas, resulting in large fluctuations in offload rates. This reliance on specific states hinders rapid adaptation to new situations, suggesting that DDPG may be unable to explore effective strategies in regions with large state changes. In contrast, KNN-DDPG effectively balances exploration and utilization through KNN and prioritized empirical replay, dynamically adapting to strategies that explore new states while ensuring high utilization, thus maintaining a stable offloading ratio. The state space coverage is more uniform, adapts well to different battery power, distance, and offloading ratios, and maintains a high offloading ratio, even at low power or distance. These features indicate that KNN-DDPG has better balance and stability under different state conditions. In conclusion, DDPG struggles with complex or rapidly changing environments, leading to poor adaptability and suboptimal offloading ratios in several states. However, KNN-DDPG demonstrates superior environmental adaptability, finding effective strategies in diverse state spaces and maintaining stable performance, thereby demonstrating deeper exploration and optimized decision-making.
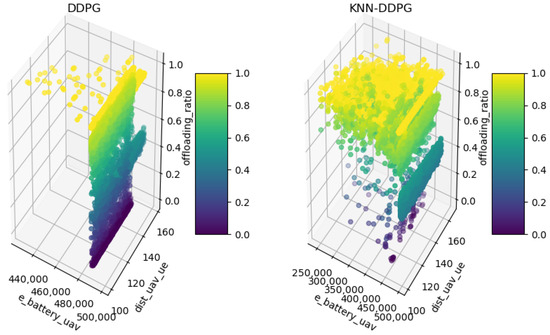
Figure 5.
Exploration of the state spaces of KNN-DDPG and DDPG.
As presented in Figure 6, as the amount of UE increases, each algorithm shows delayed growth. The growth rate and the final delay of DDPG are significantly higher than that of the KNN-DDPG algorithm in the multiuser task environment. When the number of users increased from 6 to 8, the DDPG algorithm delay increased by 5.8% and the KNN-DDPG algorithm increased by 3.74%. Although the KNN-DDPG algorithm at a constant learning rate is less stable than the KNN-DDPG algorithm, the final experimental results are similar. Herein, the constant learning rate for the actor network and the critical network of both KNN-DDPG and DDPG algorithms are set to 0.01 and 0.02, respectively.
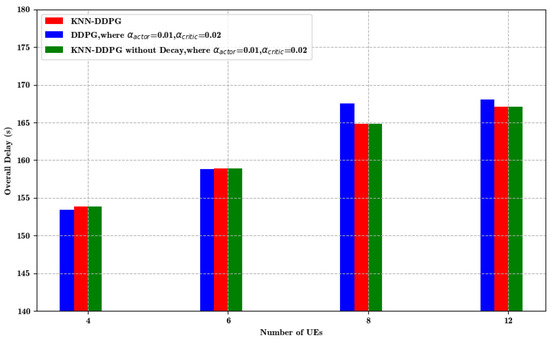
Figure 6.
Delay with different amounts of UE.
Figure 7 compares the impact of different discount factors on the convergence performance of the proposed algorithm. For , the delay distribution of KNN-DDPG is relatively centralized, but its median is higher than that of DDPG. However, KNN-DDPG has a narrower range of latencies and a shorter box (interquartile range), suggesting the performance is more stable at this discount factor. On the other hand, DDPG has more fluctuating delay performance and outliers (points well above the box), suggesting that its performance is less stable than that of KNN-DDPG under this condition. For , more centralized and stable performance of KNN-DDPG compared to DDPG. The box plot shows a narrower range and less variation in the median. Despite some outliers, there are fewer fluctuations in delay overall. The delay performance of DDPG still fluctuates. For , stability is improved relative to the case. For , KNN-DDPG has the most stable delay performance. All delay values are concentrated in a narrow range with very short boxes and no significant outliers, indicating that KNN-DDPG is consistent and stable in this condition. In contrast, DDPG has significantly fewer delay fluctuations at this discount factor. However, some outliers are present, showing that its improved performance is not as stable as KNN-DDPG.
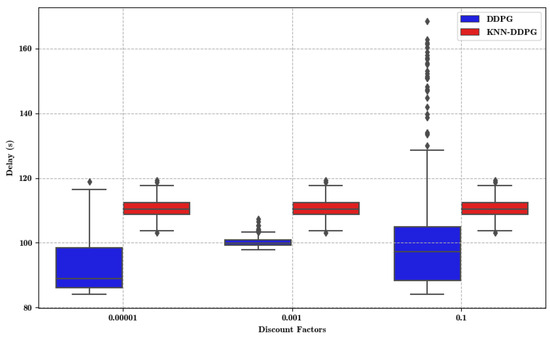
Figure 7.
Delay with different discount factors.
Figure 8 compares the KNN-DDPG algorithm using decaying learning rate and fixed learning rate approach, inferring that when no learning rate decay is applied, the algorithm converges slower in the early stages with higher and more fluctuating delay and performs poorly, especially in the first 200 rounds. However, when the learning rate decay is applied, the algorithm quickly reduces the delay and stabilizes after about 200 rounds. This result suggests that learning rate decay improves the convergence speed and stability of KNN-DDPG, allowing it to find a better strategy more quickly and keep the delay fluctuations small in later rounds.
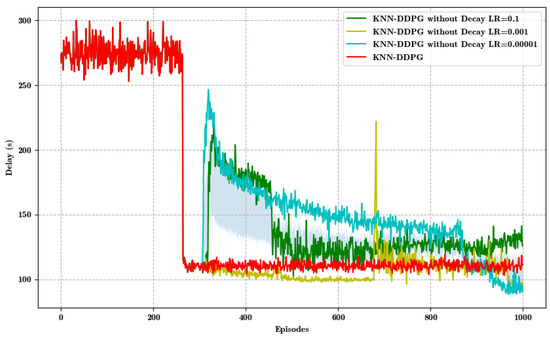
Figure 8.
Delay with different learning rates.
6. Conclusions
This paper addressed the challenge of computation offloading and trajectory planning for UAV-assisted MEC system, where a UAV serves multiple pieces of UE. Correspondingly, the JCOT problem was formulated to optimize UE scheduling, computation offloading ratio and UAV trajectory. To solve this problem, the KNN-DDPG algorithm with PER was proposed and validated by simulations. The results demonstrated that KNN-DDPG achieve 3.23% lower delay than DDPG. Future works will extend to more complex scenarios that the MEC systems involving multiple UAVs to enhance computation offloading and edge computing.
Author Contributions
Methodology, Y.L.; Validation, Y.L.; Investigation, Y.W.; Resources, Y.W.; Data curation, Y.L.; Writing—original draft, Y.L.; Writing—review & editing, C.X.; Supervision, C.X. and Y.W.; Project administration, C.X.; Funding acquisition, C.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China under Grants 92267108 and 62173322, Science and Technology Program of Liaoning Province under Grants 2023JH3/10200004 and 2022JH25/10100005.
Data Availability Statement
The original contributions presented in the study are included in the paper, further inquiries can be directed to authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cheng, J.; Chen, W.; Tao, F.; Lin, C. Industrial IoT in 5G Environment Towards Smart Manufacturing. J. Ind. Inf. Integr. 2018, 10, 10–19. [Google Scholar] [CrossRef]
- Xu, C.; Yu, H.; Jin, X.; Xia, C.; Li, D.; Zeng, P. Industrial Internet for intelligent manufacturing: Past, present, and future. Front. Inf. Technol. Electron. Eng. 2024, 25, 1173–1192. [Google Scholar] [CrossRef]
- Mach, P.; Becvar, Z. Mobile edge computing: A Survey on Architecture and Computation Offloading. IEEE Commun. Surv. Tutor. 2017, 19, 1628–1656. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, P.; Yu, H.; Li, Y. D3QN-Based Multi-Priority Computation Offloading for Time-Sensitive and Interference-Limited Industrial Wireless Networks. IEEE Trans. Veh. Technol. 2024, 73, 13682–13693. [Google Scholar] [CrossRef]
- Zhao, J.; Li, Q.; Zhang, K. Computation Offloading and Resource Allocation for Cloud Assisted Mobile Edge Computing in Vehicular Networks. IEEE Trans. Veh. Technol. 2019, 18, 7944–7956. [Google Scholar] [CrossRef]
- Lyu, J.; Zeng, Y.; Zhang, R. UAV-Aided Offloading for Cellular Hotspot. IEEE Trans. Wirel. Commun. 2018, 17, 3988–4001. [Google Scholar] [CrossRef]
- Wang, H.; Ding, G.; Gao, F.; Chen, J.; Wang, J.; Wang, L. Power Control in UAV-Supported Ultra Dense Networks: Communications, Caching, and Energy Transfer. IEEE Commun. Mag. 2017, 56, 28–34. [Google Scholar] [CrossRef]
- Mao, Y.; You, C.; Zhang, J.; Huang, K.; Letaief, K.B. A Survey on Mobile Edge Computing: The Communication Perspective. IEEE Commun. Surv. Tutor. 2017, 19, 28–34. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless Communications with Unmanned Aerial Vehicles: Opportunities and Challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.; He, Q.; Bian, K.; Song, L. Joint Trajectory and Power Optimization for UAV Relay Networks. IEEE Commun. Lett. 2018, 22, 161–164. [Google Scholar] [CrossRef]
- Xu, C.; Tang, Z.; Yu, H.; Zeng, P.; Kong, L. Digital Twin-Driven Collaborative Scheduling for Heterogeneous Task and Edge-End Resource via Multi-Agent Deep Reinforcement Learning. IEEE J. Sel. Areas Commun. 2023, 41, 3056–3069. [Google Scholar] [CrossRef]
- Ren, X.; Chen, X.; Jiao, L.; Dai, X.; Dong, Z. Joint Optimization of Trajectory, Caching and computation offloading for Multi-Tier UAV MEC Networks. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 1–6. [Google Scholar]
- Wei, Q.; Zhou, Z.; Chen, X. DRL-Based Energy-Efficient Trajectory Planning, Computation Offloading, and Charging Scheduling in UAV-MEC Network. In Proceedings of the 2022 IEEE/CIC International Conference on Communications in China (ICCC), Foshan, China, 11–13 August 2022; pp. 1056–1061. [Google Scholar]
- Du, S.; Chen, X.; Jiao, L.; Wang, Y.; Ma, Z. Deep Reinforcement Learning-Based UAV-assisted Mobile Edge Computing Offloading and Resource Allocation Decision. In Proceedings of the 2022 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Prague, Czech Republic, 9–12 October 2022; pp. 2728–2734. [Google Scholar]
- Peng, Y.; Liu, Y.; Zhang, H. Deep Reinforcement Learning Based Path Planning for UAV-assisted Edge Computing Networks. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March–1 April 2021; pp. 1–6. [Google Scholar]
- He, H.; Yang, X.; Mi, X.; Shen, H.; Liao, X. Multi-Agent Deep Reinforcement Learning Based Dynamic computation offloading in a Device-to-Device Mobile-Edge Computing Network to Minimize Average Task Delay with Deadline Constraints. Sensors 2024, 24, 5141. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, Y.; Gao, Z.; He, X. An Improved DDPG and its Application Based on the Double-Layer BP neural network. IEEE Access 2020, 8, 177734–177744. [Google Scholar] [CrossRef]
- Wang, M.; Li, R.; Jing, F.; Gao, M. Multi-UAV Assisted Air–Ground Collaborative MEC System: DRL-Based Joint computation offloading and Resource Allocation and 3D UAV Trajectory Optimization. Drones 2021, 8, 510. [Google Scholar] [CrossRef]
- Wang, D.; Tian, J.; Zhang, H.; Wu, D. Task offloading and Trajectory Scheduling for UAV-Enabled MEC Networks: An Optimal Transport Theory Perspective. IEEE Wirel. Commun. Lett. 2022, 11, 150–154. [Google Scholar] [CrossRef]
- Nath, S.; Wu, J. Deep Reinforcement Learning for Dynamic Computation Offloading and Resource Allocation in Cache-Assisted Mobile Edge Computing Systems. Intell. Converg. Netw. 2020, 1, 181–198. [Google Scholar] [CrossRef]
- Gao, Y.; Ding, Y.; Wang, Y.; Lu, W.; Guo, Y.; Wang, P.; Cao, J. Deep Reinforcement Learning-Based Trajectory Optimization and Resource Allocation for Secure UAV-Enabled MEC Networks. In Proceedings of the 2024 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Vancouver, BC, Canada, 20–23 May 2024; pp. 1–5. [Google Scholar]
- Zeng, Y.; Chen, S.; Li, J.; Cui, Y.; Du, J. Online Optimization in UAV-Enabled MEC System: Minimizing Long-Term Energy Consumption Under Adapting to Heterogeneous Demands. IEEE Internet Things J. 2024, 11, 32143–32159. [Google Scholar] [CrossRef]
- Zhang, J. Stochastic Computation Offloading and Trajectory Scheduling for UAV-Assisted Mobile Edge Computing. IEEE Internet Things J. 2019, 6, 3688–3699. [Google Scholar] [CrossRef]
- Yan, T.; Liu, C.; Gao, M.; Jiang, Z.; Li, T. A Deep Reinforcement Learning-Based Intelligent Maneuvering Strategy for the High-Speed UAV Pursuit-Evasion Game. Drones 2024, 8, 309. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, Y.; Li, D.; Zhang, H. Deep Reinforcement Learning Based Freshness-Aware Path Planning for UAV-Assisted Edge Computing Networks with Device Mobility. Remote Sens. 2022, 14, 4016. [Google Scholar] [CrossRef]
- Dai, Y.; Xu, D.; Maharjan, S.M. Artificial Intelligence Empowered Edge Computing and Caching for Internet of Vehicles. IEEE Wirel. Commun. 2019, 26, 12–18. [Google Scholar] [CrossRef]
- Xiong, J.; Guo, H.; Liu, J. Task offloading in UAV Aided Edge Computing: Bit Allocation and Trajectory Optimization. IEEE Commun. Lett. 2019, 23, 538–541. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Y.; Yu, H.; Hou, Y. Three-Dimensional Trajectory and Resource Allocation Optimization in Multi-Unmanned Aerial Vehicle Multicast System: A Multi-Agent Reinforcement Learning Method. Drones 2023, 7, 641. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, W.; Ding, Y. Computation Offloading Optimization for UAV-Assisted Mobile Edge Computing: A Deep Deterministic Policy Gradient Approach. Wirel. Netw. 2021, 27, 2991–3006. [Google Scholar] [CrossRef]
- Hu, Q.; Cai, Y.; Yu, G.; Qin, Z.; Zhao, M.; Li, G. Joint Offloading and Trajectory Design for UAV-Enabled Mobile Edge Computing Systems. IEEE Internet Things J. 2019, 6, 879–1892. [Google Scholar] [CrossRef]
- Zhan, C.; Hu, H.; Sui, X.; Liu, Z.; Niyato, D. Completion Time and Energy Optimization in the UAV-Enabled Mobile-Edge Computing System. IEEE Internet Things J. 2020, 7, 7808–7822. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).