A Survey of the Routing Problem for Cooperated Trucks and Drones
Abstract
1. Introduction
1.1. Advantages of Cooperation with Drones and Trucks
1.2. Motivation and Organization of This Review
1.3. Overview of Existing Surveys
2. Application Background
2.1. Logistics and Delivery
2.2. Intelligence Surveillance Reconnaissance and Data Collection
2.3. Area Monitoring and Patrol
2.4. Application of Truck–Drone Collaboration in Practical Scenarios
3. Cooperative Modes of Trucks and Drones
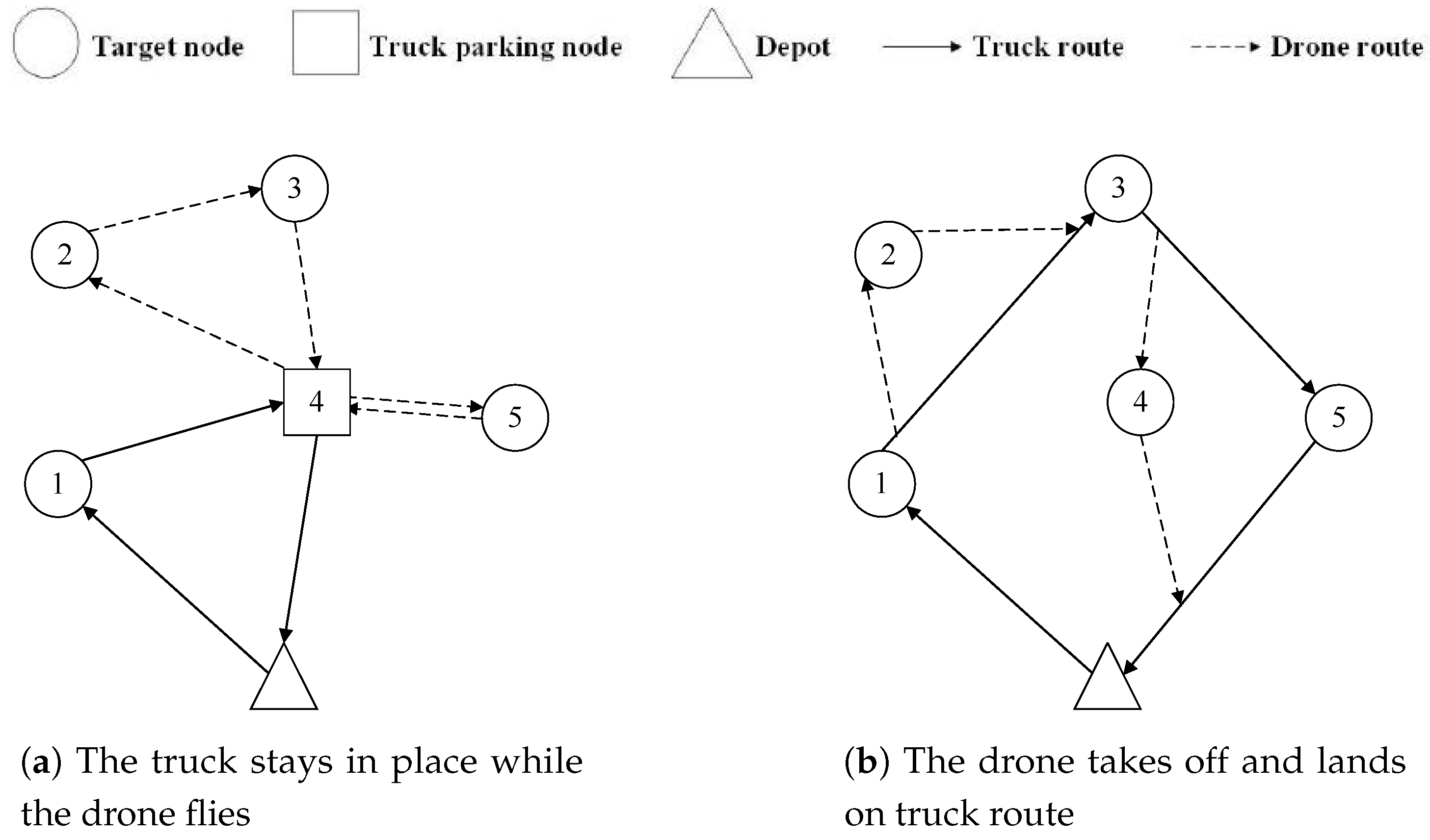
3.1. Synchronous Operation of Truck and Drone
3.2. Independent Operation of Truck and Drone
3.3. The Truck Serving as Auxiliary Support to the Drone
3.4. The Drone Serving as Auxiliary Support to the Truck
4. Configurations of Trucks and Drones
4.1. Single Truck and Single Drone
4.2. Single Truck and Multiple Drones
4.3. Multiple Combinations of Single Truck and Single Drone
4.4. Multiple Combinations of Single Truck and Multiple Drones
4.5. Multiple Trucks and Multiple Drones
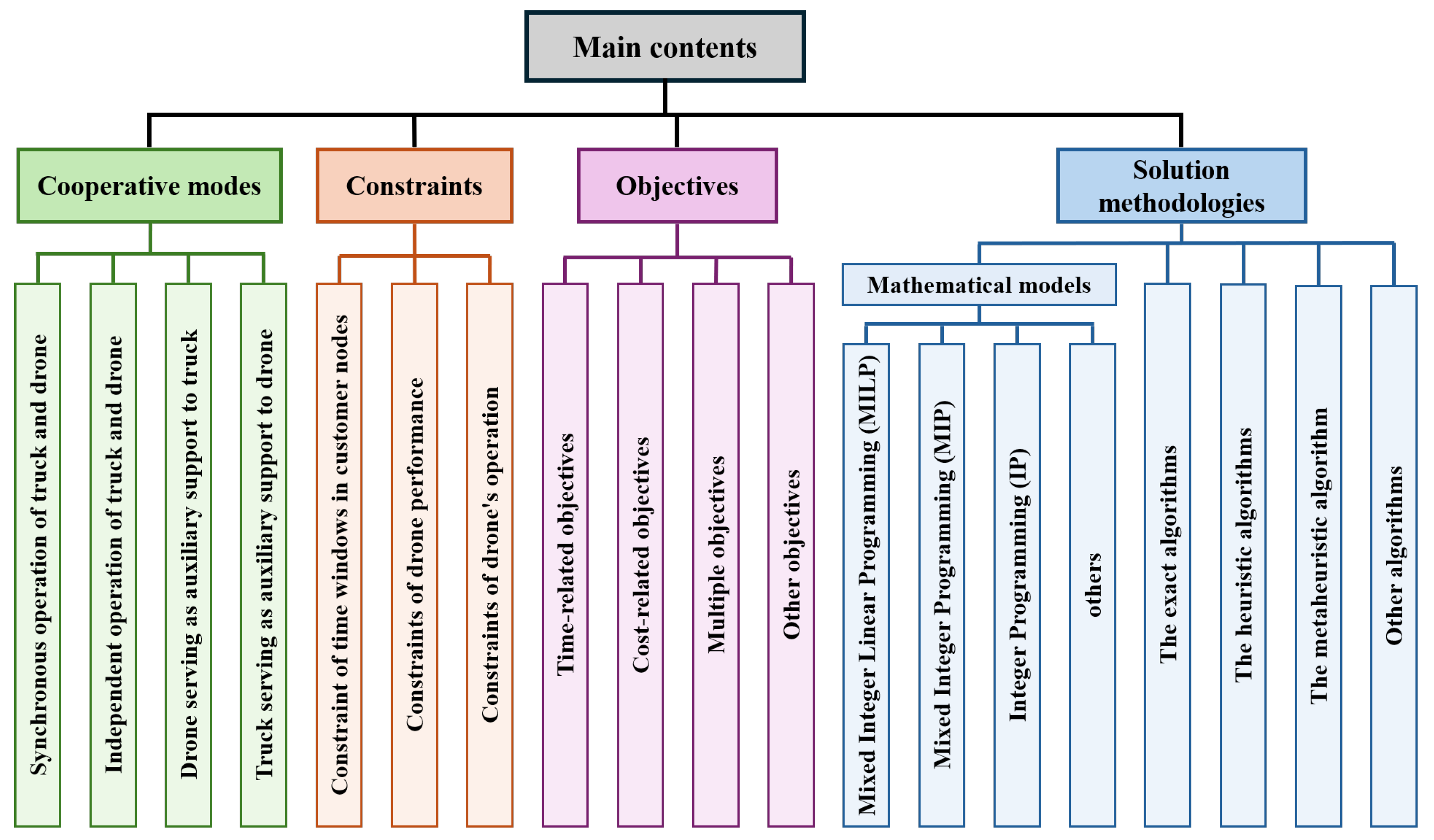
5. The Issues That Have Been Taken into Consideration
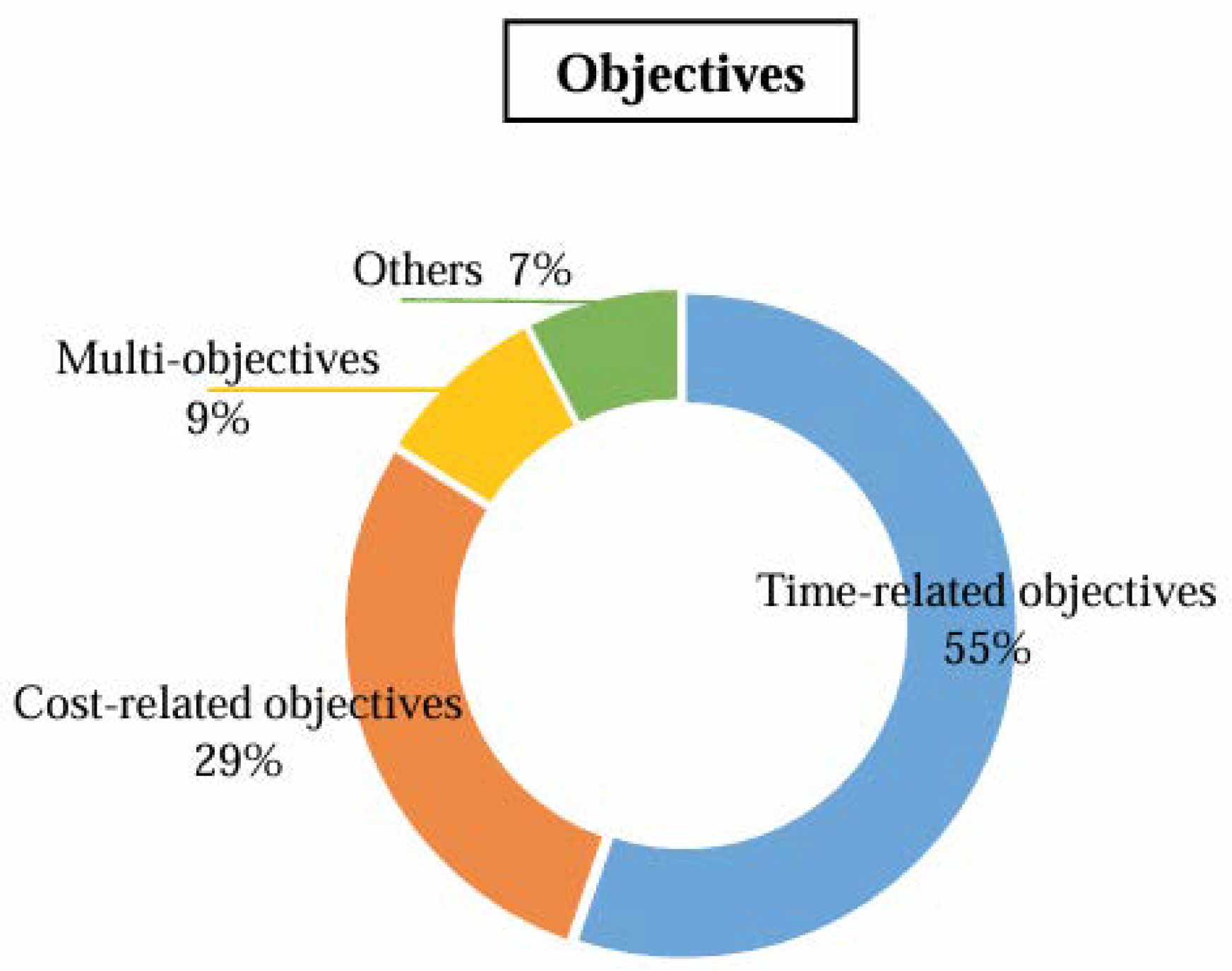
5.1. Objectives
5.1.1. Time-Related Objectives
5.1.2. Cost-Related Objectives
5.1.3. Multiple Objectives
5.1.4. Other Objectives
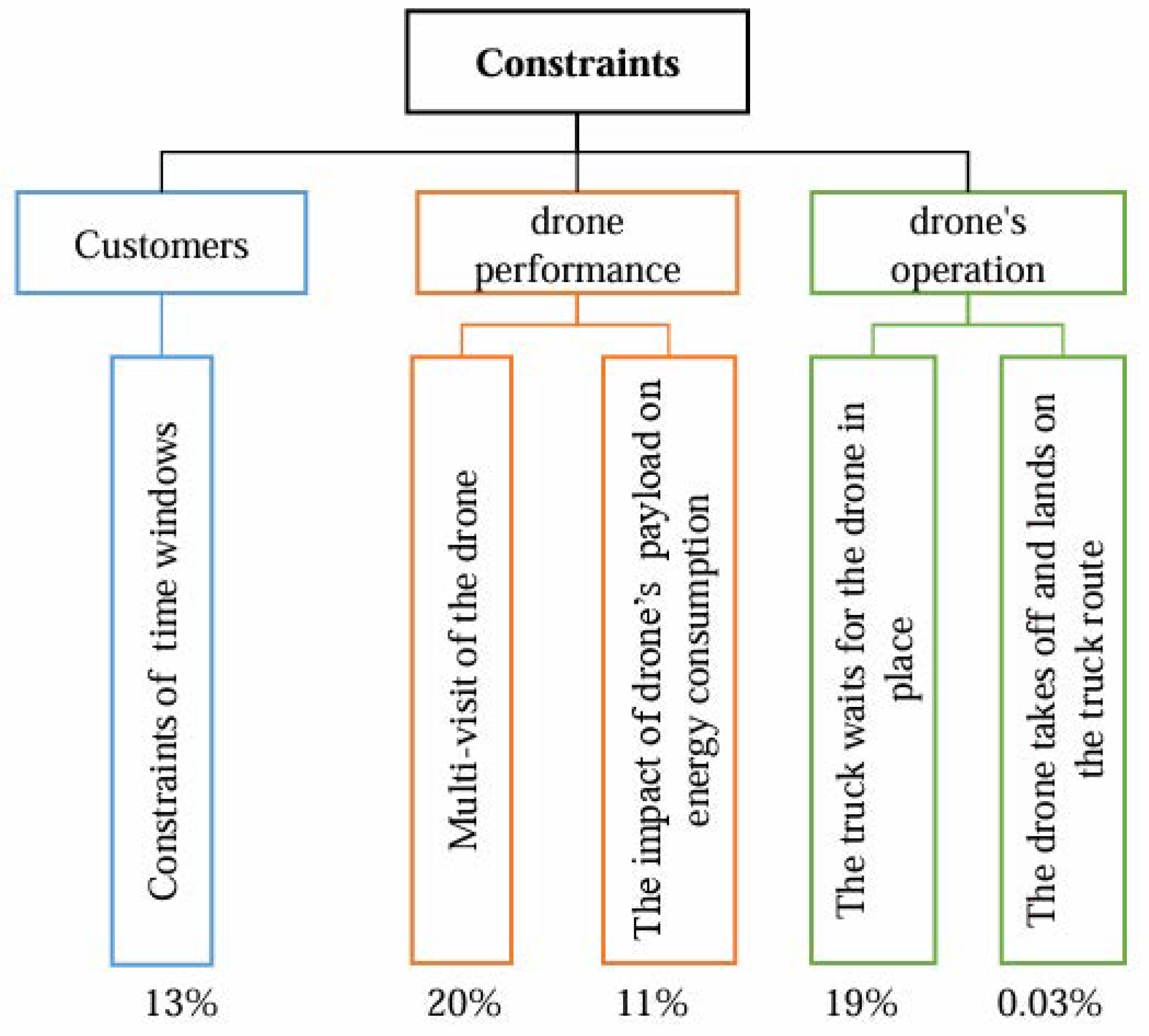
5.2. Constraints
5.2.1. Constraint of Time Windows in Customer Nodes
5.2.2. Constraints of Drone Performance
5.2.3. Constraints of Drone’s Operation
5.3. Dynamic Issues
6. Solution Methodologies
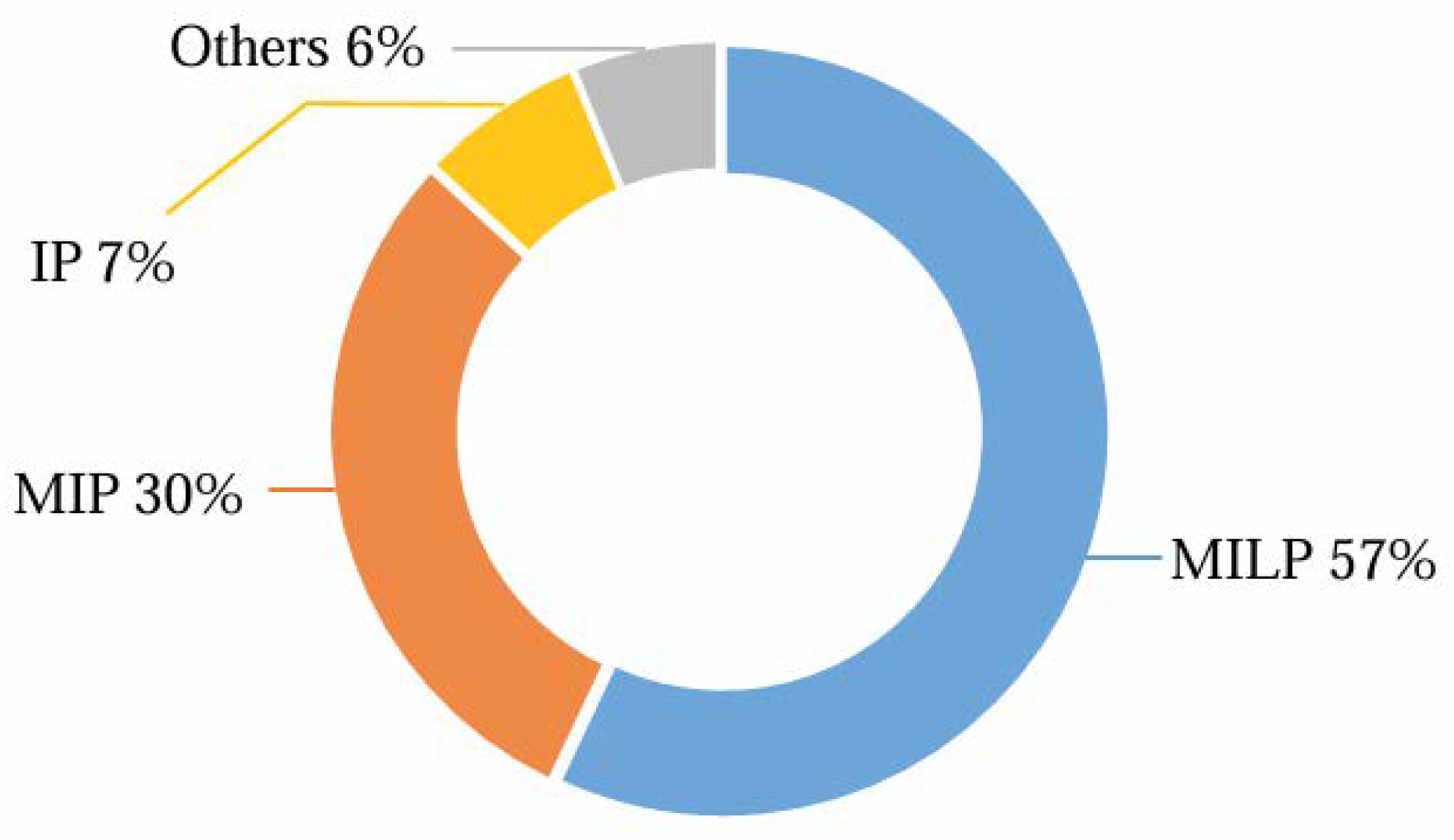
6.1. The Exact Algorithms
6.2. The Heuristic Algorithms
6.3. The Metaheuristic Algorithms
6.4. Other Algorithms
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Murray, C.C.; Chu, A.G. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transp. Res. Part Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
- Khoufi, I.; Laouiti, A.; Adjih, C. A Survey of Recent Extended Variants of the Traveling Salesman and Vehicle Routing Problems for Unmanned Aerial Vehicles. Drones 2019, 3, 66. [Google Scholar] [CrossRef]
- Chung, S.H.; Sah, B.; Lee, J. Optimization for drone and drone-truck combined operations: A review of the state of the art and future directions. Comput. Oper. Res. 2020, 123, 105004. [Google Scholar] [CrossRef]
- Macrina, G.; Di Puglia Pugliese, L.; Guerriero, F.; Laporte, G. Drone-aided routing: A literature review. Transp. Res. Part Emerg. Technol. 2020, 120, 102762. [Google Scholar] [CrossRef]
- Li, H.; Chen, J.; Wang, F.; Bai, M. Ground-vehicle and unmanned-aerial-vehicle routing problems from two-echelon scheme perspective: A review. Eur. J. Oper. Res. 2021, 294, 1078–1095. [Google Scholar] [CrossRef]
- Jazemi, R.; Alidadiani, E.; Ahn, K.; Jang, J. A review of literature on vehicle routing problems of last-mile delivery in urban areas. Appl. Sci. 2023, 13, 13015. [Google Scholar] [CrossRef]
- Baldisseri, A.; Siragusa, C.; Seghezzi, A.; Mangiaracina, R.; Tumino, A. Truck-based drone delivery system: An economic and environmental assessment. Transp. Res. Part D Transp. Environ. 2022, 107, 103296. [Google Scholar] [CrossRef]
- Chiang, W.C.; Li, Y.; Shang, J.; Urban, T.L. Impact of drone delivery on sustainability and cost: Realizing the UAV potential through vehicle routing optimization. Appl. Energy 2019, 242, 1164–1175. [Google Scholar] [CrossRef]
- Banyai, T. Impact of the Integration of First-Mile and Last-Mile Drone-Based Operations from Trucks on Energy Efficiency and the Environment. Drones 2022, 6, 249. [Google Scholar] [CrossRef]
- Kitjacharoenchai, P.; Min, B.C.; Lee, S. Two echelon vehicle routing problem with drones in last mile delivery. Int. J. Prod. Econ. 2020, 225, 107598. [Google Scholar] [CrossRef]
- Salama, M.; Srinivas, S. Joint optimization of customer location clustering and drone-based routing for last-mile deliveries. Transp. Res. Part C Emerg. Technol. 2020, 114, 620–642. [Google Scholar] [CrossRef]
- Di Puglia Pugliese, L.; Macrina, G.; Guerriero, F. Trucks and drones cooperation in the last-mile delivery process. Networks 2021, 78, 371–399. [Google Scholar] [CrossRef]
- Pugliese, L.D.P.; Guerriero, F.; Scutella, M.G. The Last-Mile Delivery Process with Trucks and Drones Under Uncertain Energy Consumption. J. Optim. Theory Appl. 2021, 191, 31–67. [Google Scholar] [CrossRef]
- Arishi, A.; Krishnan, K.; Arishi, M. Machine learning approach for truck-drones based last-mile delivery in the era of industry 4.0. Eng. Appl. Artif. Intell. 2022, 116, 105439. [Google Scholar] [CrossRef]
- Betti Sorbelli, F.; Corò, F.; Das, S.K.; Palazzetti, L.; Pinotti, C.M. On the Scheduling of Conflictual Deliveries in a last-mile delivery scenario with truck-carried drones. Pervasive Mob. Comput. 2022, 87, 101700. [Google Scholar] [CrossRef]
- Borghetti, F.; Caballini, C.; Carboni, A.; Grossato, G.; Maja, R.; Barabino, B. The Use of Drones for Last-Mile Delivery: A Numerical Case Study in Milan, Italy. Sustainability 2022, 14, 1766. [Google Scholar] [CrossRef]
- Gao, J.; Zhen, L.; Laporte, G.; He, X. Scheduling trucks and drones for cooperative deliveries. Transp. Res. Part E Logist. Transp. Rev. 2023, 178, 103267. [Google Scholar] [CrossRef]
- Imran, N.M.; Mishra, S.; Won, M. A-VRPD: Automating Drone-Based Last-Mile Delivery Using Self-Driving Cars. IEEE Trans. Intell. Transp. Syst. 2023, 24, 9599–9612. [Google Scholar] [CrossRef]
- Zhao, L.; Bi, X.; Li, G.; Dong, Z.; Xiao, N.; Zhao, A. Robust traveling salesman problem with multiple drones: Parcel delivery under uncertain navigation environments. Transp. Res. Part E Logist. Transp. Rev. 2022, 168, 102967. [Google Scholar] [CrossRef]
- Liu, Z.; Li, X.; Khojandi, A. The flying sidekick traveling salesman problem with stochastic travel time: A reinforcement learning approach. Transp. Res. Part E Logist. Transp. Rev. 2022, 164, 102816. [Google Scholar] [CrossRef]
- Zhao, L.; Bi, X.; Dong, Z.; Xiao, N.; Zhao, A. Robust traveling salesman problem with drone: Balancing risk and makespan in contactless delivery. Int. Trans. Oper. Res. 2024, 31, 167–191. [Google Scholar] [CrossRef]
- Weng, Y.Y.; Wu, R.Y.; Zheng, Y.J. Cooperative truck-drone delivery path optimization under urban traffic restriction. Drones 2023, 7, 59. [Google Scholar] [CrossRef]
- Liu, W.; Li, W.; Zhou, Q.; Die, Q.; Yang, Y. The optimization of the “UAV-vehicle” joint delivery route considering mountainous cities. PLoS ONE 2022, 17, e0265518. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Li, Y.; Cao, Z.; Xiao, J. Cooperative trucks and drones for rural last-mile delivery with steep roads. Comput. Ind. Eng. 2024, 187, 109849. [Google Scholar] [CrossRef]
- Wang, X.; Poikonen, S.; Golden, B. The vehicle routing problem with drones: Several worst-case results. Optim. Lett. 2017, 11, 679–697. [Google Scholar] [CrossRef]
- Yin, Y.; Yang, Y.; Yu, Y.; Wang, D.; Cheng, T. Robust vehicle routing with drones under uncertain demands and truck travel times in humanitarian logistics. Transp. Res. Part B Methodol. 2023, 174, 102781. [Google Scholar] [CrossRef]
- Bansal, S.; Goel, R.; Maini, R. Ground vehicle and UAV collaborative routing and scheduling for humanitarian logistics using random walk based ant colony optimization. Sci. Iran. 2022, 29, 632–644. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, Y.; Lin, H. Optimizing synchronized truck-drone delivery with priority in disaster relief. J. Ind. Manag. Optim. 2023, 19, 5143–5162. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, C.; Yang, J. A multi-objective humanitarian pickup and delivery vehicle routing problem with drones. Ann. Oper. Res. 2022, 319, 291–353. [Google Scholar] [CrossRef]
- Manshadian, H.; Sadegh Amalnick, M.; Torabi, S.A. Synchronized truck and drone routing under disastrous conditions (case study: Urban thoroughfares disinfection). Comput. Oper. Res. 2023, 159, 106295. [Google Scholar] [CrossRef]
- Gao, W.; Luo, J.; Zhang, W.; Yuan, W.; Liao, Z. Commanding Cooperative UGV-UAV with Nested Vehicle Routing for Emergency Resource Delivery. IEEE Access 2020, 8, 215691–215704. [Google Scholar] [CrossRef]
- Long, Y.; Xu, G.; Zhao, J.; Xie, B.; Fang, M. Dynamic Truck–UAV Collaboration and Integrated Route Planning for Resilient Urban Emergency Response. IEEE Trans. Eng. Manag. 2023, 71, 1–13. [Google Scholar] [CrossRef]
- Lin, M.; Chen, Y.; Han, R.; Chen, Y. Discrete Optimization on Truck-Drone Collaborative Transportation System for Delivering Medical Resources. Discret. Dyn. Nat. Soc. 2022, 2022, 1811288. [Google Scholar] [CrossRef]
- Van Steenbergen, R.; Mes, M.; Van Heeswijk, W. Reinforcement learning for humanitarian relief distribution with trucks and UAVs under travel time uncertainty. Transp. Res. Part C Emerg. Technol. 2023, 157, 104401. [Google Scholar] [CrossRef]
- Ramos, T.R.P.; Vigo, D. A new hybrid distribution paradigm: Integrating drones in medicines delivery. Expert Syst. Appl. 2023, 234, 120992. [Google Scholar] [CrossRef]
- Deng, X.; Guan, M.; Ma, Y.; Yang, X.; Xiang, T. Vehicle-Assisted UAV Delivery Scheme Considering Energy Consumption for Instant Delivery. Sensors 2022, 22, 2045. [Google Scholar] [CrossRef]
- Gu, Q.; Fan, T.; Pan, F.; Zhang, C. A vehicle-UAV operation scheme for instant delivery. Comput. Ind. Eng. 2020, 149, 106809. [Google Scholar] [CrossRef]
- Chen, X.; Ulmer, M.W.; Thomas, B.W. Deep Q-learning for same-day delivery with vehicles and drones. Eur. J. Oper. Res. 2022, 298, 939–952. [Google Scholar] [CrossRef]
- Dayarian, I.; Savelsbergh, M.; Clarke, J.P. Same-Day Delivery with Drone Resupply. Transp. Sci. 2020, 54, 229–249. [Google Scholar] [CrossRef]
- Ulmer, M.W.; Thomas, B.W. Same-day delivery with heterogeneous fleets of drones and vehicles. Networks 2018, 72, 475–505. [Google Scholar] [CrossRef]
- Lee, S.Y.; Han, S.R.; Song, B.D. Simultaneous cooperation of Refrigerated Ground Vehicle (RGV) and Unmanned Aerial Vehicle (UAV) for rapid delivery with perishable food. Appl. Math. Model. 2022, 106, 844–866. [Google Scholar] [CrossRef]
- Yan, R.; Zhu, X.; Zhu, X.; Peng, R. Optimal routes and aborting strategies of trucks and drones under random attacks. Reliab. Eng. Syst. Saf. 2022, 222, 108457. [Google Scholar] [CrossRef]
- Zandieh, F.; Farid Ghannadpour, S.; Mahdavi Mazdeh, M. Integrated ground vehicle and drone routing with simultaneous surveillance coverage for evading intentional disruption. Transp. Res. Part E Logist. Transp. Rev. 2023, 178, 103266. [Google Scholar] [CrossRef]
- Zandieh, F.; Ghannadpour, S.F.; Mazdeh, M.M. New integrated routing and surveillance model with drones and charging station considerations. Eur. J. Oper. Res. 2024, 313, 527–547. [Google Scholar] [CrossRef]
- Redi, A.A.N.P.; Sopha, B.M.; Asih, A.M.S.; Liperda, R.I. Collaborative Hybrid Aerial and Ground Vehicle Routing for Post-Disaster Assessment. Sustainability 2021, 13, 12841. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, N.; Ma, S.; Xia, J. Humanitarian relief network assessment using collaborative truck-and-drone system. Transp. Res. Part E Logist. Transp. Rev. 2021, 152, 102417. [Google Scholar] [CrossRef]
- Ribeiro, R.G.; Cota, L.P.; Euzebio, T.A.M.; Ramirez, J.A.; Guimaraes, F.G. Unmanned-Aerial-Vehicle Routing Problem with Mobile Charging Stations for Assisting Search and Rescue Missions in Postdisaster Scenarios. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 6682–6696. [Google Scholar] [CrossRef]
- Ermagun, A.; Tajik, N. Multiple-Drones-Multiple-Trucks Routing Problem for Disruption Assessment. Transp. Res. Rec. 2023, 2677, 725–740. [Google Scholar] [CrossRef]
- Yan, R.; Zhu, X.; Zhu, X.; Peng, R. Joint optimisation of task abortions and routes of truck-and-drone systems under random attacks. Reliab. Eng. Syst. Saf. 2023, 235, 109249. [Google Scholar] [CrossRef]
- Hu, M.; Liu, W.; Lu, J.; Fu, R.; Peng, K.; Ma, X.; Liu, J. On the joint design of routing and scheduling for Vehicle-Assisted Multi-UAV inspection. Future Gener. Comput. Syst. 2019, 94, 214–223. [Google Scholar] [CrossRef]
- Hu, M.; Liu, W.; Peng, K.; Ma, X.; Cheng, W.; Liu, J.; Li, B. Joint Routing and Scheduling for Vehicle-Assisted Multi-drone Surveillance. IEEE Internet Things J. 2019, 6, 1781–1790. [Google Scholar] [CrossRef]
- Maini, P.; Sundar, K.; Singh, M.; Rathinam, S.; Sujit, P.B. Cooperative Aerial–Ground Vehicle Route Planning with Fuel Constraints for Coverage Applications. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 3016–3028. [Google Scholar] [CrossRef]
- Amorosi, L.; Puerto, J.; Valverde, C. Coordinating drones with mothership vehicles: The mothership and drone routing problem with graphs. Comput. Oper. Res. 2021, 136, 105445. [Google Scholar] [CrossRef]
- Alkaabneh, F. Matheuristic for synchronized vehicle routing problem with multiple constraints and variable service time: Managing a fleet of sprayers and a tender tanker. Comput. Oper. Res. 2024, 162, 106454. [Google Scholar] [CrossRef]
- Momeni, M.; Soleimani, H.; Shahparvari, S.; Afshar-Nadjafi, B. Coordinated routing system for fire detection by patrolling trucks with drones. Int. J. Disaster Risk Reduct. 2022, 73, 102859. [Google Scholar] [CrossRef]
- Luo, H.; Zhang, P.; Wang, J.; Wang, G.; Meng, F. Traffic Patrolling Routing Problem with Drones in an Urban Road System. Sensors 2019, 19, 5164. [Google Scholar] [CrossRef]
- Rosenfeld, A.; Maksimov, O. Optimal cruiser-drone traffic enforcement under energy limitation. Artif. Intell. 2019, 277, 103166. [Google Scholar] [CrossRef]
- Liu, B.; Ni, W.; Liu, R.P.; Zhu, Q.; Guo, Y.J.; Zhu, H. Novel Integrated Framework of Unmanned Aerial Vehicle and Road Traffic for Energy-Efficient Delay-Sensitive Delivery. IEEE Trans. Intell. Transp. Syst. 2022, 23, 10692–10707. [Google Scholar] [CrossRef]
- Tian, S.; Chen, H.; Wu, G.; Cheng, J. Asymmetric Arc Routing by Coordinating a Truck and Multiple Drones. Sensors 2022, 22, 6077. [Google Scholar] [CrossRef]
- Xu, B.; Zhao, K.; Luo, Q.; Wu, G.; Pedrycz, W. A GV-drone arc routing approach for urban traffic patrol by coordinating a ground vehicle and multiple drones. Swarm Evol. Comput. 2023, 77, 101246. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, J.; Liu, Z.; Huang, J.; Zhou, T. Two-Layer Routing for High-Voltage Powerline Inspection by Cooperated Ground Vehicle and Drone. Energies 2019, 12, 1385. [Google Scholar] [CrossRef]
- Mcglaun, S. Mercedes, Matternet, and Siroop Launch Drone Pilot Program For On-Demand Same-Day Delivery. 2017. Available online: https://www.slashgear.com/mercedes-matternet-and-siroop-launch-drone-pilot-program-for-on-demand-same-day-delivery-02502365 (accessed on 26 May 2024).
- Stewart, J. A Drone-Slinging UPS Van Delivers the Future. Wired Magazine, 21 February 2017. Available online: https://mendoza.nd.edu/news/a-drone-slinging-ups-van-delivers-the-future/#:~:text=A%20Drone-Slinging%20UPS%20Van%20Delivers%20the%20Future.%20Published: (accessed on 26 May 2024).
- Soldiersystems. Elistair Unveils Long—Endurance Orion 2 Tethered Drone for Military, Security, and Industrial Use; Elistair: Dardilly, France, 2020. [Google Scholar]
- Turner, A. Drones Used by the Police. 2020. Available online: https://www.met.police.uk/foi-ai/metropolitan-police/d/november-2022/use-of-drones-in-policing/?__cf_chl_tk=P3Yxc9PWf4qn4J2SmOuZI2NCUVsL5Hz7DvAYMXNfy_w-1727784689-0.0.1.1-5311 (accessed on 26 May 2024).
- Mbiadou Saleu, R.G.; Deroussi, L.; Feillet, D.; Grangeon, N.; Quilliot, A. The parallel drone scheduling problem with multiple drones and vehicles. Eur. J. Oper. Res. 2022, 300, 571–589. [Google Scholar] [CrossRef]
- Nguyen, M.A.; Dang, G.T.H.; Ha, M.H.; Pham, M.T. The min-cost parallel drone scheduling vehicle routing problem. Eur. J. Oper. Res. 2022, 299, 910–930. [Google Scholar] [CrossRef]
- Montemanni, R.; Dell’Amico, M.; Corsini, A. Parallel drone scheduling vehicle routing problems with collective drones. Comput. Oper. Res. 2024, 163, 106514. [Google Scholar] [CrossRef]
- Ham, A.M. Integrated scheduling of m-truck, m-drone, and m-depot constrained by time-window, drop-pickup, and m-visit using constraint programming. Transp. Res. Part C Emerg. Technol. 2018, 91, 1–14. [Google Scholar] [CrossRef]
- Sawadsitang, S.; Niyato, D.; Tan, P.S.; Wang, P. Joint Ground and Aerial Package Delivery Services: A Stochastic Optimization Approach. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2241–2254. [Google Scholar] [CrossRef]
- Momeni, M.; Al-e-Hashem, S.M.J.M.; Heidari, A. A new truck-drone routing problem for parcel delivery by considering energy consumption and altitude. Ann. Oper. Res. 2023, 337, 25. [Google Scholar] [CrossRef]
- Han, Y.q.; Li, J.q.; Liu, Z.; Liu, C.; Tian, J. Metaheuristic algorithm for solving the multi-objective vehicle routing problem with time window and drones. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420920031. [Google Scholar] [CrossRef]
- Zeng, F.; Chen, Z.; Clarke, J.P.; Goldsman, D. Nested vehicle routing problem: Optimizing drone-truck surveillance operations. Transp. Res. Part Emerg. Technol. 2022, 139, 103645. [Google Scholar] [CrossRef]
- Luo, Z.; Liu, Z.; Shi, J. A Two-Echelon Cooperated Routing Problem for a Ground Vehicle and Its Carried Unmanned Aerial Vehicle. Sensors 2017, 17, 1144. [Google Scholar] [CrossRef]
- Dukkanci, O.; Kara, B.Y.; Bektas, T. The Drone Delivery Problem. SSRN Electron. J. 2019. [CrossRef]
- Peng, K.; Du, J.; Lu, F.; Sun, Q.; Dong, Y.; Zhou, P.; Hu, M. A Hybrid Genetic Algorithm on Routing and Scheduling for Vehicle-Assisted Multi-Drone Parcel Delivery. IEEE Access 2019, 7, 49191–49200. [Google Scholar] [CrossRef]
- Teimoury, E.; Rashid, R. A hybrid variable neighborhood search heuristic for the sustainable time-dependent truck-drone routing problem with rendezvous locations. J. Heuristics 2023, 30, 1–41. [Google Scholar] [CrossRef]
- Teimoury, E.; Rashid, R. The paired pickup and delivery problem with profit in a two-echelon delivery system with multiple trucks and drones. Transp. Lett. 2023, 9, 1–7. [Google Scholar] [CrossRef]
- Ghiasvand, M.R.; Rahmani, D.; Moshref-Javadi, M. Data-driven robust optimization for a multi-trip truck-drone routing problem. Expert Syst. Appl. 2024, 241, 122485. [Google Scholar] [CrossRef]
- Pina-Pardo, J.C.; Silva, D.F.; Smith, A.E. The traveling salesman problem with release dates and drone resupply. Comput. Oper. Res. 2021, 129, 105170. [Google Scholar] [CrossRef]
- Dienstknecht, M.; Boysen, N.; Briskorn, D. The traveling salesman problem with drone resupply. OR Spectrum 2022, 44, 1045–1086. [Google Scholar] [CrossRef]
- Boysen, N.; Briskorn, D.; Fedtke, S.; Schwerdfeger, S. Drone delivery from trucks: Drone scheduling for given truck routes. Networks 2018, 72, 506–527. [Google Scholar] [CrossRef]
- Agatz, N.; Bouman, P.; Schmidt, M. Optimization Approaches for the Traveling Salesman Problem with Drone. Transp. Sci. 2018, 52, 965–981. [Google Scholar] [CrossRef]
- Ha, Q.M.; Deville, Y.; Pham, Q.D.; Hà, M.H. On the min-cost Traveling Salesman Problem with Drone. Transp. Res. Part C Emerg. Technol. 2018, 86, 597–621. [Google Scholar] [CrossRef]
- Liu, Y.; Luo, Z.; Liu, Z.; Shi, J.; Cheng, G. Cooperative Routing Problem for Ground Vehicle and Unmanned Aerial Vehicle: The Application on Intelligence, Surveillance, and Reconnaissance Missions. IEEE Access 2019, 7, 63504–63518. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Z.; Shi, J.; Wu, G.; Pedrycz, W. Two-Echelon Routing Problem for Parcel Delivery by Cooperated Truck and Drone. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 51, 7450–7465. [Google Scholar] [CrossRef]
- El-Adle, A.M.; Ghoniem, A.; Haouari, M. The cost of carrier consistency: Last-mile delivery by vehicle and drone for subscription-based orders. J. Oper. Res. Soc. 2023, 75, 821–840. [Google Scholar] [CrossRef]
- Najy, W.; Archetti, C.; Diabat, A. Collaborative truck-and-drone delivery for inventory-routing problems. Transp. Res. Part C Emerg. Technol. 2023, 146, 103791. [Google Scholar] [CrossRef]
- Campuzano, G.; Lalla-Ruiz, E.; Mes, M. The drone-assisted variable speed asymmetric traveling salesman problem. Comput. Ind. Eng. 2023, 176, 109003. [Google Scholar] [CrossRef]
- Marinelli, M.; Caggiani, L.; Ottomanelli, M.; Dell’Orco, M. En route truck-drone parcel delivery for optimal vehicle routing strategies. IET Intell. Transp. Syst. 2018, 12, 253–261. [Google Scholar] [CrossRef]
- Zhu, T.; Boyles, S.D.; Unnikrishnan, A. Battery electric vehicle traveling salesman problem with drone. Netw. Spat. Econ. 2023, 24, 49–97. [Google Scholar] [CrossRef]
- Mara, S.T.W.; Sarker, R.; Essam, D.; Elsayed, S. Solving electric vehicle-drone routing problem using memetic algorithm. Swarm Evol. Comput. 2023, 79, 101295. [Google Scholar] [CrossRef]
- Yurek, E.E.; Ozmutlu, H.C. Traveling salesman problem with drone under recharging policy. Comput. Commun. 2021, 179, 35–49. [Google Scholar] [CrossRef]
- Peng, K.; Liu, W.; Sun, Q.; Ma, X.; Hu, M.; Wang, D.; Liu, J. Wide-Area Vehicle-Drone Cooperative Sensing: Opportunities and Approaches. IEEE Access 2019, 7, 1818–1828. [Google Scholar] [CrossRef]
- Chang, Y.S.; Lee, H.J. Optimal delivery routing with wider drone-delivery areas along a shorter truck-route. Expert Syst. Appl. 2018, 104, 307–317. [Google Scholar] [CrossRef]
- Moshref-Javadi, M.; Lee, S.; Winkenbach, M. Design and evaluation of a multi-trip delivery model with truck and drones. Transp. Res. Part E Logist. Transp. Rev. 2020, 136, 101887. [Google Scholar] [CrossRef]
- Kang, M.; Lee, C. An Exact Algorithm for Heterogeneous Drone-Truck Routing Problem. Transp. Sci. 2021, 55, 1088–1112. [Google Scholar] [CrossRef]
- Lu, S.H.; Kuo, R.; Ho, Y.T.; Nguyen, A.T. Improving the efficiency of last-mile delivery with the flexible drones traveling salesman problem. Expert Syst. Appl. 2022, 209, 118351. [Google Scholar] [CrossRef]
- Moshref-Javadi, M.; Hemmati, A.; Winkenbach, M. A comparative analysis of synchronized truck-and-drone delivery models. Comput. Ind. Eng. 2021, 162, 107648. [Google Scholar] [CrossRef]
- Kim, S.; Moon, I. Traveling Salesman Problem with a Drone Station. IEEE Trans. Syst. Man, Cybern. Syst. 2019, 49, 42–52. [Google Scholar] [CrossRef]
- Karak, A.; Abdelghany, K. The hybrid vehicle-drone routing problem for pick-up and delivery services. Transp. Res. Part C Emerg. Technol. 2019, 102, 427–449. [Google Scholar] [CrossRef]
- Faiz, T.I.; Vogiatzis, C.; Noor-E-Alam, M. Computational approaches for solving two-echelon vehicle and UAV routing problems for post-disaster humanitarian operations. Expert Syst. Appl. 2024, 237, 121473. [Google Scholar] [CrossRef]
- Kloster, K.; Moeini, M.; Vigo, D.; Wendt, O. The multiple traveling salesman problem in presence of drone- and robot-supported packet stations. Eur. J. Oper. Res. 2023, 305, 630–643. [Google Scholar] [CrossRef]
- Zou, B.; Wu, S.; Gong, Y.; Yuan, Z.; Shi, Y. Delivery network design of a locker-drone delivery system. Int. J. Prod. Res. 2023, 62, 4097–4121. [Google Scholar] [CrossRef]
- Moshref-Javadi, M.; Hemmati, A.; Winkenbach, M. A truck and drones model for last-mile delivery: A mathematical model and heuristic approach. Appl. Math. Model. 2020, 80, 290–318. [Google Scholar] [CrossRef]
- Murray, C.C.; Raj, R. The multiple flying sidekicks traveling salesman problem: Parcel delivery with multiple drones. Transp. Res. Part C Emerg. Technol. 2020, 110, 368–398. [Google Scholar] [CrossRef]
- Lin, M.; Lyu, J.Y.; Gao, J.J.; Li, L.Y. Model and Hybrid Algorithm of Collaborative Distribution System with Multiple Drones and a Truck. Sci. Program. 2020, 2020, 8887057. [Google Scholar] [CrossRef]
- Luo, Z.; Poon, M.; Zhang, Z.; Liu, Z.; Lim, A. The Multi-visit Traveling Salesman Problem with Multi-Drones. Transp. Res. Part C Emerg. Technol. 2021, 128, 103172. [Google Scholar] [CrossRef]
- Raj, R.; Murray, C. The multiple flying sidekicks traveling salesman problem with variable drone speeds. Transp. Res. Part C Emerg. Technol. 2020, 120, 102813. [Google Scholar] [CrossRef]
- Leon-Blanco, J.M.; Gonzalez-R, P.; Andrade-Pineda, J.L.; Canca, D.; Calle, M. A multi-agent approach to the truck multi-drone routing problem. Expert Syst. Appl. 2022, 195, 116604. [Google Scholar] [CrossRef]
- Gomez-Lagos, J.; Candia-Vejar, A.; Encina, F. A New Truck-Drone Routing Problem for Parcel Delivery Services Aided by Parking Lots. IEEE Access 2021, 9, 11091–11108. [Google Scholar] [CrossRef]
- Mahmoudi, B.; Eshghi, K. Energy-constrained multi-visit TSP with multiple drones considering non-customer rendezvous locations. Expert Syst. Appl. 2022, 210, 118479. [Google Scholar] [CrossRef]
- Salama, M.R.; Srinivas, S. Collaborative truck multi-drone routing and scheduling problem: Package delivery with flexible launch and recovery sites. Transp. Res. Part E Logist. Transp. Rev. 2022, 164, 102788. [Google Scholar] [CrossRef]
- Young Jeong, H.; Lee, S. Drone routing problem with truck: Optimization and quantitative analysis. Expert Syst. Appl. 2023, 227, 120260. [Google Scholar] [CrossRef]
- Chen, Y.; Ren, S.; Chen, Z.; Chen, M.; Wu, H. Path Planning for Vehicle-borne System Consisting of Multi Air–ground Robots. Robotica 2020, 38, 493–511. [Google Scholar] [CrossRef]
- Morandi, N.; Leus, R.; Matuschke, J.; Yaman, H. The TSP with drones: The benefits of retraversing the arcs. Transp. Sci. 2023, 57, 1340–1358. [Google Scholar] [CrossRef]
- Sacramento, D.; Pisinger, D.; Ropke, S. An adaptive large neighborhood search metaheuristic for the vehicle routing problem with drones. Transp. Res. Part C Emerg. Technol. 2019, 102, 289–315. [Google Scholar] [CrossRef]
- Schermer, D.; Moeini, M.; Wendt, O. A hybrid VNS/Tabu search algorithm for solving the vehicle routing problem with drones and en route operations. Comput. Oper. Res. 2019, 109, 134–158. [Google Scholar] [CrossRef]
- Huang, S.H.; Huang, Y.H.; Blazquez, C.A.; Chen, C.Y. Solving the vehicle routing problem with drone for delivery services using an ant colony optimization algorithm. Adv. Eng. Inform. 2022, 51, 101536. [Google Scholar] [CrossRef]
- Lei, D.; Cui, Z.; Li, M. A dynamical artificial bee colony for vehicle routing problem with drones. Eng. Appl. Artif. Intell. 2022, 107, 104510. [Google Scholar] [CrossRef]
- Wang, D.; Hu, P.; Du, J.; Zhou, P.; Deng, T.; Hu, M. Routing and Scheduling for Hybrid Truck-Drone Collaborative Parcel Delivery with Independent and Truck-Carried Drones. IEEE Internet Things J. 2019, 6, 10483–10495. [Google Scholar] [CrossRef]
- Luo, Z.; Gu, R.; Poon, M.; Liu, Z.; Lim, A. A last-mile drone-assisted one-to-one pickup and delivery problem with multi-visit drone trips. Comput. Oper. Res. 2022, 148, 106015. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Han, J.; Zhang, Y.; Li, Y.; Jiang, T. Multivisit Drone-Vehicle Routing Problem with Simultaneous Pickup and Delivery considering No-Fly Zones. Discret. Dyn. Nat. Soc. 2023, 2023, 1–21. [Google Scholar] [CrossRef]
- Mulumba, T.; Najy, W.; Diabat, A. The drone-assisted pickup and delivery problem: An adaptive large neighborhood search metaheuristic. Comput. Oper. Res. 2024, 161, 106435. [Google Scholar] [CrossRef]
- Xia, Y.; Wu, T.; Xia, B.; Zhang, J. Truck-drone pickup and delivery problem with drone weight-related cost. Sustainability 2023, 15, 16342. [Google Scholar] [CrossRef]
- Stodola, P.; Kutej, L. Multi-depot vehicle routing problem with drones: Mathematical formulation, solution algorithm and experiments. Expert Syst. Appl. 2024, 241, 122483. [Google Scholar] [CrossRef]
- Coindreau, M.A.; Gallay, O.; Zufferey, N. Parcel delivery cost minimization with time window constraints using trucks and drones. Networks 2021, 78, 400–420. [Google Scholar] [CrossRef]
- Das, D.N.; Sewani, R.; Wang, J.; Tiwari, M.K. Synchronized Truck and Drone Routing in Package Delivery Logistics. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5772–5782. [Google Scholar] [CrossRef]
- Tamke, F.; Buscher, U. A branch-and-cut algorithm for the vehicle routing problem with drones. Transp. Res. Part B Methodol. 2021, 144, 174–203. [Google Scholar] [CrossRef]
- Kuo, R.; Lu, S.H.; Lai, P.Y.; Mara, S.T.W. Vehicle routing problem with drones considering time windows. Expert Syst. Appl. 2022, 191, 116264. [Google Scholar] [CrossRef]
- Li, H.; Zhao, J.; Zhan, Z. Truck and Unmanned Vehicle Routing Problem with Time Windows: A Satellite Synchronization Perspective. J. Adv. Transp. 2022, 2022, 1–20. [Google Scholar] [CrossRef]
- Li, J.; Liu, H.; Lai, K.K.; Ram, B. Vehicle and UAV Collaborative Delivery Path Optimization Model. Mathematics 2022, 10, 3744. [Google Scholar] [CrossRef]
- Yin, Y.; Li, D.; Wang, D.; Ignatius, J.; Cheng, T.; Wang, S. A branch-and-price-and-cut algorithm for the truck-based drone delivery routing problem with time windows. Eur. J. Oper. Res. 2023, 309, 1125–1144. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y. Collaborative vehicle-drone distribution network optimization for perishable products in the epidemic situation. Comput. Oper. Res. 2023, 149, 106039. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Hu, X.; Xue, G.; Guan, X. Truck–drone hybrid routing problem with time-dependent road travel time. Transp. Res. Part C Emerg. Technol. 2022, 144, 103901. [Google Scholar] [CrossRef]
- Xing, J.; Su, L.; Hong, W.; Tong, L.; Lyu, R.; Du, W. Aerial-ground collaborative routing with time constraints. Chin. J. Aeronaut. 2023, 36, 270–283. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, J.; Yang, C. A humanitarian vehicle routing problem synchronized with drones in time-varying weather conditions. Comput. Ind. Eng. 2023, 184, 109563. [Google Scholar] [CrossRef]
- Zang, X.; Jiang, L.; Liang, C.; Dong, J.; Lu, W.; Mladenovic, N. Optimization approaches for the urban delivery problem with trucks and drones. Swarm Evol. Comput. 2022, 75, 101147. [Google Scholar] [CrossRef]
- Kuo, R.; Edbert, E.; Zulvia, F.E.; Lu, S.H. Applying NSGA-II to vehicle routing problem with drones considering makespan and carbon emission. Expert Syst. Appl. 2023, 221, 119777. [Google Scholar] [CrossRef]
- Li, H.; Wang, H.; Chen, J.; Bai, M. Two-echelon vehicle routing problem with time windows and mobile satellites. Transp. Res. Part B Methodol. 2020, 138, 179–201. [Google Scholar] [CrossRef]
- Chen, C.; Demir, E.; Huang, Y. An adaptive large neighborhood search heuristic for the vehicle routing problem with time windows and delivery robots. Eur. J. Oper. Res. 2021, 294, 1164–1180. [Google Scholar] [CrossRef]
- Gao, J.; Zhen, L.; Wang, S. Multi-trucks-and-drones cooperative pickup and delivery problem. Transp. Res. Part C Emerg. Technol. 2023, 157, 104407. [Google Scholar] [CrossRef]
- Kitjacharoenchai, P.; Ventresca, M.; Moshref-Javadi, M.; Lee, S.; Tanchoco, J.M.; Brunese, P.A. Multiple traveling salesman problem with drones: Mathematical model and heuristic approach. Comput. Ind. Eng. 2019, 129, 14–30. [Google Scholar] [CrossRef]
- Wang, Z.; Sheu, J.B. Vehicle routing problem with drones. Transp. Res. Part B Methodol. 2019, 122, 350–364. [Google Scholar] [CrossRef]
- Amine Masmoudi, M.; Mancini, S.; Baldacci, R.; Kuo, Y.H. Vehicle routing problems with drones equipped with multi-package payload compartments. Transp. Res. Part E Logist. Transp. Rev. 2022, 164, 102757. [Google Scholar] [CrossRef]
- Jiang, J.; Dai, Y.; Yang, F.; Ma, Z. A multi-visit flexible-docking vehicle routing problem with drones for simultaneous pickup and delivery services. Eur. J. Oper. Res. 2024, 312, 125–137. [Google Scholar] [CrossRef]
- Kim, D.; Ko, C.S.; Moon, I. Coordinated logistics with trucks and drones for premium delivery. Transp. Transp. Sci. 2023, 1–29. [Google Scholar] [CrossRef]
- Rave, A.; Fontaine, P.; Kuhn, H. Drone location and vehicle fleet planning with trucks and aerial drones. Eur. J. Oper. Res. 2023, 308, 113–130. [Google Scholar] [CrossRef]
- Li, H.; Wang, F.; Zhan, Z. Truck and rotary-wing drone routing problem considering flight-level selection. J. Oper. Res. Soc. 2023, 75, 205–223. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, G.; Pang, Z.; Li, L. Continuum approximation models for joint delivery systems using trucks and drones. Enterp. Inf. Syst. 2020, 14, 406–435. [Google Scholar] [CrossRef]
- De Freitas, J.C.; Penna, P.H.V. A Randomized Variable Neighborhood Descent Heuristic to Solve the Flying Sidekick Traveling Salesman Problem. Electron. Notes Discret. Math. 2018, 66, 95–102. [Google Scholar] [CrossRef]
- Crişan, G.C.; Nechita, E. On a cooperative truck-and-drone delivery system. In Proceedings of the Knowledge-Based and Intelligent Information & Engineering Systems: Proceedings of the 23rd International Conference KES2019, Budapest, Hungary, 4–6 September 2019; Volume 159, pp. 38–47. [Google Scholar] [CrossRef]
- De Freitas, J.C.; Penna, P.H.V. A variable neighborhood search for flying sidekick traveling salesman problem. Int. Trans. Oper. Res. 2020, 27, 267–290. [Google Scholar] [CrossRef]
- Boccia, M.; Masone, A.; Sforza, A.; Sterle, C. A column-and-row generation approach for the flying sidekick travelling salesman problem. Transp. Res. Part C Emerg. Technol. 2021, 124, 102913. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Montemanni, R.; Novellani, S. Drone-assisted deliveries: New formulations for the Flying Sidekick Traveling Salesman Problem. Optim. Lett. 2021, 15, 1617–1648. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Montemanni, R.; Novellani, S. Algorithms based on branch and bound for the flying sidekick traveling salesman problem. Omega 2021, 104, 102493. [Google Scholar] [CrossRef]
- Kundu, A.; Escobar, R.G.; Matis, I.T. An efficient routing heuristic for a drone-assisted delivery problem. IMA J. Manag. Math. 2022, 33, 583–601. [Google Scholar] [CrossRef]
- Bouman, P.; Agatz, N.; Schmidt, M. Dynamic programming approaches for the traveling salesman problem with drone. Networks 2018, 72, 528–542. [Google Scholar] [CrossRef]
- Es Yurek, E.; Ozmutlu, H.C. A decomposition-based iterative optimization algorithm for traveling salesman problem with drone. Transp. Res. Part C Emerg. Technol. 2018, 91, 249–262. [Google Scholar] [CrossRef]
- Poikonen, S.; Golden, B.; Wasil, E.A. A Branch-and-Bound Approach to the Traveling Salesman Problem with a Drone. INFORMS J. Comput. 2019, 31, 335–346. [Google Scholar] [CrossRef]
- Poikonen, S.; Wang, X.; Golden, B. The vehicle routing problem with drones: Extended models and connections. Networks 2017, 70, 34–43. [Google Scholar] [CrossRef]
- Ha, Q.M.; Deville, Y.; Pham, Q.D.; Hà, M.H. A hybrid genetic algorithm for the traveling salesman problem with drone. J. Heuristics 2020, 26, 219–247. [Google Scholar] [CrossRef]
- El-Adle, A.M.; Ghoniem, A.; Haouari, M. Parcel delivery by vehicle and drone. J. Oper. Res. Soc. 2021, 72, 398–416. [Google Scholar] [CrossRef]
- Roberti, R.; Ruthmair, M. Exact Methods for the Traveling Salesman Problem with Drone. Transp. Sci. 2021, 55, 315–335. [Google Scholar] [CrossRef]
- Vásquez, S.A.; Angulo, G.; Klapp, M.A. An exact solution method for the TSP with Drone based on decomposition. Comput. Oper. Res. 2021, 127, 105127. [Google Scholar] [CrossRef]
- Tong, B.; Wang, J.; Wang, X.; Zhou, F.; Mao, X.; Zheng, W. Optimal Route Planning for Truck-Drone Delivery Using Variable Neighborhood Tabu Search Algorithm. Appl. Sci. 2022, 12, 529. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Montemanni, R.; Novellani, S. Modeling the flying sidekick traveling salesman problem with multiple drones. Networks 2021, 78, 303–327. [Google Scholar] [CrossRef]
- Mara, S.T.W.; Rifai, A.P.; Sopha, B.M. An adaptive large neighborhood search heuristic for the flying sidekick traveling salesman problem with multiple drops. Expert Syst. Appl. 2022, 205, 117647. [Google Scholar] [CrossRef]
- Rinaldi, M.; Primatesta, S.; Bugaj, M.; Rostas, J.; Guglieri, G. Development of heuristic approaches for last-mile delivery TSP with a truck and multiple drones. Drones 2023, 7, 407. [Google Scholar] [CrossRef]
- Seifried, K. The Traveling Salesman Problem with One Truck and Multiple Drones. SSRN Electron. J. 2019, 57, 1115–1401. [Google Scholar] [CrossRef]
- Cavani, S.; Iori, M.; Roberti, R. Exact methods for the traveling salesman problem with multiple drones. Transp. Res. Part C Emerg. Technol. 2021, 130, 103280. [Google Scholar] [CrossRef]
- Schermer, D.; Moeini, M.; Wendt, O. A matheuristic for the vehicle routing problem with drones and its variants. Transp. Res. Part C Emerg. Technol. 2019, 106, 166–204. [Google Scholar] [CrossRef]
- Ibroska, B.; Ozpeynirci, S.; Ozpeynirci, O. Multiple traveling salesperson problem with drones: General variable neighborhood search approach. Comput. Oper. Res. 2023, 160, 106390. [Google Scholar] [CrossRef]
- Mulumba, T.; Diabat, A. Optimization of the drone-assisted pickup and delivery problem. Transp. Res. Part E Logist. Transp. Rev. 2024, 181, 103377. [Google Scholar] [CrossRef]
- Xia, Y.; Zeng, W.; Zhang, C.; Yang, H. A branch-and-price-and-cut algorithm for the vehicle routing problem with load-dependent drones. Transp. Res. Part B Methodol. 2023, 171, 80–110. [Google Scholar] [CrossRef]
- Omagari, H.; Higashino, S. Provisional-Ideal-Point-Based Multi-objective Optimization Method for Drone Delivery Problem. Int. J. Aeronaut. Space Sci. 2018, 19, 262–277. [Google Scholar] [CrossRef]
- Wang, K.; Yuan, B.; Zhao, M.; Lu, Y. Cooperative route planning for the drone and truck in delivery services: A bi-objective optimisation approach. J. Oper. Res. Soc. 2020, 71, 1657–1674. [Google Scholar] [CrossRef]
- Momeni, M.; Soleimani, H.; Shahparvari, S.; Afshar-Nadjafi, B. A multi-agency coordination resource allocation and routing decision-making problem: A coordinated truck-and-drone DSS for improved wildfire detection coverage. Int. J. Disaster Risk Reduct. 2023, 97, 104027. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, S.; Xu, W.; Wang, W. A novel multi-objective optimization model for the vehicle routing problem with drone delivery and dynamic flight endurance. Comput. Ind. Eng. 2022, 173, 108679. [Google Scholar] [CrossRef]
- Cao, Q.; Zhang, X.; Ren, X. Path Optimization of Joint Delivery Mode of Trucks and UAVs. Math. Probl. Eng. 2021, 2021, 4670997. [Google Scholar] [CrossRef]
- Luo, Q.; Wu, G.; Ji, B.; Wang, L.; Suganthan, P.N. Hybrid Multi-Objective Optimization Approach with Pareto Local Search for Collaborative Truck-Drone Routing Problems Considering Flexible Time Windows. IEEE Trans. Intell. Transp. Syst. 2022, 23, 13011–13025. [Google Scholar] [CrossRef]
- Meng, Z.; Zhou, Y.; Li, E.Y.; Peng, X.; Qiu, R. Environmental and economic impacts of drone-assisted truck delivery under the carbon market price. J. Clean. Prod. 2023, 401, 136758. [Google Scholar] [CrossRef]
- Gonzalez-R, P.L.; Sanchez-Wells, D.; Andrade-Pineda, J.L. A bi-criteria approach to the truck-multidrone routing problem. Expert Syst. Appl. 2024, 243, 122809. [Google Scholar] [CrossRef]
- Montaña, L.C.; Malagon-Alvarado, L.; Miranda, P.A.; Arboleda, M.M.; Solano-Charris, E.L.; Vega-Mejía, C.A. A novel mathematical approach for the Truck-and-Drone Location-Routing Problem. Procedia Comput. Sci. 2022, 200, 1378–1391. [Google Scholar] [CrossRef]
- Li, D.; Ignatius, J.; Wang, D.; Yin, Y.; Cheng, T.C.E. A branch-and-price-and-cut algorithm for the truck-drone routing problem with simultaneously delivery and pickup. Nav. Res. Logist. 2024, 71, 241–285. [Google Scholar] [CrossRef]
- Cheng, L.; Xin, L.; XueDong, C.; Bin, H. Route planning of truck and multi-drone rendezvous with available time window constraints of drones. Sci.-China-Technol. Sci. 2022, 65, 2190–2204. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, C.; Cao, Y.; Roberti, R. Planning robust drone-truck delivery routes under road traffic uncertainty. Eur. J. Oper. Res. 2023, 309, 1145–1160. [Google Scholar] [CrossRef]
- Luo, Q.; Wu, G.; Trivedi, A.; Hong, F.; Wang, L.; Srinivasan, D. Multi-Objective Optimization Algorithm with Adaptive Resource Allocation for Truck-Drone Collaborative Delivery and Pick-Up Services. IEEE Trans. Intell. Transp. Syst. 2023, 24, 9642–9657. [Google Scholar] [CrossRef]
- Kong, F.; Jiang, B.; Wang, J.; Wang, H.; Song, H. Collaborative Delivery Optimization with Multiple Drones via Constrained Hybrid Pointer Network. IEEE Internet Things J. 2023, 11, 773–7755. [Google Scholar] [CrossRef]
- Li, H.; Chen, J.; Wang, F.; Zhao, Y. Truck and drone routing problem with synchronization on arcs. Nav. Res. Logist. 2022, 69, 884–901. [Google Scholar] [CrossRef]
- Jeong, H.Y.; Song, B.D.; Lee, S. Truck-drone hybrid delivery routing: Payload-energy dependency and No-Fly zones. Int. J. Prod. Econ. 2019, 214, 220–233. [Google Scholar] [CrossRef]
- Zhang, Q.; Huang, X.; Zhang, H.; He, C. Research on logistics path optimization for a two-stage collaborative delivery system using vehicles and UAVs. Sustainability 2023, 15, 13235. [Google Scholar] [CrossRef]
- Baik, H.; Valenzuela, J. An optimization drone routing model for inspecting wind farms. Soft Comput. 2021, 25, 2483–2498. [Google Scholar] [CrossRef]
- Masone, A.; Poikonen, S.; Golden, B.L. The multivisit drone routing problem with edge launches: An iterative approach with discrete and continuous improvements. Networks 2022, 80, 193–215. [Google Scholar] [CrossRef]
- Thomas, T.; Srinivas, S.; Rajendran, C. Collaborative truck multi-drone delivery system considering drone scheduling and en route operations. Ann. Oper. Res. 2023, 339, 693–739. [Google Scholar] [CrossRef]
- Yu, V.F.; Lin, S.W.; Jodiawan, P.; Lai, Y.C. Solving the flying sidekick traveling salesman problem by a simulated annealing heuristic. Mathematics 2023, 11, 4305. [Google Scholar] [CrossRef]
- Boccia, M.; Mancuso, A.; Masone, A.; Sterle, C. A new MILP formulation for the flying sidekick traveling salesman problem. Networks 2023, 82, 254–276. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Montemanni, R.; Novellani, S. Exact models for the flying sidekick traveling salesman problem. Int. Trans. Oper. Res. 2022, 29, 1360–1393. [Google Scholar] [CrossRef]
- Schermer, D.; Moeini, M.; Wendt, O. A branch-and-cut approach and alternative formulations for the traveling salesman problem with drone. Networks 2020, 76, 164–186. [Google Scholar] [CrossRef]
- Tiniç, G.O.; Karasan, O.E.; Kara, B.Y.; Campbell, J.F.; Ozel, A. Exact solution approaches for the minimum total cost traveling salesman problem with multiple drones. Transp. Res. Part B Methodol. 2023, 168, 81–123. [Google Scholar] [CrossRef]
- Gu, R.; Poon, M.; Luo, Z.; Liu, Y.; Liu, Z. A hierarchical solution evaluation method and a hybrid algorithm for the vehicle routing problem with drones and multiple visits. Transp. Res. Part C Emerg. Technol. 2022, 141, 103733. [Google Scholar] [CrossRef]
- Tamke, F.; Buscher, U. The vehicle routing problem with drones and drone speed selection. Comput. Oper. Res. 2023, 152, 106112. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Montemanni, R.; Novellani, S. Matheuristic algorithms for the parallel drone scheduling traveling salesman problem. Ann. Oper. Res. 2020, 289, 211–226. [Google Scholar] [CrossRef]
- Boschetti, M.A.; Novellani, S. Last-mile delivery with drone and lockers. Networks 2023, 83, 213–235. [Google Scholar] [CrossRef]
- Morandi, N.; Leus, R.; Yaman, H. The orienteering problem with drones. Transp. Sci. 2023, 58, 240–256. [Google Scholar] [CrossRef]
- Zhou, H.; Qin, H.; Cheng, C.; Rousseau, L.M. An exact algorithm for the two-echelon vehicle routing problem with drones. Transp. Res. Part B Methodol. 2023, 168, 124–150. [Google Scholar] [CrossRef]
- Zhen, L.; Gao, J.; Tan, Z.; Wang, S.; Baldacci, R. Branch-price-and-cut for trucks and drones cooperative delivery. IISE Trans. 2023, 55, 271–287. [Google Scholar] [CrossRef]
- Li, H.; Wang, F. Branch-price-and-cut for the truck–drone routing problem with time windows. Nav. Res. Logist. 2023, 70, 184–204. [Google Scholar] [CrossRef]
- Blufstein, M.; Lera-Romero, G.; Soulignac, F.J. Decremental state-space relaxations for the basic traveling salesman problem with a drone. INFORMS J. Comput. 2024, 36, 939–1146. [Google Scholar] [CrossRef]
- Gonzalez-R, P.L.; Canca, D.; Andrade-Pineda, J.L.; Calle, M.; Leon-Blanco, J.M. Truck-drone team logistics: A heuristic approach to multi-drop route planning. Transp. Res. Part C Emerg. Technol. 2020, 114, 657–680. [Google Scholar] [CrossRef]
- Erdoğan, G.; Yıldırım, E.A. Exact and Heuristic Algorithms for the Carrier–Vehicle Traveling Salesman Problem. Transp. Sci. 2021, 55, 101–121. [Google Scholar] [CrossRef]
- Wu, G.; Mao, N.; Luo, Q.; Xu, B.; Shi, J.; Suganthan, P.N. Collaborative Truck-Drone Routing for Contactless Parcel Delivery During the Epidemic. IEEE Trans. Intell. Transp. Syst. 2022, 23, 25077–25091. [Google Scholar] [CrossRef]
- Bai, X.; Cao, M.; Yan, W.; Ge, S.S. Efficient Routing for Precedence-Constrained Package Delivery for Heterogeneous Vehicles. IEEE Trans. Autom. Sci. Eng. 2020, 17, 248–260. [Google Scholar] [CrossRef]
- Bai, X.; Ye, Y.; Zhang, B.; Ge, S.S. Efficient Package Delivery Task Assignment for Truck and High Capacity Drone. IEEE Trans. Intell. Transp. Syst. 2023, 24, 13422–13435. [Google Scholar] [CrossRef]
- Park, H.J.; Mirjalili, R.; Cote, M.J.; Lim, G.J. Scheduling Diagnostic Testing Kit Deliveries with the Mothership and Drone Routing Problem. J. Intell. Robot. Syst. 2022, 105, 38. [Google Scholar] [CrossRef]
- Morim, A.; Campuzano, G.; Amorim, P.; Mes, M.; Lalla-Ruiz, E. The drone-assisted vehicle routing problem with robot stations. Expert Syst. Appl. 2024, 238, 121741. [Google Scholar] [CrossRef]
- Zhou, X.; Feng, Y. Research on path optimization of vehicle-drone joint distribution considering customer priority. Complexity 2024, 2024, 4933311. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, W.; Yang, S.; Shi, J. A novel truck-drone collaborative service network for wide-range drone delivery using a modified variable neighborhood search algorithm. J. Intell. Fuzzy Syst. 2022, 43, 5165–5184. [Google Scholar] [CrossRef]
- Ndiaye, M.; Osman, A.; Salhi, S.; Madani, B. The truck-drone routing optimization problem: Mathematical model and a VNS approach. Optim. Lett. 2023, 18, 1023–1052. [Google Scholar] [CrossRef]
- Yanpirat, N.; Silva, D.F.; Smith, A.E. Sustainable last mile parcel delivery and return service using drones. Eng. Appl. Artif. Intell. 2023, 124, 106631. [Google Scholar] [CrossRef]
- AlMuhaideb, S.; Alhussan, T.; Alamri, S.; Altwaijry, Y.; Aljarbou, L.; Alrayes, H. Optimization of Truck-Drone Parcel Delivery Using Metaheuristics. Appl. Sci. 2021, 11, 6443. [Google Scholar] [CrossRef]
- Vu, L.; Vu, D.M.; Ha, M.H.; Nguyen, V.P. The two-echelon routing problem with truck and drones. Int. Trans. Oper. Res. 2022, 29, 2968–2994. [Google Scholar] [CrossRef]
- Ostermeier, M.; Heimfarth, A.; Hübner, A. The multi-vehicle truck-and-robot routing problem for last-mile delivery. Eur. J. Oper. Res. 2023, 310, 680–697. [Google Scholar] [CrossRef]
- Mourelo Ferrandez, S.; Harbison, T.; Weber, T.; Sturges, R.; Rich, R. Optimization of a truck-drone in tandem delivery network using k-means and genetic algorithm. J. Ind. Eng. Manag. 2016, 9, 374. [Google Scholar] [CrossRef]
- Karakose, E. A new last mile delivery approach for the hybrid truck multi-drone problem using a genetic algorithm. Appl. Sci. 2024, 14, 616. [Google Scholar] [CrossRef]
- Meng, S.; Guo, X.; Li, D.; Liu, G. The multi-visit drone routing problem for pickup and delivery services. Transp. Res. Part E Logist. Transp. Rev. 2023, 169, 102990. [Google Scholar] [CrossRef]
- Carlsson, J.G.; Song, S. Coordinated Logistics with a Truck and a Drone. Manag. Sci. 2018, 64, 4052–4069. [Google Scholar] [CrossRef]
- Canca, D.; Navarro-Carmona, B.; Luis Andrade-Pineda, J. Design and Assessment of an Urban Circular Combined Truck-Drone Delivery System Using Continuum Approximation Models and Integer Programming. Sustainability 2022, 14, 13459. [Google Scholar] [CrossRef]
- Wu, G.; Fan, M.; Shi, J.; Feng, Y. Reinforcement Learning Based Truck-and-Drone Coordinated Delivery. IEEE Trans. Artif. Intell. 2023, 4, 754–763. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, X.; Chen, Z. An efficient hybrid graph network model for traveling salesman problem with drone. Neural Process. Lett. 2023, 55, 10353–10370. [Google Scholar] [CrossRef]
- Bogyrbayeva, A.; Yoon, T.; Ko, H.; Lim, S.; Yun, H.; Kwon, C. A deep reinforcement learning approach for solving the Traveling Salesman Problem with Drone. Transp. Res. Part C Emerg. Technol. 2023, 148. [Google Scholar] [CrossRef]



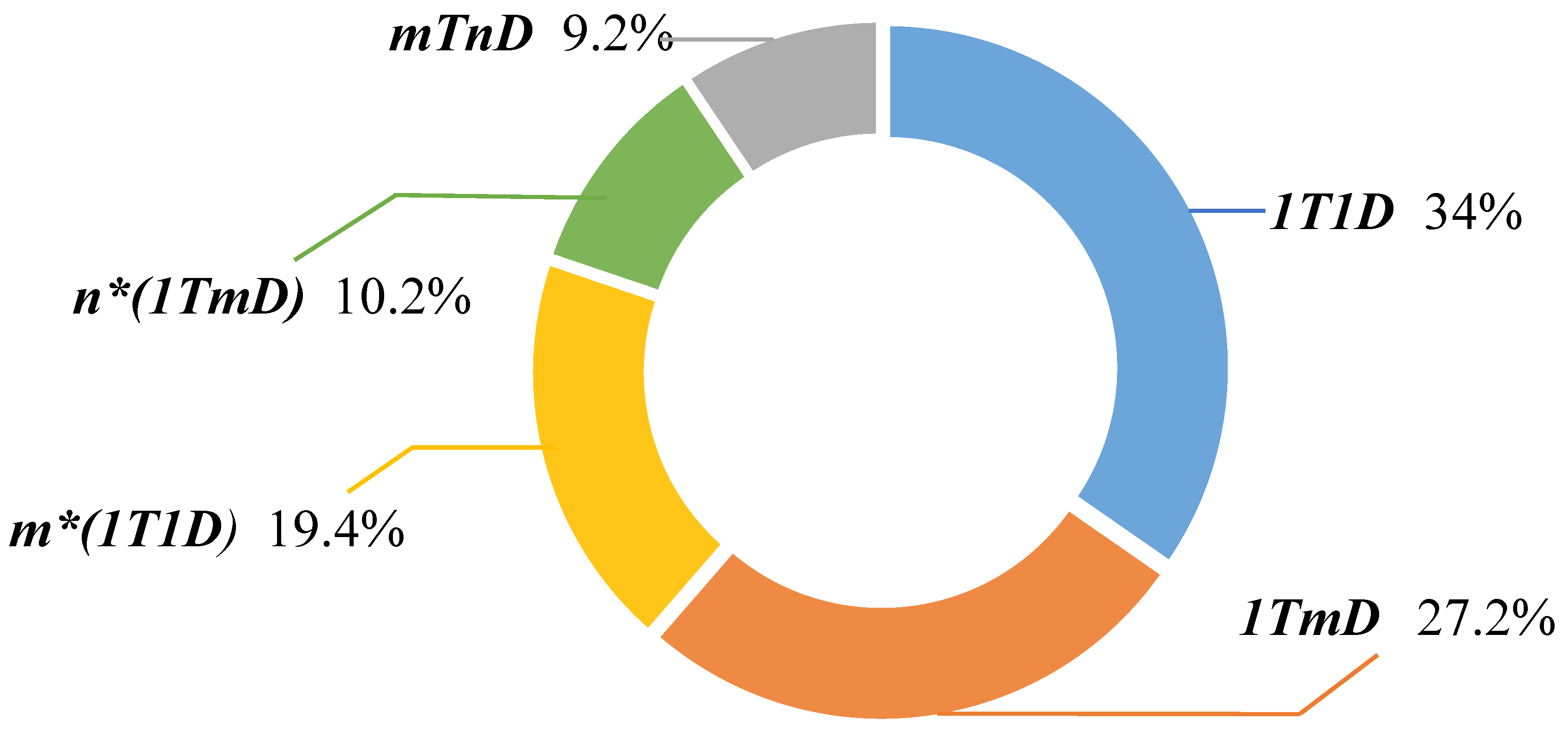


| Characteristics | Drone | Truck |
|---|---|---|
| Payload | Low | High |
| Endurance | Short | Long |
| Unit cost | Low | High |
| Route | Permitted airspace | Along road network |
| Reference | Year | Perspective | Classification Method |
|---|---|---|---|
| [2] | 2019 | Variants of the TSP and VRP | Applications; Configurations of trucks and drones; Model formulations |
| [3] | 2020 | Drone and drone–truck combined operations | Applications; Cooperation modes; Constrains; Objectives; Solution methodologies |
| [4] | 2020 | Drone-aided routing | Applications; Role of drones |
| [5] | 2021 | Two-echelon routing; Logistics | Model formulations; Solution methodologies |
| [6] | 2023 | VRP in Last-Mile Delivery | Different last-mile delivery ways |
| this paper | 2024 | Cooperation of trucks and drones | Applications; Cooperation modes; Configurations of trucks and drones; Constrains; Objectives; Model formulations; Solution methodologies |
| Reference | Configuration | Objectives | Solutions | Instance Scale |
|---|---|---|---|---|
| [1] | 1T1D | min time | Heuristics | small |
| [83] | 1T1D | min cost | Dynamic Programming | large |
| [84] | 1T1D | min cost | GRASP | large |
| [74] | 1T1D | min time | Constructive Heuristics | small |
| [85] | 1T1D | min time | Constructive Heuristics | small, medium |
| [45] | 1T1D | min time | TS | small to large |
| [86] | 1T1D | min cost | SA | small to large |
| [87] | 1T1D | min time | VNS | large |
| [88] | 1T1D | min cost | Constructive Heuristics | small, medium |
| [89] | 1T1D | min time | SA | small to large |
| [80] | 1T1D | min time | Constructive Metaheuristics | small, medium |
| [81] | 1T1D | min cost | Dynamic Programming, GA | small to large |
| [90] | 1T1D | min cost | GRASP | small, medium |
| [20] | 1T1D | min time | Reinforcement Learning | small |
| [91] | 1T1D | min time | Dynamic Programming, VNS | small |
| [92] | 1T1D | min time | MA | large |
| [93] | 1T1D | min time | Constructive Heuristics | small, medium |
| Reference | Configuration | Objectives | Solutions | Instance Scale |
|---|---|---|---|---|
| [1] | 1TmD | min time | Heuristics | small |
| [50] | 1TmD | min time | Constructive Heuristics | medium, large |
| [51] | 1TmD | min time | Constructive Metaheuristics, Dynamic Programming | large |
| [76] | 1TmD | min time, min cost | GA | large |
| [94] | 1TmD | min time, min cost | GA | large |
| [95] | 1TmD | min time | Constructive Heuristics | small to large |
| [96] | 1TmD | min time | SA, TA | small to large |
| [11] | 1TmD | min time, min cost | Integrated optimization approach | small, medium |
| [97] | 1TmD | min time | Benders Decomposition | small, medium |
| [14] | 1TmD | min cost | Machine Learning | large |
| [36] | 1TmD | min time | ACO | small to large |
| [98] | 1TmD | min time | GA, SA | medium, large |
| [99] | 1TmD | min time | Constructive Heuristics | large |
| [100] | 1TmD | min time, min drone’s number | Decomposition | small, medium |
| [101] | 1TmD | min cost | Clarke and Wright Algorithm | small to large |
| [102] | 1TmD | min cost | Decomposition Algorithm, Column Generation | medium, large |
| [103] | 1TmD | min time | Decomposition, Constructive Heuristics | small to large |
| [104] | 1TmD | min cost | GA | large |
| [105] | 1TmD | min time | LNS | small to large |
| [106] | 1TmD | min time | Constructive Heuristics | small to large |
| [107] | 1TmD | min time | GA, PSO | small to large |
| [108] | 1TmD | min time | TS | small to large |
| [109] | 1TmD | min time | Constructive Heuristics | small to large |
| [110] | 1TmD | min time | Agent-based method | medium, large |
| [111] | 1TmD | min time | GRASP | small, medium |
| [112] | 1TmD | min time | GRASP | small, medium |
| [113] | 1TmD | min time | Constructive Metaheuristics | small, medium |
| [114] | 1TmD | min time | Constructive Metaheuristics | small to large |
| [115] | 1TmD | min time | PSO | small |
| [107] | 1TmD | min time | GA, PSO | small to large |
| [54] | 1TmD | min time | ALNS | small, medium |
| [116] | 1TmD | min time | theoretical proof | small |
| Reference | Configuration | Objectives | Solutions | Instance Scale |
|---|---|---|---|---|
| [117] | (1T1D) | min cost | ALNS | small to large |
| [118] | (1T1D) | min time | VNS, TS | small, large |
| [37] | (1T1D) | min time, min stops | ACO | small to large |
| [119] | (1T1D) | min cost | ACO | medium, large |
| [120] | (1T1D) | min cost | ABC | small to large |
| [121] | (1T1D) | min cost | hybrid algorithm | large |
| [29] | (1T1D) | min time, max demand | NSGA-II, ACO | small |
| [122] | (1T1D) | min cost | ILS | small, medium |
| [123] | (1T1D) | min cost | SA | small to large |
| [124] | (1T1D) | min cost | ALNS | small to large |
| [125] | (1T1D) | min cost | ALNS | large |
| [126] | (1T1D) | min time | ACO | small to large |
| [72] | (1T1D) | min energy | ABC | large |
| [127] | (1T1D) | min cost | ALNS | medium, large |
| [128] | (1T1D) | min cost, min penalty | NSGA-II, ACO | medium |
| [129] | (1T1D) | min time | Branch and Cut Algorithm | small to large |
| [130] | (1T1D) | min cost | VNS | small, medium |
| [131] | (1T1D) | min distance | GRASP, VNS | small, large |
| [132] | (1T1D) | min cost | GA | medium |
| [133] | (1T1D) | min cost | Branch and Price Algorithm | small, medium |
| [134] | (1T1D) | min cost, min the value for products distribution | NSGA-II | small, large |
| [12] | (1T1D) | min cost | Constructive Heuristics | small |
| [135] | (1T1D) | min cost | ILS | small to large |
| [26] | (1T1D) | min cost | Branch and Price Algorithm, Branch and Cut Algorithm | small, medium |
| [136] | (1T1D) | min time | VNS | small, medium |
| [137] | (1T1D) | min time, max demand | Multi-objective evolutionary algorithm | medium, large |
| [138] | (1T1D) | min cos | Constructive Heuristics | small, medium |
| [139] | (1T1D) | min time, min carbon emission | NSGA-II | small to large |
| Reference | Configuration | Objectives | Solutions | Instance Scale |
|---|---|---|---|---|
| [140] | (1TmD) | min cost | ALNS | small to large |
| [141] | (1TmD) | min time | ALNS | small to large |
| [42] | (1TmD) | min cost | ALNS | large |
| [142] | (1TmD) | min cost | Heuristics, Dynamic Programming | small, medium |
| Reference | Configuration | Objectives | Solutions | Instance Scale |
|---|---|---|---|---|
| [69] | mTnD | min time | Heuristics | small to large |
| [40] | mTnD | max reward | Reinforcement Learning | small, medium |
| [70] | mTnD | min cost | Benders Decomposition, Column Generation | small, medium |
| [66] | mTnD | min time | ILS, Dynamic Programming | small, medium |
| [67] | mTnD | min cost | Constructive Heuristics | medium, large |
| [68] | mTnD | min time | Constraint programming | small to large |
| [34] | mTnD | max number of goods and nodes, min penalties | Reinforcement Learning | small, large |
| [35] | mTnD | min cost | Dynamic Programming | small, medium |
| [71] | mTnD | min time | Accelerate Benders Decomposition, Column Constraint Generation | small |
| [143] | mTnD | min time | Adaptive Insertion Algorithm, | small, medium |
| [144] | mTnD | min time | hybrid algorithm | large |
| [145] | mTnD | max profit | SA | medium, large |
| [146] | mTnD | min cost | ALNS | small to large |
| [147] | mTnD | min cost | Savings Algorithm | small to large |
| [48] | mTnD | max number of drone nodes | Greedy Heuristic Algorithm | small, large |
| [148] | mTnD | min cost | ALNS | small, large |
| [149] | mTnD | min cost | ALNS | small to large |
| [41] | mTnD | min time | GA | small to large |
| [150] | mTnD | min cost | Continuum Approximation methods | small |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, S.; Liu, Y.; Luo, Z.; Liu, Z.; Shi, J. A Survey of the Routing Problem for Cooperated Trucks and Drones. Drones 2024, 8, 550. https://doi.org/10.3390/drones8100550
Dang S, Liu Y, Luo Z, Liu Z, Shi J. A Survey of the Routing Problem for Cooperated Trucks and Drones. Drones. 2024; 8(10):550. https://doi.org/10.3390/drones8100550
Chicago/Turabian StyleDang, Shuo, Yao Liu, Zhihao Luo, Zhong Liu, and Jianmai Shi. 2024. "A Survey of the Routing Problem for Cooperated Trucks and Drones" Drones 8, no. 10: 550. https://doi.org/10.3390/drones8100550
APA StyleDang, S., Liu, Y., Luo, Z., Liu, Z., & Shi, J. (2024). A Survey of the Routing Problem for Cooperated Trucks and Drones. Drones, 8(10), 550. https://doi.org/10.3390/drones8100550






