OF-FSE: An Efficient Adaptive Equalization for QAM-Based UAV Modulation Systems
Abstract
:1. Introduction
- (1)
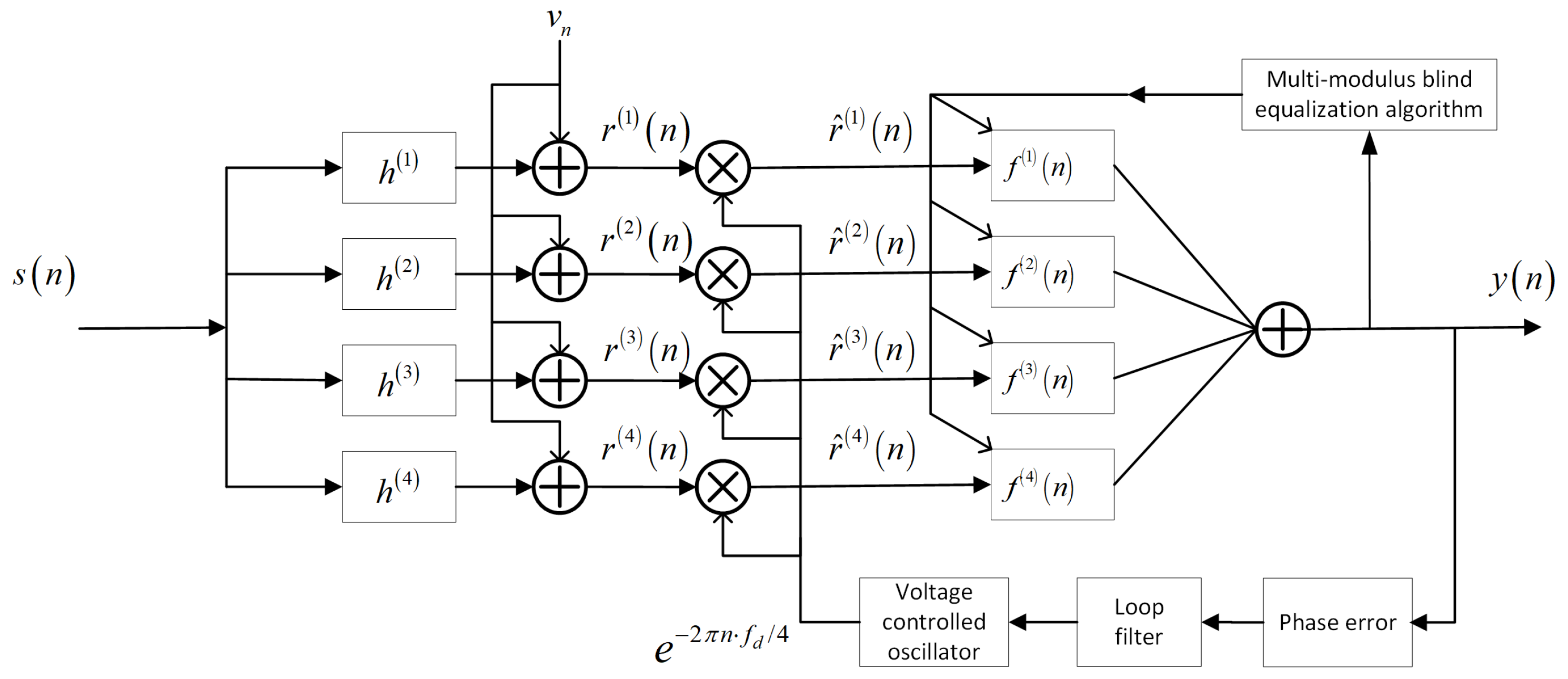
- The proposed OF-FSE architecture is used to eliminate the CFO of the equalization input signal of UAVs. In particular, a feedback loop is added to FSE. It allows the OF-FSE to estimate the phase error of the output signal through a phase discriminator. The changes are then tracked to maintain the accuracy of the estimation and thus OF-FSE enables work in non-CFO conditions.
- (2)
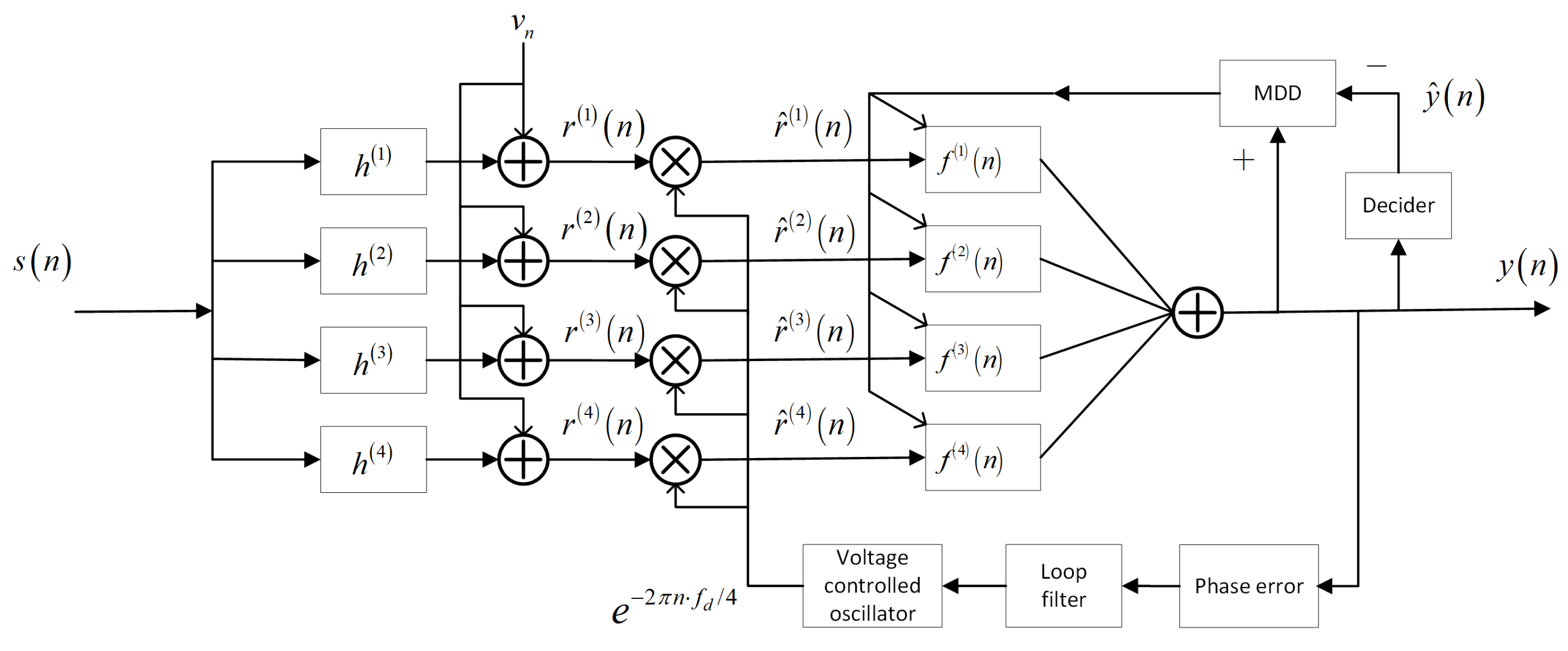
- In order to further improve the output signal accuracy, a new multi-modulus decision-directed (MDD) algorithm for the novel OF-FSE is presented. It enables adaptive adjustment of the convergence status for various dynamic environments. Hence, OF-FSE can ensure stability and further reduce errors to improve accuracy.
- (3)
- The proposed improvements are confirmed through different aspects of the QAM-based UAV modulation system by simulations. The results demonstrate that compared with MMA-FSE, our OF-FSE can eliminate the influence of the system output signal caused by the CFO. Furthermore, the proposed new MDD algorithm enhances the accuracy compared to the baseline approaches.
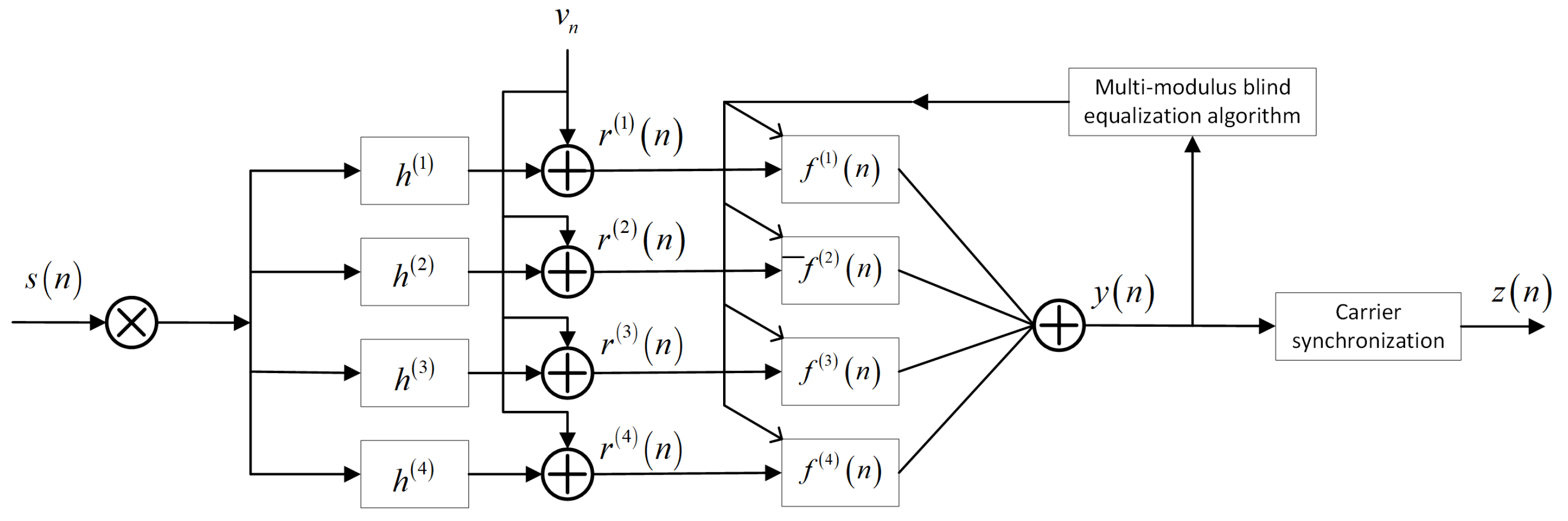
2. General FSE Architecture in QAM-Based UAV Modulation Systems
3. Proposed OF-FSE Architecture for UAVs
4. MDD Algorithm for OF-FSE
| Algorithm 1 The proposed MDD Algorithm |
| Input: received signal after communication channel |
| Output: system output signal y |
| Initialization: filters f, filter taps N, adaptive unit , number of symbols n, and |
| 1: for |
| 2: |
| 3: ⟵ Equation (28) |
| 4: if |
| 5: Calculate Equation (29) |
| 6: else if |
| 7: |
| 8: |
| 9: end for |
| 10: Return y |
5. Simulation Results
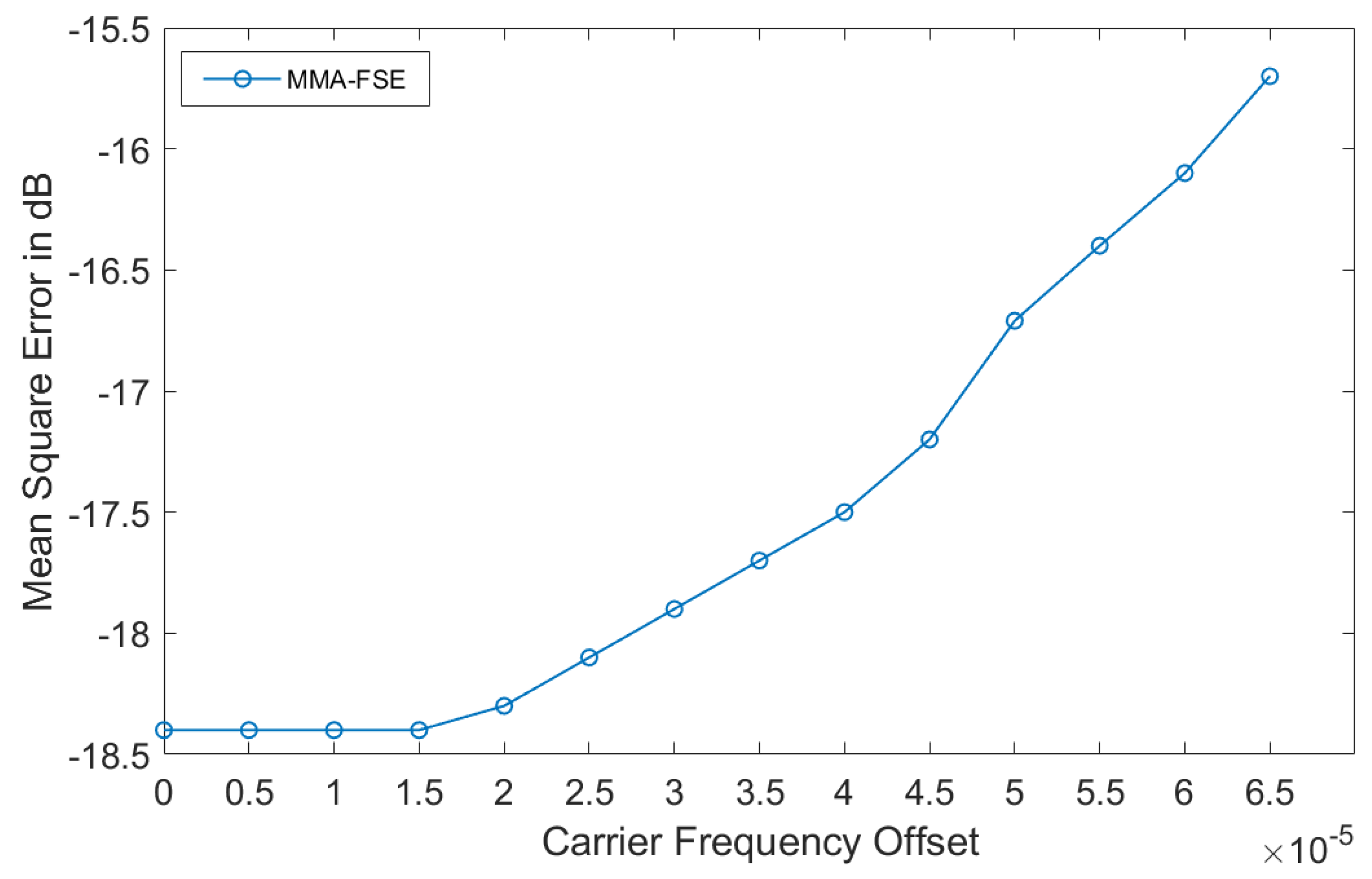
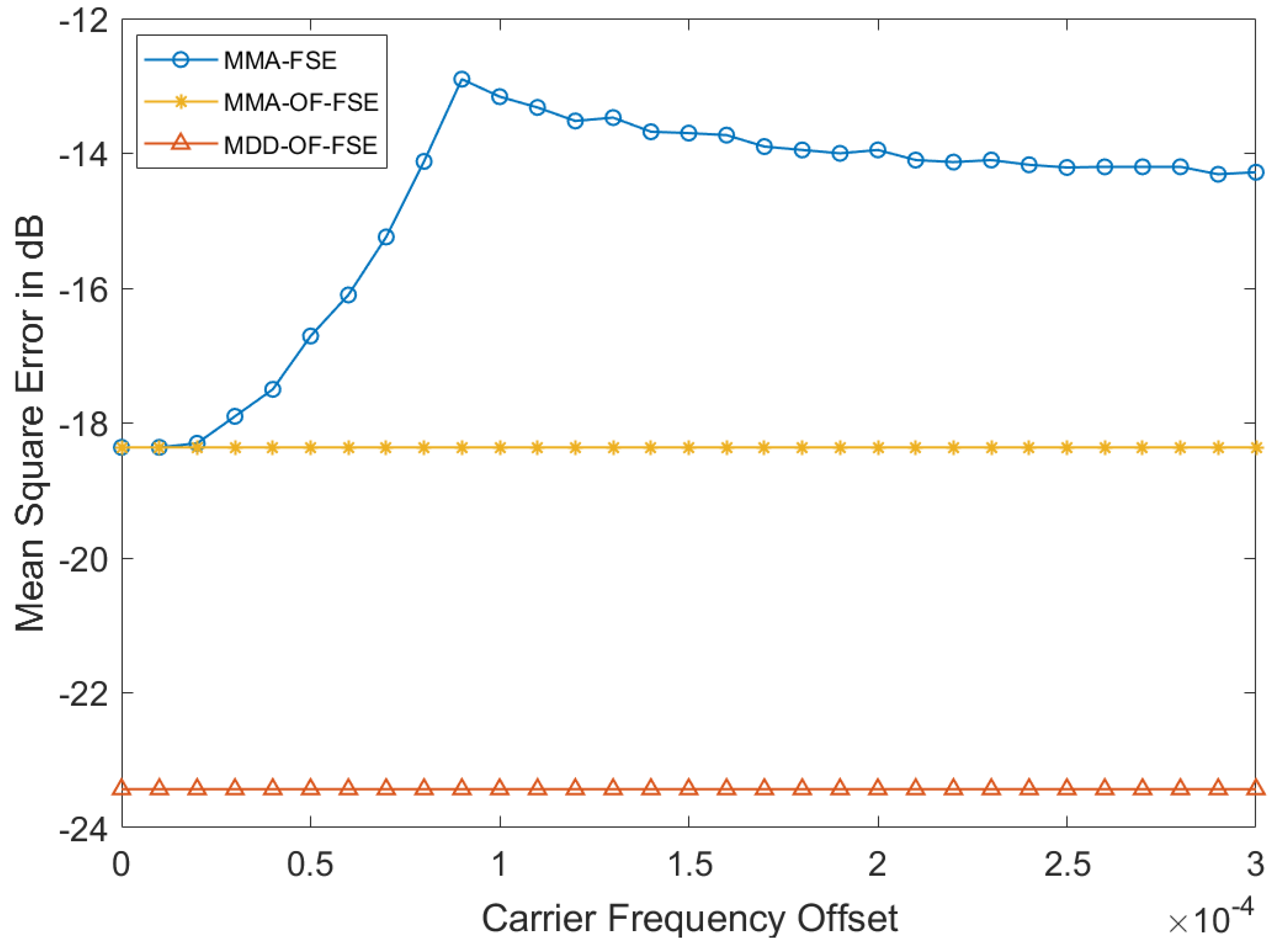
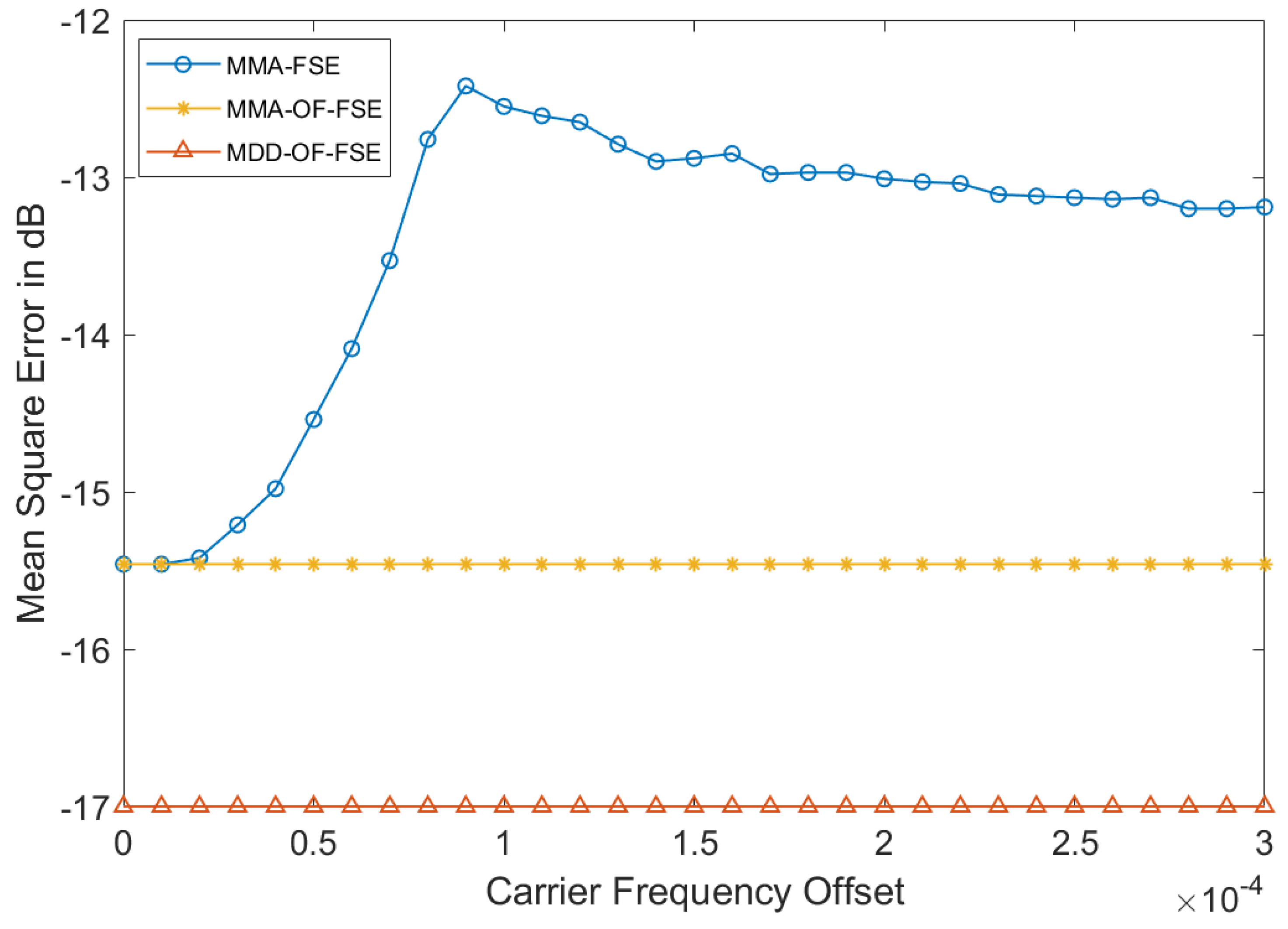
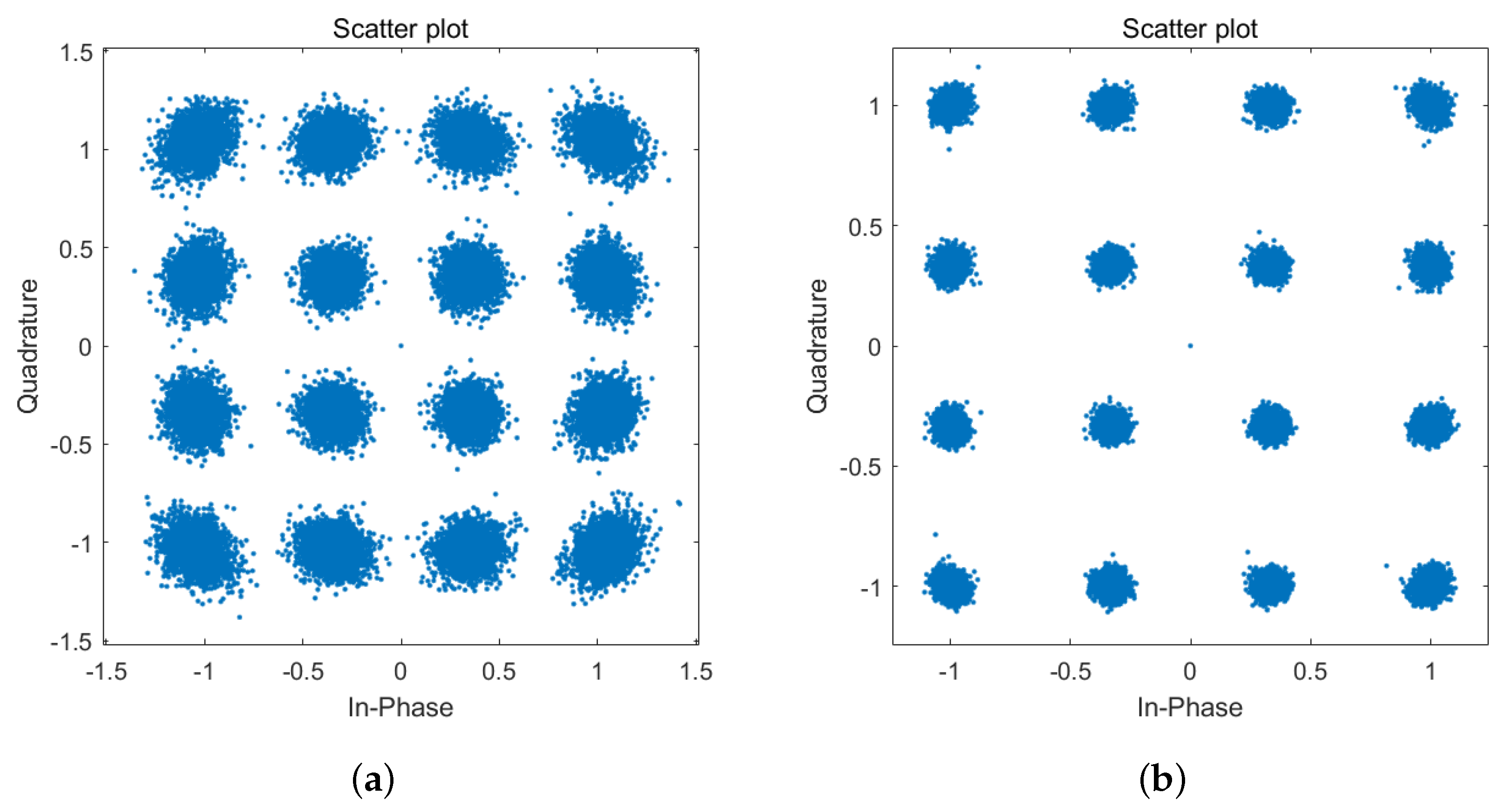
5.1. MMA-FSE Performance with CFO
5.2. Proposed Algorithm Performance with CFO
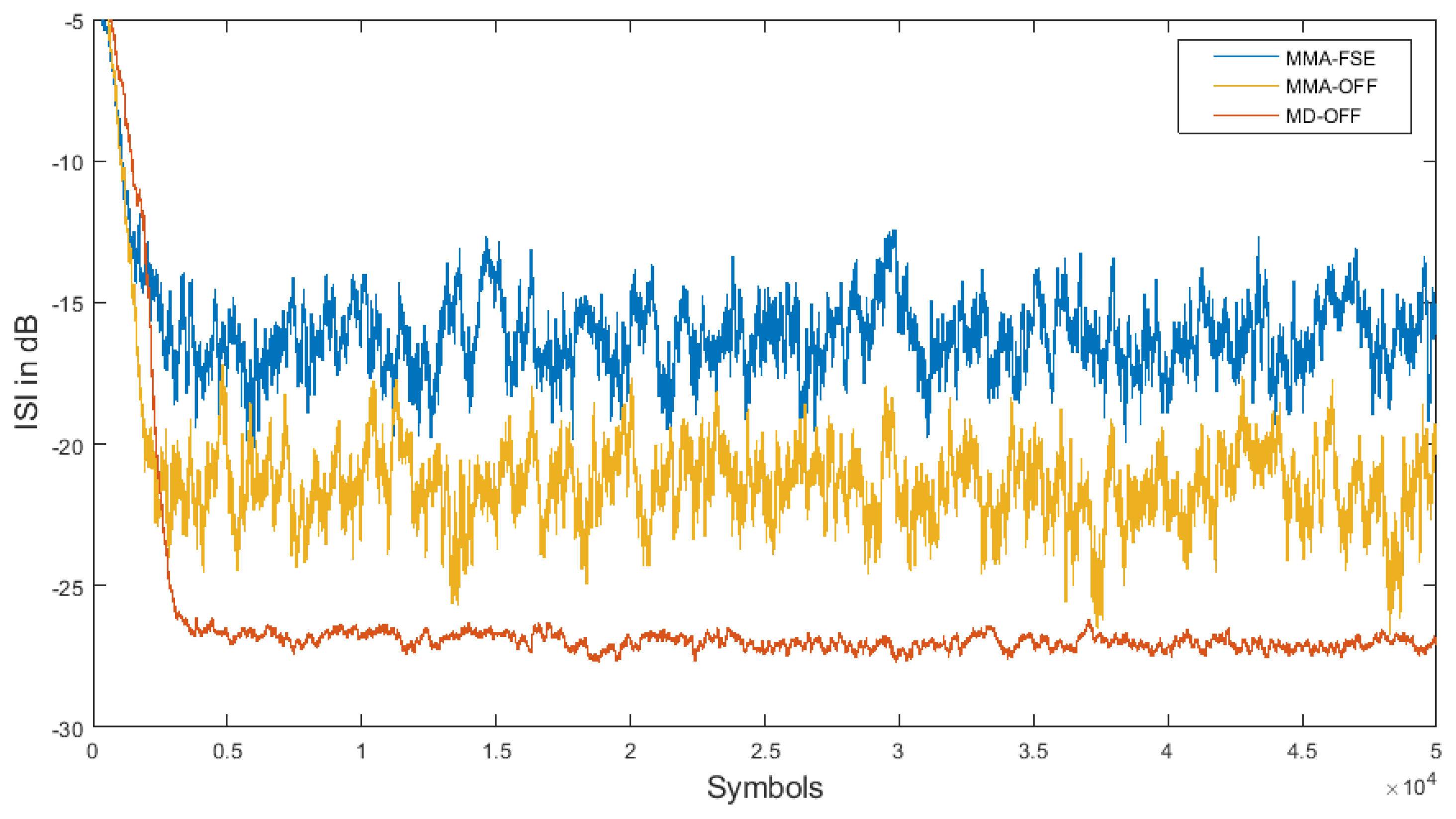
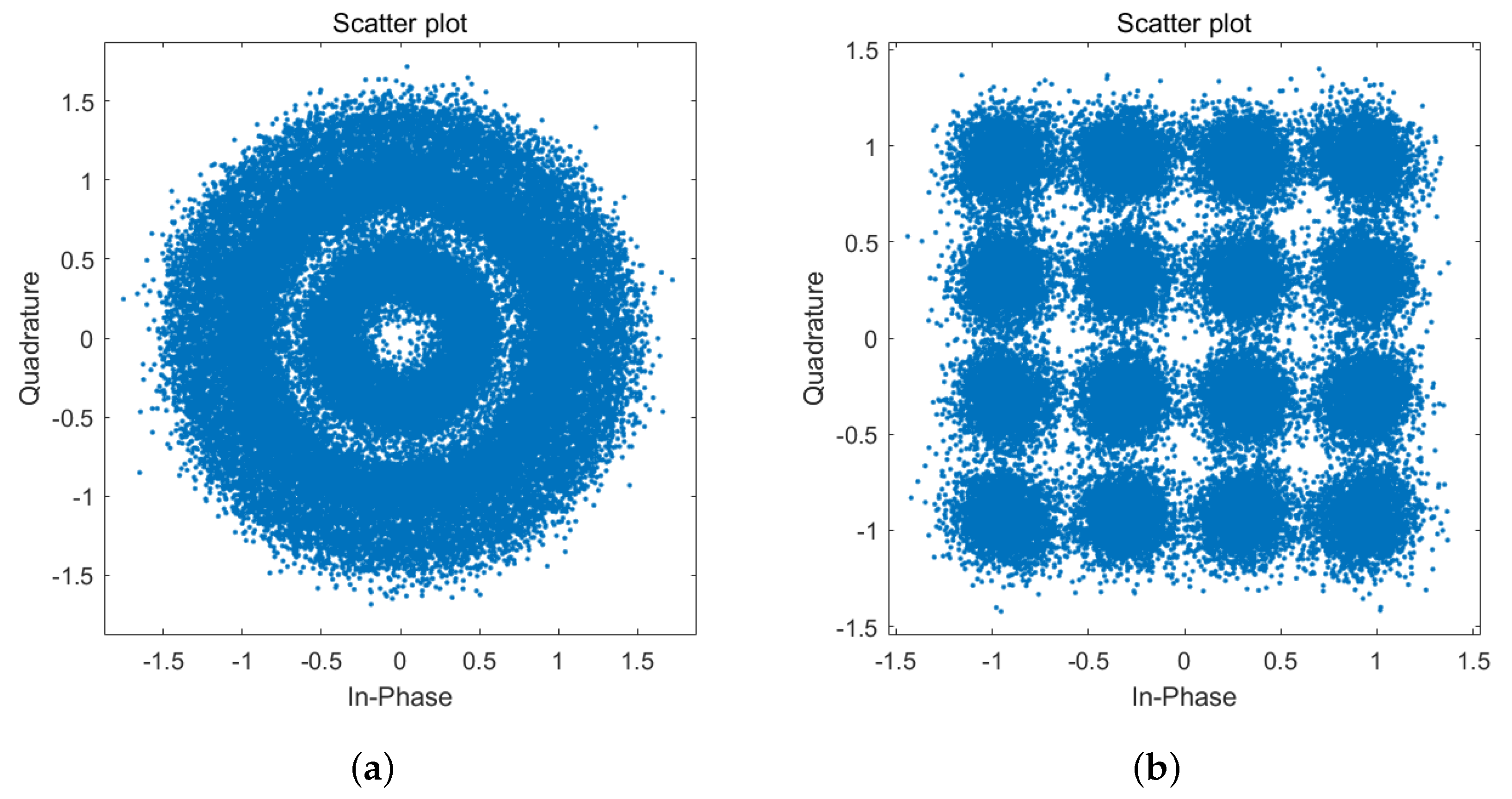
5.3. Algorithms Performance Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, B.; Li, L.; Zhao, G.; Chen, Z.; Imran, M.A. Autonomous D2D transmission scheme in URLLC for real-time wireless control systems. IEEE Trans. Commun. 2021, 69, 5546–5558. [Google Scholar]
- Li, Y. A construction of general QAM Golay complementary sequences. IEEE Trans. Inf. Theory 2010, 56, 5765–5771. [Google Scholar] [CrossRef]
- Ahmed, S.; Khan, Y.; Wahab, A. A review on training and blind equalization algorithms for wireless communications. Wireless Pers. Commun. 2019, 108, 1759–1783. [Google Scholar] [CrossRef]
- Yang, J.; Werner, J.J.; Dumont, G.A. The multimodulus blind equalization and its generalized algorithms. IEEE J. Sel. Areas Commun. 2002, 20, 997–1015. [Google Scholar] [CrossRef]
- Maruta, K.; Ahn, C.J. Multi modulus signal adaptation for semi-blind uplink interference suppression on multicell massive MIMO systems. IEICE Trans. Commun. 2021, 104, 158–168. [Google Scholar] [CrossRef]
- Sharma, V.; Raj, V.N. Convergence and performance analysis of Godard family and multimodulus algorithms for blind equalization. IEEE Trans. Signal Process. 2005, 53, 1520–1533. [Google Scholar] [CrossRef]
- Beiyuan, L.; Chen, G.; Julian, C.; Zhengyuan, X.; Jiajia, L. Blind and Semi-Blind Channel Estimation/Equalization for Poisson Channels in Optical Wireless Scattering Communication Systems. IEEE Trans. Wirel. Commun. 2022, 21, 5930–5946. [Google Scholar]
- Hamed, H.; Arman, F.; Behrouz, F. FBMC receiver design and analysis for medium and large scale antenna systems. IEEE Trans. Veh. Technol. 2022, 71, 3044–3057. [Google Scholar]
- Yao, G.; Deng, Q.; Ching, P.C.; Ding, Z. Receiver design for OTFS with a fractionally spaced sampling approach. IEEE Trans. Wirel. Commun. 2021, 20, 4072–4086. [Google Scholar]
- Li, Q.; Gao, Y.; Gong, F.K.; Li, G.; Zhai, S.H. Efficient frequency-domain linear distortion equaliser in faster-than-Nyquist systems. IET Commun. 2020, 14, 2084–2089. [Google Scholar]
- Diliyanzah, A.; Astuti, R.P.; Syihabuddin, B. Dynamic CFO reduction in various mobilities based on extended Kalman filter for broadband wireless access technology. In Proceedings of the 2014 6th International Conference on Information Technology and Electrical Engineering (ICITEE), Yogyakarta, Indonesia, 7–8 October 2014; pp. 1–6. [Google Scholar]
- Yuan, J.T.; Tsai, K.D. Analysis of the multimodulus blind equalization algorithm in QAM communication systems. IEEE Trans. Commun. 2005, 53, 1427–1431. [Google Scholar] [CrossRef]
- Ojeda, O.A.Y.; Grajal, J. The relationship between the cyclic wiener filter and fractionally spaced equalizers. IEEE Trans. Signal Process. 2019, 67, 4333–4341. [Google Scholar] [CrossRef]
- Li, D.; Wang, J.; Lu, H.; Jin, J. Performance improvement of multi-carrierless amplitude and phase modulation based visible light communication system using fractionally spaced equalizer. In Proceedings of the Optics Frontiers Online 2020: Optical Communications and Networks, Online, 24–25 July 2020; Volume 11604, pp. 110–113. [Google Scholar]
- Mayyala, Q.; Abed-Meraim, K.; Zerguine, A.; Lawal, A. Fast Multimodulus Blind Deconvolution Algorithms. IEEE Trans. Wirel. Commun. 2022, 21, 9627–9637. [Google Scholar] [CrossRef]
- Slock, D.T.; Papadias, C.B. Blind fractionally-spaced equalization based on cyclostationarity. In Proceedings of the IEEE Vehicular Technology Conference (VTC), Stockholm, Sweden, 8–10 June 1994; pp. 1286–1290. [Google Scholar]
- Yuan, J.T.; Chao, J.H.; Lin, T.C. Effect of channel noise on blind equalization and carrier phase recovery of CMA and MMA. IEEE Trans. Commun. 2012, 60, 3274–3285. [Google Scholar] [CrossRef]
- Gardner, F. A BPSK/QPSK timing-error detector for sampled receivers. IEEE Trans. Commun. 1986, 34, 423–429. [Google Scholar] [CrossRef]
- Sarkar, B. Phase error dynamics of a first-order phase locked loop in the presence of cochannel tone interference and additive noise. IEEE Trans. Commun. 1990, 38, 962–965. [Google Scholar] [CrossRef]
- Nowlan, S.J.; Hinton, G.E. A soft decision-directed LMS algorithm for blind equalization. IEEE Trans. Commun. 1993, 41, 275–279. [Google Scholar] [CrossRef]
- Li, J.; Feng, D.Z.; Zheng, W.X. A Robust Decision Directed Algorithm for Blind Equalization Under alpha-Stable Noise. IEEE Trans. Signal Process. 2021, 69, 4949–4960. [Google Scholar] [CrossRef]
- Oh, K.N.; Chin, Y.O. Modified constant modulus algorithm: Blind equalization and carrier phase recovery algorithm. In Proceedings of the Proceedings IEEE International Conference on Communications ICC’95, Seattle, WA, USA, 18–22 June 1995; Volume 1, pp. 498–502. [Google Scholar]


| Symbol | Definition |
|---|---|
| System input signal | |
| h | Channel impulse response |
| Length of channel impulse response | |
| Gaussian white noise | |
| Received signal | |
| Filters coefficients | |
| Equalizer output signal | |
| System output signal | |
| P | Oversampling multiple |
| T | Sampling interval |
| Cost function | |
| Error function | |
| Phase characteristic of loop | |
| Phase Angular frequency | |
| Frequency deviation | |
| Equalizer input signal | |
| Decision value of | |
| First-order loop filtering characteristic | |
| Second-order loop filtering characteristic | |
| Phase discrimination characteristic of first-order loop | |
| Phase discrimination characteristic of second-order loop | |
| Integral parameter | |
| Amplitude-frequency response of the channel | |
| Tracking phase of MMA | |
| Tracking phase of MMA-OF-FSE | |
| Phase of MMA-OF-FSE input signal | |
| Phase errors of first-order loop output | |
| Phase errors of second-order loop output | |
| Equalization iteration | |
| Adaptive factor of MDD algorithm | |
| Updating step size of adaptive factor |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Wang, Z.; Zheng, G. OF-FSE: An Efficient Adaptive Equalization for QAM-Based UAV Modulation Systems. Drones 2023, 7, 525. https://doi.org/10.3390/drones7080525
Zhang L, Wang Z, Zheng G. OF-FSE: An Efficient Adaptive Equalization for QAM-Based UAV Modulation Systems. Drones. 2023; 7(8):525. https://doi.org/10.3390/drones7080525
Chicago/Turabian StyleZhang, Luyao, Zhongyong Wang, and Guhan Zheng. 2023. "OF-FSE: An Efficient Adaptive Equalization for QAM-Based UAV Modulation Systems" Drones 7, no. 8: 525. https://doi.org/10.3390/drones7080525
APA StyleZhang, L., Wang, Z., & Zheng, G. (2023). OF-FSE: An Efficient Adaptive Equalization for QAM-Based UAV Modulation Systems. Drones, 7(8), 525. https://doi.org/10.3390/drones7080525






