Two Low-Complexity Efficient Beamformers for an IRS- and UAV-Aided Directional Modulation Network
Abstract
1. Introduction
- The IRS and UAV-aided DM networks were established to transmit a single CM stream by giving full play to the advantages of the DM, UAV, and IRS to improve the SR performance. To obtain a high performance SR, the CM beamforming vector was given by the rule of maximizing the SR (Max-SR), and the method of maximizing the signal-to-leakage-noise ratio (SLNR) in [41] was used to design the PSM of the IRS. The mutual iterative CM beamforming vector and the PSM of the IRS further improved the SR. AN was independently projected on the null-space of other channels, maximizing the interference with Eve through the direct channel. The iterative process was related to the initial value. Therefore, the Max-SR-SLNR method had high computational complexity.
- To reduce the computational complexity of the Max-SR-SLNR, a maximum ratio transmission (MRT)-based method is proposed. Here, the CM and AN beamforming vectors were constructed by using an MRT and an NSP, respectively, whereas the PSM of the IRS was designed by using the phase alignment (PA) method. It is particularly noted that the three optimization variables (OVs) were designed independently, and the method is called the MRT-NSP-PA. In addition, CM beamforming was only aligned to the Alice-to-IRS channel, ignoring the direct channel, etc. Therefore, the relationship between the direction of the CM beamforming and the number of IRS reflecting elements was observed from simulations. By designing different MRT methods at different IRS scales, the SR performance of the MRT-NSP-PA method was improved at small-scale and medium-scale IRSs.
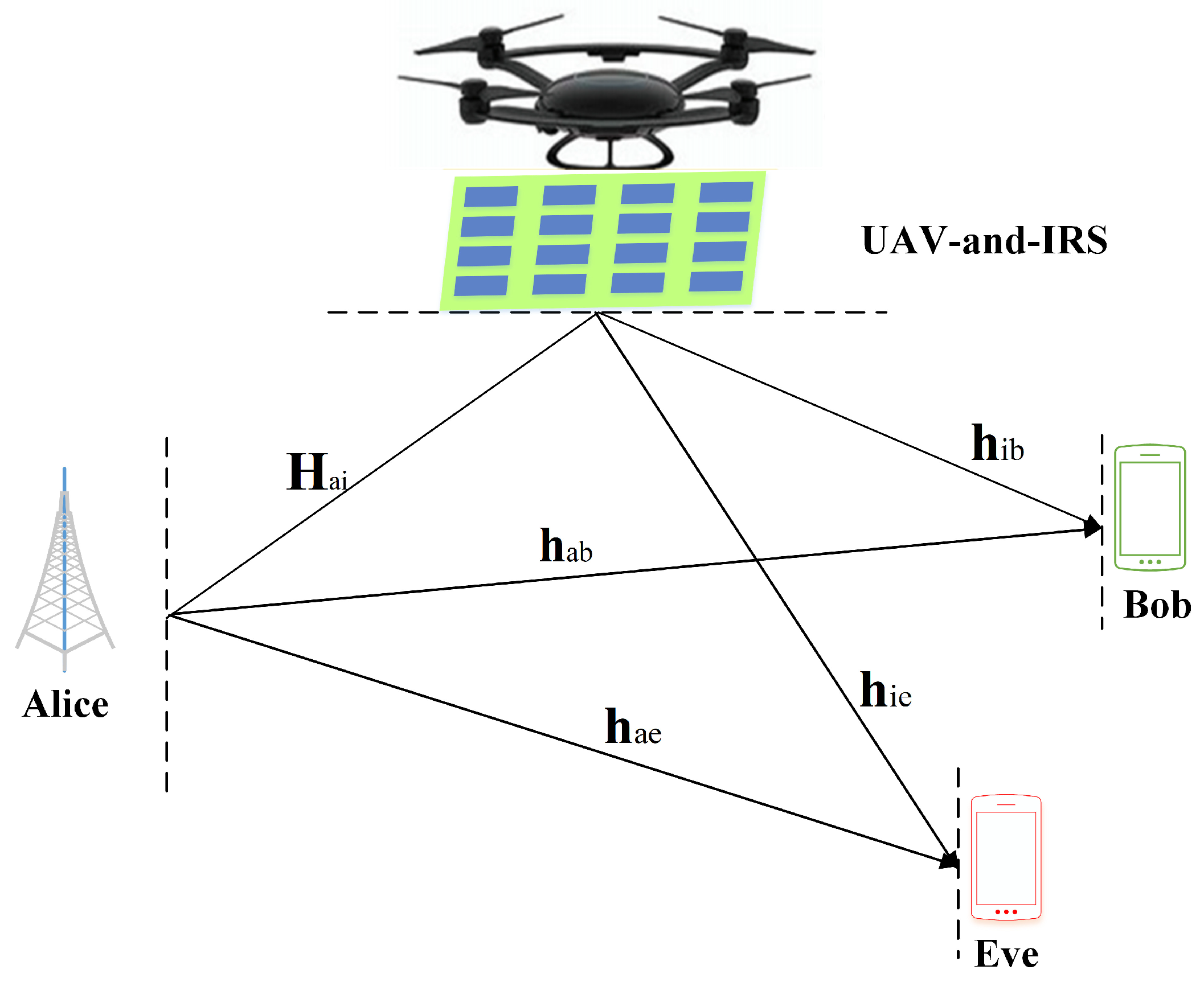
2. System Model
3. The Proposed Beamforming Methods: Max-SR-SLNR and MRT-NSP-PA
3.1. The Proposed Max-SR-SLNR
| Algorithm 1 Proposed Max-SR-SLNR method |
3.2. The Proposed MRT-NSP-PA
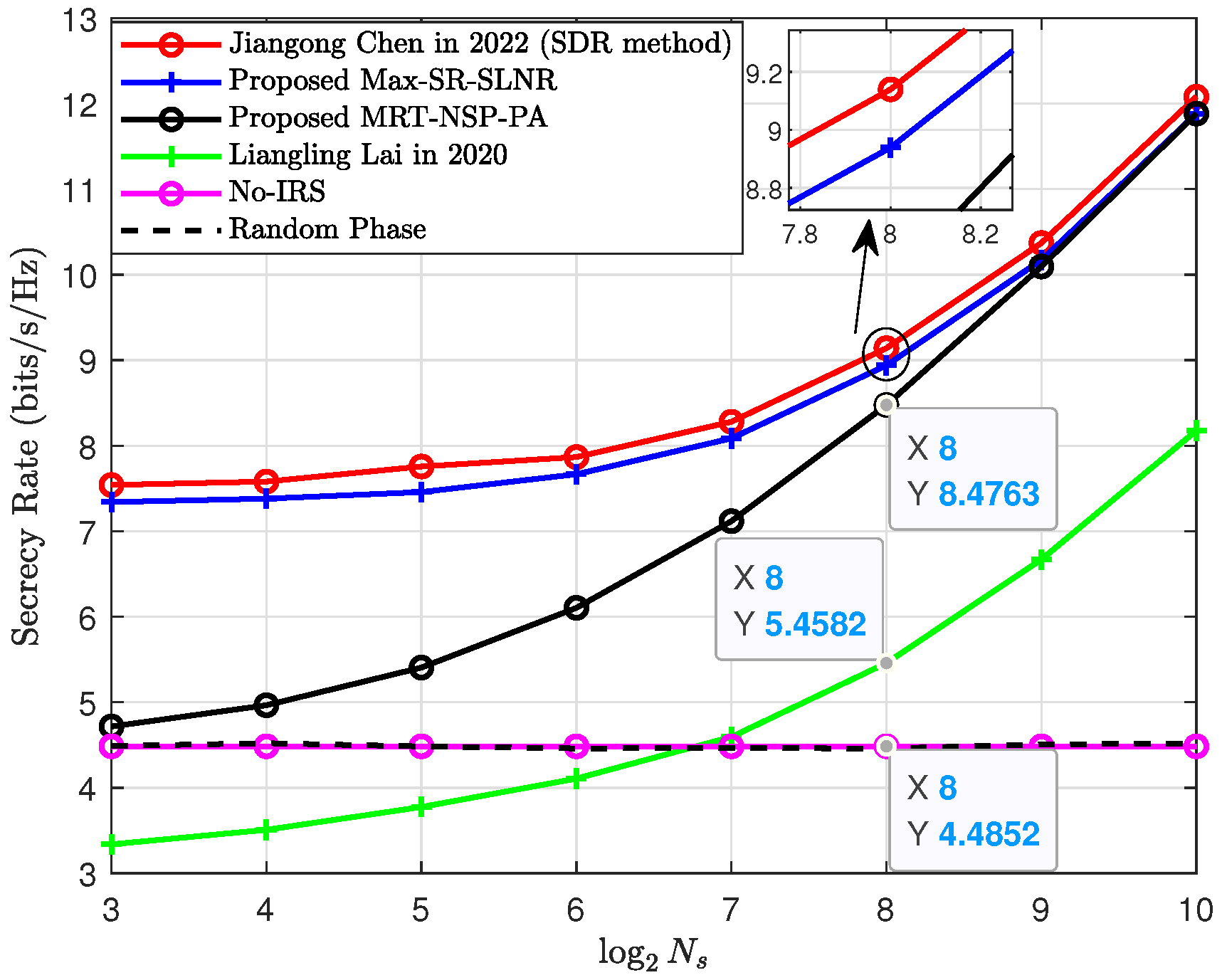
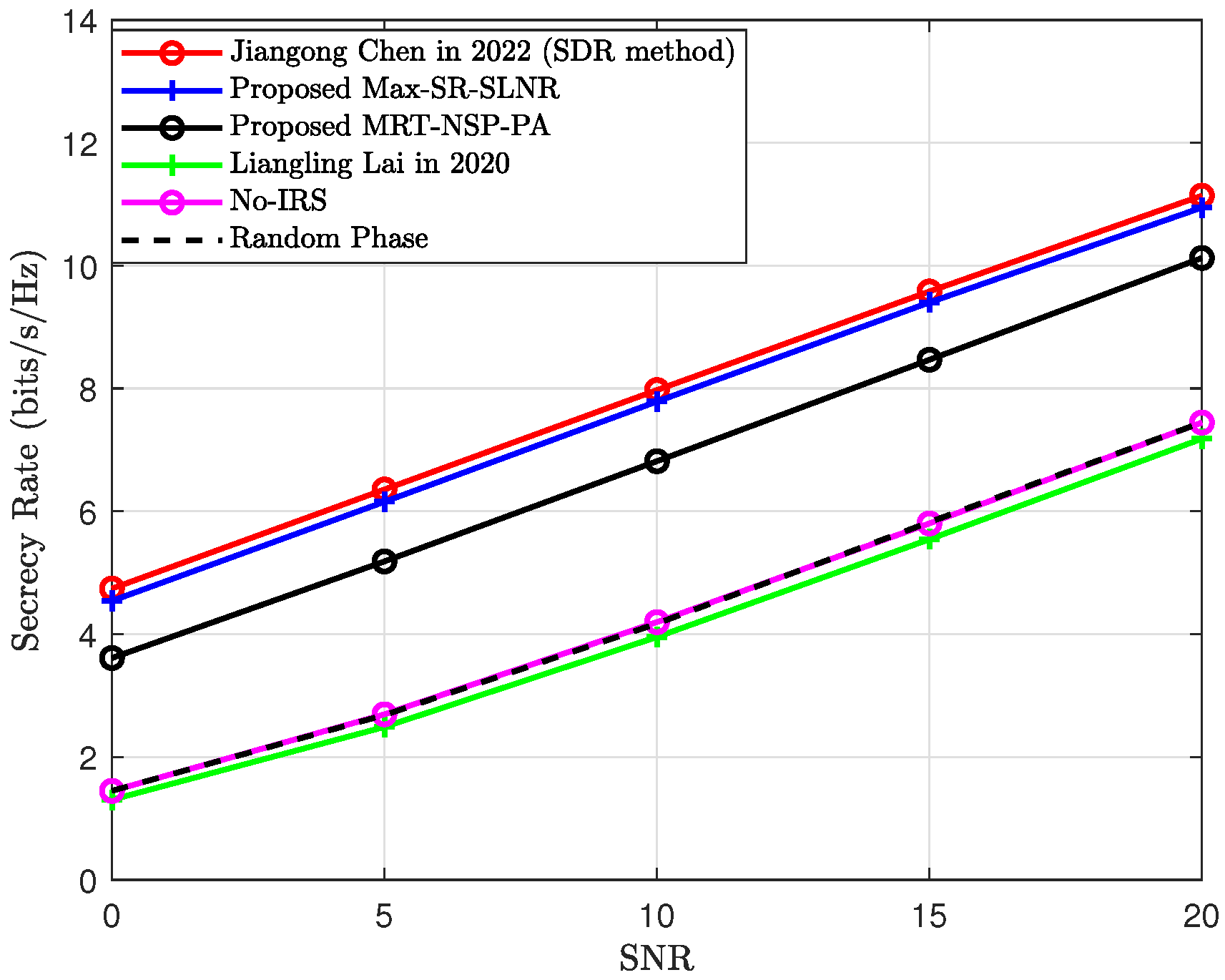
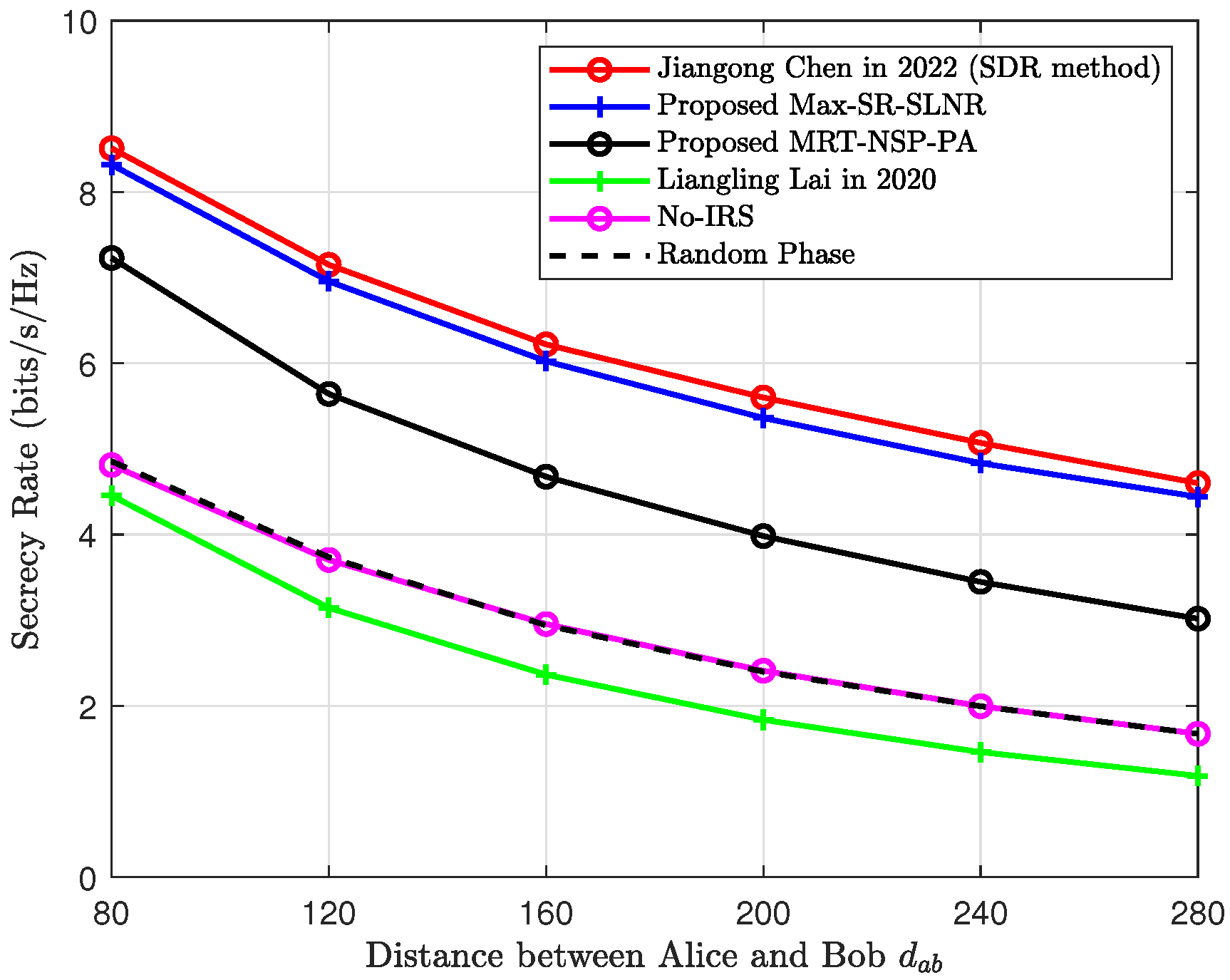
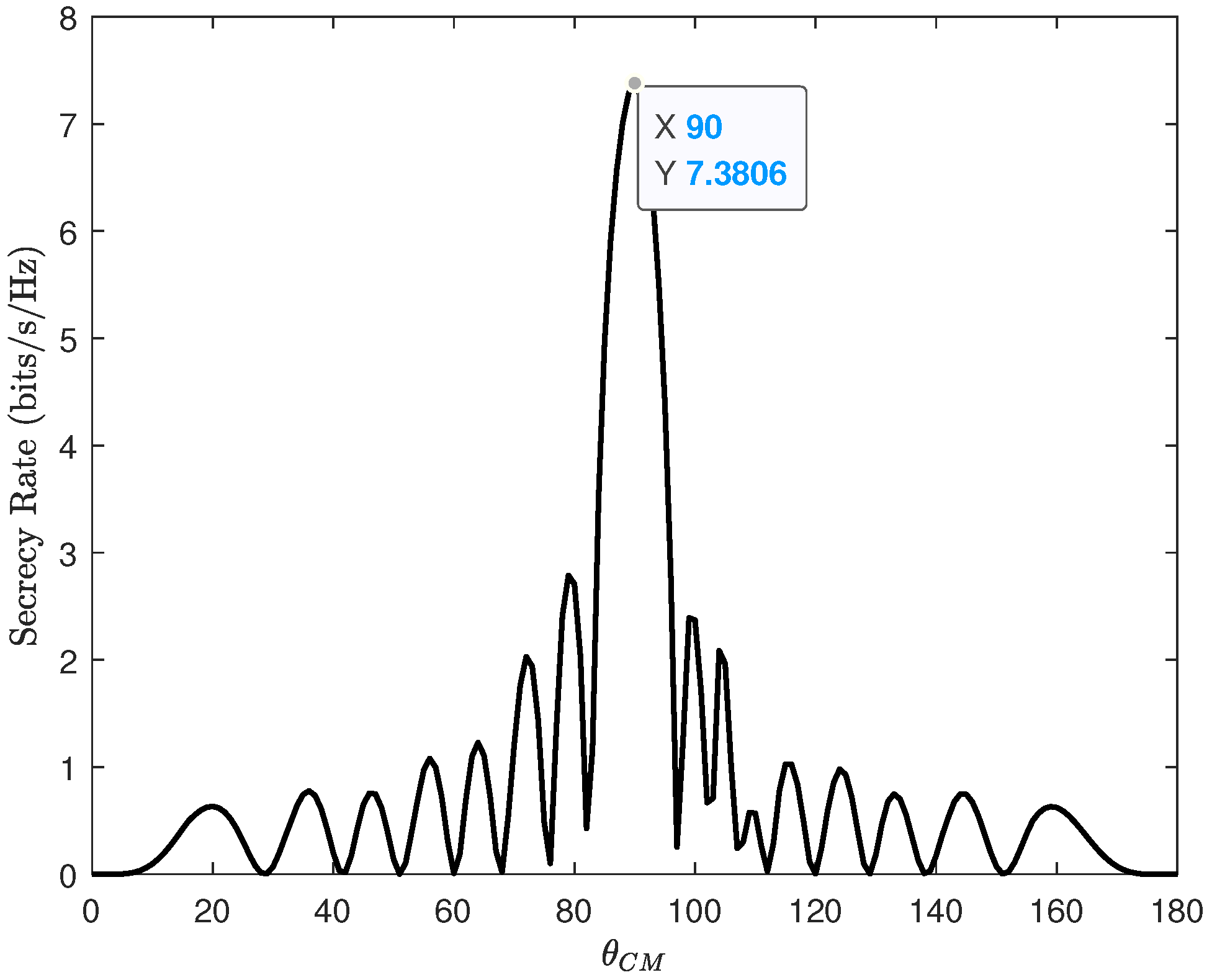
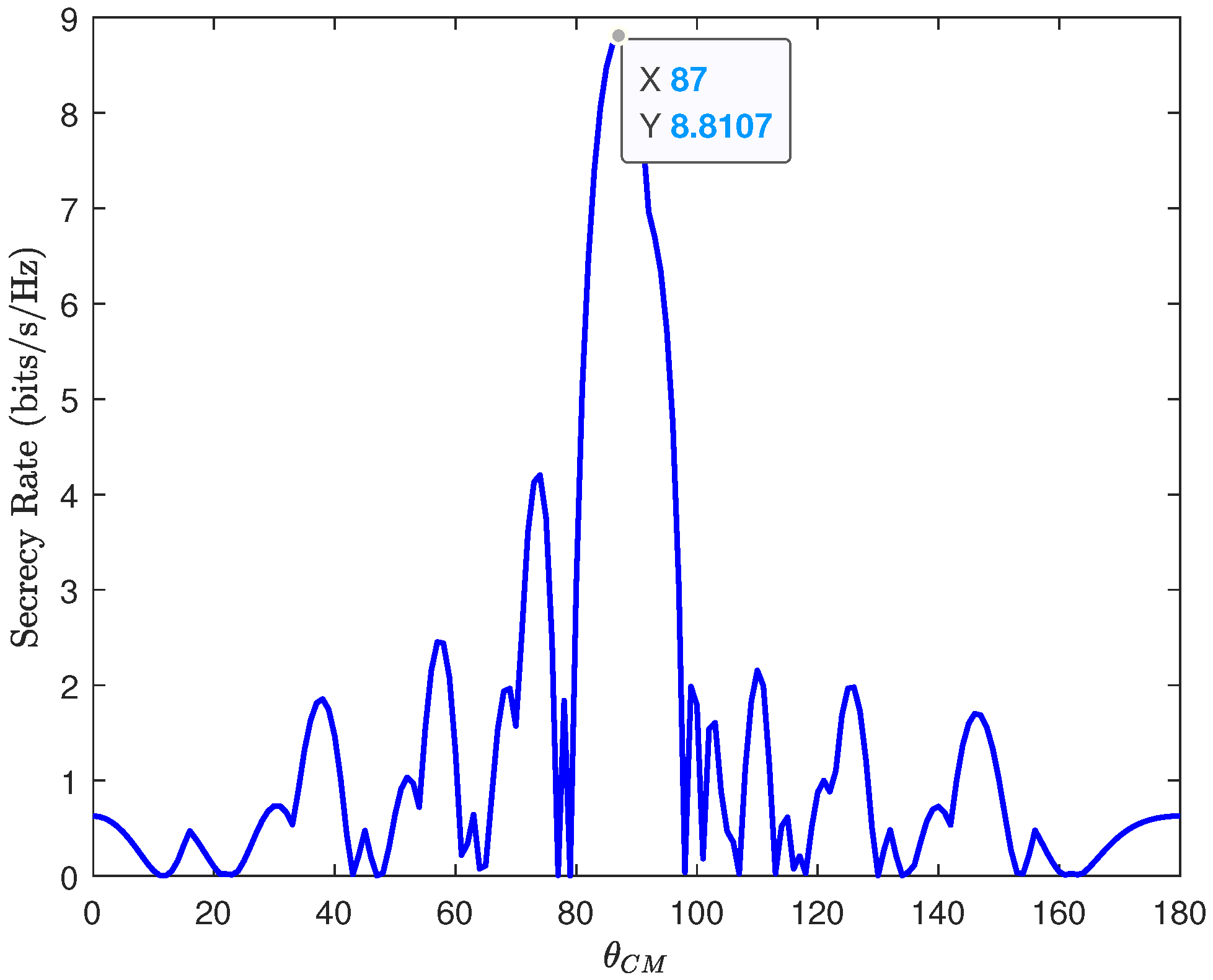
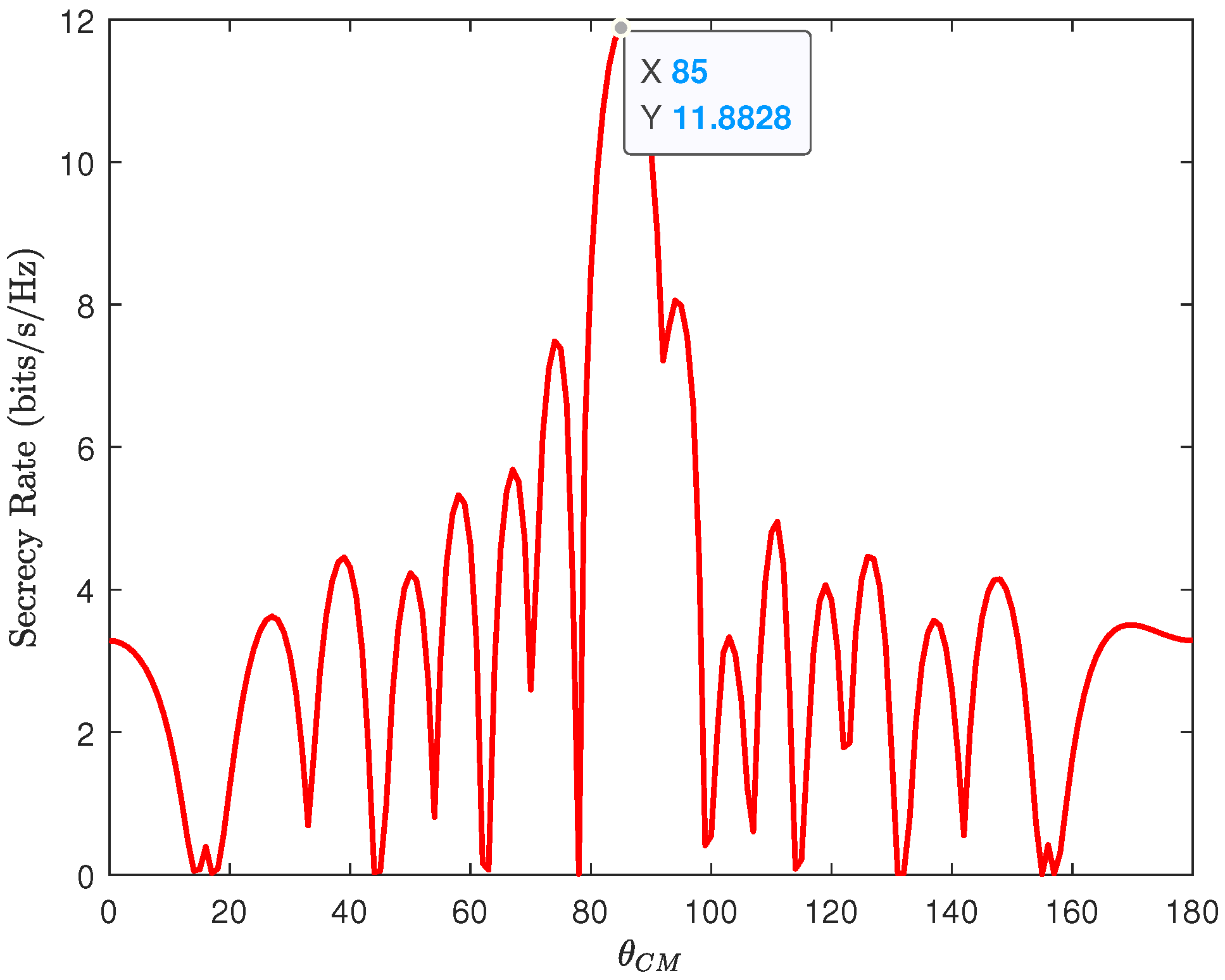
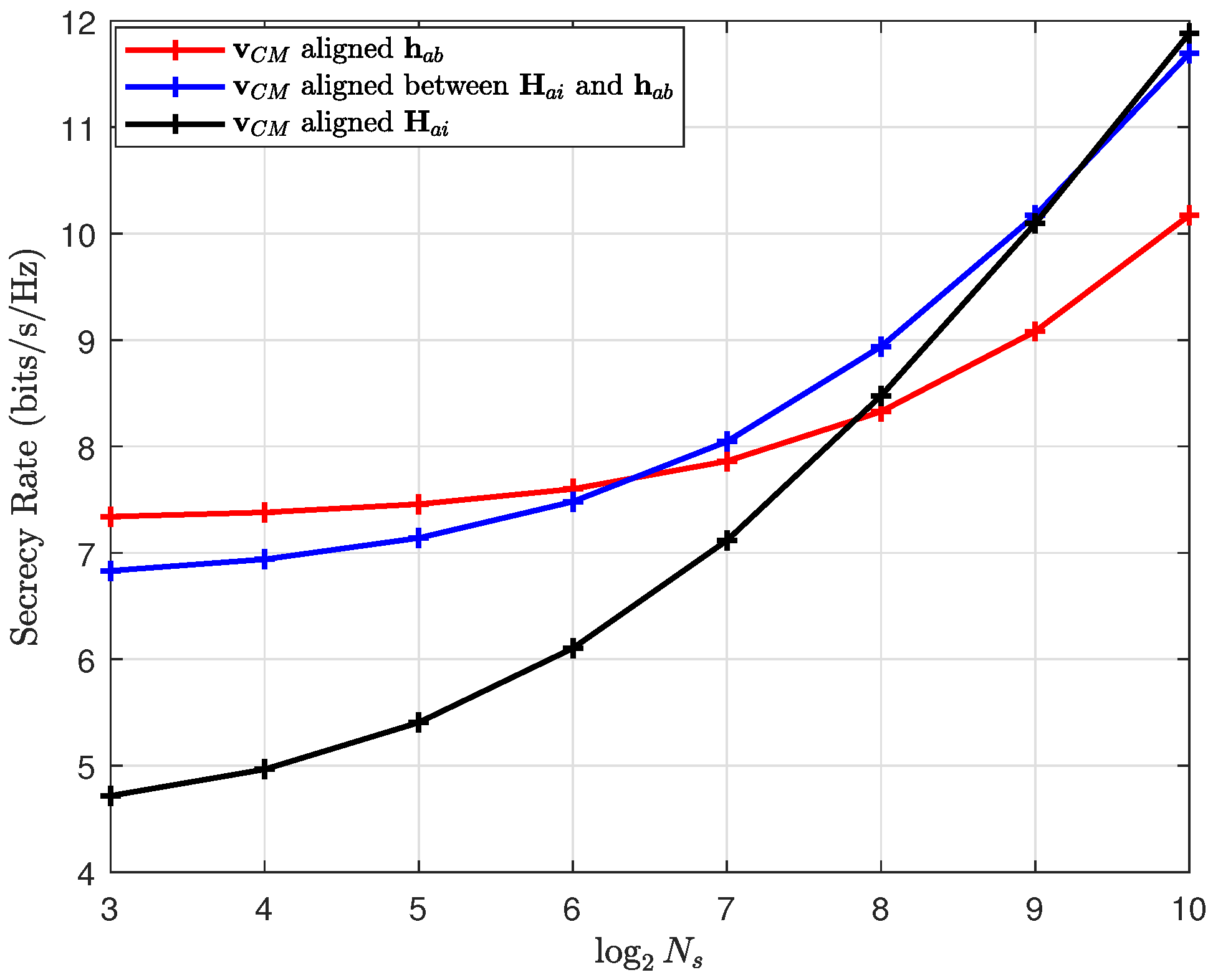
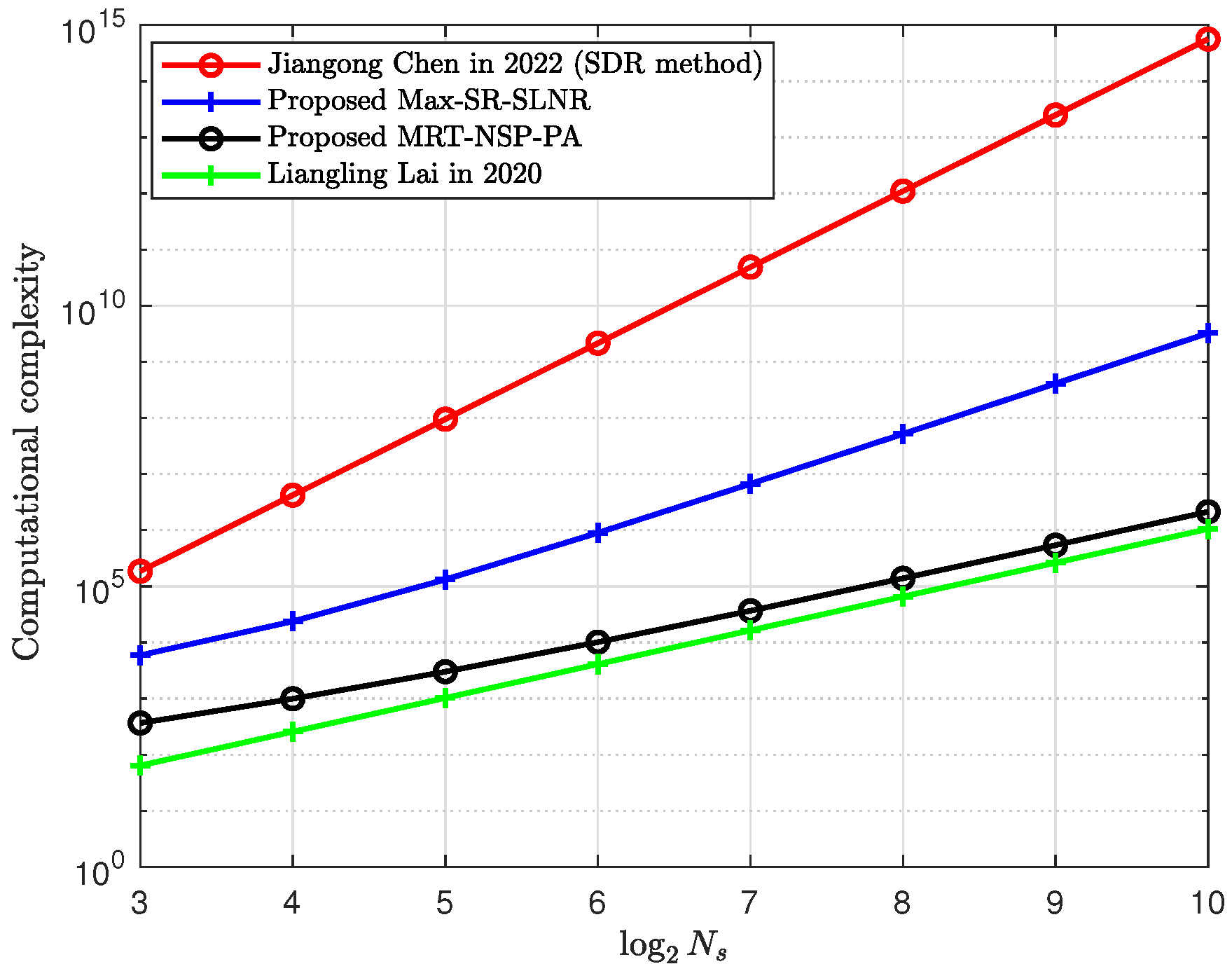
4. Simulation and Analysis
- No IRS: This scheme disregards the presence of the IRS. = .
- Random Phase: Here, the IRS phase shift value takes on a random value, and the phase of the IRS is random within the range .
Discussion of the Results
5. Conclusions and Limitations
5.1. Conclusions
5.2. Limitations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UAV | Unmanned aerial vehicle |
| LoS | Line of sight |
| IRS | Intelligent reflecting surface |
| DM | Directional modulation |
| SINR | Signal-to-interference plus noise ratio |
| PA | Phase alignment |
| SLNR | Signal-to-leakage-noise ratio |
| SR | Secrecy rate |
| Max-SR-SLNR | Maximum SR-SLNR |
| NSP | Null-space projection |
| MRT | Maximum ratio transmission |
| PSM | Phase shift matrix |
| AN | Artificial noise |
| CM | Confidential message |
| PL | Path loss |
References
- Xiao, Z.; Xia, P.; Xia, X.G. Enabling UAV cellular with millimeter-wave communication: Potentials and approaches. IEEE Commun. Mag. 2016, 54, 66–73. [Google Scholar] [CrossRef]
- Azari, M.M.; Geraci, G.; Garcia-Rodriguez, A.; Pollin, S. UAV-to-UAV communications in cellular networks. IEEE Trans. Wirel. Commun. 2020, 19, 6130–6144. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Zhao, M.M.; Shi, Q.; Zhao, M.J. Efficiency maximization for UAV-enabled mobile relaying systems with laser charging. IEEE Trans. Wirel. Commun. 2020, 19, 3257–3272. [Google Scholar] [CrossRef]
- Wen, F.; Shi, J.; Gui, G.; Gacanin, H.; Dobre, O.A. 3-D Positioning Method for Anonymous UAV Based on Bistatic Polarized MIMO Radar. IEEE Internet Things J. 2022, 10, 815–827. [Google Scholar] [CrossRef]
- Csiszar, I.; Korner, J. Broadcast channels with confidential messages. IEEE Trans. Inf. Theory 1978, 24, 339–348. [Google Scholar] [CrossRef]
- Mukherjee, A.; Fakoorian, S.A.A.; Huang, J.; Swindlehurst, A.L. Principles of physical layer security in multiuser wireless networks: A survey. IEEE Commun. Surv. Tutor. 2014, 16, 1550–1573. [Google Scholar] [CrossRef]
- Yang, N.; Yeoh, P.L.; Elkashlan, M.; Schober, R.; Yuan, J. MIMO wiretap channels: Secure transmission using transmit antenna selection and receive generalized selection combining. IEEE Commun. Lett. 2013, 17, 1754–1757. [Google Scholar] [CrossRef]
- Hamamreh, J.M.; Furqan, H.M.; Arslan, H. Classifications and applications of physical layer security techniques for confidentiality: A comprehensive survey. IEEE Commun. Surv. Tutor. 2019, 21, 1773–1828. [Google Scholar] [CrossRef]
- Yang, N.; Yan, S.; Yuan, J.; Malaney, R.; Subramanian, R.; Land, I. Artificial noise: Transmission optimization in multi-input single-output wiretap channels. IEEE Trans. Commun. 2015, 63, 1771–1783. [Google Scholar] [CrossRef]
- Diffie, W.; Hellman, M.E. New directions in cryptography. IEEE Trans. Inform. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef]
- Wyner, A.D. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Sarkar, M.Z.I.; Ratnarajah, T. Secure communications through Rayleigh fading SIMO channel with multiple eavesdroppers. In Proceedings of the 2010 IEEE International Conference on Communications, Cape Town, South Africa, 23–27 May 2010; pp. 1–5. [Google Scholar]
- Khisti, A.; Tchamkerten, A.; Wornell, G.W. Secure broadcasting over fading channels. IEEE Trans. Inf. Theory 2008, 54, 2453–2469. [Google Scholar] [CrossRef]
- Ju, Y.; Wang, H.M.; Zheng, T.X.; Yin, Q.; Lee, M.H. Safeguarding millimeter wave communications against randomly located eavesdroppers. IEEE Trans. Wirel. Commun. 2018, 17, 2675–2689. [Google Scholar] [CrossRef]
- Shu, F.; Wu, X.; You, X.; Lu, J.; Hu, J.; Zhu, W.; Yu, H.; Xu, Z.; Chen, R. Directional modulation-based secure wireless transmission: Basic principles, key techniques, and applications. Sci. Sin. Inform. 2017, 47, 1209–1225. [Google Scholar]
- Hu, J.; Shu, F.; Li, J. Robust synthesis method for secure directional modulation with imperfect direction angle. IEEE Commun. Lett. 2016, 20, 1084–1087. [Google Scholar] [CrossRef]
- Qiu, B.; Tao, M.; Wang, L.; Xie, J.; Wang, Y. Multi-beam directional modulation synthesis scheme based on frequency diverse array. IEEE Trans. Inf. Forensics Secur. 2019, 14, 2593–2606. [Google Scholar] [CrossRef]
- Mamaghani, M.T.; Hong, Y. On the performance of low-altitude UAV-enabled secure AF relaying with cooperative jamming and SWIPT. IEEE Access 2019, 7, 153060–153073. [Google Scholar] [CrossRef]
- Sun, X.; Yang, W.; Cai, Y.; Xiang, Z.; Tang, X. Secure transmissions in millimeter wave SWIPT UAV-based relay networks. IEEE Wireless Commun. Lett. 2019, 8, 785–788. [Google Scholar] [CrossRef]
- Shu, F.; Xu, L.; Wang, J.; Zhu, W.; Xiaobo, Z. Artificial-noise-aided secure multicast precoding for directional modulation systems. IEEE Trans. Veh. Technol. 2018, 67, 6658–6662. [Google Scholar] [CrossRef]
- Shu, F.; Wu, X.; Hu, J.; Li, J.; Chen, R.; Wang, J. Secure and precise wireless transmission for random-subcarrier-selection-based directional modulation transmit antenna array. IEEE J. Sel. Areas Commun. 2018, 36, 890–904. [Google Scholar] [CrossRef]
- Li, C.; Wang, X.; Yang, L.; Zhu, W.P. A joint source and relay power allocation scheme for a class of MIMO relay systems. IEEE Trans. Signal Process 2009, 57, 4852–4860. [Google Scholar]
- Wu, Q.; Zhang, R. Beamforming optimization for wireless network aided by intelligent reflecting surface with discrete phase shifts. IEEE Trans. Commun. 2019, 68, 1838–1851. [Google Scholar] [CrossRef]
- Dong, R.; Teng, Y.; Sun, Z.; Zou, J.; Huang, M.; Li, J.; Shu, F.; Wang, J. Performance Analysis of Wireless Network Aided by Discrete-Phase-Shifter IRS. J. Commun. Netw. 2022, 24, 603–612. [Google Scholar] [CrossRef]
- Tang, W.; Chen, M.Z.; Chen, X.; Dai, J.Y.; Han, Y.; Di Renzo, M.; Zeng, Y.; Jin, S.; Cheng, Q.; Cui, T.J. Wireless communications with reconfigurable intelligent surface: Path loss modeling and experimental measurement. IEEE Trans. Wirel. Commun. 2020, 20, 421–439. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Intelligent reflecting surface enhanced wireless network via joint active and passive beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef]
- Hum, S.V.; Perruisseau-Carrier, J. Reconfigurable reflectarrays and array lenses for dynamic antenna beam control: A review. IEEE Trans. Antennas Propag. 2013, 62, 183–198. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, S.; Duan, L.; Zhang, R. Double-IRS aided MIMO communication under LoS channels: Capacity maximization and scaling. IEEE Trans. Commun. 2022, 70, 2820–2837. [Google Scholar] [CrossRef]
- Pan, C.; Ren, H.; Wang, K.; Xu, W.; Elkashlan, M.; Nallanathan, A.; Hanzo, L. Multicell MIMO communications relying on intelligent reflecting surfaces. IEEE Trans. Wirel. Commun. 2020, 19, 5218–5233. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, P.; Shu, F.; Shi, W.; Wang, J. Power Allocation for IRS-aided Two-way Decode-and-Forward Relay Wireless Network. IEEE Trans. Veh. Technol. 2023, 72, 1337–1342. [Google Scholar] [CrossRef]
- Zhou, X.; Yan, S.; Wu, Q.; Shu, F.; Ng, D.W.K. Intelligent reflecting surface (IRS)-aided covert wireless communications with delay constraint. IEEE Trans. Wirel. Commun. 2022, 21, 532–547. [Google Scholar] [CrossRef]
- Shi, W.; Zhou, X.; Jia, L.; Wu, Y.; Shu, F.; Wang, J. Enhanced secure wireless information and power transfer via intelligent reflecting surface. IEEE Commun. Lett. 2020, 25, 1084–1088. [Google Scholar] [CrossRef]
- Shu, F.; Yang, L.; Jiang, X.; Cai, W.; Shi, W.; Huang, M.; Wang, J.; You, X. Beamforming and transmit power design for intelligent reconfigurable surface-aided secure spatial modulation. IEEE J. Sel. Topics Signal Process. 2022, 16, 933–949. [Google Scholar] [CrossRef]
- Pang, X.; Zhao, N.; Tang, J.; Wu, C.; Niyato, D.; Wong, K.K. IRS-assisted secure UAV transmission via joint trajectory and beamforming design. IEEE Trans. Commun. 2021, 70, 1140–1152. [Google Scholar] [CrossRef]
- Lai, L.; Hu, J.; Chen, Y.; Zheng, H.; Yang, N. Directional modulation-enabled secure transmission with intelligent reflecting surface. In Proceedings of the 2020 IEEE 3rd International Conference on Information Communication and Signal Processing (ICICSP), Shanghai, China, 12–15 September 2020; pp. 450–453. [Google Scholar]
- Chen, J.; Xiao, Y.; Lei, X.; Niu, H.; Yuan, Y. Artificial noise aided directional modulation via reconfigurable intelligent surface: Secrecy guarantee in range domain. IET Commun. 2022, 16, 1558–1569. [Google Scholar] [CrossRef]
- Shu, F.; Teng, Y.; Li, J.; Huang, M.; Shi, W.; Li, J.; Wu, Y.; Wang, J. Enhanced secrecy rate maximization for directional modulation networks via IRS. IEEE Trans. Commun. 2021, 69, 8388–8401. [Google Scholar] [CrossRef]
- Dong, R.; Jiang, S.; Hua, X.; Teng, Y.; Shu, F.; Wang, J. Low-Complexity Joint Phase Adjustment and Receive Beamforming for Directional Modulation Networks via IRS. IEEE Open J. Commun. Soc. 2022, 3, 1234–1243. [Google Scholar] [CrossRef]
- Wang, R.; Talgat, A.; Kishk, M.A.; Alouini, M.S. Conditional Contact Angle Distribution in LEO Satellite-Relayed Transmission. IEEE Commun. Lett. 2022, 26, 2735–2739. [Google Scholar] [CrossRef]
- Sadek, M.; Tarighat, A.; Sayed, A.H. A leakage-based precoding scheme for downlink multi-user MIMO channels. IEEE Trans. Wirel. Commun. 2007, 6, 1711–1721. [Google Scholar] [CrossRef]
| Conjugate Transpose | Inverse | Pseudo-Inverse | Two-Norm | Diagonal Operator |
|---|---|---|---|---|
| Previous Work | Aim of the Method | Strong Point | Limitation |
|---|---|---|---|
| Existing method in [36] | Boost SR | Low complexity | Poor SR |
| SDR in [37] | Maximize SR | High SR | High complexity |
| Parameter | Value |
|---|---|
| Alice coordinate | (0, 0, 0) m |
| IRS and UAV coordinate | (39.8, 3.5, 3.5) m |
| Bob coordinate | (90, 0, 0) m |
| Eve coordinate | (96.6, −25.9, 0) m |
| Transmitting power, | 30 dBm |
| Noise power, and | −40 dBm |
| PA factor, | 0.8 |
| distance of Alice-to-IRS, | 40 m |
| distance of Alice-to-Bob, | 90 m |
| distance of Alice-to-Eve, | 100 m |
| angle of departure of Alice-to-IRS | |
| angle of departure of Alice-to-Bob | |
| angle of departure of Alice-to-Eve |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Shu, F.; Zheng, Y.; Liu, J.; Dong, R.; Chen, X.; Wu, Y.; Yan, S.; Wang, J. Two Low-Complexity Efficient Beamformers for an IRS- and UAV-Aided Directional Modulation Network. Drones 2023, 7, 489. https://doi.org/10.3390/drones7080489
Lin Y, Shu F, Zheng Y, Liu J, Dong R, Chen X, Wu Y, Yan S, Wang J. Two Low-Complexity Efficient Beamformers for an IRS- and UAV-Aided Directional Modulation Network. Drones. 2023; 7(8):489. https://doi.org/10.3390/drones7080489
Chicago/Turabian StyleLin, Yeqing, Feng Shu, Yuxiang Zheng, Jing Liu, Rongen Dong, Xun Chen, Yue Wu, Shihao Yan, and Jiangzhou Wang. 2023. "Two Low-Complexity Efficient Beamformers for an IRS- and UAV-Aided Directional Modulation Network" Drones 7, no. 8: 489. https://doi.org/10.3390/drones7080489
APA StyleLin, Y., Shu, F., Zheng, Y., Liu, J., Dong, R., Chen, X., Wu, Y., Yan, S., & Wang, J. (2023). Two Low-Complexity Efficient Beamformers for an IRS- and UAV-Aided Directional Modulation Network. Drones, 7(8), 489. https://doi.org/10.3390/drones7080489






