Fast Tube-Based Robust Compensation Control for Fixed-Wing UAVs
Abstract
:1. Introduction
| Methods | Robustness | Characteristics | |||
|---|---|---|---|---|---|
| External Disturbances | Dynamic Uncertainties | Nonlinearity | Fast Solving | Handling Constraint | |
| Feedback linearization [2] | √ | √ | √ | ||
| Nonlinear dynamic inversion (NDI) [3] | √ | √ | √ | ||
| Sliding mode control (SMC) [4,5] | √ | √ | |||
| Model predictive control (MPC) [6] | √ | √ | √ | ||
| Fuzzy control [7] | √ | √ | √ | ||
| Artificial neural network (ANN) [8] | √ | √ | |||
| Reinforcement learning (RL) [9] | √ | √ | |||
| Safe RL [10] | √ | √ | √ | √ | |
| Adaptive control [11] | √ | √ | √ | √ | |
| Adaptive backstepping [12] | √ | √ | √ | ||
| RL-based SMC [13] | √ | √ | √ | ||
| ANN-based adaptive NDI [14] | √ | √ | |||
| LQR with robust compensation [15,16] | √ | √ | √ | ||
| Tube MPC [17] | √ | √ | √ | √ | |
| Homothetic tube MPC [18] | √ | √ | √ | √ | |
| Parameterized tube MPC [19] | √ | √ | √ | √ | |
| Nonlinear tube MPC [20] | √ | √ | √ | √ | |
| Robust LQR-Trees [21] | √ | √ | √ | ||
| TRCC [22,23] | √ | √ | √ | √ | |
| TRCC with direct HJB solving [24,25] | √ | √ | √ | √ | |
| TRCC with SOSP and tube library [27] | √ | √ | √ | √ | |
- Parallel computing method for trajectory tube computation: This paper presents a novel method for solving discrete trajectory tubes that simplifies the solution process by eliminating temporal correlations between tubes at different states. This approach enables the efficient parallel processing of trajectory tubes at different state points.
- Dimensionality reduction technique for TRCC of fixed-wing UAVs: Efficient dimensionality reduction techniques, including decoupling and stepwise approaches, are proposed to address higher fast-solving requirements according to fixed-wing UAV characteristics. These techniques are incorporated into a fast TRCC algorithm to enhance online applications.
2. TRCC Algorithm Based on Discrete Trajectory Tubes
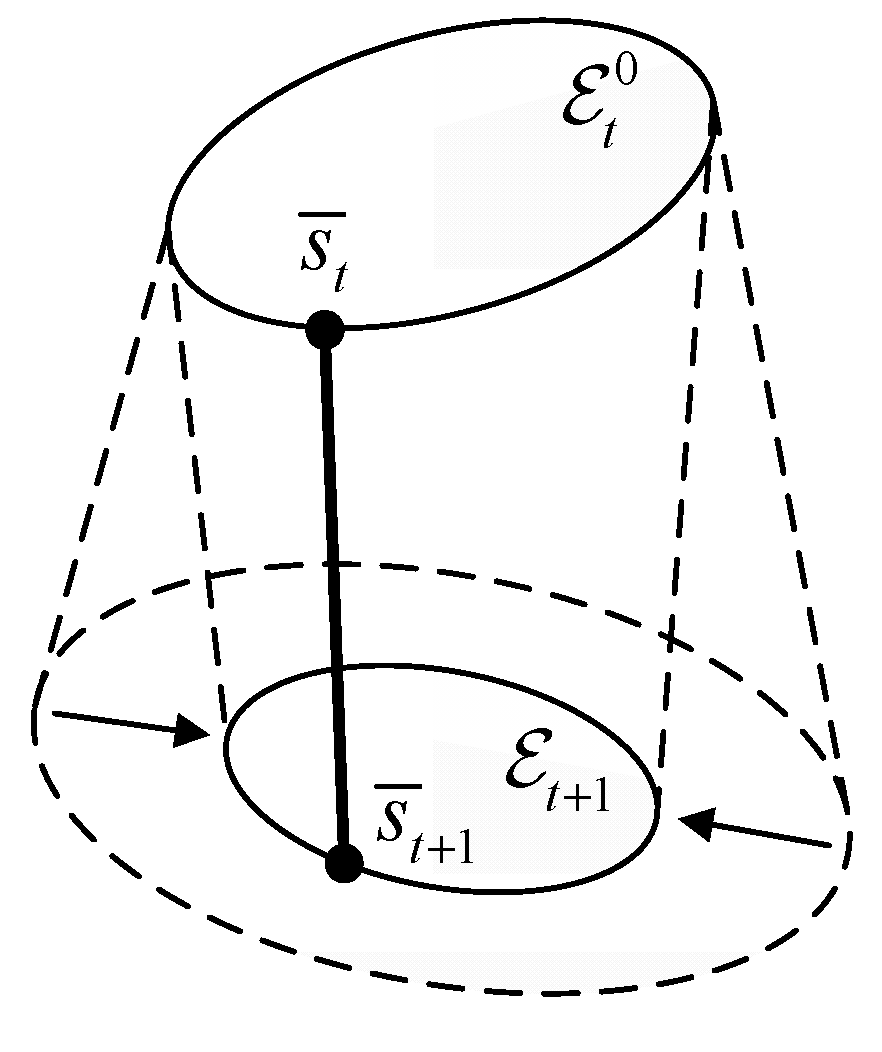
2.1. Discrete Trajectory Tube Calculation Method
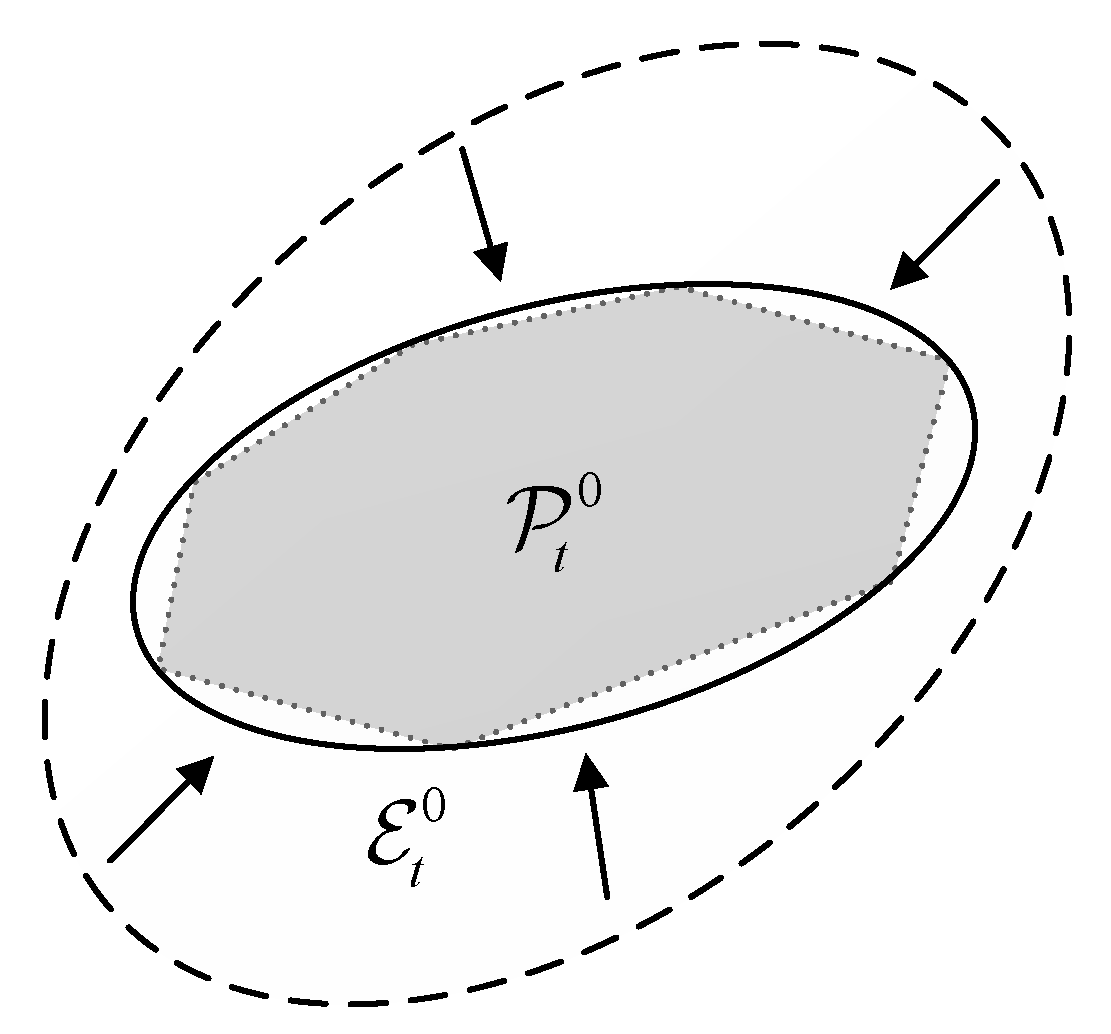
2.1.1. Initial Ellipsoid Calculation
2.1.2. Terminal Ellipsoid Calculation
2.2. Sum-of-Squares Programming
2.2.1. Constraints
2.2.2. Optimization Variables
2.2.3. Optimization Objectives
2.3. TRCC Algorithm
| Algorithm 1 TRCC |
 |
3. Fast TRCC for UAV
3.1. Control Reuse
3.2. Dimensionality Reduction
3.2.1. Decoupling
| Algorithm 2 Decoupling TRCC for UAV |
 |
3.2.2. Stepwise Method
| Algorithm 3 3-step decoupling TRCC for UAV |
 |
4. Simulation Test for Fast TRCC Performance
4.1. UAV Nonlinear Dynamics
4.1.1. Dynamic Equations
4.1.2. Aerodynamic Characteristics
4.2. Performance Analysis for TRCC
4.2.1. Trajectory Tube
4.2.2. Performance in Tracking Tasks
4.3. Performance Analysis for TRCC with Control Reuse
4.4. Time Consumption and Performance Analysis for Decoupling TRCC
4.4.1. Time Consumption
4.4.2. Performance in Tracking Tasks
4.5. Time Consumption and Performance Analysis for Stepwise TRCC
4.5.1. Time Consumption
4.5.2. Performance in Tracking Tasks
4.6. Runtime Simulation
4.7. Sensitivity Analysis
5. Conclusions
- The TRCC method for UAVs reduces the RMS tracking error by 66% compared to the uncompensated control, significantly enhancing robustness during maneuver trajectory tracking.
- By utilizing one-step reuse, UAV decoupling, and a three-step algorithm, the TRCC fast generation requirement of 50 ms per beat can be achieved in a 16-thread environment. Simulations demonstrate that the fast TRCC method reduces the RMS tracking error by 60% compared to the uncompensated control. However, when subjected to the same range of disturbances, the fast TRCC exhibits an approximate 9% increase in the RMS tracking error compared to the slow nominal TRCC, indicating lower robustness.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, M.; Wang, L.; Yue, T.; Liu, H. Influence of unmanned combat aerial vehicle agility on short-range aerial combat effectiveness. Aerosp. Sci. Technol. 2020, 96, 105534. [Google Scholar] [CrossRef]
- Pereira, L.A.A.; Pimenta, L.C.A.; Raffo, G.V. MPC Based Feedback-Linearization Strategy of a Fixed-Wing UAV. Automática 2020, 2, 1. [Google Scholar] [CrossRef]
- Pfeifle, O.; Fichter, W. Cascaded incremental nonlinear dynamic inversion for three-dimensional spline-tracking with wind compensation. J. Guid. Control Dyn. 2021, 44, 1559–1571. [Google Scholar] [CrossRef]
- Olguin-Roque, J.; Salazar, S.; González-Hernandez, I.; Lozano, R. A Robust Fixed-Time Sliding Mode Control for Quadrotor UAV. Algorithms 2023, 16, 229. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, W.; Suzuki, S.; Namiki, A.; Liu, H.; Li, Z. Design and implementation of UAV velocity controller based on reference model sliding mode control. Drones 2023, 7, 130. [Google Scholar] [CrossRef]
- Mothes, F. Trajectory planning in time-varying adverse weather for fixed-wing aircraft using robust model predictive control. Aerospace 2019, 6, 68. [Google Scholar] [CrossRef] [Green Version]
- Melo, A.G.; Andrade, F.A.A.; Guedes, I.P.; Carvalho, G.F.; Zachi, A.R.L.; Pinto, M.F. Fuzzy gain-scheduling PID for UAV position and altitude controllers. Sensors 2022, 22, 2173. [Google Scholar] [CrossRef] [PubMed]
- Alsaade, F.W.; Jahanshahi, H.; Yao, Q.; Al-Zahrani, M.S.; Alzahrani, A.S. A new neural network-based optimal mixed H2/H∞ control for a modified unmanned aerial vehicle subject to control input constraints. Adv. Space Res. 2023, 71, 3631–3643. [Google Scholar] [CrossRef]
- Wan, K.; Gao, X.; Hu, Z.; Wu, G. Robust motion control for UAV in dynamic uncertain environments using deep reinforcement learning. Remote Sens. 2020, 12, 640. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Zhao, W.; Liu, L. Safe Reinforcement Learning for Transition Control of Ducted-Fan UAVs. Drones 2023, 7, 332. [Google Scholar] [CrossRef]
- Popov, A.M.; Kostrygin, D.G.; Shevchik, A.A.; Andrievsky, B. Speed-Gradient Adaptive Control for Parametrically Uncertain UAVs in Formation. Electronics 2022, 11, 4187. [Google Scholar] [CrossRef]
- Lungu, M. Auto-landing of UAVs with variable centre of mass using the backstepping and dynamic inversion control. Aerosp. Sci. Technol. 2020, 103, 105912. [Google Scholar] [CrossRef]
- Wang, Q.; Namiki, A.; Asignacion, A., Jr.; Li, Z.; Suzuki, S. Chattering Reduction of Sliding Mode Control for Quadrotor UAVs Based on Reinforcement Learning. Drones 2023, 7, 420. [Google Scholar] [CrossRef]
- Cao, S.; Shen, L.; Zhang, R.; Yu, H.; Wang, X. Adaptive incremental nonlinear dynamic inversion control based on neural network for UAV maneuver. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019; IEEE: Tampa, FL, USA, 2019. [Google Scholar] [CrossRef]
- Liu, H.; Lu, G.; Zhong, Y. Robust LQR attitude control of a 3-DOF laboratory helicopter for aggressive maneuvers. IEEE Trans. Ind. Electron. 2012, 60, 4627–4636. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Zhong, Y. Quaternion-based robust attitude control for uncertain robotic quadrotors. IEEE Trans. Ind. Inform. 2015, 11, 406–415. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Seron, M.M.; Raković, S.V. Robust model predictive control of constrained linear systems with bounded disturbances. Automatica 2005, 41, 219–224. [Google Scholar] [CrossRef]
- Raković, S.V.; Kouvaritakis, B.; Findeisen, R.; Cannon, M. Homothetic tube model predictive control. Automatica 2012, 48, 1631–1638. [Google Scholar] [CrossRef]
- Raković, S.V.; Kouvaritakis, B.; Cannon, M.; Panos, C.; Findeisen, R. Parameterized tube model predictive control. IEEE Trans. Autom. Control 2012, 57, 2746–2761. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Kerrigan, E.C.; Van Wyk, E.J.; Falugi, P. Tube-based robust nonlinear model predictive control. Int. J. Robust Nonlinear Control 2011, 21, 1341–1353. [Google Scholar] [CrossRef]
- Moore, J.; Cory, R.; Tedrake, R. Robust post-stall perching with a simple fixed-wing glider using LQR-Trees. Bioinspir. Biomim. 2014, 9, 025013. [Google Scholar] [CrossRef] [Green Version]
- Majumdar, A.; Ahmadi, A.A.; Tedrake, R. Control design along trajectories with sums of squares programming. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: Tampa, FL, USA, 2013. [Google Scholar] [CrossRef] [Green Version]
- Tobenkin, M.M.; Manchester, I.R.; Tedrake, R. Invariant funnels around trajectories using sum-of-squares programming. IFAC Proc. Vol. 2011, 44, 9218–9223. [Google Scholar] [CrossRef]
- Herbert, S.L.; Bansal, S.; Ghosh, S.; Tomlin, C.J. Reachability-based safety guarantees using efficient initializations. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; IEEE: Tampa, FL, USA, 2019. [Google Scholar] [CrossRef] [Green Version]
- Seo, H.; Son, C.Y.; Kim, H.J. Fast funnel computation using multivariate Bernstein polynomial. IEEE Robot. Autom. Lett. 2021, 6, 1351–1358. [Google Scholar] [CrossRef]
- Cunis, T.; Legat, B. Sequential sum-of-squares programming for analysis of nonlinear systems. In Proceedings of the 2023 American Control Conference (ACC), San Diego, CA, USA, 31 May–2 June 2013; IEEE: Tampa, FL, USA, 2013. [Google Scholar] [CrossRef]
- Majumdar, A.; Tedrake, R. Funnel libraries for real-time robust feedback motion planning. Int. J. Robot. Res. 2017, 36, 947–982. [Google Scholar] [CrossRef]
- Prajna, S.; Papachristodoulou, A.; Parrilo, P.A. Introducing SOSTOOLS: A general purpose sum of squares programming solver. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; IEEE: Tampa, FL, USA, 2002. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, I.M.; Bayen, A.M.; Tomlin, C.J. A time-dependent Hamilton-Jacobi formulation of reachable sets for continuous dynamic games. IEEE Trans. Autom. Control 2005, 50, 947–957. [Google Scholar] [CrossRef] [Green Version]
- Waldspurger, I.; d’Aspremont, A.; Mallat, S. Phase recovery, maxcut and complex semidefinite programming. Math. Program. 2015, 149, 47–81. [Google Scholar] [CrossRef] [Green Version]
- Papachristodoulou, A.; Anderson, J.; Valmorbida, G.; Prajna, S.; Seiler, P.; Parrilo, P.; Peet, M.M.; Jagt, D. SOSTOOLS version 4.00 sum of squares optimization toolbox for MATLAB. arXiv 2013, arXiv:1310.4716. [Google Scholar]
- Sturm, J.F. Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones. Optim. Methods Softw. 1999, 11, 625–653. [Google Scholar] [CrossRef]
- El-kenawy, E.S.M.; Ibrahim, A.; Bailek, N.; Bouchouicha, K.; Hassan, M.A.; Jamei, M.; Al-Ansari, N. Sunshine duration measurements and predictions in Saharan Algeria region: An improved ensemble learning approach. Theor. Appl. Climatol. 2022, 147, 1015–1031. [Google Scholar] [CrossRef]
















| Parameter | Value | Parameter | Value |
|---|---|---|---|
| (m/s) | 185 | (m/s) | [−5, 5] |
| (°) | 19.3 | (°) | [−0.5, 0.5] |
| (°/s) | 28.2 | (°/s) | [−0.5, 0.5] |
| (°) | −50.5 | (°) | [−1, 1] |
| (°) | 0.7 | (°) | [−0.5, 0.5] |
| (°/s) | −19.7 | (°/s) | [−1, 1] |
| (°/s) | −9.4 | (°/s) | [−0.5, 0.5] |
| (°) | 0 | (°) | [−1, 1] |
| (km) | 3 | (°) | −5.3 |
| (-) | 0.75 | (°) | 3.0 |
| (°) | 0 | (% mmax) | [−5, 5] |
| Parameter | Range | Parameter | Range |
|---|---|---|---|
| (m/s) | [200, 350] | (°) | [−10, 25] |
| (°/s) | [−30, 30] | (°) | [−60, 60] |
| (°) | [−10, 10] | (°/s) | [−50, 50] |
| (°/s) | [−10, 10] | (°) | [−90, 90] |
| (°) | [−15, 15] | (-) | [0.2, 0.8] |
| (°) | [−15, 15] | (°) | [−25, 25] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zheng, S.; Wang, W.; Wang, H.; Liu, H.; Yue, T. Fast Tube-Based Robust Compensation Control for Fixed-Wing UAVs. Drones 2023, 7, 481. https://doi.org/10.3390/drones7070481
Wang L, Zheng S, Wang W, Wang H, Liu H, Yue T. Fast Tube-Based Robust Compensation Control for Fixed-Wing UAVs. Drones. 2023; 7(7):481. https://doi.org/10.3390/drones7070481
Chicago/Turabian StyleWang, Lixin, Sizhuang Zheng, Weijia Wang, Hao Wang, Hailiang Liu, and Ting Yue. 2023. "Fast Tube-Based Robust Compensation Control for Fixed-Wing UAVs" Drones 7, no. 7: 481. https://doi.org/10.3390/drones7070481
APA StyleWang, L., Zheng, S., Wang, W., Wang, H., Liu, H., & Yue, T. (2023). Fast Tube-Based Robust Compensation Control for Fixed-Wing UAVs. Drones, 7(7), 481. https://doi.org/10.3390/drones7070481






