Quality-Aware Autonomous Navigation with Dynamic Path Cost for Vision-Based Mapping toward Drone Landing
Abstract
1. Introduction
- A probabilistic sparse elevation map generation algorithm with Bayes inference using SVO point cloud data and a down-looking single-camera setup. The generated map enables the representation of the sensor measurement accuracy to increase map quality by cooperating with the planner.
- A novel QABV planner for autonomous navigation with a dual focus: map exploration and quality. Generated paths via the novel information gain allow for visiting viewpoints that provide new measurements that increase the performance of the probabilistic sparse elevation map concerning exploration and accuracy.
- A novel dynamic path cost representation for the QABV planner to reduce the distance traveled and escape from a low-information area. To dynamically adjust the path cost, we propose four control methods: method 1 offers a simple approach with an on–off controller while method 2 employs a PD controller to adjust the path cost, and method 3 switches its control action depending on the reference while method 4 generates its reference depending on the map information.
- To show the performance improvements of the proposed approach, we present comparative simulation results. We demonstrate that the developed QABV planners have significantly better performances compared to the NBV planner regarding measurement accuracy and distance traveled.
- To verify the performance, we also solve the safe landing problem of a delivery drone within a realistic simulation environment. The results verify the usefulness of the proposed mapping and exploration approach.
2. Probabilistic Sparse Elevation Map Generation with SVO Point Cloud Data
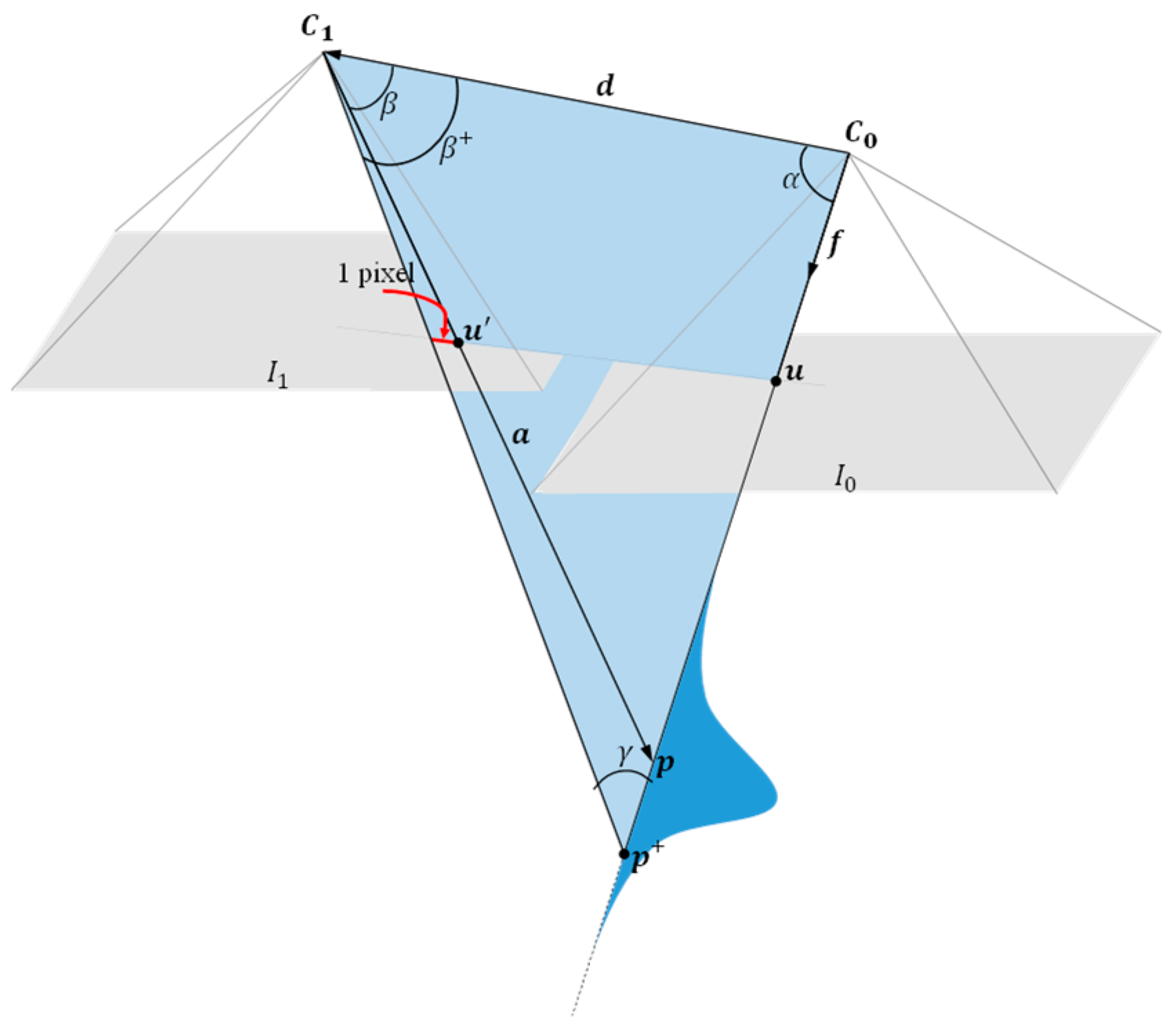
2.1. SVO Point Cloud Data Generation
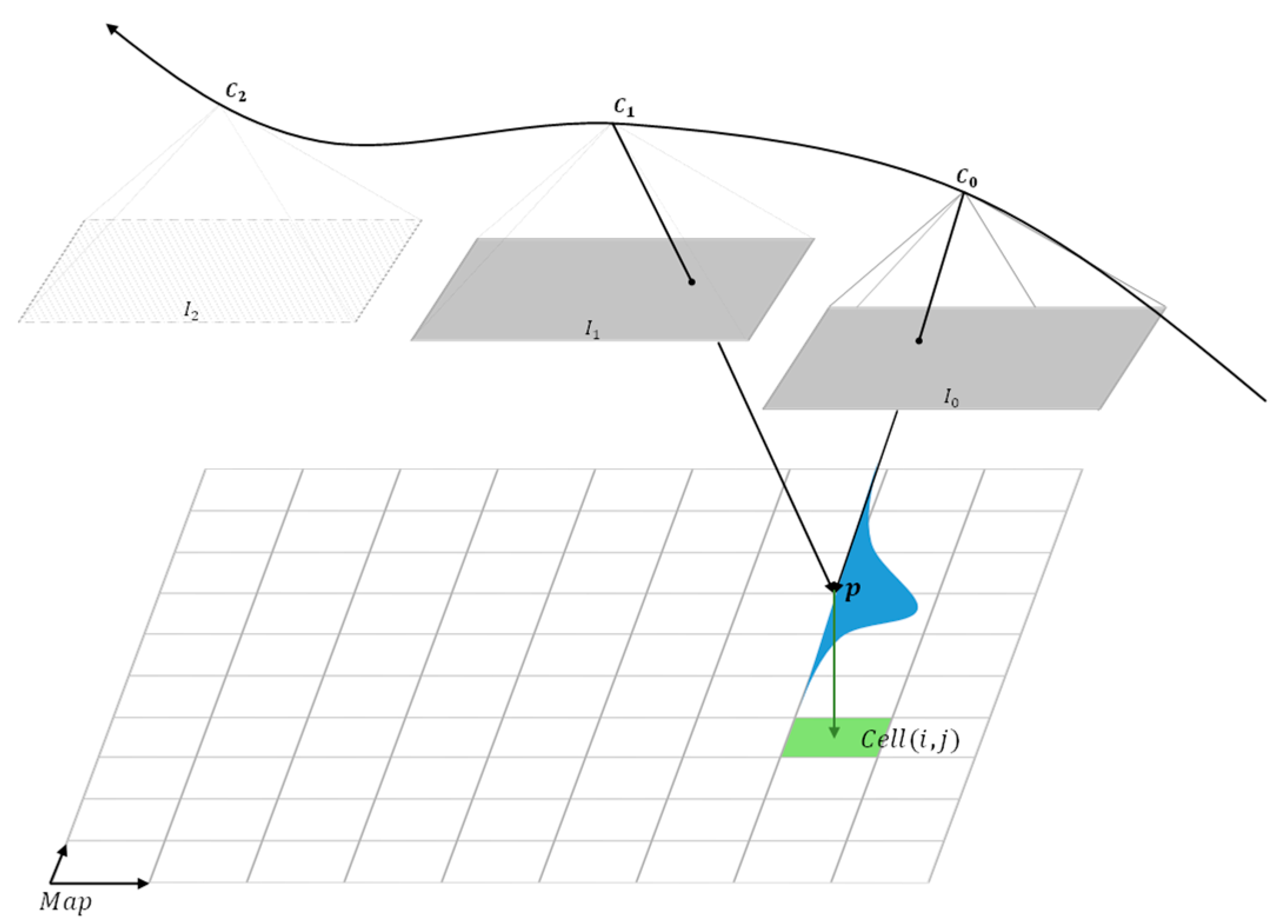
2.2. Probabilistic Sparse Elevation Map Generation via Bayesian Inference
- If it is an unmapped cell, then its height and variance are updated via .
- If it is updated before but has more than height error (i.e., a threshold value), then it is defined as an inaccurate cell as follows:
| Algorithm 1. Sparse Elevation Map Generation via Bayes Inference |
| 1: Initialize with unmapped cells 2: while the stop criterion is not satisfied ( or ) 3: 4: for each in do 5: 6: if is 7: 8: 9: else if is 10: 11: 12: end if 13: end for 14: end while |
3. Autonomous Navigation for Map Exploration and Accuracy
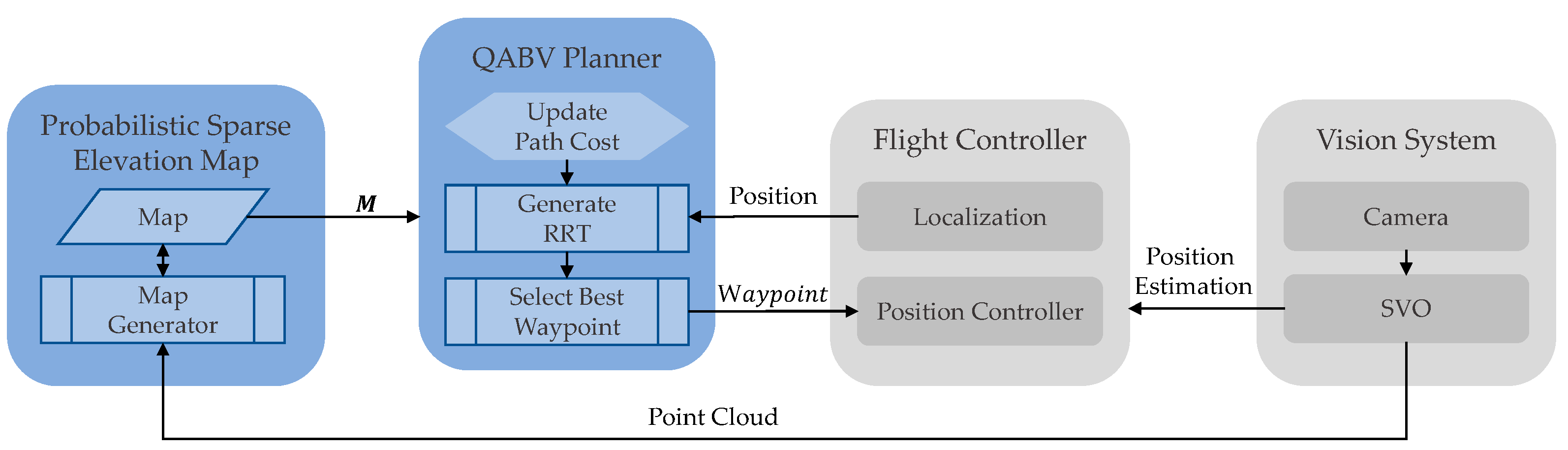
- The QABV planner is capable of acquiring information and guiding the drone with a single down-looking camera unlike using a dual camera as in the NBV planner, as it uses the generated sparse probabilistic elevation map described in Section 2.
- Unlike the NBV planner which focuses only on map exploration, the proposed QABV planner has a dual focus on map exploration and quality thanks to a novel information gain function definition. The QABV analyzes the unmapped and inaccurate cells defined in (8) and (9) to generate the best waypoints such that new map cells are updated while the accuracy of previously updated cells is improved.
- Especially in real-world applications, the path cost of the NBV planner becomes ineffective when the drone operates at a constant speed and the planner algorithm runs periodically. The QABV planner tackles this issue by processing the node numbers of the RRT branch as the path cost and adjusting its behavior dynamically while the map is being generated.
3.1. The NBV Planner: The Receding Horizon Next Best View Planner
| Algorithm 2. Receding Horizon Next Best View Planner [20] |
| 1: Current vehicle position 2: Initialize with and, unless the first planner call, also previous best branch 3:, set the best gain to zero 4:(), set the best node to the root 5: Number of initial nodes in 6: while or do 7: Incrementally build by adding 8: 9: if then 10: 11: 12: end if 13: if then 14: Terminate exploration 15: end if 16: end while 17: 18: Delete 17: return |
- (P-i)
- The gain function presented in (16) focuses only on map exploration without considering map quality; however, the measurement accuracy of the camera affects the quality of the map. By improving the function, determining the exploration progress can be performed while improving the map quality.
- (P-ii)
- The path cost function in (15) uses the distance between adjacent nodes; when the algorithm runs periodically and drone speed is constant, then the distance between adjacent nodes is equal. Thus, the NBV planner cannot punish long-path costs. For a clear understanding, let us explain this issue via the scenario depicted in Figure 5. In this case, the path cost (15) is the same for the following paths:
- (P-iii)
- As mentioned in [21,22], the NBV planner has a global map coverage problem and gets stuck in large environments. This can partly be handled by the careful tuning of the λ parameter in (16); however, this has to be completed for every environment and it typically requires several attempts. As a better approach, λ can be updated while the map is being explored rather than keeping it constant as is in the NBV planner.
3.2. The Proposed QABV Planner: Quality-Aware Best View Planner
| Algorithm 3. Quality-Aware Best View Planner |
| 1: Current vehicle position 2: Initialize with in the first run, unless the previous best branch 3: Initialize with −1 in the first run, unless the previous 4: Initialize as an empty vector in the first run 5: Initialize with in the first run 6: Set , update method in the first run: 7:, set the best gain to zero 8:(), set the best node to the root 9: Number of initial nodes in 10: switch 11: case 1: ) 12: case 2: ) 13: case 3: ) 14: case 4: 15: 16: 17: end switch 18: while or do 19: Incrementally build by adding 20: ← 21: if then 22: 23: 24: end if 25: end while 26: if 27: 28: Append to 29: end if 30: 31: Delete 32: return |
- As a solution to (P-i), with a novel information gain function, the QABV planner determines the best branch of to increase the measurement accuracy of and explores new areas. We propose the , instead of of the NBV planner, to calculate the information contribution of the visible unmapped and inaccurate cells from position . The is defined as follows:
- As stated in (P-ii), if the planner algorithm runs periodically every seconds, where r is the planning iteration, and T is the sampling period, while the drone flies at a constant speed, then the cost function given in (15) of the NBV planner becomes ineffective. Here, we solve (P-ii) by using the number of nodes between the subject node and the root node as the path cost instead of (15). Together with the new path cost and the information gain, the new gain function for RRT nodes to determine the best branch in Algorithm 3 in steps 21 and 23 is constructed as follows:
- For (P-iii), we propose updating to dynamically change the path cost within (26) while is being generated or updated. This allows the QABV planner to reduce the distance traveled while maintaining map coverage as follows:
- ○
- When there are many areas to explore nearby the drone, the information contribution of the nodes in increases. In this case, we increase λ to aggressively penalize long paths. This increases the focus of the drone to explore nearby information-rich areas. Additionally, the distance traveled reduces since closer paths are being followed.
- ○
- The information contribution of the nodes diminishes while the nearby areas are being explored. In this case, the drone should exit the area, but aggressive path cost prevents further exploration and causes the drone to get stuck. We decrease λ to prevent this situation so that the drone can reach information-rich areas at longer distances.
3.2.1. λ Update Method 1: On–Off Controller Approach
| Algorithm 4. Method 1: On–off controller |
| 1: ) 2: if 3: 4: if 5: 6: else 7: 8: end if 9: else 10: 11: end if 12: return |
3.2.2. λ Update Method 2: PD Controller Approach
- If the value of R is too big, then λ may become saturated at later stages of the map generation process. Because when the stop criterion is close to being met, there will be limited information available in the environment, so the drone may not be able to collect enough information and the PD controller keeps decreasing λ to elevate to a big R value until λ saturates.
- If R is too small, then the PD controller may increase λ excessively at the first stages of the map generation process. Because in the beginning, there is plenty of information to gather from the environment, and information gain is at its highest point, this situation can slow down the exploration process and even make the drone get stuck in the early stages.
| Algorithm 5. Method 2: PD controller |
| 1: ) 2: if 3: calculate using (36) 4: 5: 6: 7: if 8: 9: end if 10: else 11: 12: end if 13: return |
3.2.3. λ Update Method 3: Switching Controller Approach
- When , the proportional action in the forward loop is activated to update λ using (35). Because when is small, only derivative action cannot decrease λ fast enough, and the drone gets stuck in the information-poor area. The proportional action solves this problem by reducing λ proportionally to the magnitude of E.
- When , the proportional action is deactivated. Because, in this case, map exploration and accuracy will increase beyond the desired level, therefore, only a derivative action updates λ to allow extra information and stabilize as follows:
| Algorithm 6. Method 3: Switching controller |
| 1: ) 2: if 3: calculate using (36) 4: initialize with zero 5: if 6: 7: end if 8: 9: 10: if 11: 12: end if 13: else 14: 15: end if 16: return |
3.2.4. λ Update Method 4: 2 DOF PD Controller Approach
- In the first planning iterations, the drone can gather maximum information from the environment as there is no prior information on the map and is zero. That is why we prefer a big value in the first planning iteration and set it to , which is equal to the value of in the first planning iteration.
- As we progress through the planning iterations and represent the gathered information on the map, increases. As a result, available information in the environment becomes limited; therefore, we gradually decrease until it reaches its minimum value, , towards the end of the map generation process.
| Algorithm 7. Method 4: 2 DOF PD controller |
| 1: 2: if 3: calculate using (36) 4: + 5: 6: 7: 8: if 9: 10: end if 11: else 12: 13: end if 14: return |
4. Comparative Performance Analysis
- Map exploration as defined in (13);
- Map accuracy as defined in (14);
- Distance traveled to indicate the path length followed by the drone during the execution of Algorithm 1.
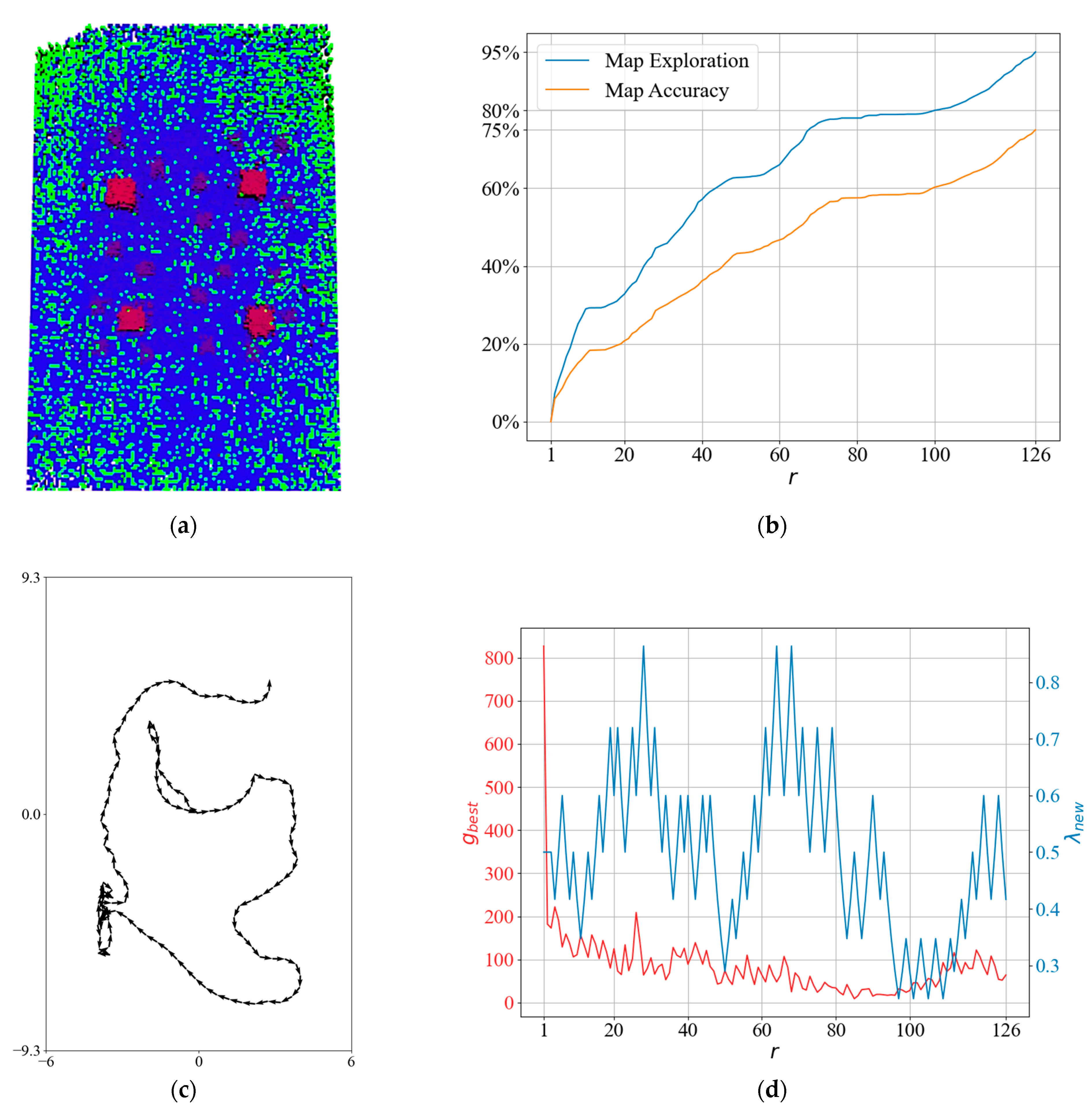
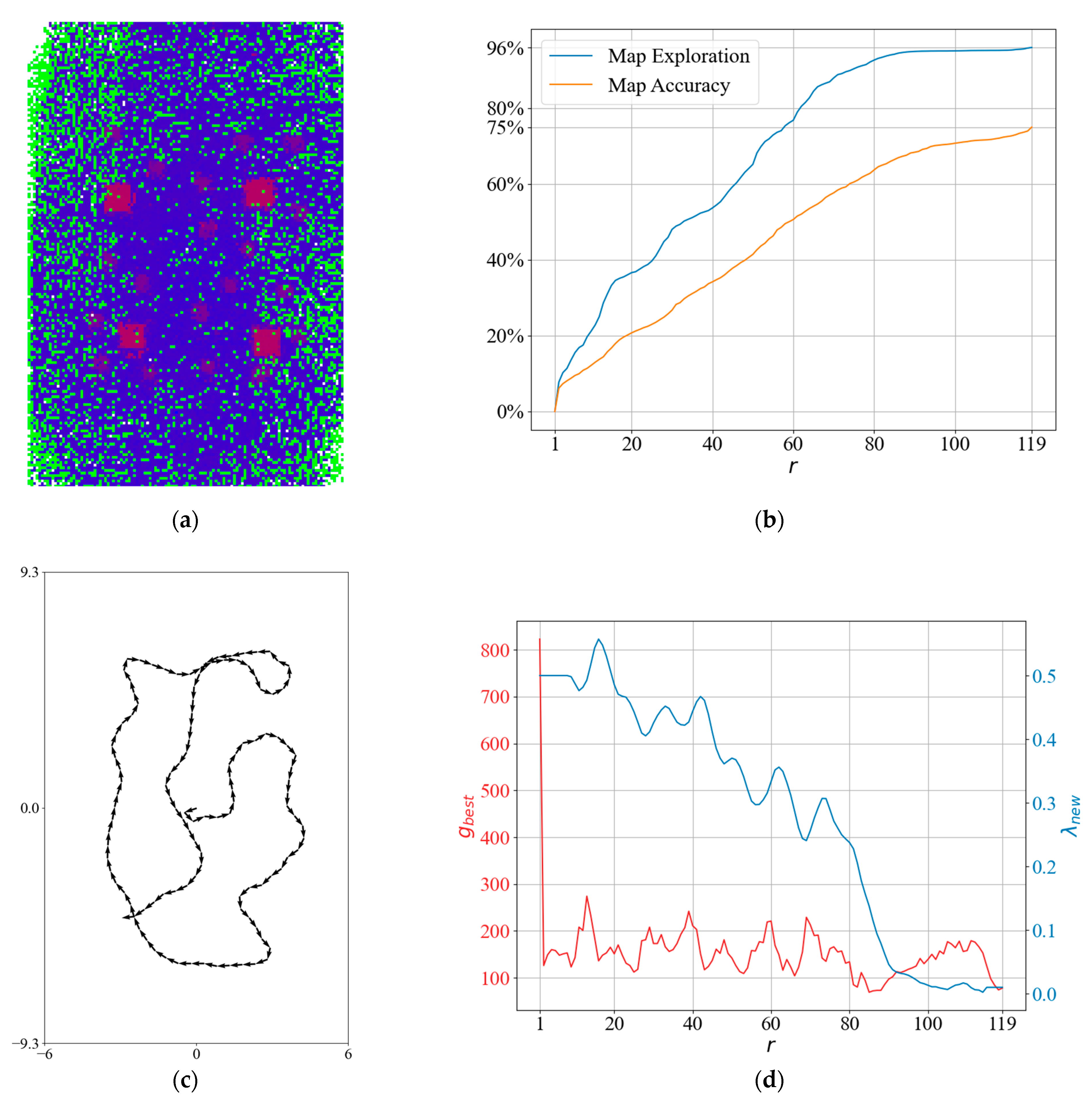
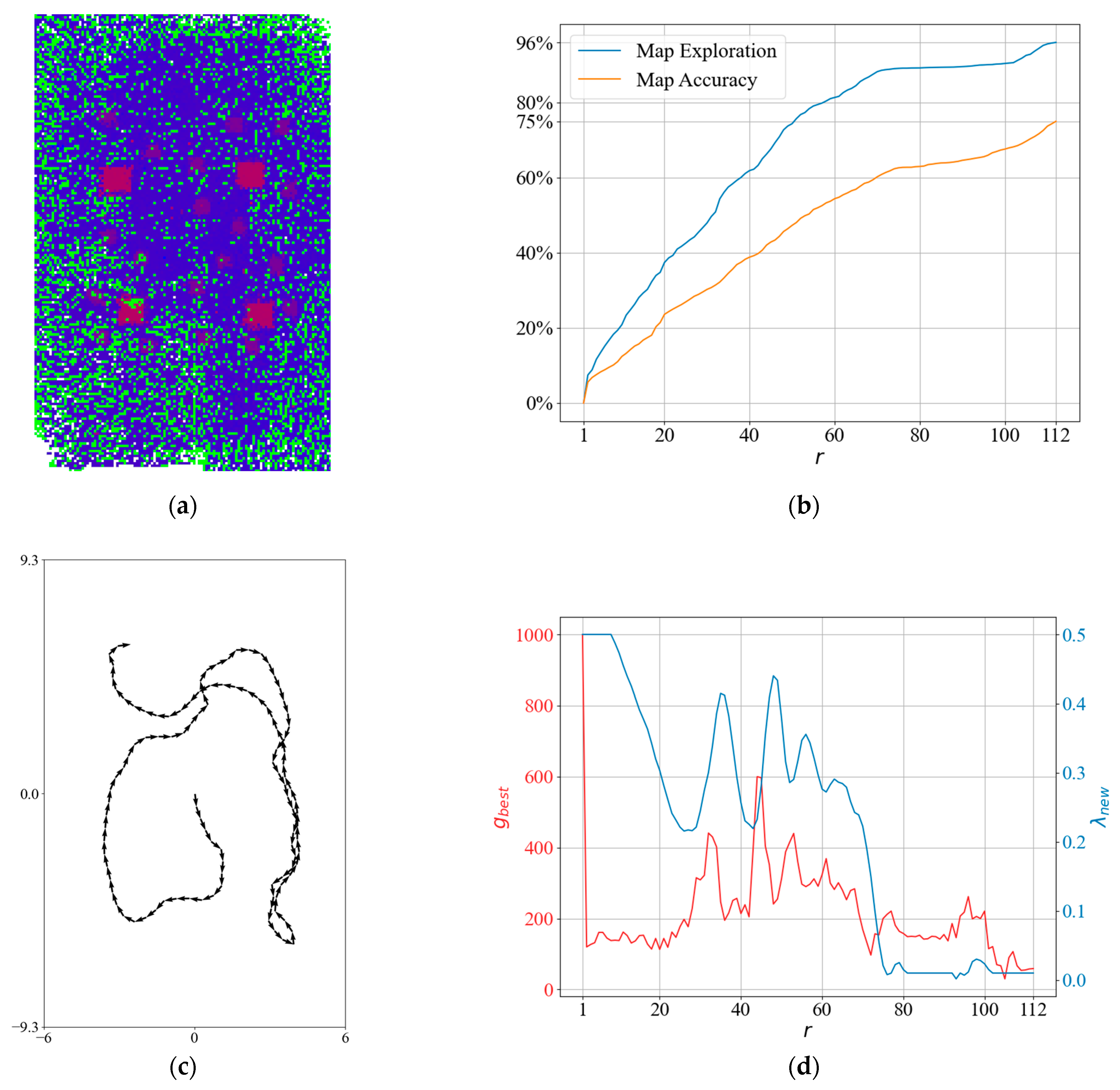
4.1. NBV Planner Results
4.2. QABV-1 Planner Results
4.3. QABV-2 Planner Results
4.4. QABV-3 Planner Results
4.5. QABV-4 Planner Results
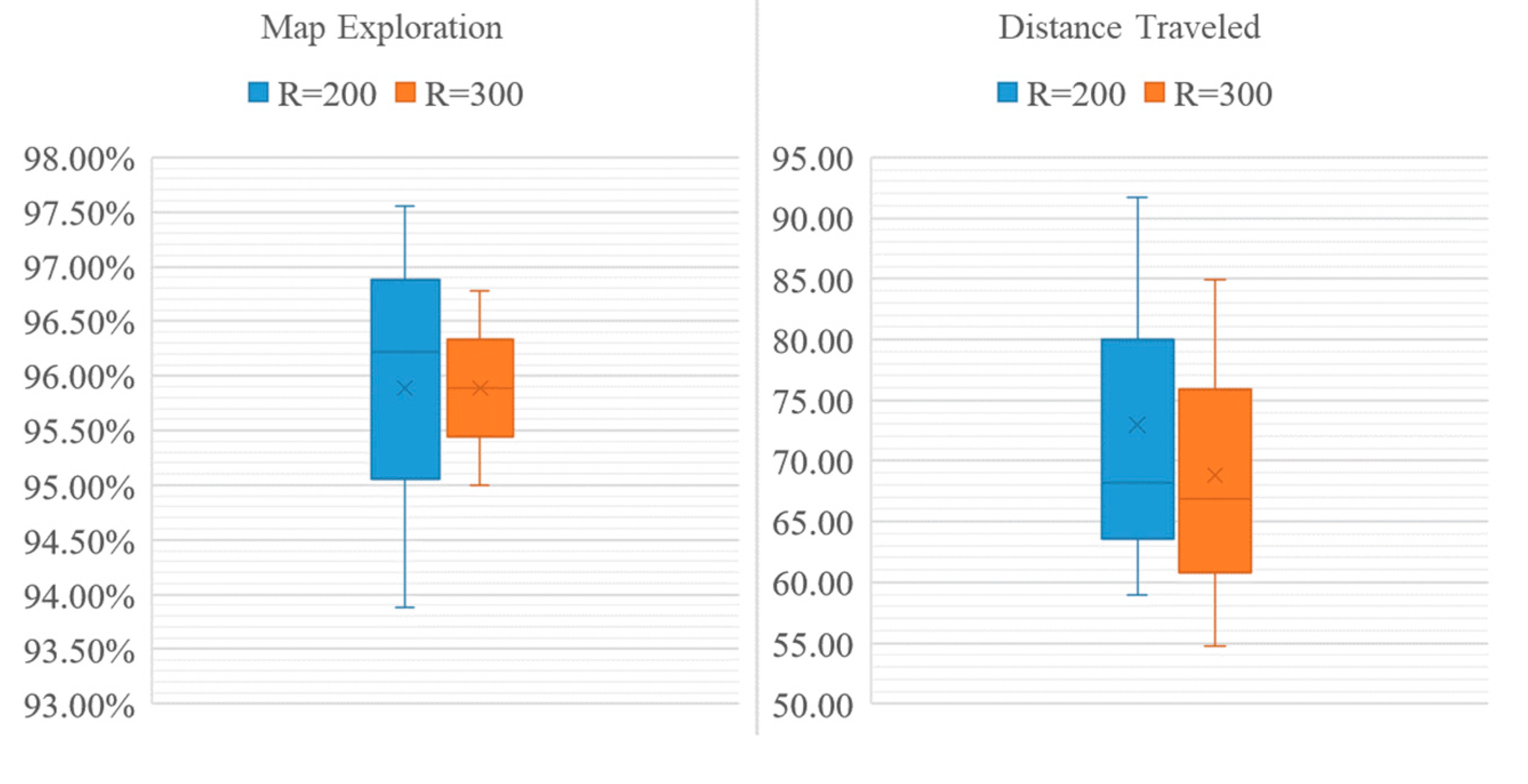
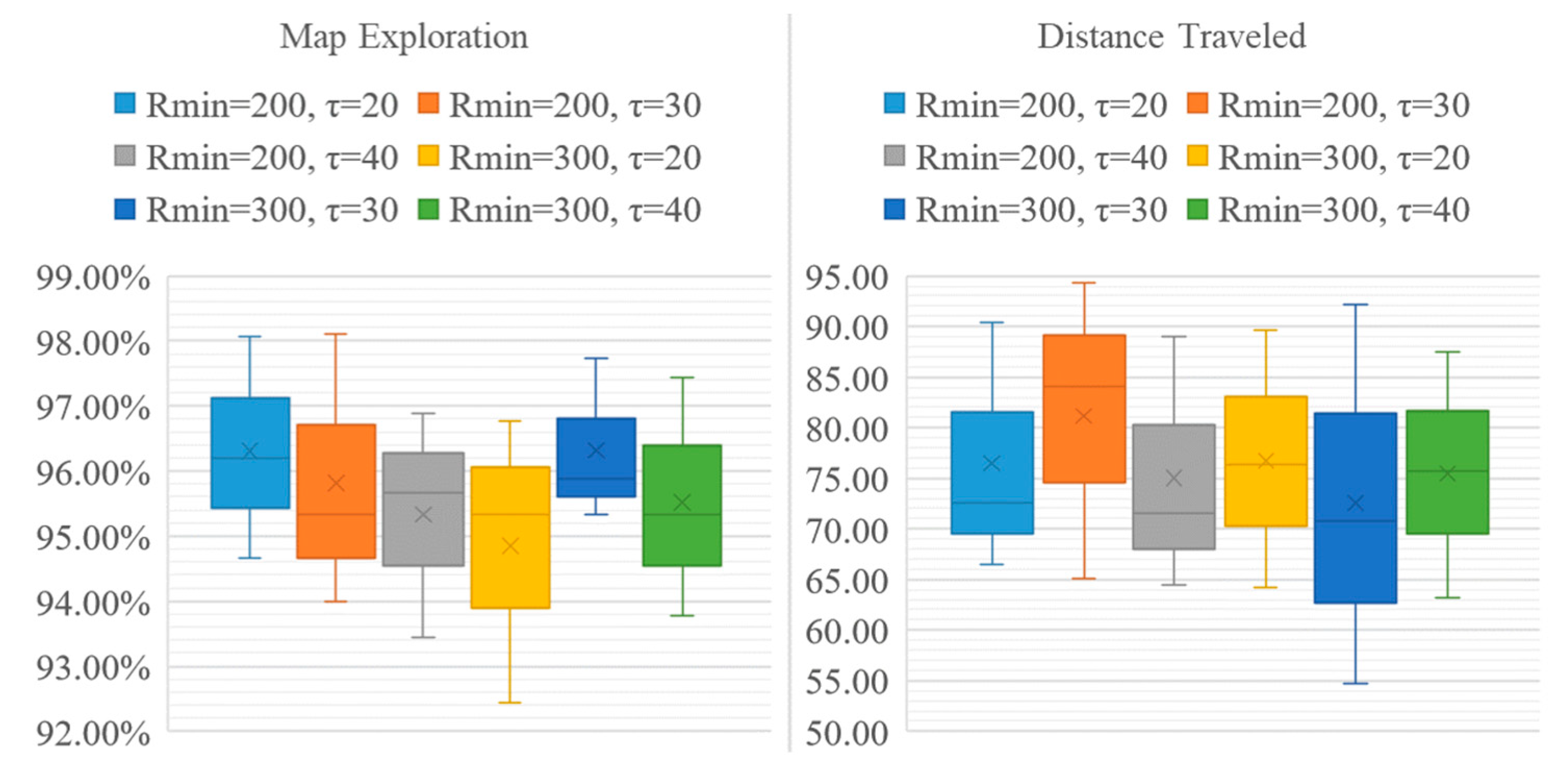
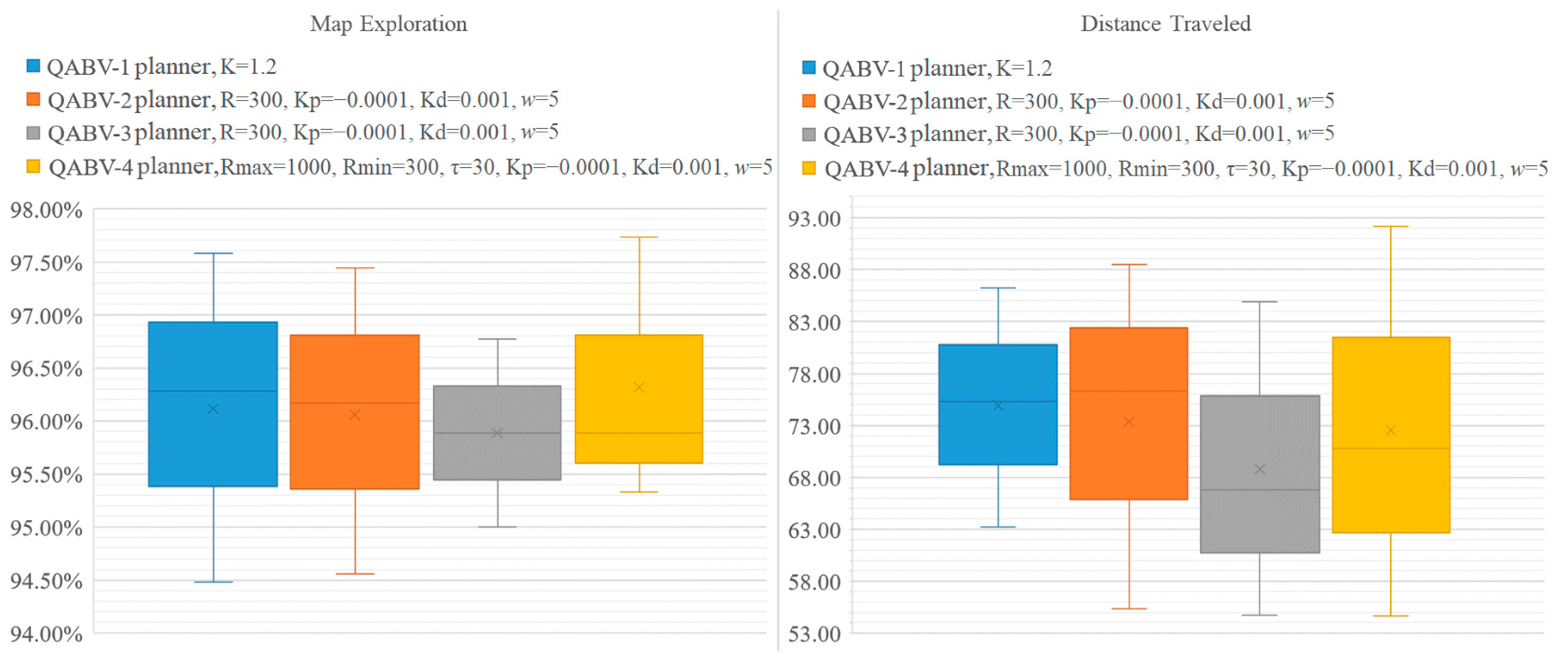
4.6. Overall Performance Comparison
- QABV-1 when ;
- QABV-2 when ;
- QABV-3 when ;
- QABV-4 when .
- 20.28% less distance traveled using QABV-1;
- 30.19% less distance traveled using QABV-2;
- 31% less distance traveled using QABV-3;
- 31.02% less distance traveled using QABV-4;
- 5% less distance traveled using QABV-1;
- 3.72% less distance traveled using QABV-2;
- 15.69% less distance traveled using QABV-3;
- 10.76% less distance traveled using QABV-4;
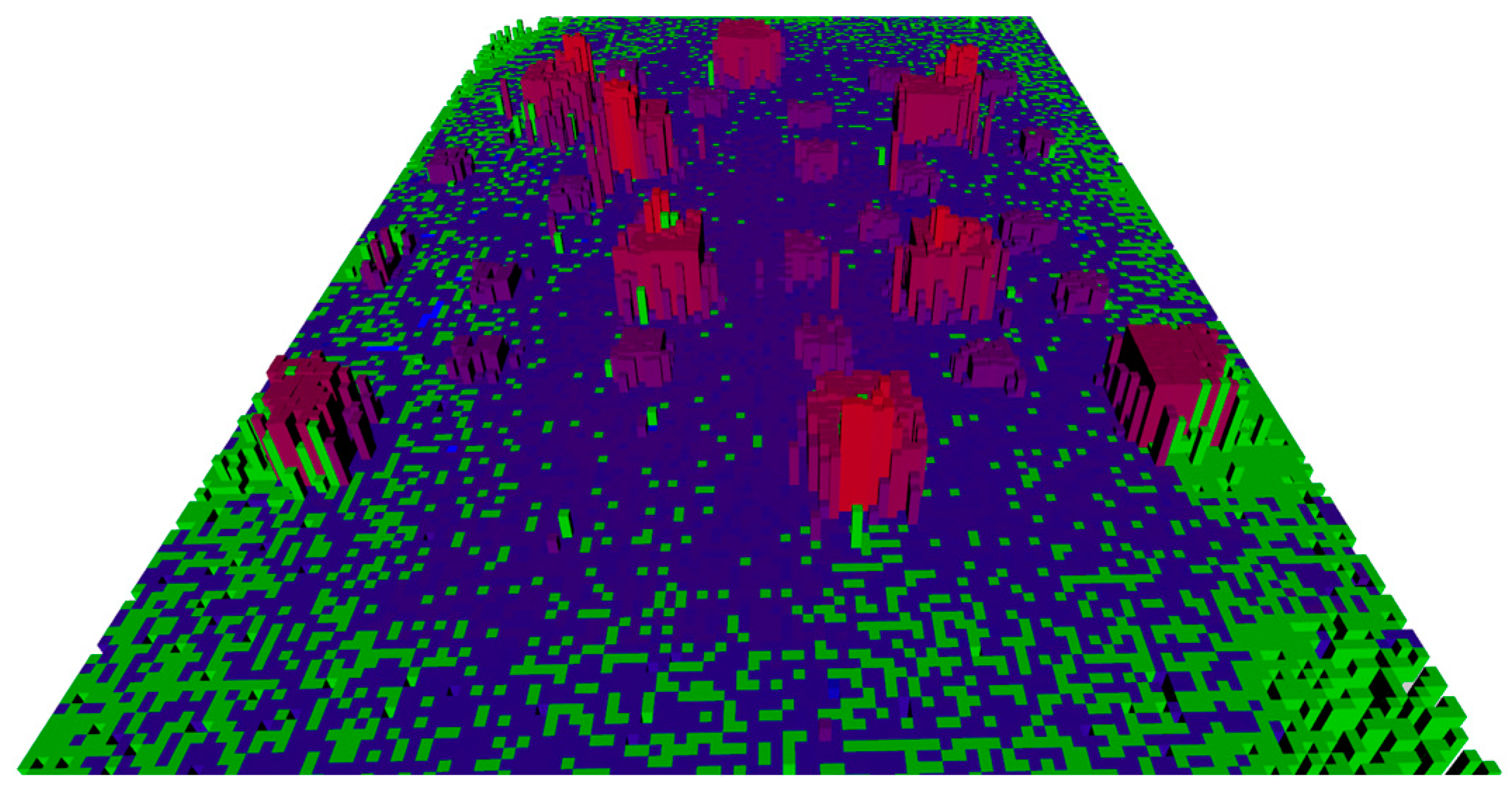
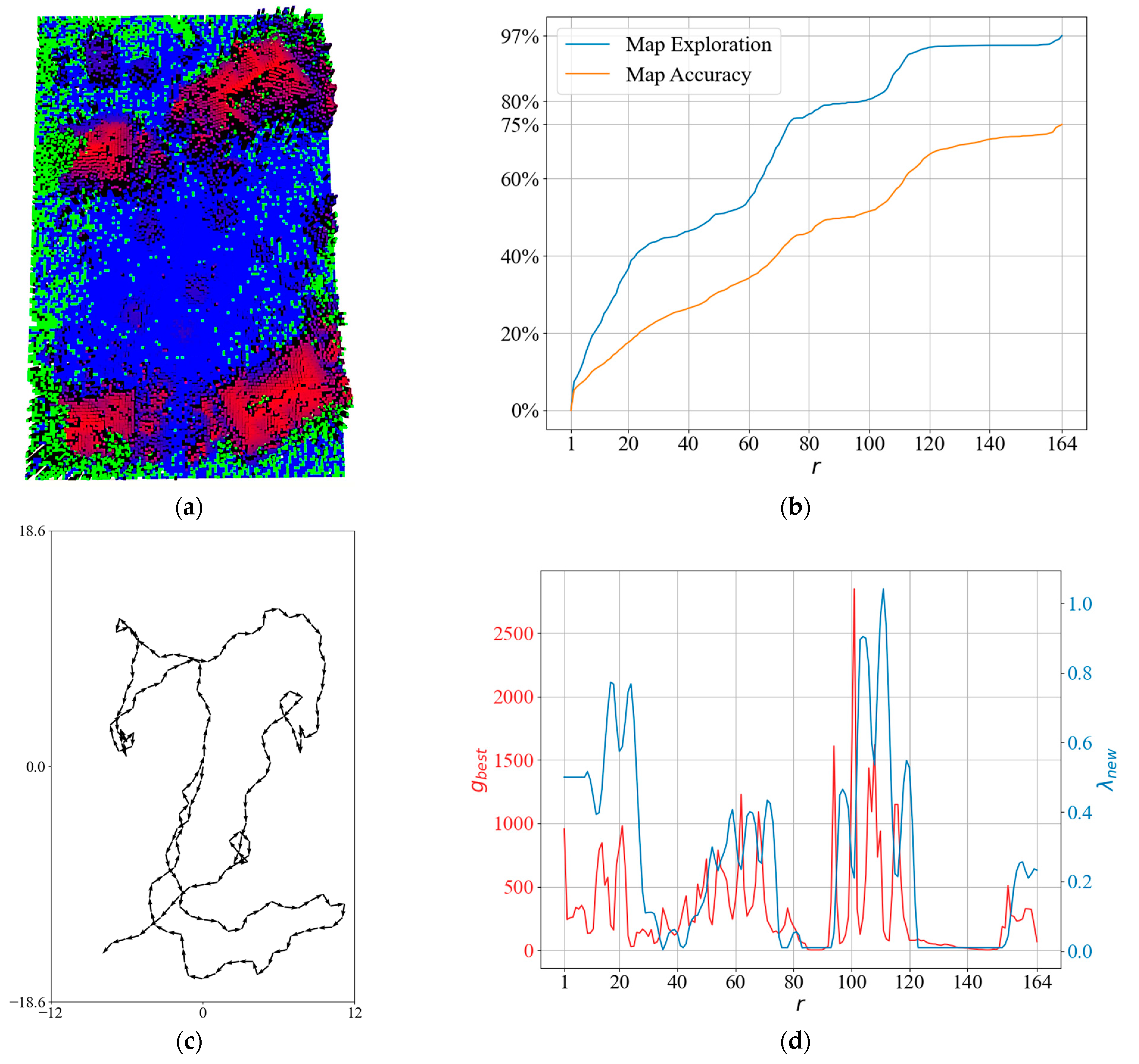
5. A Real-World Scenario
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, S.; Han, Y.; Chen, J.; Zhang, Z.; Wang, G.; Du, N. A Deep-Learning-Based Sea Search and Rescue Algorithm by UAV Remote Sensing. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; IEEE: New York, NY, USA, 2018; pp. 1–5. [Google Scholar]
- Wang, C.; Liu, P.; Zhang, T.; Sun, J. The Adaptive Vortex Search Algorithm of Optimal Path Planning for Forest Fire Rescue UAV. In Proceedings of the 2018 IEEE 3rd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 October 2018; IEEE: New York, NY, USA, 2018; pp. 400–403. [Google Scholar]
- Chen, S.; Meng, W.; Xu, W.; Liu, Z.; Liu, J.; Wu, F. A Warehouse Management System with UAV Based on Digital Twin and 5G Technologies. In Proceedings of the 2020 7th International Conference on Information, Cybernetics, and Computational Social Systems (ICCSS), Guangzhou, China, 13–15 November 2020; IEEE: New York, NY, USA, 2020; pp. 864–869. [Google Scholar]
- Liu, H.; Chen, Q.; Pan, N.; Sun, Y.; An, Y.; Pan, D. UAV Stocktaking Task-Planning for Industrial Warehouses Based on the Improved Hybrid Differential Evolution Algorithm. IEEE Trans. Ind. Inform. 2021, 18, 582–591. [Google Scholar] [CrossRef]
- Masmoudi, N.; Jaafar, W.; Cherif, S.; Abderrazak, J.B.; Yanikomeroglu, H. UAV-Based Crowd Surveillance in Post COVID-19 Era. IEEE Access 2021, 9, 162276–162290. [Google Scholar] [CrossRef]
- Song, H.; Yoo, W.-S.; Zatar, W. Interactive Bridge Inspection Research Using Drone. In Proceedings of the 2022 IEEE 46th Annual Computers, Software, and Applications Conference (COMPSAC), Alamitos, CA, USA, 27 June–1 July 2022; IEEE: New York, NY, USA, 2022; pp. 1002–1005. [Google Scholar]
- Worakuldumrongdej, P.; Maneewam, T.; Ruangwiset, A. Rice Seed Sowing Drone for Agriculture. In Proceedings of the 2019 19th International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 15–18 October 2019; IEEE: New York, NY, USA, 2019; pp. 980–985. [Google Scholar]
- Raivi, A.M.; Huda, S.M.A.; Alam, M.M.; Moh, S. Drone Routing for Drone-Based Delivery Systems: A Review of Trajectory Planning, Charging, and Security. Sensors 2023, 23, 1463. [Google Scholar] [CrossRef] [PubMed]
- PX4 Autopilot. Available online: https://px4.io/ (accessed on 19 February 2023).
- ArduPilot. Available online: https://ardupilot.org/copter (accessed on 19 February 2023).
- Johnson, A.E.; Klumpp, A.R.; Collier, J.B.; Wolf, A.A. Lidar-Based Hazard Avoidance for Safe Landing on Mars. J. Guid. Control. Dyn. 2002, 25, 1091–1099. [Google Scholar] [CrossRef]
- Scherer, S.; Chamberlain, L.; Singh, S. Autonomous Landing at Unprepared Sites by a Full-Scale Helicopter. Robot. Auton. Syst. 2012, 60, 1545–1562. [Google Scholar] [CrossRef]
- Templeton, T.; Shim, D.H.; Geyer, C.; Sastry, S.S. Autonomous Vision-Based Landing and Terrain Mapping Using an MPC-Controlled Unmanned Rotorcraft. In Proceedings of the Proceedings 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; IEEE: New York, NY, USA, 2007; pp. 1349–1356. [Google Scholar]
- Geyer, C.; Templeton, T.; Meingast, M.; Sastry, S.S. The Recursive Multi-Frame Planar Parallax Algorithm. In Proceedings of the Third International Symposium on 3D Data Processing, Visualization, and Transmission (3DPVT’06), Chapel Hill, NC, USA, 14–16 June 2006; IEEE: New York, NY, USA, 2006; pp. 17–24. [Google Scholar]
- Desaraju, V.R.; Michael, N.; Humenberger, M.; Brockers, R.; Weiss, S.; Nash, J.; Matthies, L. Vision-Based Landing Site Evaluation and Informed Optimal Trajectory Generation toward Autonomous Rooftop Landing. Auton. Robot. 2015, 39, 445–463. [Google Scholar] [CrossRef]
- Yang, T.; Li, P.; Zhang, H.; Li, J.; Li, Z. Monocular Vision SLAM-Based UAV Autonomous Landing in Emergencies and Unknown Environments. Electronics 2018, 7, 73. [Google Scholar] [CrossRef]
- Forster, C.; Faessler, M.; Fontana, F.; Werlberger, M.; Scaramuzza, D. Continuous On-Board Monocular-Vision-Based Elevation Mapping Applied to Autonomous Landing of Micro Aerial Vehicles. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; IEEE: New York, NY, USA, 2015; pp. 111–118. [Google Scholar]
- Forster, C.; Pizzoli, M.; Scaramuzza, D. SVO: Fast Semi-Direct Monocular Visual Odometry. In Proceedings of the 2014 IEEE international conference on robotics and automation (ICRA), Hong Kong, China, 31 May–5 June 2014; IEEE: New York, NY, USA, 2014; pp. 15–22. [Google Scholar]
- Delmerico, J.; Scaramuzza, D. A Benchmark Comparison of Monocular Visual-Inertial Odometry Algorithms for Flying Robots. In Proceedings of the 2018 IEEE international conference on robotics and automation (ICRA), Brisbane, Australia, 21–26 May 2018; IEEE: New York, NY, USA, 2018; pp. 2502–2509. [Google Scholar]
- Bircher, A.; Kamel, M.; Alexis, K.; Oleynikova, H.; Siegwart, R. Receding Horizon"next-Best-View" Planner for 3d Exploration. In Proceedings of the 2016 IEEE international conference on robotics and automation (ICRA), Stockholm, Sweden, 16–20 May 2016; IEEE: New York, NY, USA, 2016; pp. 1462–1468. [Google Scholar]
- Schmid, L.; Pantic, M.; Khanna, R.; Ott, L.; Siegwart, R.; Nieto, J. An Efficient Sampling-Based Method for Online Informative Path Planning in Unknown Environments. IEEE Robot. Autom. Lett. 2020, 5, 1500–1507. [Google Scholar] [CrossRef]
- Selin, M.; Tiger, M.; Duberg, D.; Heintz, F.; Jensfelt, P. Efficient Autonomous Exploration Planning of Large-Scale 3-d Environments. IEEE Robot. Autom. Lett. 2019, 4, 1699–1706. [Google Scholar] [CrossRef]
- Mittal, M.; Mohan, R.; Burgard, W.; Valada, A. Vision-Based Autonomous UAV Navigation and Landing for Urban Search and Rescue. In Proceedings of the Robotics Research: The 19th International Symposium ISRR, Hanoi, Vietnam, 6–10 October 2019; Springer: Cham, Switzerland, 2022; pp. 575–592. [Google Scholar]
- Zhang, Z.; Scaramuzza, D. Perception-Aware Receding Horizon Navigation for MAVs. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–26 May 2018; IEEE: New York, NY, USA, 2018; pp. 2534–2541. [Google Scholar]
- Davison, A.J.; Murray, D.W. Simultaneous Localization and Map-Building Using Active Vision. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 865–880. [Google Scholar] [CrossRef]
- Mueller, M.W.; Hehn, M.; D’Andrea, R. A Computationally Efficient Algorithm for State-to-State Quadrocopter Trajectory Generation and Feasibility Verification. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; IEEE: New York, NY, USA, 2013; pp. 3480–3486. [Google Scholar]
- LaValle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning. Annu. Res. Rep. 1998. [Google Scholar]
- Karaman, S.; Frazzoli, E. Sampling-Based Algorithms for Optimal Motion Planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Yamauchi, B. A Frontier-Based Approach for Autonomous Exploration. In Proceedings of the 1997 IEEE International Symposium on Computational Intelligence in Robotics and Automation CIRA’97.’Towards New Computational Principles for Robotics and Automation, Monterey, CA, USA, 10–11 July 1997; IEEE: New York, NY, USA, 1997; pp. 146–151. [Google Scholar]
- Pizzoli, M.; Forster, C.; Scaramuzza, D. REMODE: Probabilistic, Monocular Dense Reconstruction in Real Time. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–5 June 2014; IEEE: New York, NY, USA, 2014; pp. 2609–2616. [Google Scholar]
- Hornung, A.; Wurm, K.M.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: An Efficient Probabilistic 3D Mapping Framework Based on Octrees. Auton. Robot. 2013, 34, 189–206. [Google Scholar] [CrossRef]
- Ogata, K. Two-Position or On–Off Control Action. In Modern Control Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2010; Volume 5, pp. 22–23. [Google Scholar]
- Ogata, K. PI-D Control. In Modern Control Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2010; Volume 5, pp. 590–591. [Google Scholar]
- Gazebo. Available online: https://gazebosim.org/home (accessed on 22 February 2023).
- System Identification Toolbox. Available online: https://nl.mathworks.com/products/sysid.html (accessed on 22 February 2023).











| Drone Specifications | |
|---|---|
| Motor-to-motor dimension | 550 mm |
| Height | 100 mm |
| Weight (with battery) | 1282 g |
| Propellers | (2) 10 × 4.7 normal-rotation (2) 10 × 4.7 reverse-rotation |
| Motors | AC 2830, 850 kV |
| Camera Specifications | |
| Image width | 752 pixels |
| Image height | 480 pixels |
| Image format | Black and white |
| Horizontal FOV | 115 degrees |
| Update rate | 20 Hz |
| Simulation Environment Apecifications for Rendering | |
| Near clip plane | 0.05 |
| Far clip plane | 15,000 |
| Performance Criteria | Map 1 | Map 2 | Map 3 | Average |
|---|---|---|---|---|
| Map Exploration (%) | 95.00 | 95.00 | 95.00 | 95.00 |
| Map Accuracy (%) | 72.00 | 73.00 | 77.70 | 74.20 |
| Distance Traveled (m) | 82.60 | 73.50 | 81.76 | 79.29 |
| Performance Criteria | Map 1 | Map 2 | Map 3 | Average | |
|---|---|---|---|---|---|
| Map Accuracy 75% | Map Exploration (%) | 96.60 | 93.60 | 93.25 | 94.48 |
| Distance Traveled (m) | 68.03 | 64.45 | 57.15 | 63.21 | |
| Map Accuracy 80% | Map Exploration (%) | 96.80 | 96.80 | 95.25 | 96.28 |
| Distance Traveled (m) | 87.00 | 71.94 | 67.06 | 75.33 | |
| Map Accuracy 85% | Map Exploration (%) | 98.50 | 97.75 | 96.50 | 97.58 |
| Distance Traveled (m) | 101.48 | 83.85 | 73.35 | 86.23 | |
| Performance Criteria | Map 1 | Map 2 | Map 3 | Average | |
|---|---|---|---|---|---|
| Map Accuracy 75% | Map Exploration (%) | 95.00 | 93.33 | 91.66 | 93.33 |
| Distance Traveled (m) | 63.59 | 68.13 | 68.28 | 66.67 | |
| Map Accuracy 80% | Map Exploration (%) | 97.20 | 97.00 | 95.50 | 96.57 |
| Distance Traveled (m) | 81.55 | 73.15 | 73.00 | 75.90 | |
| Map Accuracy 85% | Map Exploration (%) | 98.60 | 98.00 | 97.66 | 98.09 |
| Distance Traveled (m) | 91.50 | 94.37 | 77.15 | 87.67 | |
| Performance Criteria | Map 1 | Map 2 | Map 3 | Average | |
|---|---|---|---|---|---|
| Map Accuracy 75% | Map Exploration (%) | 95.00 | 94.80 | 89.00 | 92.93 |
| Distance Traveled (m) | 82.8 | 59.21 | 59.69 | 67.23 | |
| Map Accuracy 80% | Map Exploration (%) | 97.20 | 95.00 | 95.33 | 95.84 |
| Distance Traveled (m) | 95.24 | 74.00 | 69.70 | 79.65 | |
| Map Accuracy 85% | Map Exploration (%) | 98.60 | 97.25 | 97.00 | 97.62 |
| Distance Traveled (m) | 119.55 | 85.29 | 87.82 | 97.55 | |
| Performance Criteria | Map 1 | Map 2 | Map 3 | Average | |
|---|---|---|---|---|---|
| Map Accuracy 75% | Map Exploration (%) | 95.67 | 93.33 | 91.66 | 93.55 |
| Distance Traveled (m) | 62.81 | 65.27 | 59.12 | 62.40 | |
| Map Accuracy 80% | Map Exploration (%) | 97.33 | 94.66 | 94.66 | 95.55 |
| Distance Traveled (m) | 75.56 | 79.75 | 71.65 | 75.65 | |
| Map Accuracy 85% | Map Exploration (%) | 98.00 | 98.66 | 96.00 | 97.55 |
| Distance Traveled (m) | 102.5 | 84.18 | 83.08 | 89.92 | |
| Performance Criteria | Map 1 | Map 2 | Map 3 | Average | |
|---|---|---|---|---|---|
| Map Accuracy 75% | Map Exploration (%) | 95.67 | 94.33 | 93.67 | 94.56 |
| Distance Traveled (m) | 57.45 | 56.00 | 52.61 | 55.35 | |
| Map Accuracy 80% | Map Exploration (%) | 97.00 | 96.50 | 95.00 | 96.17 |
| Distance Traveled (m) | 73.79 | 77.13 | 78.10 | 76.34 | |
| Map Accuracy 85% | Map Exploration (%) | 97.67 | 98.00 | 96.67 | 97.45 |
| Distance Traveled (m) | 93.18 | 80.66 | 91.55 | 88.46 | |
| Performance Criteria | Map 1 | Map 2 | Map 3 | Average | |
|---|---|---|---|---|---|
| Map Accuracy 75% | Map Exploration (%) | 94.00 | 94.66 | 93.00 | 93.89 |
| Distance Traveled (m) | 68.41 | 54.86 | 53.62 | 58.96 | |
| Map Accuracy 80% | Map Exploration (%) | 97.33 | 96.00 | 95.33 | 96.22 |
| Distance Traveled (m) | 75.18 | 66.16 | 63.27 | 68.20 | |
| Map Accuracy 85% | Map Exploration (%) | 97.33 | 97.33 | 98.00 | 97.55 |
| Distance Traveled (m) | 89.76 | 95.88 | 89.62 | 91.75 | |
| Performance Criteria | Map 1 | Map 2 | Map 3 | Average | |
|---|---|---|---|---|---|
| Map Accuracy 75% | Map Exploration (%) | 96.00 | 95.00 | 94.00 | 95.00 |
| Distance Traveled (m) | 55.30 | 52.12 | 56.70 | 54.71 | |
| Map Accuracy 80% | Map Exploration (%) | 97.00 | 96.33 | 94.33 | 95.89 |
| Distance Traveled (m) | 66.46 | 62.78 | 71.31 | 66.85 | |
| Map Accuracy 85% | Map Exploration (%) | 97.66 | 96.66 | 96.00 | 96.77 |
| Distance Traveled (m) | 77.90 | 87.43 | 89.42 | 84.92 | |
| Decay Constant | Performance Criteria | Map 1 | Map 2 | Map 3 | Average | |
|---|---|---|---|---|---|---|
| τ = 20 | Map Accuracy 75% | Map Exploration (%) | 95.00 | 94.00 | 95.00 | 94.67 |
| Distance Traveled (m) | 71.99 | 64.82 | 62.52 | 66.44 | ||
| Map Accuracy 80% | Map Exploration (%) | 96.60 | 96.00 | 96.00 | 96.20 | |
| Distance Traveled (m) | 73.53 | 72.56 | 71.67 | 72.59 | ||
| Map Accuracy 85% | Map Exploration (%) | 98.00 | 98.60 | 97.60 | 98.07 | |
| Distance Traveled (m) | 95.78 | 88.61 | 86.86 | 90.42 | ||
| τ = 30 | Map Accuracy 75% | Map Exploration (%) | 93.66 | 93.00 | 95.33 | 94.00 |
| Distance Traveled (m) | 67.87 | 64.78 | 62.52 | 65.06 | ||
| Map Accuracy 80% | Map Exploration (%) | 96.00 | 93.66 | 96.33 | 95.33 | |
| Distance Traveled (m) | 92.26 | 88.13 | 71.67 | 84.02 | ||
| Map Accuracy 85% | Map Exploration (%) | 98.33 | 98.33 | 97.66 | 98.11 | |
| Distance Traveled (m) | 96.18 | 100.1 | 86.86 | 94.38 | ||
| τ = 40 | Map Accuracy 75% | Map Exploration (%) | 95.66 | 93.33 | 91.33 | 93.44 |
| Distance Traveled (m) | 69.37 | 60.07 | 64.12 | 64.52 | ||
| Map Accuracy 80% | Map Exploration (%) | 95.66 | 96.33 | 95.00 | 95.66 | |
| Distance Traveled (m) | 72.24 | 70.76 | 71.56 | 71.52 | ||
| Map Accuracy 85% | Map Exploration (%) | 97.33 | 97.66 | 95.66 | 96.88 | |
| Distance Traveled (m) | 94.74 | 86.67 | 85.76 | 89.06 | ||
| Decay Constant | Performance Criteria | Map 1 | Map 2 | Map 3 | Average | |
|---|---|---|---|---|---|---|
| τ = 20 | Map Accuracy 75% | Map Exploration (%) | 93.00 | 92.33 | 92.00 | 92.44 |
| Distance Traveled (m) | 70.36 | 62.40 | 60.00 | 64.25 | ||
| Map Accuracy 80% | Map Exploration (%) | 96.00 | 96.33 | 93.66 | 95.33 | |
| Distance Traveled (m) | 80.94 | 78.72 | 69.45 | 76.37 | ||
| Map Accuracy 85% | Map Exploration (%) | 97.33 | 97.00 | 96.00 | 96.78 | |
| Distance Traveled (m) | 93.29 | 97.04 | 78.58 | 89.64 | ||
| τ = 30 | Map Accuracy 75% | Map Exploration (%) | 96.33 | 95.66 | 94.00 | 95.33 |
| Distance Traveled (m) | 50.39 | 56.61 | 57.08 | 54.69 | ||
| Map Accuracy 80% | Map Exploration (%) | 96.33 | 95.33 | 96.00 | 95.89 | |
| Distance Traveled (m) | 70.5 | 73.19 | 68.6 | 70.76 | ||
| Map Accuracy 85% | Map Exploration (%) | 98.00 | 98.20 | 97.00 | 97.73 | |
| Distance Traveled (m) | 107.6 | 92.61 | 76.35 | 92.19 | ||
| τ = 40 | Map Accuracy 75% | Map Exploration (%) | 94.33 | 94.00 | 93.00 | 93.70 |
| Distance Traveled (m) | 69.81 | 58.06 | 61.81 | 63.23 | ||
| Map Accuracy 80% | Map Exploration (%) | 96.00 | 95.00 | 95.00 | 95.33 | |
| Distance Traveled (m) | 78.95 | 78.71 | 69.51 | 75.72 | ||
| Map Accuracy 85% | Map Exploration (%) | 97.66 | 97.66 | 97.00 | 97.44 | |
| Distance Traveled (m) | 93.02 | 82.93 | 86.56 | 87.50 | ||
| Planner | Performance Criteria | Map 1 | Map 2 | Map 3 | Average |
|---|---|---|---|---|---|
| NBV planner | Map Accuracy (%) | 72.00 | 73.00 | 77.70 | 74.20 |
| Map Exploration (%) | 95.00 | 95.00 | 95.00 | 95.00 | |
| Distance Traveled (m) | 82.60 | 73.50 | 81.76 | 79.29 | |
| QABV-1 planner | Map Accuracy (%) | 75.00 | 75.00 | 75.00 | 75.00 |
| Map Exploration (%) | 96.60 | 93.60 | 93.25 | 94.48 | |
| Distance Traveled (m) | 68.03 | 64.45 | 57.15 | 63.21 | |
| QABV-2 planner | Map Accuracy (%) | 75.00 | 75.00 | 75.00 | 75.00 |
| Map Exploration (%) | 95.67 | 94.33 | 93.67 | 94.56 | |
| Distance Traveled (m) | 57.45 | 56.00 | 52.61 | 55.35 | |
| QABV-3 planner | Map Accuracy (%) | 75.00 | 75.00 | 75.00 | 75.00 |
| Map Exploration (%) | 96.00 | 95.00 | 94.00 | 95.00 | |
| Distance Traveled (m) | 55.30 | 52.12 | 56.70 | 54.71 | |
| QABV-4 planner | Map Accuracy (%) | 75.00 | 75.00 | 75.00 | 75.00 |
| Map Exploration (%) | 96.33 | 95.66 | 94.00 | 95.33 | |
| Distance Traveled (m) | 50.39 | 56.61 | 57.08 | 54.69 |
| Planner | Performance Criteria | Map 1 | Map 2 | Map 3 | Average | |
|---|---|---|---|---|---|---|
| QABV-1 planner | Map Accuracy 80% | Map Exploration (%) | 96.80 | 96.80 | 95.25 | 96.28 |
| Distance Traveled (m) | 87.00 | 71.94 | 67.06 | 75.33 | ||
| Map Accuracy 85% | Map Exploration (%) | 98.50 | 97.75 | 96.50 | 97.58 | |
| Distance Traveled (m) | 101.48 | 83.85 | 73.35 | 86.23 | ||
| QABV-2 planner | Map Accuracy 80% | Map Exploration (%) | 97.00 | 96.50 | 95.00 | 96.17 |
| Distance Traveled (m) | 73.79 | 77.13 | 78.10 | 76.34 | ||
| Map Accuracy 85% | Map Exploration (%) | 97.67 | 98.00 | 96.67 | 97.45 | |
| Distance Traveled (m) | 93.18 | 80.66 | 91.55 | 88.46 | ||
| QABV-3 planner | Map Accuracy 80% | Map Exploration (%) | 97.00 | 96.33 | 94.33 | 95.89 |
| Distance Traveled (m) | 66.46 | 62.78 | 71.31 | 66.85 | ||
| Map Accuracy 85% | Map Exploration (%) | 97.66 | 96.66 | 96.00 | 96.77 | |
| Distance Traveled (m) | 77.90 | 87.43 | 89.42 | 84.92 | ||
| QABV-4 planner | Map Accuracy 80% | Map Exploration (%) | 96.33 | 95.33 | 96.00 | 95.89 |
| Distance Traveled (m) | 70.5 | 73.19 | 68.6 | 70.76 | ||
| Map Accuracy 85% | Map Exploration (%) | 98.00 | 98.20 | 97.00 | 97.73 | |
| Distance Traveled (m) | 107.6 | 92.61 | 76.35 | 92.19 | ||
| Performance Criteria | NBV Planner | QABV-1 Planner | QABV-2 Planner | QABV-3 Planner | QABV-4 Planner |
|---|---|---|---|---|---|
| Map Exploration (%) | 95.00 | 95.00 | 95.50 | 95.50 | 95.50 |
| Map Accuracy (%) | 74.00 | 75.00 | 75.00 | 75.00 | 75.00 |
| Distance Traveled (m) | 276.34 | 216.41 | 205.90 | 200.88 | 203.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sözer, O.; Kumbasar, T. Quality-Aware Autonomous Navigation with Dynamic Path Cost for Vision-Based Mapping toward Drone Landing. Drones 2023, 7, 278. https://doi.org/10.3390/drones7040278
Sözer O, Kumbasar T. Quality-Aware Autonomous Navigation with Dynamic Path Cost for Vision-Based Mapping toward Drone Landing. Drones. 2023; 7(4):278. https://doi.org/10.3390/drones7040278
Chicago/Turabian StyleSözer, Onuralp, and Tufan Kumbasar. 2023. "Quality-Aware Autonomous Navigation with Dynamic Path Cost for Vision-Based Mapping toward Drone Landing" Drones 7, no. 4: 278. https://doi.org/10.3390/drones7040278
APA StyleSözer, O., & Kumbasar, T. (2023). Quality-Aware Autonomous Navigation with Dynamic Path Cost for Vision-Based Mapping toward Drone Landing. Drones, 7(4), 278. https://doi.org/10.3390/drones7040278






