GCP and PPK Utilization Plan to Deal with RTK Signal Interruption in RTK-UAV Photogrammetry
Abstract
1. Introduction
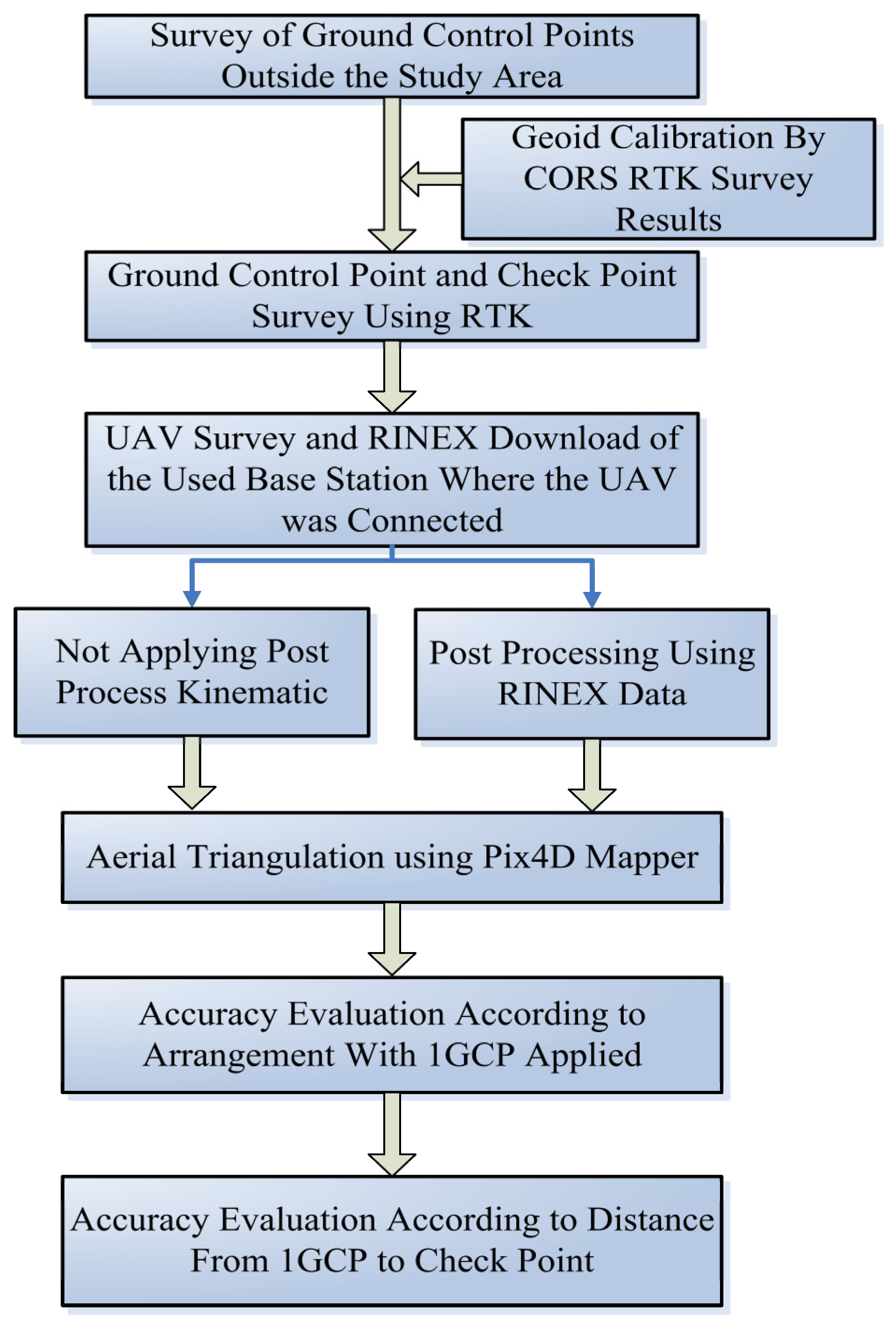
2. Data Acquisition and Experimental Method Setting
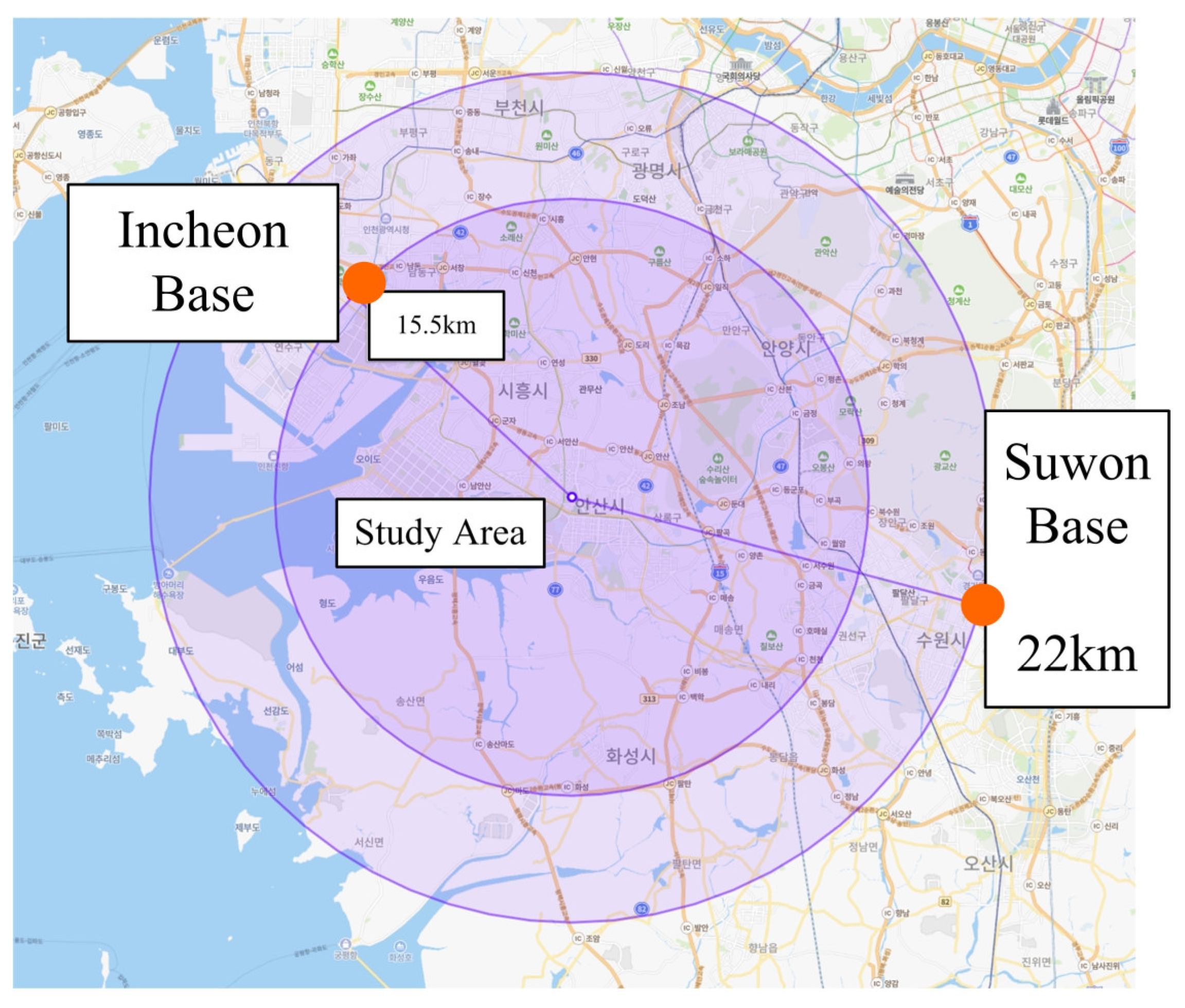
2.1. In Situ Geoid Model Calibration of Study Area
2.2. UAV Surveying and Internal Orientation
2.3. Post-Process Kinematics and Aerial Triangulation Relative Orientation
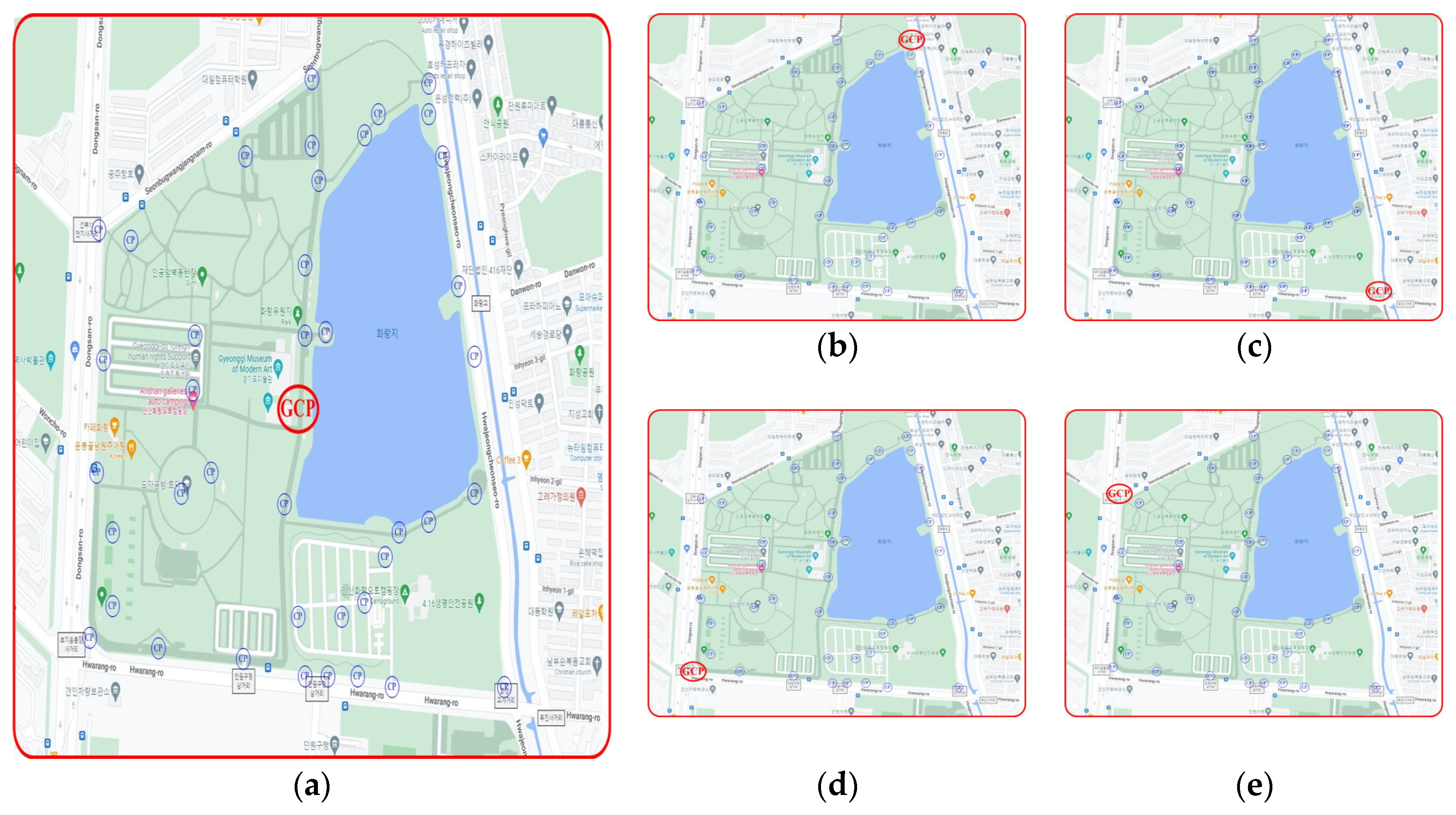
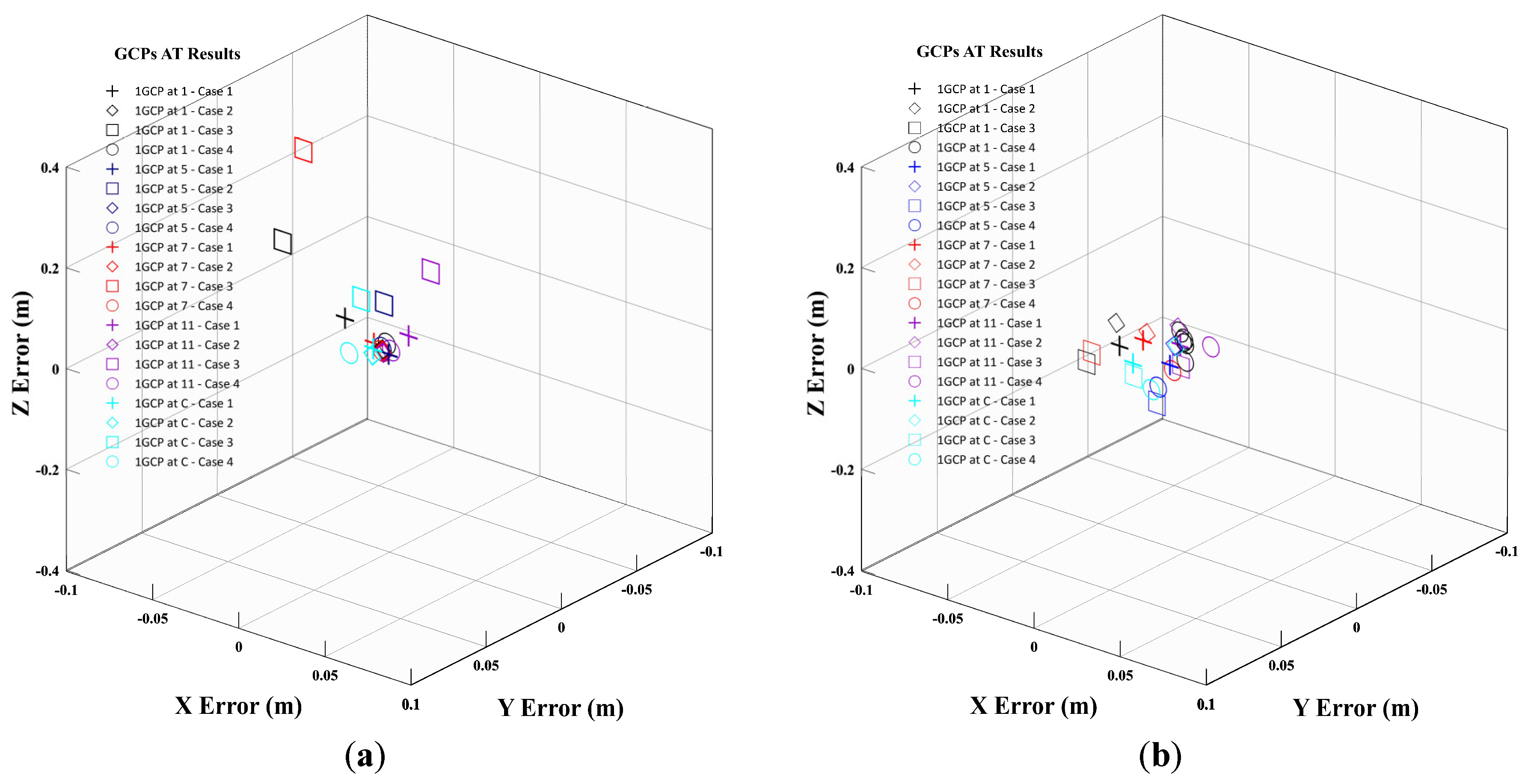
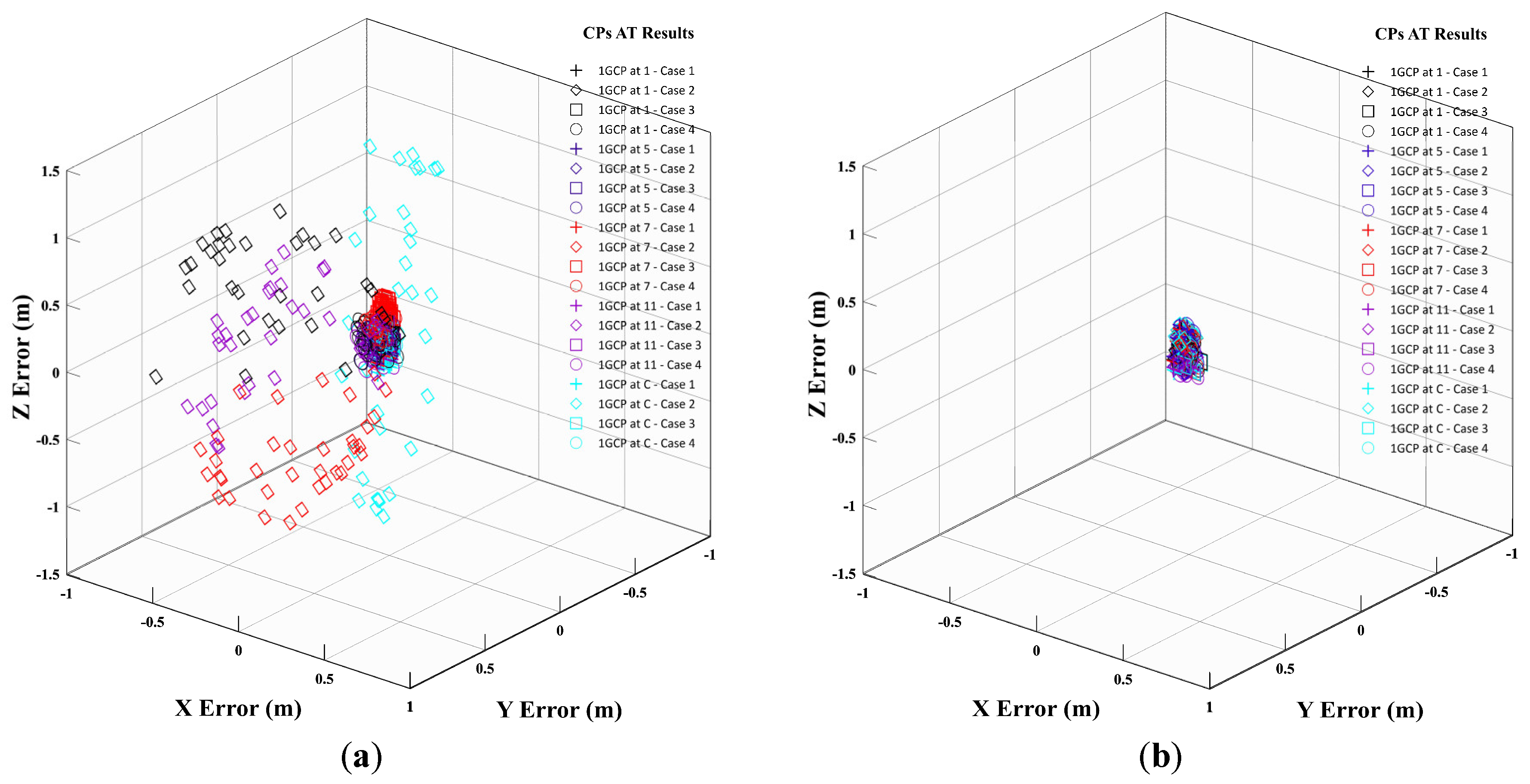
3. Evaluation of Aerial Triangulation Accuracy according to RTK Reception Rate and 1GCP Deployment
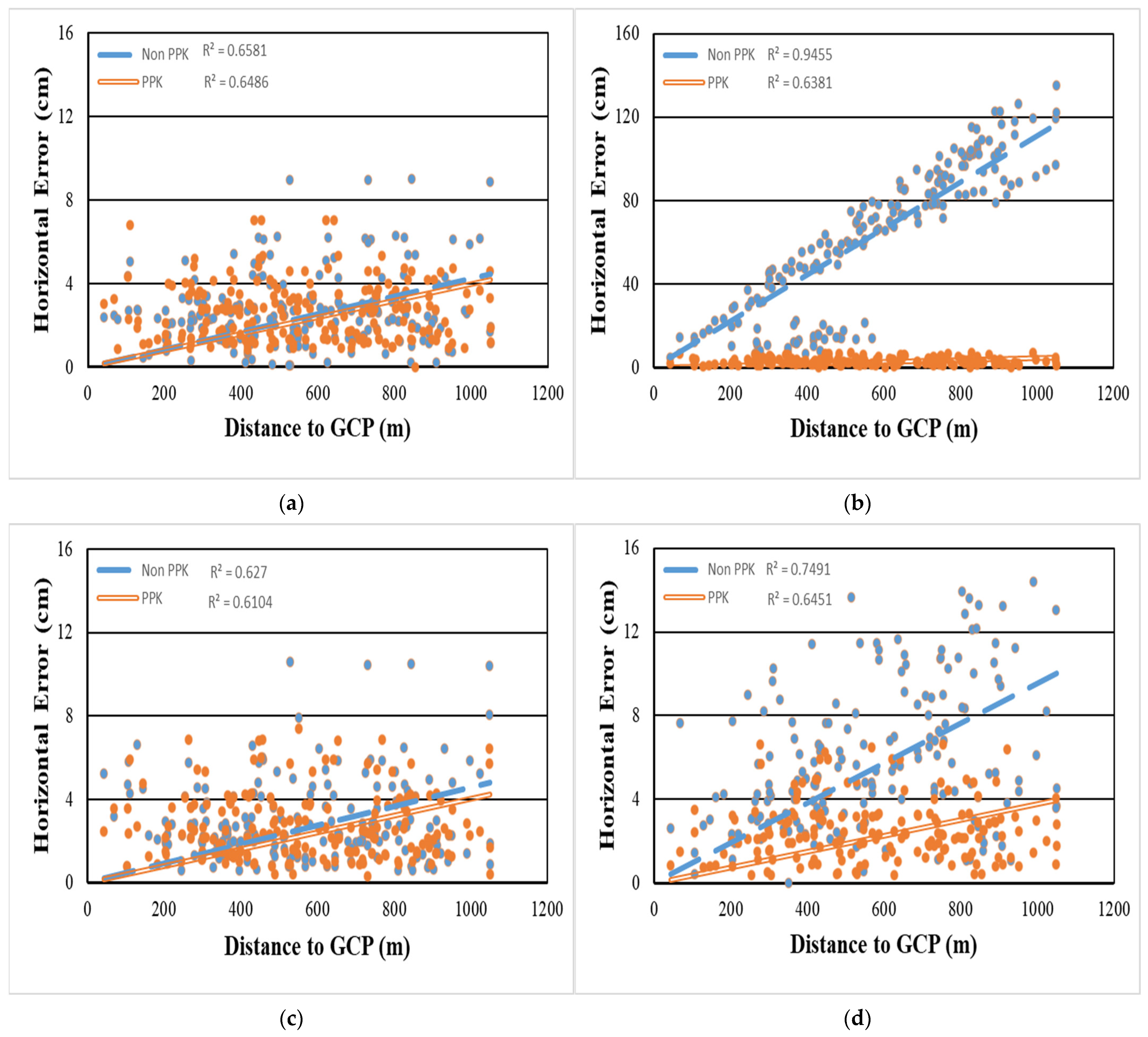
4. Accuracy Evaluation According to the Distance before and after PPK According to the Arrangement of GCP When 1GCP Is Applied
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AT | (Aerial Triangulation) |
| CORS | (Continuously Observation Reference Station) |
| CP | (Check Point) |
| GCP | (Ground Control Point) |
| GNSS | (Global Navigation Satellite System) |
| IMU | (Inertial Measurement Unit) |
| PDOP | (Position Dilution of Precision) |
| PPK | (Post Process Kinematic) |
| PPP | (Precise Point Positioning) |
| RINEX | (Receiver Independent Exchange Format) |
| RMSE | (Root Mean Square Error) |
| RTCM | (Radio Technical Commission for Maritime Services) |
| RTK | (Real Time Kinematic) |
| UAV | (Unmanned Aerial Vehicle) |
| UAM | (Urban Air Mobility) |
| VRS | (Virtual Reference Station) |
References
- Kim, J.; Lee, S.; Seo, J.; Lee, D.; Choi, H.S. The integration of earthwork design review and planning using uav-based point cloud and bim. Appl. Sci. 2021, 11, 3435. [Google Scholar] [CrossRef]
- Eker, R.; Elvanoglu, N.; Ucar, Z.; Bilici, E.; Aydın, A. 3D modelling of a historic windmill: PPK-aided terrestrial photogrammetry vs smartphone app. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 43, 787–792. [Google Scholar] [CrossRef]
- Kim, D.; Song, Y.; Kim, G.; Kim, C. A study on the application of UAV for Korean land monitoring. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2014, 32, 29–38. [Google Scholar] [CrossRef]
- Pádua, L.; Marques, P.; Adão, T.; Guimarães, N.; Sousa, A.; Peres, E.; Sousa, J.J. Vineyard variability analysis through UAV-based vigour maps to assess climate change impacts. Agronomy 2019, 9, 581. [Google Scholar] [CrossRef]
- Chivasa, W.; Mutanga, O.; Biradar, C. UAV-based multispectral phenotyping for disease resistance to accelerate crop improvement under changing climate conditions. Remote Sens. 2020, 12, 2445. [Google Scholar] [CrossRef]
- Feifei, X.; Zongjian, L.; Dezhu, G.; Hua, L. Study on construction of 3D building based on UAV images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, B1. [Google Scholar]
- Park, S.; Choi, Y.; Bae, J.; Hong, S.; Sohn, H. Three-dimensional positional accuracy analysis of uav imagery using ground control points acquired from multisource geospatial data. Korean J. Remote Sens. 2020, 36, 1013–1025. [Google Scholar]
- Laporte-Fauret, Q.; Marieu, V.; Castelle, B.; Michalet, R.; Bujan, S.; Rosebery, D. Low-cost UAV for high-resolution and large-scale coastal dune change monitoring using photogrammetry. J. Mar. Sci. Eng. 2019, 7, 63. [Google Scholar] [CrossRef]
- National Geographic Information Institute Regulations for Unmanned Aerial Vehicle Surveying Work. Suwon, Korea, Notice No. 2020–5670. 2020. Available online: https://www.ngii.go.kr/kor/board/view.do?sq=69672&board_code=lawinfo: (accessed on 11 March 2023).
- Eisenbeiss, H.; Sauerbier, M. Investigation of UAV systems and flight modes for photogrammetric applications. Photogramm. Rec. 2011, 26, 400–421. [Google Scholar] [CrossRef]
- Gómez-Gutiérrez, Á.; Sánchez-Fernández, M.; Juan de Sanjosé-Blasco, J. Performance of different UAS platforms, techniques (LIDAR and photogrammetry) and referencing approaches (RTK, PPK or GCP-based) to acquire 3D data in coastal cliffs. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–27 May 2022; p. EGU22-9881. [Google Scholar]
- Bulgakov, A.; Sayfeddine, D.; Yu, W.; Buzalo, N. Comparing Embedded Technologies for Aerial Geomatics Using Unmanned Aerial Systems. In Modern Problems in Construction: Selected Papers from MPC 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 13–20. [Google Scholar]
- Štroner, M.; Urban, R.; Seidl, J.; Reindl, T.; Brouček, J. Photogrammetry using UAV-mounted GNSS RTK: Georeferencing strategies without GCPs. Remote Sens. 2021, 13, 1336. [Google Scholar] [CrossRef]
- Bertin, S.; Stéphan, P.; Ammann, J. Assessment of RTK Quadcopter and Structure-from-Motion Photogrammetry for Fine-Scale Monitoring of Coastal Topographic Complexity. Remote Sens. 2022, 14, 1679. [Google Scholar] [CrossRef]
- Henkel, P.; Sperl, A.; Mittmann, U.; Fritzel, T.; Strauss, R.; Steiner, H. Precise 6D RTK positioning system for UAV-based near-field antenna measurements. In Proceedings of the 2020 14th European Conference on Antennas and Propagation (EuCAP), Copenhagen, Denmark, 15–20 March 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Kang, I.; Kim, T. Accuracy evaluation of 3D slope model produced by drone taken images. J. Korean GEO-Environ. Soc. 2020, 21, 13–17. [Google Scholar]
- Cho, J.; Lee, J.; Lee, B. Application of UAV Photogrammetry to Slope-Displacement Measurement. KSCE J. Civ. Eng. 2022, 26, 1904–1913. [Google Scholar] [CrossRef]
- Nesbit, P.R.; Hubbard, S.M.; Hugenholtz, C.H. Direct georeferencing UAV-SfM in high-relief topography: Accuracy assessment and alternative ground control strategies along steep inaccessible rock slopes. Remote Sens. 2022, 14, 490. [Google Scholar] [CrossRef]
- Ocalan, T.; Turk, T.; Tunalioglu, N.; Gurturk, M. Investigation of accuracy of PPP and PPP-AR methods for direct georeferencing in UAV photogrammetry. Earth Sci. Inform. 2022, 15, 2231–2238. [Google Scholar] [CrossRef]
- Pix4D Documentation; Pix4D SA: Lausanne, Switzerland, 2022.
- Chiabrando, F.; Tonolo, F.G.; Lingua, A. Uav direct georeferencing approach in an emergency mapping context. the 2016 central Italy earthquake case study. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 247–253. [Google Scholar] [CrossRef]
- Dreier, A.; Janßen, J.; Kuhlmann, H.; Klingbeil, L. Quality analysis of direct georeferencing in aspects of absolute accuracy and precision for a UAV-based laser scanning system. Remote Sens. 2021, 13, 3564. [Google Scholar] [CrossRef]
- Famiglietti, N.A.; Cecere, G.; Grasso, C.; Memmolo, A.; Vicari, A. A test on the potential of a low cost unmanned aerial vehicle RTK/PPK solution for precision positioning. Sensors 2021, 21, 3882. [Google Scholar] [CrossRef] [PubMed]
- Zeybek, M. Accuracy assessment of direct georeferencing UAV images with onboard global navigation satellite system and comparison of CORS/RTK surveying methods. Meas. Sci. Technol. 2021, 32, 065402. [Google Scholar] [CrossRef]
- Leandro, R.F.; Santos, M.C.; Langley, R.B. Analyzing GNSS data in precise point positioning software. GPS Solut. 2011, 15, 1–13. [Google Scholar] [CrossRef]
- Håkansson, M.; Jensen, A.B.; Horemuz, M.; Hedling, G. Review of code and phase biases in multi-GNSS positioning. GPS Solut. 2017, 21, 849–860. [Google Scholar] [CrossRef]
- Vierinen, J.; Coster, A.J.; Rideout, W.C.; Erickson, P.J.; Norberg, J. Statistical framework for estimating GNSS bias. Atmos. Meas. Tech. 2016, 9, 1303–1312. [Google Scholar] [CrossRef]
- Berber, M.; Munjy, R.; Lopez, J. Kinematic GNSS positioning results compared against Agisoft Metashape and Pix4dmapper results produced in the San Joaquin experimental range in Fresno County, California. J. Geod. Sci. 2021, 11, 48–57. [Google Scholar] [CrossRef]
- Yan, L.; Wan, J.; Sun, Y.; Fan, S.; Yan, Y.; Chen, R. A novel absolute orientation method using local similarities representation. ISPRS Int. J. Geo-Inf. 2016, 5, 135. [Google Scholar] [CrossRef]
- Zhang, H.; Aldana-Jague, E.; Clapuyt, F.; Wilken, F.; Vanacker, V.; Van Oost, K. Evaluating the potential of post-processing kinematic (PPK) georeferencing for UAV-based structure- from-motion (SfM) photogrammetry and surface change detection. Earth Surf. Dyn. 2019, 7, 807–827. [Google Scholar] [CrossRef]
- Bolkas, D. Assessment of GCP number and separation distance for small UAS surveys with and without GNSS-PPK positioning. J. Surv. Eng. 2019, 145, 04019007. [Google Scholar] [CrossRef]
- Zhang, K.; Okazawa, H.; Hayashi, K.; Hayashi, T.; Fiwa, L.; Maskey, S. Optimization of ground control point distribution for unmanned aerial vehicle photogrammetry for inaccessible fields. Sustainability 2022, 14, 9505. [Google Scholar] [CrossRef]
- Park, J.W.; Yeom, D.J. Method for establishing ground control points to realize UAV-based precision digital maps of earthwork sites. J. Asian Archit. Build. Eng. 2022, 21, 110–119. [Google Scholar] [CrossRef]
- Hastaoglu, K.O.; Kapicioglu, H.S.; Gül, Y.; Poyraz, F. Investigation of the effect of height difference and geometry of GCP on position accuracy of point cloud in UAV photogrammetry. Surv. Rev. 2022, 1–13. [Google Scholar] [CrossRef]
- Choi, H.J.; Lee, B.; Yeon, S.H. A study on the site calibration of Network RTK surveying. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2013, 31, 99–107. [Google Scholar] [CrossRef]
- Žabota, B.; Kobal, M. Accuracy assessment of uav-photogrammetric-derived products using PPK and GCPs in challenging terrains: In search of optimized rockfall mapping. Remote Sens. 2021, 13, 3812. [Google Scholar] [CrossRef]
- Kim, K.B.; Yun, H.S.; Choi, H.J. Accuracy evaluation of geoid heights in the national control points of south Korea using high-degree geopotential model. Appl. Sci. 2020, 10, 1466. [Google Scholar] [CrossRef]
- Lee, J.; Kwon, J.H. Review the status of Korean geoid model development since 2000s and future improvement plan. Terr. Atmos. Ocean. Sci. 2022, 33, 12. [Google Scholar] [CrossRef]
- DJI Phantom 4 RTK User Manual; v2.4. 2021. DJI Phantom 4 RTK User Manual; v2.4. 2021. Available online: https://dl.djicdn.com/downloads/phantom_4_rtk/20210716/Phantom_4_RTK_User_Manual_v2.4_EN.pdf: (accessed on 11 March 2023).
- Lee, K.; Lee, W.H. Earthwork Volume Calculation, 3D Model Generation, and Comparative Evaluation Using Vertical and High-Oblique Images Acquired by Unmanned Aerial Vehicles. Aerospace 2022, 9, 606. [Google Scholar] [CrossRef]
- Przybilla, H.; Gerke, M.; Dikhoff, I.; Ghassoun, Y. Investigations on the Geometric Quality of Cameras for Uav Applications Using the High Precision Uav Test Field Zollern Colliery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W13, 531–538. [Google Scholar] [CrossRef]
- Zhou, Y.; Daakir, M.; Rupnik, E.; Pierrot-Deseilligny, M. A two-step approach for the correction of rolling shutter distortion in UAV photogrammetry. ISPRS J. Photogramm. Remote Sens. 2020, 160, 51–66. [Google Scholar] [CrossRef]
- Choi, Y.W.; Yoon, H.W.; Choo, M.J.; Yoon, D.K. A Study on Precision of 3D Spatial Model of a Highly Dense Urban Area based on Drone Images. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2022, 40, 69–77. [Google Scholar]
- Kong, L.; Chen, T.; Kang, T.; Chen, Q.; Zhang, D. An Automatic and Accurate Method for Marking Ground Control Points in Unmanned Aerial Vehicle Photogrammetry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 16, 278–290. [Google Scholar] [CrossRef]
- Cho, J.; Lee, J.; Lee, B. A study on the optimal shooting conditions of UAV for 3D production and orthophoto generation. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2020, 38, 645–653. [Google Scholar]
- No, S.; Han, J.; Kwon, J.H. Accuracy analysis of network-RTK (VRS) for real time kinematic positioning. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2012, 30, 389–396. [Google Scholar] [CrossRef]



| Survey Point | Reference Point | dN (m) | dE (m) | Geoid Height (m) | Hor. Residual (m) | Ver. Residual (m) |
|---|---|---|---|---|---|---|
| U19 | U Anyang 19 | −0.001 | 0.002 | 23.057 | 0.002 | −0.027 |
| U20 | U Anyang 20 | 0.002 | 0.006 | 22.974 | 0.007 | 0.022 |
| U22 | U Anyang 22 | −0.010 | −0.005 | 23.038 | 0.011 | −0.011 |
| U75 | U Anyang 75 | 0.009 | −0.004 | 23.261 | 0.010 | 0.016 |
| Case | UAV Survey Date | Front and Side Overlap (%) | Flight Height (m) | Camera Angle | Flight Speed (m/s) | Course | Images | ||
|---|---|---|---|---|---|---|---|---|---|
| GeoReference | |||||||||
| Disconnect | GNSS | RTK | |||||||
| 1 | 16 December 2020 | 70 | 100 | Nadir | 10 | Single Grid | 658 | ||
| 2 | 17 December 2020 | 70 | 100 | Nadir | 10 | Single Grid | 646 | ||
| 3 | 10 February 2021 | 75 | 100 | Nadir | 10 | Double Grid | 113 | 65 | 1477 |
| 4 | 23 February 2021 | 75 | 100 | Nadir | 10 | Double Grid | 1599 | 91 | |
| Focal Length Pixel/mm | Principal Point x Pixel/mm | Principal Point y Pixel/mm | R1 | R2 | R3 | T1 | T2 | |
|---|---|---|---|---|---|---|---|---|
| Initial Value | 3658.3/ 8.580 | 2722.5/6.385 | 1835.1/ 4.304 | −0.269 | 0.112 | −0.033 | 0.000 | −0.001 |
| Optimized Values | 3683.661/ 8.639 | 2731.889/6.407 | 1845.674/4.329 | −0.267 | 0.109 | −0.031 | 0.000 | −0.000 |
| Uncertainties (Sigma) | 0.663/0.002 | 0.119/0.000 | 0.083/0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Case | Original Image Accuracy Data | PPK Image Accuracy Data | ||
|---|---|---|---|---|
| H (cm) | Z (cm) | H (mm) | Z (mm) | |
| 1 | 2.35 | 4.25 | 5.62 | 9.59 |
| 2 | 116.92 | 274.61 | 6.23 | 9.24 |
| 3 | 41.10 | 84.69 | 5.63 | 9.70 |
| 4 | 116.84 | 254.02 | 14.73 | 22.72 |
| GCP Location | Case | Error | H (cm) | Z (cm) | Reprojection Error |
|---|---|---|---|---|---|
| 1 o’clock direction | 1 | Mean | −1.39 | 14.59 | 0.268 |
| RMSE | 2.74 | 15.53 | |||
| 2 | Mean | 66.30 | 90.77 | 0.346 | |
| RMSE | 78.05 | 98.72 | |||
| 3 | Mean | 1.55 | 16.14 | 0.312 | |
| RMSE | 3.27 | 16.66 | |||
| 4 | Mean | 5.69 | 11.54 | 0.275 | |
| RMSE | 8.14 | 13.32 | |||
| 5 o’clock direction | 1 | Mean | −1.73 | 7.19 | 0.275 |
| RMSE | 3.23 | 8.83 | |||
| 2 | Mean | 72.87 | 23.11 | 0.346 | |
| RMSE | 85.67 | 68.52 | |||
| 3 | Mean | 1.54 | 11.94 | 0.303 | |
| RMSE | 3.26 | 12.66 | |||
| 4 | Mean | 4.73 | 11.55 | 0.283 | |
| RMSE | 6.61 | 12.61 | |||
| 7 o’clock direction | 1 | Mean | −1.66 | 5.56 | 0.274 |
| RMSE | 3.20 | 7.49 | |||
| 2 | Mean | 59.85 | −41.15 | 0.352 | |
| RMSE | 68.74 | 45.75 | |||
| 3 | Mean | 1.96 | 32.59 | 0.271 | |
| RMSE | 3.46 | 32.87 | |||
| 4 | Mean | 3.55 | 19.15 | 0.282 | |
| RMSE | 5.94 | 19.96 | |||
| 11 o’clock direction | 1 | Mean | −1.69 | 2.78 | 0.269 |
| RMSE | 3.19 | 5.82 | |||
| 2 | Mean | 61.01 | 33.05 | 0.347 | |
| RMSE | 74.76 | 60.40 | |||
| 3 | Mean | 1.55 | 16.00 | 0.306 | |
| RMSE | 3.25 | 16.53 | |||
| 4 | Mean | 5.67 | 4.70 | 0.279 | |
| RMSE | 8.19 | 8.65 | |||
| Center of study area | 1 | Mean | −1.68 | −1.23 | 0.273 |
| RMSE | 3.20 | 5.32 | |||
| 2 | Mean | 1.58 | 25.42 | 0.347 | |
| RMSE | 13.63 | 94.20 | |||
| 3 | Mean | 1.58 | 11.46 | 0.312 | |
| RMSE | 3.27 | 12.20 | |||
| 4 | Mean | 2.11 | 8.45 | 0.281 | |
| RMSE | 4.29 | 11.22 |
| GCP Location | Case | Error | H (cm) | Z (cm) | Reprojection Error |
|---|---|---|---|---|---|
| 1 o’clock direction | 1 | Mean | 1.89 | 5.70 | 0.333 |
| RMSE | 3.02 | 7.65 | |||
| 2 | Mean | 1.25 | 0.42 | 0.332 | |
| RMSE | 3.44 | 5.00 | |||
| 3 | Mean | 1.64 | −5.15 | 0.414 | |
| RMSE | 3.09 | 6.98 | |||
| 4 | Mean | 1.49 | 0.31 | 0.327 | |
| RMSE | 2.99 | 5.64 | |||
| 5 o’clock direction | 1 | Mean | 1.97 | 8.11 | 0.328 |
| RMSE | 3.07 | 9.58 | |||
| 2 | Mean | 1.36 | 7.55 | 0.329 | |
| RMSE | 3.49 | 8.97 | |||
| 3 | Mean | 1.66 | −5.22 | 0.338 | |
| RMSE | 3.09 | 7.04 | |||
| 4 | Mean | 1.39 | 6.52 | 0.335 | |
| RMSE | 2.98 | 8.58 | |||
| 7 o’clock direction | 1 | Mean | 1.93 | 5.28 | 0.333 |
| RMSE | 3.04 | 7.35 | |||
| 2 | Mean | 1.32 | 7.41 | 0.334 | |
| RMSE | 3.47 | 8.84 | |||
| 3 | Mean | 1.71 | −5.42 | 0.322 | |
| RMSE | 3.15 | 7.19 | |||
| 4 | Mean | 1.41 | 2.67 | 0.338 | |
| RMSE | 2.96 | 6.21 | |||
| 11 o’clock direction | 1 | Mean | 1.94 | 0.13 | 0.331 |
| RMSE | 3.06 | 5.13 | |||
| 2 | Mean | 1.33 | −6.47 | 0.331 | |
| RMSE | 3.44 | 8.27 | |||
| 3 | Mean | 1.67 | −5.21 | 0.339 | |
| RMSE | 3.08 | 7.02 | |||
| 4 | Mean | 1.41 | −4.64 | 0.333 | |
| RMSE | 3.00 | 7.31 | |||
| Center of study area | 1 | Mean | 1.92 | −1.73 | 0.328 |
| RMSE | 3.04 | 5.43 | |||
| 2 | Mean | 1.34 | 7.68 | 0.331 | |
| RMSE | 3.49 | 9.08 | |||
| 3 | Mean | 1.66 | −4.97 | 0.399 | |
| RMSE | 3.09 | 6.86 | |||
| 4 | Mean | 1.39 | 4.00 | 0.335 | |
| RMSE | 2.95 | 6.87 |
| GCP Arrangement (m) | ||||||
|---|---|---|---|---|---|---|
| Center | 1 | 5 | 7 | 11 | ||
| Horz. Accuracy | 0.014 | 0.014 | 0.014 | 0.014 | 0.014 | |
| Vert. Accuracy | 0.020 | 0.030 | 0.020 | 0.032 | 0.030 | |
| Distance | Min | 101.9 | 42.2 | 181.7 | 67.6 | 76.9 |
| Avg | 356.7 | 589.3 | 637.9 | 630.3 | 590.6 | |
| Max | 568.5 | 1048.9 | 1051.0 | 1048.9 | 1051.0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, J.M.; Lee, B.K. GCP and PPK Utilization Plan to Deal with RTK Signal Interruption in RTK-UAV Photogrammetry. Drones 2023, 7, 265. https://doi.org/10.3390/drones7040265
Cho JM, Lee BK. GCP and PPK Utilization Plan to Deal with RTK Signal Interruption in RTK-UAV Photogrammetry. Drones. 2023; 7(4):265. https://doi.org/10.3390/drones7040265
Chicago/Turabian StyleCho, Jung Min, and Byoung Kil Lee. 2023. "GCP and PPK Utilization Plan to Deal with RTK Signal Interruption in RTK-UAV Photogrammetry" Drones 7, no. 4: 265. https://doi.org/10.3390/drones7040265
APA StyleCho, J. M., & Lee, B. K. (2023). GCP and PPK Utilization Plan to Deal with RTK Signal Interruption in RTK-UAV Photogrammetry. Drones, 7(4), 265. https://doi.org/10.3390/drones7040265






