Event-Trigger-Based Finite-Time Privacy-Preserving Formation Control for Multi-UAV System
Abstract
1. Introduction
- (1)
- A local (implemented independently by each UAV), deterministic, time-varying output mapping function was adopted to cope with the privacy-preserving formation control issues for a continuous-time multi-UAV system. All UAVs encode the internal states prior to their public transmission, hence the true value information of each UAV’s states can be kept indecipherable for honest-but-curious UAVs or other malicious eavesdroppers. Compared with the existing privacy-preserving methods based on incorporating noises [36] and state decomposition [15], the method has a simpler control structure and a lower computation complexity;
- (2)
- The finite-time stability theory was introduced to ensure the convergence performance of privacy-preserving formation control. Then, through the theoretical derivation, this paper obtained a settling time related to the UAVs’ initial states. Meanwhile, the convergence time obtained by the final experimental results can verify the settling time obtained by the theoretical results;
- (3)
- An event-triggered-based finite-time privacy-preserving formation controller was designed by selecting proper triggering conditions. To some extent, with the help of an event-triggered mechanism, the lower bandwidth usage and lower frequency of controller updates can be implemented. Additionally, the paper provides the convergence analysis and privacy analysis of the proposed controller, and simultaneously excludes Zeno behavior. Compared with the research of [15,37], the controller designed in this paper relieves pressure on the actuator and bandwidth;
2. Preliminaries
2.1. Graph Theory
2.2. Privacy-Preserving Based on Output Mask
2.3. Some Useful Lemmas
3. Problem Formulation
- (1)
- (2)
- there exists an output mapping called a privacy mask g in a condition whereby ; assures the indecipherability of the UAVs’ initial states; the neighborhoods of any are not preserved by ; is strictly increasing with respect to for any certain t, and [44].
4. Control Design with Event-Triggered Strategy
- (i)
- If the vector x holds
- (ii)
- Else if the vector x holds
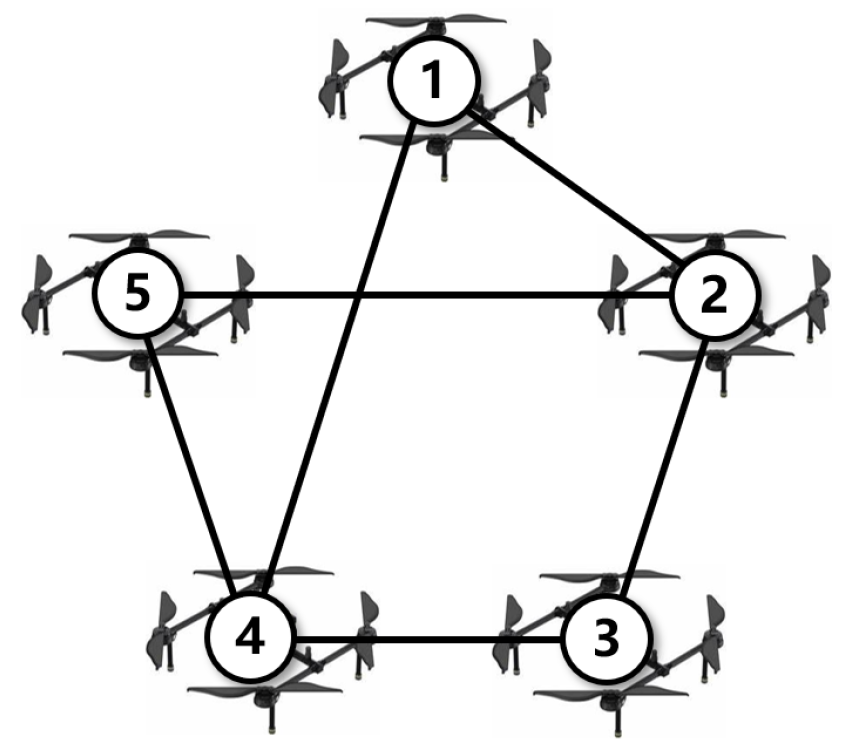
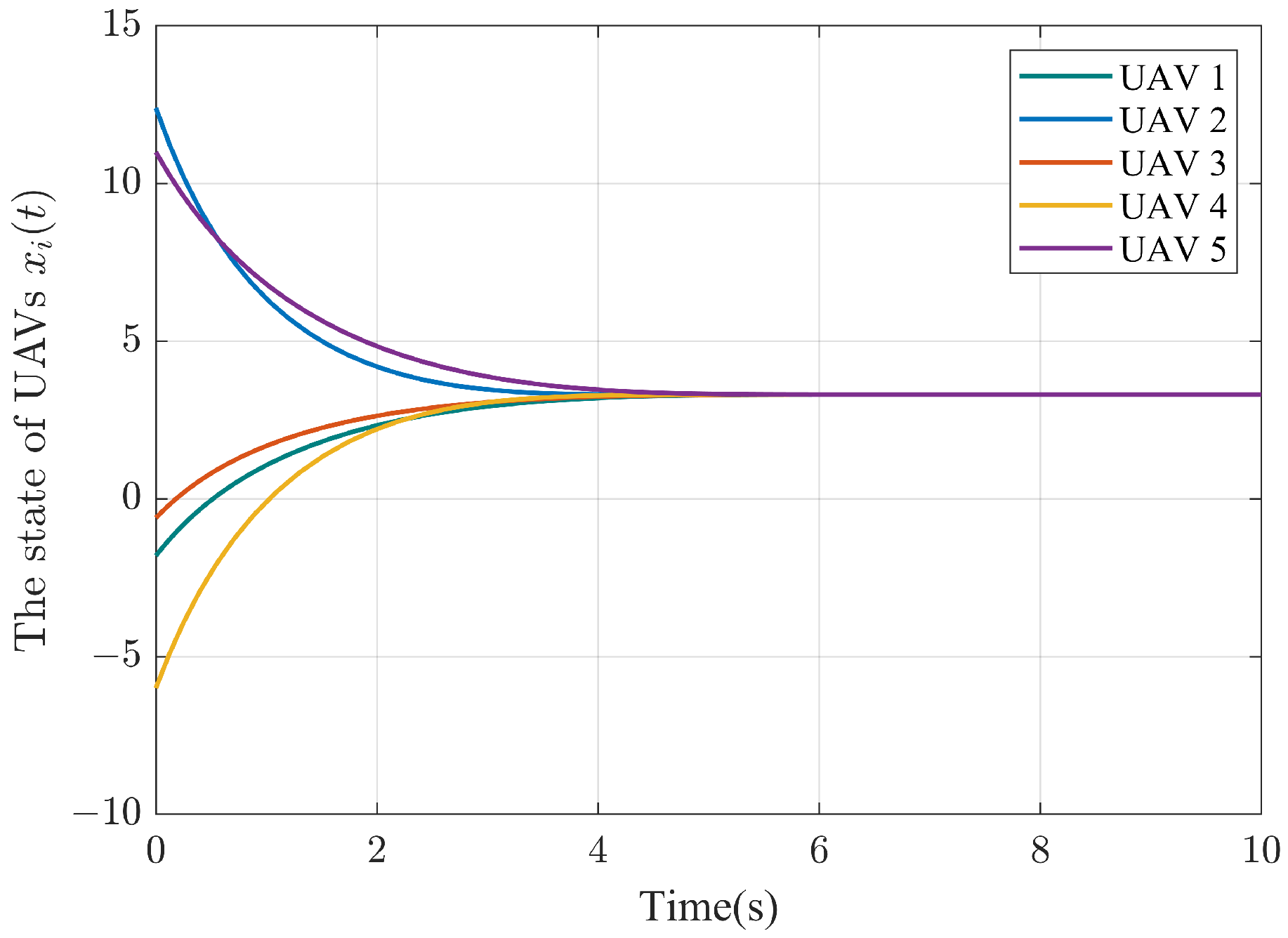
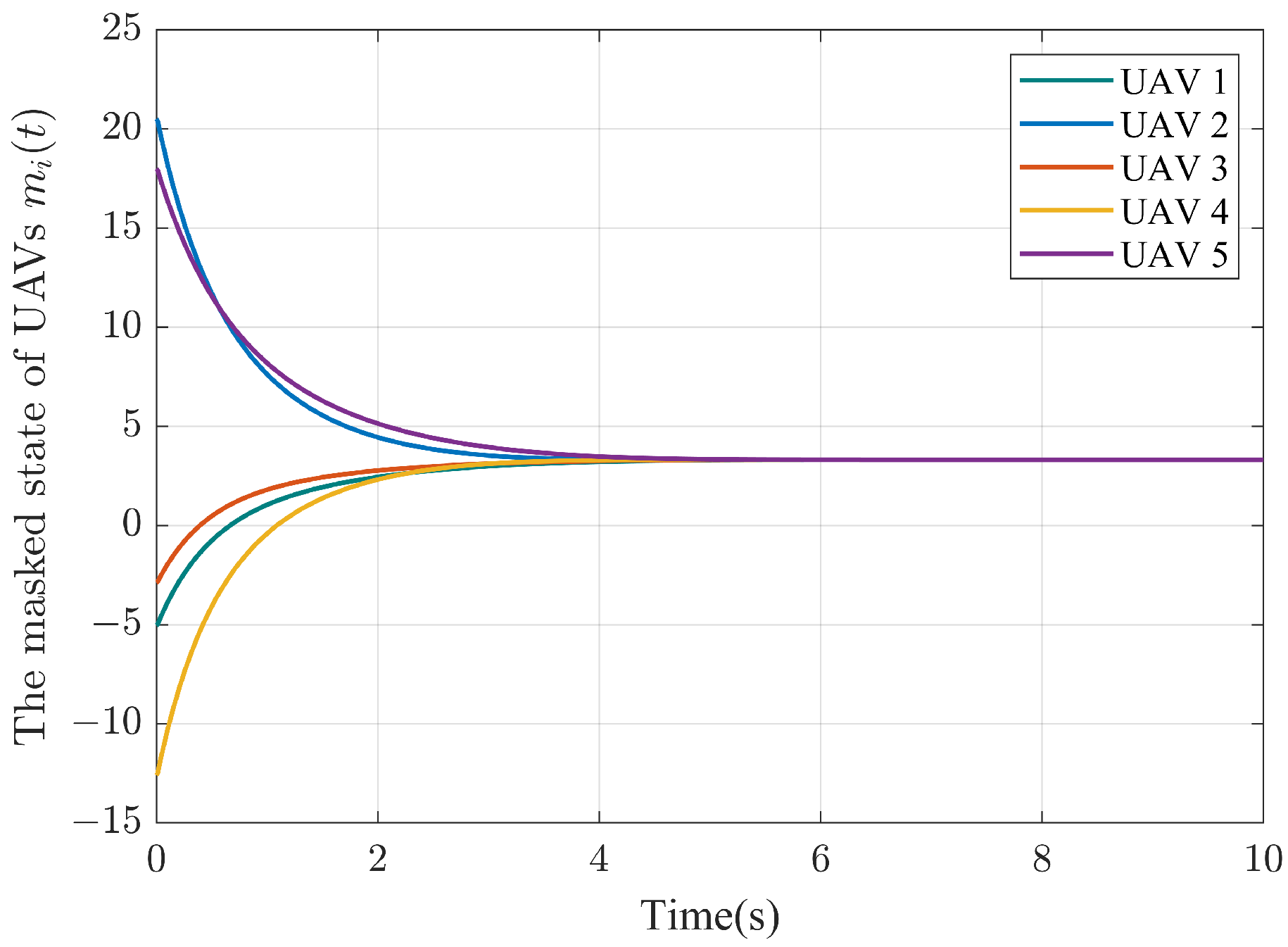
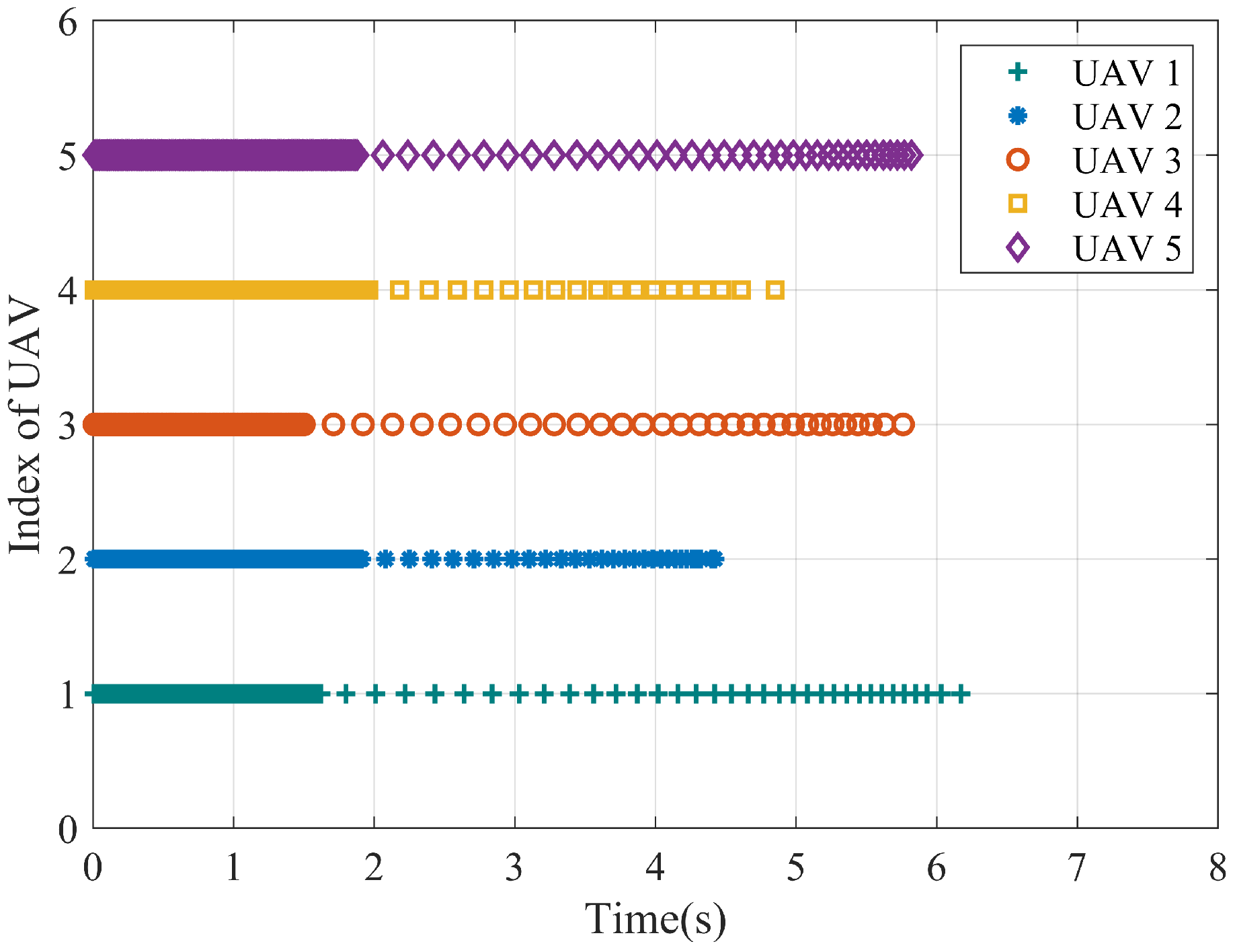
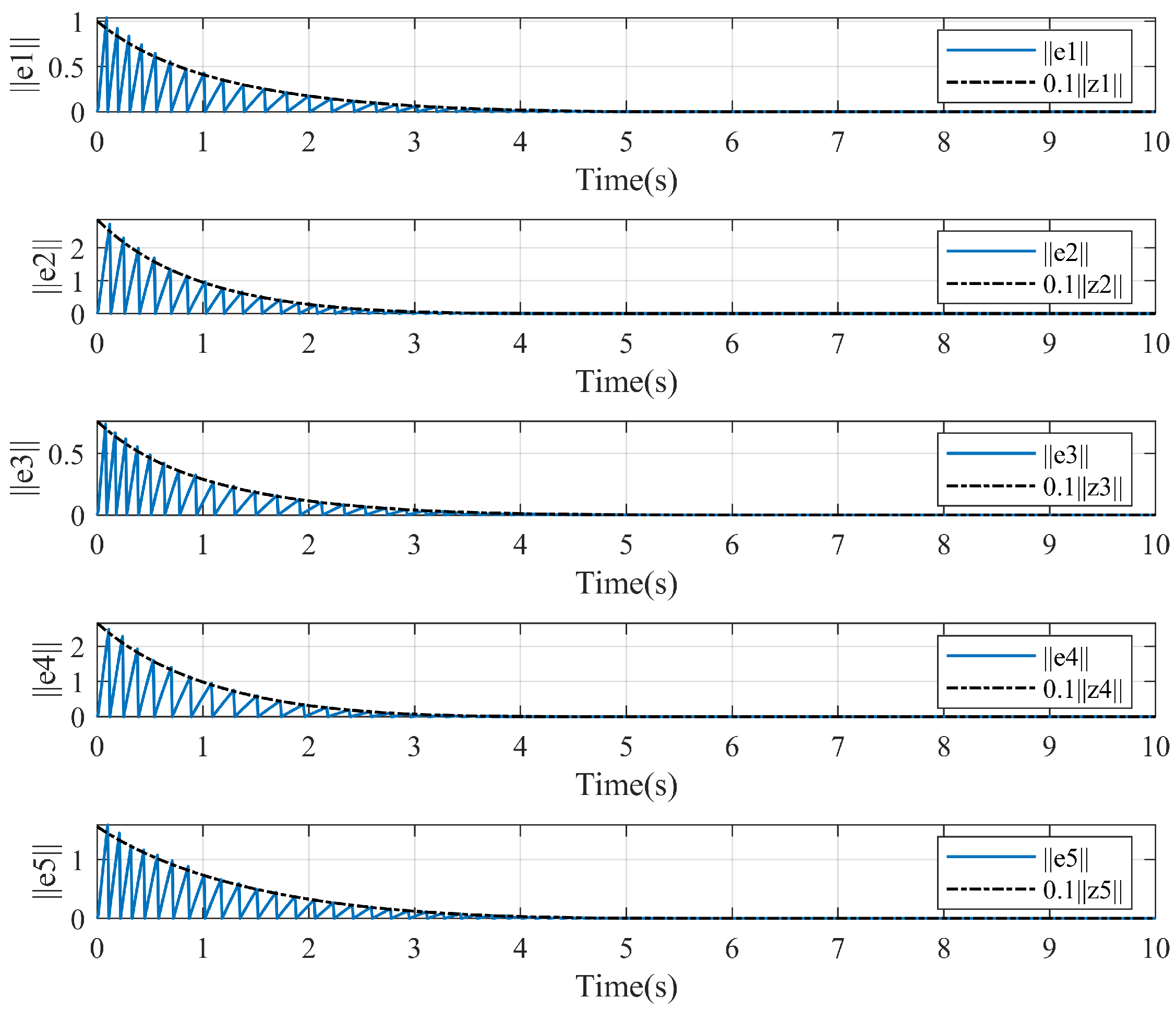
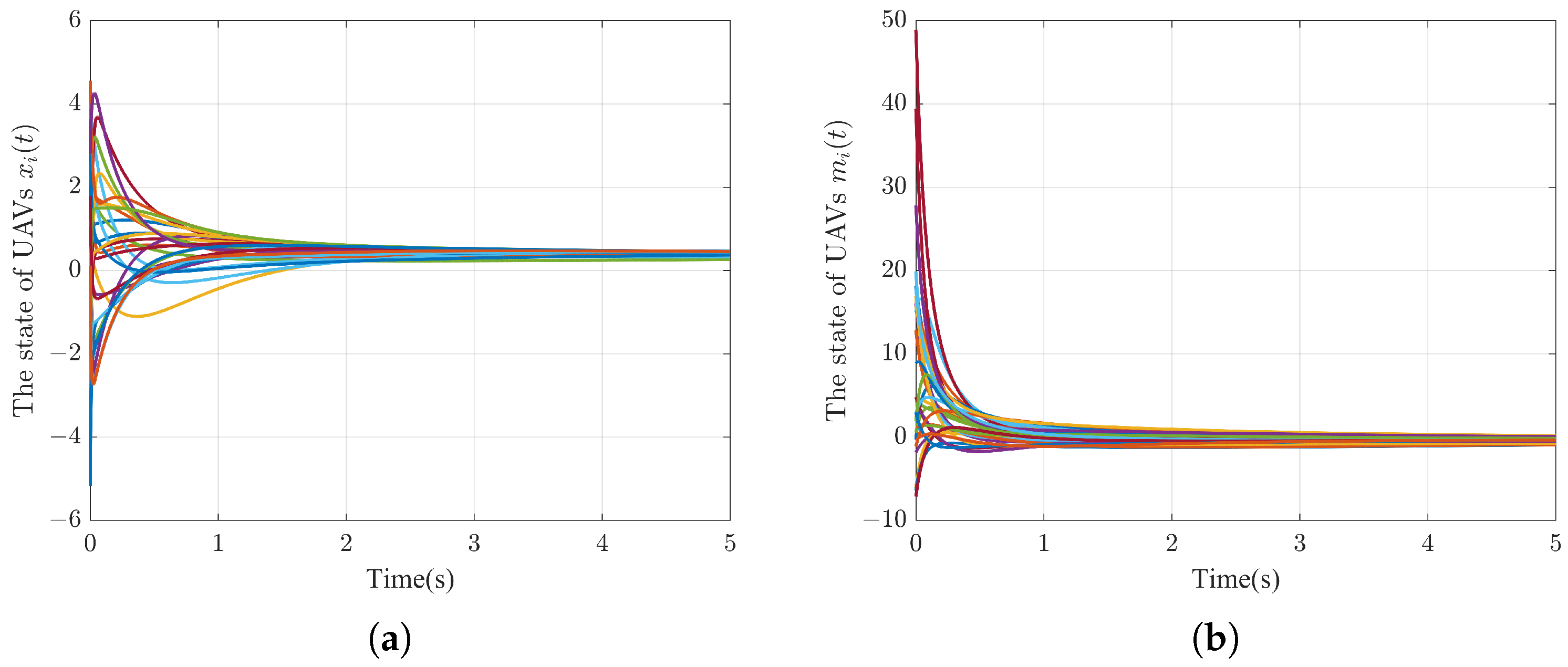
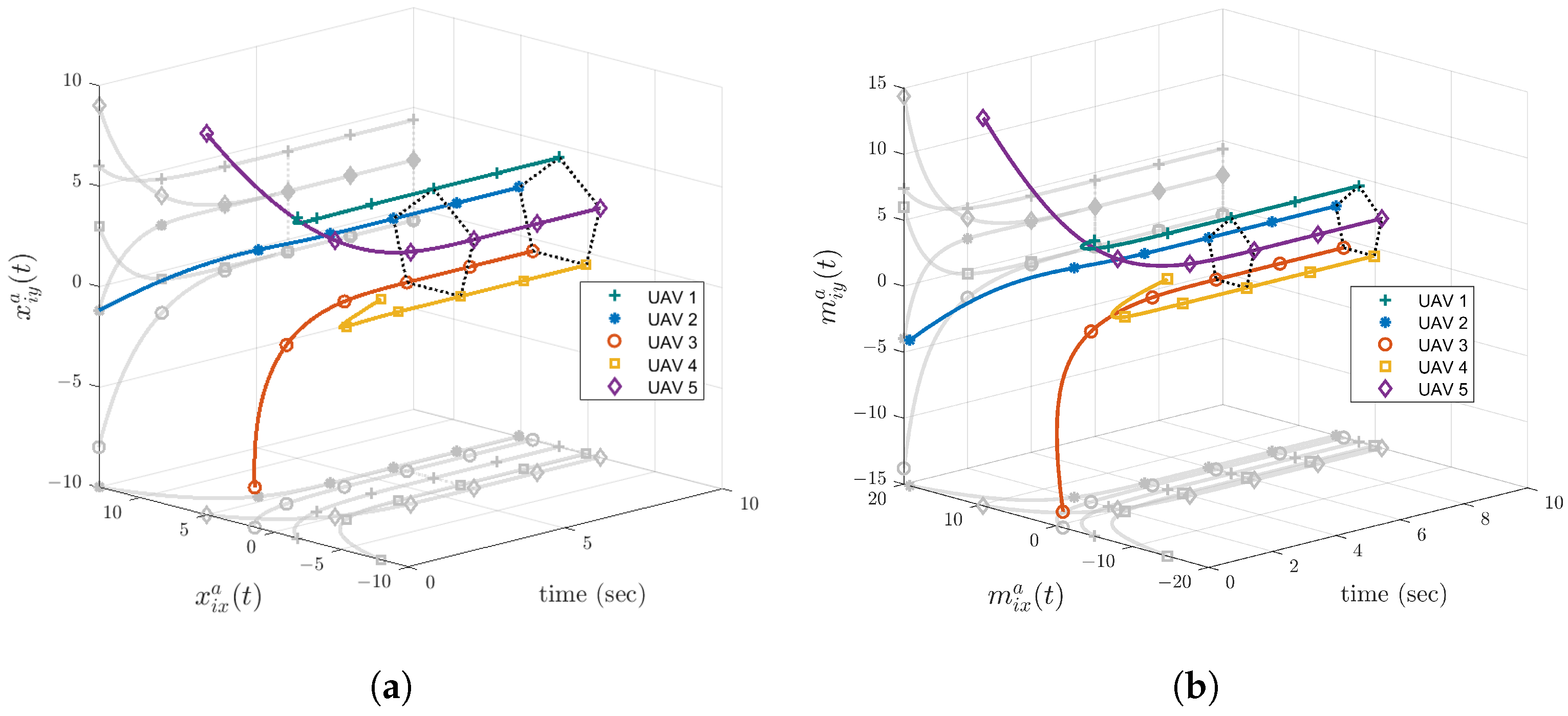
5. Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chleboun, J.; Amorim, T.; Nascimento, A.M.; Nascimento, T.P. An Improved Spanning Tree-Based Algorithm for Coverage of Large Areas Using Multi-UAV Systems. Drones 2022, 7, 9. [Google Scholar] [CrossRef]
- Cui, W.; Li, R.; Feng, Y.; Yang, Y. Distributed Task Allocation for a Multi-UAV System with Time Window Constraints. Drones 2022, 6, 226. [Google Scholar] [CrossRef]
- Lu, Y.; Zhu, M. A control-theoretic perspective on cyber-physical privacy: Where data privacy meets dynamic systems. Annu. Rev. Control 2019, 47, 423–440. [Google Scholar] [CrossRef]
- Basan, E.; Basan, A.; Nekrasov, A.; Fidge, C.; Abramov, E.; Basyuk, A. A Data Normalization Technique for Detecting Cyber Attacks on UAVs. Drones 2022, 6, 245. [Google Scholar] [CrossRef]
- Shi, L.; Liu, Q.; Shao, J.; Cheng, Y.; Zheng, W.X. A Cooperation-Competition Evolutionary Dynamic Model Over Signed Networks. IEEE Trans. Autom. Control 2023. [Google Scholar] [CrossRef]
- Shi, L.; Zheng, W.X.; Shao, J.; Cheng, Y. Sub-super-stochastic matrix with applications to bipartite tracking control over signed networks. SIAM J. Control. Optim. 2021, 59, 4563–4589. [Google Scholar] [CrossRef]
- Shi, L.; Cheng, Y.; Shao, J.; Sheng, H.; Liu, Q. Cucker-Smale flocking over cooperation-competition networks. Automatica 2022, 135, 109988. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, W.; Zheng, G. Optimum Placement of UAV as Relays. IEEE Commun. Lett. 2017, 22, 248–251. [Google Scholar] [CrossRef]
- Mo, Y.; Murray, R.M. Privacy preserving average consensus. IEEE Trans. Autom. Control 2016, 62, 753–765. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, F.; Duan, F.; Liu, Z.; Chen, Z. Anonymous Privacy-Preserving Consensus via Mixed Encryption Communication. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3445–3449. [Google Scholar] [CrossRef]
- Liu, X.K.; Zhang, J.F.; Wang, J. Differentially private consensus algorithm for continuous-time heterogeneous multi-agent systems. Automatica 2020, 122, 109283. [Google Scholar] [CrossRef]
- Wang, Y. Privacy-preserving average consensus via state decomposition. IEEE Trans. Autom. Control 2019, 64, 4711–4716. [Google Scholar] [CrossRef]
- Xu, H.; Ni, Y.H.; Liu, Z.; Chen, Z. Privacy-preserving leader-following consensus via node-augment mechanism. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 2117–2121. [Google Scholar] [CrossRef]
- Bellink, K. Secure and Private Formation Control of the Nexus Robot Using Fully Homomorphic Encryption. Ph.D. Thesis, University of Groningen, Groningen, The Netherlands, 2019. [Google Scholar]
- Zhang, K.; Li, Z.; Wang, Y.; Louati, A.; Chen, J. Privacy-preserving dynamic average consensus via state decomposition: Case study on multi-robot formation control. Automatica 2022, 139, 110182. [Google Scholar] [CrossRef]
- Li, W.; Qin, K.; Shi, M.; Shao, J.; Lin, B. Dynamic Target Enclosing Control Scheme for Multi-Agent Systems via a Signed Graph-Based Approach. IEEE/CAA J. Autom. Sin. 2023, 10, 560–562. [Google Scholar] [CrossRef]
- Li, W.; Qin, K.; Li, G.; Shi, M.; Zhang, X. Robust bipartite tracking consensus of multi-agent systems via neural network combined with extended high-gain observer. ISA Trans. 2022. [Google Scholar] [CrossRef]
- Shafiq, M.; Tian, Z.; Bashir, A.K.; Du, X.; Guizani, M. CorrAUC: A malicious bot-IoT traffic detection method in IoT network using machine-learning techniques. IEEE Internet Things J. 2020, 8, 3242–3254. [Google Scholar] [CrossRef]
- Shafiq, M.; Tian, Z.; Bashir, A.K.; Du, X.; Guizani, M. IoT malicious traffic identification using wrapper-based feature selection mechanisms. Comput. Secur. 2020, 94, 101863. [Google Scholar] [CrossRef]
- Shafiq, M.; Tian, Z.; Bashir, A.K.; Jolfaei, A.; Yu, X. Data mining and machine learning methods for sustainable smart cities traffic classification: A survey. Sustain. Cities Soc. 2020, 60, 102177. [Google Scholar] [CrossRef]
- Tedeschi, P.; Sciancalepore, S.; Di Pietro, R. PPCA-Privacy-Preserving Collision Avoidance for Autonomous Unmanned Aerial Vehicles. IEEE Trans. Dependable Secur. Comput. 2022, 20, 1541–1558. [Google Scholar] [CrossRef]
- Ng, J.S.; Lim, W.Y.B.; Dai, H.N.; Xiong, Z.; Huang, J.; Niyato, D.; Hua, X.S.; Leung, C.; Miao, C. Joint auction-coalition formation framework for communication-efficient federated learning in UAV-enabled internet of vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 22, 2326–2344. [Google Scholar] [CrossRef]
- Han, Y.; Li, C.; Zeng, Z. Asynchronous event-based sampling data for impulsive protocol on consensus of non-linear multi-agent systems. Neural Netw. 2019, 115, 90–99. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Long, Y.; Li, T.; Chen, C.P. Consensus of linear multi-agent systems by distributed event-triggered strategy with designable minimum inter-event time. Inf. Sci. 2022, 609, 644–659. [Google Scholar] [CrossRef]
- Chen, Z.; Niu, B.; Zhao, X.; Zhang, L.; Xu, N. Model-based adaptive event-triggered control of nonlinear continuous-time systems. Appl. Math. Comput. 2021, 408, 126330. [Google Scholar] [CrossRef]
- Tang, X.; Li, M.; Wei, S.; Ding, B. Event-triggered synchronous distributed model predictive control for multi-agent systems. Int. J. Control. Autom. Syst. 2021, 19, 1273–1282. [Google Scholar] [CrossRef]
- Peng, C.; Zhang, J.; Han, Q.L. Consensus of multiagent systems with nonlinear dynamics using an integrated sampled-data-based event-triggered communication scheme. IEEE Trans. Syst. Man, Cybern. Syst. 2018, 49, 589–599. [Google Scholar] [CrossRef]
- Rikos, A.I.; Charalambous, T.; Johansson, K.H.; Hadjicostis, C.N. Privacy-preserving event-triggered quantized average consensus. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju Island, Republic of Korea, 14–18 December 2020; pp. 6246–6253. [Google Scholar]
- Wang, A.; Liu, Y.; Huang, T. Event-Triggered privacy-preserving average consensus for continuous-time multi-agent network systems. J. Frankl. Inst. 2022, 359, 4959–4975. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Park, D.; Ngoc, D.N.; Xuan-Mung, N.; Huynh, T.T.; Nguyen, T.N.; Hong, S.K. Quadrotor formation control via terminal sliding mode approach: Theory and experiment results. Drones 2022, 6, 172. [Google Scholar] [CrossRef]
- Bingöl, Ö.; Güzey, H.M. Finite-Time Neuro-Sliding-Mode Controller Design for Quadrotor UAVs Carrying Suspended Payload. Drones 2022, 6, 311. [Google Scholar] [CrossRef]
- Gao, H.; Li, W.; Cai, H. Fully Distributed Robust Formation Flying Control of Drones Swarm Based on Minimal Virtual Leader Information. Drones 2022, 6, 266. [Google Scholar] [CrossRef]
- Hao, L.; Zhan, X.; Wu, J.; Han, T.; Yan, H. Bipartite Finite Time and Fixed Time Output Consensus of Heterogeneous Multiagent Systems Under State Feedback Control. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2067–2071. [Google Scholar] [CrossRef]
- Ren, Y.; Zhou, W.; Li, Z.; Liu, L.; Sun, Y. Prescribed-time cluster lag consensus control for second-order non-linear leader-following multiagent systems. ISA Trans. 2021, 109, 49–60. [Google Scholar] [CrossRef] [PubMed]
- Rikos, A.I.; Charalambous, T.; Johansson, K.H.; Hadjicostis, C.N. Distributed event-triggered algorithms for finite-time privacy-preserving quantized average consensus. IEEE Trans. Control Netw. Syst. 2022, 10, 38–50. [Google Scholar] [CrossRef]
- He, J.; Cai, L.; Zhao, C.; Cheng, P.; Guan, X. Privacy-preserving average consensus: Privacy analysis and algorithm design. IEEE Trans. Signal Inf. Process. Over Netw. 2018, 5, 127–138. [Google Scholar] [CrossRef]
- Xie, A.; Wang, X.; Ren, X. Privacy-Preserving Average Consensus in Finite Time. In Proceedings of the 2021 60th IEEE Conference on Decision and Control (CDC), Austin, TX, USA, 13–15 December 2021; pp. 2743–2749. [Google Scholar]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control. Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Li, Q.; Hua, Y.; Dong, X.; Yu, J.; Ren, Z. Time-varying formation tracking control for unmanned aerial vehicles with the leader’s unknown input and obstacle avoidance: Theories and applications. Electronics 2022, 11, 2334. [Google Scholar] [CrossRef]
- Ren, W. Consensus tracking under directed interaction topologies: Algorithms and experiments. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 742–747. [Google Scholar]
- Yang, J.; Zhang, H.; Chu, H.; Zhang, W. Output event triggered consensus control of nonlinear multi-agent systems with relative state constraints. ISA Trans. 2021, 108, 164–177. [Google Scholar] [CrossRef]
- Zhao, Z.; Shi, L.; Li, T.; Shao, J.; Cheng, Y. Opinion Dynamics of Social Networks With Intermittent-Influence Leaders. IEEE Trans. Comput. Soc. Syst. 2022. [Google Scholar] [CrossRef]
- Shi, L.; Li, W.; Shi, M.; Shi, K.; Cheng, Y. Opinion Polarization Over Signed Social Networks With Quasi Structural Balance. IEEE Trans. Autom. Control 2023. [Google Scholar] [CrossRef]
- Altafini, C. A dynamical approach to privacy preserving average consensus. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; pp. 4501–4506. [Google Scholar]



| Literature | Privacy-Preserving | Object | PA | BC | CP | Results |
|---|---|---|---|---|---|---|
| [9] | Superimposed noise | discrete-time | ✓ | ✓ | average consensus | |
| [10] | Encryption method | discrete-time | ✓ | leader-following | ||
| [11] | Differential privacy | continuous-time | ✓ | output consensus | ||
| [12] | State decomposition | discrete-time | ✓ | ✓ | average consensus | |
| [13] | Node augment | discrete-time | ✓ | leader-following | ||
| [35] | Quantized offset | discrete-time | ✓ | ✓ | ✓ | average consensus |
| This article | Ouput mapping | continuous-time | ✓ | ✓ | ✓ | formation control |
| UAV | Triggering Events | Inforamtion Transmission | ||||
|---|---|---|---|---|---|---|
| Algorithm 1 | Algorithm 2 | This Paper | Algorithm 1 | Algorithm 2 | This Paper | |
| 1 | 248 | 231 | 198 | 496 | 462 | 396 |
| 2 | 248 | 306 | 223 | 744 | 918 | 669 |
| 3 | 248 | 220 | 181 | 496 | 440 | 362 |
| 4 | 248 | 298 | 214 | 744 | 894 | 642 |
| 5 | 248 | 258 | 223 | 496 | 516 | 446 |
| Total | 1240 | 1313 | 1039 | 2976 | 3230 | 2515 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, J.; Qin, K.; Shi, M.; Jiang, B.; Li, W.; Shi, L. Event-Trigger-Based Finite-Time Privacy-Preserving Formation Control for Multi-UAV System. Drones 2023, 7, 235. https://doi.org/10.3390/drones7040235
Yue J, Qin K, Shi M, Jiang B, Li W, Shi L. Event-Trigger-Based Finite-Time Privacy-Preserving Formation Control for Multi-UAV System. Drones. 2023; 7(4):235. https://doi.org/10.3390/drones7040235
Chicago/Turabian StyleYue, Jiangfeng, Kaiyu Qin, Mengji Shi, Bing Jiang, Weihao Li, and Lei Shi. 2023. "Event-Trigger-Based Finite-Time Privacy-Preserving Formation Control for Multi-UAV System" Drones 7, no. 4: 235. https://doi.org/10.3390/drones7040235
APA StyleYue, J., Qin, K., Shi, M., Jiang, B., Li, W., & Shi, L. (2023). Event-Trigger-Based Finite-Time Privacy-Preserving Formation Control for Multi-UAV System. Drones, 7(4), 235. https://doi.org/10.3390/drones7040235






