Optimal UAV Hangar Locations for Emergency Services Considering Restricted Areas

Abstract

With unmanned aerial vehicle(s) (UAV), swift responses to urgent needs (such as search and rescue missions or medical deliveries) can be realized. Simultaneously, legislators are establishing so-called geographical zones, which restrict UAV operations to mitigate air and ground risks to third parties. These geographical zones serve particular safety interests but they may also hinder the efficient usage of UAVs in time-critical missions with range-limiting battery capacities. In this study, we address a facility location problem for up to two UAV hangars and combine it with a routing problem of a standard UAV mission to consider geographical zones as restricted areas, battery constraints, and the impact of wind to increase the robustness of the solution. To this end, water rescue missions are used exemplary, for which positive and negative location factors for UAV hangars and areas of increased drowning risk as demand points are derived from open-source georeferenced data. Optimum UAV mission trajectories are computed with an A* algorithm, considering five different restriction scenarios. As this pathfinding is very time-consuming, binary occupancy grids and image-processing algorithms accelerate the computation by identifying either entirely inaccessible or restriction-free connections beforehand. For the optimum UAV hangar locations, we maximize accessibility while minimizing the service times to the hotspots, resulting in a decrease from the average service time of 570.4 s for all facility candidates to 351.1 s for one and 287.2 s for two optimum UAV hangar locations.

1. Introduction

According to the World Health Organization [1], drowning is the third leading cause (7%) of unintentional injury-related deaths worldwide. Thus, alerting emergency responders and localizing victims in the water are particular challenges at the start of the rescue chain. Autonomous Unmanned Aircraft Systems (UAS) for Search & Rescue (SAR) operations may detect persons in distress faster than helicopters, boats, or lifeguards. Furthermore, the precise dropping of a flotation device may extend the chance of survival until conventional rescue services arrive on site. However, such UAS also require safe integration into the airspace, well-suited operational automation, and ensuring the safety of third parties on the ground, e.g., according to the UAS geographical zones of the Commission Implementing Regulation (EU) 2019/947 [2].

This paper uses open-source georeferenced data to solve a Facility Location Problem (FLP) for decentralized autonomous Unmanned Aerial Vehicle (UAV). The UAV hangar locations are optimized by minimizing the service times to hotspot areas with increased risk for accidents, while considering optimum standard SAR missions to incorporate the routing problem including the avoidance of UAS geographical zones and potentially crowded areas. As an application, we utilize the model region of the research project RescueFly, which studies the prototypical implementation of two non-holonomic UAV at the remote Lusatian Lake District in the Federal State of Brandenburg and the Free State of Saxony in Germany. Figure 1 shows the 109 georeferenced layers from open data sources, which we discretize and merge to determine the solution space for planning optimized safe flight routes and to derive positive and negative location factors to solve the FLP given two finite sets of potential hangar locations and hotspots.

A standard SAR mission is defined for the UAV, which includes the planning of a restriction-free path to and from the hotspot area and a complete search of the hotspot, limited by the maximum endurance of the UAV. As the used A* algorithm for path planning is reliable but computationally expensive, we transform the georeferenced data into a binary occupancy grid image and labeled the solution space using a fast connected-component algorithm to identify non-permissible connections between potential UAV hangar locations and hotspots. In addition, direct connections, i.e., paths not affected by restrictive areas, are identified using a fast ray–occupancy intersection algorithm. The proposed methodology determines location candidates from open-source data and provides accessibility scores for these candidates to find the optimum UAV hangar locations. To increase the robustness of the solution, we consider various UAV geographical zones and different wind cases affecting the UAV endurance.

This section continues with a review of the state of the art, focusing on other SAR applications for UAS, UAV mission planning, automated detection of persons in distress, and approaches to the FLP for UAS. The following section then describes the methodology for solving the FLP with multi-objective optimization, considering positive and negative location factors and constraints, such as the battery capacity or the external risk for up to two locations. Subsequently, the results of our work are shown, indicating candidate locations for the UAV hangars. Finally, we conclude by discussing possible next steps.

1.1. SAR Concepts with UAS

Various SAR concepts have been studied using UAS as a component in the rescue chain. Ajgaonkar et al. [6] developed a UAV to assist lifeguards at coastal beaches. They assumed that the lifeguard provides the initial identification of the person in distress to a UAV operator, who then searches the area to drop a flotation device. Similarly, Seguin et al. [7] conducted a study with UAV delivering flotation devices to swimmers at the lifeguard’s remote control, showing that the faster delivery compared to the lifeguard or a jet ski reduces the submersion time and therefore the risk of drowning significantly. Dufek and Murphy [8] introduced the concept of combining an UAV with an Unmanned Surface Vehicle (USV) for offshore emergencies, which searches the person in distress and serves as a flotation device. The UAV serves to first guide the USV to the victims and then to track the drift of the USV for the emergency responders.

Liu et al. [9] presented an operational concept for UAV usage in SAR missions over rivers, in which they predicted the drift using Monte Carlo simulations to delimit the search area. For the faster coverage of larger areas, authors, such as Ruetten et al. [10], proposed swarm networks consisting of many UAVs that organize themselves to reach optimal search coverage with minimal overlapping. While this approach ensures fast detection over large areas, it poses an additional external risk to persons and significantly increases the required infrastructure and equipment. Thus, it is deemed unfeasible for SAR missions at bathing lakes.

1.2. UAV Flight Path Planning

The most crucial factor in SAR is the time since the early detection of a drowning person substantially improves the chances of survival. From the technical standpoint, the battery capacity also limits the flight time of an UAV, which requires efficient path planning from the UAS hangar to identify, reach and search the target area. Brühl et al. [11] provided a methodology to estimate energy consumption based on the flight phase for various large air taxis, including multi-copter designs similar to UAV for SAR. Citroni et al. [12] developed a model to estimate the energy consumption of very light and small Micro Air Vehicles, including options for energy harvesting to extend the endurance. While the concept is promising, it cannot be adapted to larger multi-copter UAV in the ’specific’ category yet. Chu et al. [13] analyzed the impact of wind on the battery capacity of small quad-copter UAV, considering wind speed, direction, and turbulence in a simulation. They found wind conditions up to 11 m s⁻¹ suitable for surveying crash areas regarding the additional energy consumption, but also emphasized the significant increase in consumption in higher turbulence.

Lin and Goodrich [14] created a probability distribution map to accelerate wilderness SAR with a UAV flying 60 m above ground. With this map, they converted the path search into a discretized combinatorial optimization problem and applied variants of complete-coverage, local hill climbing, and evolutionary algorithms with and without a defined destination, finding that the local hill-climbing algorithm with a convolution kernel performs best. Hayat et al. [15] developed a multi-objective path planning based on a genetic algorithm that minimizes the search time, which balances the search area coverage with the network connectivity coverage to ensure communication with the emergency responders. Wang et al. [16] proposed a vortex search algorithm for multi-objective path optimization to guide UAV to forest fires, considering obstacles and terrain described with a cubic interpolation method. Jayaweera and Hanoun [17] studied a path-planning problem for an UAV to follow a ground-moving target with variable speed and direction. They used an artificial potential field to correct the wind disturbance, demonstrating a maximum deviation of the camera aim point of 0.41 m for a vehicle speed of 10 m s⁻¹ and a wind speed of 8 m s⁻¹.

After reaching the search area, an efficient method for scanning this area is required. Zuo et al. [18] suggested an extended square search, which expands from the center of the search area, assuming that positions closer to the center are more likely than distant ones. Liang et al. [19] developed a heuristic to avoid redundant image coverage and maximize image quality during a SAR mission with an energy-constrained UAV. Dakulović et al. [20] developed a complete coverage D* algorithm for a floor-cleaning mobile robot, minimizing path length and search time in a constrained area with unknown obstacles. Xu et al. [21] studied a Complete Coverage Neural Network (CCNN) for an unmanned surface vehicle for complete coverage of a search area and combined it with an improved A* algorithm to escape deadlock situations efficiently. Sun et al. [22] proposed a two-step auction method to coordinate multiple UAV to cover a mutual search area, considering the avoidance of obstacles and the energy constraints of the UAV. Sun and Ma [23] proposed a two-phase search for aircraft maintenance. Initially, a high-altitude scan is performed. The information is then used in a Monte Carlo tree search algorithm to find a safe path for the inspection afterward. Approaches such as these can accelerate the time-critical search for a person in distress, but they also raise concerns regarding the air and ground risks for both multiple UAV and higher altitudes; there is also the risk of missing persons entirely in the initial scan.

1.3. Automated Detection of a Person in Distress

When covering the search area with the UAV, the person in distress must be detected swiftly, even when large groups are swimming simultaneously. For this, Qingqing et al. [24] analyzed different altitudes and camera angles for human detection in marine SAR to find a trade-off between speed and detection accuracy with the real-time object detection model of YOLOv3. They found that individuals can be detected from greater distances when the camera angle is closer to facing straight down (known as nadir). Above 100 m, however, confidence and accuracy drop significantly since it is a function of the camera lens and image resolution. Rudol and Doherty [25] presented a method to detect human bodies lying or sitting on the ground by combining video and thermal sensors. For maritime SAR, it remains unclear if a thermal sensor can produce similar results, especially for submerged persons. Bejiga et al. [26] trained a Convolutional Neural Network (CNN) to assist avalanche SAR with faster detection of victims utilizing optical cameras fitted to UAV. Lygouras et al. [27] used CNN to detect persons swimming in open water with an autonomous UAV. Feraru et al. [28] proposed a concept to deploy autonomous UAV for man-overboard incidents using a probabilistic leeway model with a Faster Region-based Convolutional Neural Network (R-CNN) to detect a person in the water. Liu and Szirányi [29] studied a two-stage approach, in which they first detected persons in UAV video footage and then interpreted basic gestures used by persons in distress using neural networks. Wang et al. [30] proposed a different two-stage approach. First, persons are located with simpler features to reduce the search space, and second, a CNN is applied to the previously selected areas. Liu and Szirányi [31] used UAV to detect main and secondary roads from image data, and provide an optimum route with an A* algorithm for people in the field. However, the planning of the mission trajectory for the UAV was rarely considered in these studies.

1.4. Facility Location Problem

A FLP models the selection and localization of facilities to serve demand at specific points or areas, such as hospitals, fire stations, or warehouses. The Uncapacitated Facility Location Problem (UFLP) is one of the most commonly considered combinatorial optimization problems, in which two finite sets of potential facilities and demand points are considered by assessing the associated costs for the facility construction and the distance or cost for each combination of demand point and facility location. The objective of the optimization problem is to select the facility locations to be established and allocate the demand points by minimizing the total operational costs [32,33]. The k-facility problem is a UFLP with the additional constraint of $k\in \mathbb{N}$ facilities being allowed to open. For facility construction costs equal to zero, k-median clustering can be applied to determine centroids as optimized facility locations. This approach, however, assumes that all distances are as the crow flies [34]. Another option is the lower-bounded FLP, e.g., with the algorithm of Ahmadian and Swamy [35], where each facility must serve a certain minimum amount of demand.

For the delivery of first-aid products using UAVs, Zhu et al. [36] developed a robust two-stage FLP optimization that accounts for customer demand uncertainty. They proposed three models for the problem that outperform a deterministic FLP. Lynskey et al. [37] studied the distribution of UAV ground facilities. They solved the problem with k-means clustering while adding the energy consumption of the UAV as costs using a traveling salesman algorithm to enable UAV to perform multiple tasks with one flight.

As the review shows, there are various studies dealing with optimal routing for UAV. However, any flight restrictions, such as the UAS geographical zones according to EU 2019/947 [2] and § 21h Luftverkehrsordnung (LuftVO) [38] (German Federal Regulation for aircraft operations, which supplements EU 2019/947.), have been rarely considered. Concerning the FLP for UAV, those restrictions are quite significant, as they will extend the flight times and may render location candidates inaccessible. Furthermore, methods on how to obtain suitable information on location candidates, e.g., for positive and negative location standards, are seldom discussed as well.

2. Materials and Methods

2.1. Overview of the Approach

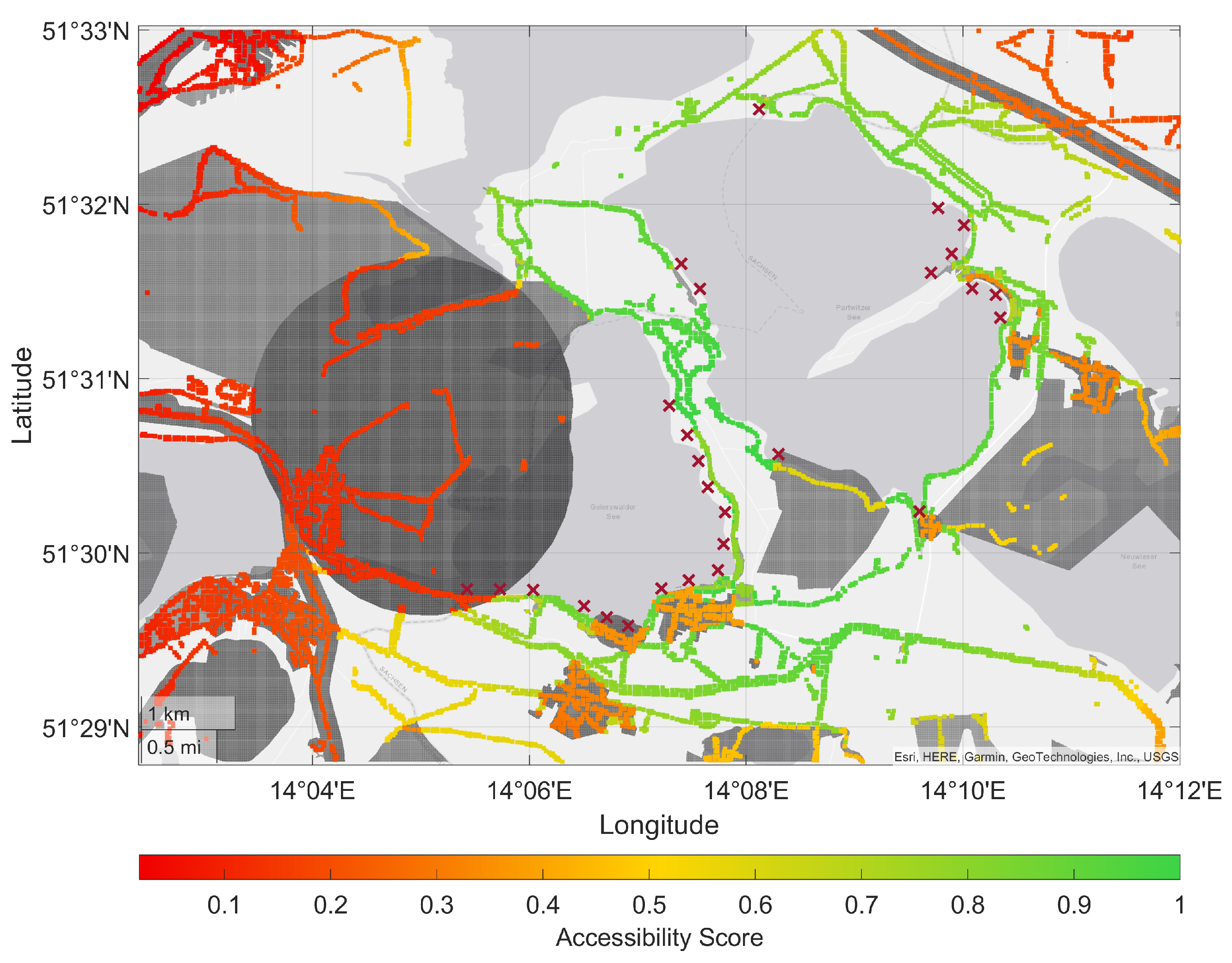
The RescueFly concept of operations plans to assist SAR missions at Lake Geierswalde and Lake Partwitz utilizing automated UAS based in decentralized hangars. We use this opportunity to develop an optimization model to solve the related FLP for UAV hangars, which shall provide minimum service time to hotspot areas where accidents are expected more frequently. These hotspots serve as demand for the FLP, so they must be identified based on their geographic characteristics and nearby amenities. Furthermore, positive and negative location factors must be determined to identify hangar candidate locations. We propose to derive the required information from open-source geographical data, so it is easily transferable to other regions or other FLP.

Furthermore, restricted areas and varying wind conditions affect the service times. This is considered in the FLP with the development of a standard SAR mission, which is optimized individually for each combination of hangar candidate and hotspot location in different scenarios. For the flight time to and from the hotspot area, we consider national and European regulations as well as external risk factors, such as potentially crowded areas with an A* algorithm [39] on a binary occupancy grid to determine the shortest restriction-free flight path. Furthermore, we determine the search time required to find the person in distress in the derived hotspot area. Finally, the endurance of the UAV is also considered a constraint to the FLP.

A location candidate must provide solid ground, power supply, and reasonable access for installing and maintaining the system while being located outside restrictive areas (e.g., hazard areas, UAS geographical zones, natural reserves). In addition, vegetation shading must be avoided to permit reliable communication links to the emergency centers. Furthermore, the location shall grant swift access to designated beaches, recreation sites, hotel and camping facilities, grasslands, and other facilities where people are engaged in activities adjacent to lakes e.g., barbecue areas, boat slipways, and boat rentals. When planning a SAR mission, the risk to third parties, i.e., the air and ground risk, must be considered. SAR operations are excluded from the remit of Regulation (EU) 2018/1139 [40], so the competent national authority is responsible for regulating SAR operations. 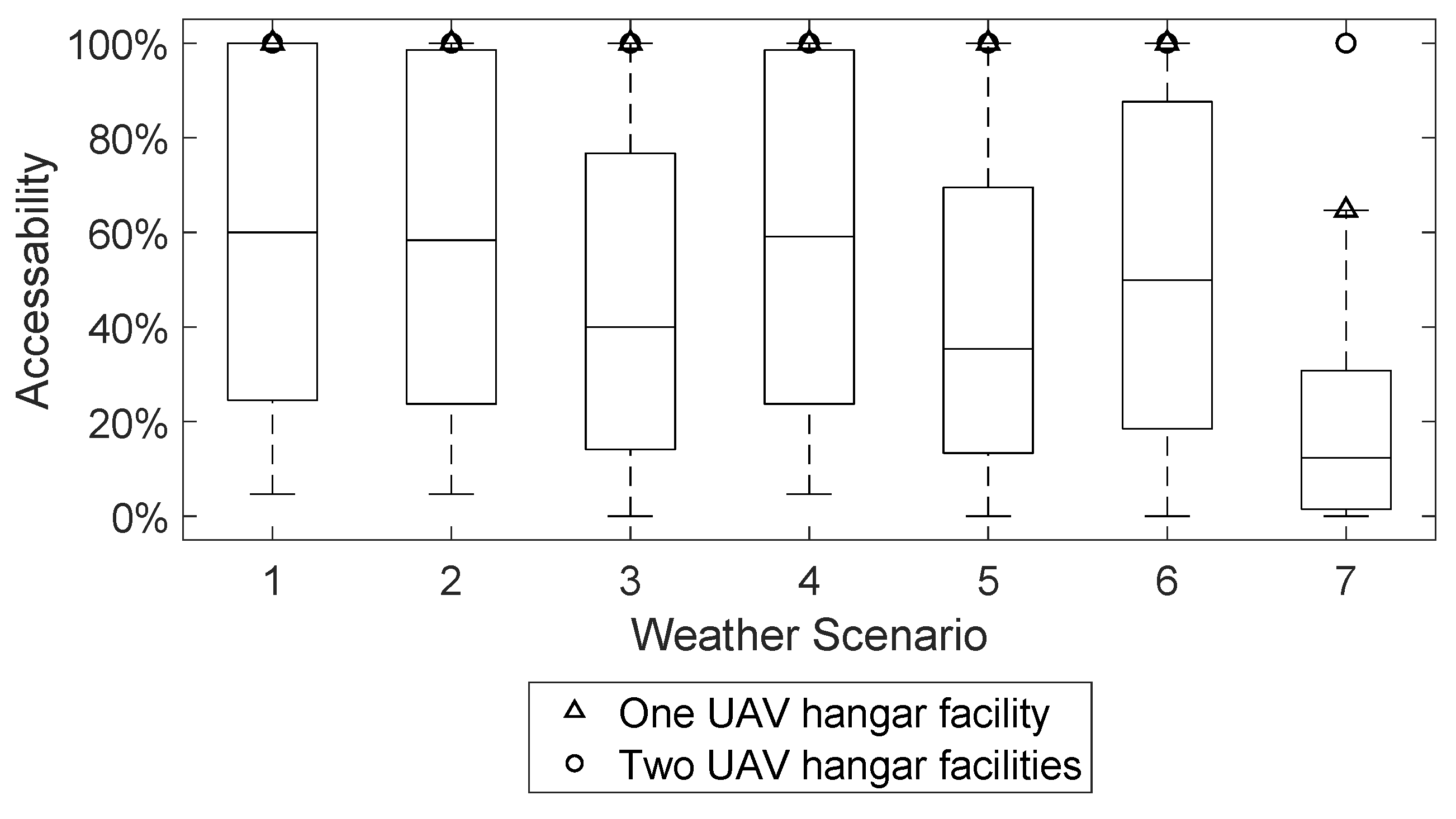According to § 21k LuftVO [38], authorities conducting SAR operations are permitted to fly through UAS geographical zones [2,38]. As the UAV hangar locations shall provide a robust and optimum solution, complying with or flying through various UAS geographical zones can be selected operationally, e.g., depending on the urgency or the exposed crowd size. For this purpose, this paper considers five different scenarios:

1.

Restriction-free flight from the hangar to the hotspot by invoking the special rights of SAR authorities according to § 21k LuftVO [38];

2.

Compliance with specified air risk relevant UAS geographical zones according to EU 2019/947 [2] and § 21h LuftVO [38], e.g., required distance to airfields;

3.

Compliance with UAS geographical zones relevant to air and ground risk;

4.

Compliance with all UAS geographical zones; and

5.

Compliance with all UAS geographical zones and avoidance of crowded areas.

Furthermore, the solution should be robust against the wind. Therefore, different wind cases are considered for each scenario based on the extensive study of Chu et al. [13].

2.2. Acquisition of Open-Source Data

This section reviews open-source data to retrieve relevant information for identifying UAV hangar location candidates, which are divided into three georeferenced data-requirement groups, i.e., (1) positive and negative location factors for establishing UAV hangars. (2) Data are required to identify areas of high intrinsic risks for waterside accidents. (3) The UAS geographical zones according to EU 2019/947 [2] and § 21h LuftVO [38] must be identified for the mission planning with incrementally minimized external risks and environmental impacts according to our scenarios.

The primary source for the former two is the OpenStreetMap (OSM) (Available online: https://www.openstreetmap.org/ (accessed on 22 November 2022)), a community-driven database for georeferenced data layers. OSM defines the georeferenced data with nodes, ways, and relations to describe the geometry, supplemented by tags (key-value principle) describing the object’s function. Using the Overpass API (Available online: https://overpass-turbo.eu/ (accessed on 22 November 2022)), it is possible to define queries for extracting data based on region, layers, and tags. The location factors are based on the surface and its ability to accommodate UAV hangars. As listed in

Table 1. OSM map features for positive UAV hangar location factors.

Key	Values
landuse	grass, greenfield
natural	grassland, heath, scrub, scree

, six tags for areas with grass and minimal vegetation are considered positive. Eight tags for areas with forests, large groups of trees, or wetlands will require additional construction work or shade the communication links, leading to negative location factors in

Table 2. OSM map features for negative UAV hangar location factors.

Key	Value(s)
boundary	forest, forest_compartment, hazard
landuse	forest
natural	tree, tree_row, wood, wetland

. Furthermore, each potential UAV hangar location requires road access for maintenance with a maximum permitted distance of 20 m from the road tags in

Table 3. OSM map features for road access to the UAV hangar location with a maximum distance of 20 m.

Key	Values
highway	motorway, trunk, primary, secondary, tertiary, unclassified, residential, motorway_link, trunk_link, primary_link, secondary_link, living_street, service, pedestrian, track, bus_guideway, escape, raceway, road, busway, cycleway
tracktype	grade1, grade2, grade3

. In addition, the UAV hangar cannot be established on water surfaces, provided as Web Map Service (WMS) (Available online: https://geoportal.brandenburg.de/de/cms/portal/start (accessed on 22 November 2022)). Finally, the power supply should be another positive location factor, but the required data are not public.

Table 4. OSM map features for hotspot areas.

Key	Value(s)
amenity	boat_rental, boat_sharing, ferry_terminal, public_bath, parking, parking_space, lounger
building	beach_hut
emergency	lifeguard, life_ring, phone
landuse	grass
leisure	marina, slipway, swimming_area, swimming_pool, water_park, beach_resort, park, picnic_table
lifeguard	tower
man_made	pier
natural	beach, shingle, shoal, sand
sport	sailing, swimming, surfing, wakeboarding, water_polo, water_ski
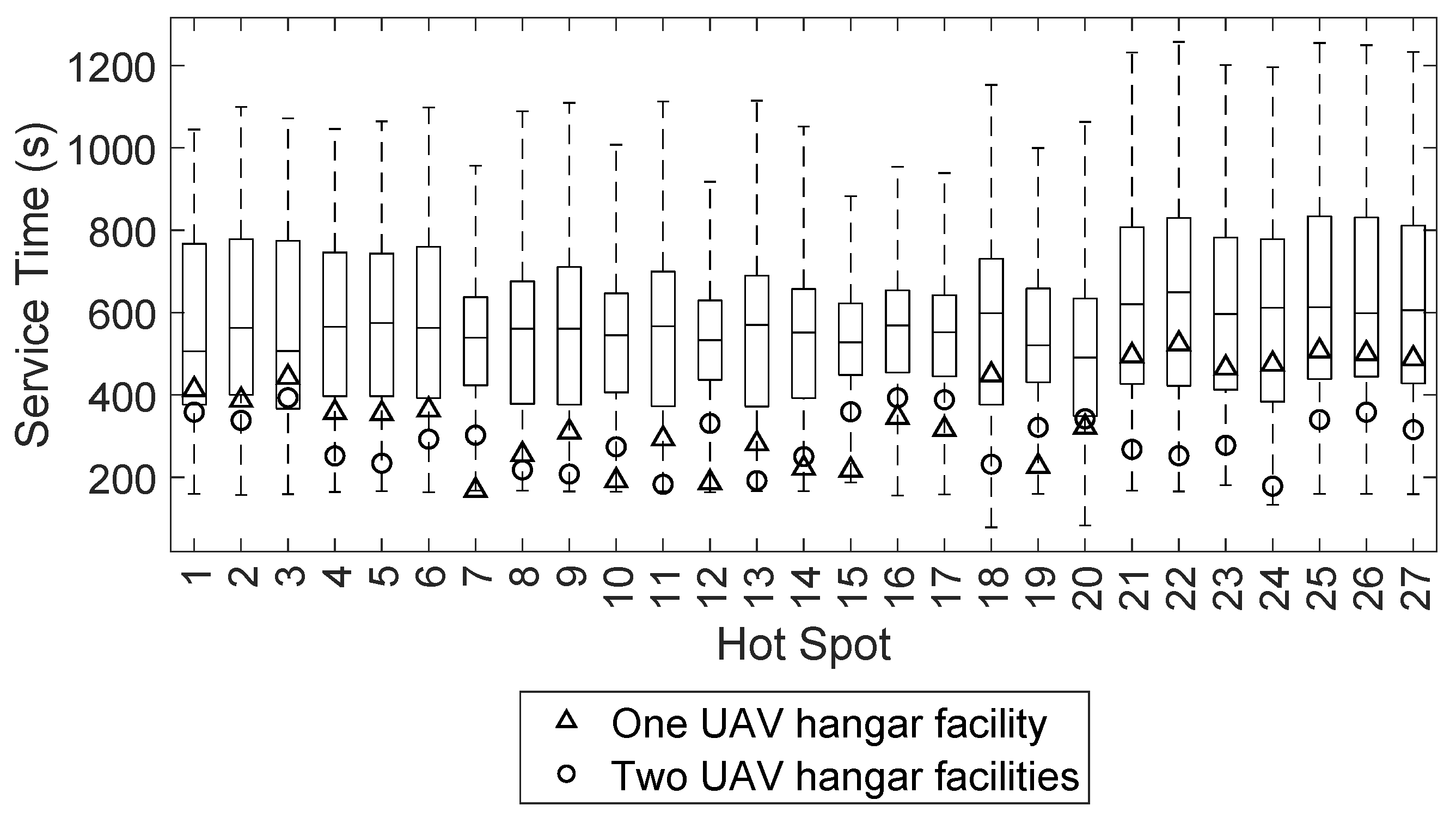
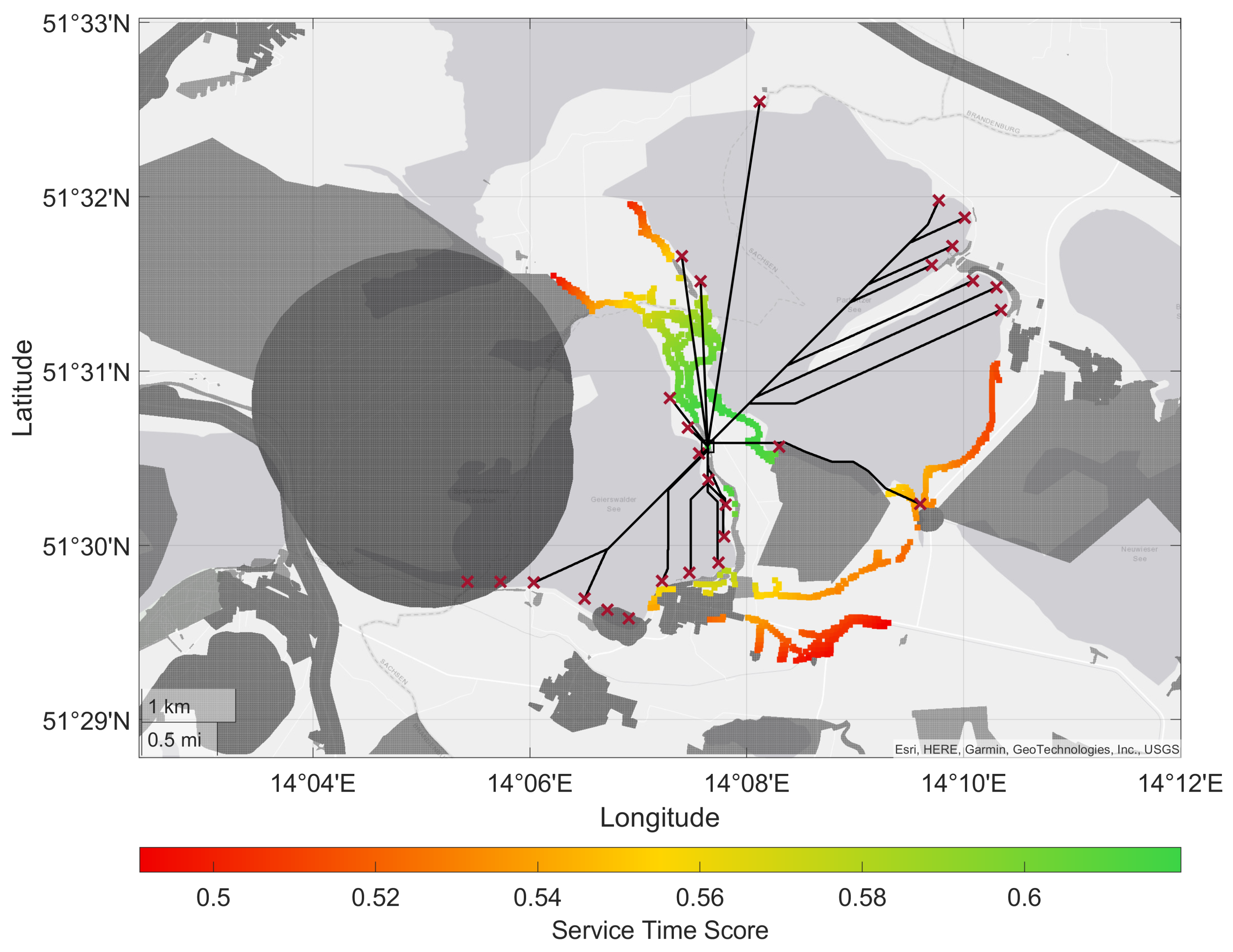
tourism	camp_site, caravan_site

lists 34 map features representing hotspot indicators. We assume that these features increase the probability of an accident on the water. For this purpose, we extrude the resulting map feature nodes and areas with a radius of 150 m in size, followed by an intersection with the water surfaces of the investigated lakes. If an area is a subset of the extruded hotspot indicators and a subset of either of the water areas at the same time, it is identified as a hotspot area. The radius of 150 m is based on the distance between buoys and shoreline of approximately 120 m plus an additional 30 m buffer since the OSM features may be georeferenced slightly outside of the shorelines. We assume that most swimmers tend to stay within the prescribed limits, increasing the risk of accidents in these areas.

For the planning of the standard SAR mission, the UAS geographical zones [2,38] are required. For UAV operations in Germany, the Digital Platform for Unmanned Aviation (dipul) provides a map tool (available online: https://maptool-dpul-prod.dfs.de/ (accessed on 22 November 2022)) and web map service indicating the UAS geographical zones as separate layers. For data transmission, the availability of a sufficient broadband connection should be considered as well. However, the so-called Breitband monitor (available online: https://www.breitband-monitor.de/mobilfunkmonitoring (accessed on 16 December 2022)) of the German Bundesnetzagentur provides only coverage at the ground level, so open-source data at cruising and search altitudes cannot be retrieved thus far.

2.3. Definition of the Standard SAR Mission

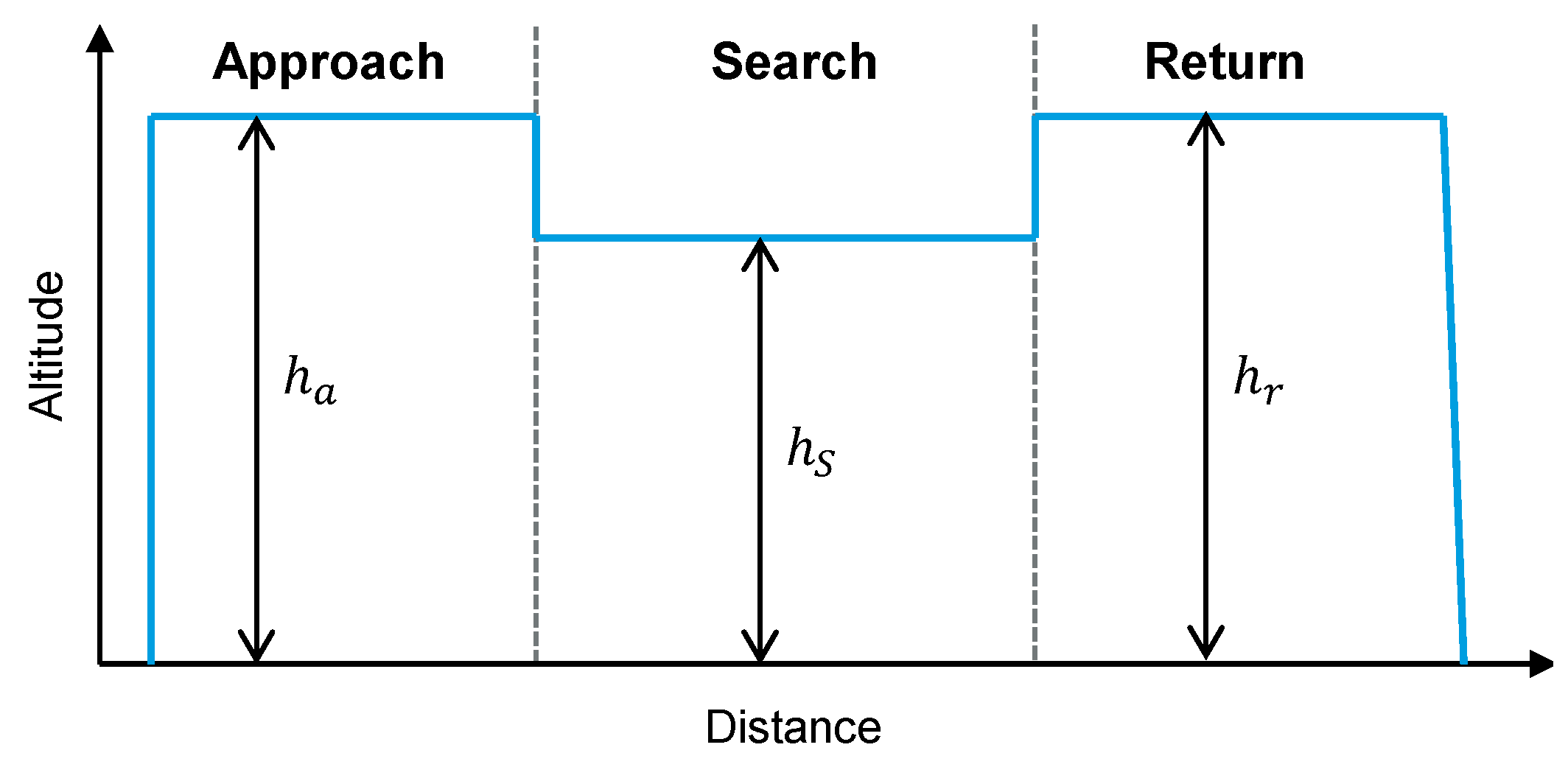
As the battery capacity limits the operation duration of the UAV, a restriction-free flight path between each potential UAV hangar location and each hotspot, and a standard search mission must be defined to assess the accessibility of the hotspot and feasibility of the search mission, given varying UAS geographical zones and wind scenarios. Each standard SAR mission consists of three phases: the approach, the search mission, and the return to the hangar. For consistency, we assume that the approach and return flights have the same paths and vertical profiles. Furthermore, as shown in Figure 2, we assume a vertical climb at the UAV hangar to the approach altitude $h_a$, which is maintained until the UAV reaches the hotspot area. There, the UAV descends vertically to the search altitude $h_s$, which depends on the required resolution to detect a person in distress, and continues with a search pattern at $h_s$. After the search, the UAV climbs to maintain the return altitude $h_r$ until reaching the hangar.

A maximum altitude of $h_a=h_r=$ 100 m above ground is assumed for approach and return, leaving a safety buffer to the maximum permitted altitude of 120 m for the ‘specific’ category [2]. $h_s$ depends on the characteristics and orientation of the camera and the required resolution for the automated detection of a person in distress. The camera of our UAV has an aspect ratio of 4:3 with a resolution of $R=12$ Mpx, a lateral field of view $\alpha =56°$, a vertical field of view $\beta =45°$, and a 1/2.3″ CMOS sensor.

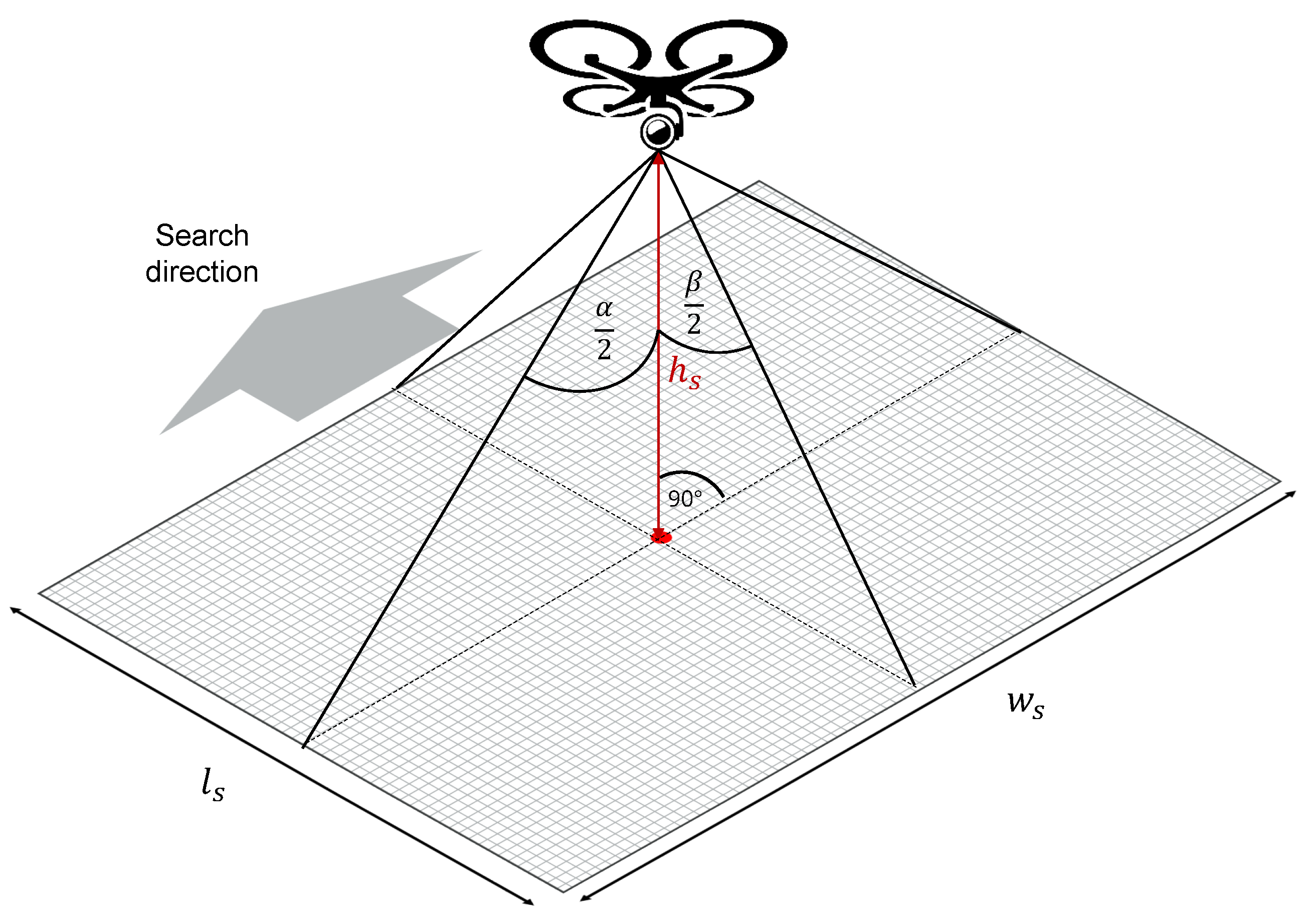
The camera faces perpendicularly downward (i.e., nadir) to the water surface, guaranteeing the best coverage and detection [24]. Furthermore, the larger $\alpha$ is perpendicular to the search direction so that the UAV is centered above the middle of the covered surface in a single camera frame, as shown in Figure 3. Then, the achieved pixel density D in [px m⁻²] per frame is given with the search width $w_s$ and length $l_s$ in [m] according to:

$$D=\frac{R}{w_s·l_s}$$

(1)

Using the tangent of two assumed right-angle triangles, $w_s$ and $l_s$ can be determined at given $h_s$ with $\alpha$ and $\beta$:

$$\begin{array}{cc}\hfill w_s& =2·h_s·tan\left(0.5·\alpha \right)\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill l_s& =2·h_s·tan\left(0.5·\beta \right)\hfill \end{array}$$

(3)

The required minimum pixel density $D_{min}$ significantly drives the optimum $h_s$ to detect persons in distress autonomously. A trade-off is necessary between a high-as-possible $h_s$ for minimum-time coverage of the search area for the fastest SAR, and a sufficiently high pixel density to solve the detection and recognition task reliably, i.e., to distinguish persons in distress from all other swimmers. For estimating $D_{min}$, a set of test images of 35 swimming volunteers has been taken at Lake Partwitz under sunny and clear conditions without any significant wind. From the set, 96 images of different pixel densities between 5 to 3300 px m⁻² were generated, an example set is shown in Figure 4. Those images were presented to 10 test persons (3 female, 7 male) aged 30 to 40 ($\mu =33.4,\sigma =3.34$), thus equaling 960 samples. The test person’s tasks are (a) detecting objects in the image and (b) recognizing and describing the activity of the swimming persons. If all persons per image are detected, task (a) is classified as positive; if at least one person remains undetected, it is considered negative. If the test persons describe all activities of the swimmers correctly (e.g., breaststroke with drawn legs), task (b) is classified as positive.

The experiments show an average $D_{min,\left(a\right)}$ = 9 px m⁻² with ${\sigma }_{\left(a\right)}$ = 8 px m⁻², and $D_{min,\left(b\right)}$ = 503 px m⁻² with ${\sigma }_{\left(b\right)}$ = 493 px m⁻². The task complexity correlates strongly with the number and types of objects per test image resulting in high standard deviations. Thus, images containing few volunteers or volunteers on floating objects (e.g., surfboards) show significantly lower $D_{min}$ due to contrast and size. Moreover, their activities are recognized more reliably than images with many volunteers swimming closely together. The obtained $D_{min}$ from the test persons serve as estimates for the Deep Convolutional Neural Network (DCNN) intended to automatically detect a person in distress, assuming it will not perform significantly better or worse than humans. van Dyck et al. [41] confirm this hypothesis, in which the DCNNs ResNet18 and vNet achieved $79.05\%$ and $84.76\%$ accuracy, respectively, compared to $89.96\%$ of human observers. With $D_{min}$, Equations (1)–(3) are rearranged to solve for $h_s$:

$$h_s\le \sqrt{\frac{R}{4·D_{min}·tan\left(0.5\alpha \right)·tan\left(0.5\beta \right)}}$$

(4)

Since the goal of the search mission is the reliable recognition of the person in distress, it is assumed that $D_{min}=D_{min,\left(b\right)}+3{\sigma }_{\left(b\right)}$ = 1981 px m⁻² is required to avoid misdetection, which is a ground sampling distance of 0.0225 m. With Equation (4), $h_s\le$ 82.92 m is determined to fulfill the task (b).

With the standard UAV mission, a set can be generated from the potential UAV hangar location F (Facility), a hotspot H as the demand, a wind scenario W, and a UAS geographical zone scenario Z. The corresponding total flight time $t_{i,j}^{m,n}\in \mathbb{R}+$, for $i\in F$, $j\in H$, $m\in W,n\in Z$ constitutes the evaluation metric. The flight distance $d_{i,j}^n$ results from the shortest restriction-free flight path from $i\in F$ to $j\in H$ considering $n\in Z$. For this, the approach and return flight are assumed identical, i.e., $d_{i,j}^n:=d_{j,i}^n$. Since various shapes of hotspot areas exist and the search time depends on the coverage algorithm, we simplify the resulting hotspot areas $a_j$ [m²] to rectangles with the identical area and the edge length $w_s$ [m] of Figure 3. Furthermore, an additional search detour factor $f_s=1.1$ accounts for different coverage algorithms and shapes, resulting in a search distance $s_j$:

$$s_j=\left(\frac{a_j}{w_s}-l_s\right)·f_s$$

(5)

According to the UAV manufacturer, a reliable cruise speed during approach and return $v_1$ = 10 m s⁻¹ and a vertical rate $v_2$ = 2.5 m s⁻¹ is achieved. During the search phase, we assume a slower search speed $v_3$ = 5 m s⁻¹ to provide suitable coverage and reduced motion blur. The total flight time for successive maneuvers (cf. Figure 2) is:

$$t_{i,j}^{m,n}=\left(2\frac{h_a}{v_2}+2\frac{d_{i,j}^n}{v_1}+2\frac{h_a-h_s}{v_2}+\frac{s_j}{v_3}\right)·f_m$$

(6)

$f_m$ in Equation (6) represents the detour factor per wind scenario $m\in W$. The actual values are derived from Chu et al. [13], using wind speeds below 11 m s⁻¹ as recommended. We computed $f_m$ for seven wind scenarios in

Table 5. Wind scenarios with detour factors $f_m$ derived from the battery use studied by Chu et al. [13].

Wind Scenario	Wind Speed	Turbulence Index	Detour Factor
$\mathit{m}\in \mathit{W}$	[m s−1]		${\mathit{f}}_{\mathit{m}}$
1	0	0	1.0
2	3.5	0	1.023
3	10.5	0	1.237
4	3.5	10	1.018
5	10.5	10	1.311
6	3.5	20	1.109
7	10.5	20	2.199

with the battery use from Table 10 [13], averaging over all wind directions and normalized on 1 s of flight time. Furthermore, the wind scenario $m=1$ with 0 m s⁻¹ and turbulence index 0 is added as a baseline case with $f_m=1$.

Given the flight endurance E = 22 min, each rescue mission from i to j is evaluated, so $t_{i,j}^{m,n}\le E$ from Equation (6) are only classified as accessible:

$$A_{i,j}^{m,n}·(E-t_{i,j}^{m,n}+ϵ)·M\ge E-t_{i,j}^{m,n}+ϵ$$

(7)

Thus, $A_{i,j}^{m,n}\in \{0,1\}$ is the binary accessibility variable from $i\in F$ to $j\in H$, avoiding $n\in Z$ and considering $m\in W$, with the Big-M parameter M and an infinitesimally small positive quantity $ϵ$.

2.4. Optimization Model for UAV Hangar Positions

This section describes the FLP model to determine $P\in \mathbb{N}$ optimum UAV hangar locations with maximum accessibility to all hotspots $j\in H$ across all wind scenarios $n\in W$ and all UAS geographical zone scenarios $n\in Z$ while minimizing the respective total flight time. For that, we consider a finite set H of hotspots and a finite set F of potential facilities with the binary success variable $A_{i,j}^{m,n}\in \{0,1\}$ from Equation (7) and total flight time $t_{i,j}^{m,n}\in \mathbb{R}+$ from Equation (6), such that:

$$max\sum _{i\in F}\sum _{j\in H}\sum _{m\in W}\sum _{n\in Z}(A_{i,j}^{m,n}-t_{i,j}^{m,n})$$

(8)

With the binary parameter $y_j\in 0,1$ and P facility locations to be established, while $x_{i,j}^n\in 0,1$ ensures that each i is connected to only one j:

$$\begin{array}{cccc}\sum _{i\in F}{y}_i\hfill & \le P\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall i& \in F\hfill \end{array}$$

(9)

$$\begin{array}{cccc}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{x}_{i,j}^n\hfill & \le y_i\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall i& \in F,j\in H,n\in Z\hfill \end{array}$$

(10)

$$\begin{array}{cccc}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\sum _{i\in F}{x}_{i,j}^n\hfill & \le 1\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \forall i& \in F,j\in H,n\in Z\hfill \end{array}$$

(11)

To this end, we process the data of Section 2.2 in a georeferenced 5 m × 5 m grid inside $[51.48°,51.55°]$ latitude and $[14.04°,14.20°]$ longitude. Then, the location factors from Table 1 and Table 2 identify the solution space for candidate locations. To reduce the computational effort, a spacing of 50 m between the candidates for UAV hangar locations is chosen, resulting in $\left|F\right|=5949$ candidate locations. The hotspot areas from Section 2.2 are processed with connected component labeling, resulting in 11 separate hotspot areas of varying extents across the two lakes. Each hotspot area is represented by hotspot centroids of a k-means clustering algorithm where k is the quotient of the respective hotspot area and the smallest hotspot area as an integer, resulting in a total of $\left|H\right|=27$ hotspot locations. Consequently, a total of $27·5949·7·5=5.622\times {10}^6$ path computations for one optimum facility location and $27·\left(\genfrac{}{}{0pt}{}{5949}{2}\right)·7·5=1.672\times {10}^{10}$ calculations for two hangar locations is required. 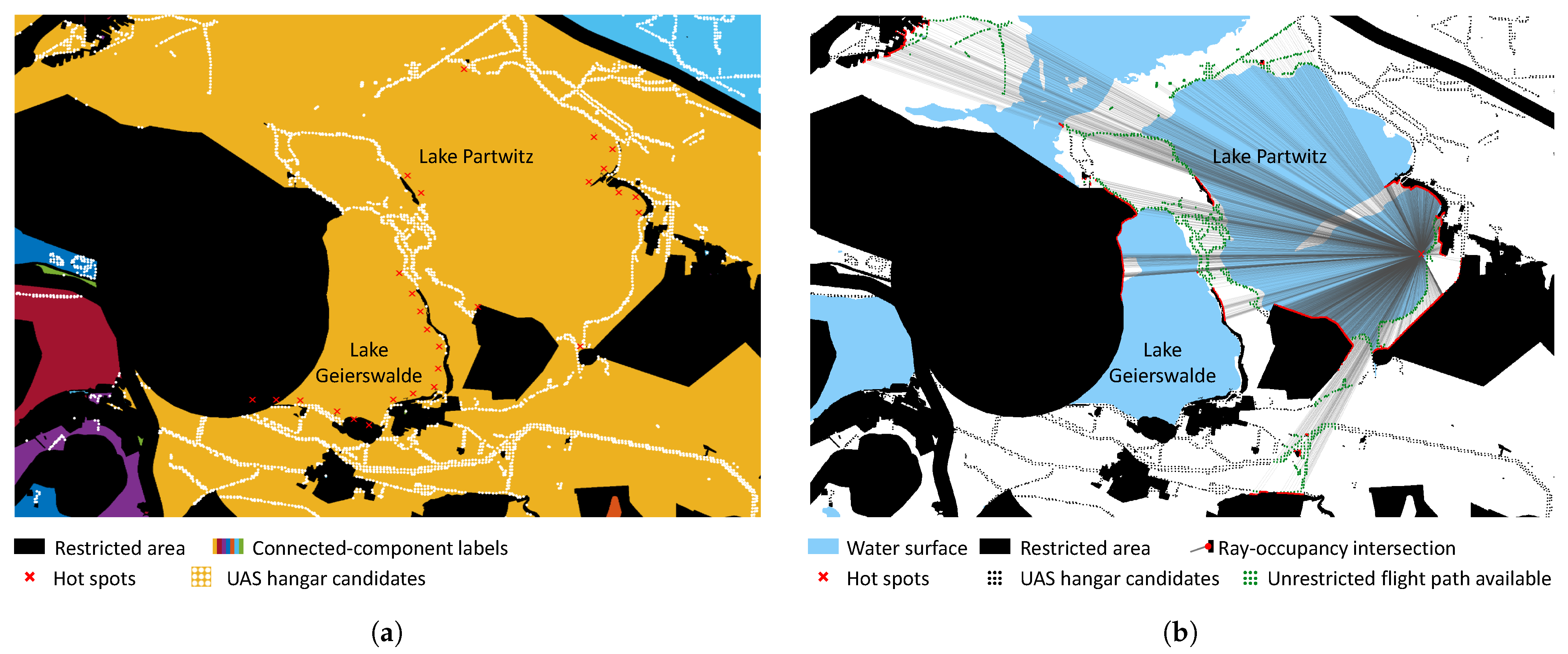Since the restriction-free pathfinding with the A* algorithm [39] has a high computational effort, we reduce the number of paths by applying the two techniques illustrated in Figure 5.

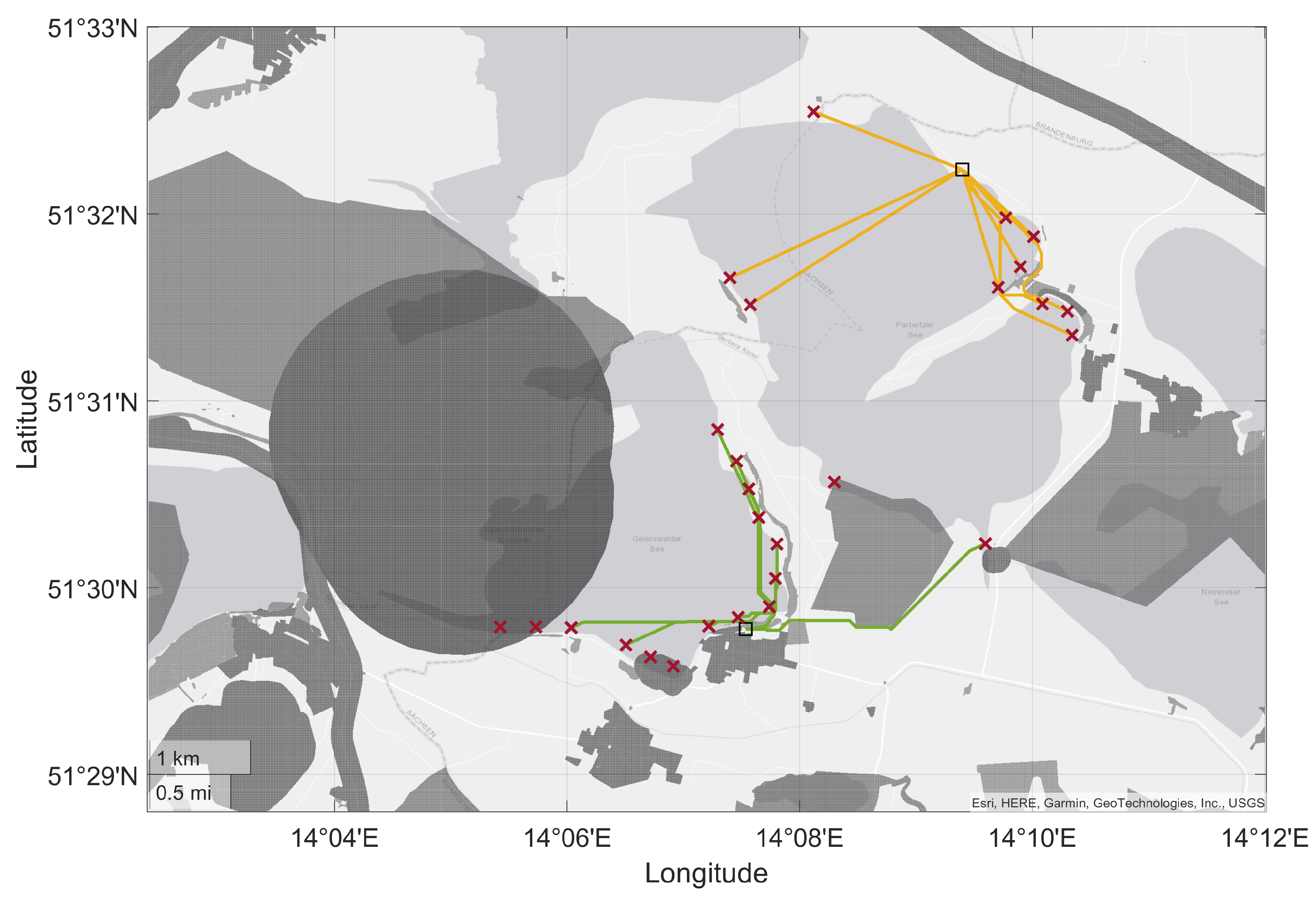
First, we label the discretized binary occupancy grid using a connected components algorithm removing all inaccessible candidates due to restrictions. Figure 5a illustrates the method for $n=5$ as an example. All candidate locations labeled ‘yellow’ are valid connections to the hotspots, removing invalid candidate locations (e.g., ‘purple’) from the later pathfinding.

Second, a fast ray occupancy intersection algorithm checks if straight paths from j to i exist that do not infringe on restricted areas. If this is the case, the shortest path is already found, and the A* pathfinding around restricted areas is not required for this particular combination. Figure 5b illustrates the procedure using $n=5$ as an example. Green-marked location candidates permit direct paths, given one example hotspot at Lake Geierswalde. Red borders show interruptions due to the occupancy envelope, respectively, invalid direct paths.

With these two steps, all UAV hangar candidates without valid connections were removed, and the shortest path to all candidates with unrestricted straight connections were successfully found. Accordingly, only the candidates with the same connected component label in Figure 5a and intersecting with the occupancy envelope in Figure 5b require calculating a restriction-free path with the A* algorithm [39] in the two-dimensional discretized operation space. Horizontal, vertical, and diagonal movements are allowed. The cumulative great circle distance of the georeferenced path nodes along the shortest path from each source to each sink was subsequently calculated, considering UAS geographical zones for all $n\in Z$.

3. Results

Using $P=1$ and $P=2$ planned UAV hangar facilities as examples, we demonstrate the resulting optimum locations according to Equations (8)–(11), and compare their performance with the remaining candidates. For the shortest path calculation, the two methods described in Section 2.4, cf. Figure 5, predetermine 100% of the distances for $n=1$, 79.89% for $n=2$, 73.94% for $n=3$, 66.51% for $n=4$, and 47.15% for $n=5$, resulting in a significant reduction in the computational time. The remaining shortest paths are calculated with an A* algorithm [39] to determine $d_{i,j}^n$ for Equation (6).

Figure 6 visualizes the accessibility score $A_i\forall i\in F$. It is derived from the accessibility $A_{i,j}^{m,n}$ according to Equations (8)–(11) but additionally normalized for all scenarios n and m based on the maximum number of accessible hotspots. $A_i=0$ in red indicates hangar location candidates with the lowest accessibility across all scenarios, while $A_i=1$ in green represents the hangar location candidates with the most accessible hotspots in all scenarios. Different shades of gray indicate the UAS geographical zones of the scenarios n.

Since some hotspots, e.g., $j=1$, are located inside UAS geographical zones, they cannot be reached from any location candidate in those scenarios containing this particular UAS geographical zone. For $n=1$, all hotspots are located outside UAS geographical zones, so they can be served as desired. For $n=2$, two hotspots are inside a UAS geographical zone, reducing the maximum accessible hotspots to 25. In this case, the inaccessible hotspots are removed from the score, resulting in $A_i=1$ for the best candidates. Analogously, a maximum of $[27,25,23,22,22]$ hotspots is achievable for all n. So for $P=1$, five potential locations exist that cover the most hotspots across all scenarios $n\in W$ and $m\in Z$.

Table 6. Number of hotspots served by the $P=1$ optimum UAV hangar locations per wind and UAS geographical zone scenario.

Geographical Zone	Wind Scenarios $\mathit{m}\in \mathit{W}$
$\mathit{n}\in \mathit{Z}$	1	2	3	4	5	6	7
1	27	27	27	27	27	27	17
2	25	25	25	25	25	25	17
3	23	23	23	23	23	23	15
4	22	22	22	22	22	22	14
5	22	22	22	22	22	22	14

shows the resulting number of hotspots covered by them.

Figure 7 summarizes $A_i$ per wind scenario m, in which the zero- and low-wind cases $m=\{1,2,4\}$ provide a high median accessibility of approximately 60% for all location candidates. Furthermore, the optimum locations for both $P=1$ and $P=2$ guarantee 100% accessibility in all wind scenarios except $m=7$, where the optimum solution for $P=1$ achieves a mean accessibility of approximately 65%. In this high-wind–high-turbulence case, E is smaller than a subset j of $t_{i,j}^{7,n}$, so some hotspots cannot be reached in such weather conditions.

For analyzing the SAR performance, we compute the service time $S_{i,j}^{m,n}$ in [s], which is the duration until the search mission ends and the return to the UAV hangar starts. Thus, it indicates the worst case until the person in distress will be discovered in the search area, with:

$$S_{i,j}^{m,n}=\left(\frac{h_a}{v_3}+\frac{d_{i,j}^n}{v_1}+\frac{h_a-h_s}{v_3}+\frac{s_i}{v_2}\right)·f_m$$

(12)

Figure 8 summarizes the service times across all $n\in Z$ for all $i\in H$ as a box plot. As indicated by the markers, the $P=1$ and $P=2$ optimized locations provide excellent service times compared to all other candidates, significantly below the median and close to the minimum for each hotspot. This results in a decrease in the average service time from 570.4 s for all facility candidates and weather scenarios to 351.1 s for $P=1$ and 287.2 s for $P=2$, respectively. Only hotspots $j=21$ to $j=27$, located at the farther side of Lake Partwitz, cf. Figure 9, show slightly worse service times due to the balanced optimization among all hotspots.

Figure 9 shows the optimum location for $P=1$, satisfying Equations (8)–(11), and the shortest flight paths from the optimum facility to all hotspots $j\in H$ while respecting the UAS geographical zones, using $n=5$ as an example. The heatmap indicates the average service time to all j across all $m\in W$ and $n\in Z$ as a normalized score for all facility candidates with $A_i>0.9$ indicating near-optimal locations with a slightly inferior result, which may be used as alternatives if the optimum location is not available for building the UAV hangar.

For $P=2$, 40 possible combinations of candidates achieve the maximum accessibility score. Figure 10 shows the combination satisfying Equation (8). The plotted paths indicate the hotspot assignment according to Equations (9)–(11) for $n=5$ as an example. This assignment is part of the optimization process and represents the shortest service time in each case. However, for operational reasons, the other facility may also serve as the hotspot if satisfying Equation (7). Furthermore, the service time Equation (12) is significantly better compared to $P=1$, especially for hotspots $j=21$ to $j=27$, cf. Figure 8.

4. Discussion

4.1. Validation of the Hotspots Obtained from Open-Source Data

As described before, the determination of the hotspots is built on public georeferenced data. As the RescueFly project also plans to install emergency phones around the two lakes, an inspection of the shorelines has been conducted. Those observations serve to validate the hotspots generated from the open-source data to identify possible shortcomings. The inspection found most of the OSM hotspots to be suitable. However, the northernmost hotspot is a larger beach area, which OSM identifies as a single point (with tag leisure=beach_resort, see Figure 6), which underestimates the search area at Lake Partwitz. Furthermore, the inspection found the marinas at both lakes to be less significant for the aims of RescueFly, as swimmers are not expected in these areas. However, it may be argued that a marina still induces the risk of water-related incidents according to our initial assumptions.

For the validation of our open-source approach, we computed the service times from our optimum UAV hangar locations for $P=1$ and $P=2$ with the hotspots from the inspection. For $P=1$, the previously determined UAV hangar location performs better than 94.9% of the candidates. Furthermore, the average service time per hotpot increased from 400 s to 421 s for $P=1$ and from 307 s to 311 s for $P=2$. Thus, the determined UAV hangar locations are close to the optimum even if a few nearby areas are added afterward.

Our methodology is purposely based on open-source data, as it should be transferable to any similar problem without needing an inspection. For $P=2$, an error of 4s in the average service time is deemed to be very low. Yet, it highlights the need for validation of the input data, especially on community-drive platforms, such as OSM.

4.2. Analysis of the Applicability of the Hangar Locations

Using open-source data, we demonstrated a fast and robust method for optimizing UAV hangar locations considering restrictive areas and wind scenarios. The optimum locations show significantly greater accessibility and lower service time than the other hangar location candidates. Furthermore, the rescue times are significantly below the maximum response time regulated for each federal state in Germany. Typically, rescue stations shall be established to reach any emergency site along a public road within 15 min for $95\%$ of all annual cases, e.g., in Brandenburg [42]. Consequently, emergency services should arrive at the closest public road to the accident site at the lake in about 900 s. Then, additional time is required to reach the shoreline area, which may be difficult to access, and the SAR time in the water. With the optimum UAV hangar locations, average service times over all $n\in Z$ for $m=1$ of ${\overline{S}}_{P=1}$ = 351.1 s and ${\overline{S}}_{P=2}$ = 287.2 s, respectively, were achieved. During this time, the UAV will provide a flotation device to the person in distress. Thus, it reacts earlier than required, provides measures to increase survivability, and guides emergency responders to the right location faster. If even faster UAV responses are deemed necessary, a maximum permissible service time may serve as an additional constraint to our optimization model.

However, the currently defined standard SAR mission uses a worst-case approach in which an unfavorable wind delays the arrival of the UAV at the hotspot, and the person in distress is only detected after the search area has been overflown completely. For the facility location problem, we deem this assumption effective as the given service times are guaranteed even in adverse situations. In reality, the person in distress will be detected earlier in most cases, especially if the distress call specifies the position with sufficient precision or the wind accelerates the UAV on the approach. Furthermore, the search phase may be accelerated by surveying the area on approach and selecting an appropriate search pattern based on the current conditions, e.g., the number of persons in the water, precision of the emergency call, and wind conditions. Such a refinement from the standard SAR mission to a case-by-case mission trajectory will be studied further.

The currently used positive and negative location factors are selected according to the needs of the UAV hangar FLP but also based on data availability. Accordingly, the power supply and property situation could not be assessed, as the required data are not accessible to the public. However, if suitable information will be available, our methodology is able to incorporate it as another data layer in the optimization. Additionally, our work provides a set of second-best options based on $A_i$ in case the optimum spot is unavailable, as indicated by the heatmap in Figure 9.

5. Conclusions

Our work demonstrated an approach to determine optimum UAV hangar locations in an environment with restricting factors both regarding the facility location itself and the airspace. Thus, it combines a FLP with the mission planning for the proposed UAS. Since the determination of the UAV hangar candidates, the hotspots as well as the derived positive and negative location factors rely solely on open-source data, see Section 2.2, they can be applied to any other area of interest directly. In this study, we used the SAR missions with $P=2$ and $P=1$ UAV hangar locations at bathing lakes as one intended application. However, the proposed methodology can easily transfer to other UAV use cases. Similarly, the number of locations P may be increased as well, although it will impact the computation time. As the proposed method computes the accessibility $A_i$ for all location candidates, second-best solutions can always be determined if the optimum solutions are not available, e.g., due to land use issues.

The integration of the mission planning in the FLP allowed modeling additional constraints beyond the UAV endurance, such as non-direct routing due to airspace restrictions and the impact of wind on flight time. The considered restricted airspaces, called UAV geographical zones in the EU legislation [2], are established to reduce ground and air risk. At the same time, SAR missions are always urgent, so our scenarios $n\in Z$ permit us to ignore the UAV geographical zones if inevitable. As the A* is flexible in this regard, restrictions for other use cases, such as time-dependent or altitude restrictions, may be added to the mission description.

The current standard SAR mission represents a worst-case scenario, as it assumes the person in distress to be found only after scanning the entire search area. We deem this assumption suitable for the FLP, as it guarantees a maximum service time. As a next step, we will study the efficiency and reliability of various search patterns for the hotspot area to accelerate the service time further. Together with a UAV flight performance model to estimate the energy consumption, an optimum SAR mission can be determined given the prevailing weather situation and the size of the exposed crowds (ground risk) on the day of operation.