Designing Ultrahigh Frequency Motor Rotor Position Search Coils for Electric Propulsion in Drones
Abstract
1. Introduction
2. Ultrahigh Frequency (UHF) Search Coils—Rotor Position Detection Principle
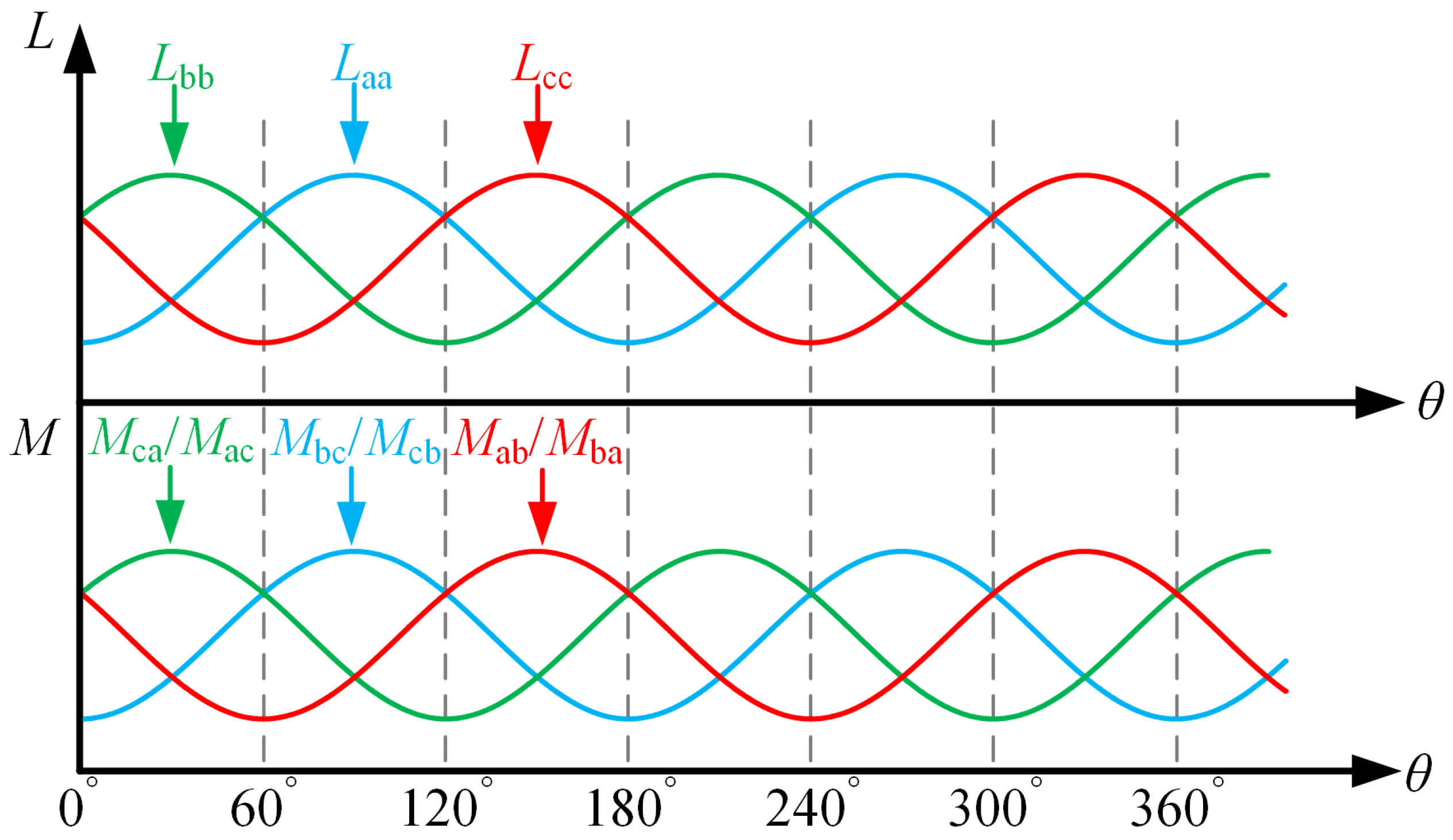
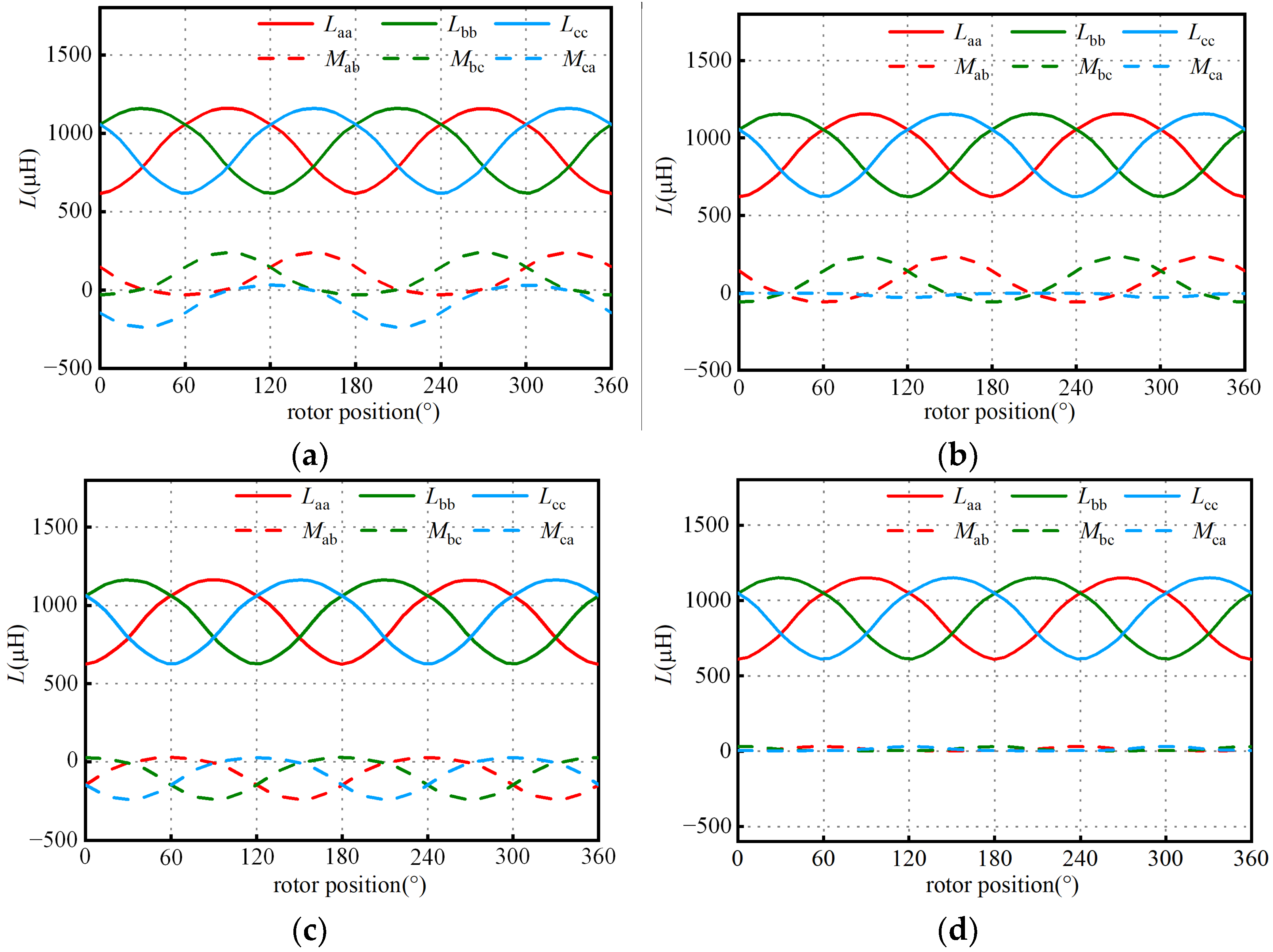
2.1. Inductance Change Due to Salient Pole Effect
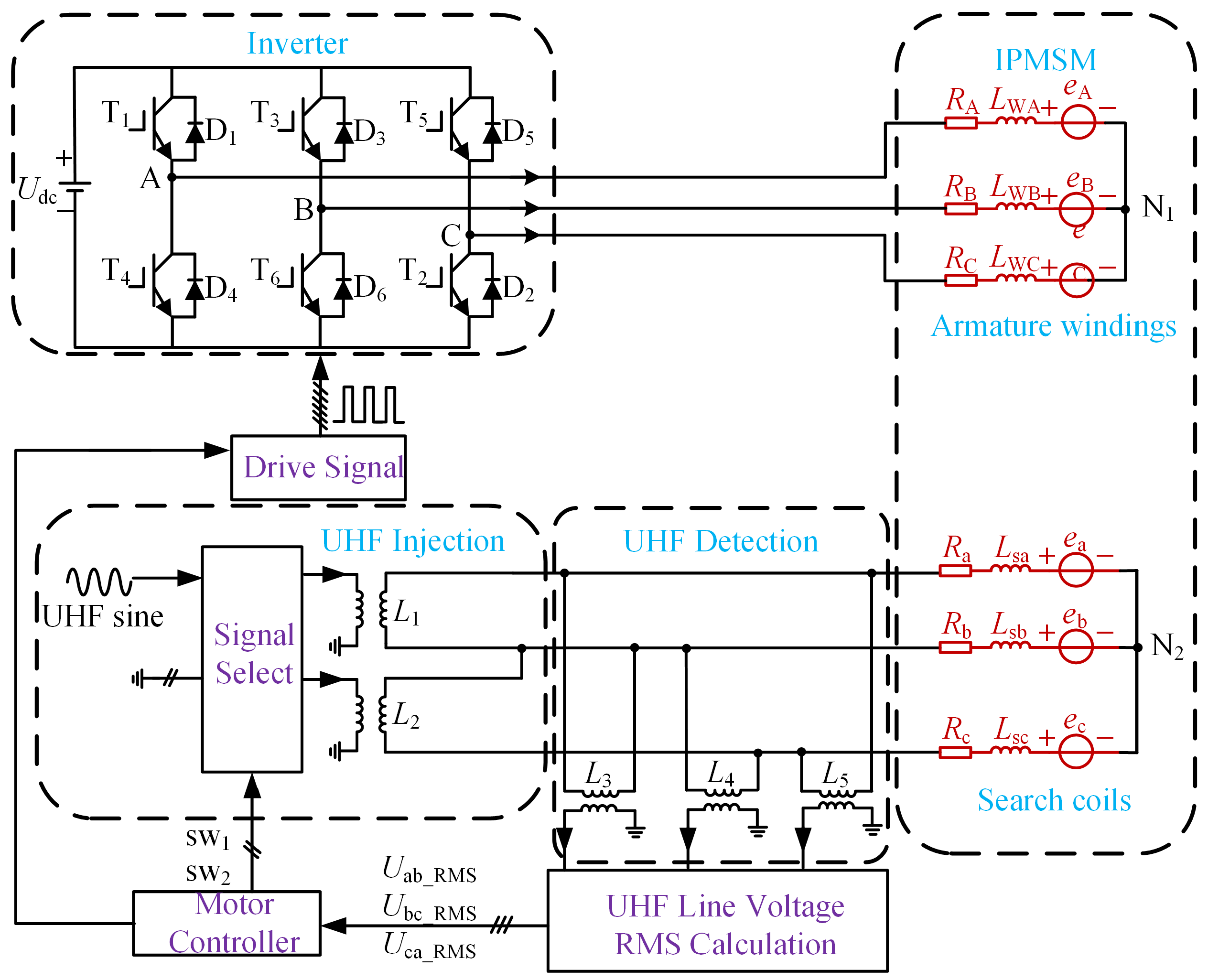
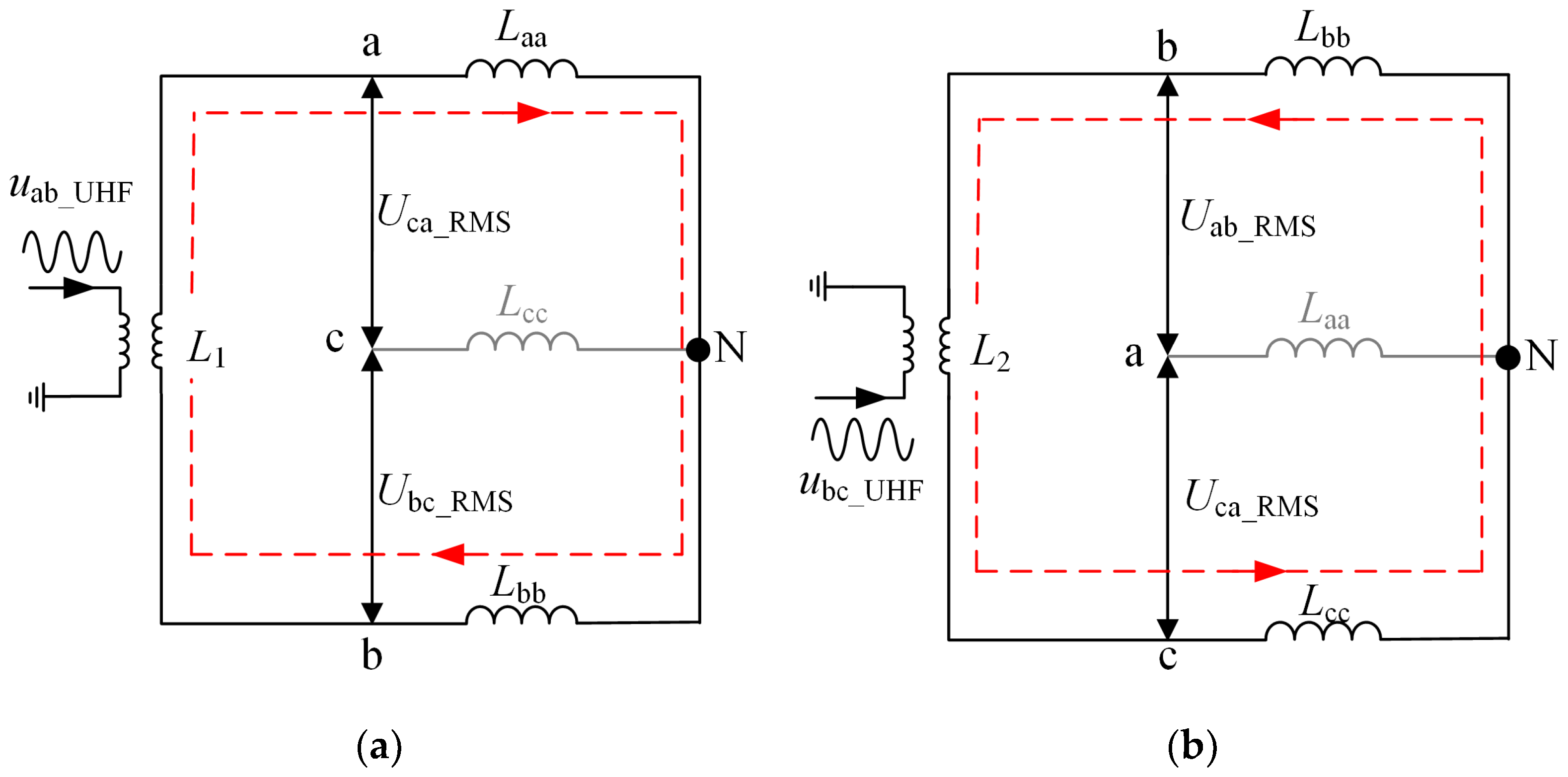
2.2. UHF Signal Injection Topology
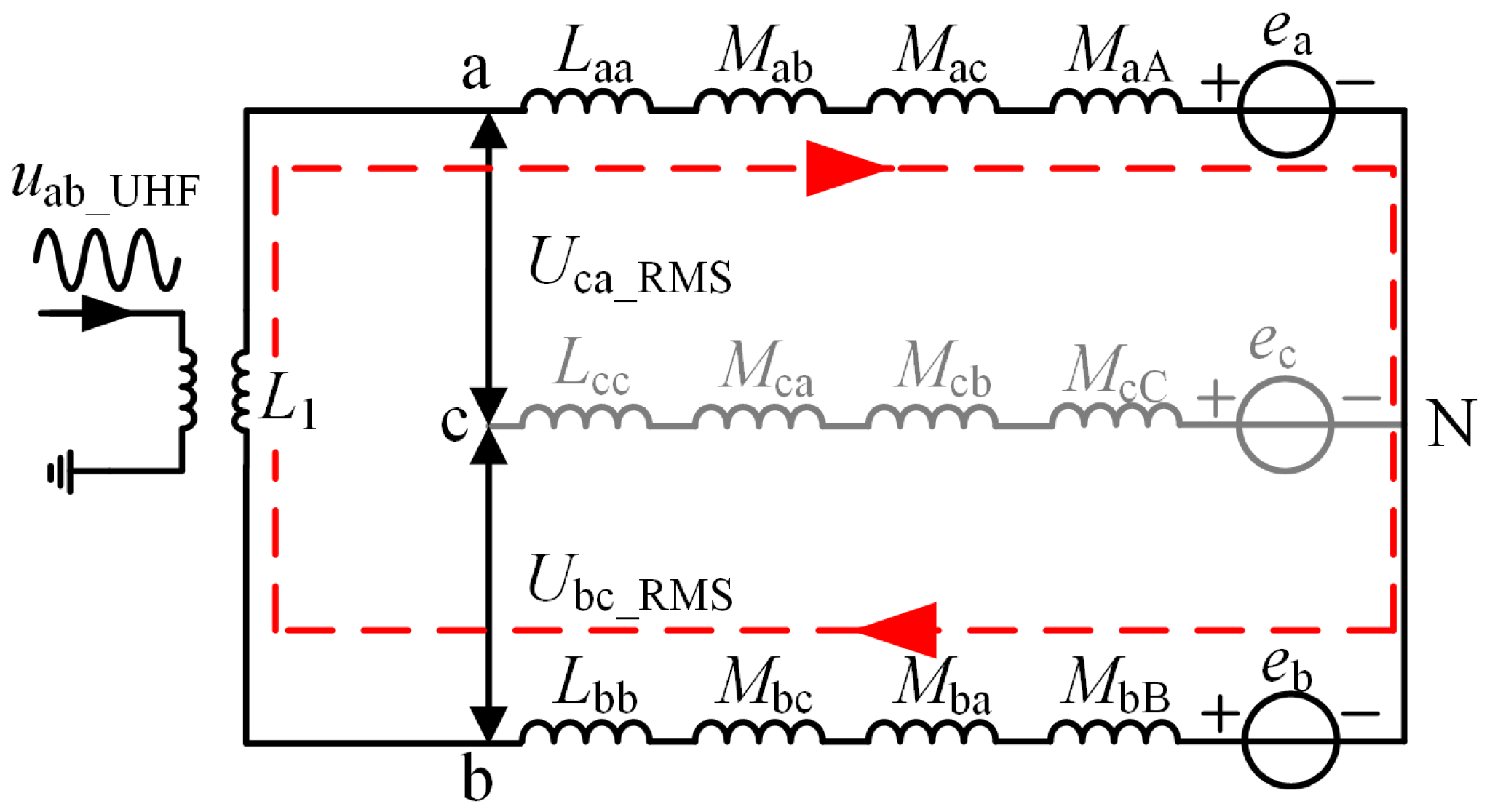
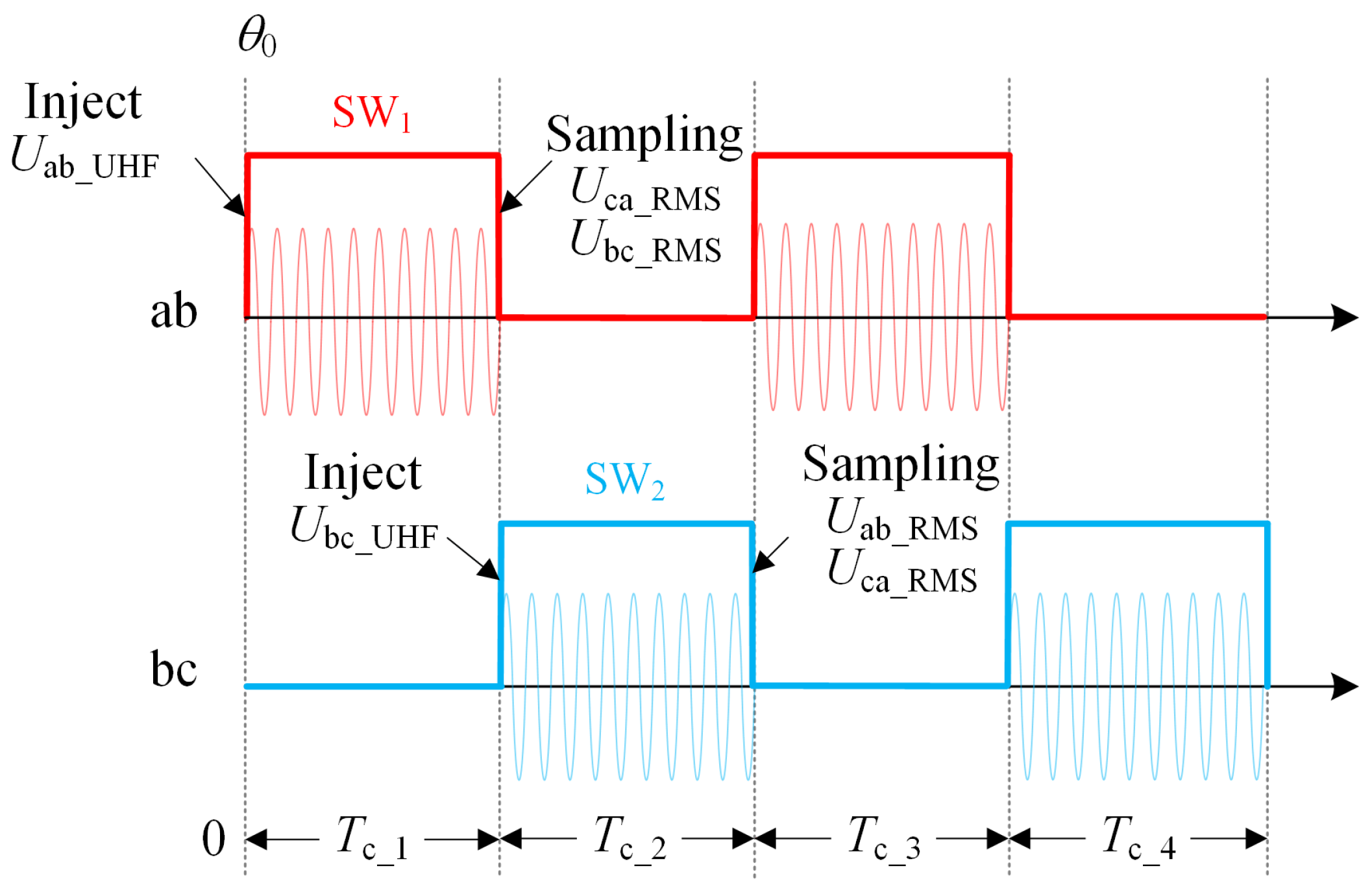
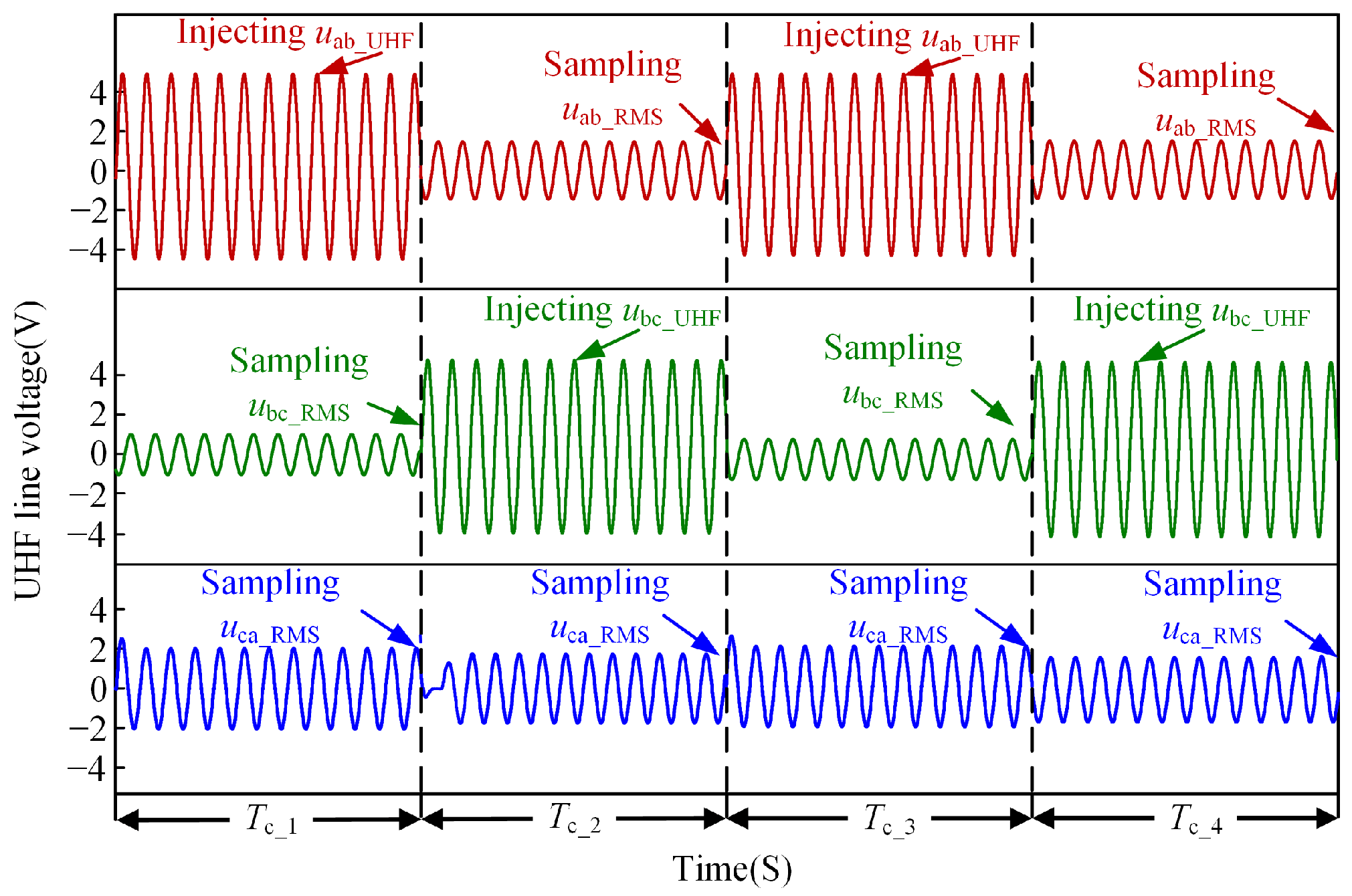
2.3. Rotor Position Detection Method
3. Search Coils—Design and Optimization
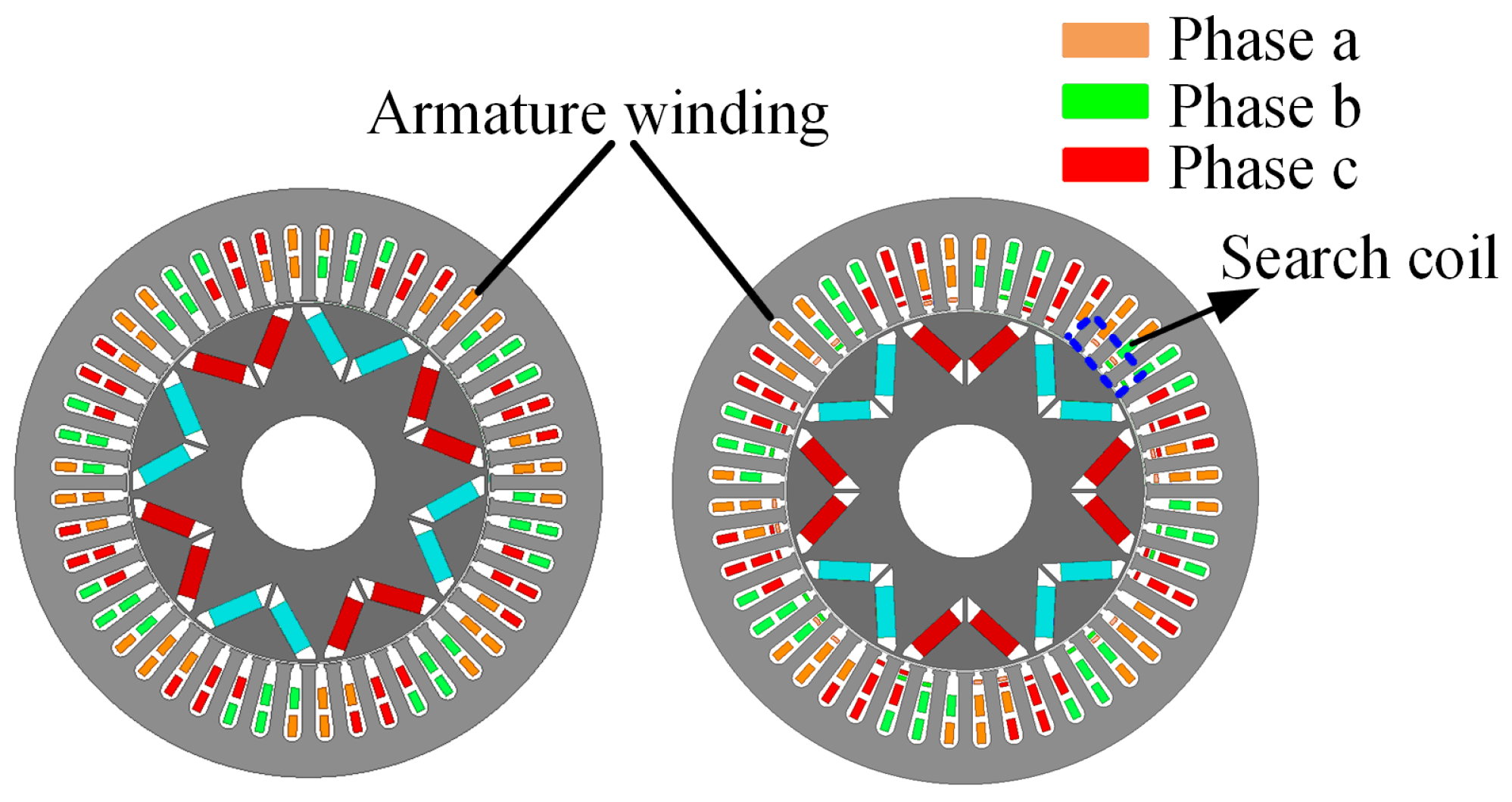
3.1. Search Coils—Design
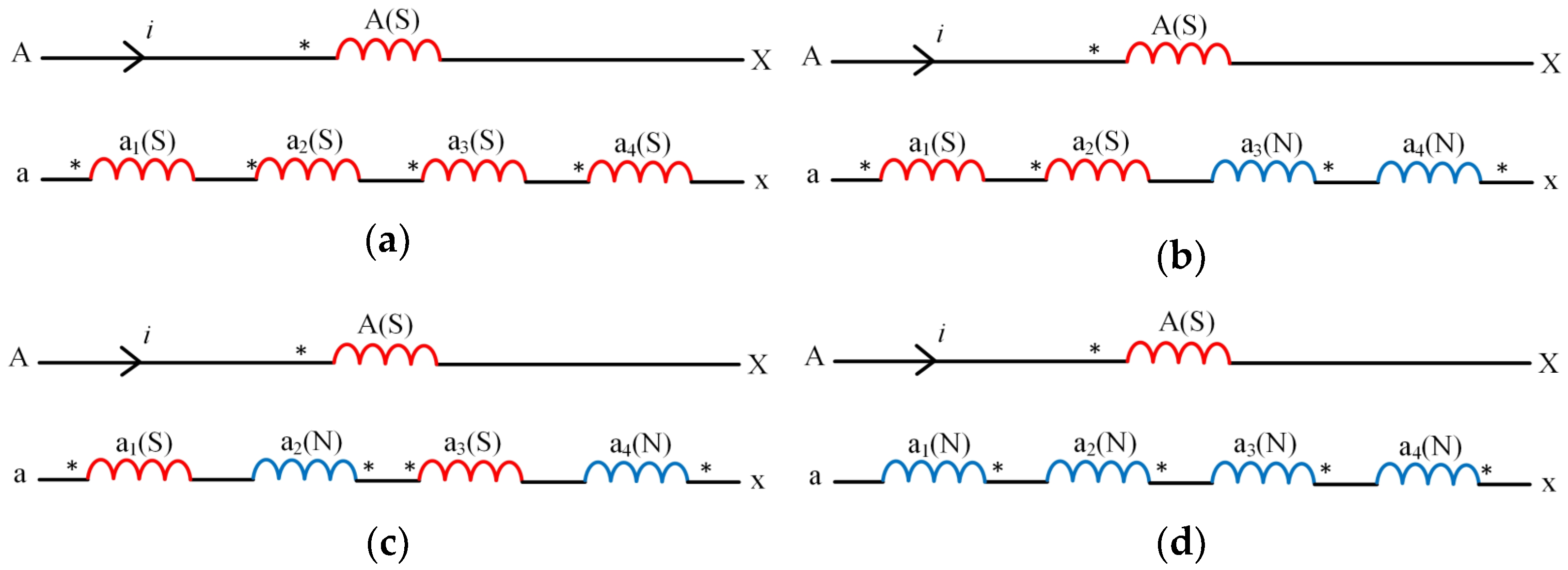
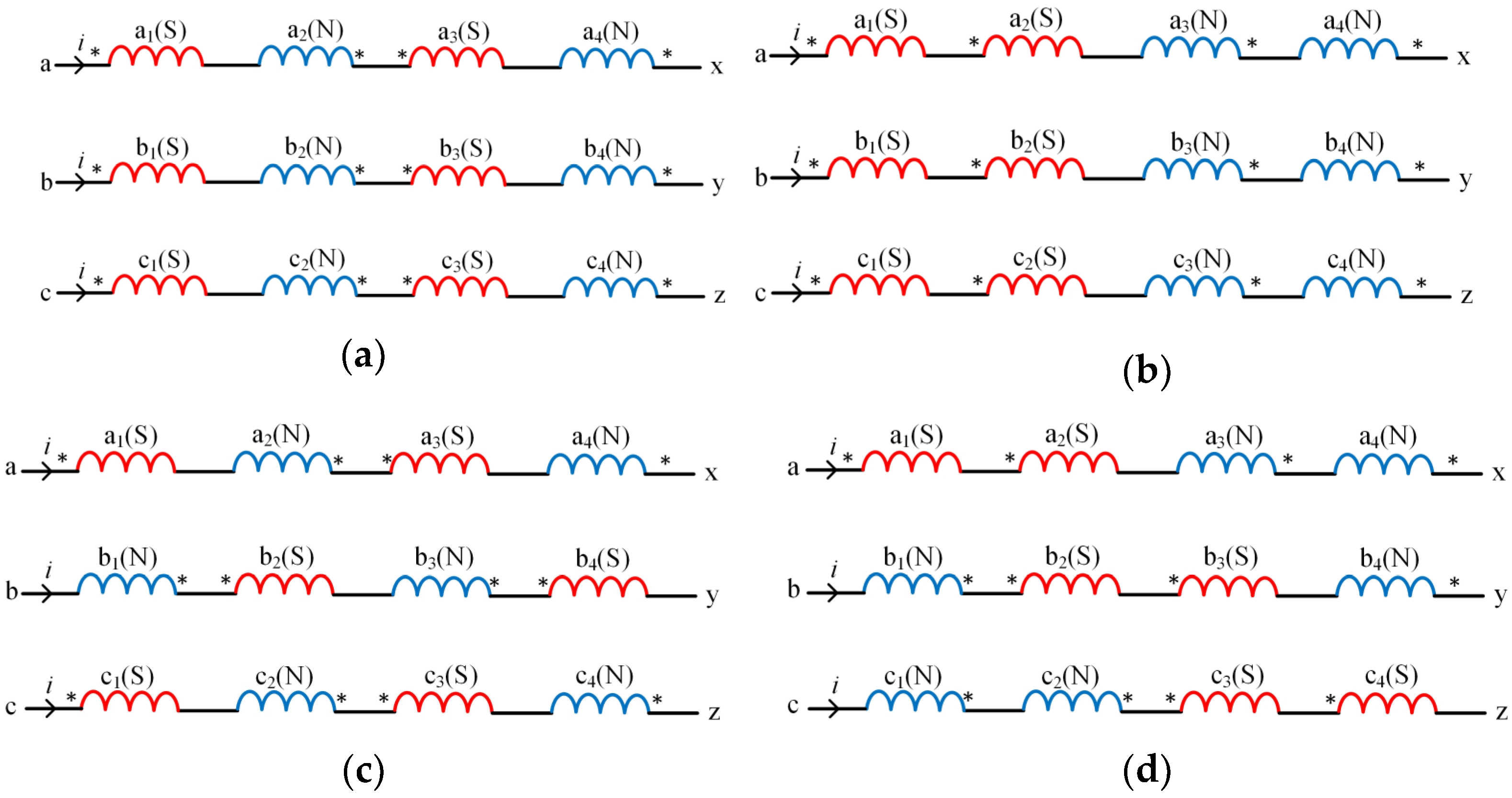
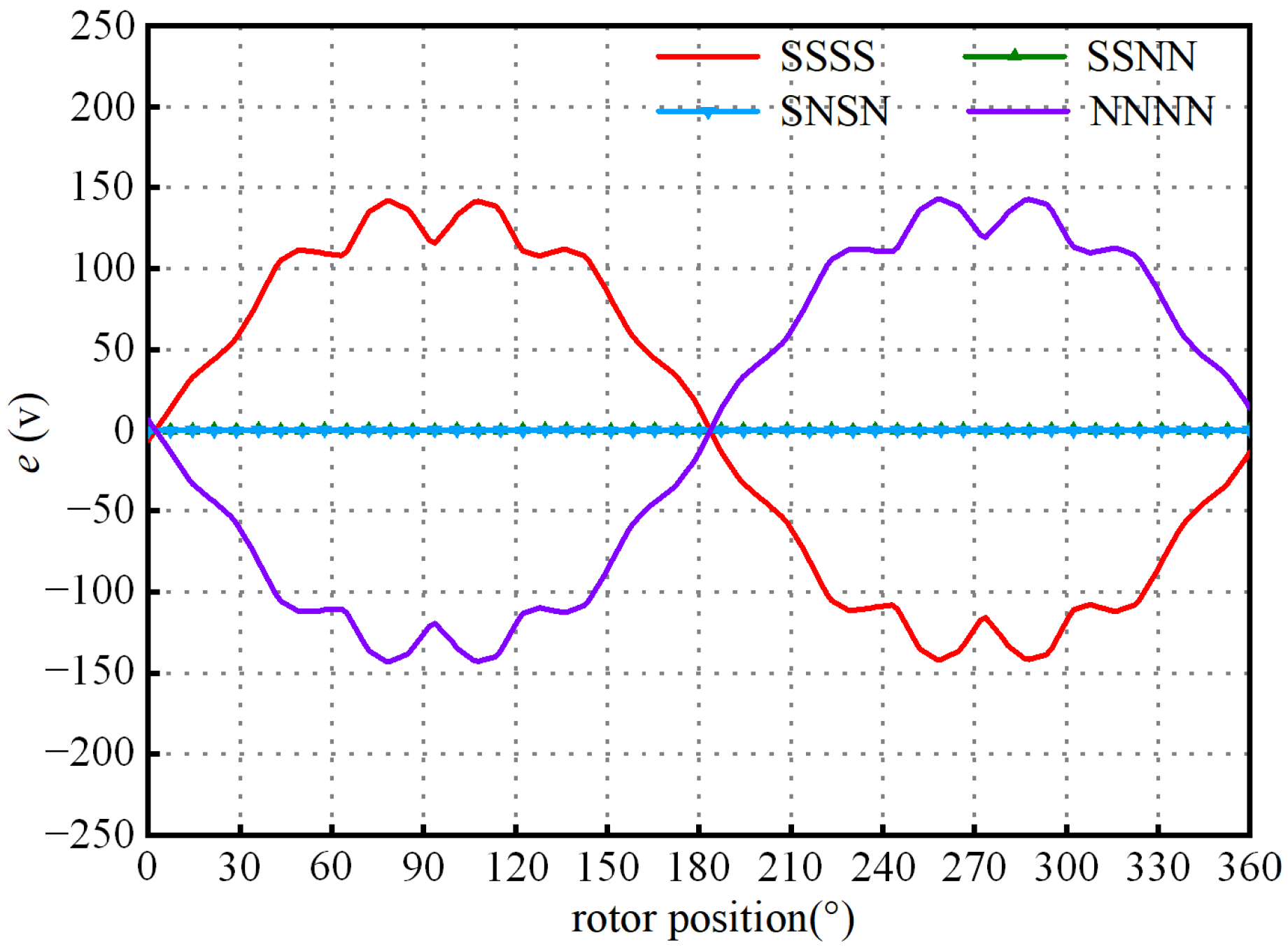
3.2. The Search Coils and Armature Winding—Mutual Inductance Optimization
3.3. The Search Coils—Mutual Inductance Optimization
4. Simulation Results and Analysis
4.1. FEA Verification
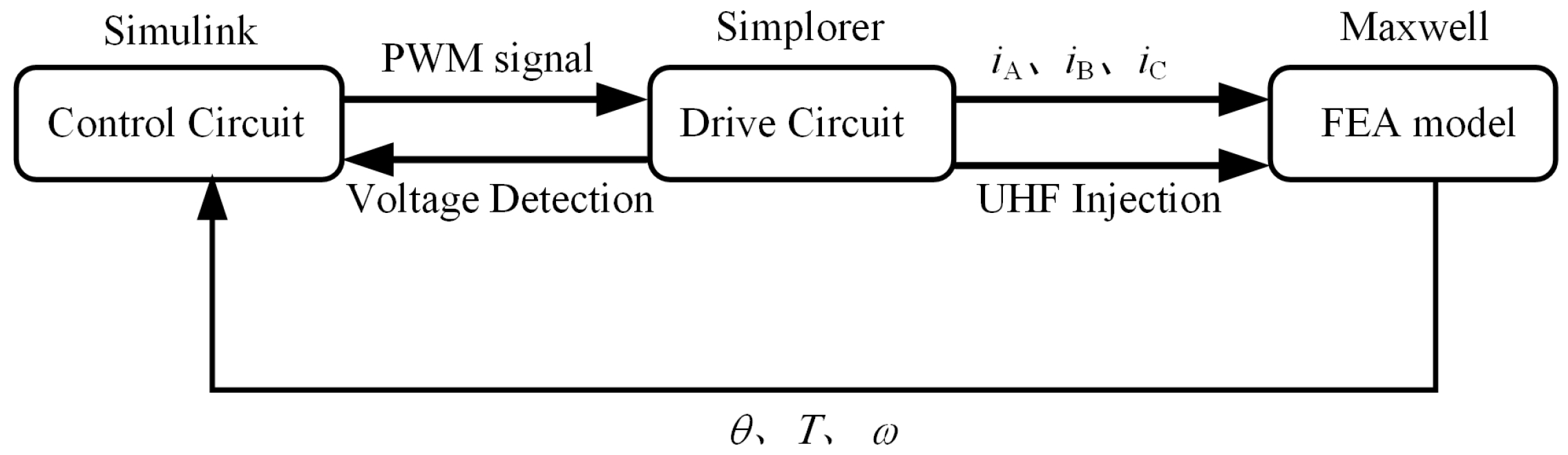
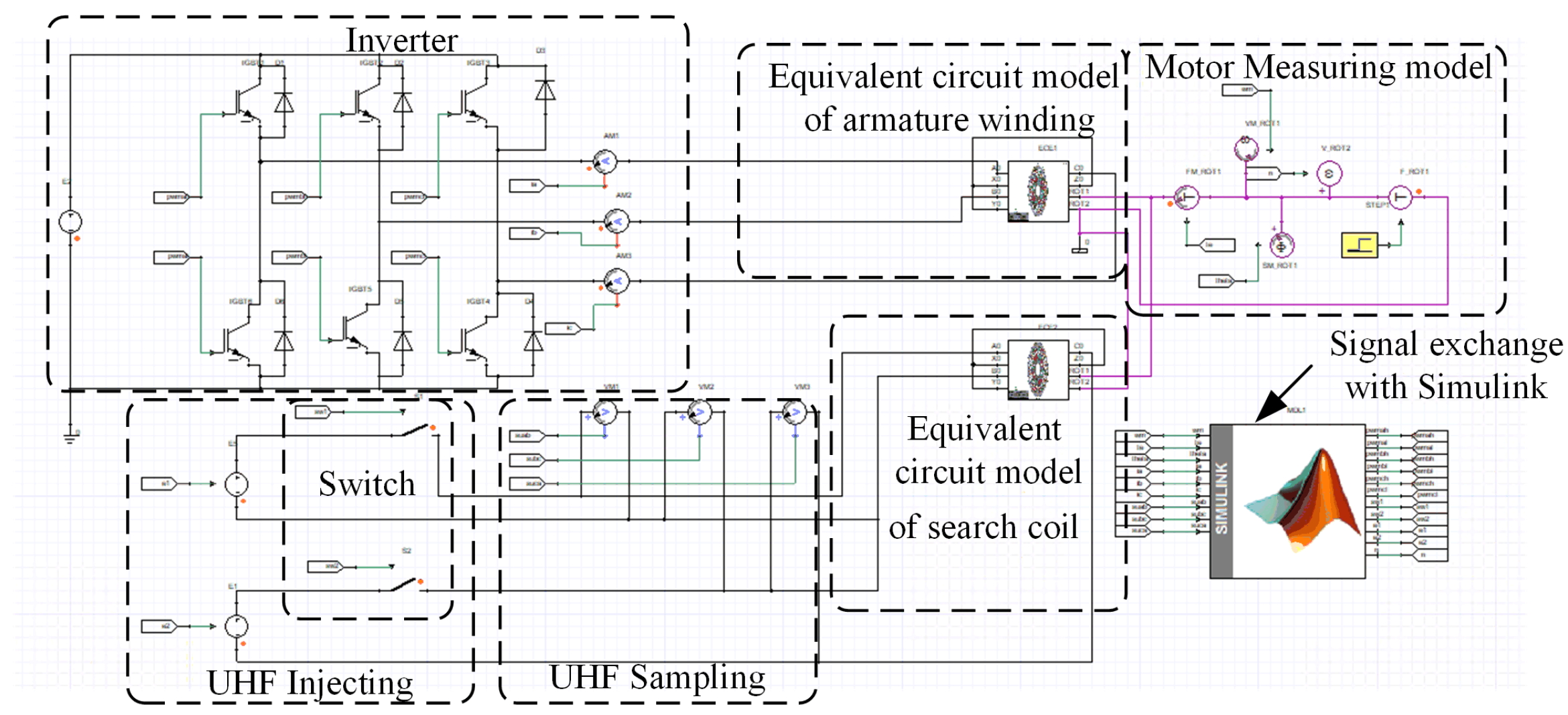
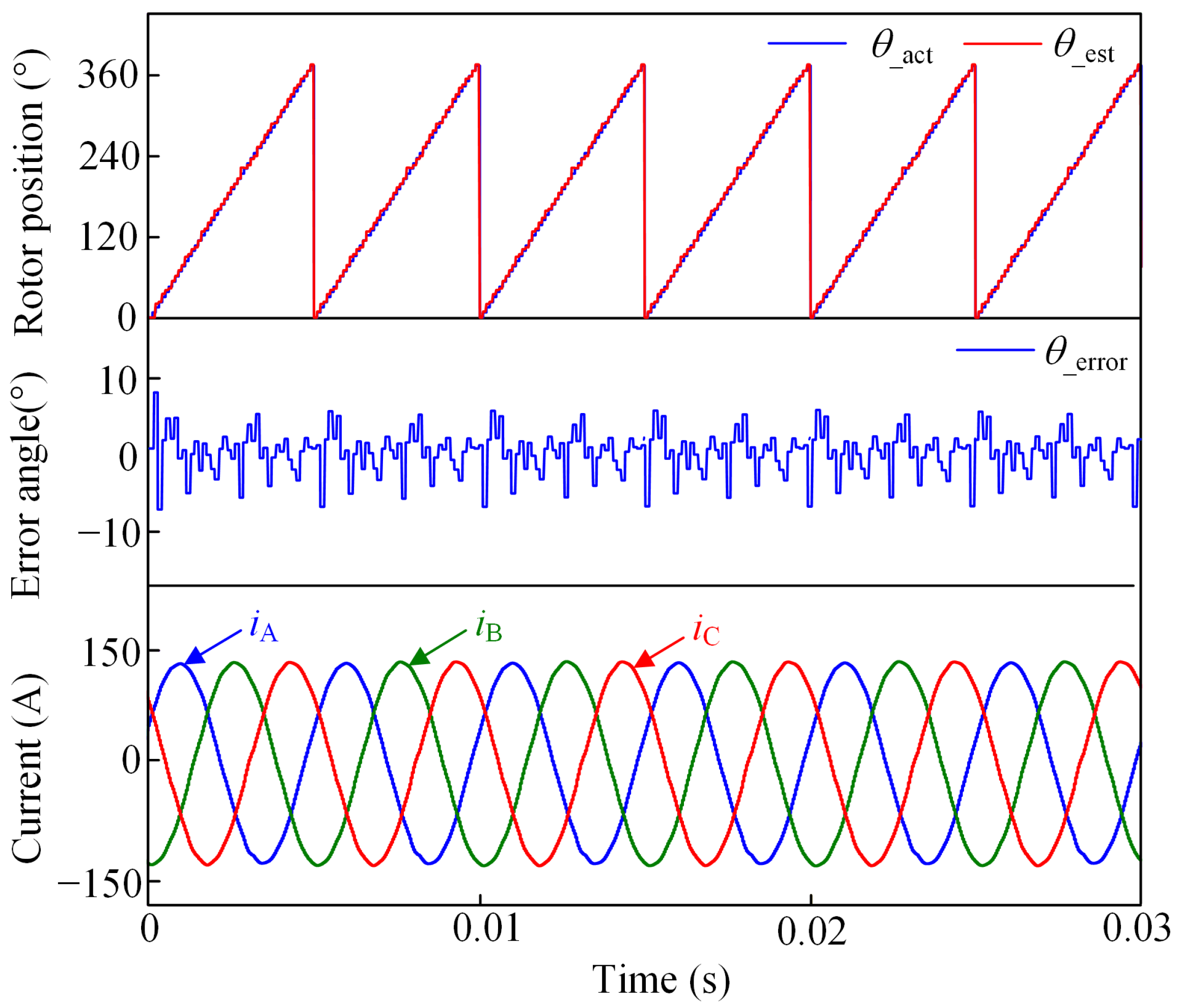
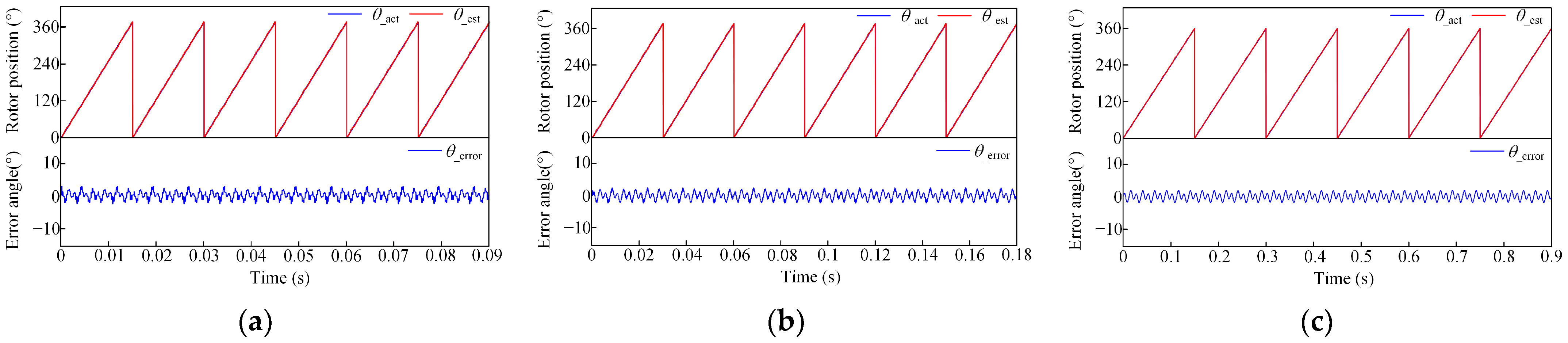
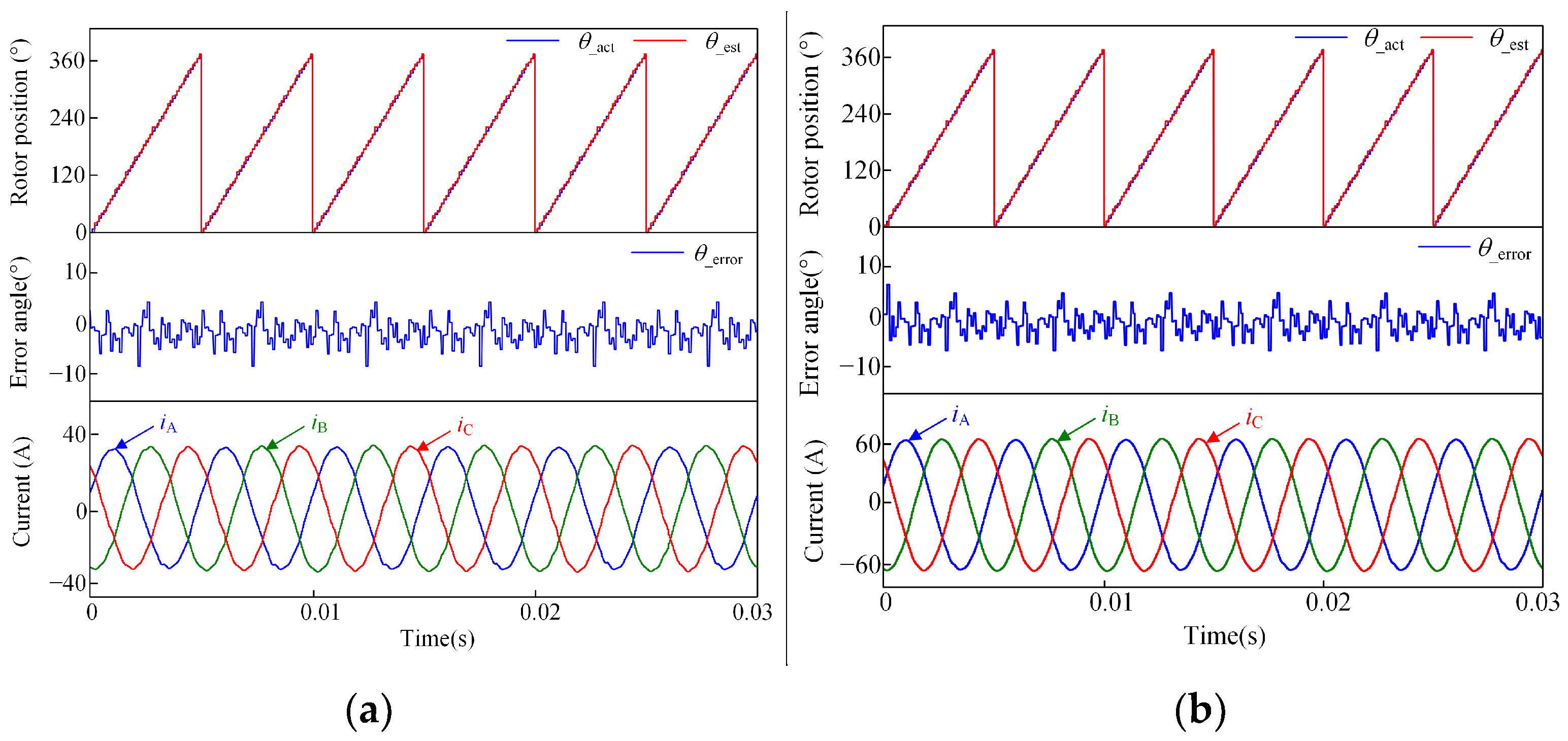
4.2. Co-Simulation Analysis and Verification
5. Conclusions
- The search coil self-inductance is large and can sensitively reflect the rotor position;
- Mutual inductance between the search coil and armature winding is small, and the coupling relationship between the two coils reaches the minimum, which does not affect the normal operation of the motor drive system;
- The equivalent circuit model with the calculation of UHF signal injection into the search coil is simplified because the search coil has less mutual inductance between phases;
- By searching the mapping relationship between search coil self-inductance and rotor position, as well as the wide detection bandwidth provided by the UHF signal, the rotor position can be detected in the full speed domain and under different loads.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Medeiros, R.L.V.; Ramos, J.G.G.S.; Nascimento, T.P.; Filho, A.C.L.; Brito, A.V. A Novel Approach for Brushless DC Motors Characterization in Drones Based on Chaos. Drones 2018, 2, 14. [Google Scholar] [CrossRef]
- Li, J.; Yang, J.; Zhang, H. Research on Modeling and Fault-Tolerant Control of Distributed Electric Propulsion Aircraft. Drones 2022, 6, 78. [Google Scholar] [CrossRef]
- Urquhart, I.; Tanaka, D.; Owen, R.; Zhu, Z.Q.; Wang, J.B.; Stone, D.A. Mechanically actuated variable flux IPMSM for EV and HEV applications. World Electr. Veh. J. 2013, 6, 684–695. [Google Scholar] [CrossRef]
- Riaz, S.; Qi, R.; Tutsoy, O.; Iqbal, J. A novel adaptive PD-type iterative learning control of the PMSM servo system with the friction uncertainty in low speeds. PLoS ONE 2023, 18, e0279253. [Google Scholar] [CrossRef]
- Saleem, O.; Abbas, F.; Iqbal, J. Complex Fractional-Order LQIR for Inverted-Pendulum-Type Robotic Mechanisms: Design and Experimental Validation. Mathematics 2023, 11, 913. [Google Scholar] [CrossRef]
- Kim, J.K.; Joo, S.W.; Hahn, S.C. Static characteristics of linear BLDC motor using equivalent magnetic circuit and finite element method. IEEE Trans. Magn. 2004, 40, 742–745. [Google Scholar] [CrossRef]
- Chen, S.H.; Liu, G.; Zhu, L.Q. Control Strategy of a 315 kW High-Speed BLDC Motor Based on a Speed-Independent Flux Linkage Function. IEEE Trans. Ind. Electron. 2017, 64, 8607–8617. [Google Scholar] [CrossRef]
- Liu, G.; Chen, B.; Song, X. High-Precision Speed and Position Estimation Based on Hall Vector Frequency Tracking for PMSM With Bipolar Hall-Effect Sensors. IEEE Sens. J. 2019, 19, 2347–2355. [Google Scholar] [CrossRef]
- Cui, C.; Liu, G.; Wang, K.; Song, X. Sensorless Drive for High-Speed Brushless DC Motor Based on the Virtual Neutral Voltage. IEEE Trans. Power Electron. 2015, 30, 3275–3285. [Google Scholar] [CrossRef]
- Lee, W.J.; Sul, S.K. A new starting method of BLDC motors without position sensor. IEEE Ind. Appl. Conf. 2004, 4, 2397–2402. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, M.; Xu, L. Sensorless control of BLDC motor from zero to low speed based on rotor saliency. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014. [Google Scholar] [CrossRef]
- Jang, G.H.; Kim, M.G. Optimal Commutation of a BLDC Motor by Utilizing the Symmetric Terminal Voltage. IEEE Trans. Magn. 2006, 42, 3473–3475. [Google Scholar] [CrossRef]
- Hinkkanen, M.; Saarakkala, S.E.; Awan, H.A. Observers for Sensorless Synchronous Motor Drives: Framework for Design and Analysis. IEEE Trans. Ind Appl. 2018, 54, 6090–6100. [Google Scholar] [CrossRef]
- Consoli, A.; Cavallaro, C.; Scarcella, G. Sensorless torque control of Syncrel motor drives. IEEE Trans. Power Electron. 2000, 15, 28–35. [Google Scholar] [CrossRef]
- Consoli, A.; Scarcella, G.; Testa, A. Slip frequency detection for indirect field oriented control drives. IEEE Ind Appl. 2004, 40, 194–201. [Google Scholar] [CrossRef]
- Da, Y.; Shi, X.; Krishnamurthy, M. A New Approach to Fault Diagnostics for Permanent Magnet Synchronous Machines Using Electromagnetic Signature Analysis. IEEE Trans. Power Electron. 2013, 28, 4104–4112. [Google Scholar] [CrossRef]
- Da, Y.; Shi, X.; Krishnamurthy, M. A Novel Universal Sensor Concept for Survivable PMSM Drives. IEEE Trans. Power Electron. 2013, 28, 5630–5638. [Google Scholar] [CrossRef]
- Da, Y.; Shi, X.; Krishnamurthy, M. Position and current estimation for Permanent Magnet Synchronous Machines using search coils. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011. [Google Scholar] [CrossRef]
- Tornello, L.D. Combined Rotor-Position Estimation and Temperature Monitoring in Sensorless Synchronous Reluctance Motor Drives. IEEE Trans. Ind. Appl. 2019, 55, 3851–3862. [Google Scholar] [CrossRef]
- Kwon, Y.C.; Sul, S.K.; Baloch, N.A.; Morimoto, S. Design, Modeling, and Control of an IPMSM with an Asymmetric Rotor and Search coils for Absolute Position Sensorless Drive. IEEE Trans. Ind. Appl. 2016, 52, 3839–3850. [Google Scholar] [CrossRef]
- Li, G.; Xu, J.D.; Cheng, Z.J. Position Sensorless Based on the Added Coil for Switched Reluctance Motor. Small Spec. Elect. Mach. 2016, 44, 51–54. [Google Scholar]
- Mao, L.M.; Jing, Y.Z.; Fan, X.M. Study on Application of Indirect Rotor-Position Detecting Technique with Opposite-Connect Sensing Coils Method in SRD Generator System. Proc. CSEE 2000, 20, 27–34. [Google Scholar]
- Liu, C.; Feng, L.; Zhou, Q. Rotor Position Eigenvalue detection for SRD based on Opposite-Connect Sensing Coils Technique. Trans. China Electrotech. Soc. 2008, 23, 24–29. [Google Scholar]
- Li, X.M.; Yan, Y.; Xu, Y.M. Low-Speed Rotating Restart and Speed Recording for Free-Running Sensorless IPMSM Based on Ultrahigh Frequency Sinusoidal Wave Injection. IEEE Trans. Power Electron. 2022, 12, 15245–15259. [Google Scholar] [CrossRef]





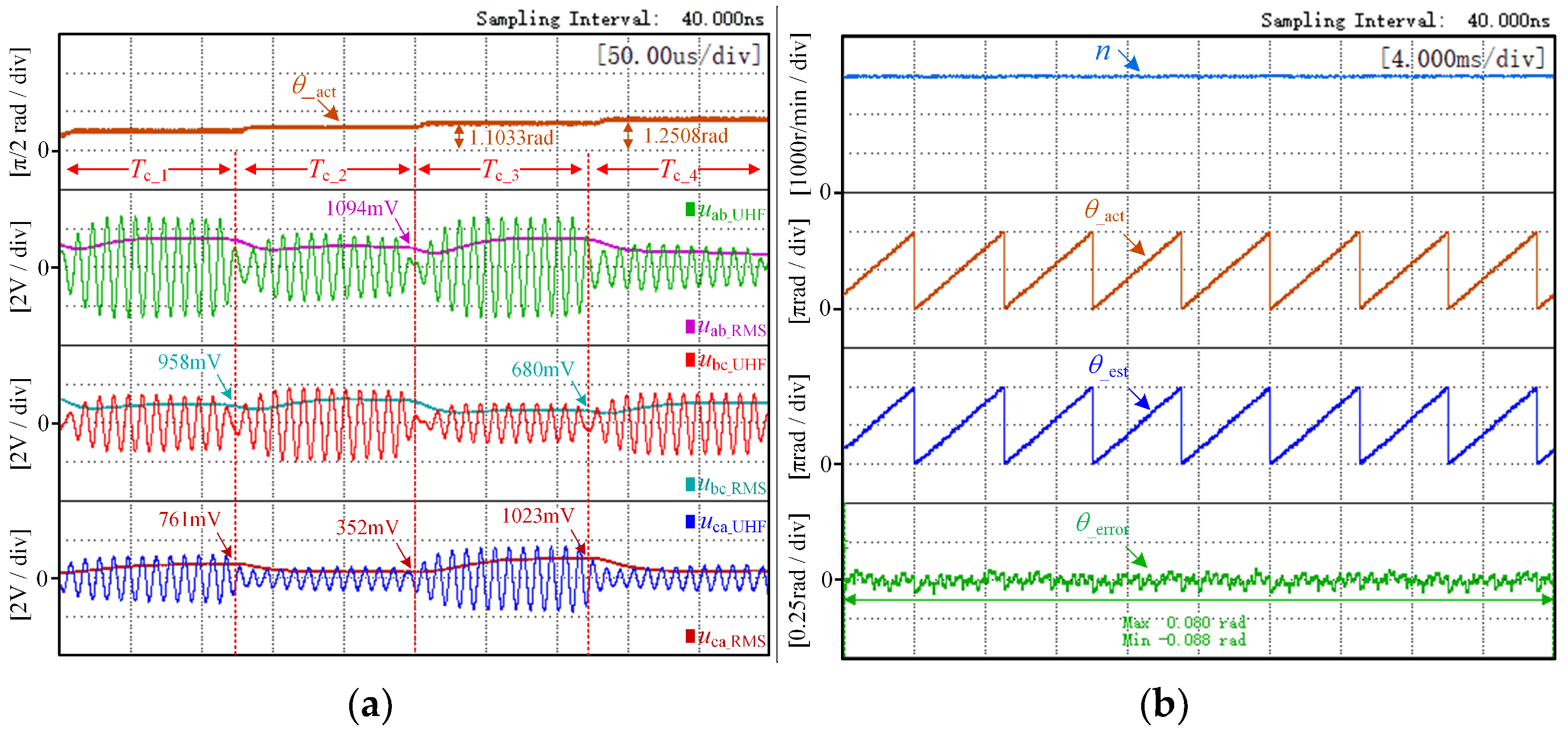
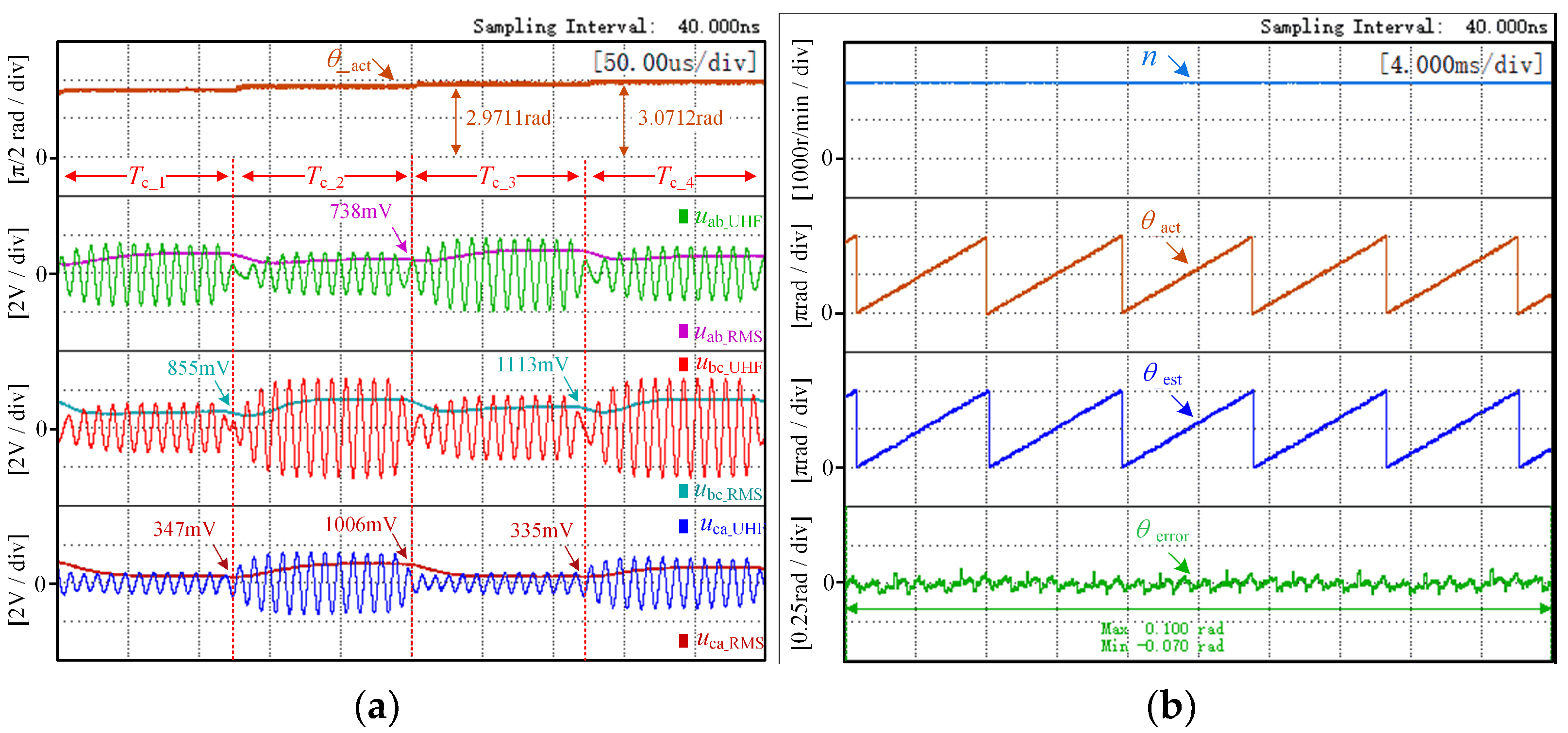
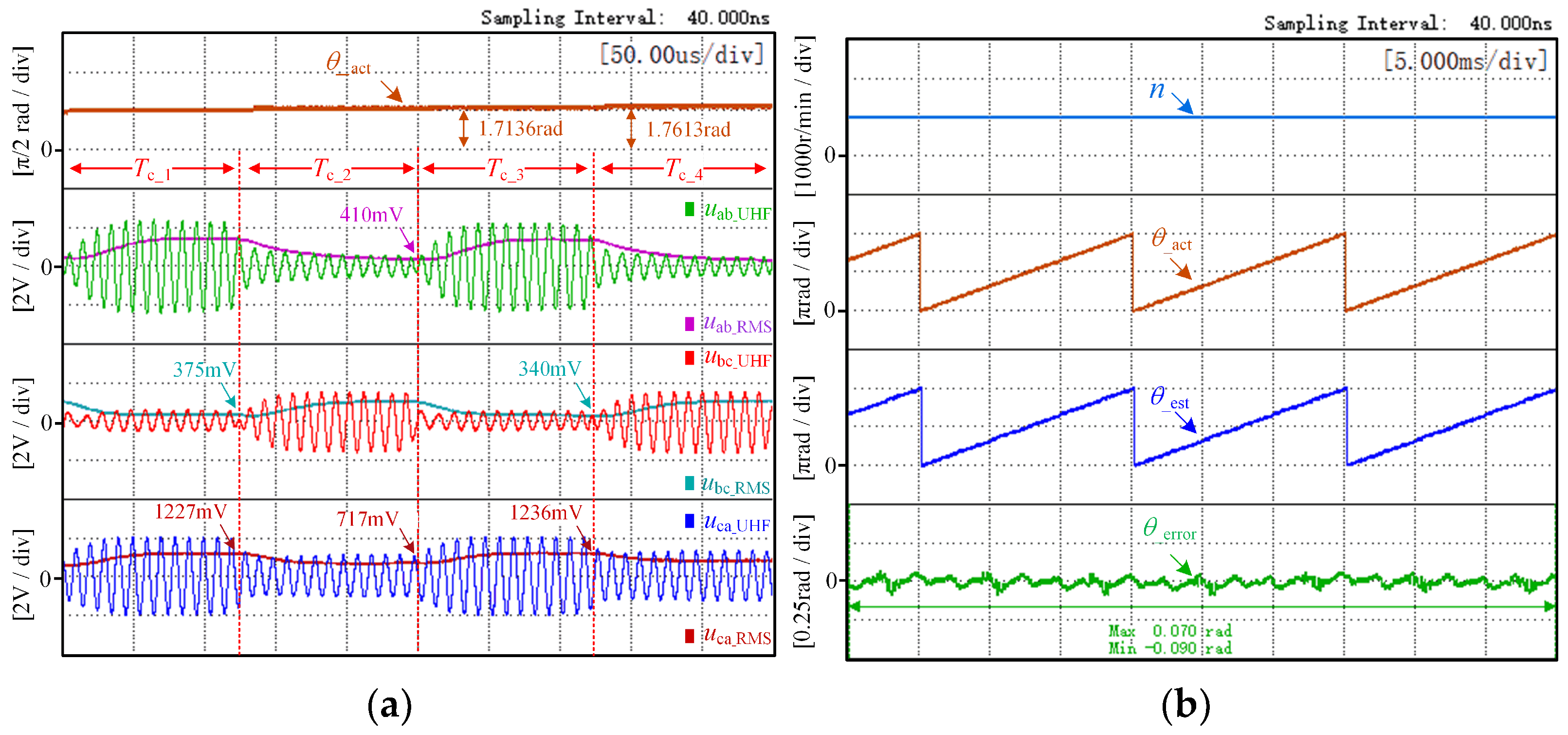

| Parameters | Symbol | Value | Unit |
|---|---|---|---|
| Pole pairs | p | 4 | - |
| Slots | s | 48 | - |
| Rated power | P | 18 | kW |
| Rated speed | n | 3000 | r/min |
| Rated torque | Te | 58 | N·m |
| Stator inner radius | D0 | 130 | mm |
| Rotor outer radius | D1 | 128 | mm |
| Turns of search coils | Nsc | 4 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wang, H.; Wang, H.; Guo, L.; Chen, W. Designing Ultrahigh Frequency Motor Rotor Position Search Coils for Electric Propulsion in Drones. Drones 2023, 7, 181. https://doi.org/10.3390/drones7030181
Li X, Wang H, Wang H, Guo L, Chen W. Designing Ultrahigh Frequency Motor Rotor Position Search Coils for Electric Propulsion in Drones. Drones. 2023; 7(3):181. https://doi.org/10.3390/drones7030181
Chicago/Turabian StyleLi, Xinmin, Huan Wang, Huimin Wang, Liyan Guo, and Wei Chen. 2023. "Designing Ultrahigh Frequency Motor Rotor Position Search Coils for Electric Propulsion in Drones" Drones 7, no. 3: 181. https://doi.org/10.3390/drones7030181
APA StyleLi, X., Wang, H., Wang, H., Guo, L., & Chen, W. (2023). Designing Ultrahigh Frequency Motor Rotor Position Search Coils for Electric Propulsion in Drones. Drones, 7(3), 181. https://doi.org/10.3390/drones7030181












