Factored Multi-Agent Soft Actor-Critic for Cooperative Multi-Target Tracking of UAV Swarms
Abstract
1. Introduction
- We formulate a UAV swarm-based MTT problem within a Dec-POMDP setting. The UAVs are partially observable, can only perceive the targets within the observation range, and can communicate with the neighboring UAVs. A recurrent neural network (RNN) is added to the actor-critic network to gather the historical information from the hidden state of the RNN, which solves the problem of incomplete information caused by partial observations. To increase the detection coverage and boost the tracking efficiency, inspired by the concept of spatial entropy, we design a shaping-reward SER. In addition, safe distance constraints are considered in the reward function to avoid collisions.
- MARL is used to solve the MTT optimization problem, which does not need a pre-set target trajectory and can learn to track targets in an unknown environment. Here, the CTDE paradigm is adopted, where global observation–action history can be accessed during centralized training, and trained policies are executed conditioned only on local information in a decentralized way. Moreover, the trained model can generalize to an unknown and dynamic changing environment.
- We propose using the FMASAC algorithm, which adopts an entropy maximization MARL for greater exploration and introduces the idea of value decomposition. This algorithm effectively combines the advantages of the value decomposition and MASAC methods, which reduces the variance in policy updates, achieves efficient credit assignment [29], and enables the scalable learning of a centralized critic in Dec-POMDP.
2. Related Work
2.1. Traditional Optimization Methods
2.2. Reinforcement Learning Methods
2.3. UAV Swarm Communication
3. Preliminary Analysis
3.1. Dec-POMDP
3.2. MASAC
4. Problem Formulation
4.1. UAV Kinematic Model
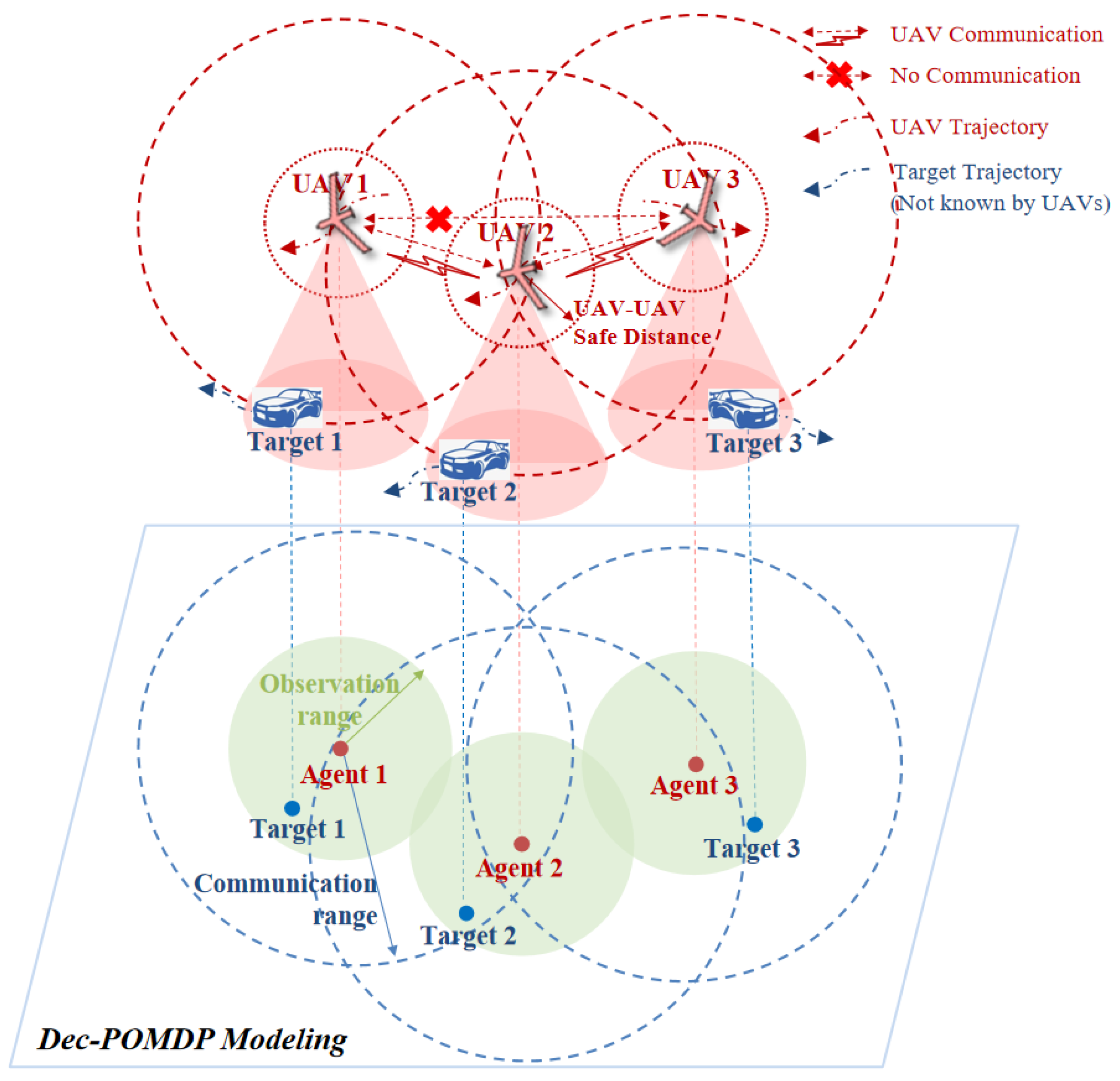
4.2. Dec-POMDP Modeling
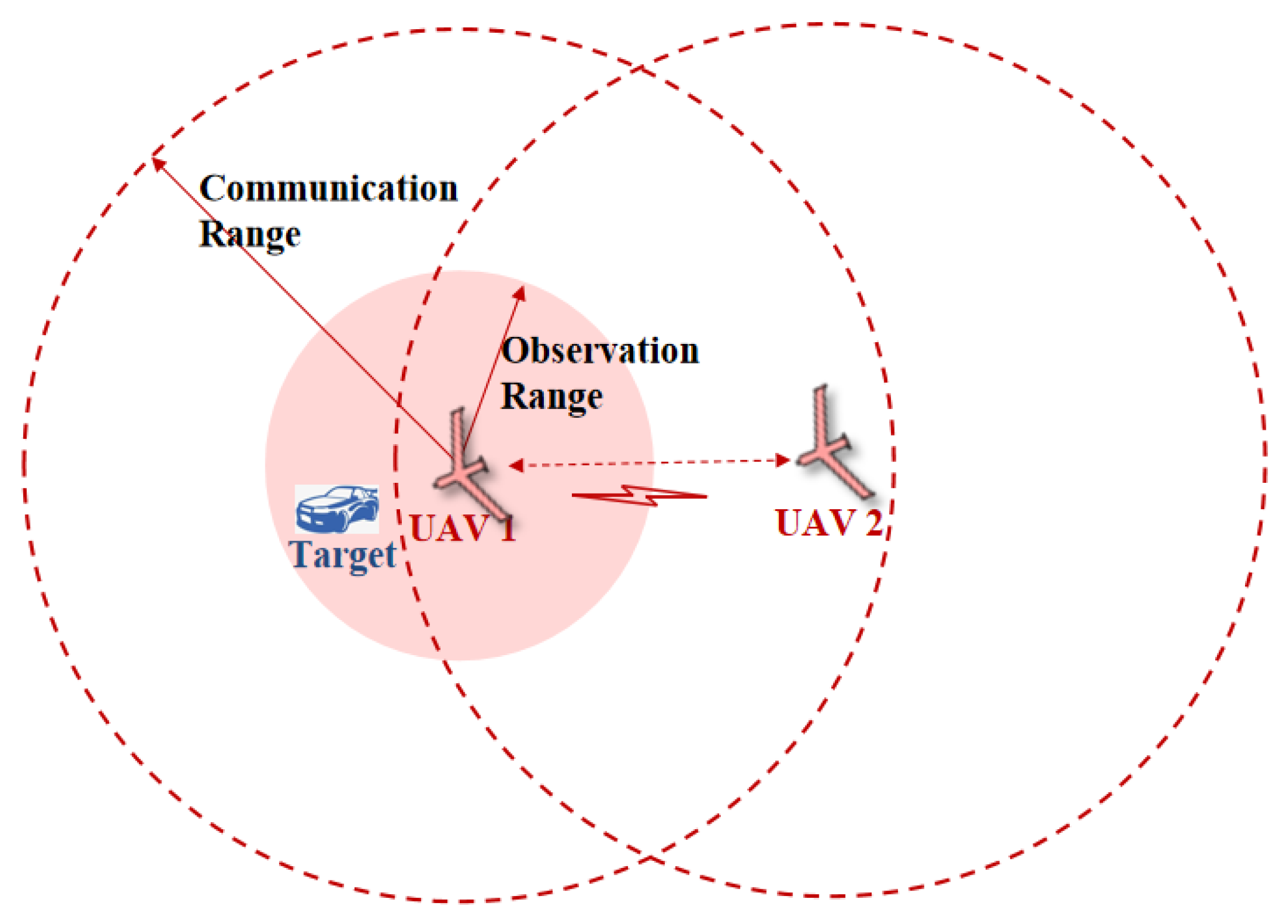
4.2.1. Observation Space
4.2.2. Action Space
4.2.3. Reward Function
4.3. Spatial Entropy Reward
5. Method
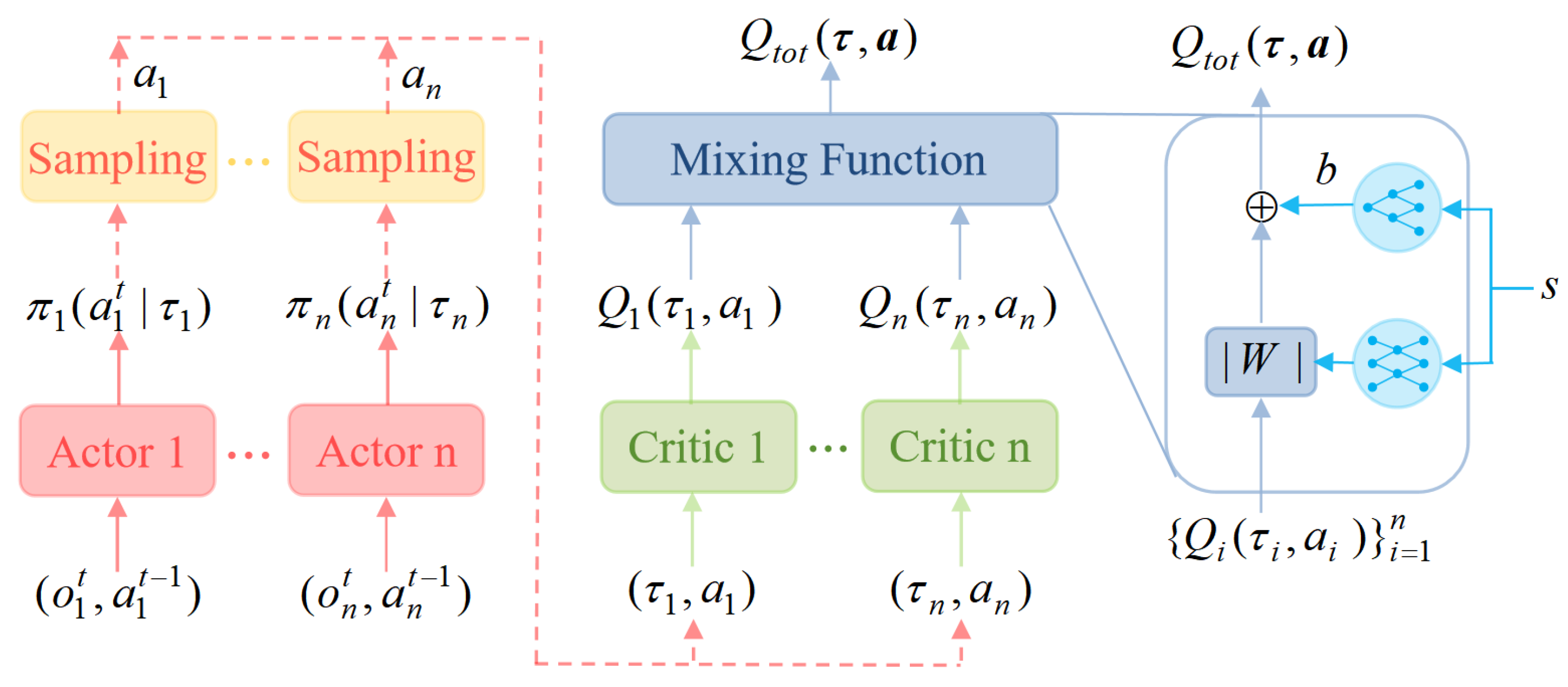
5.1. Learning a Centralized but Factored Critic
5.2. Factored Soft Policy Iteration
5.3. FMASAC-Based MTT of the UAV Swarm
| Algorithm 1: Factored multi-agent soft actor-critic (FMASAC) |
| # Initialize phase # 1: Initialize critic networks , actor networks , and mixing network with random parameters , , 2: Initialize target networks: , , 3: Initialize a replay buffer 4: for episode = 1 to max_train_episodes do 5: Reset environment # Experience collection phase # 6: for = 0 to max_episode_steps do 7: For each agent , take action 8: Execute joint action 9: Observe observation , and reward , done, info 10: Store in replay buffer 11: end for # Actor and critic network update phase # 12: for = 1 to do 13: Sample a minibatch trajectory from 14: Calculate 15: Update critic networks and mixing network w.r.t. Equation (22) 16: Update decentralized policies using the gradients w.r.t. Equation (25) 17: Update temperature parameter w.r.t. Equation (26) 18: if update target network then 19: , , 20: end if 21: end for 22:end for 23:Return π |
6. Experiments
6.1. Parameter Setup
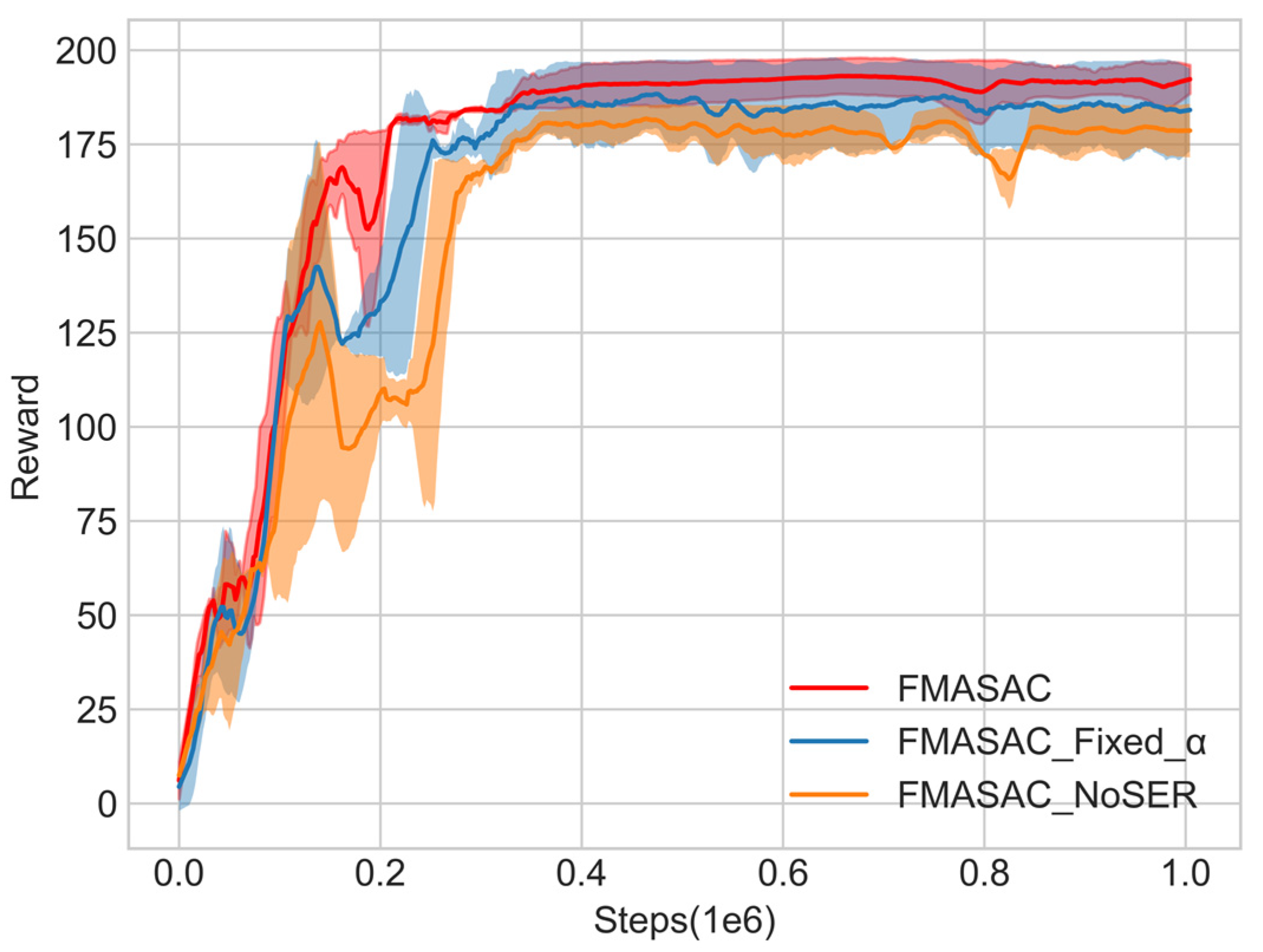
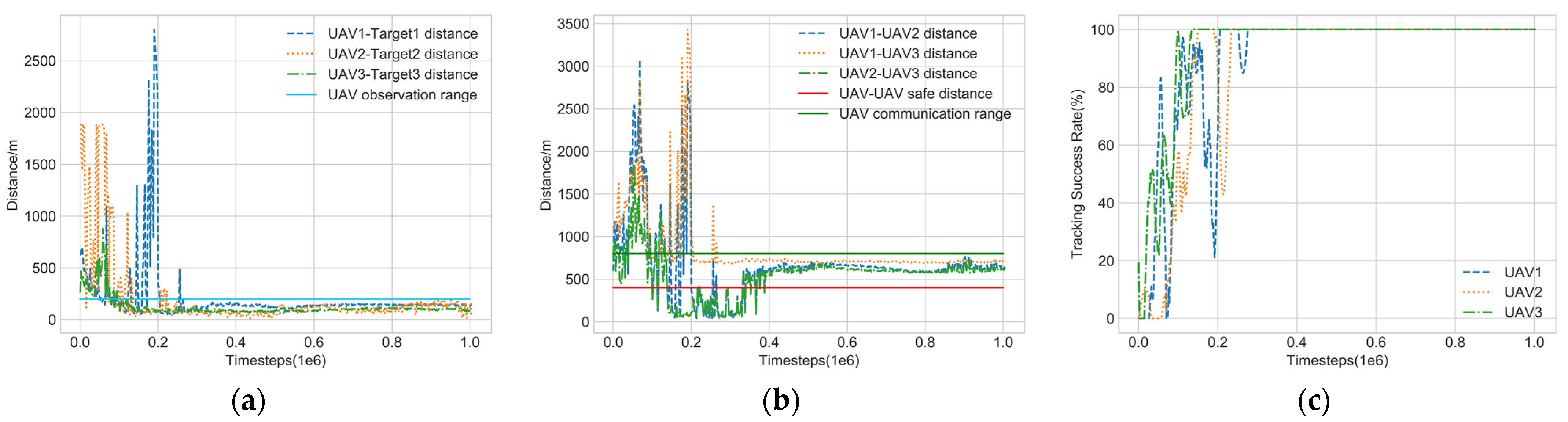
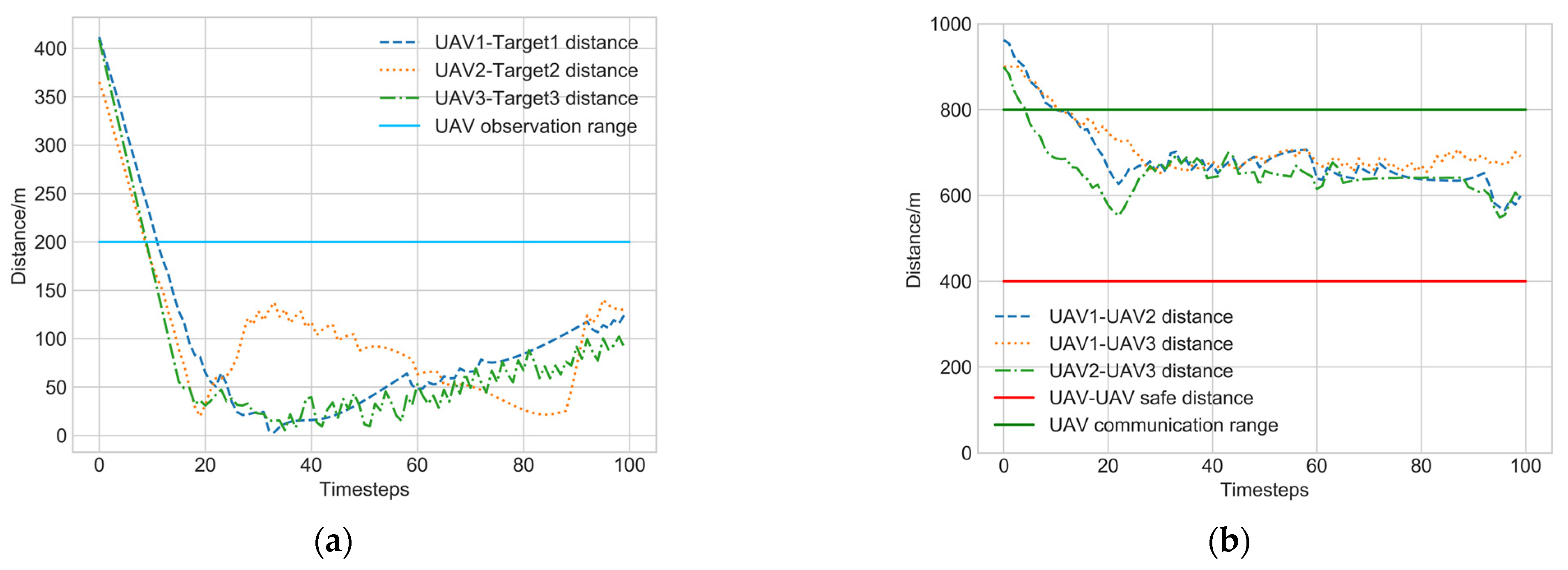
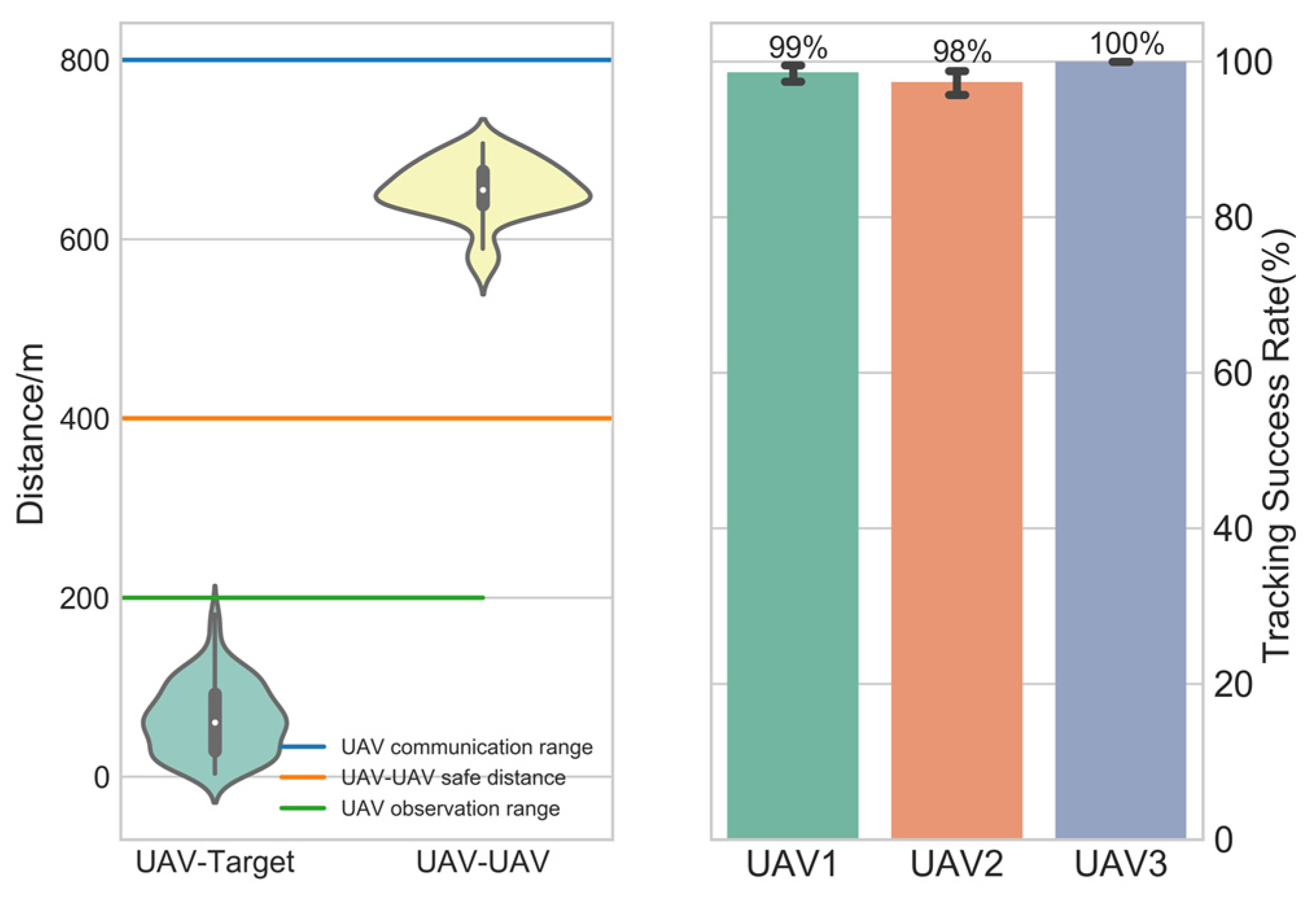
6.2. Effectiveness
6.3. Generalization
6.4. Scalability
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, L.Y.; Leng, S.P.; Liu, Q.; Wang, Q. Intelligent UAV Swarm Cooperation for Multiple Targets Tracking. IEEE Internet Things J. 2022, 9, 743–754. [Google Scholar] [CrossRef]
- Chen, Y.; Dong, Q.; Shang, X.Z.; Wu, Z.Y.; Wang, J.Y. Multi-UAV autonomous path planning in reconnaissance missions considering incomplete information: A reinforcement learning method. Drones 2022, 7, 10. [Google Scholar] [CrossRef]
- Shi, W.; Li, J.; Wu, H.; Zhou, C.; Chen, N.; Shen, X. Drone-cell trajectory planning and resource allocation for highly mobile networks: A hierarchical DRL approach. IEEE Internet Things J. 2020, 99, 9800–9813. [Google Scholar] [CrossRef]
- Serna, J.G.; Vanegas, F.; Brar, S.; Sandino, J.; Flannery, D.; Gonzalez, F. UAV4PE: An open-source framework to plan UAV autonomous missions for planetary exploration. Drones 2022, 6, 391. [Google Scholar] [CrossRef]
- Kumar, M.; Mondal, S. Recent developments on target tracking problems: A review. Ocean Eng. 2021, 236, 109558. [Google Scholar] [CrossRef]
- Vo, B.N.; Mallick, M.; Bar-Shalom, Y.; Coraluppi, S.; Osborne, R., III; Mahler, R.; Vo, B.T. Multitarget Tracking. In Wiley Encyclopedia of Electrical and Electronics Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; pp. 1–25. [Google Scholar] [CrossRef]
- Pitre, R.R.; Li, X.R.; Delbalzo, R. UAV route planning for joint search and track missions-an information-value approach. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2551–2565. [Google Scholar] [CrossRef]
- Jilkov, V.P.; Li, X.R. On fusion of multiple objectives for UAV search and track path optimization. J. Adv. Inf. Fusion 2009, 4, 27–39. [Google Scholar]
- Botts, C.H.; Spall, J.C.; Newman, A.J. Multi-Agent Surveillance and Tracking Using Cyclic Stochastic Gradient. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 270–275. [Google Scholar]
- Khan, A.; Rinner, B.; Cavallaro, A. Cooperative robots to observe moving targets: Review. IEEE Trans. Cybern. 2018, 48, 187–198. [Google Scholar] [CrossRef]
- Li, B.; Yang, Z.P.; Chen, D.Q.; Liang, S.Y.; Ma, H. Maneuvering target tracking of UAV based on MN-DDPG and transfer learning. Def. Technol. 2021, 17, 457–466. [Google Scholar] [CrossRef]
- Wang, T.; Qin, R.X.; Chen, Y.; Hichem, S.; Chang, C. A reinforcement learning approach for UAV target searching and tracking. Multimed. Tools Appl. 2019, 78, 4347–4364. [Google Scholar] [CrossRef]
- Rosello, P.; Kochenderfer, M.J. Multi-agent reinforcement learning for multi-object tracking. In Proceedings of the 17th International Conference on Autonomous Agents and Multi-Agent Systems (AAMAS), Richland, SC, USA, 9–11 July 2018; pp. 1397–1404. [Google Scholar]
- Zhou, W.H.; Li, J.; Liu, Z.H.; Shen, L.C. Improving multi-target cooperative tracking guidance for UAV swarms using multi-agent reinforcement learning. Chin. J. Aeronaut. 2022, 35, 100–112. [Google Scholar] [CrossRef]
- Kraemer, L.; Banerjee, B. Multi-agent reinforcement learning as a rehearsal for decentralized planning. Neurocomputing 2016, 190, 82–94. [Google Scholar] [CrossRef]
- Sunehag, P.; Lever, G.; Gruslys, A.; Czarnecki, W.M.; Zambaldi, V.; Jaderberg, M.; Lanctot, M.; Sonnerat, N.; Leibo, J.Z.; Tuyls, K.; et al. Value-Decomposition Networks for Cooperative Multi-Agent Learning Based on Team Reward. In Proceedings of the 17th International Conference on Autonomous Agents and Multiagent Systems (AAMAS), Richland, SC, USA, 9–11 July 2018; pp. 2085–2087. [Google Scholar]
- Rashid, T.; Samvelyan, M.; Schroeder, C.; Farquhar, G.; Foerster, J.; Whiteson, S. Qmix: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning. In Proceedings of the International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018; pp. 1–14. [Google Scholar]
- Son, K.; Kim, D.; Kang, W.J.; Hostallero, D.E.; Yi, Y. Qtran: Learning to Factorize with Transformation for Cooperative Multi-Agent Reinforcement Learning. In Proceedings of the International Conference on Machine Learning (ICML), Long Beach, CA, USA, 10–15 June 2019; pp. 1–18. [Google Scholar]
- Rashid, T.; Farquhar, G.; Peng, B.; Whiteson, S. Weighted QMIX: Expanding Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Virtual, 6–12 December 2020; pp. 1–20. [Google Scholar]
- Yang, Y.; Hao, J.; Liao, B.; Shao, K.; Chen, G.; Liu, W.; Tang, H. Qatten: A general framework for cooperative multiagent reinforcement learning. arXiv 2020, arXiv:2002.03939. [Google Scholar]
- Wang, J.H.; Ren, Z.Z.; Liu, T.; Yu, Y.; Zhang, C.J. Qplex: Duplex Dueling Multi-Agent Q-Learning. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual, 3–7 May 2021; pp. 1–27. [Google Scholar]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-Agent Actor-Critic for Mixed Cooperative Competitive Environments. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 24–28 January 2018; pp. 1–12. [Google Scholar]
- Foerster, J.; Farquhar, G.; Afouras, T.; Nardelli, N.; Whiteson, S. Counterfactual Multi-Agent Policy Gradients. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), New Orleans, LA, USA, 2–7 February 2018; pp. 1–10. [Google Scholar]
- Wei, E.; Wicke, D.; Freelan, D.; Luke, S. Multiagent Soft Q-Learning. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), New Orleans, LA, USA, 2–7 February 2018; pp. 1–7. [Google Scholar]
- Iqbal, S.; Sha, F. Actor-Attention-Critic for Multi-Agent Reinforcement Learning. In Proceedings of the International Conference on Machine Learning (ICML), Long Beach, CA, USA, 10–15 June 2019; pp. 1–14. [Google Scholar]
- Wang, Y.H.; Han, B.N.; Wang, T.H.; Dong, H.; Zhang, C.J. DOP: Off-Policy Multi-Agent Decomposed Policy Gradients. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual, 26 April–1 May 2020; pp. 1–20. [Google Scholar]
- Tumer, K.; Agogino, A.K.; Wolpert, D.H. Learning Sequences of Actions in Collectives of Autonomous Agents. In Proceedings of the the First International Joint Conference on Autonomous Agents and Multiagent Systems: Part 1, Bologna Italy, 15–19 July 2002; pp. 378–385. [Google Scholar] [CrossRef]
- Batty, M. Spatial entropy. Geogr. Anal. 1974, 6, 1–31. [Google Scholar] [CrossRef]
- Agogino, A.K.; Tumer, K. Unifying Temporal and Structural Credit Assignment Problems. In Proceedings of the Third International Joint Conference on Autonomous Agents and Multiagent Systems (AAMAS), New York, NY, USA, 19–23 July 2004; pp. 980–987. [Google Scholar]
- Cheriguene, Y.; Bousbaa, F.Z.; Kerrache, C.A.; Djellikh, S.; Lagraa, N.; Lahby, M.; Lakas, A. COCOMA: A resource-optimized cooperative UAVs communication protocol for surveillance and monitoring applications. Wirel. Netw. 2022. [Google Scholar] [CrossRef]
- Zhou, W.H.; Li, J.; Zhang, Q.J. Joint communication and action learning in multi-target tracking of UAV swarms with deep reinforcement learning. Drones 2022, 6, 339. [Google Scholar] [CrossRef]
- Mishra, D.; Trotta, A.; Traversi, E.; Felice, M.D.; Natalizio, E. Cooperative cellular UAV-to-Everything (C-U2X) communication based on 5G sidelink for UAV swarms. Comput. Commun. 2022, 192, 173–184. [Google Scholar] [CrossRef]
- Gao, N.; Liang, L.; Cai, D.H.; Li, X.; Jin, S. Coverage control for UAV swarm communication networks: A distributed learning approach. IEEE Internet Things J. 2022, 9, 19854–19867. [Google Scholar] [CrossRef]
- Dibangoye, J.S.; Amato, C.; Buffet, O.; Charpillet, F. Optimally solving dec-POMDPs as continuous-state MDPs. J. Artif. Intell. Res. 2016, 55, 443–497. [Google Scholar] [CrossRef]
- Oliehoek, F.A.; Amato, C. A Concise Introduction to Decentralized POMDPs; Springer: Berlin/Heidelberg, Germany, 2016; Volume 1. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. In Proceedings of the 35th international conference on machine learning (ICML), Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Zhang, T.H.; Li, Y.H.; Wang, C.; Xie, G.M.; Lu, Z.Q. Fop: Factorizing Optimal Joint Policy of Maximum-Entropy Multi-Agent Reinforcement Learning. In Proceedings of the International Conference on Machine Learning (ICML), Virtual, 18–24 July 2021; pp. 12491–12500. [Google Scholar]
- Wolpert, D.H.; Tumer, K. Optimal payoff functions for members of collectives. Adv. Complex Syst. 2002, 4, 355–369. [Google Scholar]
- Xia, Z.Y.; Du, J.; Wang, J.J.; Jiang, C.X.; Ren, Y.; Li, G.; Han, Z. Multi-Agent Reinforcement Learning Aided Intelligent UAV Swarm for Target Tracking. IEEE Trans. Veh. Technol. 2021, 71, 931–945. [Google Scholar] [CrossRef]
- Yu, C.; Velu, A.; Vinitsky, E.; Wang, Y.; Bayen, A.; Wu, Y. The Surprising Effectiveness of PPO in Cooperative Multi-Agent Games. In Proceedings of the 36th Conference on Neural Information Processing Systems (NeurIPS 2022), New Orleans, LA, USA, 28 November–9 December 2022; pp. 1–30. [Google Scholar]
- Yu, C.; Velu, A.; Vinitsky, E.; Wang, Y.; Bayen, A.; Wu, Y. Benchmarking Multi-Agent Deep Reinforcement Learning Algorithms. In Proceedings of the Workshop in Conference on Neural Information Processing Systems (NeurIPS), Virtual, 6–12 December 2020; pp. 1–22. [Google Scholar]
- Lv, M.; Yu, W.; Cao, J.; Baldi, S. A separation-based methodology to consensus tracking of switched high-order nonlinear multi-agent systems. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 5467–5479. [Google Scholar] [CrossRef] [PubMed]
- Lv, M.; Schutter, B.D.; Cao, J.; Baldi, S. Adaptive prescribed performance asymptotic tracking for high-order odd-rational-power nonlinear systems. IEEE Trans. Autom. Control 2023, 68, 1047–1053. [Google Scholar] [CrossRef]
- Lv, M.; Schutter, B.D.; Baldi, S. Non-recursive control for formation-containment of HFV swarms with dynamic event-triggered communication. IEEE Trans. Ind. Inform. 2022, early access. [CrossRef]



| Symbol | Definition |
|---|---|
| The numbers of the UAVs and targets. | |
| The indexes of each UAV, each neighbor, and each target. | |
| The position, velocity, and heading of UAV . | |
| The maximum heading angular rate and the action of UAV . | |
| The UAV’s cardinality of the discrete action space, and the corresponding index of its discrete action. | |
| The maximum observation distance and maximum communication distance. | |
| The distance between UAV and UAV , target , and scenario center . | |
| The UAV ’s observation information about target . | |
| The UAV ’s communication information from neighbor . | |
| The UAV ’s local observation information. | |
| The global state of the environment. |
| Methods | Advantage | Limitation |
|---|---|---|
| Traditional optimization | Powerful non-convex optimization and convergence performance; robust. | Computationally expensive; poor real-time performance of online searching; limitations in large-scale variable problems. |
| Reinforcement learning | Implicit modeling unknown environment; data-driven; offline training and online decision framework; near real-time solving speed. | Learning inefficiency; credit assignment; poor interpretation; scalability. |
| Entity | Physical Meaning | Notation | Value |
|---|---|---|---|
| Environment | Size | 2000 m × 2000 m | |
| Scenario boundary length | 2000 m | ||
| UAV | Observation range | 200 m | |
| Communication range | 800 m | ||
| Safe distance | 400 m | ||
| Speed | 60 m/s | ||
| Maximum heading angular rate | /6 rad/s | ||
| Target | Speed | 40 m/s |
| Hyperparameter | Value |
|---|---|
| Episode limit | 100 |
| Max step | 1,005,000 |
| Buffer size | 5000 |
| Minibatch size | 64 |
| Target update interval | 200 |
| Actor learning rate | 0.0001 |
| Critic learning rate | 0.0005 |
| TD lambda | 0.6 |
| Gamma | 0.99 |
| Minimum policy entropy | −1 |
| Equivalent spatial entropy distance | 500 |
| Scenarios | Map Size (km) | Indicators | FMASAC | MASAC | MAPPO | MADDPG |
|---|---|---|---|---|---|---|
| 3 UAVs and 3 targets | 2 × 2 | Mean reward | 172.63 | 144.54 | 160.51 | 54.28 |
| Reward standard deviation | 1.11 | 18.84 | 1.26 | 8.07 | ||
| Average tracked targets | 3 | 2.44 | 2.96 | 1.05 | ||
| Tracking success rate | 100% | 81.25% | 98.75% | 35% | ||
| 5 UAVs and 5 targets | 5 × 5 | Mean reward | 315.23 | 289.72 | 308.88 | 124.36 |
| Reward standard deviation | 1.32 | 16.95 | 1.45 | 9.87 | ||
| Average tracked targets | 4.88 | 4.19 | 4.81 | 1.56 | ||
| Tracking success rate | 97.5% | 83.75% | 96.25% | 31.25% | ||
| 10 UAVs and 10 targets | 10 × 10 | Mean reward | 611.97 | 457.42 | 543.83 | 277.19 |
| Reward standard deviation | 1.64 | 23.63 | 1.58 | 13.42 | ||
| Average tracked targets | 9.5 | 7.38 | 8.63 | 4.13 | ||
| Tracking success rate | 95% | 73.75% | 86.25% | 41.25% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, L.; Yang, R.; Zuo, J.; Yan, M.; Zhao, X.; Lv, M. Factored Multi-Agent Soft Actor-Critic for Cooperative Multi-Target Tracking of UAV Swarms. Drones 2023, 7, 150. https://doi.org/10.3390/drones7030150
Yue L, Yang R, Zuo J, Yan M, Zhao X, Lv M. Factored Multi-Agent Soft Actor-Critic for Cooperative Multi-Target Tracking of UAV Swarms. Drones. 2023; 7(3):150. https://doi.org/10.3390/drones7030150
Chicago/Turabian StyleYue, Longfei, Rennong Yang, Jialiang Zuo, Mengda Yan, Xiaoru Zhao, and Maolong Lv. 2023. "Factored Multi-Agent Soft Actor-Critic for Cooperative Multi-Target Tracking of UAV Swarms" Drones 7, no. 3: 150. https://doi.org/10.3390/drones7030150
APA StyleYue, L., Yang, R., Zuo, J., Yan, M., Zhao, X., & Lv, M. (2023). Factored Multi-Agent Soft Actor-Critic for Cooperative Multi-Target Tracking of UAV Swarms. Drones, 7(3), 150. https://doi.org/10.3390/drones7030150







