Fast Marching Techniques for Teaming UAV’s Applications in Complex Terrain

Abstract

In this paper, we present a study on coverage missions carried out by UAV formations in 3D environments. These missions are designed to be applied in tracking and search and rescue missions, especially in the case of accidents. In this manner, the presented method focuses on the path planning stage, the objective of which is to compute a convenient trajectory to completely cover a certain area in a determined environment. The methodology followed uses a Gaussian mixture to approximate a probability of containment distribution along with the Fast Marching Square (FM²) as path planner. The Gaussians permit to define a zigzag trajectory that optimizes the path. Next, a first 2D geometric path perpendicular to the Voronoi diagram of the Gaussian distribution is calculated, obtained by skeletonization. To this path, the height above the ground is added plus the desired flight height to make it 3D. Finally, the FM² method for formations is applied to make the path smooth and safe enough to be followed by UAVs. The simulation experiments show that the proposed method achieves good results for the zigzag path in terms of smoothness, safety and distance to cover the desired area through the formation of UAVs.

1. Introduction

Target search and thus the covering of a big area goes back years in history. This task has been mainly focused on carrying out rescue operations and tracking of subjects missions. There exist four types of searching problems, regarding their application field: maritime, combat, urban and wilderness [1].

Searching tasks gained value in the maritime field since the Second World War due to the efforts made by the US Army to detect enemy submarines [2]. Currently, interest in this area has been highlighted by diverse civilian applications such as monitoring and exploration of varied environments and largely by unfortunate events such as rescuing in disaster scenarios, for instance, the unsuccessful search for Malaysian Flight 370 (MH370) disappearing in the ocean in midflight in March 2014 after takeoff from Kuala Lumpur and on its way to Beijing and carrying 239 passengers. The search operations involved a total of 40 ships and aircraft covering an area of over 4.6 million square kilometers in the waters of the Indian Ocean. However, efforts were eventually stood down without finding any conclusive evidences [3].

These tasks have attracted the attention of researchers in many fields dealing with problems in different areas, namely computer vision [4,5], wireless sensor network design [6,7,8], ask assignment formula [9,10] and Optimal Path Planning Computing for Self-Driving Vehicles to Facilitate Search [11,12]. In this work, we address the latter and present an algorithm able to provide search vehicles with appropriate routes to follow and explore target areas.

There are two main factors hindering the development process of search missions, mainly related to field applications at sea [13]:

• Definition of the target area. Due to uncertainty given by adverse weather conditions and unclear or unknown lead locations, these being remaining debris from a disaster event as well as last known position of the objective, for instance. Furthermore, in the case of open ocean search missions, the complex drift dynamics of the surface and the inaccuracy of its predictive models considerably increase the error margin in the estimation of these targets whereabouts.
• Search path design. Although the target region is well defined, the design of the search path problem is not known to have an optimal solution. The goal here is to calculate the path of the search agent over the entire target area to maximize the probability of target detection at a given time.

When determining a target area, the first factor to determine is containment capability. This metric is defined as the probability of finding the object the agent is looking for in each given region of the search area. In this way, the region is initially discretized into cells, which are then transformed into a probability map by assigning these partitions a probability value related to the aforementioned probability of containing the object of interest. The resulting map will represent the likely location of the object you are looking for, taking possible ocean and wind currents (or other uncertainties) that may change its original location into account. It can also be considered as the motion of solid particles through a moving fluid, which can then be studied using Lagrangian particle tracking algorithms (also known as Euler–Lagrangian methods). Examples of these probability plots are shown in Figure 1 containing regions of lower and higher exponential probability differentiated by color codes.

There might be scenarios in which the search area does not consist of a single compact area but a set of nonconnected regions. In these cases, the probability map could be treated as a mixture model. A common example of these probability models is given by the Gaussian mixture model [14], which allows to gather all possible observations under a group of normal distributions of different parameters, as shown in Figure 2.

Once the search area is well defined, the trajectory to conveniently reach its full breadth must be designed. This task is widely known as coverage. Researchers in the literature distinguish two different approaches, namely [15]: lawnmower algorithms and control of the agents through optimization processes.

In a lawnmower strategy, search agents will sweep the target area by going back and forth following a specific pattern. These patterns are conveniently designed to find the target in shorter time. Figure 3 shows different patterns proposed by authors working on the matter. What makes this strategy interesting is that, just on the basis of these primitive patterns and adding some custom design criteria, good results can be obtained for a low computational cost.

Researchers in [17] use this approach to study and improve the calculation method of the aforementioned probability of containment measure, as well as the probability of detection and thus the probability of success values. This probability of detection is mainly related to the efficiency of the path designed and available sensors to cover the full search area and therefore detect the targets. Then, the probability of coverage success would depend on these other factors.

One could look at this path planning task as an optimization problem. Then, the goal would be to compute this search trajectory by minimizing a certain performance metric that may be related to, for instance: fuel consumption, travel times, path length or, as in the well-known salesman problem, visiting all target areas (if more than one exists) just once while following the shortest path. This issue is commonly addressed through swarm optimization algorithms, as its aim is to provide ’best locations’ within a search space using swarms [18,19,20]. Particle Swarm Optimization is notably highlighted in the literature from this whole family of algorithms [21,22]. For its part, authors in [23] study the problem of dynamically covering a given region through a designed closed-loop control strategy. Their goal was to provide, for each target point of the domain, a certain amount of effective coverage.

Finally, once the coverage problem has been formulated, it seems interesting to underline that most of these tasks are usually carried out not just by a single search vehicle but by a swarm, following a specific formation or not [24]. Multirobot (or multivehicle) systems have certain advantages over single-robot missions. Several tasks can be executed in parallel, provide a wider sensing range and the whole system can be more robust to failures of one of the vehicles [20,25,26,27,28,29]. Regarding this topic, our group has worked on the robot formations planning problem (both in 2D and 3D) using the Fast Marching Square (FM²) algorithm [30,31].

In this work, we are going to study the coverage and robot formation problems, introducing probability maps and implementing the FM² algorithm, in two closely related situations. The first aimed at search missions in mountain areas using Unmanned Autonomous Vehicle (UAV) formations and the latter focusing on maritime search tasks carried out by an Unmanned Autonomous System (UAS).

The main contributions of this paper are: (1) a simple approach lawnmower strategy is presented to face the coverage path planning problem for search and rescue tasks carried out by UAVs in different 3D environments; (2) the coverage method is based on the use of Gaussian Mixture to approximate the probability of containment distribution, Voronoi Diagrams to skeletonize the Gaussian Mixture, geometric generation of the lawnmower zigzag coverage path and Fast Marching Square to obtain smooth, optimal in terms of distance cost and collision free trajectories; (3) the method is extended to UAV team formations and the strategy is usable for different swarm configurations and numbers of team vehicle members; (4) the search environments aimed at this work may present diverse shapes and may be composed of a single compact target zone or a series of disjoint areas; (5) the target zones may constitute uneven ground terrain levels and the flight height at which the coverage mission is planned can be chosen at will and is relative to this varying ground level.

The rest of the paper is organized as follows. Section 2 describes the Eikonal Equation and the Fast Marching Method. Section 3 introduces the Coverage Path Planning carried out by a single UAV and also presents the UAVs formation approach. Section 4 shows the results from two cases of application. Finally, in Section 5, the main conclusions of the work are presented.

2. The Fast Marching Method

The Fast Marching method was proposed by J.A. Sethian in 1996 [32]. This method lead to an extremely fast scheme to solve the eikonal equation in Cartesian grids. The eikonal equation models the propagation of an isometric wave front. Rays of light, traveling through different materials, follow the least time-consuming path, according to Fermat’s principle [33]. This is an interest concept in robotics due to the fact that, if we know how light rays propagate through space, we can calculate the trajectory between two points of a map. This trajectory can be obtained with the Fast Marching method (FMM).

If we consider the target point of a trajectory as the source of a light wave front, and the Fast Marching method can be computed over the free cells of a map, the arrival time of the wave front to each point of the map is calculated. Furthermore, taking the set of all cells that represent the free space and the time of arrival to those cells into account, a Lyapunov surface in which all level curves are isochronous can be created, and the Lyapunov trajectories are orthogonal to said curves. This means that it is not possible for the method to show local minima. An example of this surface can be seen in Figure 4.

The propagation of the light wave front is given by the eikonal Equation (1). Sethian [32] proposed a first order approximation to this equation and called it FMM. The eikonal equation defines the time of arrival of the propagating wavefront, $T\left(x\right)$, to every point x, in which the wave front propagation speed depends on the point $F\left(x\right)$, according to:

$$|\nabla T\left(X\right)|F\left(x\right)=1,x\subset {\mathbb{R}}^N$$

(1)

The Fast Marching method consists of solving the Equation (1) and calculate sequentially $T\left(x\right)$ for every cell of the map starting from the wave source point where $T\left(x_o\right)=0$. After using FMM, gradient descent can be used from any distance map point to obtain a path to the wave source as a target point. The main advantage of this approach is that the resulting paths are time optimal. An example of a path generated using FMM and another calculated using $F{M}^2$ is shown in Figure 5.

The Fast Marching Square Method

As it can be seen in Figure 6a, although optimal in distance, the trajectory is neither safe in terms of possible collision with obstacles nor feasible in terms of the sharpness of the turns the trajectory requires. These series of disadvantages lead to study the use of the Fast Marching Square method (FM²) [34] as a path planner, since it gives a solution to these two disadvantages. It consists of applying FMM two times as shown in Figure 5b.

Let us consider a map in which obstacles take the value 1 and free cells take the value 0. FMM can be applied to these map considering all obstacles as wave sources. An example of this method is shown in Figure 6.

This map can be explained in many ways. It can be interpreted as a potential field of the original map, as cells move away from obstacles, the $T_i$ value gets higher, like in the case of the distances map. Furthermore, it can be seen as a velocity map: the $T_i$ value can be interpreted proportional to the maximum speed achievable for the robot in each point, which leads to permitting lower speeds when the point is close to an obstacle, and higher speeds when it is away from them. In fact, a robot which speed in each point is given by $T_i$ will never collide with obstacles, since $T_i\to 0$ as it gets closer to an obstacle. Further into this work, this first potential is referred to as potential W.

The second time the FMM is applied (obtaining potential D), the velocity at which the wave front advances can be different in each point of the map. Furthermore, this velocity is proportional to the distance to the closest obstacle, which means that the wave front advances faster when it is away from obstacles. This produces important differences in the trajectory obtained, as it can be seen in Figure 4. The final trajectory is obtained through gradient descent methods, as for the original FMM.

The $F{M}^2$ method has some properties that make it really useful to plan trajectories. The most important advantages are:

• No local minima.
• Complete.
• Smooth trajectories.
• Fast response with $O\left(n\right)$ complexity [35].

3. Problem Statement

3.1. Coverage Path Planning of the Leader of the UAVs Formation

As it has been previously mentioned, the method presented in this paper for Coverage Path Planning (CPP) aims to be applied to UAV formations. In this way, the strategy is first defined for the leader of the UAV formation team. The technique used belongs to the aforementioned lawnmower family of coverage planning algorithms, sufficiently optimized to be both efficient and easy to implement.

The 3D environment where the path planning for covering with a UAVs formation is carried out is the terrain height near Mount Washington as a function of x–y position (In this case, Mount Washington is the highest peak in the northeastern United States.)

The US Geological Survey provides terrain elevation data as a function of x–y position on the grid. To estimate the height of an arbitrary point, the objective function interpolates the height from nearby grid points.

The 3D grid map has a dimension of 550 × 550 × 40 cells, where each cell of the map is equivalent to 15 × 15 × 15 m. It is not necessary to consider the sizes of the UAVs, since it is assumed tobe smaller than the size of a cell. In Figure 7 and Figure 8, the grid map has a dimension of 750 × 750 × 40 cells to have a denser coverage.

The procedure is detailed below.

This method is based in the Gaussian Mixture approximation of the probability of containment density function that defines the searching area, which is assumed to be already characterized. The method is composed by the following steps:

1.

Find the Gaussian Mixture that approximates the probability function given. In this manner, the domain is simplified to a series of Gaussian distributions, and it is possible to apply the upcoming steps to the Gaussians. Figure 9a and Figure 7a shows a search region given by three Gaussians.

2.

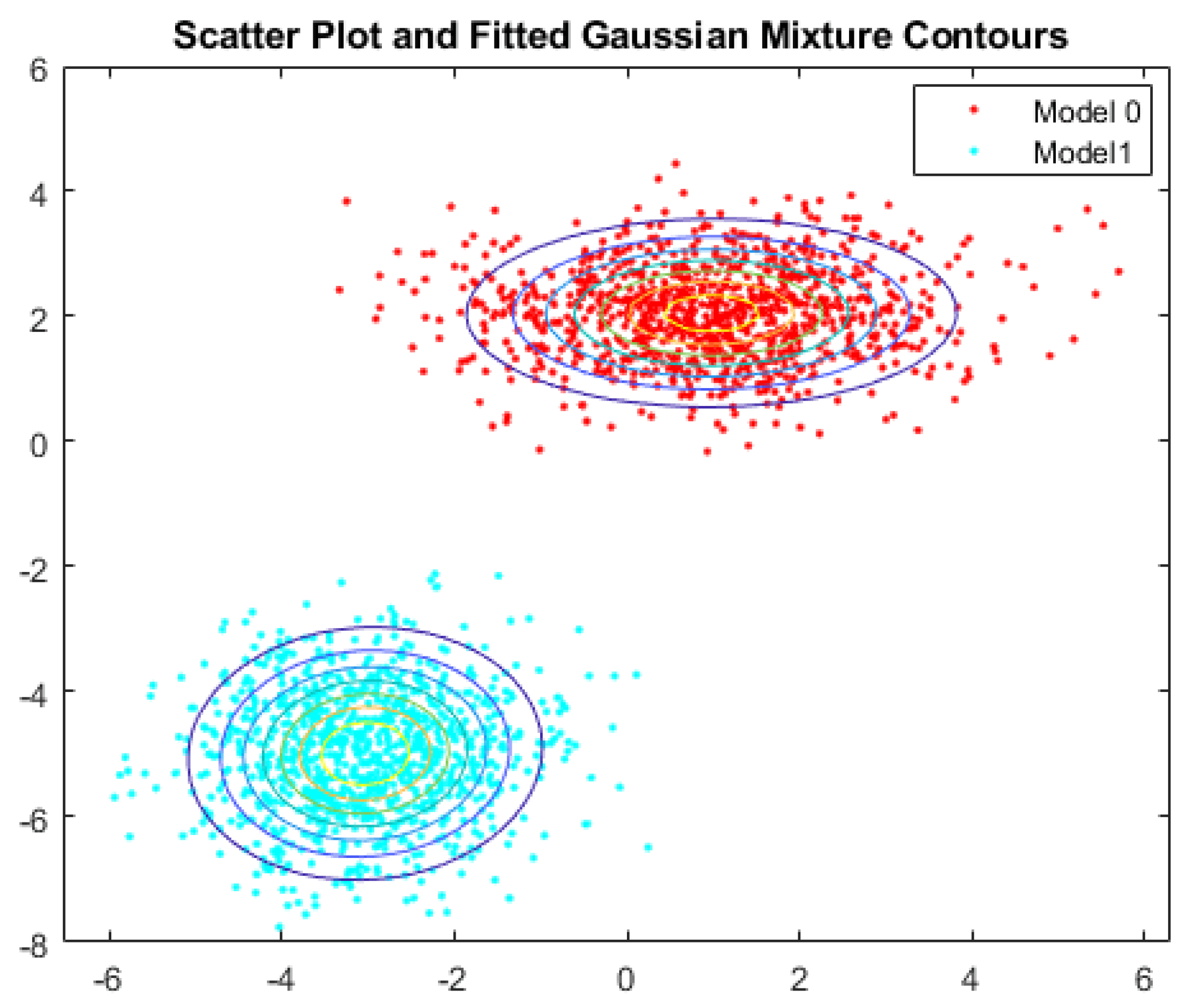
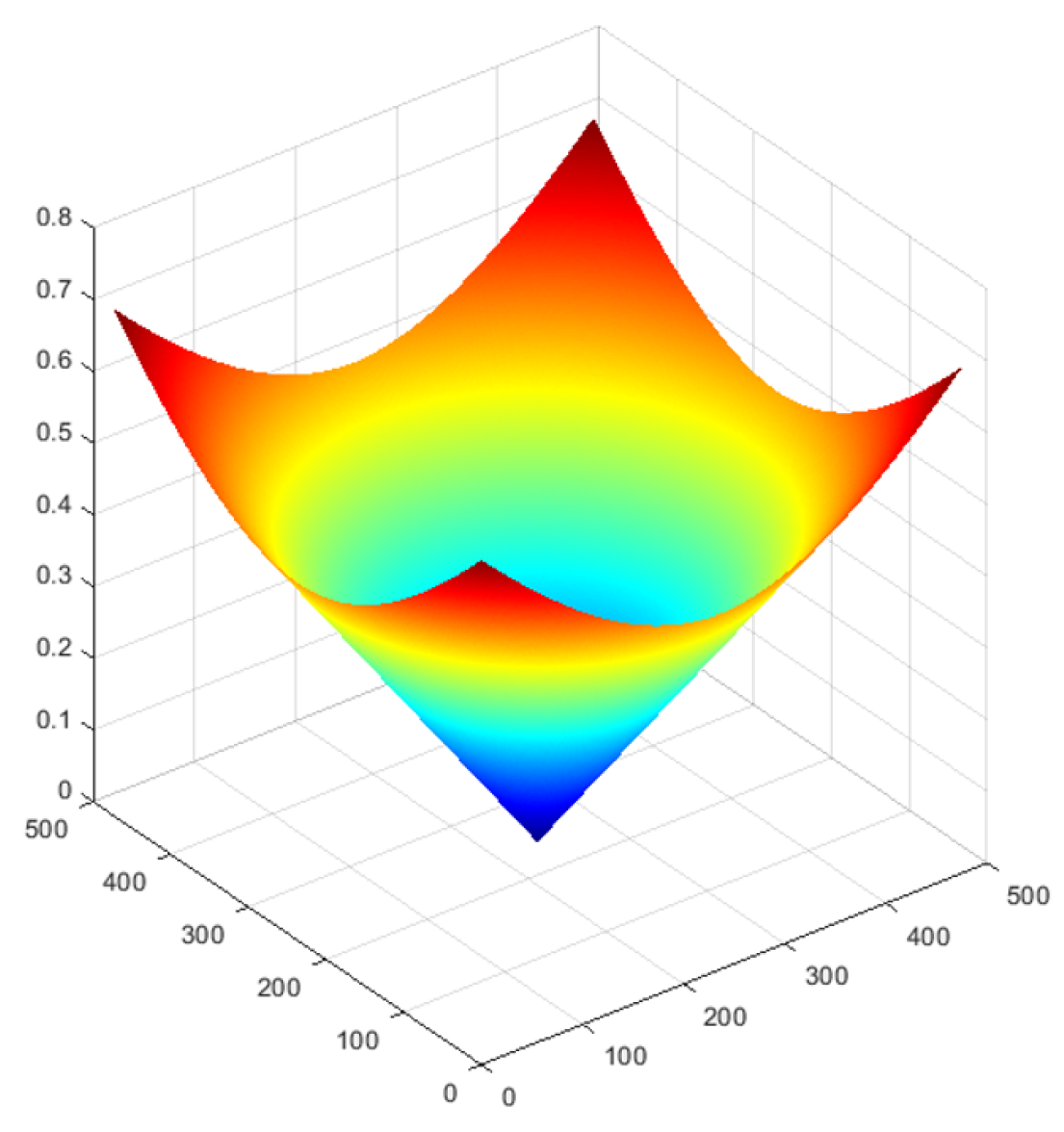
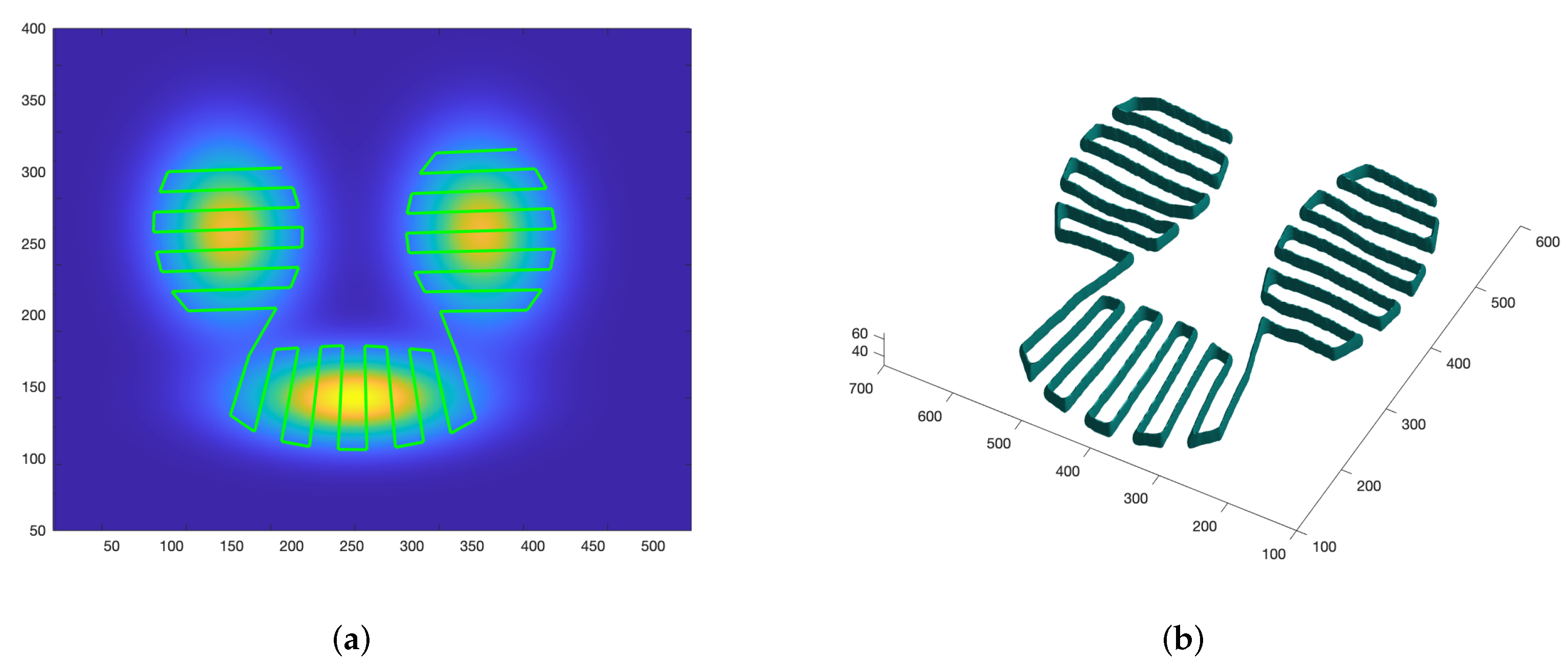
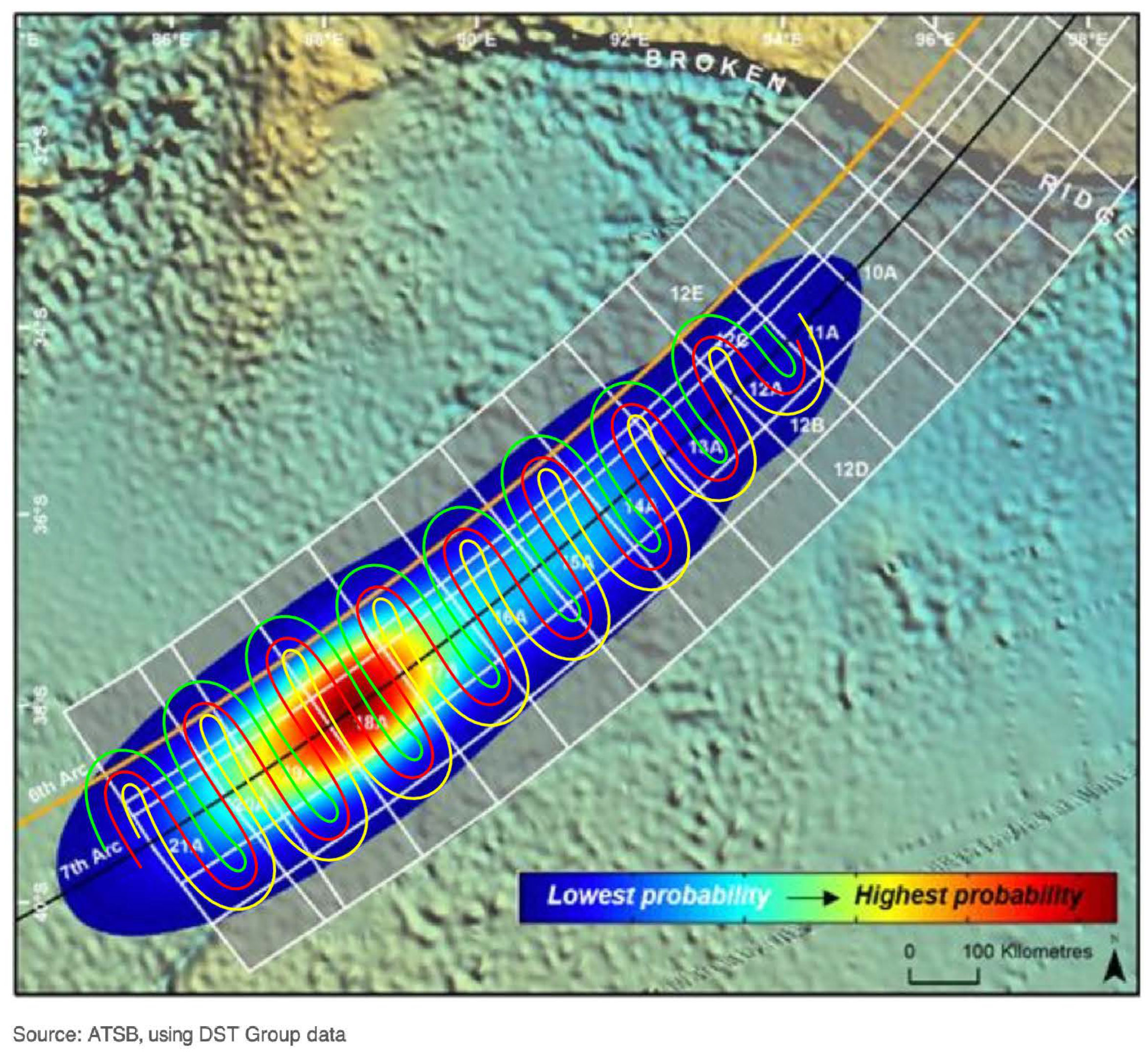
Identify the minimum level of probability to find the area to be covered. This zone can be compact or composed by different unconnected zones, as shown in Figure 7a.

3.

Using the Voronoi method, the medial axis of the zones is calculated. The medial axis may be a curve or can be made up of unconnected sections. For isolated Gaussians, the medial axis is the main axis of the Gaussian. For nonisolated Gaussians, the medial axis is a curve composed by the points that are at the same distance to the borders of the probability threshold.

4.

The next step is to find the points that divide the medial axis into segments of the same length.

5.

The line segments perpendicular to the medial axis that pass through these points are calculated. The segments end where the chosen probability threshold is reached.

6.

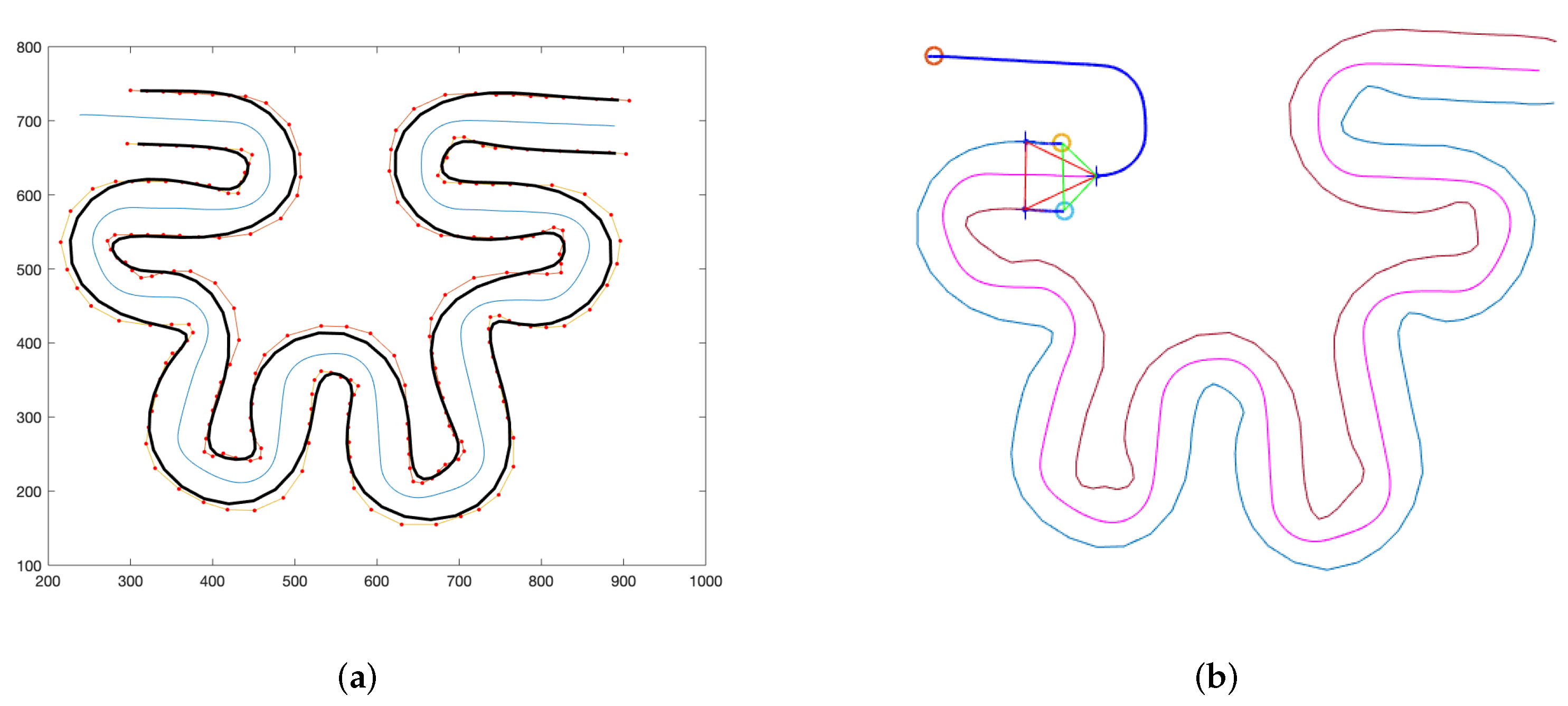
The ends of these segments are joined alternately to obtain a complete zigzag path. This is done optimally so that the overall length is minimized. Figure 9b shows a 2D zigzag path composed by segments obtained this way.

7.

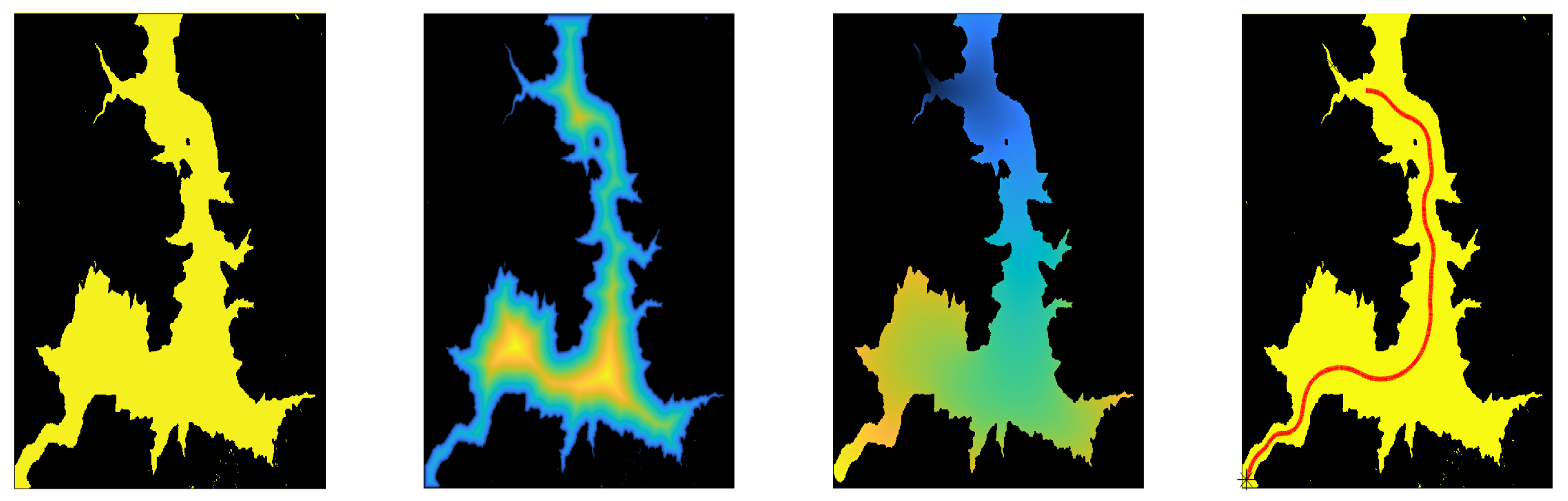
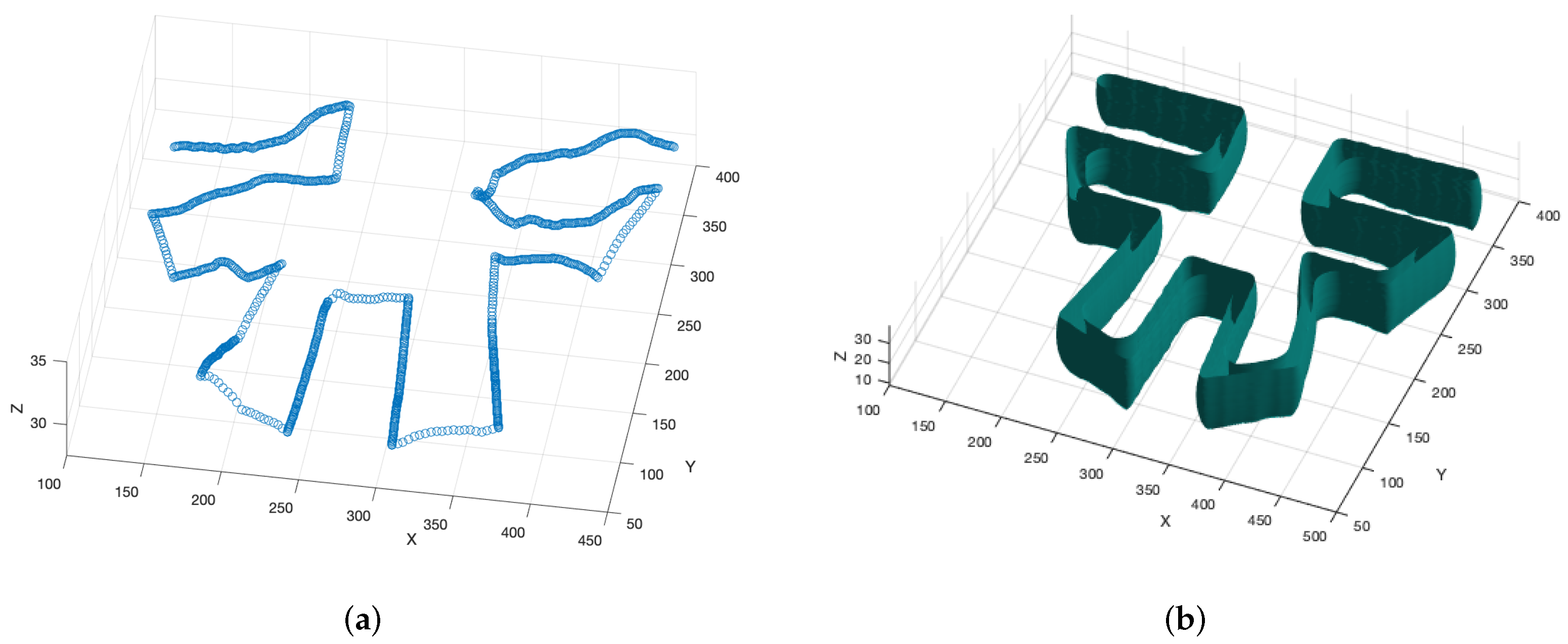
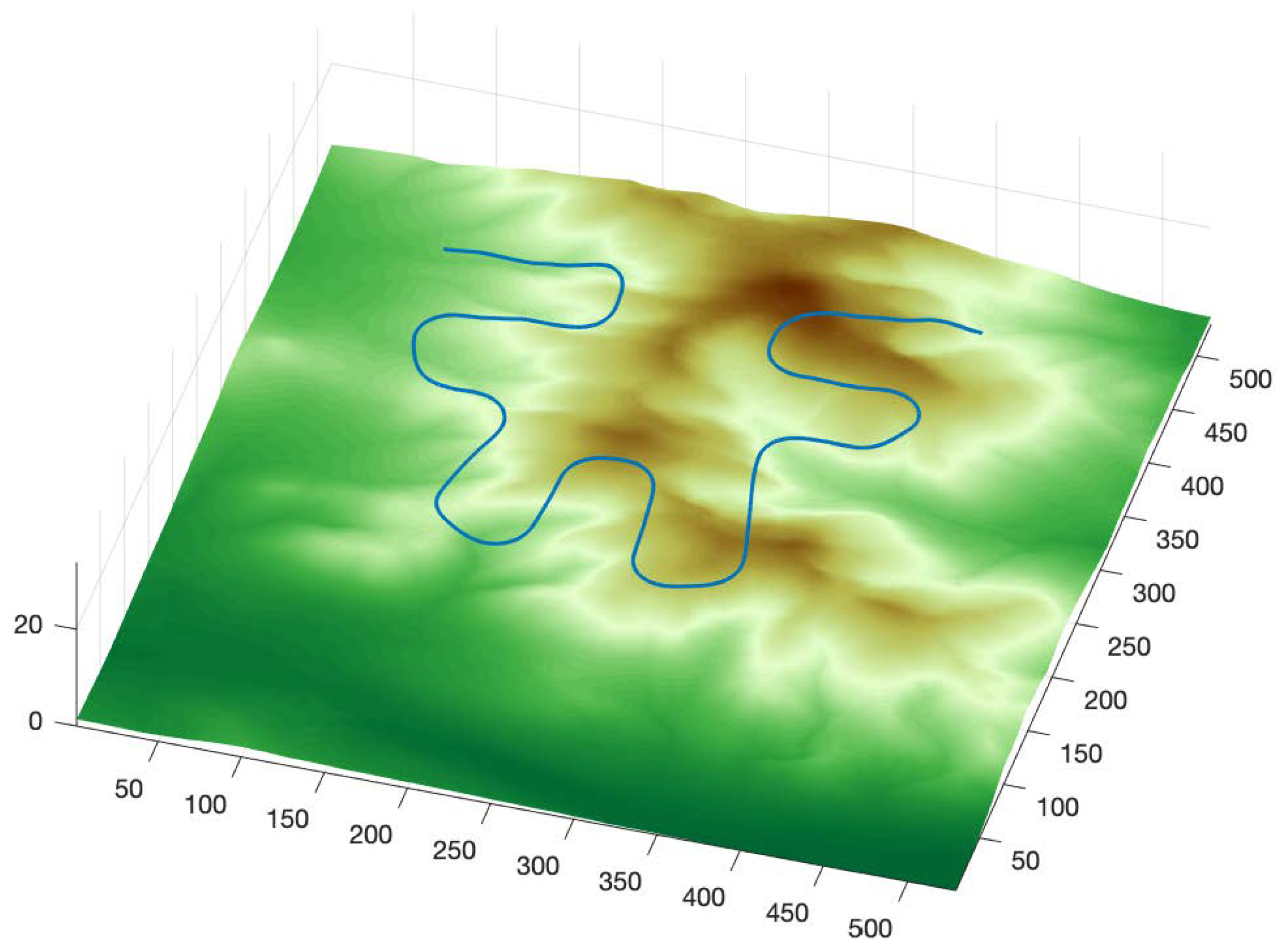
Heights are added so that the path becomes a three-dimensional path. Figure 10a shows a 3D path obtained by adding the desired height above the ground to the previous path. It is important to notice that the ground terrain level may be irregular.

8.

As it is not smooth enough, a three-dimensional tube is calculated through image processing techniques, dilating the path as shown in Figure 10b.

9.

The first Fast Marching potential W is calculated inside the tube so that the path tends to go through the middle of the tube smoothly.

10.

On this first potential W, the second potential D is calculated from the end point. This process finishes when the expansion wave reaches the start point. A slice at a certain height of this D expansion is shown in Figure 11a.

11.

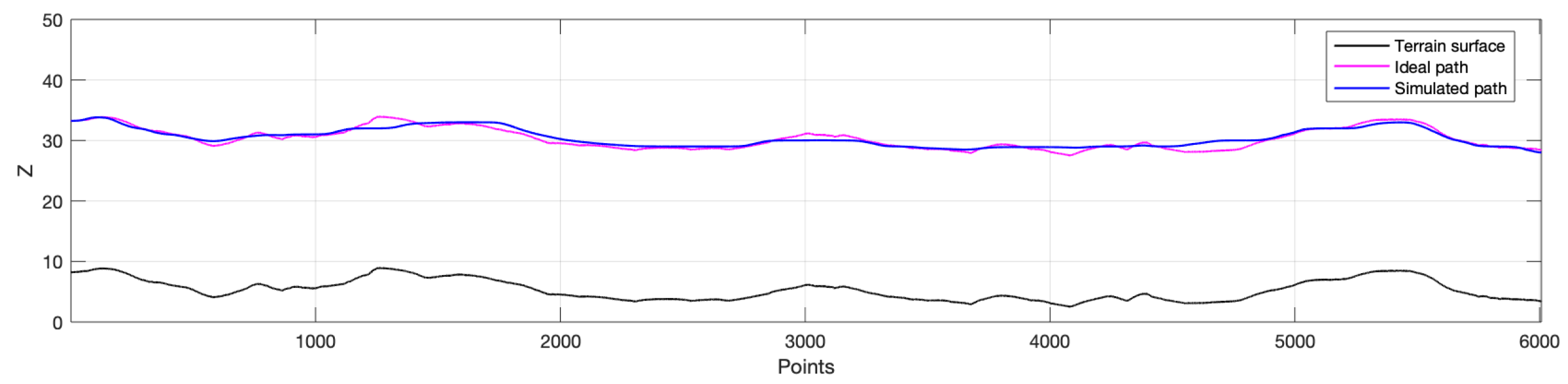
On this potential D, the 3D geodesic path is calculated, from the initial point to the goal point using the gradient descend method. Figure 11b shows the final smooth path obtained with this process.

12.

Final smooth path over the terrain surface is shown in Figure 12, whereas Figure 13 shows a lateral view of this terrain surface (in black), ideal path (in magenta) and smooth path obtained with $F{M}^2$ (in blue).

3.2. UAVs Formation Algorithm

The previous subsection shows how to find out the path for a UAV that will constitute the path of the leader of the formation. Now, it is necessary to explain how, from this path, the trajectories for every UAV in the formation are calculated, taking the possible irregularities of the terrain and the obstacles present in the environment into account.

Suppose a triangular formation, with a leading UAV and two followers. The other possible formations would be treated in a similar way. The formation consists of a first pure geometric triangular shape (magenta triangle in Figure 14) that is deformed according to the needs to avoid the obstacles that appear on the route and the path itself by using the gray levels. This second deformed triangle is the one that UAVs must follow (magenta triangle in Figure 14).

This second deformed triangle is calculated using the remaining vehicles as obstacles. Using the gray level potential present in the Fast Marching method as shown in Figure 15, each UAV sees the rest of the UAV’s as obstacles in the environment. This effect provides additional repulsion force, preventing them from colliding with the other UAVs.

Thus, the stages for planning the trajectory for a whole UAV team flying in formation are detailed hereinafter. The different steps to obtain the trajectory of the leader are:

1.

We start with a binary map $W_o$ of zeros (black area represents the obstacles) and ones (white area represents the zone without obstacles) as shown in Figure 14a.

2.

The Fast Marching method is applied to this binary map $Wo$, taking obstacles as wave origin points. In this way, a gray map W is obtained, in which the grayscale level represents the distance to the nearest obstacle. You can also do this step using the Voromoi Transform, although the performance is not that good due to its discrete nature. This map can be considered as the map of relative speeds of expansion of the wave and also of the leader. (grey potential in Figure 14b,c).

3.

On this first potential W, a wave is launched from the destination point, again using the Fast Marching method, to the origin point. This gives us the second funnel-shaped potential D (color potential in Figure 14d).

4.

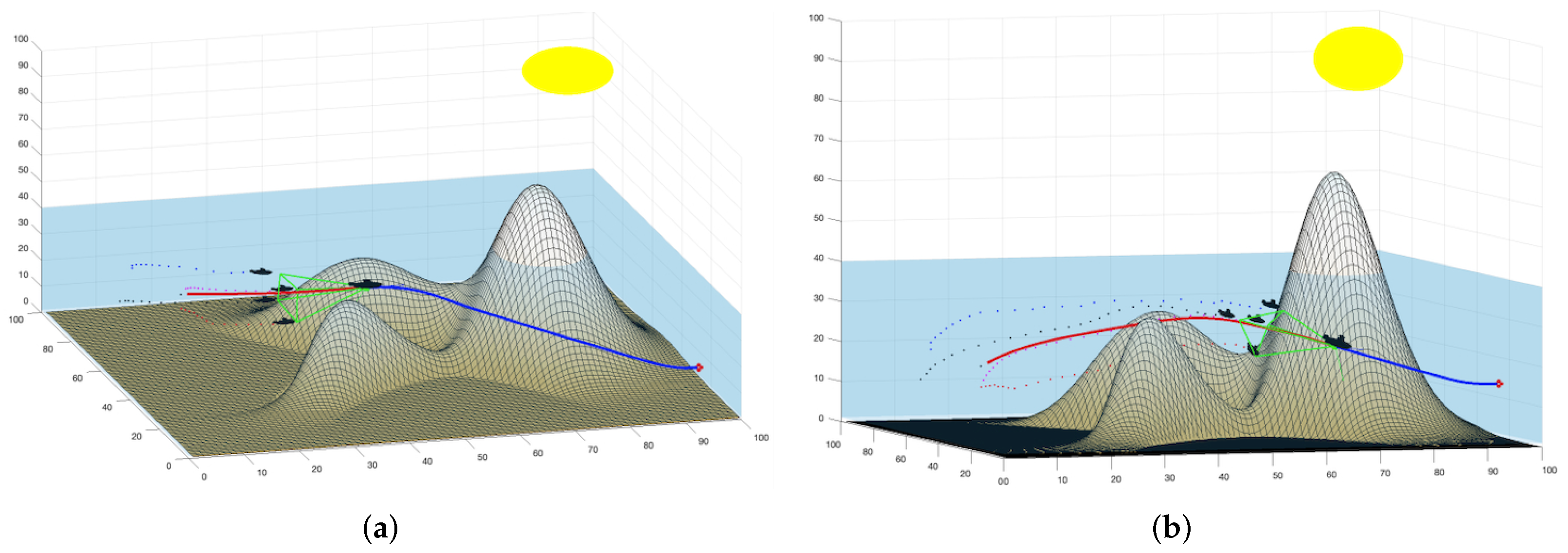
The gradient descent method is applied to D second potential to find the minimum time path. The generated path is the trajectory that the leader must follow.

The distance between the lines of the zigzag can be changed to have a denser coverage of the zone as shown in Figure 7 and Figure 8 and with more resolution (750 × 750 cells).

As for this work, the trajectory corresponding to the leader is computed following the steps described in Section 3.1. Then, when the path of the leader has been generated, the paths of the followers are calculated iteratively. In each cycle of time t and for each $UAV$, referred to as $UA{V}_i$, a partial goal and a partial path are calculated that will continue until the next cycle. The iterations t are calculated in the following way:

1.

Each $UA{V}_i$ is associated with a binary map $W^{t_{0,i}}$ which acts as obstacle map, with the leader and the other followers considered as obstacles. Figure 14a represents the binary map $W^{t_{0,i}}$ with the obstacles and the others UAV’s of the formation in black (value 0) and the allowed parts are white (value 1).

2.

For each ${\mathrm{UAV}}_i$, a new first grayscale potential $W_i^t$ is generated from the binary map $W^{t_{0,i}}$ in each cycle t by using FMM the first time, using all black points as starting points and obtaining the first potential of wave expansion velocities. Figure 14b shows the grayscale map $W_i^t$ of the right follower obtained from the corresponding binary map $W_{0,i}^t$ with two blurred black dots representing the leader and the left follower. In Figure 14c, is shown the grayscale map $W_i^t$ corresponding to the leader obtained from the initial binary map $W_{0,i}^t$, with two blurred black spots representing the two followers.

3.

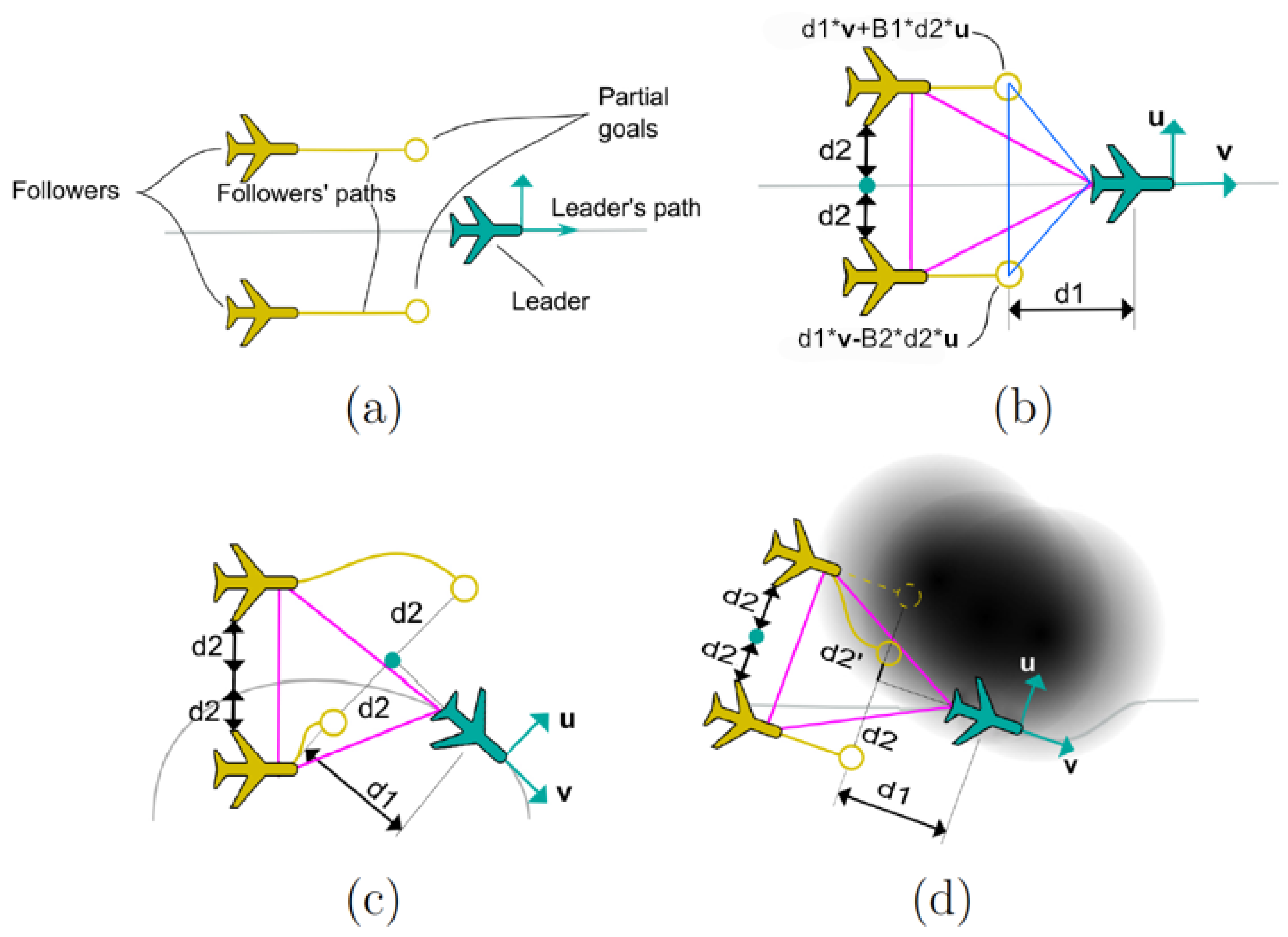
The subgoals $Pt$ ($x_{g,i}$, $y_{g,i}$, $z_{g,i}$) for each follower are calculated based on the leader’s position of the previous $F{M}^2$ leader trajectory. These partial targets indicate the next desired goal for each follower and form the deformable geometric triangle as shown in Figure 8 (magenta triangle). Obstacles in the environment (including other drones) are taken into account when calculating this position. For this purpose, the grayscale level of each subtarget goal is calculated from $W_i^t$, which conveniently changes the triangle distances (edges and vertices). This approach introduces a repulsive force against obstacles and the other UAVs in the environment. More details can be seen in [36].

Figure 16 shows the trajectories of the followers in (a) XY view and (b) the trajectories followed by the UAVs, whereas Figure 17 shows the trajectories of leader and followers over the terrain surface.

In the previous CPP example presented for a mountainous area, the Gaussians were disjoint and the medial axis coincides with the main axis of the ellipse, but when the Gaussian mixture is not composed of disjoint distributions, the medial axis is not a series of straight segments. For example, Figure 17 shows the probability function of the search zone of the accident of the Malaysia Airlines Flight MH370 with the three paths of the UAV’s formation. In this case, the medial axis is a curved line.

4. Results

As can be seen in the figures above, the paths of each member of the formation are smooth, and the trajectories are safe to be followed by real UAVs. The difference is that the trajectories calculated with FMM have sudden changes of direction and collide with the obstacles while the trajectories obtained with $F{M}^2$ are smooth and move away from the obstacles. With the word smooth, we mean that the continuous solution has all the derivatives, that is, it is of class ${\mathcal{C}}^{\infty }$. In our case, we have a discrete solution that depends on the size of the grid, and when it tends to zero, the discrete solution tends to the continuous ${\mathcal{C}}^{\infty }$ solution. The practical meaning is that this type of trajectory can be easily followed by a UAV.

In Figure 18, it can be seen that the method also works to make a covering in other probability spots such as the accident of the Malaysia Airlines Flight MH370. In Figure 7, the height relative to the ground of the leader is shown, which follows the desired values. Those of the followers are similar, as can be seen in Figure 19. The simulation results show that the formation is able to adapt its shape to avoid obstacles while respecting flight level constraints.

Likewise, Figure 17 and Figure 20 shows that the distances among the three members of the formation are correct, because the geometric triangle is deformable but has a range of action so that they do not become too close. As can be seen, the distance minimum among the UAVs formation members is bigger than 50 cells.

As the gray level potential of the first step of the calculation of $F{M}^2$ represents the relative velocity between 0 and 1, we have the recommended relative velocity for each member of the formation in each point, as shown in Figure 21. If this relative velocity is multiplied by the maximum velocity of the UAVs measured in cells per iteration, the real velocity of the three UAVs in cells/iterations is obtained as shown in Figure 22.

The method can be applied to other formations and scenarios. As an example, Figure 23 represents the approach for the case of a leader ship followed by four mini-submarines in a pyramid formation.

5. Conclusions

In this work, we present a new technique to solve the probabilistic Coverage Path Planning (CPP) problem for search and rescue by a formation of UAVs based on Gaussian Mixture to approximate the probability distribution, Voronoi Diagram for the skeletonization of the Gaussian mixture, geometric generation of a zigzag path and finally the Fast Marching Square method ($F{M}^2$) a feasible path free from obstacles for the UAV’s formation that maintains a flight level with respect to the ground. The generated path is optimal not only in terms of distance cost but also in terms of safety and smoothness and, therefore, feasible for the UAV.

One of the advantages of the $F{M}^2$ Method is its flexibility, because by conveniently modifying the first potential (first step of $F{M}^2$), it is possible to obtain the desired path properties and trajectories that can be easily followed by UAVs.

Our approach has proved successful. The tests carried out show good results, even on uneven terrain, always achieving a feasible path with minimum cost. This result shows that our method generates paths that conserve energy or fuel and, furthermore, trajectories that are safe and compatible with UAV kinematics.

In further research, other formations, in different scenarios and in real situations can be studied.