Competition and Cooperation for Multiple Solar Powered Unmanned Aerial Vehicles under Static Soaring
Abstract
:1. Introduction
2. Problem Formulation
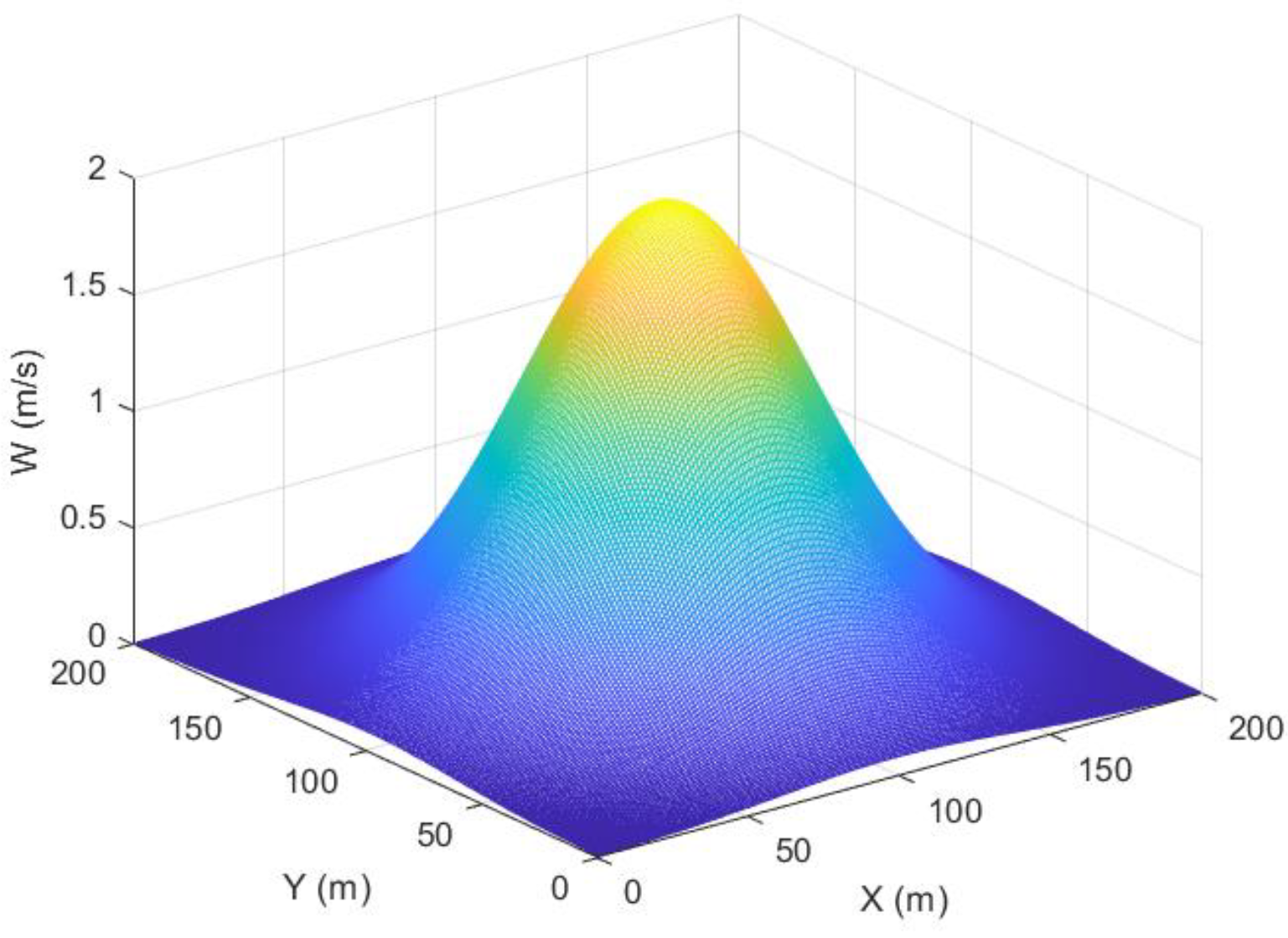
2.1. Model of Thermal
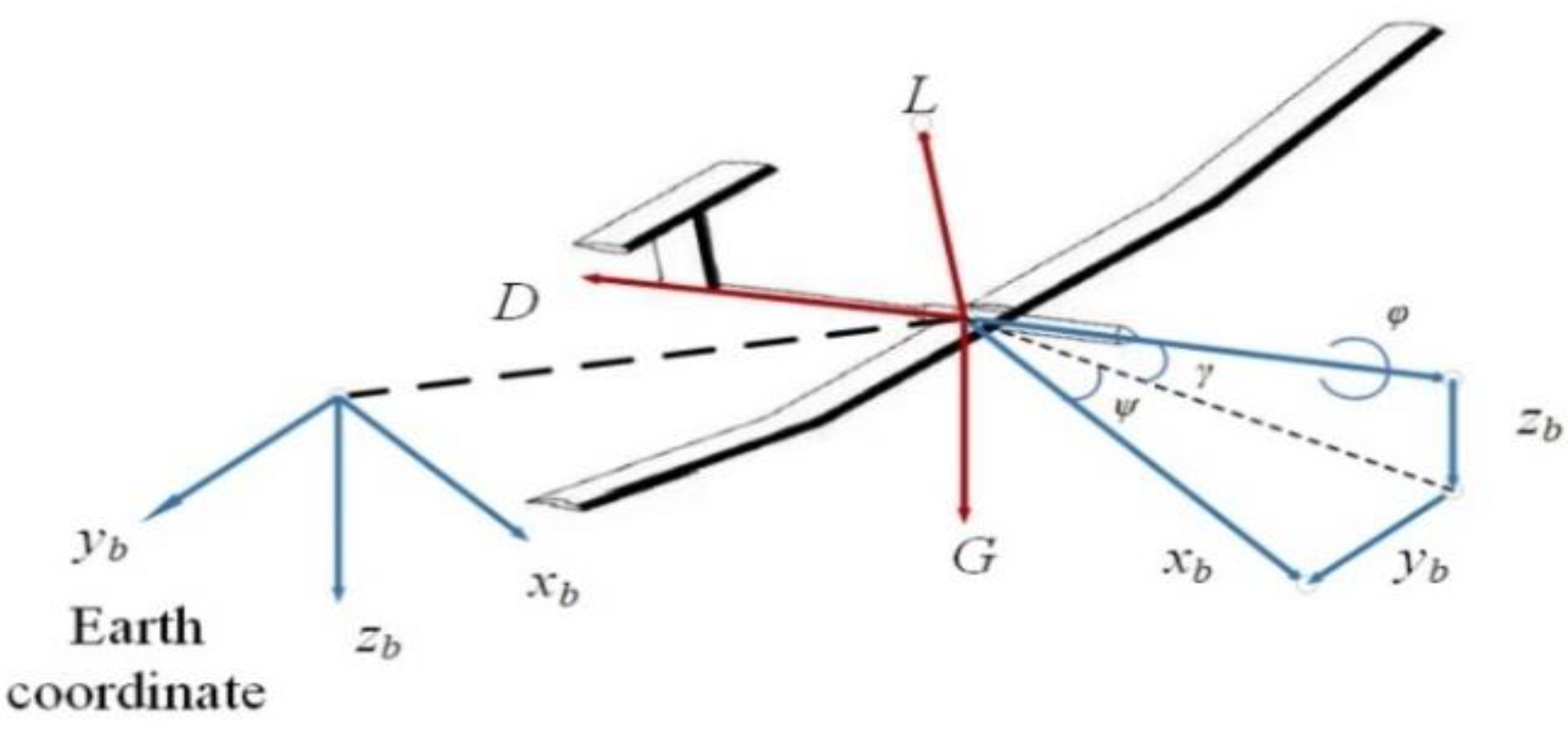
2.2. Vehicle Kinematic Model
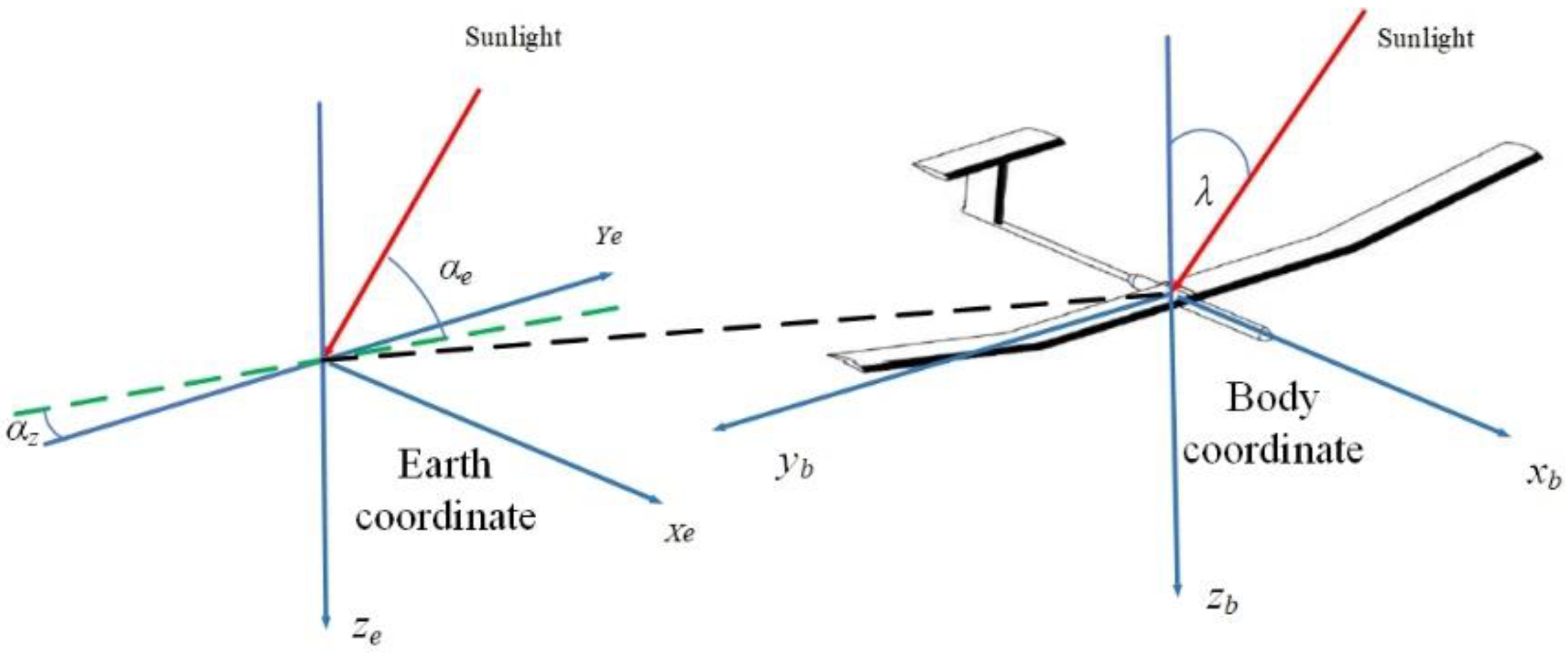
2.3. Solar Irradiance Model
2.4. Energy Model of the SUAV
3. Integrated Guidance and Control Process for Soaring
3.1. Total Energy and Autonomous Soaring Process
3.2. Control and Logic
4. Non-Cooperation and Cooperation Assignment Strategies
4.1. Non-Cooperative Competition Mode
4.2. Cooperative Assignment Mode
5. Simulation and Results
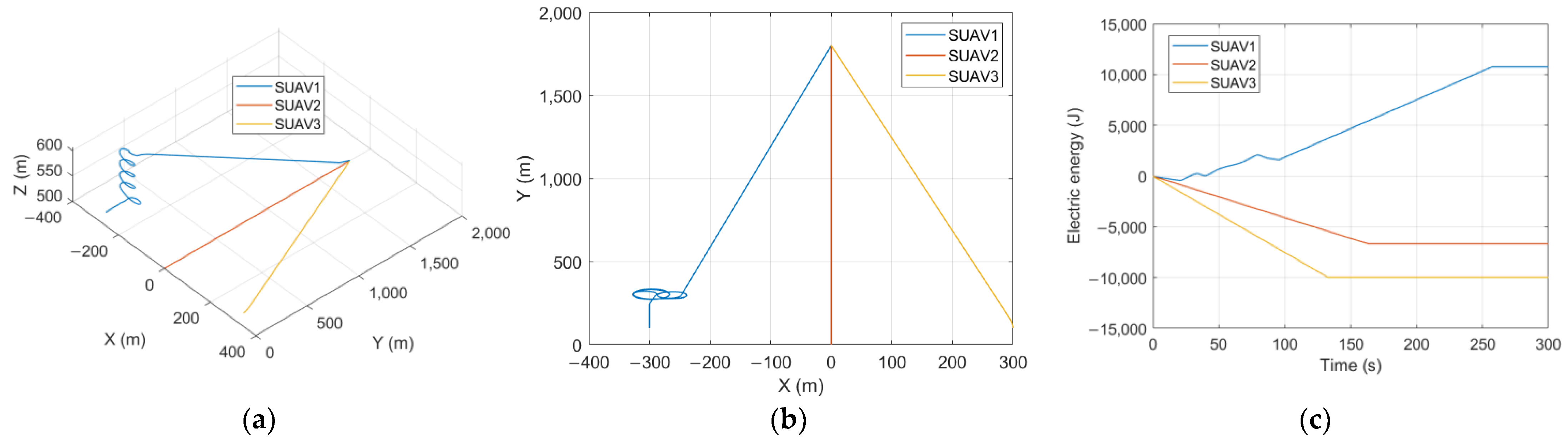
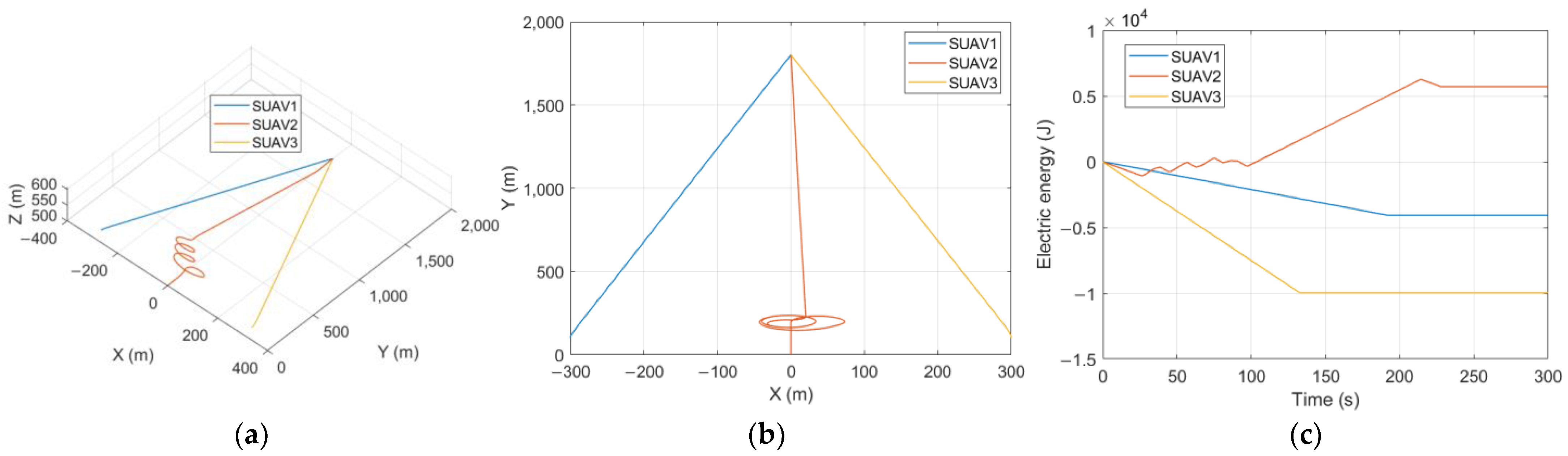
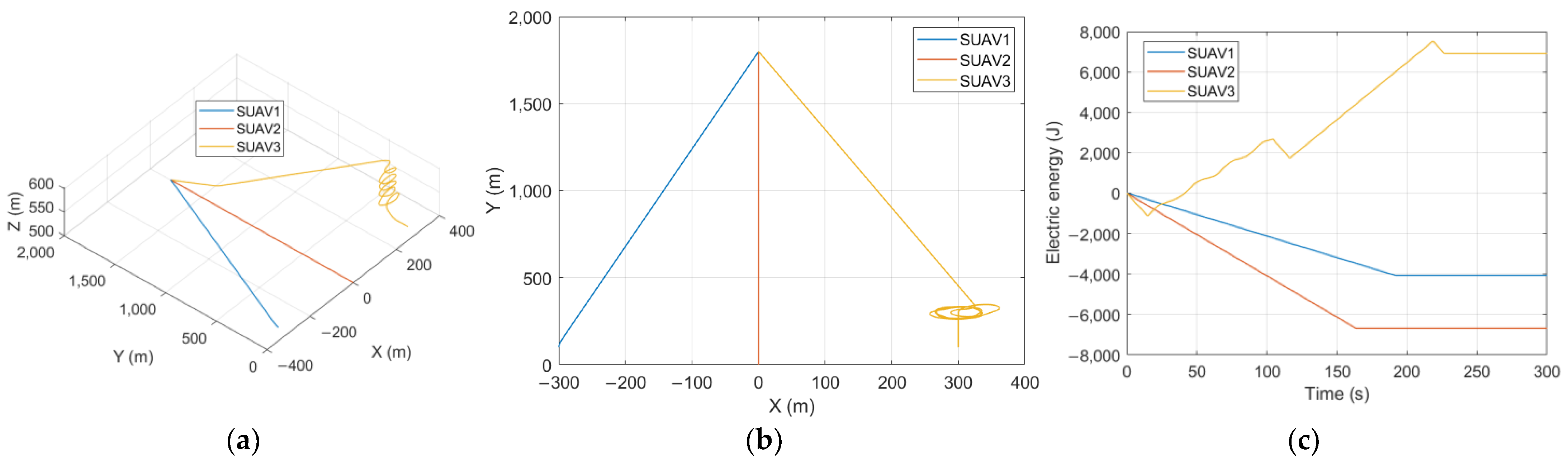
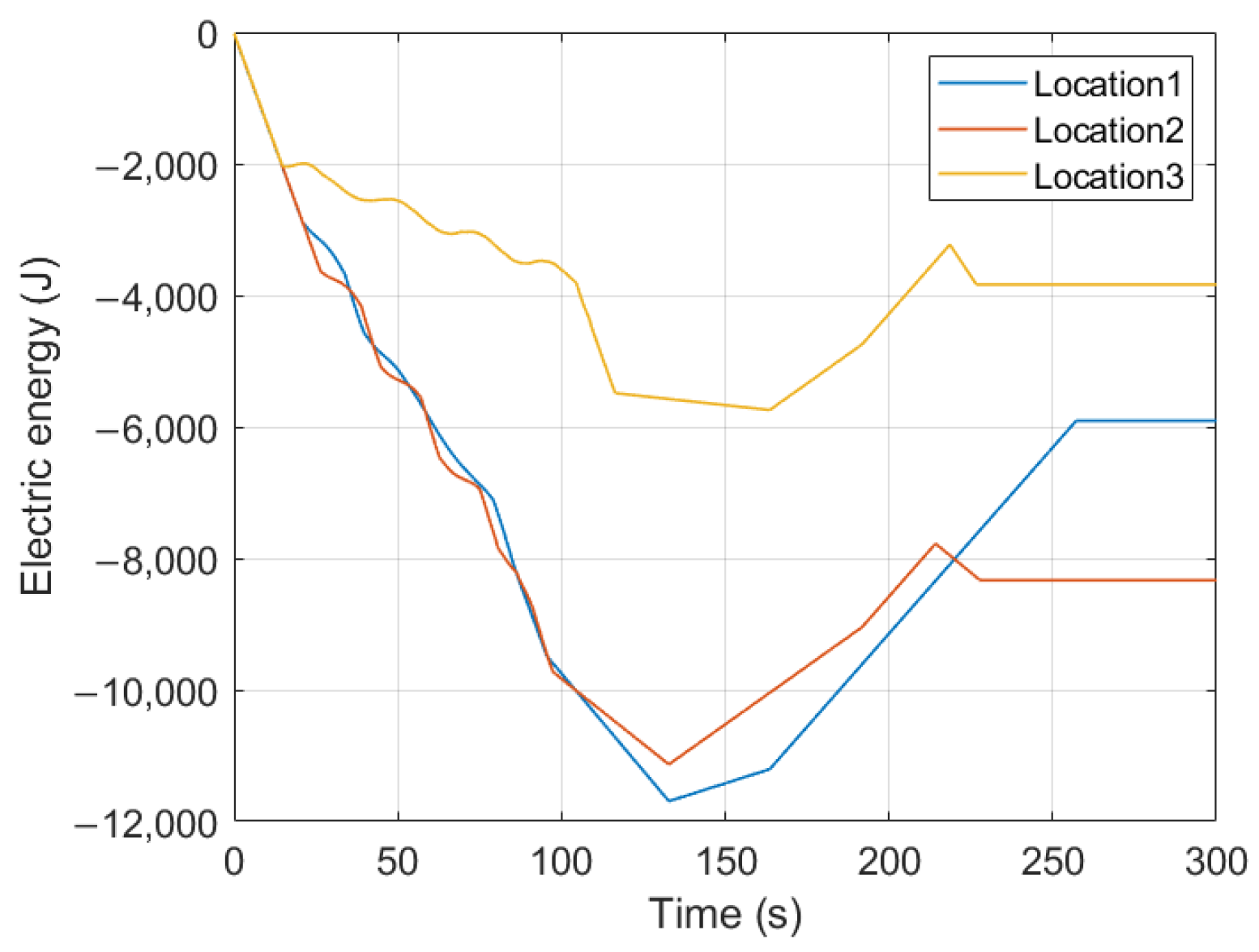
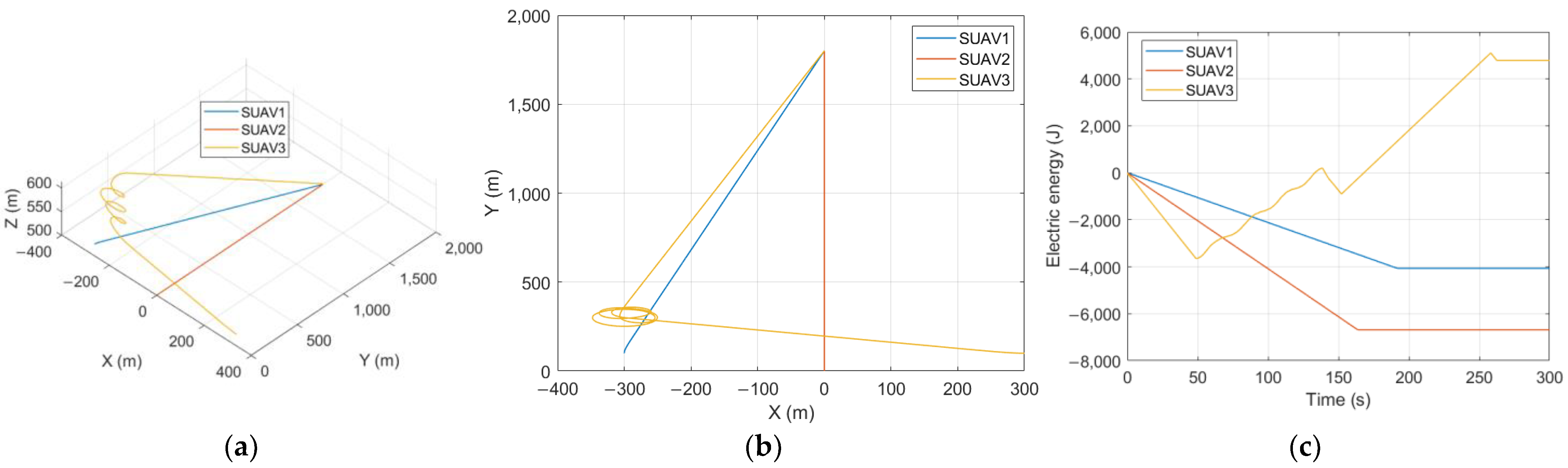
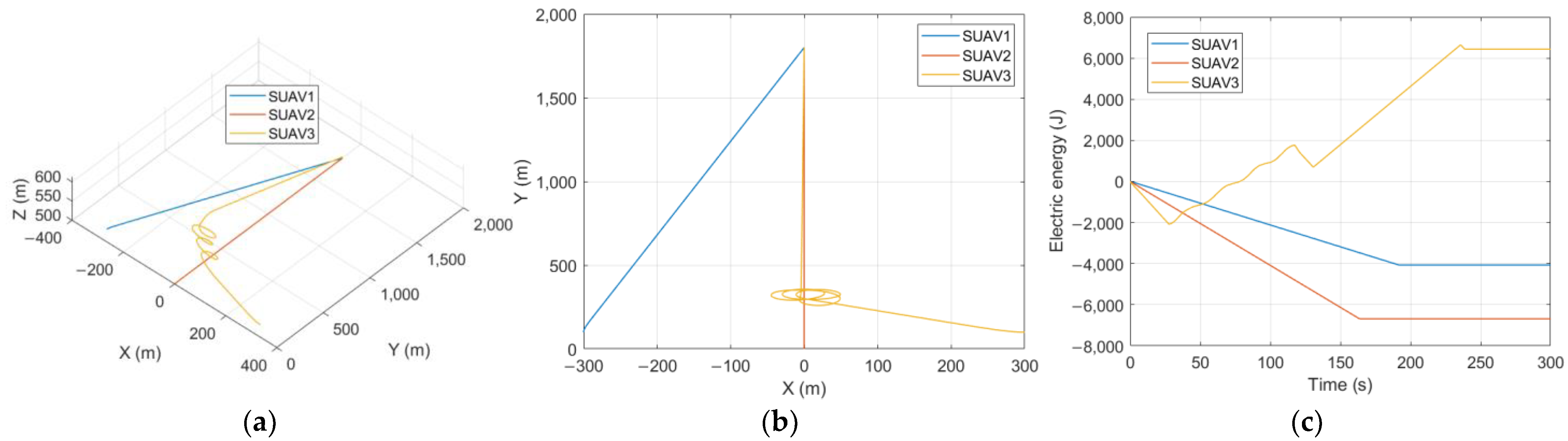
5.1. Non-Cooperative Competition Mode
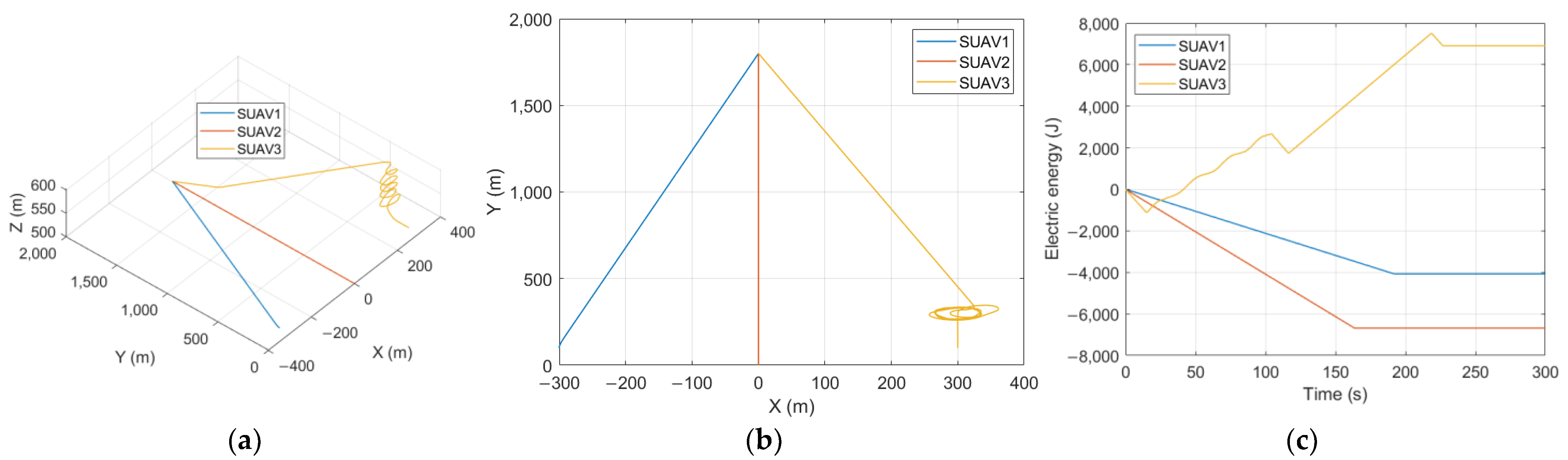
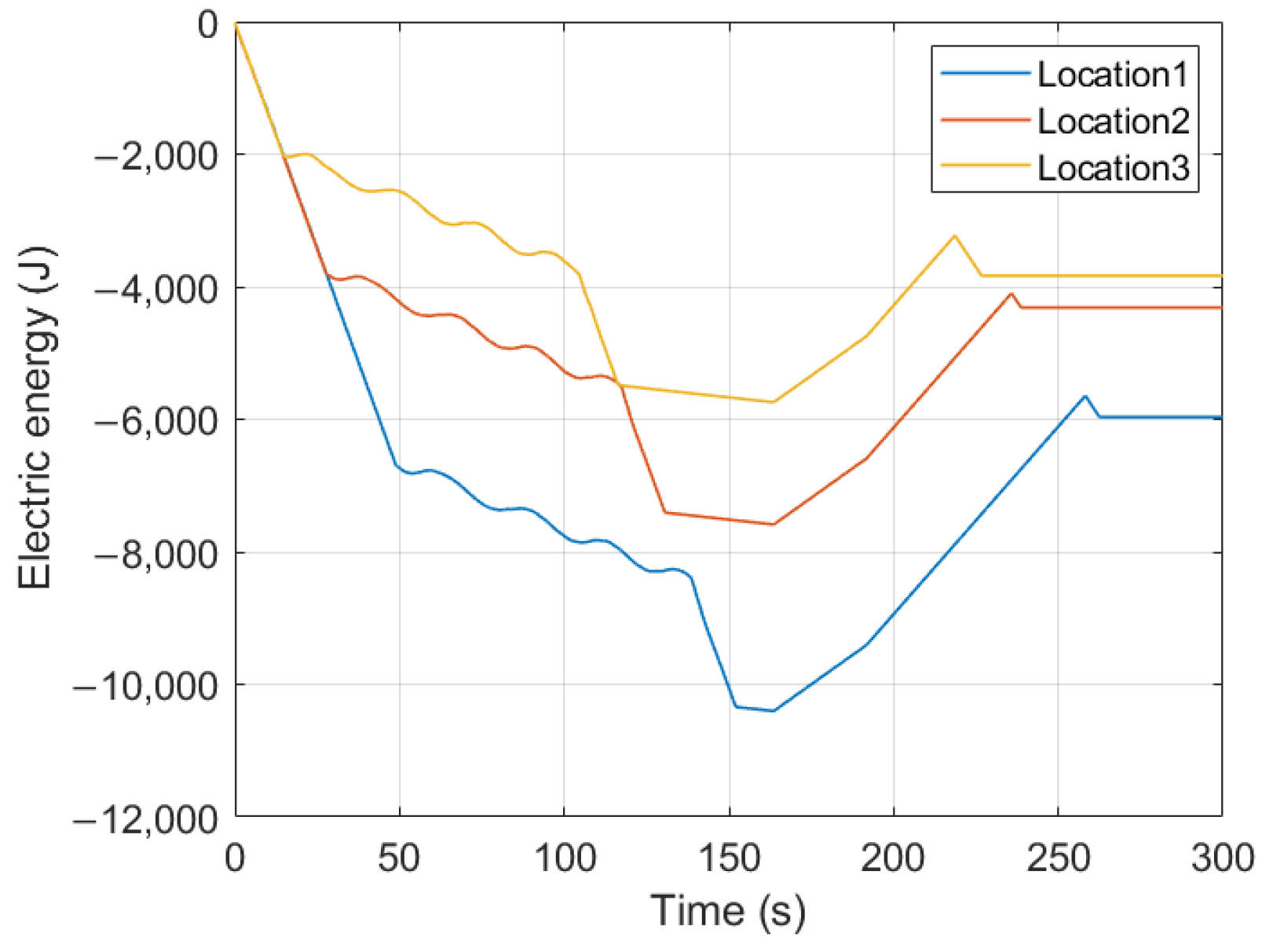
5.2. Cooperative Assignment Mode
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lun, Y.B.; Yao, P.; Wang, Y.X. Trajectory Optimization of SUAV for Marine Vessels Communication Relay Mission. IEEE Syst. J. 2020, 14, 5014–5024. [Google Scholar] [CrossRef]
- Hu, S.Y.; Ni, W.; Wang, X.; Jamalipour, A. Disguised Tailing and Video Surveillance with Solar-Powered Fixed-Wing Un-manned Aerial Vehicle. IEEE Trans. Veh. Technol. 2022, 71, 5507–5518. [Google Scholar] [CrossRef]
- Huang, H.L.; Savkin, A.V. Energy-efficient decentralized navigation of a team of solar-powered UAVs for collaborative eavesdropping on a mobile ground target in urban environments. Ad Hoc Netw. 2021, 117, 102485. [Google Scholar] [CrossRef]
- Bencate, R.; deSousa, J.T.; Girard, A. Atmospheric flow field models applicable for aircraft endurance extension. Prog. Aerosp. Sci. 2013, 61, 1–25. [Google Scholar] [CrossRef]
- Akos, Z.; Nagy, M.; Leven, S.; Vicsek, T. Thermal soaring flight of birds and unmanned aerial vehicles. Bioinspir. Biomim. 2010, 5, 045003. [Google Scholar] [CrossRef]
- Allen, M. Updraft Model for Development of Autonomous Soaring Uninhabited Air Vehicles. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–12 January 2006. [Google Scholar]
- Walton, C.; Kaminer, I. Alternate Strategies for Optimal Unmanned Aerial Vehicle Thermaling. J. Aircraft 2018, 55, 2347–2356. [Google Scholar] [CrossRef]
- Andersson, K.; Kaminer, I.; Dobrokhodov, V.; Cichella, V. Thermal Centering Control for Autonomous Soaring: Stability Analysis and Flight Test Results. J. Guid. Control Dyn. 2012, 25, 963–975. [Google Scholar] [CrossRef]
- Notter, S.; Gross, P.; Schrapel, P.; Fichte, W. Multiple Thermal Updraft Estimation and Observability Analysis. J. Guid. Control Dyn. 2020, 43, 490–503. [Google Scholar] [CrossRef]
- Notter, S.; Schimpf, F.; Muller, G.; Fichter, W. Hierarchical Reinforcement Learning Approach for Autonomous Cross-Country Soaring. J. Guid. Control Dyn. 2022, 46, 114–126. [Google Scholar] [CrossRef]
- Rosales, J.; Gross, A. Statistical Analysis of Autonomous Soaring Algorithm. J. Guid. Control Dyn. 2022, 45, 2398–2402. [Google Scholar] [CrossRef]
- Khaghani, J.; Nekoui, M.; Nasiri, R.; Ahmadabadi, M.N. Analytical Model of Thermal Soaring: Towards Energy Efficient Path Planning for Flying Robots. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Tin, F.E.; Borowczyk, A.; Sharf, I.; Nahon, M. Turn Decisions for Autonomous Thermalling of Unmanned Aerial Gliders. J. Intell. Robot. Syst. 2022, 104, 1–18. [Google Scholar] [CrossRef]
- Wu, Y.; Li, K.; Zhao, A.; Liu, H.; Li, Y.; Wen, D. Energy Analysis for Solar-Powered Unmanned Aerial Vehicle under Static Soaring. Aerospace 2023, 10, 779. [Google Scholar] [CrossRef]
- Oettershagen, P.; Stastny, T.; Hinzmann, T.; Rudin, K.; Mantel, T.; Melzer, A.; Wawrzacz, B.; Hitz, G.; Siegwart, R. Robotic technologies for solar-powered UAVs: Fully autonomous updraft-aware aerial sensing for multiday search-and-rescue missions. J. Field Robot. 2018, 35, 612–640. [Google Scholar] [CrossRef]
- Edwards, D.J.; Kahn, A.D.; Kelly, M.; Heinzen, S.; Scheiman, D.A.; Jenkins, P.P.; Walters, R.; Hoheisel, R. Maximizing net power in circular turns for solar and autonomous soaring aircraft. J. Aircraft 2016, 53, 1237–1247. [Google Scholar] [CrossRef]
- Mateja, K.; Skarka, W.; Peciak, M.; Niestrój, R.; Gude, M. Energy Autonomy Simulation Model of Solar Powered UAV. Energies 2023, 16, 479. [Google Scholar] [CrossRef]
- Li, K.; Wu, Y.; Bakar, A.; Wang, S.; Li, Y.; Wen, D. Energy System Optimization and Simulation for Low-Altitude So-lar-Powered Unmanned Aerial Vehicles. Aerospace 2022, 9, 331. [Google Scholar] [CrossRef]
- Wu, J.F.; Wang, H.L.; Huang, Y.; Zhang, M.H.; Su, Z.K. Solar-Powered Aircraft Endurance Map. J. Guid. Control Dyn. 2019, 42, 687–694. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, H.L.; Yao, P. Energy-optimal path planning for Solar-powered UAV with tracking moving ground target. Aerosp. Sci. Technol. 2016, 53, 241–251. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, J.G.; Wang, H.L.; Su, G.F. A method of 3D path planning for solar-powered UAV with fixed target and solar tracking. Aerosp. Sci. Technol. 2019, 92, 831–838. [Google Scholar] [CrossRef]
- Hosseini, S.; Mesbahi, M. Energy-Aware Aerial Surveillance for a Long-Endurance Solar-Powered Unmanned Aerial Vehicles. J. Guid. Control Dyn. 2016, 39, 1980–1993. [Google Scholar] [CrossRef]
- Xin, W.; Yao, P.; Xie, Z. Comprehensive optimization of energy storage and standoff tracking for solar-powered UAV. IEEE Syst. J. 2020, 14, 5133–5143. [Google Scholar]
- Wu, J.F.; Wang, H.L.; Li, N.; Yao, P.; Huang, Y.; Yang, H.M. Path planning for solar-powered UAV in urban environment. Neurocomputing 2018, 275, 2055–2065. [Google Scholar] [CrossRef]
- Wu, J.; Wang, H.; Li, N.; Yao, P.; Huang, Y.; Su, Z.; Yu, Y. Distributed trajectory optimization for multiple solar-powered UAVs target tracking in urban environment by Adaptive Grasshopper Optimization Algorithm. Aerosp. Sci. Technol. 2017, 70, 497–510. [Google Scholar] [CrossRef]
- Le, W.X.; Xue, Z.T.; Chen, J.; Zhang, Z.C. Coverage Path Planning Based on the Optimization Strategy of Multiple Solar Powered Unmanned Aerial Vehicles. Drones 2022, 6, 203. [Google Scholar] [CrossRef]
- Lun, Y.B.; Wang, H.L.; Wu, J.F.; Liu, Y.H.; Wang, Y.X. Target Search in Dynamic Environments with Multiple Solar-Powered UAVs. IEEE Trans. Veh. Technol. 2022, 71, 9309–9321. [Google Scholar] [CrossRef]
- Andersson, K.; Kaminer, I.; Jones, K.; Dobrokhodov, V.; Lee, D.J. Cooperating UAVs Using Thermal Lift to Extend Endurance. In Proceedings of the AIAA Infotech@Aerospace Conference, Seattle, WA, USA, 6–9 April 2009. [Google Scholar]
- Antal, C.; Granichin, O.; Levi, S. Adaptive Autonomous Soaring of Multiple UAVs Using Simultaneous Perturbation Stochastic Approximation. In Proceedings of the 49th IEEE Conference on Decision and Control, Atlanta, GA, USA, 15–17 December 2010. [Google Scholar]
- Cobano, J.A.; Alejo, D.; Vera, S.; Heredia, G.; Ollero, A. Multiple gliding UAV coordination for static soaring in real time applications. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013. [Google Scholar]
- Acevedo, J.; Lawrance, N.R.; Arrue, B.C.; Sukkarieh, S.; Ollero, A. Persistent monitoring with a team of autonomous gliders using static soaring. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 4842–4848. [Google Scholar]
- Cobano, J.A.; Alejo, D.; Vera, S.; Sukkarieh, S.; Heredia, G.; Ollero, A. Thermal detection and generation of collision-free trajectories for cooperative soaring UAVs. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Karlsruhe, Germany, 6–10 May 2013. [Google Scholar]
- Yu, Y.; Ding, X.A. Global Tracking Controller for Underactuated Aerial Vehicles: Design, Analysis, and Experimental Tests on Quadrotor. IEEE ASME Trans. Mechatronics 2016, 21, 2499–2511. [Google Scholar] [CrossRef]
- Allen, M.; Lin, V.; Samuel, T. Guidance and Control of an Autonomous Soaring Vehicle with Flight Test Results. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar]

| Sign | Parameter | Value | Unit |
|---|---|---|---|
| I0 | Solar irradiance | 1367 | W/m2 |
| τb | Beam optical depths | 0.626 | N/A |
| τd | Diffuse optical depths | 1.707 | N/A |
| Ssolar | Solar cell area | 1.37 | m2 |
| S | Wing area | 1.75 | m2 |
| m | Mass | 6.93 | kg |
| ρ | Air density | 1.26 | kg/m3 |
| CD0 | Parasitic drag | 0.025 | N/A |
| ε | Oswald efficiency factor | 0.92 | N/A |
| Ra | Aspect ratio of the wing | 18.5 | N/A |
| ηprop | Propeller efficiency | 60% | N/A |
| ηsolar | Solar cell efficiency | 22% | N/A |
| SUAV1 | SUAV2 | SUAV3 | |
|---|---|---|---|
| Initial position | (−300, 100) | (0, 0) | (300, 100) |
| Velocity | 9 m/s | 11 m/s | 13 m/s |
| Thermal Locations | Assignment Result |
|---|---|
| (−300, 300) | SUAV1 |
| (0, 300) | SUAV2 |
| (300, 300) | SUAV3 |
| Thermal Locations | Assignment Result |
|---|---|
| (−300, 300) | SUAV3 |
| (0, 300) | SUAV3 |
| (300, 300) | SUAV3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Li, K.; Zhao, A.; Wang, S.; Li, Y.; Chen, X. Competition and Cooperation for Multiple Solar Powered Unmanned Aerial Vehicles under Static Soaring. Drones 2023, 7, 653. https://doi.org/10.3390/drones7110653
Wu Y, Li K, Zhao A, Wang S, Li Y, Chen X. Competition and Cooperation for Multiple Solar Powered Unmanned Aerial Vehicles under Static Soaring. Drones. 2023; 7(11):653. https://doi.org/10.3390/drones7110653
Chicago/Turabian StyleWu, Yansen, Ke Li, Anmin Zhao, Shaofan Wang, Yuangan Li, and Xiaodan Chen. 2023. "Competition and Cooperation for Multiple Solar Powered Unmanned Aerial Vehicles under Static Soaring" Drones 7, no. 11: 653. https://doi.org/10.3390/drones7110653
APA StyleWu, Y., Li, K., Zhao, A., Wang, S., Li, Y., & Chen, X. (2023). Competition and Cooperation for Multiple Solar Powered Unmanned Aerial Vehicles under Static Soaring. Drones, 7(11), 653. https://doi.org/10.3390/drones7110653







