Dual-UAV Collaborative High-Precision Passive Localization Method Based on Optoelectronic Platform
Abstract
:1. Introduction
- Two noise transfer models are established to obtain the noise distributions of the UAV position and the AOA of the target relative to the UAV in the ECEF coordinate system;
- A WLS algorithm is proposed, taking into account the noise distributions of both the UAV position and the AOA;
- The optimal placement for two coplanar UAVs relative to the target is investigated using the D-optimality criterion, based on the FIM obtained from 3D space AOA measurements.
2. Estimation of Measurements and Their Error Distributions
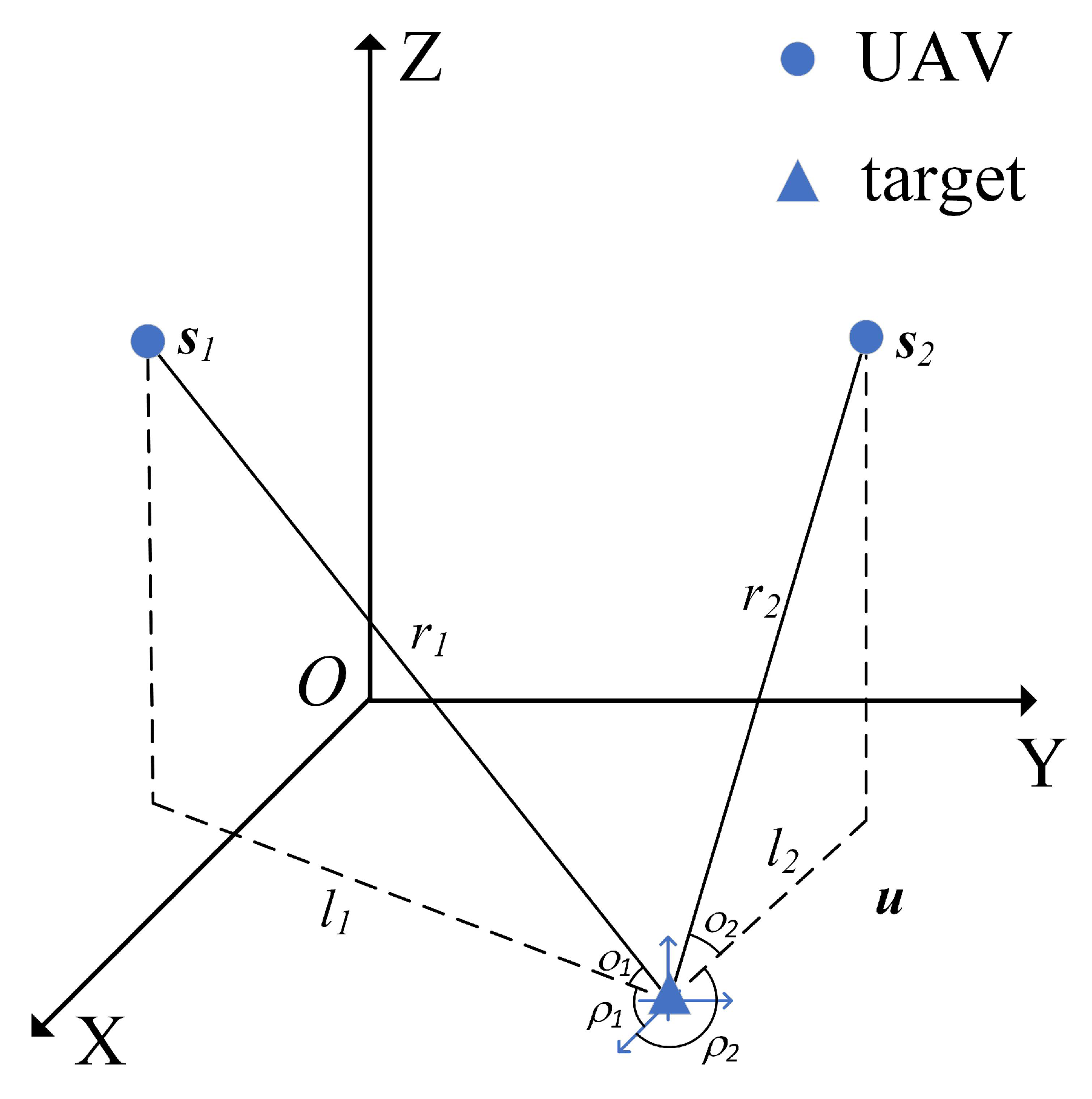
2.1. AOA of the Target Relative to UAV in the ECEF Coordinate System
2.2. The Position of UAV in ECEF Coordinate System
3. The Proposed Weighted Least Squares Algorithm
3.1. Formulate the Localization Problem
3.2. The Proposed Weighted Least Squares Estimator
3.3. Performance Analysis
4. Optimal Placement of Coplanar UAVs Relative to Target
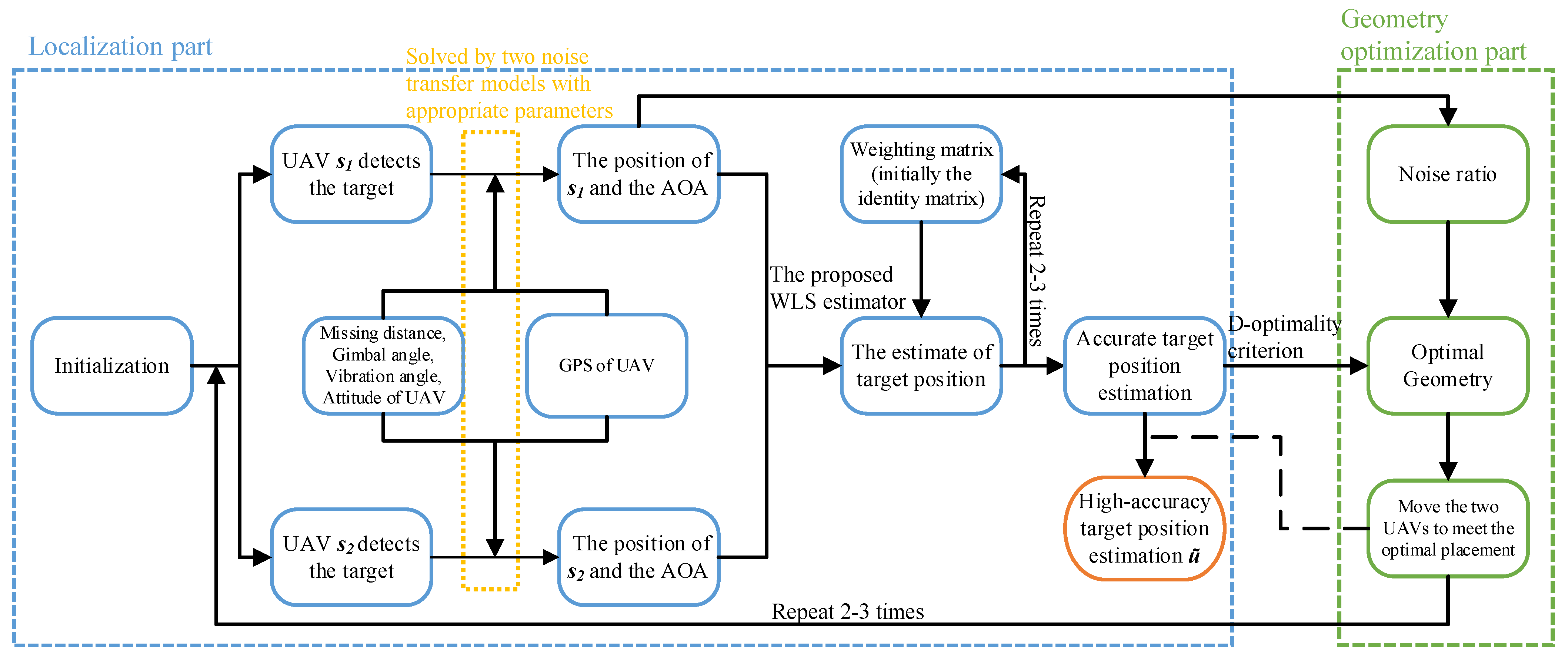
| Algorithm 1: The scheme of two UAVs using the photoelectric platform to achieve high-precision localization target |
 |
5. Simulation and Discussion
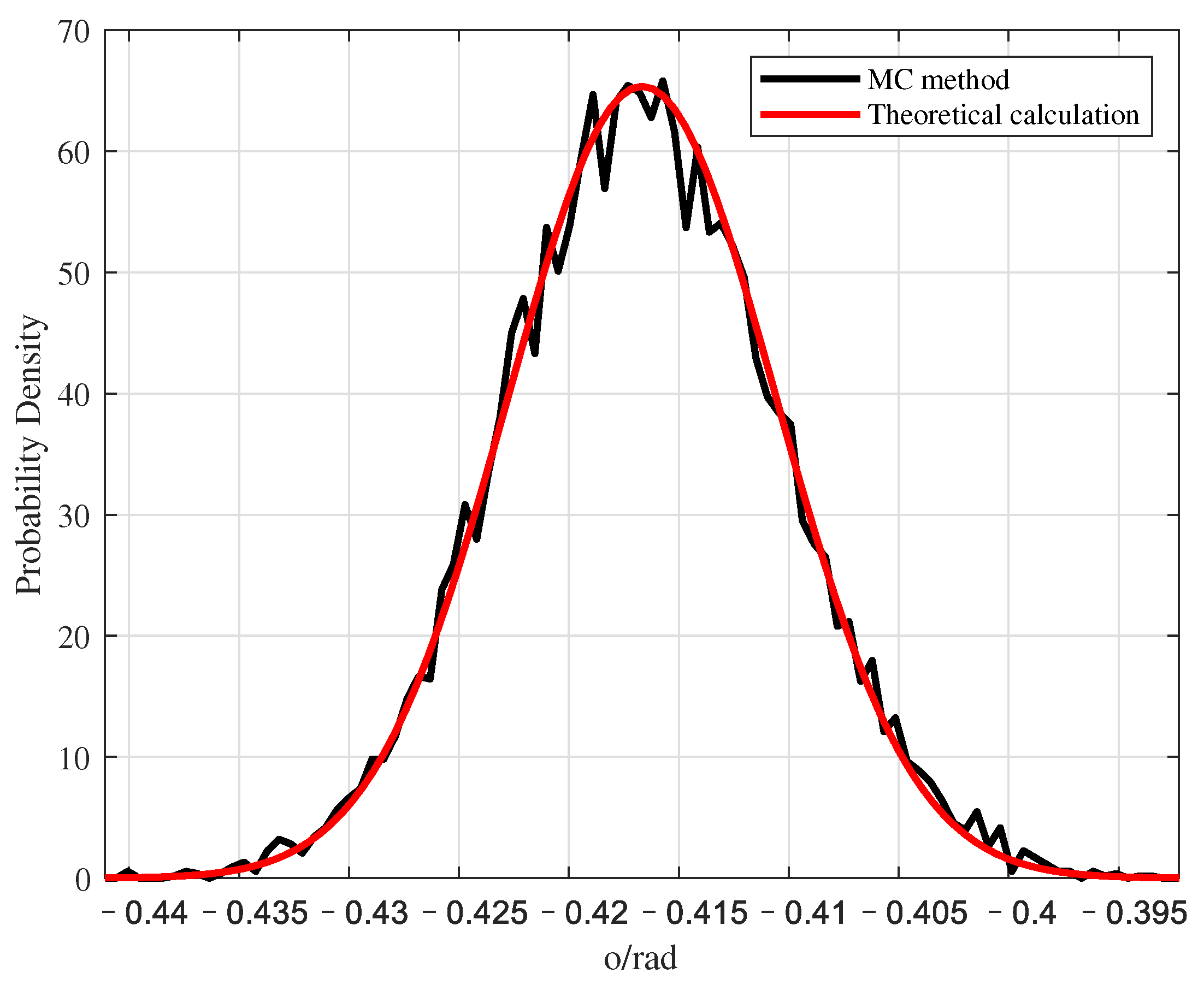
5.1. Estimate the Variances of AOA and UAV Positions
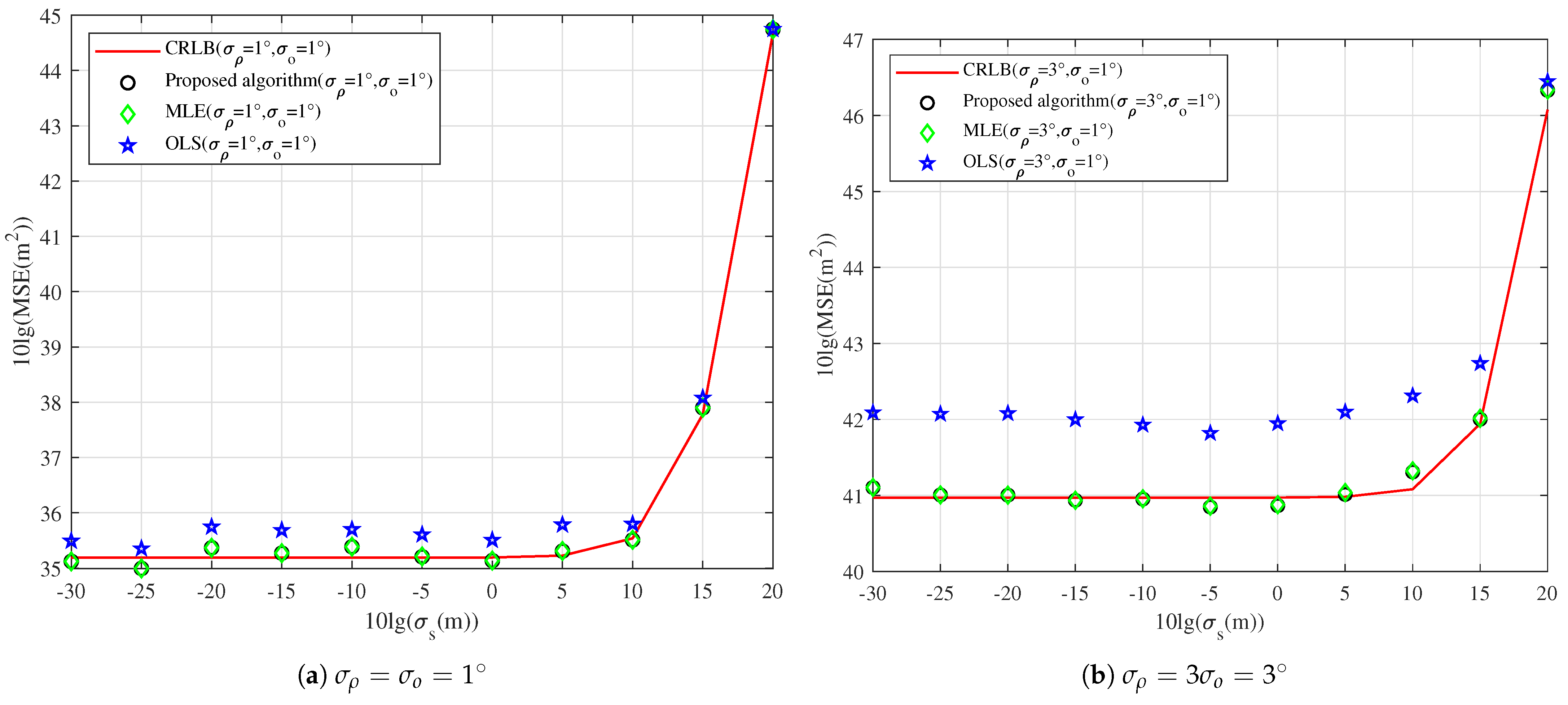
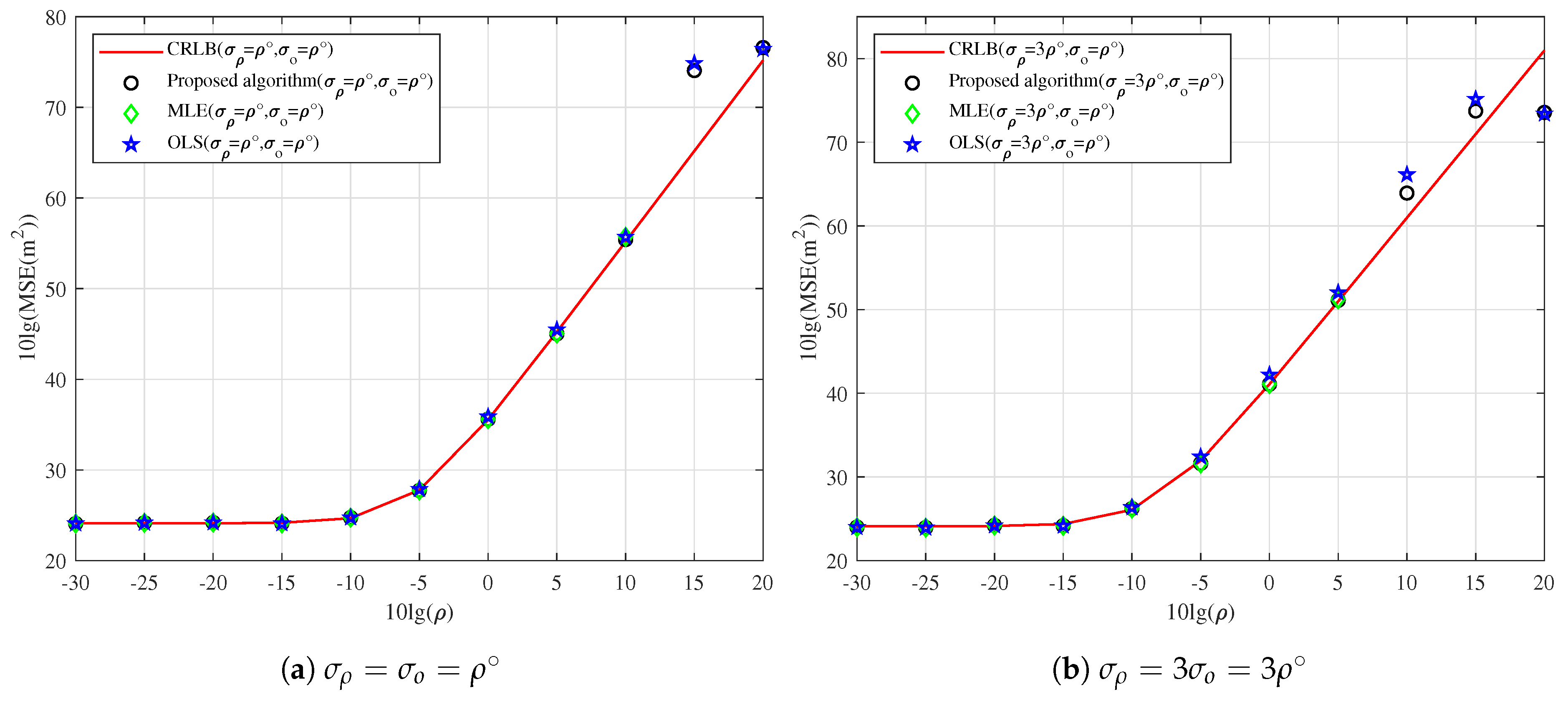
5.2. Performance of Localization Algorithms
5.3. Optimize Placement
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Rotation Matrix between Different Coordinate Systems
Appendix B. The Error of the Rotation Matrix Caused by the First-Order Noise of the Variable
References
- Zhao, S.; Zhang, X.P.; Cui, X.; Lu, M. A Closed-Form Localization Method Utilizing Pseudorange Measurements From Two Nonsynchronized Positioning Systems. IEEE Internet Things J. 2021, 8, 1082–1094. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.Y.; Jeon, S.; Baik, J.W.; Cho, S.H.; Kim, C. Super-Resolution Localization Photoacoustic Microscopy Using Intrinsic Red Blood Cells as Contrast Absorbers. Light Sci. Appl. 2019, 8, 103. [Google Scholar] [CrossRef] [PubMed]
- Heil, H.S.; Schreiber, B.; Götz, R.; Emmerling, M.; Dabauvalle, M.C.; Krohne, G.; Höfling, S.; Kamp, M.; Sauer, M.; Heinze, K.G. Sharpening Emitter Localization in Front of a Tuned Mirror. Light Sci. Appl. 2018, 7, 99. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Ho, K.C. An Asymptotically Efficient Estimator in Closed-Form for 3-D AOA Localization Using a Sensor Network. IEEE Trans. Wireless Commun. 2015, 14, 6524–6535. [Google Scholar] [CrossRef]
- Masullo, L.A.; Stefani, F.D. Multiphoton Single-Molecule Localization by Sequential Excitation with Light Minima. Light Sci. Appl. 2022, 11, 70. [Google Scholar] [CrossRef]
- Masullo, L.A.; Szalai, A.M.; Lopez, L.F.; Pilo-Pais, M.; Acuna, G.P.; Stefani, F.D. An Alternative to MINFLUX That Enables Nanometer Resolution in a Confocal Microscope. Light Sci. Appl. 2022, 11, 199. [Google Scholar] [CrossRef]
- Cao, S.; Chen, X.; Zhang, X.; Chen, X. Combined Weighted Method for TDOA-Based Localization. IEEE Trans. Instrum. Meas. 2020, 69, 1962–1971. [Google Scholar] [CrossRef]
- Shen, H.; Ding, Z.; Dasgupta, S.; Zhao, C. Multiple source localization in wireless sensor networks based on time of arrival measurement. IEEE Trans. Signal Process. 2014, 62, 1938–1949. [Google Scholar] [CrossRef]
- Park, P.; Marco, P.D.; Jung, M.; Santucci, F.; Sung, T.K. Multidirectional Differential RSS Technique for Indoor Vehicle Navigation. IEEE Internet Things J. 2023, 10, 241–253. [Google Scholar] [CrossRef]
- Dogancay, K. Bias Compensation for the Bearings-Only Pseudolinear Target Track Estimator. IEEE Trans. Signal Process. 2006, 54, 59–68. [Google Scholar] [CrossRef]
- Kang, X.; Wang, D.; Shao, Y.; Ma, M.; Zhang, T. An Efficient Hybrid Multi-Station TDOA and Single-Station AOA Localization Method. IEEE Trans. Wireless Commun. 2023, 22, 5657–5670. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, X.; Zheng, C.; Fu, J.; Zhao, C. Underwater Acoustical Localization of the Black Box Utilizing Single Autonomous Underwater Vehicle Based on the Second-Order Time Difference of Arrival. IEEE J. Ocean. Eng. 2020, 45, 1268–1279. [Google Scholar] [CrossRef]
- Kim, T.y.; Hwang, S.s. Cascade AOA Estimation Algorithm Based on Flexible Massive Antenna Array. Sensors 2020, 20, 6797. [Google Scholar] [CrossRef] [PubMed]
- Bai, G.; Liu, J.; Song, Y.; Zuo, Y. Two-UAV Intersection Localization System Based on the Airborne Optoelectronic Platform. Sensors 2017, 17, 98. [Google Scholar] [CrossRef]
- Rui, L.; Ho, K. Bias Analysis of Maximum Likelihood Target Location Estimator. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2679–2693. [Google Scholar] [CrossRef]
- Wang, Y.; Ho, K.C. Unified Near-Field and Far-Field Localization for AOA and Hybrid AOA-TDOA Positionings. IEEE Trans. Wireless Commun. 2018, 17, 1242–1254. [Google Scholar] [CrossRef]
- Chen, X.; Wang, G.; Ho, K. Semidefinite Relaxation Method for Unified Near-Field and Far-Field Localization by AOA. Signal Process. 2021, 181, 107916. [Google Scholar] [CrossRef]
- Sun, Y.; Ho, K.C.; Wan, Q. Eigenspace Solution for AOA Localization in Modified Polar Representation. IEEE Trans. Signal Process. 2020, 68, 2256–2271. [Google Scholar] [CrossRef]
- Sadeghi, M.; Behnia, F.; Amiri, R. Optimal Sensor Placement for 2-D Range-Only Target Localization in Constrained Sensor Geometry. IEEE Trans. Signal Process. 2020, 68, 2316–2327. [Google Scholar] [CrossRef]
- Doğançay, K.; Hmam, H. Optimal Angular Sensor Separation for AOA Localization. Signal Process. 2008, 88, 1248–1260. [Google Scholar] [CrossRef]
- Fang, X.; Li, J.; Zhang, S.; Chen, W.; He, Z. Optimal AOA Sensor-Source Geometry With Deployment Region Constraints. IEEE Commun. Lett. 2022, 26, 793–797. [Google Scholar] [CrossRef]
- Xu, S.; Dogancay, K. Optimal Sensor Placement for 3-D Angle-of-Arrival Target Localization. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1196–1211. [Google Scholar] [CrossRef]
- Smith, W.H.F. Direct Conversion of Latitude and Height from One Ellipsoid to Another. J. Geod. 2022, 96, 36. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; JHU Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Wang, Y.; Ho, K.C. TDOA Positioning Irrespective of Source Range. IEEE Trans. Signal Process. 2017, 65, 1447–1460. [Google Scholar] [CrossRef]
- Moreno-Salinas, D.; Pascoal, A.; Aranda, J. Optimal sensor placement for acoustic underwater target positioning with range-only measurements. IEEE J. Ocean. Eng. 2016, 41, 620–643. [Google Scholar] [CrossRef]
- Zhang, Y.; Ho, K. Multistatic localization in the absence of transmitter position. IEEE Trans. Signal Process. 2019, 67, 4745–4760. [Google Scholar] [CrossRef]




| Source of Error | Parameter | Random Distribution | Mean | Standard Deviation |
|---|---|---|---|---|
| Missing distance | x | Gaussian distribution | 0 | 10 µm |
| y | Gaussian distribution | 0 | 10 µm | |
| Gimbal angle | (Azimuth) | Uniform distribution | 0 | |
| (Elevation) | Uniform distribution | 0 | ||
| Vibration angle | (Heading) | Uniform distribution | 0 | |
| (Pitch) | Uniform distribution | 0 | ||
| (Yaw) | Uniform distribution | 0 | ||
| Attitude of UAV | (Heading) | Gaussian distribution | 0 | |
| (Pitch) | Gaussian distribution | 0 | ||
| (Yaw) | Gaussian distribution | 0 | ||
| GPS of UAV | L (Longitude) | Gaussian distribution | 0 | |
| M (Latitude) | Gaussian distribution | 0 | ||
| H (Height) | Gaussian distribution | 0 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Missing distance of | 0 | Missing distance of | 0 |
| Azimuth of gimbal angle | −62.1712 | Elevation of gimbal angle | −60.1477 |
| Heading of vibration angle | 0 | Heading of UAV | 0 |
| Pitch of vibration angle | 0 | Pitch of UAV | 0 |
| Yaw of vibration angle | 0 | Yaw of UAV | 0 |
| Longitude of UAV | 125.67412 | Latitude of UAV | 42.13541 |
| The Position Component of the UAV | Variance of the MC Estimate | Variance of Theoretical Estimate |
|---|---|---|
| x | 279.3674 | 275.2468 |
| y | 256.2604 | 256.0767 |
| z | 232.9268 | 234.8598 |
| Algorithm | Running Time | Bias | MSE |
|---|---|---|---|
| OLS | 0.0128 | 2.1358 | 10,065 |
| Proposed algorithm | 0.0180 | 2.6249 | 6573 |
| MLE | 7.1674 | 1.8918 | 6588 |
| CRLB | ∖ | ∖ | 6583 |
| Noise Ratio | (Elevation, Separation Angle) | CRLB | Proposed Algorithm | MLE |
|---|---|---|---|---|
| 1322 | 1408 | 1335 | ||
| 650 | 665 | 654 | ||
| 605 | 612 | 607 | ||
| 612 | 645 | 618 | ||
| 662 | 674 | 665 | ||
| 2366 | 2445 | 2370 | ||
| 960 | 974 | 963 | ||
| 836 | 842 | 838 | ||
| 770 | 791 | 774 | ||
| 755 | 758 | 756 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, X.; Shao, Y.; Bai, G.; Sun, H.; Zhang, T.; Wang, D. Dual-UAV Collaborative High-Precision Passive Localization Method Based on Optoelectronic Platform. Drones 2023, 7, 646. https://doi.org/10.3390/drones7110646
Kang X, Shao Y, Bai G, Sun H, Zhang T, Wang D. Dual-UAV Collaborative High-Precision Passive Localization Method Based on Optoelectronic Platform. Drones. 2023; 7(11):646. https://doi.org/10.3390/drones7110646
Chicago/Turabian StyleKang, Xu, Yu Shao, Guanbing Bai, He Sun, Tao Zhang, and Dejiang Wang. 2023. "Dual-UAV Collaborative High-Precision Passive Localization Method Based on Optoelectronic Platform" Drones 7, no. 11: 646. https://doi.org/10.3390/drones7110646
APA StyleKang, X., Shao, Y., Bai, G., Sun, H., Zhang, T., & Wang, D. (2023). Dual-UAV Collaborative High-Precision Passive Localization Method Based on Optoelectronic Platform. Drones, 7(11), 646. https://doi.org/10.3390/drones7110646








