UAV Formation Trajectory Planning Algorithms: A Review

Abstract

With the continuous development of UAV technology and swarm intelligence technology, the UAV formation cooperative mission has attracted wide attention because of its remarkable function and flexibility to complete complex and changeable tasks, such as search and rescue, resource exploration, reconnaissance and surveillance. The collaborative trajectory planning of UAV formation is a key part of the task execution. This paper attempts to provide a comprehensive review of UAV formation trajectory planning algorithms. Firstly, from the perspective of global planning and local planning, a simple framework of the UAV formation trajectory planning algorithm is proposed, which is the basis of comprehensive classification of different types of algorithms. According to the proposed framework, a classification method of existing UAV formation trajectory planning algorithms is proposed, and then, different types of algorithms are described and analyzed statistically. Finally, the challenges and future research directions of the UAV formation trajectory planning algorithm are summarized and prospected according to the actual requirements. It provides reference information for researchers and workers engaged in the formation flight of UAVs.

1. Introduction

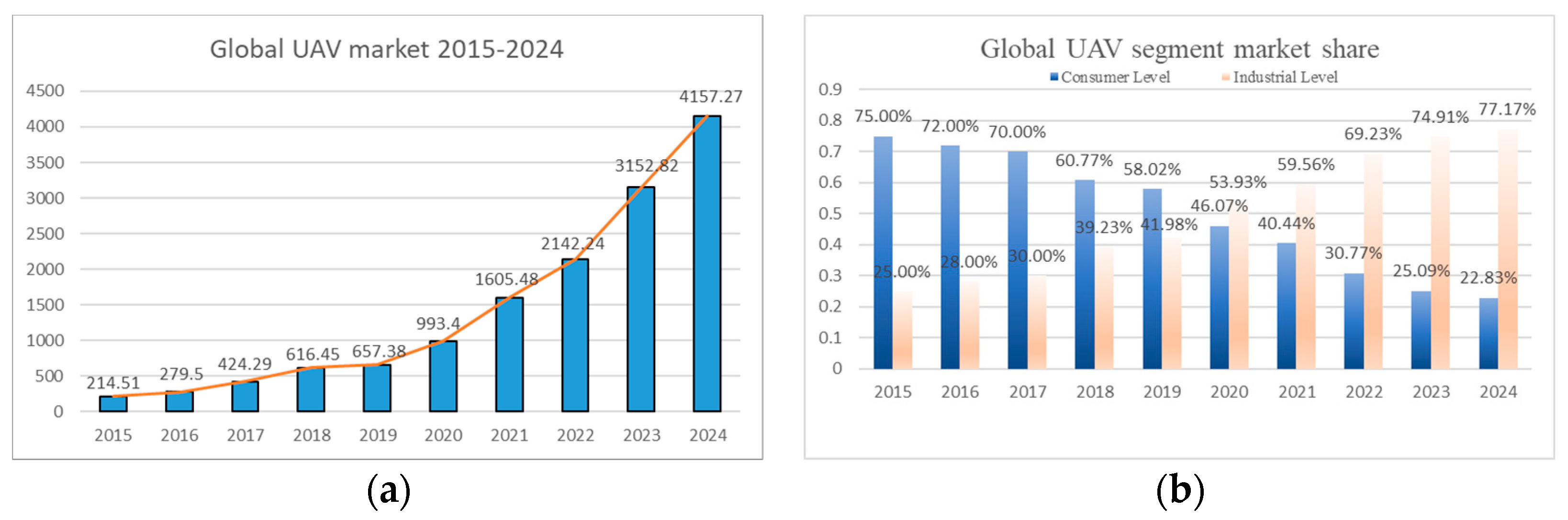
Since its outstanding performance in the Gulf War in 1991, drones have made good achievements in the Afghanistan War, the Iraq War, the fight against the Islamic State (ISIS) terrorist group, the “Neptune Spear” decapitation operation in 2011, and the Russia–Ukraine conflict in 2022. Their success has caused countries around the world to invest a large amount of manpower and financial resources in the research of UAV [1], as shown in Figure 1. After decades of development, UAVs have not only been applied in the military fields of reconnaissance, surveillance, communication relay, electronic countermeasures, combat assessment, harassment, decoy, anti-submarine, target attack, etc. At the same time, they have been widely used in agriculture [2], energy [3], civil [4] and other very important fields. However, there are some problems with a single drone performing its mission. For example, when a single UAV performs a reconnaissance mission, it may be limited by the observation angle and cannot observe the target area from multiple different orientations [5]; when faced with a large-scale search task, a single UAV cannot effectively cover the entire reconnaissance area [6]; during the attack, the combat range, killing radius, destruction capability and attack accuracy are limited, thus affecting the success rate of the entire combat mission [7]; if a single drone fails in the middle of a mission, it must immediately interrupt the mission and return, but in a war, it may delay the aircraft and destroy the entire operation plan. In order to improve combat effectiveness and make up for the deficiency of a single UAV, a multi-UAV cooperative formation (cluster) combat task is proposed. It refers to the formation, maintenance or reconstruction of a certain geometric formation during the execution of a task by multiple UAVs to adapt to the battlefield situation and task requirements.

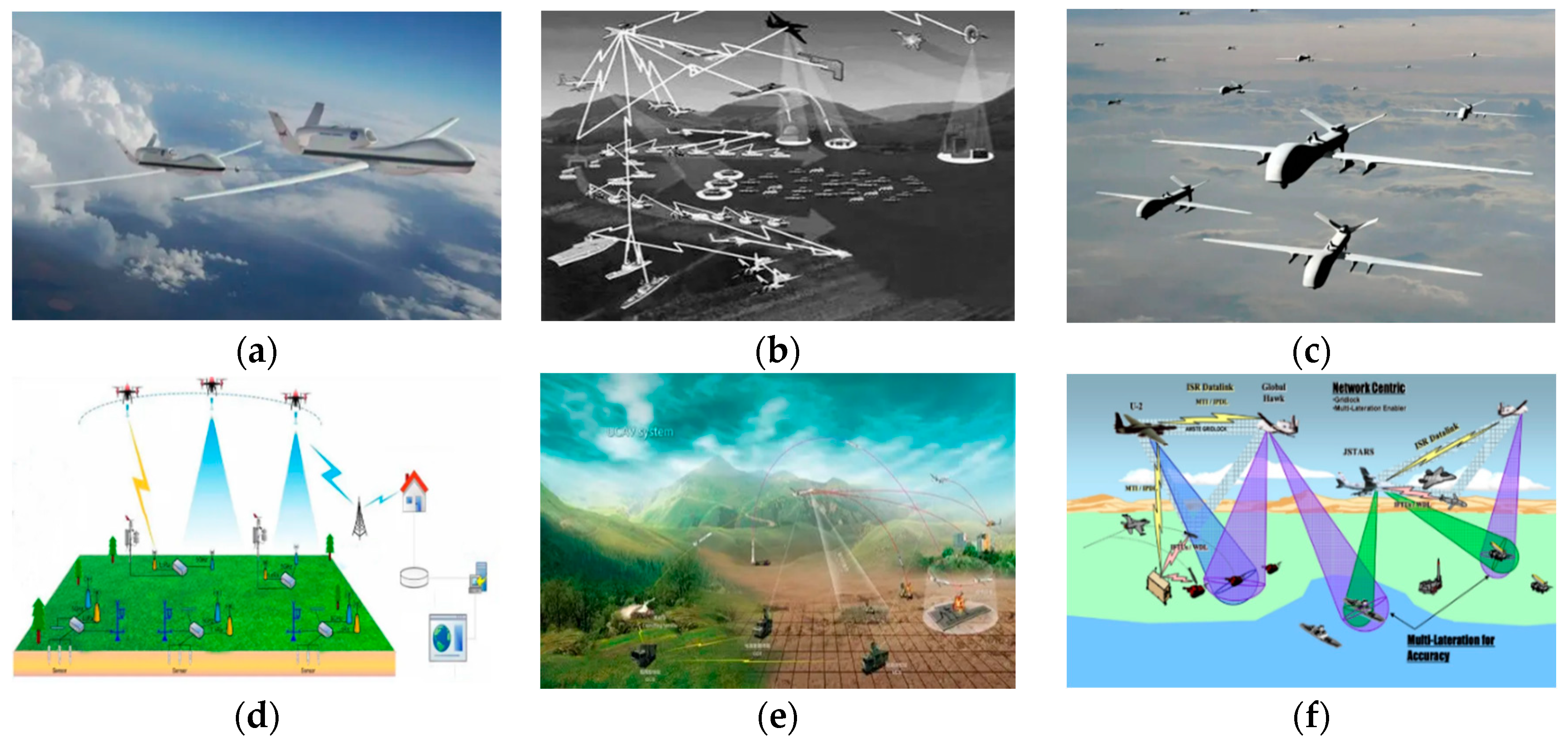
Unmanned aerial vehicle formation has incomparable advantages over a single unmanned aerial vehicle. When UAV formation is not possible in extreme weather, maintaining different formations can improve the aerodynamic efficiency of UAVs to varying degrees, thus reducing the overall flight resistance and saving fuel [8]; it can realize the all-round reconnaissance or observation of the target, such as the enemy target monitoring and reconnaissance, resource exploration and so on, and it can greatly improve the scope of target monitoring; 0069t can also realize simultaneous strikes on multiple mission targets, disrupt the enemy’s combat command system, improve the lethality and hit rate of targets, and improve combat effectiveness, as shown in Figure 2. In the process of use, UAVs are equipped with intelligent devices, which can simulate the transport environment in real time, determine their own position, control their flight status, select effective trajectory points, and calculate safe trajectory. These are important guarantees for UAVs formation to reach the target point from the take-off point as well as important prerequisites for a UAV formation to complete tasks. Therefore, it is important to select a suitable algorithm for UAV formation trajectory planning.

The purpose of trajectory planning of UAV formation is based on the specific tasks, terrain, weather and other environmental factors of each UAV as well as its own flight performance. Under the premise of satisfying multiple constraints, the specified performance index can be optimized or better so that all UAVs in the formation can safely reach the target from the starting point. The trajectory planning of UAV formation is a complex multi-objective optimization and decision problem under multiple constraints. With the increasing number of UAVs, the analytic space of the problem will increase exponentially. In the study of UAV trajectory planning, the algorithm is the soul of UAV trajectory planning, which is directly related to the efficiency and results of trajectory planning. Compared with single UAV trajectory planning, the complexity of UAV formation trajectory planning is mainly reflected as follows:

(1)

In many cases, the scope of planning space is large and complex: for example, there are various spatial obstacles and dynamic threats in the modern battlefield environment;

(2)

There are many constraints. Not only should the planned flyable trajectory conform to the actual dynamics and kinematic characteristics of the UAV, but also the coordination between time and space and the concealment of the trajectory should be considered;

(3)

Multi-UAV trajectory planning can adapt to battlefield dynamic changes and adjust trajectories online in real time.

For the trajectory planning of UAV formation, many papers have proposed solutions from different perspectives, but there are still many unsolved problems and many limitations, resulting in numerous and complex papers without a comprehensive and systematic classification, which is not conducive to research and reading.

The reference [9] classifies and statistically analyzes the cooperative flight path planning of various UAV formations from the three elements of a UAV system (mission, UAV crew and environment) and the three elements of UAV formation cooperative flight path planning (UAV flight path, target and constraint), but it does not discuss the flight path planning algorithm of UAV formation.

Stochastic Heuristic Algorithms (SHA) are reviewed in reference [10], and the characteristics, improvements, applications, advantages and disadvantages of some of them are discussed, but non-SHA algorithms in UAV formation flight paths are not discussed.

The reference [11] divides the flight path planning algorithms of UAV formation into five categories, including optimal algorithm, graph theoretics-based planning method, heuristic information-based planning algorithm, swarm intelligence algorithm and neural network algorithm. Then, a simple description is given to these categories, but no specific algorithms are discussed.

Reference [12] reviews swarm intelligence algorithms from four aspects, such as collision avoidance processing, task allocation, track planning and formation recombination, and it discusses classical algorithms among them. However, it does not discuss non-swarm intelligence algorithms, which has certain limitations.

Compared with many studies in the literature on UAV formation trajectory planning [9,10,11,12], the contributions of this paper are as follows.

In this review, the UAV formation trajectory planning algorithms used in recent decades are classified in detail, and the basic principles of these algorithms are described and compared so as to find out the shortcomings of UAV formation trajectory planning algorithms. The challenges and future research directions of the algorithm are summarized and prospected, which provides reference information for researchers and workers engaged in the formation flight of UAVs.

This paper can be divided into the following parts: Firstly, a simple classification framework of the UAV formation trajectory planning algorithm is introduced in Section 2. Then, the global trajectory planning algorithms are summarized in time order in Section 3 and Section 4. Among them, Section 3 summarizes the traditional algorithm and Section 4 summarizes the intelligent algorithm. Section 5 summarizes the local trajectory planning algorithm. Section 6 summarizes the challenges the algorithm faces. Section 7 summarizes the focus and direction of future research. Section 8 summarizes the full text.

2. Classification Framework of UAV Formation Trajectory Planning Algorithm

This paper provides a classification framework of the UAV formation trajectory planning algorithm, which includes two elements: global planning and local planning.

The global trajectory planning algorithm belongs to the static programming algorithm, which carries out trajectory planning based on existing map information and seeks an optimal trajectory from the starting point to the target point. In this paper, global trajectory planning algorithms are divided into traditional algorithms and intelligent algorithms according to whether they are inspired by natural organisms; the intelligent algorithms are divided into machine learning algorithms and heuristic algorithms according to whether they imitate human behavior or other animal behavior. The global trajectory planning algorithm framework is shown in Figure 3.

The local trajectory planning algorithm belongs to the dynamic trajectory planning algorithm, which means that the pilot aircraft collects the current position information and local obstacle information in real time according to the UAV sensor in the formation and then obtains the optimal trajectory between the starting point and the ending point. The local trajectory planning algorithm framework is shown in Figure 4.

3. Traditional Algorithm

Traditional methods must build the map environment for the target before performing trajectory planning. Firstly, the map environment was discretized into graphs, and feasible trajectories were generated by the search algorithm to complete the global trajectory planning of UAV formation. The existing algorithms are the Dijkstra algorithm, Dubins Curve, Floyd algorithm, Voronoi graph method, Probabilistic Roadmaps (PRM), and Rapidly-Exploring Random Tree (RRT).

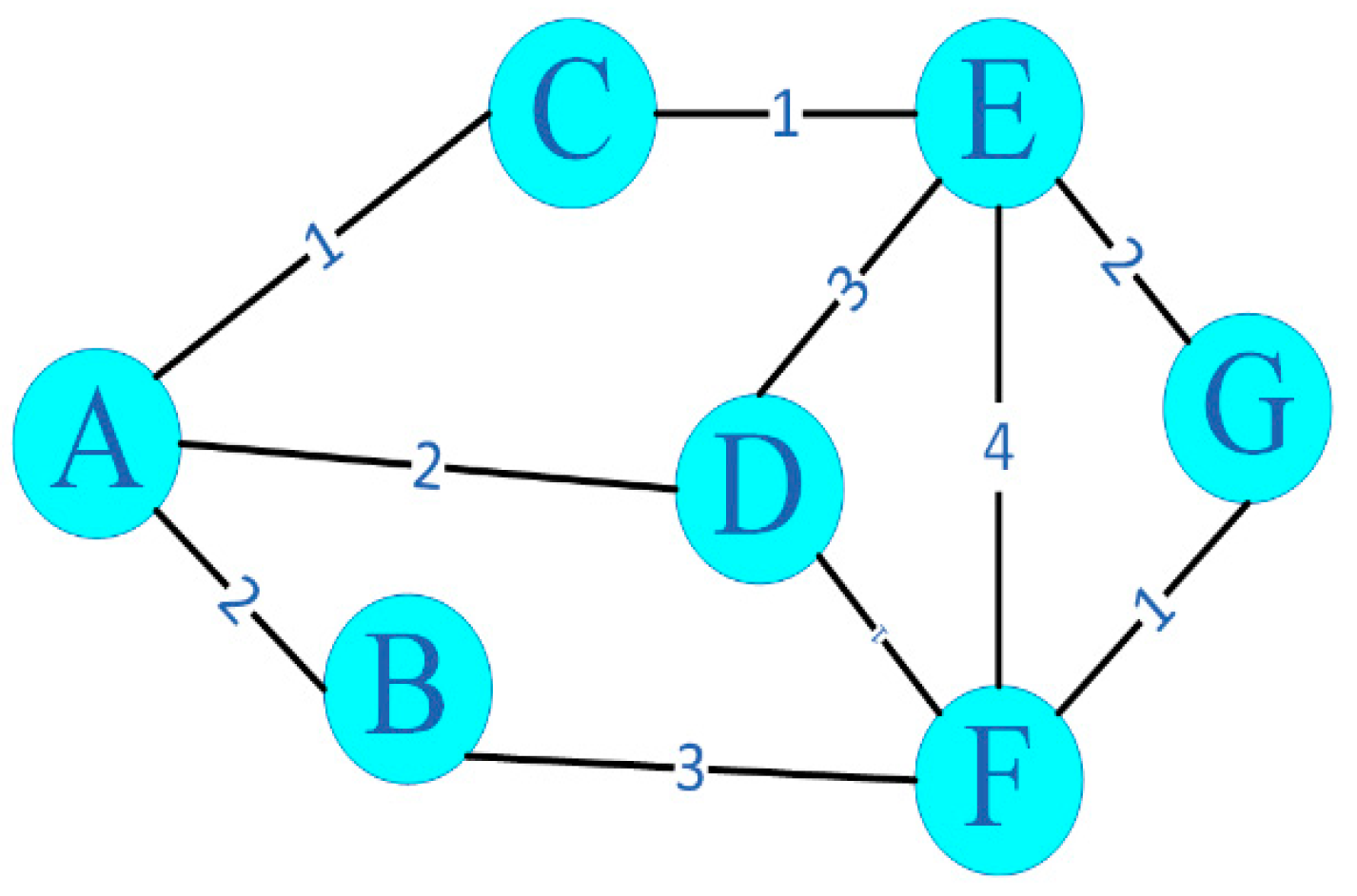
3.1. Dijkstra Algorithm

The Dijkstra algorithm is the classical shortest trajectory method in the geometric graph method, in which the vertex represents trajectory points, the edge represents a feasible trajectory, the line between nodes is called an edge, and each edge has a corresponding weight, which is the distance or cost of the journey; it is suitable for two-dimensional static obstacle avoidance scenes with a non-negative side weight. The key to using this algorithm is to select effective trajectory points, shorten the planning time, expand from the starting point, find the shortest trajectory for a node in each step, select the node with the smallest distance from the node that has never been visited to register, then traverse the adjacent nodes of the node after the node is included, and then update the distance. The cost diagram of a Dijkstra algorithm is shown in Figure 5.

Aiming at the uncertain region search problem, Sujit and Ghose [13] proposed a search algorithm based on the K-shortest trajectory algorithm for UAV to search targets in an unknown environment. It satisfies the requirements of endurance time of each UAV and the location of the base station of UAV operation, and it enables each UAV to search in the area of maximum uncertainty so as to maximize the search benefit.

In order to meet the needs of searching an unknown environment and tracking moving targets in a balanced way, Tin [14] improved on Dijkstra’s algorithm and proposed a robust shortest algorithm (ARSP) to deal with arc uncertainty. The influence of information uncertainty and environmental change on the trajectory planning algorithm is overcome, and the trajectory is quickly replanned at the same time.

Ueno and Kwon [15] applied the Dijkstra algorithm to the minimum time reconstruction of UAV formation in order to meet the requirements of optimality and short computing time, and the trajectory generated within the shortest time is close to the optimal trajectory.

Aggarwal et al. [16] proposed an approximate trajectory generation method to generate an approximate trajectory length under the condition of meeting the safety constraints of a UAV. This method is based on the total cost of the Lagrange relaxation (LARAC) algorithm, and it iteratively uses the Dijkstra algorithm (iDijkstra) to modify the edge cost, which solves the safety constraints and flight energy consumption of UAV caused by extreme high temperature.

3.2. Dubins Curve

The Dubins curve is the shortest locus connecting two two-dimensional planes (i.e., the X-Y plane) under the condition that the curvature constraint is satisfied and the tangent directions of the specified beginning and end are satisfied. In 1957, Lester Eli Dubins proved that any locus can consist of a maximum curvature arc or straight segment (the locus between two points must exist). In other words, the shortest path connecting two points will be constituted by the circular arc of the maximum curvature and the straight line segment. The Dubins of any starting point to the end point are composed of not more than three original motions, and the sequence constituted by the three original motions is called a kind of trajectory. As two continuous and identical primordial motions can be combined into one primordial motion, Dubins proved that the optimal trajectory can only be one of the following six combinations: namely, RSR, LSL, RSL, LSR, RLR, LRL. The first four are collectively called a CSC trajectory, and the last two are collectively called a CCC trajectory, where the primordial motion R represents right turn, S stands for straight and L stands for left. Figure 6 is the trajectory diagram of one Dubins curve LRL.

D’Amato, Mattei, and Notaro [17] modeled the UAV as a Dubins vehicle, using a method based on the Reduced Visibility Graph (RVG), connecting selected nodes by arcs and segments, and adding the Rendez-Vous Waypoints (RVWs). It was based on the leader–follower Stackelberg model’s two-layer game theory method to optimize the location of the trajectory point and the trajectory of the UAV as much as possible in order to find the optimal trajectory while maintaining the shape of the formation in many places.

3.3. Floyd Algorithm

The Floyd algorithm, also known as the interpolation method, is a relatively classic algorithm for solving graph theory problems. It is an algorithm to solve the shortest trajectory between vertices in a given weighted graph, and it can correctly handle the shortest trajectory problem of directed graphs. At the same time, it is a dynamic programming algorithm, and the connection weight between nodes can be positive or negative; similar to Dijkstra’s algorithm, but different from it is that Floyd’s algorithm is used to find the distance between any two points, which is the shortest path of multiple sources, and it can be calculated with negative weights, while Dijkstra’s algorithm is used to find the shortest route from one vertex to all other vertices, is the single-source shortest path, and negative weight circuits cannot be calculated.

Faced with the problem of multi-UAV cooperative patrol trajectory planning under constraints such as time windows, mandatory patrol nodes, UAV flight time and imaging sensors, Yang et al. [18] proposed a new cooperative patrol trajectory planning method, using the Floyd algorithm to generate the initial trajectory, and then used the improved forward insertion heuristic algorithm (PFIH) to obtain the optimal trajectory.

Zhou and Nie [19] proposed a graph-based trajectory planning method for multi-UAV systems, using the Floyd algorithm to update the adjacent cost matrix and trajectory matrix, and solved the problem of UAV formation trajectory planning.

3.4. Fast Marching Method

The fast marching method (FM) is an efficient numerical algorithm for solving the optical path function equation (Eikonal equation), and the optical path function equation is as follows:

$$\left|\nabla T\left(x,y\right)\right|V\left(x,y\right)=1$$

(1)

where (x, y) is the coordinate of the calculation point in the pose space, T(x, y) is the time when the interface function arrives at the calculation point, V(x, y) is the propagation velocity set by the interface function, and it is a fixed value in trajectory planning. The optical path function solution model is shown in Figure 7.

The fast marching method first establishes a rasterized space for storing time values, and then, the time cost will be converted into the distance cost during planning. Then, we set reachable points and unreachable points and complete the minimum value search operation by continuously updating the distance cost to obtain the distance matrix. We use it to construct the potential field and then use the gradient descent method to iterate continuously from the starting point along the direction of the fastest gradient descent in the generated potential field, obtaining a smooth trajectory without collision.

Aiming at the problem that the trajectory obtained by the traditional FM algorithm in the 3D environment will be too close to obstacles and the trajectory is not smooth enough, López et al. [20,21] proposed a fast marching square algorithm (FM2), which improves the FM algorithm by changing the propagation speed in space so that the wave will tend to follow the track travel.

3.5. Voronoi Diagram Method

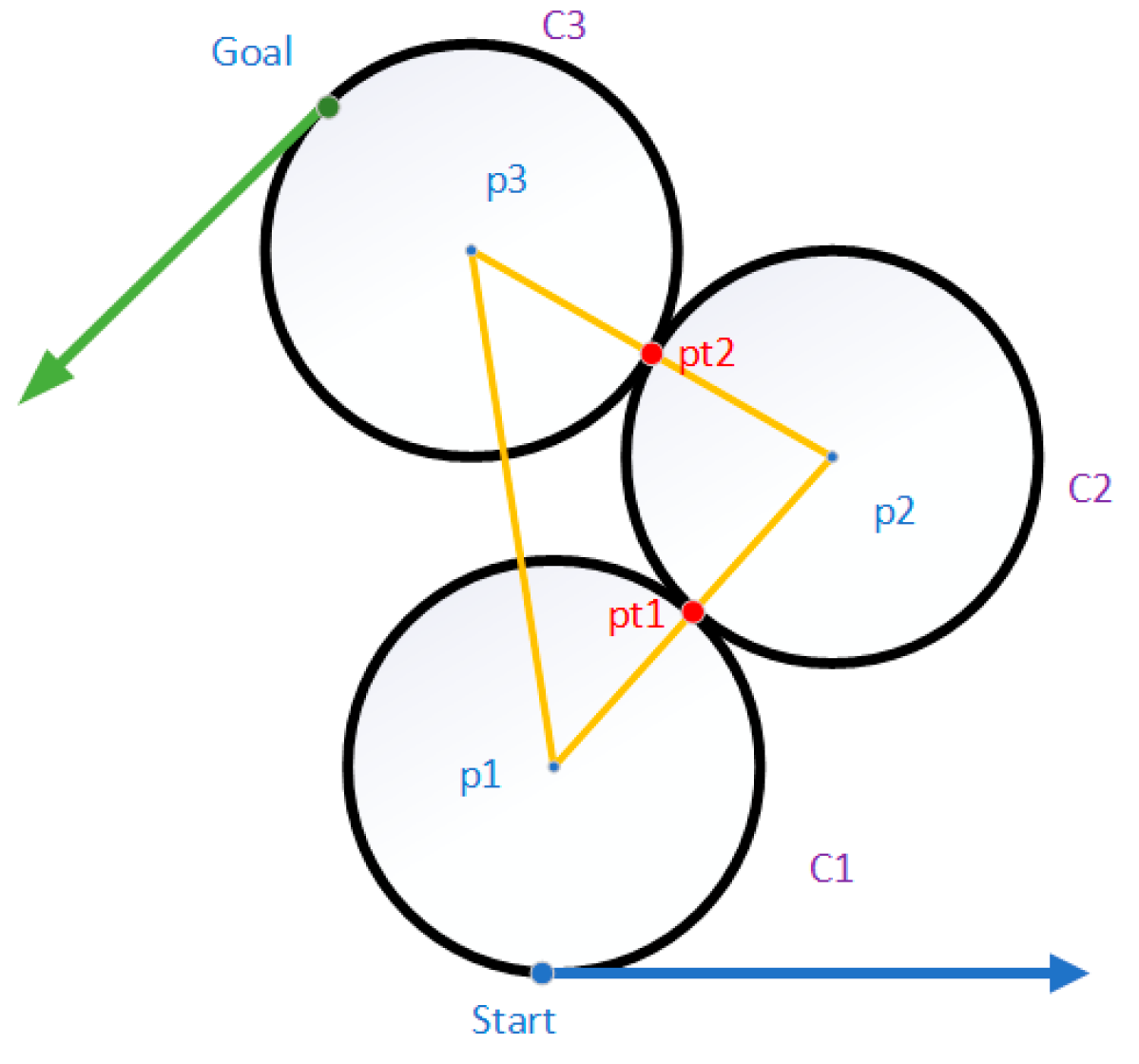
The Voronoi graph method (also known as Dirichlet tessellation) is a space segmentation algorithm proposed by Russian mathematician Georgy Voronoy. It divides the space into many sub-regions through a series of seed nodes (Seed Points), each sub-region is called a Cell, and the distance between all points in each Cell and the Seed Points in the current Cell is less than Distance to all other Seed Points. According to the distribution of obstacles, the Voronoi diagram squares the free space between the edges of the obstacles, and at the same time, it draws the vertical line of adjacent obstacles to form a polygon around the obstacles so that each side is equidistant from the surrounding obstacles. Then, the origin and destination nodes can be connected into the graph by constructing trajectories from the nodes to the edges closest to each node. Figure 8 is a Voronoi trajectory diagram.

Unavoidable accidents or environmental interference problems will inevitably occur when UAV formations perform multi-mission planning and collaborative trajectory planning. In order to cope with this situation, Meng et al. [22] proposed an algorithm to deal with multi-UAV multi-task trajectory re-planning in an unexpected event environment. Each UAV uses a Voronoi diagram to plan its own initial, optimal or sub-optimal trajectory; then, it replans its trajectory according to the new multi-task requirements corresponding to some unexpected events.

To solve the coverage problem with average Voronoi partitions, Chen et al. [23] proposed a distributed coverage algorithm to cover the convex area of the average Voronoi partition of the UAV formation. By exchanging local information with neighbors, the Voronoi partition is continuously iteratively updated, and the UAV direction of movement is calculated. The algorithm can theoretically make the area difference infinitely small so as to achieve the actual average area coverage.

Chen et al. [24] proposed a method based on consistency theory, using the Voronoi diagram method to create a threat domain, and designing a cost function for trajectory planning of multiple UAVs, so that multiple UAVs can take off at the same time and reach the specified target Point, solving the problem of UAV formation attacking multiple targets in a static threat environment.

Hu et al. [25] proposed a distributed formation control and collision avoidance method based on the Voronoi partition and traditional artificial potential field, using the Voronoi partition theory to divide the entire space into non-overlapping regions, and further proposed the target switching scheme; this method solves the problem of local optimum when an artificial potential field is used as motion control law.

3.6. Probabilistic Roadmap Algorithm

The Probabilistic Roadmap Algorithm (PRM) is a method based on graph search, which converts continuous space into discrete space. Trajectory planning is mainly divided into two stages. In the offline learning stage, a large number of robot pose points are randomly sampled; then, neighbor nodes are searched and connections are established to construct a landmark map. In the online query phase, a feasible trajectory is searched from the landmark map using a heuristic search algorithm based on the starting point, target point and landmark map information. Figure 9 is a trajectory diagram of a roadmap algorithm.

Madridano et al. [26] proposed a multi-trajectory PRM-based planning method by establishing a parameter to define three different modes, so that different UAVs in the UAV formation can achieve different mission goals.

3.7. Rapidly Exploring Random Trees

Rapidly exploring Random Trees (RRT) is a single query random search algorithm based on sampling. Its basic idea is to randomly sample in the state space, use the graph structure or tree structure extension to build a feasible trajectory set, and then find a complete feasible trajectory from the trajectory set. The RRT algorithm takes the starting point in the state space as the root node and then generates a random extended tree by gradually increasing the leaf nodes at random. If the newly generated node conflicts with the obstacle area during the generation process, the node is discarded and reselected. When the target point is included in the leaf node of the random tree, the expansion of the random tree stops, and an obstacle avoidance route from the starting point to the target point can be obtained. A fast random search tree locus is shown in Figure 10.

Aiming at the trajectory planning problem of UAV formation with static, ejection and dynamic obstacles, Kothar et al. [27] proposed a trajectory planning algorithm based on fast search random tree (RRTs) and introduced an anytime algorithm and guidance law based on tracking and line of sight into the algorithm to generate low-cost UAV formation trajectories under kinematic constraints in real time.

Zu et al. [28] proposed an improved Rapid Exploration Random Trees (RRTs) UAV formation collaborative trajectory planning algorithm, using a trajectory pruning method to delete redundant nodes on the trajectory. The UAV uses a trajectory planner, which enables the UAV to share information within the communication range.

When UAV formation faces sudden threat trajectory replanning, the classical RRT algorithm has some problems such as low efficiency, large storage space and slow convergence. Huang and Sun [29] proposed a bidirectional fast search random tree algorithm based on greedy strategy, improved the expansion mode of algorithm nodes, and adopted an adaptive step size rolling detection method to improve the sensitivity of UAV formation to sudden threats.

In addition, the traditional RRT algorithm also has the problem that it cannot adapt to the possible changes in the high-order dynamic characteristics of the autonomous movement of the UAV and the mission process during trajectory planning. In response to this problem, Shi et al. [30] proposed a trajectory generation algorithm based on the integration of the RRT algorithm and the minimum capture algorithm, using the RRT algorithm to generate the initial trajectory, and then using the minimum capture algorithm to smooth the initial trajectory, and using the concept of flight corridors to limit the flight trajectory of drones.

Table 1. Content of traditional trajectory planning algorithm in our survey.

Reference	Challenge	Optimization Criteria	Method	Dimension
P. Sujit and D. Ghose [13]	Environment	Trajectory of deviation	KSP	2D
C. Tin [14]	Information, Environment	ARSP	Dijkstra	2D
S. Ueno and S. J. Kwon [15]	Time, Optimality	Optimal control	Dijkstra	2D
R. Aggarwal et al. [16]	Security	LARAC	Dijkstra	2D
E. D’Amato, M. Mattei, and I. Notaro [17]	Environment	RVG, Bi-level optimization	Dubins	3D
J. Yang et al. [18]	Resources	PFIH	Floyd	2D
F. Zhou and H. Nie [19]	Environment	Shortest path	Floyd	2D
B. López et al. [20,21]	Trajectory	Lead–Follow, Multiple applications	FM	3D
B.-b. Meng et al. [22]	Environment	Task allocation	Voronoi + Dijkstra	2D
S. Chen et al. [23]	coverage problem	Distributed coverage	Voronoi	2D
X. Chen et al. [24]	Environment, Multiple objectives	Consistency theory	Voronoi	2D
J. Hu et al. [25]	UAV clustering	Target switching	Voronoi + APF	3D
Á. Madridano et al. [26]	Trajectory	Multiple trajectories	PRM	2D/3D
M. Kothari et al. [27]	Environment	Anytime, Guide rate	RRT	2D
W. Zu et al. [28]	Environment	pruning	RRT	2D
J. Huang and W. Sun [29]	Environment	Greedy strategy, Adaptive step size	RRT	3D
B. Shi et al. [30]	Environment	Minimum snap, Flight corridor	RRT	2D

summarizes the contents of our survey on traditional trajectory planning algorithms.

4. Intelligent Algorithm

The intelligent algorithm is based on the principle of bionics computing, simulating the process of group biological behaviors to collaboratively search for the optimal solution in the space; for high-latitude, nonlinear, multi-constrained optimization problems, it can often converge to the optimal value in UAV formation trajectory planning at the same time, and it also solves the problem of UAV formation obstacle avoidance. In this paper, intelligent algorithms are divided into two types: heuristic algorithms and machine learning algorithms.

4.1. Heuristic Algorithm

Most heuristic algorithms are optimization algorithms that search approximate optimal solutions based on empirical rules under acceptable computational costs to find solutions to problems. It is not a systematic search for answers, but the use of previous experience to select effective methods, and it cannot guarantee the speed of solutions and optimization degree of feasible solutions [31]. At present, the heuristic algorithms are mainly natural body-like algorithms. The heuristic algorithms used for UAV formation trajectory planning include the Simulated Annealing Algorithm (SA), A* Algorithm, Evolutionary Algorithm (EA), Particle Swarm Optimization (PSO), Pigeon-Inspired Optimization (PIO), Fruit Fly Optimization Algorithm (FOA), Artificial Bee Colony (ABC), Salp Swarm Algorithm (SSA), Ant Colony Optimization algorithm (ACO), Gray Wolf Optimization algorithm (GWO), Harmony Search algorithm (HS), etc.

4.1.1. Simulated Annealing Algorithm

The Simulated Annealing Algorithm (SA) is derived from the annealing of solid matter in physics. Usually, when a solid material is annealed, it is heated to allow its particles to move freely, and then, the particle system descends slowly enough to slow down sufficiently. The system is approximately at a thermodynamic equilibrium point, and finally, the particle system will reach its lowest energy state, the ground state, which corresponds to the global minimum of the energy function. The objective function of the optimization problem is equivalent to the energy, and the optimal solution is equivalent to the lowest energy state. The simulated annealing algorithm changes randomly from one state to another state at a given temperature and uses the random acceptance criterion to judge. When the temperature slowly drops to a very low value, it remains at the optimal solution with a probability of 1. When the UAV formation is performing trajectory planning, we first define a solution space, arrange the fixed starting point to the end point by unit, use the Monte Carlo method as the initial solution, and iterate to create a new solution for the next trajectory point program. The exchange order of the two trajectory points in the obtained solution will generate a new solution. Then, we set the target function of the trajectory length of the UAV and use the simulated annealing criterion to test the cost function according to the data of the distance matrix. We use the difference between the cost functions to determine whether to accept the new trajectory planning and set the cooling process control parameters, initial temperature, cooling coefficient, end temperature, and current temperature iteration number. When the temperature drops to the end temperature, the algorithm stops, reaches the minimum temperature, and outputs the formation. The optimal trajectory of the UAV using a simulated annealing algorithm trajectory is shown in Figure 11.

Turker et al. [32] proposed an alternative method to effectively calculate the cost-fair flight path of a single-station multi-UAV system, using a data parallel computing mechanism to improve the simulated annealing algorithm, and solve the problem of the UAV formation trajectory planning calculation time index problem of growth.

Yue and Zhang [33] proposed a method of UAV formation trajectory planning based on the K-means algorithm and Simulated Annealing (SA) algorithm, using decomposition technology to reasonably decompose the effective area into multiple sub-target points. They use the K-means algorithm to cluster the UAV cruise target points and then use the Simulated Annealing (SA) algorithm for similar sub-target trajectory planning, which solves the problem of UAV cruise distance and scheduling under complex constraints and leads to improved coverage of drones in the sub-target area of the cruise effective area.

4.1.2. A* Algorithm

The A* algorithm is a graph search algorithm that introduces heuristic information factors into the target information of the problem to be solved, making the search direction more accurate and reducing the convergence time. The basic idea of this algorithm for UAV formation trajectory planning is as follows: firstly, the flight space is rasterized and decomposed into some units with regular shapes, and it is judged whether these units are covered by obstacles or intersected with obstacles. Then, find the unit containing the starting point and the target point and use the A* algorithm to find a series of connected units to connect the starting unit and the target unit. The search process of the A* algorithm is based on the value of the heuristic function in the direction of the lower cost; that is, for the node n, the algorithm uses the cost function to evaluate its surrounding nodes and selects the point with the smallest estimated value as the next node. The expression of the cost function is:

$$f(n)=g(n)+h(n)$$

(2)

where h(n) is the heuristic function; g(n) represents the prediction cost function from the current node position to the target point and represents the trajectory cost from the starting point to the current node n; and f(n) is the estimated value, which is obtained by adding h(n) and g(n). In the grid graph, the heuristic function is usually expressed by the distance between two points. The calculation process of algorithm A* is a step-by-step search process, continuously extending to the direction of the minimum estimated value trajectory, calculating the optimal solution and outputting the optimal trajectory. Figure 12 is a trajectory diagram of an A* algorithm.

The traditional A* algorithm convergence speed is slow, and the trajectory may not be optimal. Hu et al. [34] proposed a distributed velocity perception and trajectory planning algorithm, which introduced a velocity perception strategy and collision prediction into the A* algorithm and carried out trajectory planning of UAV formation.

Su et al. [35] proposed a cooperative search A* algorithm, which introduced cooperation strategies, cooperation constraints and cooperation costs into the constraint model, and they solved the problem of multi-aircraft formation trajectory planning with complex space–time constraints.

Zhang et al. [36] proposed a collaborative tactical planning method of UAV formation based on hierarchical structure, which introduced a hierarchical structure into UAV formation collaborative combat and solved the autonomous control problem of UAV formation in modern air combat.

Haghighi et al. [37] proposed a method based on the cell revisit time value and other effective cost functions such as height, minimum distance, collision avoidance and turning cost to realize multi-objective collaborative trajectory planning of multiple UAVs. A modification of the A* algorithm (MA*) was made to define a new criterion for individual revisit time unit values and extend it to the entire 3D mountain environment area, introducing revisit time and application-specific settings to reduce the computational complexity degree, which solves the problems of the traditional A* algorithm, such as high computational complexity, small number of extension units and low ratio of coverage.

Nagasawa et al. [38] proposed a multi-UAV trajectory planning method in the case of three-dimensional building damage investigation or disaster, which combined the fuzzy c-means method of assigning positioning points to UAVs and the A* algorithm to calculate the access sequence of each UAV camera positioning point so as to obtain the feasible trajectory of multiple UAVs, which solves the problem of multi-UAV coverage trajectory planning for the 3D reconstruction of damaged buildings after disasters.

Luo et al. [39] proposed a convergent method to ensure autonomous non-collision trajectory planning of UAVs in the presence of static obstacles and dynamic threats. They extended the jump point search algorithm (JPS), parent node transfer law, seventh-order polynomial interpolation method of minimum capture, virtual gravity field and improved artificial potential field (APF) algorithm to a three-dimensional UAV. Based on a static environment, a collision-free trajectory is generated, which solves the trajectory planning problem of UAV formation flying at low altitude in urban and mountainous areas.

Table 2. Summary of simulated annealing algorithm and A* algorithm in our review.

Reference	Challenge	Optimization Criteria	Method	Dimension
T. Turker et al. [32]	Trajectory	Parallel computing	SA	2D
X. Yue and W. Zhang [33]	coverage problem	K-means	SA	2D
Y. Hu et al. [34]	Trajectory	Speed perception, collision prediction	A*	3D
H. Su et al. [35]	UAV clustering	Constraint model	A*	2D
Z. Zhang et al. [36]	UAV clustering	Hierarchy	A*	3D
H. Haghighi et al. [37]	Trajectory and Multiple objectives	Revisit Time	A*	3D
R. Nagasawa et al. [38]	Environment	Fuzzy c-means method	A*	3D
Y. Luo et al. [39]	Environment	parent node, seventh-order polynomial interpolation	JPS + APF	3D

summarizes the contents of our review about the simulated annealing algorithm and the A* algorithm.

4.1.3. Evolutionary Algorithm

The Evolutionary Algorithm (EA) is a stochastic optimization search algorithm summed up on the basis of biological evolution in nature. The most widely used algorithm is the Genetic Algorithm (GA). Its main idea is to rasterize the flight space first, find the area covered by obstacles or conflict with obstacles, and then randomly generate starting points in the map. To ensure the collision-free trajectory to the target point, in the trajectory planning process, each collision-free trajectory from the starting point to the goal point is represented as an individual, and each individual has a chromosome, so each collision-free trajectory can also become a chromosome. Each segment in the trajectory is represented as a gene. The collection of all individuals, that is, all generated collision-free trajectories from the starting point to the target point, are called the population. We design the corresponding fitness function to screen out the required individuals from the population. Individuals with high fitness are elite individuals; through the cross-mutation operation between elite individuals, better elite individuals are continuously screened until the termination conditions are met, and finally, what remains is the required obstacle avoidance route. Figure 13 is a diagram of a cross-mutation operation and a trajectory diagram of an Evolutionary Algorithm (EA).

Tian et al. [40] proposed an algorithm based on model predictive control (MPC) and the Genetic Algorithm (GA) for multiple UAVs to search for unknown areas cooperatively, combining the flexibility of the Genetic Algorithm and the predictive ability of MPC. The combination avoids the problem where the search process enters into local optimality.

Shen et al. [41] proposed a method based on Genetic Algorithm (GA) to solve the multi-UAV cooperative reconnaissance mission planning problem, introduced integer string chromosome representation and designed a new subsequence crossover algorithm to meet the requirements of reconnaissance resolution. They also inserted mutation operators forward to increase the population diversity, which solves the problems of reconnaissance resolution and the time window when UAV formations perform reconnaissance missions.

Nikolos et al. [42] proposed a trajectory planner suitable for a group of cooperative UAVs to avoid collisions with environmental obstacles, combining b-spline curves, potential fields, and differential evolution (DE) to generate smooth the trajectory curve of the UAV formation, which solves the trajectory planning problem of the UAV formation in a known or unknown static environment.

Lamont et al. [43] proposed a multi-objective evolutionary algorithm (MOEA) for trajectory planning that introduces a Genetic Vector Router (GVR) while combining trajectory tracking capabilities with existing swarm behavior to measure the impact of these capabilities on the impact of swarm characteristics. By using “immigrant” population members to increase the search space and generate trajectories that meet mission requirements, they solved the problem of UAV formations exploring the terrain of larger areas and threatening regional trajectory planning.

Eun and Bang [44] developed an efficient strategy for the assignment and trajectory planning of homogeneous UAVs, combining Voronoi diagrams and Genetic Algorithms (GAs) to generate efficient flyable trajectories in network shapes, solving the problem of task assignment, and trajectory planning in the presence of time constraints is addressed.

Pehlivanoglu and Volkan [45] proposed a new multi-frequency Vibration Genetic Algorithm (mVGA), which constructed a Voronoi diagram using height filtering and fuzzy c-means clustering methods. They generated some initial individuals based on Voronoi vertices to improve the initial population, thereby generating efficient and fast flyable trajectories and solving the local optimization problem in a relatively short optimization period.

Sahingoz [46] proposed a flight-able trajectory planning method for multi-UAV systems, which combines the Genetic Algorithm (GA) and Bezier curves to generate an efficient and feasible trajectory of the UAV formation, solving the problem in which the curve is not smooth when using the traditional Genetic Algorithm (GA) for trajectory planning.

Zhang and Duan [47] proposed an improved constrained Differential Evolution (DE) algorithm, which combines the global search capability of the Differential Evolution (DE) algorithm and the constraint processing technology of level comparison, and they designed a level update strategy that solves the trajectory planning problem of formations under multiple constraints in real scenes.

Cekmez et al. [48] used a parallel Genetic Algorithm on the CUDA architecture to plan feasible trajectories for multiple UAVs; the algorithm first used a clustering method to find a subset of control points and then parallelized it on the programming computing platform. The Genetic Algorithm is used to solve each cluster and generate the feasible trajectory of the UAV formation, which solves the problem of long calculation time of the serial algorithm.

Sørli et al. [49] proposed a co-evolutionary multi-UAV cooperative trajectory planning method, which applied the co-evolutionary Genetic Algorithm to trajectory planning, and they considered the sensors carried by each UAV in the formation quantity and location effects, real-time or near-real-time trajectory planning for each UAV, solving the problem of trajectory planning for UAV formations in dynamic environments.

Chen et al. [50] proposed a parallel optimization method, which uses real coding methods and effective selection operations, crossover operations, and mutation operations to improve the Genetic Algorithm (GA), and at the same time, the Particle Swarm Optimization algorithm (the combination of PSO) and Ant Colony Optimization algorithm (ACO) makes the ants in the PSO-ACO system have particle characteristics. Then, it uses the two algorithms to generate formation trajectories simultaneously, which solves the weak global search ability of the Genetic Algorithm (GA) and the Ant Colony Optimization algorithm (ACO) premature maturation problem.

Binol et al. [51] proposed an improved evolution method of Genetic Algorithm (GA) and Harmony Search (HS); the improved search method utilizes various evolution operators with the same properties at the starting position to determine the overall shortest trajectories, which solves the problem of trajectory planning for drone formations when collecting data from multiple roadside units (RSUs).

Harounabadi et al. [52] proposed a Genetic Algorithm for the trajectory planning of multiple UAVs in message ferry networks. The Genetic Algorithm is used to create node clusters, and then, node scheduling in each cluster is defined according to the traffic between nodes and the message load in nodes. The problem of the average message passing delay of traditional mTSP schemes is solved.

Cao et al. [53] established a global optimization model that takes into account UAVs with various sensors located in different bases and multiple constraints, converts the time into an easily measurable way, and then uses the Genetic Algorithm analysis to solve the optimal detection track problem in the case of a multi-base.

Ma et al. [54] proposed a coordination optimization algorithm combining the Genetic Algorithm and clustering algorithm, using the task time constraint method to determine the number of UAVs required. They find the optimal trajectory for each UAV, solving the problem of multi-task assignment and trajectory planning of multiple UAVs.

Li et al. [55] proposed an improved trajectory planning algorithm based on GA. On the basis of a Genetic Algorithm, the optimal trajectory is obtained by the K-means target clustering algorithm and multi-chromosomal Genetic Algorithm, which solves the trajectory planning problem of multi-UAV maritime target search.

Xiong et al. [56] proposed a trajectory planning algorithm based on Genetic Algorithm with adaptive interference operators. The algorithm can realize the multi-directional attack target by setting intermediate points around the target point. A reasonable fitness function is designed by using the regionalization method, and the adaptive disturbance operator is added to plan the trajectory of each UAV, which solves the trajectory planning problem of multiple UAVs attacking targets in a complex combat environment.

Li et al. [57] proposed an optimized Genetic Algorithm method, which applied the augmented stochastic framework to evaluate the task completion probability (PoC) of the strategy in a three-dimensional grid environment, and then, they used the Genetic Algorithm optimization method to find feasible trajectories that maximize PoC, addressing the Reliability-Aware Multi-Agent Coverage Trajectory Planning (RA-MCTP) problem.

Li et al. [58] proposed a gray Genetic Algorithm, which iteratively uses the Genetic Algorithm to continuously find the agent trajectory that maximizes the PoC and solves the reliability-aware multi-agent coverage trajectory planning in continuous time (RA- MCTP) problem.

Zhang et al. [59] proposed a collaborative trajectory planning model, introduced decision variables into the trajectory cost model, and then improved the Genetic Algorithm to generate a formation flight trajectory, which solved the problems of short effective flight time and low mission success rate when multiple UAVs were threatened.

Asim et al. [60] proposed a variable population size genetic trajectory planning algorithm (GTPA-VP), which improves the Genetic Algorithm through three operators of insertion, replacement and deletion, and updates the stop point adaptively. Using the number and location, on this basis, a multi-color Genetic Algorithm is used to find the association between UAVs and stopping points, the optimal number of UAVs and the optimal order of UAV stopping points. Finally, a Genetic Algorithm is used to construct the flight trajectory of all drones, solving the problem of high energy consumption of drones hovering and flying in IoT services.

Yan et al. [61] proposed an improved Particle Swarm Optimization and Genetic Algorithm (GA-PSO), which introduced partial matching crossover and secondary transposition mutation to the traditional Particle Swarm Optimization (PSO) algorithm and solved the intelligent marine task assignment problem and trajectory planning problem for multiple UAVs.

Wang et al. [62] proposed a trajectory planning method based on the Genetic Algorithm (GA). Through the task analysis of the decision-making part and trajectory planning part, a Genetic Algorithm is used to initialize the trajectory; the fitness value calculation, selection, crossover, mutation and other operations are optimized to obtain the optimal search trajectory, which solves the trajectory planning problem of multiple UAV collaborative search tasks.

Table 3. Summary of evolutionary algorithms in our review.

Reference	Challenge	Optimization Criteria	Method	Dimension
J. Tian et al. [40]	Environment	Region division	MPC + GA	2D
L. Shen et al. [41]	UAV clustering	Subsequence crossover, Forward insertion mutation	GA	2D
I. Nikolos et al. [42]	Environment	B-Spline, DE	DE	3D
G. B. Lamont et al. [43]	Environment	GVR, Parallel computing	MOEAs	3D
Y. Eun and H. Bang [44]	Trajectory	Task allocation	Voronoi + GA	2D
Pehlivanoglu and Y. Volkan [45]	Trajectory	Height filtration, Fuzzy c-mean	Voronoi + GA	3D
O. K. Sahingoz [46]	Trajectory	Curves	GA	2D
X. Zhang and H. Duan [47]	Environment	Level update	DE	3D
U. Cekmez et al. [48]	Time, Trajectory	Cluster and parallel computing	GA	2D
J.-V. Sørli et al. [49]	Environment, UAV	Coevolution	GA	2D
J. Chen et al. [50]	Trajectory	Parallel optimization	GA + PSO +ACO	2D
H. Binol et al. [51]	Trajectory, Multiple objectives	Evolutionary operator	GA + HS	2D
M. Harounabadi et al. [52]	Time	Node scheduling	GA	2D
Y. Cao et al. [53]	Trajectory, Multiple objectives	Time conversion	GA	2D
Y. Ma et al. [54]	Trajectory, coverage problem	Clustering, Task time	GA	2D
L. Li et al. [55]	Trajectory, coverage problem	K-means, Multiple chromosome	GA	2D
C. Xiong et al. [56]	Trajectory	Adaptive interference operator, Regionalization	GA	3D
M. Li et al. [57]	coverage problem	Augmented random frame	GA	3D
M. Li et al. [58]	Time, coverage problem	Iterative use	GA	3D
J. Zhang et al. [59]	Environment	Decision variable, Adaptive	GA	2D
M. Asim et al. [60]	Environment, UAV	Variable population	GTPA-VP	2D
M. Yan et al. [61]	Trajectory, Multiple objectives	Partially matched crossover, Secondary transposition mutations	GA + PSO	2D
S. Wang et al. [62]	Multiple objectives, UAV clustering	Task analysis	GA	2D

summarizes the content of evolutionary algorithms in our review.

4.1.4. Particle Swarm Optimization

Particle Swarm Optimization (PSO) is an adaptive stochastic optimization algorithm with a population search strategy developed by simulating the foraging behavior of birds, which is used to solve various problems in engineering and science. Particle Swarm Optimization initializes the trajectory planning problem into a group of random particles and then iterates to find the optimal solution. In each iteration, particles update their position and velocity by tracking individual and global extreme values, and then, they use the search space to complete the optimal trajectory planning. Figure 14 shows a particle motion diagram.

Sujit et al. [63] proposed a random time algorithm based on the Particle Swarm Optimization algorithm. Tracking guidance law and line of sight guidance law are used to track the trajectory generated by the Particle Swarm Optimization algorithm at any time, which solves the problem of using a pop-up window when multiple UAV tracks may collide and trajectory planning when there are moving obstacles.

Wang et al. [64] proposed a collaborative trajectory planning method for multiple UAVs based on the Particle Swarm Optimization (PSO) algorithm, analyzed the main influencing factors of the cost function after modeling, and carried out collaborative dynamic analysis of multiple UAVs, including static three-dimensional trajectory planning, which solves the problems of unsatisfactory trajectory and poor real-time performance in multi-UAV collaborative trajectory planning.

Alejo et al. [65] proposed a system for automatically planning collision-free four-dimensional trajectories; the system is based on the Particle Swarm Optimization (PSO) algorithm of axis-aligned minimum bounding boxes and stochastic global optimization techniques, and it uses a strategy to quickly calculate the initial point, solving the problems of high computational overhead and slow convergence in evolutionary algorithms.

Liu et al. [66] proposed a cooperative competitive Particle Swarm Optimization (PSO) algorithm, which uses two-stage optimization to reduce the dimensionality of the problem and generates the optimal collaborative trajectory for multiple UAVs in three-dimensional space, solving the trajectory planning problem for UAV formation in cooperative and competitive situations.

Zhang et al. [67] designed an improved PSO algorithm (IPSO), which used a binary value coding matrix and adaptive inertial weight adjustment strategy to generate a feasible trajectory for multiple UAVs, solving the decision-making problem of a multi-UAVs cooperative reconnaissance mission.

In this paper, Li et al. [68] proposed a new trajectory planning method for multiple UAVs by introducing a variable neighborhood drop (VND)-enhanced genetic Particle Swarm Optimization algorithm to optimize flight trajectory with minimum span and solve the problem of limited flight endurance of UAVs in agricultural applications.

Hoang et al. [69] proposed an angle-encoded Particle Swarm Optimization method, which realized the communication between UAVs through the Internet of Things board, minimized the cost function of multiple constraints including the shortest trajectory and the safe operation of UAVs, and found a feasible and frictionless trajectory for the whole formation. The trajectory planning problem of UAV formation in building infrastructure inspection is solved.

Chen et al. [70] proposed a trajectory planning method based on Dubins trajectory and the Particle Swarm Optimization (PSO) algorithm, using Dubins trajectory to reduce the dimensionality of the aircraft kinematics model. Then, using the Particle Swarm Optimization algorithm to optimize the trajectory after the formation reconstruction, it solves the trajectory planning problem when the task adjustment or the environment changes in the UAV formation.

Patley et al. [71] proposed an improved Particle Swarm Optimization method (ODPSO) based on orthogonal design and formulated a point sequence strategy to redefine the objective function. They searched for each the three-dimensional trajectory points within the time step, used the relative particle directivity to improve the search accuracy, and solved the trajectory planning problem of the UAV formation under the conditions of threats and terrain constraints.

Shao et al. [72] proposed a 3D trajectory planning algorithm for UAV formation based on Comprehensive Improved Particle Swarm Optimization (CIPSO). This method uses chaos-based logical mapping to improve the initial distribution of particles, designs commonly used constant acceleration coefficients and maximum speeds to adapt to linear change coefficients, and uses a mutation strategy in which the desired particles replace undesired particles, solving the terrain and threat constraints problems of UAV formation trajectory planning under the condition.

Yang et al. [73] proposed a 4D coordinated trajectory planning algorithm for multiple UAVs, which constructed the solution boundary of the search space and the distance to the destination based on the properties of all threats, and then designed a spatial refinement voting mechanism that solves the problems of local optimum and slow convergence of the standard Particle Swarm Optimization algorithm.

Shao et al. [74] proposed a Distributed Cooperative Particle Swarm Optimization (DCPSO) algorithm with an elite-preserving strategy, which parameterizes the trajectory using a Pythagorean Heatmap (PH) curve. Then, evolutionary theory is used to improve the Particle Swarm Optimization algorithm to generate a flyable and safe trajectory for each UAV, which solves the kinematic constraint problem of multi-UAV trajectory planning.

Liu and Lu [75] proposed an algorithm based on Dubins trajectory and Coevolutionary Particle Swarm Optimization (CCPSO). This algorithm determines the initial reference trajectory by the Dubins trajectory and then converts the time co-constraint into an equal trajectory length, and the trajectory parameters are optimized by CCPSO, which solves the problem of multi-UAV collaborative trajectory planning.

He et al. [76] proposed a new hybrid Particle Swarm Optimization and improved symbiotic search algorithm (HIPSO-MSOS), which introduces a time-stamp segmentation (TSS) model and a multi-objective optimization function to simplify the cost. Using HIPSO-MSOS to generate feasible trajectories and then smoothing trajectories by cubic b-spline curves, the problem of coordinated trajectory planning for multiple UAVs in complex 3D environments is solved.

Ahmed et al. [77] proposed a trajectory planner based on the Particle Swarm Optimization (PSO) algorithm, which uses distributed full coverage and dynamic fitness function to generate the optimal trajectory and solves the problem of trajectory planning for multiple UAVs.

Mobarez et al. [78] proposed an improved Particle Swarm Optimization method, improved the optimization problem by using evolutionary computing technology, added parallel recombination into trajectory planning, and solved the problems of long processing time and non-optimal trajectory in the dynamic trajectory planning of UAV formation.

Xiao et al. [79] proposed a Heterogeneous Adaptive Comprehensive Learning Dynamic Multi-population Particle Swarm Optimization algorithm (HACLDMS-PSO), which incorporated a population dynamic adjustment strategy, disturbance mechanism and adaptive learning probability mechanism into the Particle Swarm Optimization algorithm, which better solved the NP-hard problem in multi-UAV trajectory planning.

Meng-yun et al. [80] proposed a tracking planning method based on multi-strategy improved symbiosis search (MSISOS); this method uses an adaptive strategy and interference strategy to assist the search trajectory and coordinates space–time through UAV information interaction layer constraints. Then, a distributed method is designed for formation trajectory planning, which solves the problems of poor accuracy and slow convergence in multi-UAV trajectory planning in complex battlefield environments.

Chung et al. [81] proposed a trajectory planning algorithm that combines gradient descent-based trajectory planning (GBPP) and Particle Swarm Optimization. The initial trajectory of the algorithm is defined as the input of GBPP, and the hierarchical concept is added to the Particle Swarm Optimization algorithm (HPSO) to generate a feasible trajectory, which solves the problem of long calculation time of the Genetic Algorithm and Particle Swarm Optimization algorithm.

Lu et al. [82] proposed a distributed hybrid Particle Swarm Optimization and differential evolution (DE) technique; this technique adds the nonlinear time-varying method to the Particle Swarm Optimization algorithm (NTVPSO) and adds the adaptive mechanism to the differential evolution (DE) evolution (ADE). Finally, it adopts the distributed method, uses NTVPSO-ADE to realize the collaborative trajectory planning of multiple UAVs, and solves the problem of difficult model establishment and large amount of calculation in formation trajectory planning.

Table 4. A summary of Particle Swarm Optimization in our review.

Reference	Challenge	Optimization Criteria	Method	Dimension
P. Sujit et al. [63]	Trajectory, Environment	Tracking, Line of sight guidance law	PSO	3D
G. Wang et al. [64]	Trajectory, Environment	Cost analysis	PSO	3D
D. Alejo et al. [65]	Time	Minimum boundary, Random optimization, One-time strategy	PSO	4D
J. Liu et al. [66]	UAV clustering	Two-stage optimization	PSO	3D
Y.-Z. Zhang et al. [67]	UAV clustering, Multiple objectives	Binary value coding matrices, Adaptive inertia weights	IPSO	2D
X. Li et al. [68]	Trajectory, UAV	VND	GPSO	2D
V. Hoang et al. [69]	Environment, coverage problem	Minimizing cost function	$\theta$-PSO	3D
Q.-y. Chen et al. [70]	Environment	Reduction in dimension	Dubins + PSO	2D
A. Patley et al. [71]	Environment	Point sequence strategy, Inclined plane, Relative particle directivity	ODPSO	2D/3D
S. Shao et al. [72]	Environment	Logical mapping, Adaptive linear change	CIPSO	3D
L. Yang et al. [73]	Trajectory	Spatial refinement voting mechanism	PSO	4D
Z. Shao et al. [74]	Environment, UAV	Pythagorean heat map, Coevolution	DCPSO	3D
Y. Liu and H. Lu [75]	UAV clustering	Constraint conversion	Dubins + CCPSO	2D
W. He et al. [76]	Environment, UAV clustering	TSS, Multiple objective optimization	HIPSO-MSOS	3D
N. Ahmed et al. [77]	UAV clustering	Distributed full coverage, dynamic fitness	PSO	3D
E. Mobarez et al. [78]	Time, Trajectory	Evolutionary computation, Parallel recombination	PSO	3D
J. Xiao et al. [79]	Trajectory	Adaptive, interference, Interactive coordination	MSISOS	3D
W. Chung et al. [81]	Trajectory	GBPP, layered	HPSO	3D
L. Lu et al. [82]	Trajectory	Nonlinear time variation, adaptive, Distributed	NTVPSO-ADE	3D

summarizes the content of PSO algorithms in our review.

4.1.5. Pigeon-Inspired Optimization

The Pigeon-Inspired Optimization algorithm (PIO) is a swarm intelligent optimization algorithm designed to simulate pigeon homing behavior. First of all, three kinds of pigeon swarm optimization models were proposed: the map model based on the geomagnetic field, the pointer operator model based on the sun and the landmark operator model based on the landmark operator model. Secondly, a general direction was identified through the map and pointer operator, and then, the landmark operator was used to correct the current direction until the best track was found. Figure 15 shows a PIO map and compass operator model and a pigeon flock optimization (PIO) track chart.

Luo et al. [83] proposed a co-evolutionary Pigeon-Inspired Optimization (CPIO) algorithm based on a cooperation–competition mechanism. The search and track (ST) method is introduced to obtain the lowest-cost trajectory, and the dynamic two-stage closed search (DTCSCS) problem of UAV formation under range constraints (RC) and orientation constraints (OC) is solved.

Ruan and Duan [84] proposed a multi-objective social learning pigeon-inspired optimization algorithm (MSLPIO), which uses iterative learning to update waypoint positions, adding social learning factors and dimension-related parameter setting methods, which solves the problem of weak convergence of a traditional Genetic Algorithm.

Duan et al. [85] proposed a dynamic discrete Pigeon-Inspired Optimization algorithm based on hybrid architecture ($D^{2}PIO$), constructed and updated the probability mapping by using Bayesian formula, adopted the response threshold S-type function model (RTSM) for target allocation during attack execution, and finally used B-spline curve to generate feasible trajectory. The problem of search–attack task planning for multiple UAVs is solved.

Wang et al. [86] proposed a multi-UAV collaborative trajectory planning method based on the Cauchy mutant pigeon intelligent optimization algorithm (ECM-PIO); the algorithm uses the Cauchy mutation operator for optimization, expanding the search range and reducing the risk of falling into local optimization, which solves the shortcomings of the traditional pigeon swarm algorithm optimization process that has optimization bias and is easy to fall into local optimization.

Yu et al. [87] proposed a mutational pigeon swarm optimization algorithm (MGLPIO) based on swarm learning strategy, which introduces the swarm learning strategy, triple mutation strategy, timestamp segmentation mechanism and coordination cost function into the swarm optimization algorithm (PIO). They used it to solve the optimal trajectory, which solves the problems of low population diversity, weak global search ability and weak convergence of traditional PIO.

Lu et al. [88] proposed an improved Pigeon-Inspired Optimization algorithm (IPIO) based on natural selection and Gauss–Cauchy mutation, established an environment-aware map, and designed an integer encoding method. A discrete compass operator, discrete landmark operators, Gaussian mutation and Cauchy mutation operators are introduced to break away from local optimum. Finally, natural selection is used to accelerate convergence, which solves the problem of collaborative dynamic target search and area coverage of UAV formations in uncertain environments.

Zheng et al. [89] proposed a collaborative search decision-making method based on improved Pigeon-Inspired Optimization, which established a target probability information graph model with a normal distribution, an information graph of the search environment determinism, and a digital information graph. By adding the speed update and correction mechanism and the elite generation mechanism, they improve the traditional Pigeon-Inspired Optimization algorithm. Finally, the improved classification optimization method is used to determine the optimal search flight trajectory of the UAV, which solves the problem of multi-UAV cooperative moving target search.

Luo et al. [90] proposed a closed-loop trajectory planning method based on cooperative Pigeon-Inspired Optimization (CPIO) and artificial potential field (APF). Firstly, a probabilistic graphical model was established, and then, a rolling prediction strategy and CPIO were applied to generate multiple man–machine collaborative target search trajectories, while using Bayesian theorem to update the search probability map, and finally using the APF method to generate return trajectories for each UAV, which solves the multi-UAV cooperative target search problem.

4.1.6. Fruit Fly Optimization Algorithm

The Fruit Fly Optimization Algorithm (FOA) is a new method for deriving global optimization based on the foraging behavior of Drosophila, which uses Drosophila to be superior to other species in sensory perception, especially in the sense of smell and vision. First, fruit flies use their sense of smell to collect the smell in the air. Then, they fly to the vicinity of the food location, where they use vision to find the location where the food and companions gather and fly in that direction, so as to realize the group iterative search of the solution space and complete the multi-UAV trajectory planning. Figure 16 is an FOA iterative evolution search diagram and a Fruit Fly Optimization Algorithm (FOA) trajectory diagram.

Shi et al. [91] proposed the multi-swarm Fruit Fly Optimization Algorithm (MSFOA), which divides the entire fruit fly group into multiple multi-task sub-swarms and introduces offspring competition strategies. They propose a collision detection method to solve the problem of slow global convergence, and local optimum of the traditional Fruit Fly Optimization Algorithm is solved.

Li et al. [92] proposed an optimized Fruit Fly Optimization Algorithm (ORPFOA) to determine the optimal number and priority of UAVs while using a change task assignment algorithm combined with reference points and distance–cost matrices. Trajectory planning solves the problem of multi-UAV trajectory planning in a three-dimensional complex environment with online changing tasks.

Mao et al. [93] proposed an improved Fruit Fly Optimization Algorithm (NIFOA) based on Time Stamp Segmentation (TSS). The TSS model was introduced to solve the spatio-temporal coupling problem between multiple UAVs, and the multi-objective problem is transformed into a multi-constraint problem. Finally, the greedy strategy, the restart strategy and the evolutionary strategy of the optimal population are added to complete the multi-UAV trajectory planning, which solves the space–time coupling problem between multi-UAVs and the convergence speed of the traditional Fruit Fly Optimization Algorithm problems with slowness and local optima.

4.1.7. Artificial Bee Colony

The Artificial Bee Colony algorithm (ABC) is an optimization method to imitate the intelligent foraging behavior of bees. The process of the algorithm follows: First, assign a hired bee to the initial honey source and search according to certain rules to generate a new honey source. Then, use the greedy selection method to retain the honey source with high fitness and calculate the probability that the honey source found by the hired bee will be followed. Last, follow the peak using the same method as the hired bee. If the nectar source satisfies the condition of being abandoned, the corresponding hired bee becomes a scout bee and randomly searches in the search space to generate a new nectar source, obtaining the global optimal trajectory through the local optimization behavior of each individual artificial bee. Figure 17 is a trajectory diagram of the Artificial Bee Colony algorithm (ABC).

Tian et al. [94] proposed an improved Artificial Bee Colony (IABC) algorithm, which optimizes the trajectory points only according to the cost value of the trajectory and solves the problem of long convergence time of the traditional Artificial Bee Colony algorithm.

Bai et al. [95] proposed a hybrid algorithm based on Artificial Bee Colony algorithm (ABC) and A*. The algorithm uses the ABC algorithm to complete the preliminary planning, then uses the A* algorithm to plan the specific trajectory points, and finally combines the adaptive time coordination method to obtain the optimal trajectory, which solves the problem of three-dimensional multi-UAV trajectory planning.

Liu et al. [96] proposed a multi-UAV task assignment and trajectory planning method for disaster medical rescue. The algorithm uses the fitness function considering the current number of iterations and the maximum number of iterations and an Adaptive Genetic Algorithm (AGA) for task allocation; then, a balanced search strategy is added to improve the Artificial Bee Colony algorithm (IABC), and trajectory planning solves the problem of poor convergence efficiency and calculation effect of the traditional Artificial Bee Colony algorithm.

Table 5. Summarizes the content of our review on PIO, FOA, and ABC.

Reference	Challenge	Optimization Criteria	Method	Dimension
D. Luo et al. [83]	DTSCS	ST	CPIO	2D
W.-y. Ruan and H.-b. Duan [84]	Trajectory	Iterative learning, social learning factor	MSLPIO	2D
H. Duan et al. [85]	UAV clustering	Bayes’ formula, RTSM, B-spline curve	$D^{2}PIO$	3D
B. Wang et al. [86]	Trajectory	Cauchy mutation operator	ECM-PIO	3D
Y. Yu et al. [87]	Trajectory	triple mutation, timestamp segmentation, coordination costs	MGLPIO	3D
J. Lu et al. [88]	UAV clustering, coverage problem	Environment awareness, integer coding, discrete operators, mutation operators, natural selection	IPIO	2D
W. Zheng et al. [89]	UAV clustering	Probability graph model, pheromone graph, speed update, correction, elite generation	PIO	2D
D. Luo et al. [90]	UAV clustering	Probability graph model, rolling prediction, Bayes’ theorem	CPIO + APF	2D
K. Shi et al. [91]	Trajectory	Offspring competition, collision detection	MSFOA	2D/3D
K. Li et al. [92]	Environment	Mission change and distance cost	ORPFOA	3D
Y. Mao et al. [93]	Trajectory	TSS, greedy strategy, restart strategy and evolution strategy	NIFOA	3D
G. Tian et al. [94]	Time	Trajectory cost	IABC	2D
X. Bai et al. [95]	UAV clustering	Adaptive time coordination	ABC + A*	3D
H. Liu et al. [96]	Trajectory	Fitness function, balanced search	AGA + IABC	2D

summarizes the content of the Pigeon-Inspired Optimization algorithm, Fruit Fly Optimization algorithm and Artificial Bee Colony algorithm in our review.

4.1.8. Salp Swarm Algorithm

The Salp Swarm Algorithm (SSA) is a new method to deduce and seek global optimization based on the swarming behavior of salps when navigating and foraging in the ocean. The SSA algorithm acts as an approximate global optimum by initializing a number of salps at random locations. Then, it calculates the fitness of each salp, finds the salp with the best fitness, assigns the position of the best salp to a variable as the source food to be chased by the salp chain, and uses the formula to update the fitness coefficient. For each dimension, the positions of the leading jumping body and the following jumping body are updated iteratively, and the search space determines the global optimal trajectory. Figure 18 is a Salp Swarm Algorithm (SSA) trajectory diagram.

Dewangan and Saxena [97] proposed a new Salp group algorithm (SSA), which uses multiple random operators to solve the problems of slow convergence and poor real-time performance of other heuristic algorithms in multi-UAV trajectory planning.

4.1.9. Ant Colony Optimization Algorithm

Ant Colony Optimization (ACO) is a heuristic global optimization algorithm derived from the trajectory behavior of ants in the process of searching for food. The ant colony algorithm uses the trajectories of ants to represent the feasible solution of the problem to be optimized. All trajectories of the entire ant colony constitute the solution space of the problem to be optimized, and ants with shorter trajectories release more pheromones. The concentration of pheromone accumulated on the shorter trajectory gradually increases, and the number of ants choosing this trajectory increases; eventually, all the ants will concentrate on the best trajectory under the action of positive feedback, and the corresponding trajectory is the optimal solution to the problem. Figure 19 is a trajectory diagram of an Ant Colony Optimization algorithm (ACO).

Cekmez et al. [98] proposed a parallel Ant Colony Optimization algorithm (ACO) to calculate the trajectory of a UAV. This algorithm implements ACO on CUDA architecture, which gives full play to the parallel characteristics of ACO on GPU and solves the problem of slow convergence of a traditional ant colony algorithm.

Qiannan et al. [99] proposed an intelligent method based on the improved Ant Colony Optimization (ACO) algorithm, which cuts the trajectory generated by ACO and solves the problem that the trajectory of the traditional ACO algorithm may not be optimal.

Huang et al. [100] proposed a coordinated trajectory planning method for multiple UAVs based on K-degree smoothing. In this method, a Voronoi diagram is used to redefine the edge cost, and the redefined heuristic information function and pheromone updating method are used to change the Ant Colony Optimization algorithm. Finally, the K-degree smoothing method is used to smooth the trajectory, which solves the problem of strong coordination and weak coordination in the collaborative trajectory planning of multi-UAVs.

Li [101] proposed a multi-UAV multi-communication target and message priority UAV cooperative communication trajectory method. This method combines a delay tolerant network (DTN), light grid and ant colony algorithm. The trajectory planning is carried out to solve the contradiction between the intermittent link of the underlying communication of multi-UAVs and the continuous demand of the upper-level communication in a highly hostile battlefield.

Perez-Carabaza et al. [102] proposed a new method based on the improvement of Ant Colony Optimization (ACO), which added a new minimum time search (MTS) heuristic function to ACO to solve the traditional ACO problem of slow algorithm convergence and low initial trajectory quality.

Zhen et al. [103] proposed a multi-UAV cooperative search attack method (ISOA) based on an intelligent self-organizing algorithm, using a new state transition rule and a distributed method to improve the Ant Colony Optimization algorithm. Then, using the Dubins curve to smoothly connect the trajectory points generated by ACO, the trajectory planning problem of multiple UAVs under the constraints of maneuverability, collision avoidance and maximum range is solved.

Cekmez et al. [104] proposed an enhanced Ant Colony Optimization (ACO) algorithm, which performs multi-core computing on the parallel computing platform CUDA to solve the trajectory planning problem of multiple UAVs in complex environments.

Lin et al. [105] proposed a multi-objective optimization model of coverage and task time and introduced the similarity measure in an immune optimization algorithm into the Ant Colony Optimization algorithm to solve the problem that the traditional Ant Colony Optimization algorithm is insufficient in track repeatability.

Liu et al. [106] proposed an improved Ant Colony Optimization algorithm, which introduced the location allocation method and the new node selection strategy into the Ant Colony Optimization algorithm and solved the problem of slow trajectory planning optimization speed of the Ant Colony Optimization algorithm in formation transformation.

Ali et al. [107] proposed a hybrid meta-heuristic algorithm, which combined maximum–minimum Ant Colony Optimization and differential evolution to solve the problem of slow global convergence of traditional Ant Colony Optimization algorithms and maximum–minimum Ant Colony Optimization algorithms.

Xia et al. [108] proposed a system framework for multi-UAV collaborative task assignment and tracking planning. The framework uses a Particle Swarm Optimization algorithm based on a guidance mechanism to solve the combinatorial optimization model. Then, adaptive parameter adjustment, encounter point prediction, bidirectional search and online replanning are introduced into the Ant Colony Optimization algorithm for trajectory planning (SAP-ACO), which solves the cooperative task assignment and tracking planning problems of UAV formations facing moving targets.

Ali et al. [109] proposed a bionic optimization algorithm, which combines the maximum–minimum Ant Colony Optimization (MMACO) and the Cauchy mutant (CM) operator, and they use the CM operator to enhance the MMACO algorithm to solve the problems of slow convergence and possible local optimum in traditional ACO and MMACO.

Wei and Xu [110] proposed a distributed trajectory planning algorithm based on dual decomposition of UAV communication chains. This algorithm improves the traditional Ant Colony Optimization algorithm (ACO) from the aspects of trajectory selection, pheromone update, rollback strategy, etc., and solves the problems of poor efficiency, adaptability and robustness of the ACO algorithm.

Li et al. [111] proposed an asynchronous Ant Colony Optimization (AACO) algorithm. The visibility matrix and test track coverage matrix are added into the ACO algorithm. The search order of the population track primitive is changed from the current fitness value and the previous fitness value to the current fitness value. Finally, the incentive value is introduced to avoid track repetition, which solves the problem of optimal trajectory planning for multiple UAVs in three-dimensional space.

Majeed and Hwang [112] proposed a multi-objective coverage flight trajectory planning algorithm, which added the fitting sensor footprint scanning (SFS) and sparse trajectory point graph (SWG) to the Ant Colony Optimization (ACO) algorithm. Traversing the area of interest (AOI) solves the problem of high cost of multi-UAV coverage trajectory planning in urban environments.

4.1.10. Gray Wolf Optimization Algorithm

The Gray Wolf Optimization algorithm (GWO) is a new swarm intelligence optimization algorithm inspired by the predation behavior of gray wolves. The Gray Wolf Optimization algorithm divides gray wolf individual fitness into four different levels: optimal solution, suboptimal solution, third solution and candidate solution according to the calculated fitness; the individuals with the top three fitness guide other wolves towards the goal Iterative search, while continuously updating the solution level and position, until the best trajectory to the target point is found. Figure 20 contains a Gray Wolf Optimization algorithm position update model and a Gray Wolf Optimization algorithm (GWO) trajectory diagram.

Radmanesh et al. [113] proposed a Bayesian algorithm based on Gray Wolf Optimization, which added dynamic Bayes and range-based value function (DBVF) into GWO to solve the trajectory planning and collision avoidance problems of multiple UAVs with fixed and moving obstacles in uncertain environments.

Dewangan et al. [114] proposed a multi-UAV trajectory planning method based on the Gray Wolf Optimization algorithm (GWO) to solve the problems of slow convergence, high trajectory calculation cost and local optimization of other meta-heuristic and deterministic algorithms in multi-UAV trajectory planning.

Xu et al. [115] proposed an improved Gray Wolf Optimization algorithm (GWO), which improved the population initialization, attenuation factor updating and single position updating of the Gray Wolf Optimization algorithm and solved the NP-hard problem of multi-UAV collaborative trajectory planning.

Yang et al. [116] proposed a trajectory planning method based on multi-population chaotic Gray Wolf Optimization (MP-CGWO). The multi-population concept and chaotic search strategy are added into the Gray Wolf Optimization algorithm (GWO), which solves the problem that the traditional GWO algorithm is easy to fall into local optimization.

Huang et al. [117] proposed a hybrid discrete intelligence algorithm (HDGWO) based on gray wolf optimizer. The algorithm uses the discrete gray wolf update operator and uses integer coding and a greedy algorithm to transform between the gray wolf space and the discrete problem space. Then, it adds the center position operation and the stagnation compensation gray wolf update operation, and finally, it adds an azimuth to improve the gray wolf algorithm, which solves the GWO problems of poor global convergence ability and local search ability.

Jiaqi et al. [118] proposed an adaptive multi-UAV trajectory planning method to improve the Gray Wolf Optimization algorithm (AP-GWO). This method adds the spiral update position and self-adaptive adjustment mechanism to the Gray Wolf Optimization algorithm, which solves the problems of relatively long convergence time, relatively unsmooth trajectory and possibly not optimal trajectory of the traditional GWO algorithm.

4.1.11. Harmony Search Algorithm

Harmony Search (HS) is a music-based heuristic optimization algorithm. The Harmony Search algorithm mimics the process of musical improvisation, in which musicians continually adjust the pitch of their instruments to achieve better harmony. The search process of the global trajectory planning problem is similar to the music improvisation process; that is, each decision variable constantly updates its own value during the search process so as to converge to the global optimum and obtain the optimal trajectory. Figure 21 is a Harmony Search algorithm (HS) trajectory diagram quoted from reference [119].

Wu et al. [119] proposed an improved Harmony Search algorithm (MHS), which introduced an intersection mutation operator and Pythagorean heat map curve (PH) to improve the HS algorithm and solved the traditional HS problem of slow algorithm convergence.

Table 6. Summary of the contents of SSA, ACO, GWO and HS in the review.

Reference	Challenge	Optimization Criteria	Method	Dimension
R. K. Dewangan and P. Saxena [97]	Time, Trajectory	Random operator	SSA	3D
U. Cekmez et al. [98]	Time	Parallel computing	ACO	2D
Z. Qiannan et al. [99]	Trajectory	Trajectory cutting	IACO	2D
L. Huang et al. [100]	UAV clustering	Redefine, k degree smoothing	Voronoi + ACO	2D
Z. Li [101]	Communication, UAV clustering	DTN, Light lattice diagram	ACO	2D
S. Perez-Carabaza et al. [102]	Time, Trajectory	MTS	ACO	3D
Z. Zhen et al. [103]	UAV, Trajectory	State transitions, Distributed	ISOA	2D
U. Cekmez et al. [104]	Environment	Parallel computing	ACO	3D
W. Lin et al. [105]	Trajectory	Similarity measure	ACO	2D
G. Liu et al. [106]	Time, UAV clustering	Location allocation, Node selection	ACO	2D
Z. A. Ali et al. [107]	Time, Environment	Mixed inspiration	MMACO + DE	3D
C. Xia et al. [108]	UAV clustering, Multiple objectives	Guidance mechanism, Adaptive, Bidirectional search	BSAPACO	2D
Z. A. Ali et al. [109]	Time, Trajectory	CM	MMACO	3D
X. Wei and J. Xu [110]	Time, Trajectory	Pheromone update and rollback policies	ACO	2D
H. Li et al. [111]	Trajectory	Visibility matrix, Coverage matrix, Fitness, Reward	AACO	3D
A. Majeed and S. O. Hwang [112]	Environment, Cost	SFS, SWG	ACO	3D
R. K. Dewangan et al. [113]	Environment	DBVF	GWO	2D
R. K. Dewangan et al. [114]	Trajectory	Mapping	GWO	3D
C. Xu et al. [115]	Trajectory	Initialization, Attenuation factor, Position update	IGWO	3D
L. Yang et al. [116]	Trajectory	Multi-population, Chaotic search	MP-CGWO	3D
G. Huang et al. [117]	Trajectory	Update operators, Greedy algorithms, Stagnation compensation	HDGWO	2D
S. Jiaqi et al. [118]	Trajectory	Spiral update position, Adaptive adjustment	AP-GWO	3D
J. Wu et al. [119]	Time	Intersecting mutation operator, PH	MHS	3D

summarizes the contents of the Salp Swarm Algorithm, Ant Colony Optimization algorithm, Gray Wolf Optimization algorithm and Harmony Search algorithm in our review.

4.2. Machine Learning Algorithm

The machine learning algorithm mainly simulates or realizes human learning behavior, transforms the UAV formation trajectory planning problem into a decision-making problem, and formulates optimal or near-optimal search strategies through continuous learning and interaction in complex environments. With the rapid development of multi-agent algorithms, machine learning algorithms have gradually begun to be applied in UAV formation trajectory planning. The machine learning algorithms currently used for UAV formation trajectory planning include the neural network (NN) algorithm, reinforcement learning (RL) algorithm and deep reinforcement learning (DRL) algorithm.

4.2.1. Neural Network

The neural network (NN) algorithm is based on the information obtained by each UAV sensor, and it quickly obtains the actions that the UAV should take. The neural network has a nonlinear complex network structure composed of a large number of nonlinear unit connections. By simulating the control and feedback functions of the human brain function, a nonlinear mapping system is formed to obtain the mapping relationship between the state space and the action space; then, it completes the UAV formation trajectory planning through its own powerful learning ability and rapid planning ability. Figure 22 is a neural network model.

Xia and Yudi [120] designed a fast trajectory planning method using an improved neural network algorithm. This method combined a dynamic adjustable step size with a neural network and added adaptive learning factors for trajectory planning, which solved the problem that the trajectory of a traditional neural network algorithm may not be optimal in the presence of threats.

Sanna et al. [121] proposed a method to cover the trajectory planning problem of UAVs driven by artificial intelligence, which combined a distributed artificial neural network (ANN) and A* algorithm to solve the problems of inadequate grid resolution and low trajectory efficiency of traditional methods.

4.2.2. Reinforce Learning

The reinforcement learning (RL) algorithm is a new learning method which combines dynamic programming with supervised learning. The reinforcement learning algorithm keeps learning in the interaction with the environment, implements the “reward–punishment” mechanism, maximizes the reward index through the feedback evaluation, and realizes the optimal decision output in the UAV formation trajectory planning. Figure 23 shows a reinforcement learning (RL) model.

Luo et al. [122] proposed a strategy-based Deep-Sarsa algorithm, which combined traditional Sarsa and neural network to find the optimal trajectory of UAV formation and improved the poor trajectory planning ability of heuristic algorithm in dynamic environment.

Qie et al. [123] proposed a multi-agent reinforcement learning algorithm. The algorithm combines the Multi-Agent Deep Deterministic Policy Gradient Algorithm (MADDPG) and the Simultaneous Target Assignment and Trajectory Planning (STATP) method to solve the Multi-Agent Deep Deterministic Policy Gradient (MUTAPP) problem in dynamic environments.

Zhao et al. [124] proposed a q-learning based decentralized multi-UAV cooperative reinforcement learning algorithm (DMUCRL). The algorithm enables UAVs to independently choose their cruising strategy and charging scheduling and at the same time share the learning results in the communication network according to the specified time, which solves the problem of efficient content coverage for multi-UAV trajectory planning.

Wang et al. [125] proposed a collaborative trajectory planning method for multiple UAVs based on attentional reinforcement learning. This method uses a neural network with an attention mechanism to generate a UAV cooperative reconnaissance strategy (AM) and uses a reinforcement algorithm to test a large amount of simulation data and optimize the attention network. It solves the problem in which it is difficult for traditional heuristic algorithms to extract empirical models from large sample terrain data in time.

Liu et al. [126] proposed a trajectory planning method based on the fusion of the Sparse Search Algorithm (SSA) and Biologically Inspired Neural Network (BINN). The algorithm uses SSA to find the node with the lowest comprehensive cost and then uses the b-spline curve to fit it; then, it uses the improved BINN method to replan the local trajectory, which solves the problem where the trajectory planning stability of the heuristic algorithm is poor in a dynamic environment, or the trajectory is probably not the optimal question.

4.2.3. Deep Reinforcement Learning

Deep Reinforcement Learning (DRL) algorithms combine reinforcement learning with deep learning. The optimization goal is obtained through reinforcement learning and environment exploration, the system operation mechanism is obtained by using deep learning, and the specific state characteristics and problem solving are obtained at the same time. Relying on the perception ability of deep learning, this method uses a certain strategy to map the current state into corresponding actions; even for high-dimensional raw data input, through continuous iterative learning, the optimal strategy for UAV formation trajectory planning can finally be obtained. Figure 24 is a deep reinforcement learning (DRL) model.

Wang et al. [127] proposed a trajectory control algorithm based on multi-agent Deep Reinforcement Learning, using multi-agent deep deterministic policy gradient (MADDPG) and a low-complexity method to optimize the UAV trajectory, which solves the problem that traditional dynamic algorithms include both integer variables and continuous variables in Mobile Edge Computing (MEC).

Zhang et al. [128] proposed a constrained deep Q-network (cDQN) algorithm. The algorithm formulates the three-dimensional dynamic motion problem of the UAV under the coverage constraint as a constrained Markov decision process (CMDP). Then, it uses prior information to eliminate invalid actions in the deep Q network (DQN) to maximize the unmanned and real-time downlink connection capability between drones, solving the problem of low capacity of the drone formation communication system under coverage constraints.

Bayerlein et al. [129] proposed a dual-deep Q-network (DDQN) based on a multi-agent reinforcement learning (MARL) approach, which transformed the trajectory planning problem into a decentralized partially observable Markov decision process (Dec-POMDP) and then solved it by the Deep Reinforcement Learning method optimizing Dec-POMDP to obtain the optimal trajectory, which solves the problem where the UAV formation is difficult to collect data in distributed IoT devices.

Tianle et al. [130] proposed a multi-UAV trajectory planning method based on Deep Reinforcement Learning. This method uses the improved attention dynamic clustering algorithm to optimize the trajectory planning network model and then combines the Particle Swarm Optimization algorithm (PSO) and the Deep Reinforcement Learning (IA-DRL) algorithm to perform trajectory planning, which solves the slow convergence speed of traditional neural network algorithms.

Table 7. A summary of the content of the survey about machine learning algorithms.

Reference	Challenge	Optimization Criteria	Method	Dimension
C. Xia and A. Yudi [120]	Trajectory	Dynamic step size, Adaptive learning	NN	3D
G. Sanna et al. [121]	Trajectory	Supervised learning	ANN + A*	2D
W. Luo et al. [122]	Environment	Multi-agent	Deep-Sarsa	3D
H. Qie et al. [123]	Environment	STATP	MADDPG	2D
C. Zhao et al. [124]	coverage problem	Adaptive, Information sharing	DMUCRL	2D
T. Wang et al. [125]	Environment	Attention network	AM	2D
Q. Liu et al. [126]	Environment, Trajectory	SSA, B-spline curve	BINN	3D
L. Wang et al. [127]	MEC	Low complexity	MADDPG	2D
W. Zhang et al. [128]	Communication	CMDP	cDQN	3D
H. Bayerlein et al. [129]	Collect Data	Dec-POMDP	DDQN	2D
S. Tianle et al. [130]	Time	Note dynamic clustering	PSO + IA-DRL	2D

summarizes what we surveyed about machine learning algorithms.

5. Local Trajectory Planning Algorithm

The local trajectory planning algorithm belongs to the dynamic programming algorithm. According to the UAV sensors in the UAV formation, the current location information and local obstacle information are collected in real time so as to dynamically plan the optimal trajectory from the starting point to the target point. The algorithms for UAV formation local trajectory planning usually include the artificial potential field method (APF), dynamic window approach (DWA), mathematical optimization algorithm (MOA), and Model Predictive Control (MPC).

5.1. Artificial Potential Field

The artificial potential field method (APF) was first proposed by Khatib as a virtual force method. The artificial potential field method assumes that each UAV is moving in an artificial potential field. For UAVs, the target point generates an attractive field, and obstacles generate a repulsive force field; under the action of the gravitational field and the repulsive field, the UAV generates a feasible trajectory along the direction of the potential field. In general, in order to simplify the calculation, by calculating the negative gradient of the gravitational potential function and the repulsive potential function, the gravitational and repulsive forces on the UAV in the potential field can be obtained, and then the resultant force on the UAV can be obtained. Then, calculating according to the resultant force, each UAV makes the control amount required for attitude adjustment so as to guide the UAV formation to avoid obstacles and complete trajectory planning. Figure 25 is a schematic diagram of artificial potential field forces.

Rasche et al. [131] proposed a trajectory planning method in a 3D environment. This method adds a multi-UAV distributed work and inter-machine communication to the artificial potential field method (APF) and solves the problem of multi-UAV coordination and task assignment when exploring disaster areas.

Li et al. [132] proposed a trajectory planning method combining the artificial potential field method (APF) and Dubins curve. This method introduces the virtual leader UAV into the UAV formation and uses the Dubins curve to plan its trajectory. Then, it uses the APF to plan the trajectory of the wingman and finally completes the trajectory planning of the UAV formation by constraining the flight trajectory of the virtual leader. It solves the problem where the lead aircraft may have out-of-control failure and the UAV is restricted by the turning radius.

Tang et al. [133] proposed an optimized artificial potential field algorithm. This method simulates other UAVs as dynamic obstacles and at the same time introduces the climbing strategy and dynamic step adjustment method into APF, which solves the problems of inter-machine collision and excessive flight step length in traditional APF under the complex space conditions of multiple UAVs.

Chen et al. [134] proposed an improved artificial potential field method (IAPF). This method introduces the judging mechanism of local minimum points and the jump-out mechanism of 90° movement along the target direction into APF; it solves the problems of unreachable targets near obstacles, local minimum points and UAV track oscillations in traditional APF.

Sun et al. [135] proposed a trajectory planning algorithm for dense UAV formations based on an artificial potential field (APF). The algorithm improves the APF by improving the repulsive force model, adding the target exchange algorithm and adding constraints, and it solves the problems of traditional APF trajectory oscillation, unreachable targets and local minimum points.

Dongcheng and Jiyang [136] proposed a multi-UAV trajectory planning method based on the improved artificial potential field method (IAPF). This method introduces an improved distance factor potential field function and dynamic step size adjustment method into APF, and at the same time, it considers the influence of the force between UAVs; it solves the problem where the traditional APF target cannot be reached: it is easy to fall into a local minimum, and the trajectory shakes the problem.

Wang et al. [137] proposed a collaborative formation distributed trajectory planning method based on the improved artificial potential field (IAPF) and consensus theory. This method introduces the dynamic model and communication network topology, coordination gain factor, repulsion force and planning angle influence factor into APF. Then, the position and velocity variables in the consensus protocol are improved to solve the problem of UAV formation in 3D obstacle environment trajectory planning and position–velocity consistency problems.

Dai et al. [138] proposed a consensus algorithm for distributed cooperative formation trajectory planning. The algorithm introduces the potential field function including distance items and communication effects into APF (IAPF) and then combines the second-order system dynamic model, consistency theory and IAPF for UAV formation collaborative trajectory planning. This solves the problems that traditional APF encounters in UAV including poor convergence problems related to consistency, relative distance and velocity in formation cooperative trajectory planning.

Li et al. [139] proposed a new trajectory planning method using the improved artificial potential field algorithm (IAPF). This method increases the repulsive force between UAVs and defines the front center of mass of the cluster as another source of gravity, which solves the problem where the traditional APF target is unreachable and easily falls into a local minimum.

Wei et al. [140] proposed a UAV time-varying formation trajectory planning method with an interactive topology. This method introduces the improved potential field into APF (IAPF) and then combines distributed time-varying formation control, IAPF and model predictive control (MPC) for UAV formation trajectory planning. It solved the problem where the UAV formation has poor ability to deal with complex environments during flight.

Wang et al. [141] introduced a multi-UAV trajectory planning method based on an adaptive extended potential field. In this method, the gravitational influence factor and the repulsive force influence factor are introduced into the layered potential field function, and the auxiliary force is added to improve the APF. It solves the problems related to the slow convergence speed of a layered potential field algorithm and unreachable target of a traditional APF, easily falling into local minimum, inability to avoid obstacles and lack of a trajectory optimization strategy.

Pan et al. [142] proposed a trajectory planning method based on artificial potential functions (IAPF) for multi-UAV systems. This method introduces the improved artificial potential function (IAPF) of the rotating potential field and at the same time adds the leader–follower UAV model for UAV formation trajectory planning. It solves the problems of poor stability, local minimum and oscillation in the traditional APF system.

Table 8. Summary of the methods of artificial potential field in the survey.

Reference	Challenge	Optimization Criteria	Method	Dimension
C. Rasche et al. [131]	UAV clustering	Distributed, UAV communication	APF	3D
X. Li et al. [132]	UAV	Constrain virtual leads	APF + Dubins	2D
J. Tang et al. [133]	UAV clustering, Trajectory	Climb strategy, Dynamic step size	APF	3D
H. Chen et al. [134]	Trajectory	Judging mechanism, 90° jump mechanism	IAPF	3D
H. Sun et al. [135]	Trajectory	Improve the model, Target exchange, Add constraints	APF	3D
L. Dongcheng and D. Jiyang [136]	Trajectory, UAV clustering	Improved function, Dynamic step size	IAPF	3D
N. Wang et al. [137]	Environment, UAV clustering	Communication topology, Coordination gain, Impact factor	IAPF	3D
J. Dai et al. [138]	Trajectory, UAV clustering	Second-order model, Consistency theory	IAPF	3D
R. Li et al. [139]	Trajectory	Increase the repulsive force, Gravity source	IAPF	2D
B. Wei et al. [140]	Environment	Distributed time variation	IAPF + MPC	2D
N. Wang et al. [142]	Trajectory	Impact factor, Auxiliary force	IAPF	3D
Z. Pan et al. [141]	Trajectory	Rotational potential field, Leader–Follow	IAPF	3D

summarizes the contents of our survey regarding artificial potential field methods.

5.2. Dynamic Window Approach

The dynamic window method (DWA) is a classic UAV local trajectory planning algorithm. It determines a sampling velocity space that satisfies the hardware constraints of the UAV in the velocity space according to the current position state and velocity state of the mobile UAV and transforms the local trajectory planning problem into a motion constraint problem in space. Then, it calculates the UAV trajectory of the drone moving for a certain period of time under these speed conditions and evaluates the trajectory through the evaluation function. It selects the trajectory with the best evaluation and the corresponding speed as the movement speed of the UAV; finally, through the motion constraints, it selects the locally optimal trajectory and so on until the UAV reaches the target point. Figure 26 is a schematic diagram of the DWA velocity vector space.

Zhang et al. [143] proposed a multi-UAV consistent formation trajectory planning algorithm based on an improved dynamic window method (DWA). The algorithm introduces a new rotation cost evaluation function, A* algorithm and azimuth-related variable weight factors to improve DWA and finally adds a leader–following UAV model for UAV formation trajectory planning. It solves the problems of frequent large-angle rotation and low search efficiency in the traditional DWA algorithm.

5.3. Mathematical Optimization Algorithm

The mathematical optimization algorithm (MOA) is based on the established UAV trajectory planning model, using nonlinear optimization, mixed integer linear programming (MILP), mixed integer nonlinear programming (MINLP) and dynamic programming (DP) to solve the optimal control problem into an easily solvable model to generate feasible trajectories for formation UAVs. Figure 27 is a mathematical optimization algorithm (MOA) model.

Bellingham et al. [144] proposed CPLEX, which is a collaborative trajectory planning method for UAV formation. This method combines the failure probability of each UAV with the selected task and puts forward a new formula to solve the problem of mission failure caused by UAV loss in UAV formation trajectory planning.

Maza and Ollero [145] proposed a method based on polygonal area decomposition and efficient coverage (PADEC). This method introduces the concepts of regional division and computational scanning into the UAV formation coverage trajectory planning and solves the problem of multi-UAV cooperative search.

Dehghan et al. [146] proposed a trajectory planning method based on multi-UAV for RF source localization. The method combines the differential received signal strength indicator (DRSSI) method, the extended Kalman filter (EKF) and the Cramer–Rao lower bound (CRLB) objective function; finally, using the local value of the CRLB in the current waypoint and the next possible waypoint to determine the optimal trajectory, it solves the problem of slow convergence of the heuristic algorithm.

Wang et al. [147] proposed a decoupled sequence convex programming (SCP) collaborative trajectory planning method for UAV formations. This method represents the UAV formation trajectory planning problem as a non-convex optimal control problem; then, it uses the decoupled sequence convex programming (SCP) method to parameterize the problem into a non-convex programming sub-problem and solves it in parallel to obtain the UAV best trajectory for formation coordination tasks. The problem of insufficient efficiency of the sequence quadratic programming algorithm (SQP) in UAV formation cooperative trajectory planning is solved.

Causa et al. [148] proposed an algorithm for multi-UAV trajectory planning under heterogeneous Global Navigation Satellite System (GNSS) coverage. The algorithm conceives the multi-UAV formation as a reconfigurable distributed system and then introduces methods such as edge definition and cost evaluation, custom target assignment, UAV timing and polynomial trajectory (PT) for formation trajectory planning. It solves the problem of low efficiency of UAV formation trajectory planning task assignment in a three-dimensional heterogeneous environment.

Pengfei et al. [149] proposed an optimal trajectory planning method for multiple UAVs based on the pseudospectral method. This method uses the pseudospectral method to transform the optimal control problem with complex constraints into a nonlinear programming problem; at the same time, it uses the distributed solution and the Nash optimal coordination strategy to solve the multi-UAV trajectory planning problem under complex and multi-constrained conditions.

Li et al. [150] proposed a trajectory planning method for multi-UAV scan coverage with minimum time maximum coverage. This method introduces a Weighted Target Scan Coverage (WTSC) algorithm for greedy target assignment, which solves the problem of insufficient task time and coverage performance of two algorithms, CycleSplit and G-MSCR [151].

Xia et al. [152] proposed a gradient-based sequential minimum optimization (GB-SMO) algorithm, which uses time segmentation instead of traditional waypoint segmentation to establish a trajectory optimization model and introduces virtual line segments to adapt to the trajectory length. Constraints are converted into cost functions and then minimized using GBSMO, which solves the problem of insufficient computational performance of commonly used trajectory planning algorithms considering constraints.

Wang et al. [153] proposed a real-time trajectory planning method for UAV formation transformation based on safe flight corridors, introducing safe flight corridors to avoid UAV collisions, while considering time and space efficiency models. They addressed an issue where drones could collide when performing a formation change.

Cho et al. [154] proposed a multi-UAV search trajectory planning method covering nodes in the shortest time. The method introduces a mixed integer linear programming (MILP) model of hexagonal grid decomposition and at the same time uses the optimization time as a search function to obtain the trajectory of the formation UAVs in iterations. The trajectory planning problem of UAV formation searching for catastrophic marine accidents is solved.

Sun et al. [155] proposed a 4D trajectory planning method with temporal and spatial constraints. This method transforms the arrival time into state adaptation and at the same time transforms the collaborative penetration trajectory planning into a single-objective optimization problem. Then, it uses the multi-leader search distribution estimation algorithm (MLSEDA) to solve the problem, which solves the trajectory planning problem of UAV cooperative penetration.

Cheng et al. [156] proposed a decentralized multi-UAV trajectory planning method for obstacle environments. In this method, the UAV rendezvous trajectory planning problem under constraints is modeled as a non-convex optimal control problem, and then, the consensus protocol and sequential convex programming two-layer collaborative framework are used to solve the UAV formation trajectory. It solves the problems of low calculation efficiency and poor adaptive ability of the traditional UAV formation trajectory planning method.

Yanmaz [157] proposed a hybrid planner that uses joint optimization methods, decoupling optimization methods, and hybrid methods to calculate UAV formations. They generated feasible trajectories under two different requirements of time constraints and connectivity, solving the problem where the connection parameters are difficult to trade off and the resource utilization rate is low in the formation task.

Table 9. Summary of dynamic windowing methods and mathematical optimization algorithms in our survey.

Reference	Challenge	Optimization Criteria	Method	Dimension
S. Zhang et al. [143]	Trajectory, Time	New cost function, Variable weight factor, Lead–follow	A* + DWA	2D
J. S. Bellingham et al. [144]	UAV	Failure probability, Task selection	CPLEX	2D
I. Maza and A. Ollero [145]	UAV clustering	Area divided and conquer, Computational scan	PADEC	2D
S. M. M. Dehghan et al. [146]	Trajectory	EKF, CRLB	DRSSI	2D
Z. Wang et al. [147]	Trajectory	Non-convex optimal, Parallel solution	SCP	2D
F. Causa et al. [148]	Environment	GNSS, Custom target allocation	Multiple step path	3D
J. Pengfei et al. [149]	UAV, Environment	Distributed solutions and Nash optimal coordination	Pseudo-spectral Method	3D
J. Li et al. [150]	Trajectory	Greedy goal assignment	WTSC	2D
Q. Xia et al. [152]	Computing performance	Time division, Constraint transformation	GB-SMO	3D
G. Wang et al. [153]	Environment, UAV clustering	Efficiency model	Safe flight corridor	2D
S.-W. Cho et al. [154]	Environment	Hexagonal grid decomposition	MILP	2D
P. Sun et al. [155]	Environment, Time	State adaptation, Single objective optimization	MLSEDA	4D
Z. Cheng et al. [156]	Trajectory	Consensus protocol, Sequential convex programming	Non-convex optimal control	3D
E. Yanmaz [157]	Resource utilization	Joint optimization, Decoupling optimization, Hybrid method	Hybrid planner	2D

summarizes the contents of our survey about the dynamic window method and mathematical optimization algorithm.

5.4. Model Predictive Control

Model Predictive Control (MPC) is a typical online planning method with planning and execution at the same time. In other words, it is a rolling time window approach. In the local planning process, the algorithm first updates the environmental information in the current trajectory search domain and predicts the information change trend in the trajectory search domain on this basis. Then, it searches out the local reference trajectory according to the motion model of the UAV and executes. In the process, the trajectory is corrected according to the motion constraints and control errors of the UAV so as to make full use of real-time feedback information to gradually generate a global trajectory. Figure 28 is a schematic diagram of MPC.

Oh et al. [158] proposed a decentralized nonlinear model predictive control trajectory planning strategy (DNMPC), which introduces filtering technology and decentralized optimization into MPC to realize UAV formation for trajectory planning in relay communication to solve the problem of poor connectivity of the wireless network between the fleet of naval ships.

Cui et al. [159] proposed a multi-object tracking algorithm based on task assignment consensus. It uses the dynamic task allocation model to update the tracking tasks and uses the intermittent asynchronous communication principle to realize the sharing of local observation information. At the same time, it uses the MPC algorithm to complete the tracking trajectory planning and solved the problem of UAV formation tracking multiple moving targets within a limited communication range.

Wu et al. [160] proposed a UAV trajectory planning model (Poc-KF) based on collision probability and Kalman filter. The model uses the collision probability algorithm and the Kalman filter algorithm for UAV collision probability calculation and formation state estimation, and it calculates feasible trajectories for UAV formation in real time. It also addressed possible trajectory conflicts in high-density drone formations.

Wu et al. [161] proposed a behavior tree (BT) model. The specific operation is to combine the model prediction with the decision tree to obtain the behavior tree (BT). Then, they add the virtual target-based tracking (VTB-T) method and use the behavior tree (BT) organization trajectory planning method to construct a feasible trajectory for the UAV. The problem of multi-UAV trajectory planning in the target tracking scenario is solved.

Wang et al. [162] proposed a new trajectory planning algorithm for model predictive control (NMPC). They introduced a virtual target to move along the patrol trajectory at a predetermined speed and designed a decentralized estimator for each UAV to estimate the state of the virtual target. Then, they used a new model prediction algorithm to calculate a feasible trajectory for the formation of UAVs, which addresses the problem of formation reconstruction and trajectory planning in multi-UAV aerial patrol missions.

Chen and Liu [163] proposed a model for predicting flushing force under drones (PMDFF). It regards each UAV as a virtual structure to form a cylindrical UAV model and then uses the cluster and Optimal Interactive Collision Avoidance (ORCA) algorithm to solve the collision-free trajectory. They addressed an issue where downwash effects have an impact on neighboring drones in UAV formation trajectory planning.

Table 10. Summary of MPC algorithms in our survey.

Reference	Challenge	Optimization Criteria	Method	Dimension
H. Oh et al. [158]	Communication	Filtering technology, Dispersion optimization	DNMPC	2D
Y. Cui et al. [159]	Communication, Multiple objectives	Dynamic update, Intermittent asynchronous communication	MPC	2D
Z. Wu et al. [160]	UAV clustering	Probability calculation, KF	Poc-KF	2D
W. Wu et al. [161]	Environment	VTB-T	BT	3D
Y. Wang et al. [162]	UAV clustering, Trajectory	Virtual target, Decentralized estimates	NMPC	3D
C.-C. Chen and H. H. Liu [163]	UAV clustering	Virtual structure, ORCA	PMDFF	3D

summarizes the contents of our survey on model predictive control algorithms.

6. Problems of UAV Formation Trajectory Planning Algorithm

With the advancement of low-airspace reforms and the innovation of artificial intelligence and information technology [164], new theories and new achievements related to swarm intelligence continue to emerge, and the improvement of UAV formation trajectory planning algorithms is facing many challenges.

6.1. Physical Constraints of UAV Formation

In the process of trajectory planning, the UAV in the formation is usually simplified into three degrees of freedom particles, ignoring its own constraints such as minimum turning radius, rolling angle and other restrictions on the running state. As a result, the current trajectory planning algorithm is difficult to adapt to the UAV with high maneuverability, there are errors between the release route and the planned route when the actual formation UAV performs the task, and the execution effect will also be affected.

6.2. Performance Problems of UAV Formation Carrying Equipment

In the UAV formation trajectory planning algorithm, the performance of the UAV itself is not considered enough. An insufficient consideration of problems such as fuel consumption, load, and onboard sensor errors in practice makes it difficult to accurately detect complex environments, and the trajectory planning that can be achieved by simulation cannot be realized or has poor robustness in the actual environment.

6.3. Complex Environment Modeling Problem

Most of the current formation trajectory planning algorithms are hypothetical ideal obstacles, but the actual operating environment of UAVs is complex and diverse, especially the detection and description of scenes such as complex concave obstacle environments and dense dynamic obstacles, which need further exploration.

6.4. Algorithm Real-Time Problems

Realistic environmental information is usually time-varying. Regarding UAV formation trajectory planning in an unknown environment, the success rate of trajectory planning strategies used by traditional algorithms and local trajectory planning algorithms in the face of emergencies and dynamic environments is low; in addition, the amount of calculation is large, and the trajectory is not optimal. It is difficult for drones to complete real-time trajectory updates.

6.5. Adaptability of UAV Formation Route Planning Algorithm

When performing formation trajectory planning in a complex dynamic environment, there is a lot of information exchange between UAVs, which leads to an increase in the amount of calculations, and intelligent algorithms are prone to fall into problems such as local optima that exist in themselves.

6.6. UAV Formation Communication Problem

With the development of science and technology, the application scenarios of drones in the future will become more and more complex. In certain scenarios, there will be communication interference problems, which will cause the UAV to fail to work normally and even cause irreversible damage.

7. Future Research Focus and Direction

7.1. Improved Model

Constraints such as six degrees of freedom, minimum turning radius, roll angle, and the onboard sensor error of each UAV are added to the modeling to enhance the robustness of actual control. For complex environment modeling, the influence of multiple factors in the complex environment on the effect of trajectory planning must be considered; reliable and accurate data must be obtained through specific measurements or the use of accurate 3D maps, and at the same time, the data must be used to verify the model to make the simulation closer to reality. It can also be better applied to the actual platform in the future.

7.2. Real time Planning

In the face of increasingly complex environments and tasks, in order to meet the requirements of fast optimal solution, computational complexity, convergence speed and rationality, the computational memory is allocated reasonably. Executing trajectory planning algorithms to generate efficient trajectories in the case of limited computing power of UAVs is of great significance for UAV formations to complete tasks in complex environments.

7.3. Fusion Algorithm

It is an important current research trend to integrate different types of trajectory planning algorithms to make up for the defects and deficiencies of existing single methods.

For example, the local trajectory planning method can be combined with artificial intelligence technology represented by machine learning to complement each other. On the one hand, it can solve the problem of easy falling into local optimum in the local trajectory planning method, and on the other hand, it can also make up for the poor real-time performance of the machine learning-based track planning algorithm to a certain extent. It is also possible to combine the characteristics of heuristic algorithms and machine learning algorithms that are easy to integrate with each other to help analyze the performance of the algorithm and expand the application range of the algorithm. At the same time, experiments show that the hybrid algorithm has better adaptability.

7.4. New Algorithm

At present, the existing UAV formation trajectory planning algorithms have more or less defects. Therefore, developing an algorithm that reduces computational requirements, saves time, allows real-time planning, and is more efficient in terms of energy is also a direction worth exploring.

7.5. Fault Tolerance Mechanism

Since the maneuvering area of each UAV is very small, once a collision occurs, it will affect the adjacent UAVs, and a chain effect will be generated between the UAV clusters, which will cause the mission to fail. Therefore, the fault-tolerant redundancy mechanism is an important link to ensure the safe operation of the UAV system. At present, there is no fault-tolerant mechanism design for the core and weak links of the trajectory planning algorithm so as to improve the fault-tolerant ability of unmanned formation flight. In future research, we should focus on the design of the fault-tolerant mechanism when the function of the UAV fails to avoid uncontrollable events.

7.6. Hybrid Frame

It is unrealistic to use a centralized framework to solve problems in the process of carrying out missions in large-scale UAV formations. Therefore, a hybrid framework should be adopted; how to design an appropriate conflict resolution mechanism and how to effectively combine UAV formation trajectory planning with collaborative control to generate feasible flight trajectories are topics worthy of further study.

7.7. Behavior Decision

Recently, UAV swarm-to-swarm dynamic confrontation has become a hot research direction. At the same time, the autonomous decision-making behavior of UAV formations such as autonomous reconnaissance and detection, autonomous target recognition, and autonomous task coordination in complex terrain such as cities and mountainous areas can effectively reduce the loss of manpower and material resources. How to plan and generate the optimal trajectory of UAV formation from the perspective of game theory is undoubtedly a problem worthy of further exploration.

7.8. Allocation of Resources

In the future, drone formations will be widely used in battlefields and anti-terrorism operations. The environment in which UAVs perform these tasks may become very complex, resulting in increased mission difficulty, and the environment may provide extremely strong support for UAV formations, such as satellite links and energy supplies for continuous flight. How to reasonably allocate available resources to each UAV during mission execution is also a challenging problem.

7.9. Communication Networking

The confrontation between UAVs has become more and more information-based. When the UAV formation is performing tasks, it is necessary to ensure that the UAVs can communicate and share information normally and at the same time deal with external communication interference. Although some scholars have noticed related problems, the problem of how to solve communication interference in UAV formation trajectory planning is still a difficult problem.

8. Conclusions

From the perspective of the two key elements of global planning and local planning, this paper proposes a framework for UAV formation trajectory planning algorithms, comprehensively classifies different types of algorithms, and describes different types of algorithms and their variants in a unified way. Then, a review and statistical analysis were carried out on the basis of classification. We found the shortcomings in the UAV formation trajectory planning algorithm methods and put forward the focus and direction of future research. This paper provides reference information for the next step of research work for researchers and workers engaged in UAV formation flight-related work. We believe that with the innovation of various theories and the iterative development of technologies, the UAV formation trajectory planning algorithm will enter a new era.