Gusts Encountered by Flying Vehicles in Proximity to Buildings
Abstract
1. Background and Objectives
2. Turbulence
3. Prior Gust Models
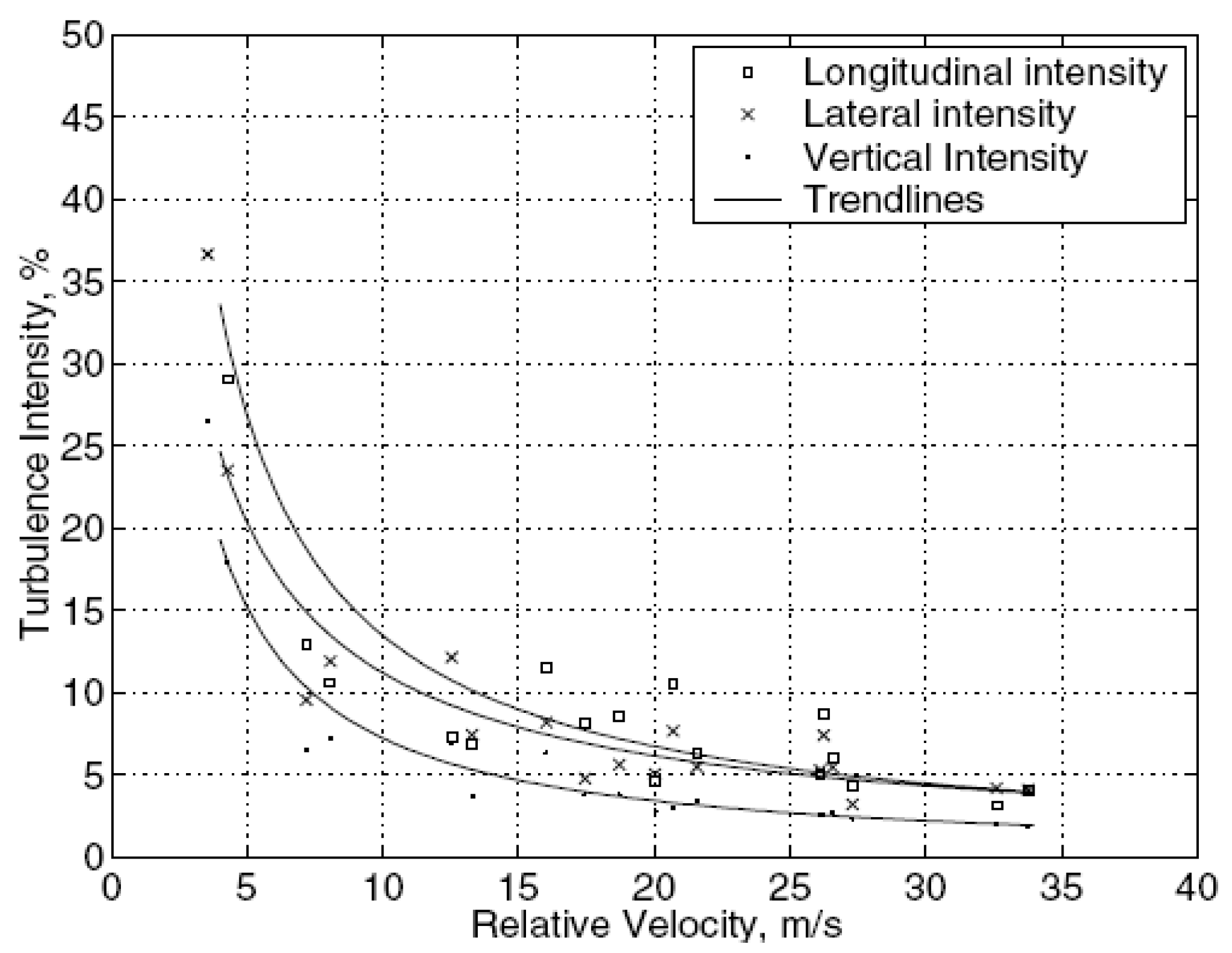
4. Turbulence Experienced by Moving Vehicles (Relative Turbulence)
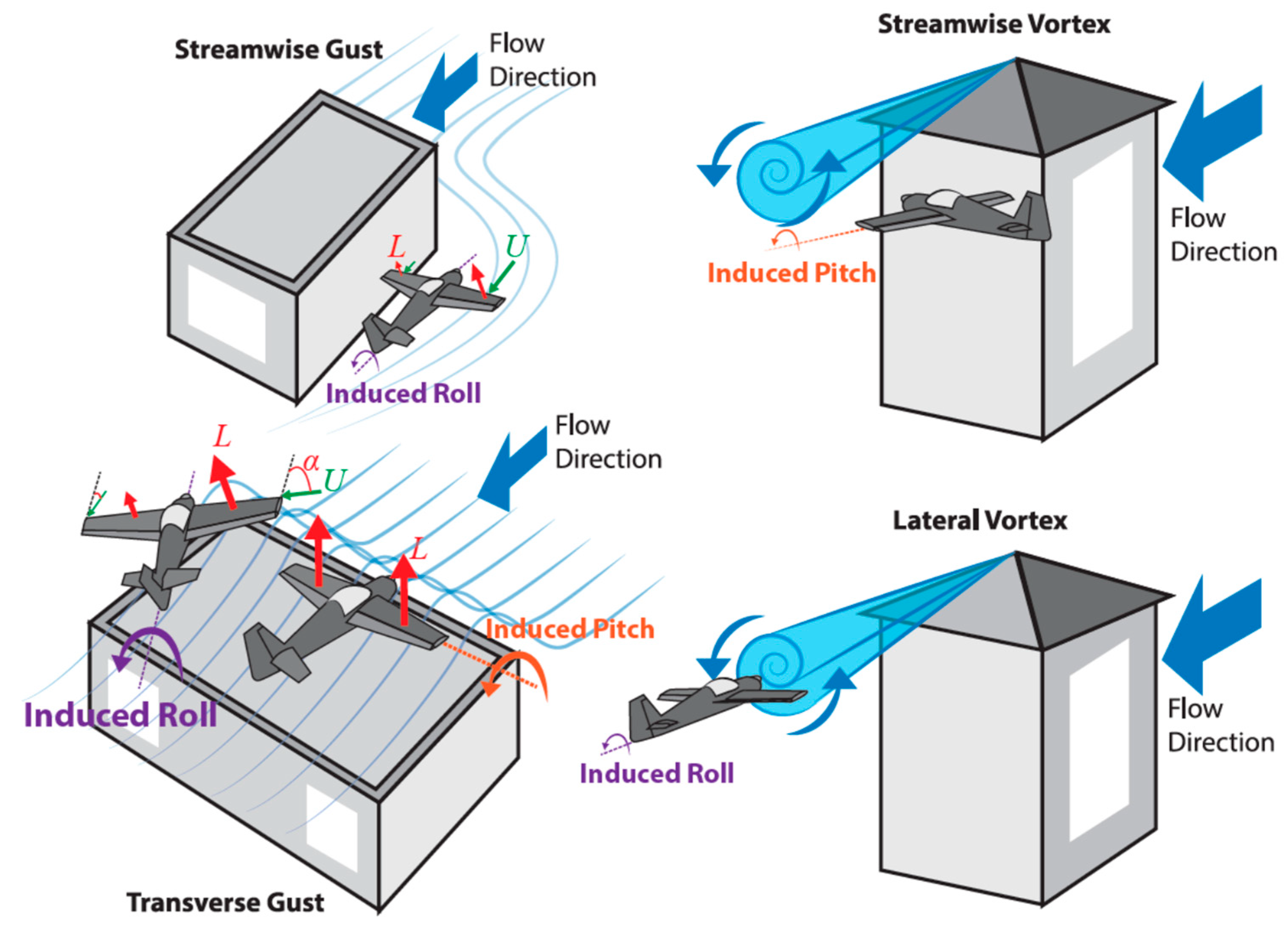
5. Relevant Gust Characteristics
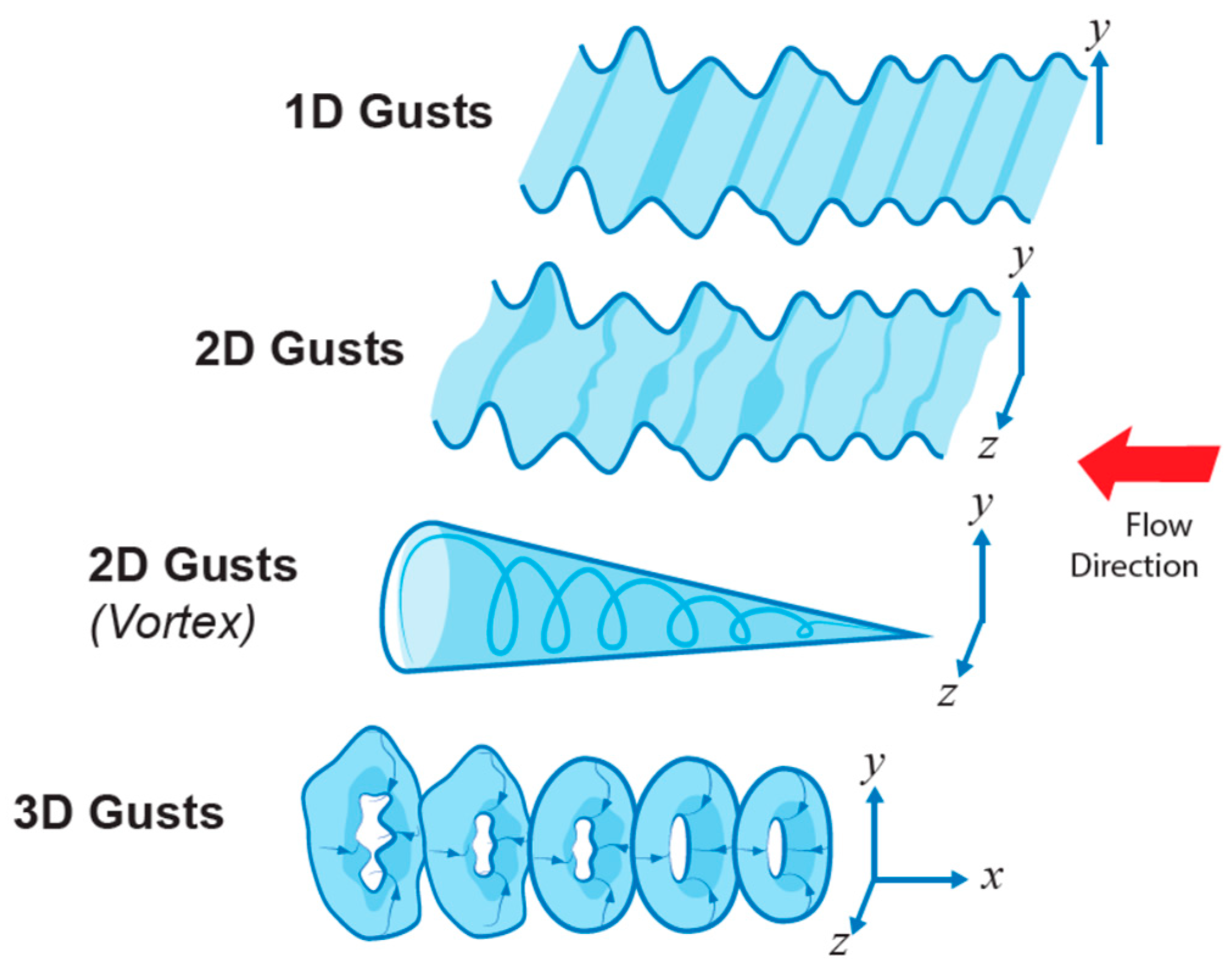
6. Gust Taxonomy
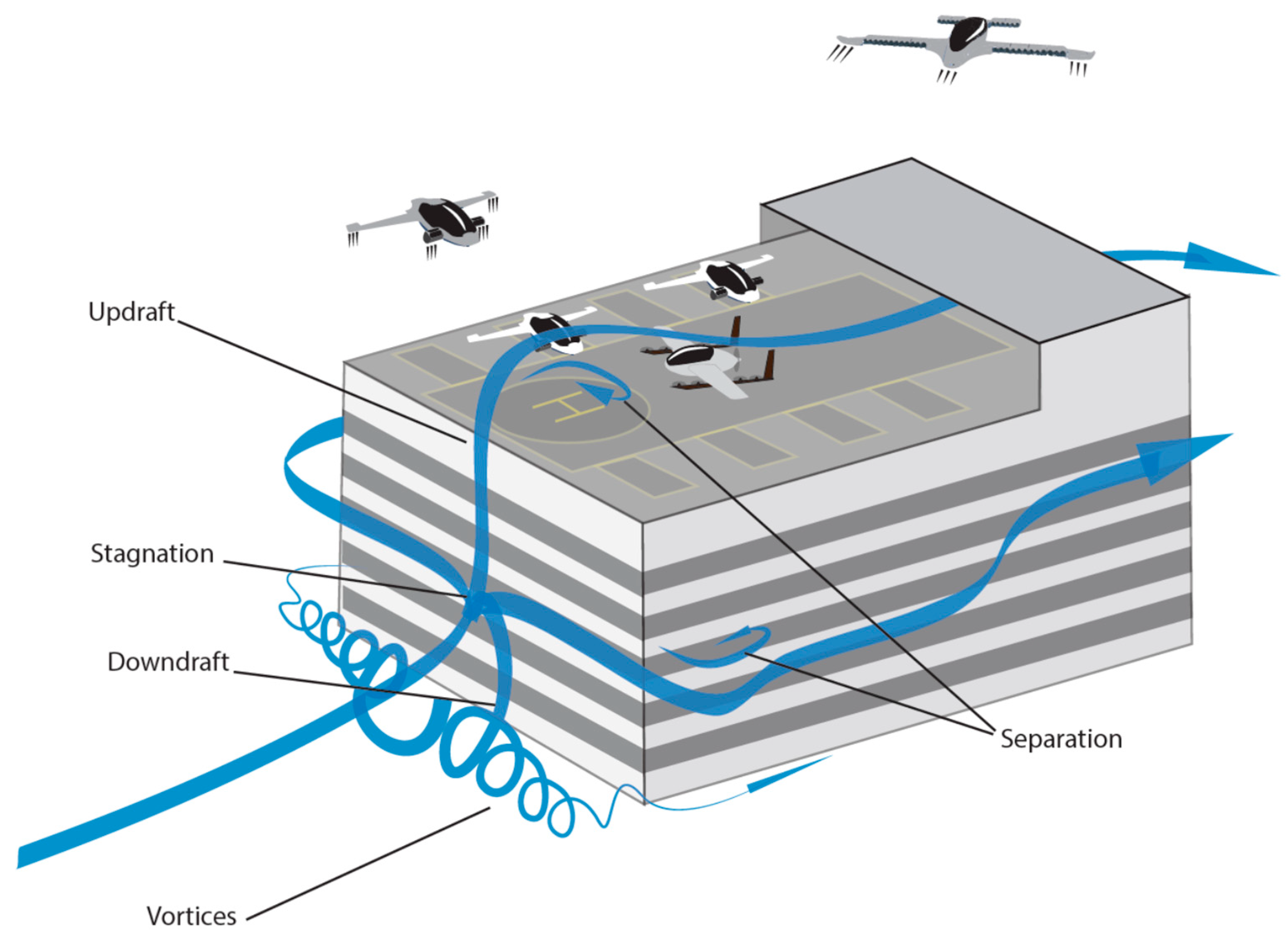
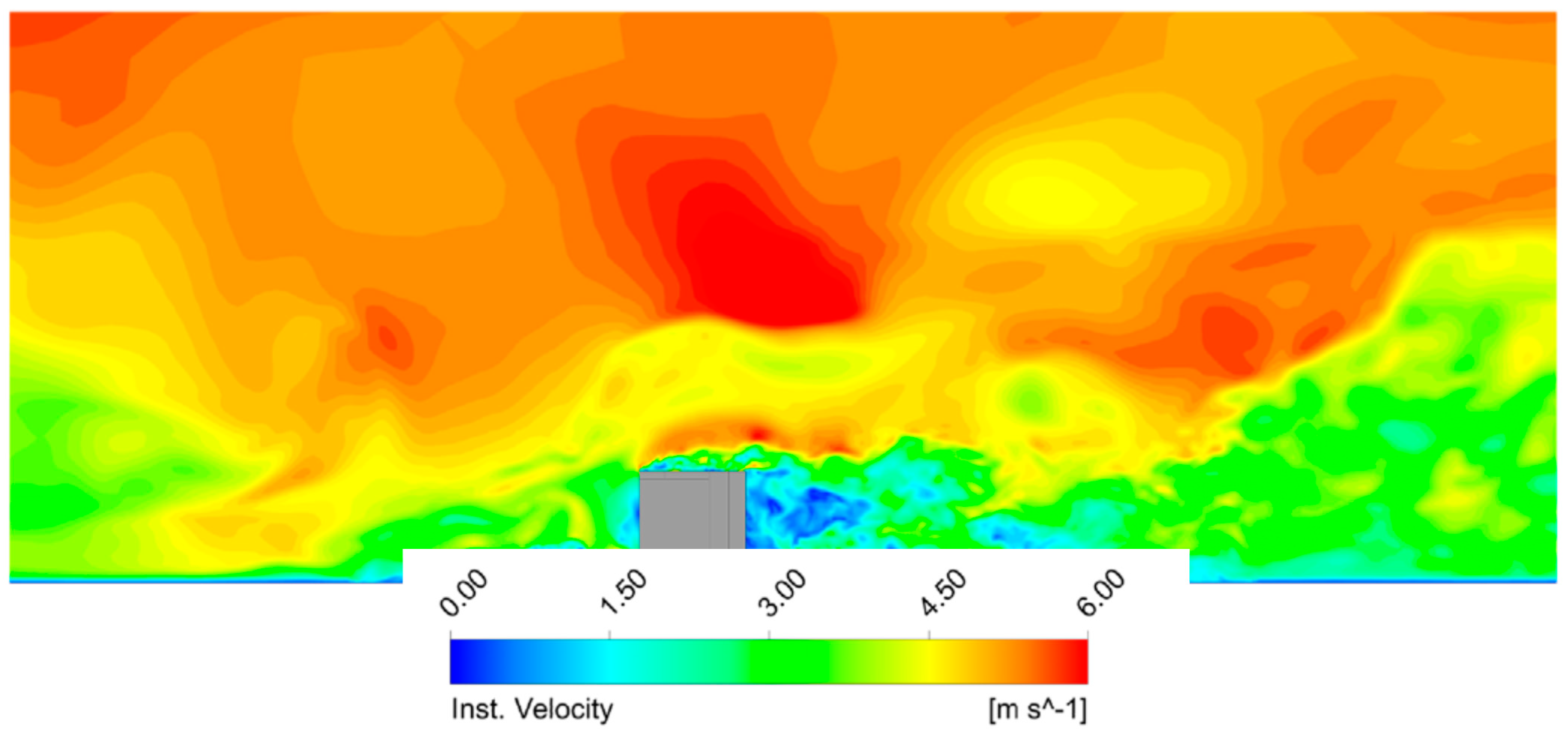
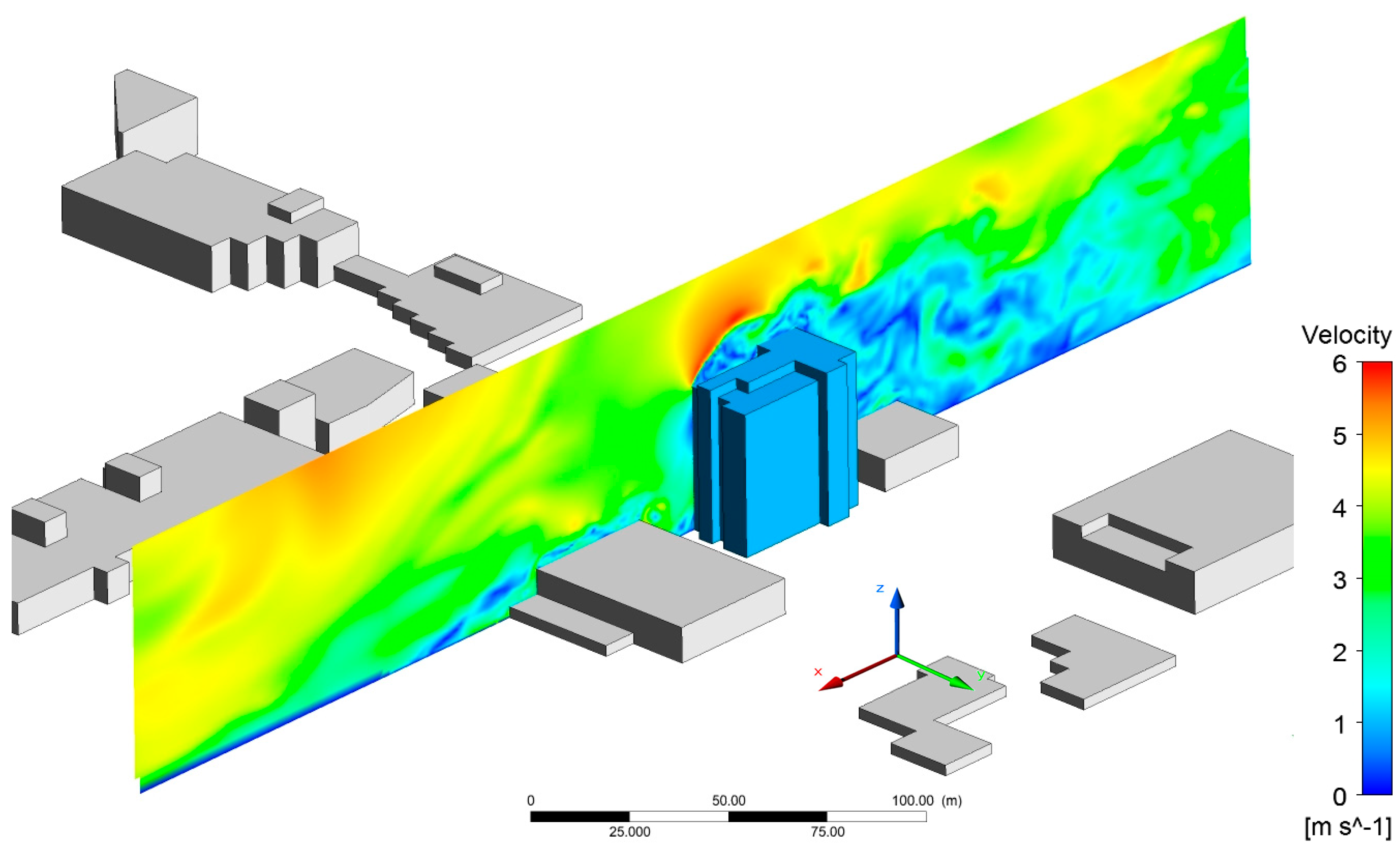
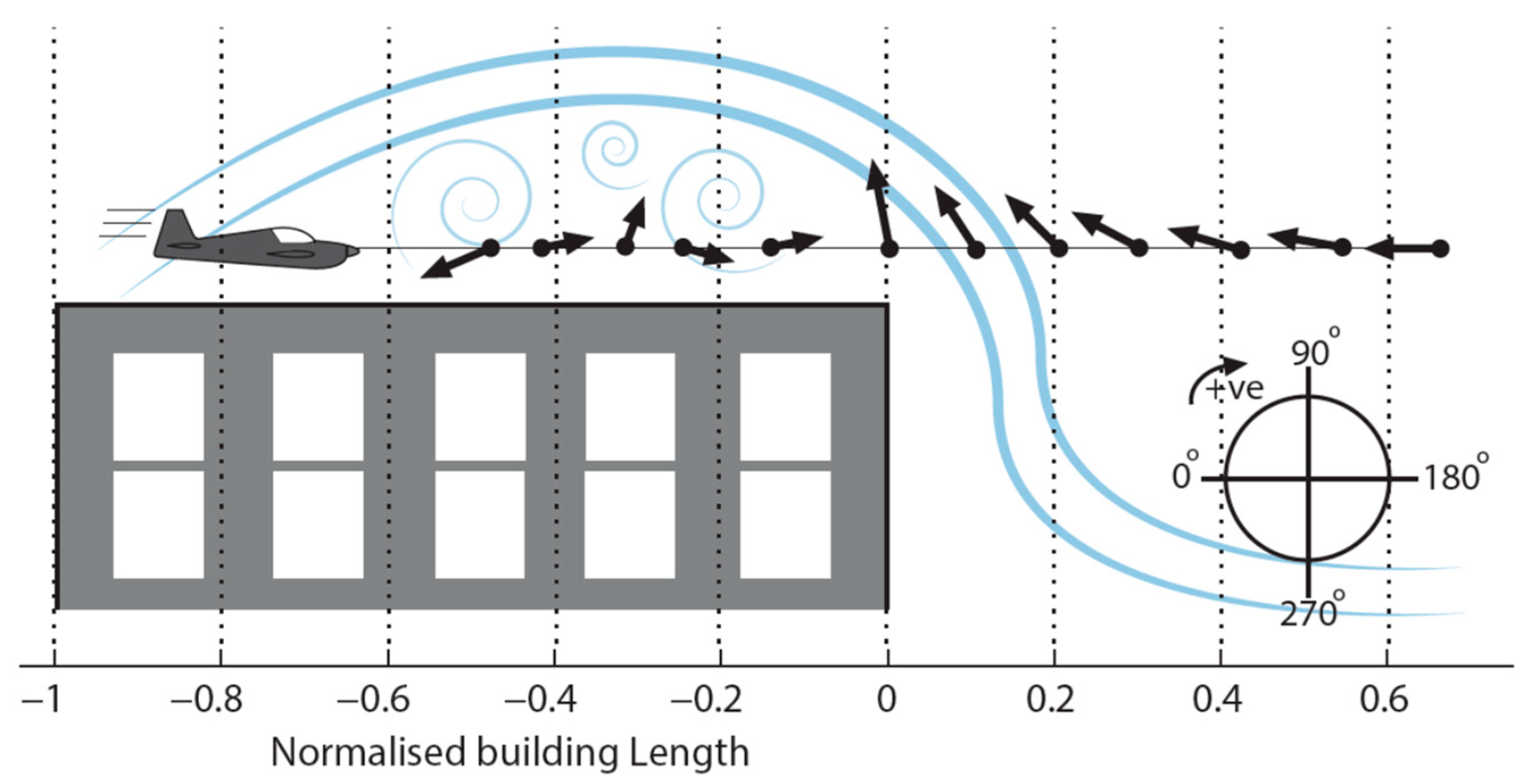
7. Severe Gusts around Buildings: Case Studies
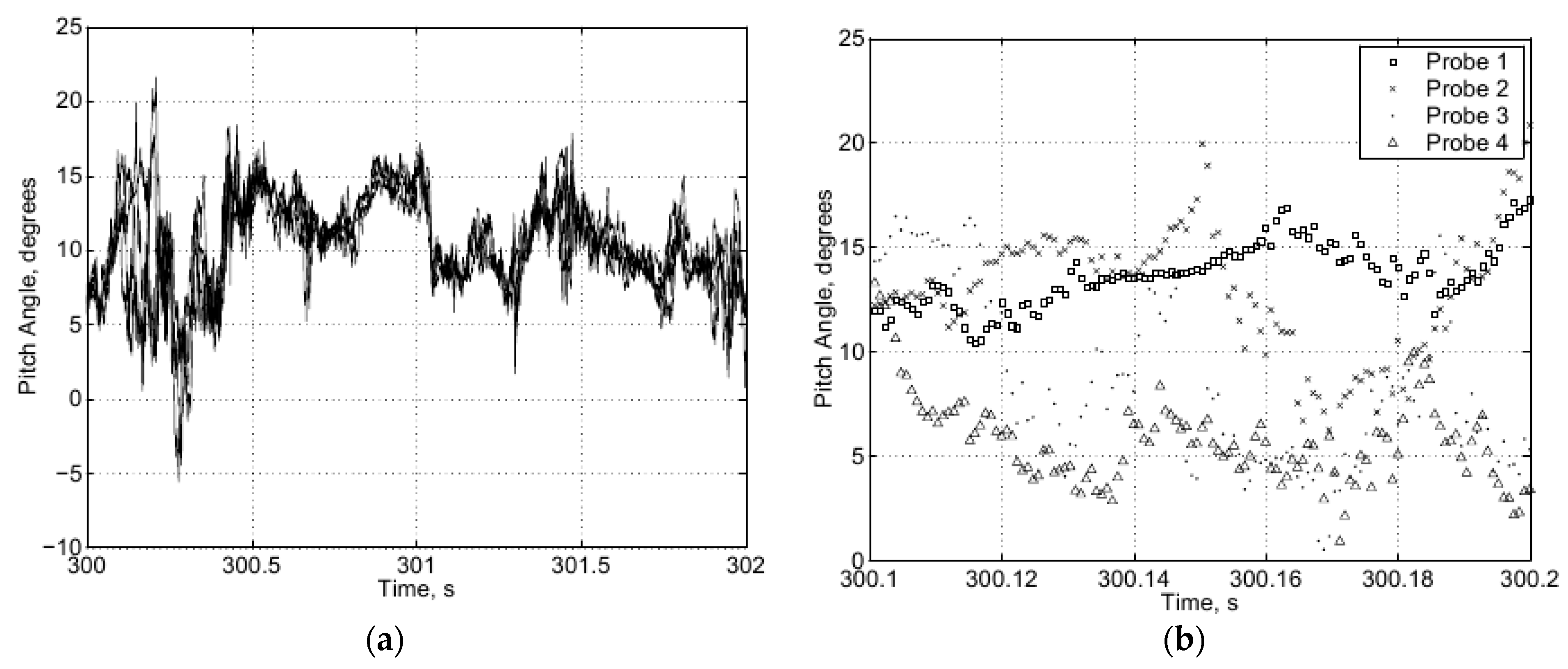
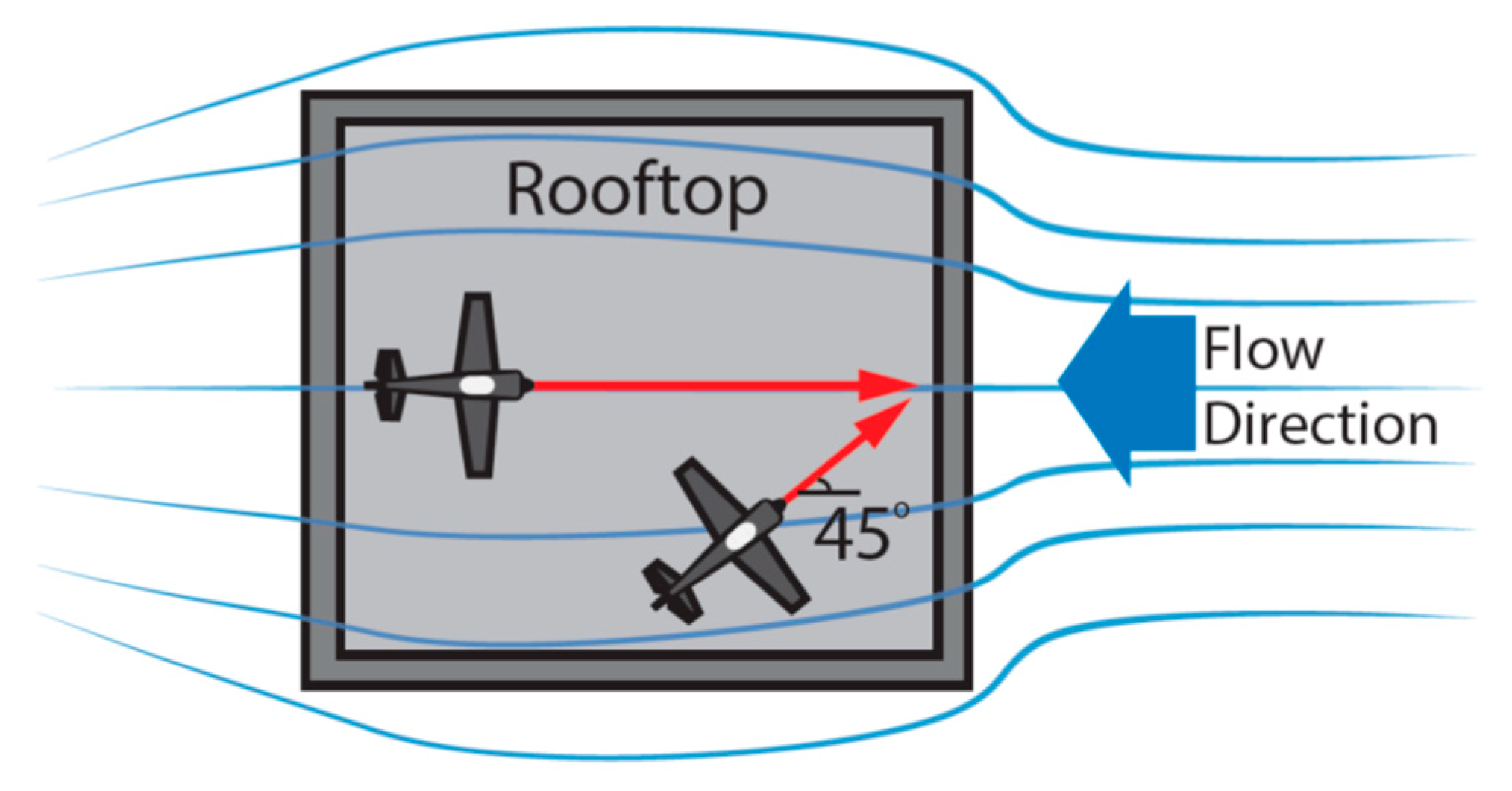
7.1. Flight Trajectory Modelling
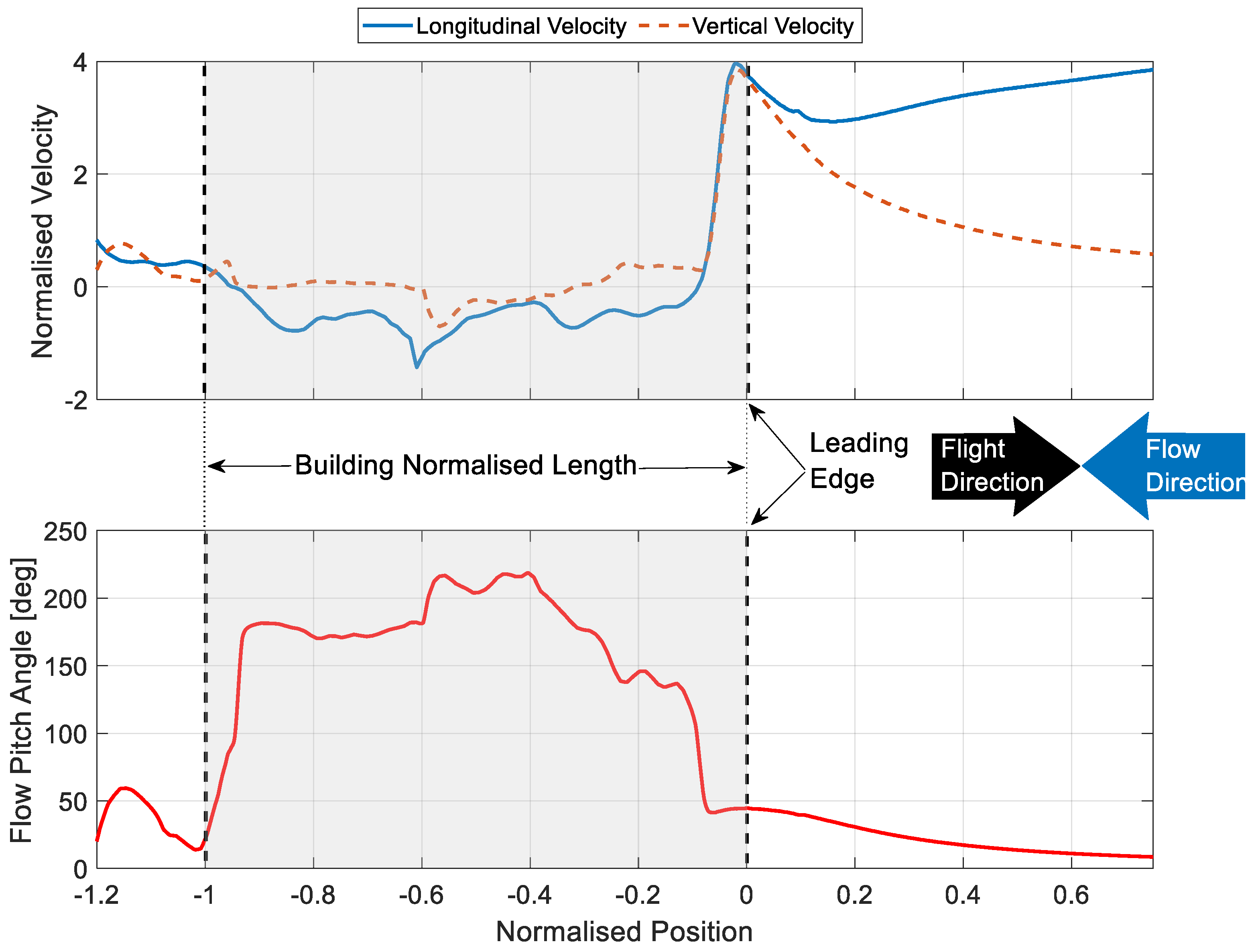
7.2. Estimations of Perceived Gust for Fixed-Wing
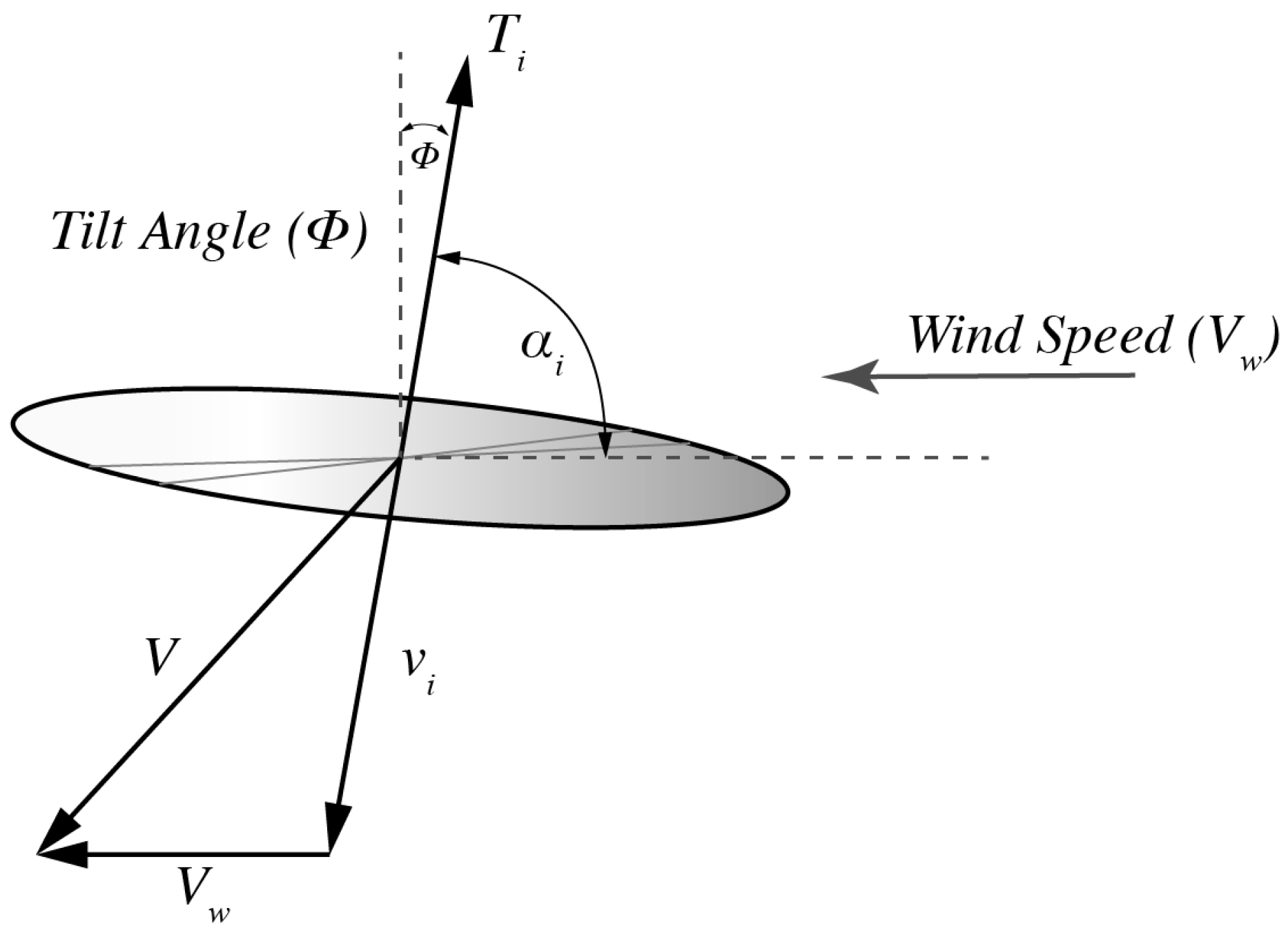
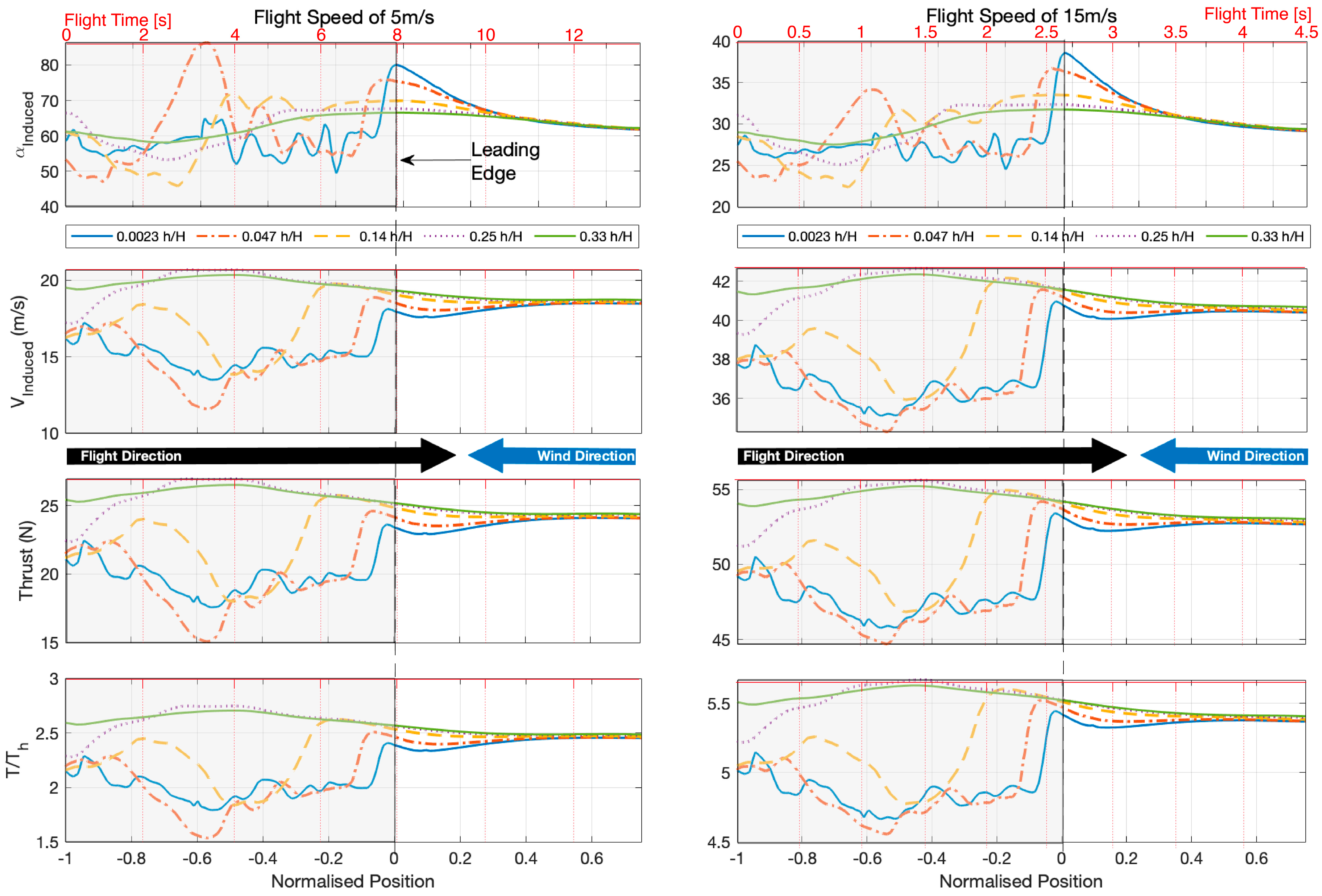
7.3. Estimations of Perceived Gust for a Rotor
7.4. Airframe Design and Certification Considerations
- “Operating in close proximity to obstructions can lead to recirculation and loss of performance. Aerodromes, geographically situated in hilly, mountainous areas, including certain coastal regions, can be subject to hazardous turbulent conditions in moderate to strong wind conditions. Pilots should be aware that, in certain cases, aircraft performance can be severely affected. History has shown, in extreme cases, that turbulence has prevented the aircraft from climbing or being controlled near the ground and has also caused structural damage”.
- “In winds below 15 kts, the turbulence may be experienced in the lee of an obstruction, vertically to about one third higher than the height of the obstruction. Above 20 kts, turbulence may be experience on the leeward side of an obstruction to a distance of 10–15 times the obstruction height and up to twice the obstruction height above the ground”.
- “During take-off or landing in gusty wind situations where wind shear is likely to be present, may require a greater power margin to deal with varying power demands or an unexpected loss of airspeed and accompanying sink. Large anti-torque pedal inputs to maintain directional control also act to reduce the excess power available”.
7.5. Vertiport Design and Certification Considerations
8. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stough, P.; Scanlon, C. Numerous research projects support efforts to overcome weather-related hazards. ICAO J. 1999, 20–29. [Google Scholar]
- Kohut, T. 21 Sent to Hospital after Severe Turbulence Diverts Flight AC088 to Calgary; Global News: Toronto, ON, Canada, 2015; Available online: https://globalnews.ca/news/2427003/flight-with-20-injuries-diverted-to-calgary-international-airport/ (accessed on 10 December 2022).
- Bedo, S. Qantas Cabin Crew Injured in Turbulence Scare. 2019. Available online: https://www.news.com.au/national/qantas-cabin-crew-injured-in-turbulence-scare/news-story/528899b3886f77242887e946a78f9c35 (accessed on 1 March 2020).
- Souza, L. Twelve Passengers Injured Due to Severe Turbulence on an Aerolineas Argentinas Airbus A330. 2022. Available online: https://simpleflying.com/twelve-passengers-injured-severe-turbulence-aerolineas-argentinas-airbus-a330/ (accessed on 10 December 2022).
- Pande, P. SpiceJet Passenger Injured In Turbulence Dies Five Months Later. 2022. Available online: https://simpleflying.com/spicejet-turbulence-passenger-death/ (accessed on 10 December 2022).
- Watkins, S.; Milbank, J.; Loxton, B.; Melbourne, W. Atmospheric winds and their effects on micro air vehicles. AIAA J. 2006, 44, 2591–2600. [Google Scholar] [CrossRef]
- Mohamed, A.; Massey, K.; Watkins, S.; Clothier, R. The Attitude Control of Fixed-Wing MAVS in Turbulent Environments. Prog. Aerosp. Sci. 2014, 66, 37–48. [Google Scholar] [CrossRef]
- Hoblit, F.M. Gust Loads on Aircraft: Concepts and Applications; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1988. [Google Scholar]
- Mohamed, A.; Watkins, S.; OL, M.; Jones, A. Flight-Relevant Gusts: Computation-Derived Guidelines for Micro Air Vehicle Ground Test Unsteady Aerodynamics. J. Aircr. 2020, 1–7. [Google Scholar] [CrossRef]
- Thorn, A. Turbulence Factor in R44 Crash that Killed Pilot and Trainee. 2022. Available online: https://australianaviation.com.au/2022/04/turbulence-factor-in-r44-crash-that-killed-pilot-and-trainee/ (accessed on 10 December 2022).
- Severe Turbulence Caused B.C. Helicopter Crash That Seriously Injured 2, Investigation Finds. 2022. Available online: https://ca.news.yahoo.com/severe-turbulence-caused-b-c-194736055.html?guccounter=1&guce_referrer=aHR0cHM6Ly93d3cuZ29vZ2xlLmNvbS8&guce_referrer_sig=AQAAAJG9lcsg3uLYEePQR4Eh2qW8ph7sHzRJsRQ-E7iDNKjjW9AlwiXj1WRyxzJs_ckdOwlVnGC2J1I_xZeZ7sgx_xdefW7GUvFAK9zMxoNmG1V6YsiR7juy2jse3VeaHKJk8y6a8j40oTrWVYIqdF_yCQ55auAOJlbJOrAFy8GdysH1 (accessed on 10 December 2022).
- Severe Turbulence Led to Helicopter Collision with Terrain on Bowen Island, British Columbia. 2022. Available online: https://canadianaviationnews.wordpress.com/2022/07/29/severe-turbulence-led-to-helicopter-collision-with-terrain-on-bowen-island-british-columbia/ (accessed on 10 December 2022).
- Smith, A.; Bell, A.; Hackett, D. Trade-Offs in Helipad Sitting & Design; Rowan Williams Davies & Irwin Inc.: Guelph, ON, Canada, 2017; pp. 1–10. [Google Scholar]
- Glaser, A. Here’s Why Facebook’s Massive Drone Crashed in the Arizona Desert. 2016. Available online: https://www.vox.com/2016/12/18/13998900/facebooks-drone-crash-aquila-arizona-structural-failure (accessed on 8 December 2020).
- Lye, H. Second Airbus Zephyr UAS Crashes during a Test Flight. 2019. Available online: https://www.airforce-technology.com/news/second-airbus-zephyr-uas-crashes-during-a-test-flight/ (accessed on 10 December 2022).
- Mangan, D.; Breuninger, K. One Dead after Helicopter Crash-Lands on Roof of Midtown Manhattan Building. 2019. Available online: https://www.cnbc.com/2019/06/10/helicopter-crashes-into-building-in-midtown-manhattan.html (accessed on 3 March 2020).
- Farell, C.; Sitheeq, M.M.; Ellis, C.R.; Voigt, R.L., Jr. Fairview Riverside Medical Center Helistop, Minneapolis, Minnesota: Design and Operational Issues; St. Anthony Falls Hydraulic Laboratory: Minneapolis, MN, USA, 1995. [Google Scholar]
- Horn, J.F.; Keller, J.D.; Whitehouse, G.R.; McKillip, R.M., Jr. Analysis of Urban Airwake Effects on Heliport Operations at the Chicago Children’s Memorial Hospital. In Final Report Submitted to Illinois Department of Transportation; Researchgate: Berlin, Germany, 2011. [Google Scholar]
- McKinley, J.B. Evaluating Wind Flow around Buildings on Heliport Placement; West Palm Beach Fl Champlain Technology; Systems Control Technology Inc.: Idaho Falls, ID, USA, 1984. [Google Scholar]
- Civil Aviation Authority. Helideck Design Considerations–Environmental Effects; CAA Paper: Norwich, UK, 2008; Volume 3. [Google Scholar]
- Nakayama, M.; Uchiami, Y.; Watagami, K.; Ui, K. Wind tunnel test to design helidecks on the rooftops of high-rise buildings. J. Wind. Eng. Ind. Aerodyn. 1991, 38, 459–468. [Google Scholar]
- Perrotta, G.; Jones, A.R. Unsteady forcing on a flat-plate wing in large transverse gusts. Exp. Fluids 2017, 58, 101. [Google Scholar]
- Andreu-Angulo, I.; Babinsky, H.; Biler, H.; Sedky, G.; Jones, A.R. Effect of transverse gust velocity profiles. AIAA J. 2020, 58, 5123–5133. [Google Scholar] [CrossRef]
- Biler, H.; Sedky, G.; Jones, A.R.; Saritas, M.; Cetiner, O. Experimental investigation of transverse and vortex gust encounters at low Reynolds numbers. AIAA J. 2021, 59, 786–799. [Google Scholar] [CrossRef]
- Granlund, K.; Monnier, B.; Ol, M.; Williams, D. Airfoil longitudinal gust response in separated vs. attached flows. Phys. Fluids 2014, 26, 027103. [Google Scholar] [CrossRef]
- Biler, H.; Badrya, C.; Jones, A.R. Experimental and computational investigation of transverse gust encounters. AIAA J. 2019, 57, 4608–4622. [Google Scholar] [CrossRef]
- Jones, A.R.; Cetiner, O.; Smith, M.J. Physics and modeling of large flow disturbances: Discrete gust encounters for modern air vehicles. Annu. Rev. Fluid Mech. 2022, 54, 469–493. [Google Scholar] [CrossRef]
- Jones, A.R.; Cetiner, O. Overview of unsteady aerodynamic response of rigid wings in gust encounters. AIAA J. 2021, 59, 731–736. [Google Scholar] [CrossRef]
- Eldredge, J.D.; Jones, A.R. Leading-edge vortices: Mechanics and modeling. Annu. Rev. Fluid Mech. 2019, 75–104. [Google Scholar] [CrossRef]
- Watkins, S.; Thompson, M.; Loxton, B.; Abdulrahim, M. On Low Altitude Flight through The Atmospheric Boundary Layer. Int. J. Micro Air Veh. 2010, 2, 55–67. [Google Scholar] [CrossRef]
- Mohamed, A.; Watkins, S.; Clothier, R.; Abdulrahim, M. Influence of Turbulence on MAV Roll Perturbations. Int. J. Micro Air Veh. 2014, 6, 175–190. [Google Scholar] [CrossRef]
- Chen, T.; Clothier, R.; Mohamed, A.; Badawy, R. An Experimental Study of Human Performance in Controlling Micro Air Vehicles in Turbulent Environment. In Proceedings of the Fourth Australasian Unmanned Systems Conference, Melbourne, Australia, 15–16 December 2014; pp. 1–8. [Google Scholar]
- Holmes, J.D. Wind Loading of Structures; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Peterka, J.; Meroney, R.; Kothari, K. Wind flow patterns about buildings. J. Wind Eng. Ind. Aerodyn. 1985, 21, 21–38. [Google Scholar] [CrossRef]
- Leuzzi, G.; Monti, P. Particle trajectory simulation of dispersion around a building. Atmos. Environ. 1998, 32, 203–214. [Google Scholar] [CrossRef]
- Zhang, Y.; Arya, S.; Snyder, W. A comparison of numerical and physical modeling of stable atmospheric flow and dispersion around a cubical building. Atmos. Environ. 1996, 30, 1327–1345. [Google Scholar] [CrossRef]
- Ferreira, A.D.; Sousa, A.C.M.; Viegas, D.X. Prediction of building interference effects on pedestrian level comfort. J. Wind Eng. Ind. Aerodyn. 2002, 90, 305–319. [Google Scholar] [CrossRef]
- Mochida, A.; Lun, I.Y.F. Prediction of wind environment and thermal comfort at pedestrian level in urban area. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1498–1527. [Google Scholar] [CrossRef]
- Lim, K.E.; Watkins, S.; Clothier, R.; Ladani, R.; Mohamed, A.; Palmer, J.L. Full-scale flow measurement on a tall building with a continuous-wave Doppler Lidar anemometer. J. Wind Eng. Ind. Aerodyn. 2016, 154, 69–75. [Google Scholar] [CrossRef]
- Tsinober, A. An Informal Conceptual Introduction to Turbulence; Springer: Berlin/Heidelberg, Germany, 2009; Volume 483. [Google Scholar]
- Baklanov, A.A.; Grisogono, B.; Bornstein, R.; Mahrt, L.; Zilitinkevich, S.S.; Taylor, P.; Larsen, S.E.; Rotach, M.W.; Fernando, H.J.S. The Nature, Theory, and Modeling of Atmospheric Planetary Boundary Layers. Bull. Am. Meteorol. Soc. 2011, 92, 123–128. [Google Scholar] [CrossRef]
- Garratt, J.R. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Thompson, M. The Small Scales of Turbulence in Atmospheric Winds at Heights Relevant to Mavs. Doctoral Dissertation, RMIT University, Melbourne, Australia, 2013. [Google Scholar]
- Mohamed, A.; Carrese, R.; Fletcher, D.; Watkins, S. Scale-resolving simulation to predict the updraught regions over buildings for MAV orographic lift soaring. J. Wind Eng. Ind. Aerodyn. 2015, 140, 34–48. [Google Scholar] [CrossRef]
- Liepmann, H. On the application of statistical concepts to the buffeting problem. J. Aeronaut. Sci. 1952, 19, 793–800. [Google Scholar] [CrossRef]
- Dowell, E.H.; Crawley, E.F.; Curtiss, H.C., Jr.; Peters, D.A.; Scanlan, R.H.; Sisto, F. A Modern Course in Aeroelasticity, 3rd revised and enlarged Ed ed.; Kluwer Academic Publishers: Boston, MA, USA, 1995; pp. 327–337. [Google Scholar]
- Von Karman, T. Progress in the statistical theory of turbulence. Proc. Natl. Acad. Sci. USA 1948, 34, 530–539. [Google Scholar] [CrossRef] [PubMed]
- Diederich, F.W.; Drischler, J.A. Effect of Spanwise Variations in Gust Intensity on the Lift Due to Atmospheric Turbulence; NACA TN 3920; 1957. [Google Scholar]
- Dryden, H.L. Turbulence investigations at the National Bureau of Standards. In Proceedings of the Fifth International Congress of Applied Mechanics, Cambridge, MA, USA, 12–16 September 1938. [Google Scholar]
- Heisenberg, W. Zur statistischen theorie der turbulenz. Z. Phys. 1948, 124, 628–657. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Proc. R. Soc. London. Ser. A-Math. Phys. Sci. 1991, 434, 9–13. [Google Scholar]
- Liepmann, H.; Laufer, J.; Liepmann, K. On the Spectrum of Isotropic Turbulence; NACA TN 2473; National Advisory Committee for Aeronautics: Washington, DC, USA, 1951. [Google Scholar]
- Standard, M. Flying Qualities of Piloted Aircraft; US Dept. of Defense MIL-STD-1797A; 1990. [Google Scholar]
- Zbrozek, J. The Relationship between the Discrete Gust and Power Spectra Presentations of Atmospheric Turbulence, with a Suggested Model of Low-Altitude Turbulence; Royal Aeronautical Establishment, Aeronautical Research Council, Reports and Memoranda; 1961. [Google Scholar]
- Etkin, B. Theory of the Flight of Airplanes in Isotropic Turbulence-Review and Extension; Advisory Group for Aeronautical Research and Development Paris (France): Neuilly-sur-Seine, France, 1961. [Google Scholar]
- Skelton, G.B. Investigation of the Effects of Gusts on V/STOL Craft in Transition and Hover; Air Force Flight Dynamics Laboratory Technical Report; 1968. [Google Scholar]
- ESDU. Characteristics of Atmospheric Turbulence near the Ground. Part II: Single Point Data for Strong Winds (Neutral Atmosphere); 1985. [Google Scholar]
- Watkins, S.; Cooper, K.R. The Unsteady Wind Environment of Road Vehicles, Part Two: Effects on Vehicle Development and Simulation of Turbulence; SAE Technical Paper; 2007. [Google Scholar]
- Lissaman, P. Effects of Turbulence on Bank Upsets of Small Flight Vehicles. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Thompson, M.; Watkins, S.; White, C.; Holmes, J. Span-wise wind fluctuations in open terrain as applicable to small flying craft. Aeronaut. J. 2011, 115, 693–701. [Google Scholar] [CrossRef]
- Wang, L.; Dai, Y.; Yang, C. Gust response analysis for helicopter rotors in the hover and forward flights. Shock Vib. 2017, 2017, 8986217. [Google Scholar] [CrossRef]
- Diederich, F.W. The dynamic response of a large airplane to continuous random atmospheric disturbances. J. Aeronaut. Sci. 1956, 23, 917–930. [Google Scholar] [CrossRef]
- Fadl, M.S.; Karadelis, J. CFD simulation for wind comfort and safety in urban area: A case study of Coventry University central campus. Int. J. Archit. Eng. Constr. 2013, 2, 131–143. [Google Scholar] [CrossRef]
- Watkins, S.; Mohamed, A.; Fisher, A.; Clothier, R.; Carrese, R.; Fletcher, D. Towards Autonomous MAV Soaring in Cities: CFD Simulation, EFD Measurement and Flight Trials. Int. J. Micro Air Veh. 2015, 7, 441–448. [Google Scholar] [CrossRef]
- Blocken, B.; Stathopoulos, T.; Carmeliet, J. CFD simulation of the atmospheric boundary layer: Wall function problems. Atmos. Environ. 2007, 41, 238–252. [Google Scholar] [CrossRef]
- Mohamed, A.; Abdulrahim, M.; Watkins, S.; Clothier, R. Development and Flight Testing of a Turbulence Mitigation System for MAVs. J. Field Robot. 2016, 35, 639–660. [Google Scholar] [CrossRef]
- Mohamed, A.; Watkins, S.; Clothier, R.; Abdulrahim, M.; Massey, K.; Sabatini, R. Fixed-Wing MAV Attitude Stability in Atmospheric Turbulence PART 2: Investigating Biologically-Inspired Sensors. Prog. Aerosp. Sci. 2014, 71, 1–13. [Google Scholar] [CrossRef]
- Panta, A.; Petersen, P.; Marino, M.; Watkins, S.; Fisher, A.; Mohamed, A. Qualitative investigation of the dynamics of a leading edge control surfaces for MAV applications. In Proceedings of the International Micro Air Vehicle Conference and Flight Competition (IMAV 2017), Toulouse, France, 18–21 September 2017; pp. 1–8. [Google Scholar]
- Medina, a.; Ol, m.V.; mancini, p.; Jones, a. Revisiting Conventional Flaps at High Deflection Rate. AIAA J. 2016, 55, 2676–2685. [Google Scholar] [CrossRef]
- Lei, Y.; Huang, Y.; Wang, H. Effects of wind disturbance on the aerodynamic performance of a quadrotor MAV during hovering. J. Sens. 2021, 2021, 6681716. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Liu, Y.; Mori, K. Experimental study for aerodynamic performance of quadrotor helicopter. Trans. Jpn. Soc. Aeronaut. Space Sci. 2018, 61, 29–39. [Google Scholar] [CrossRef]
- Zhou, Q.; Chen, G.; Da Ronch, A.; Li, Y. Reduced order unsteady aerodynamic model of a rigid aerofoil in gust encounters. Aerosp. Sci. Technol. 2017, 63, 203–213. [Google Scholar] [CrossRef]
- Guo, S.; Jing, Z.; Li, H.; Lei, W.; He, Y. Gust response and body freedom flutter of a flying-wing aircraft with a passive gust alleviation device. Aerosp. Sci. Technol. 2017, 70, 277–285. [Google Scholar] [CrossRef]
- Rajpal, D.; Gillebaart, E.; De Breuker, R. Preliminary aeroelastic design of composite wings subjected to critical gust loads. Aerosp. Sci. Technol. 2019, 85, 96–112. [Google Scholar] [CrossRef]
- Bekemeyer, P.; Timme, S. Flexible aircraft gust encounter simulation using subspace projection model reduction. Aerosp. Sci. Technol. 2019, 86, 805–817. [Google Scholar] [CrossRef]
- De Souza Siqueira Versiani, T.; Silvestre, F.J.; Neto, A.B.G.; Rade, D.A.; da Silva, R.G.A.; Donadon, M.V.; Bertolin, R.M.; Silva, G.C. Gust load alleviation in a flexible smart idealized wing. Aerosp. Sci. Technol. 2019, 86, 762–774. [Google Scholar] [CrossRef]
- Bronz, M.; Gavrilovic, N.; Drouin, A.; Hattenberger, G.; Moschetta, J.-M. Flight Testing of Dynamic Soaring Part-1: Leeward Inclined Circle Trajectory. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–15 & 19–21 January 2021. [Google Scholar]
- Gavrilovic, N.; Benard, E.; Pastor, P.; Moschetta, J.-M. Performance improvement of small unmanned aerial vehicles through gust energy harvesting. J. Aircr. 2018, 55, 741–754. [Google Scholar] [CrossRef]
- Mohamed, A.; Taylor, G.; Watkins, S.; Windsor, S. Opportunistic soaring by birds suggests new opportunities for atmospheric energy harvesting by flying robots. J. R. Soc. Interface 2022, 19, 20220671. [Google Scholar] [CrossRef] [PubMed]
- Poksawat, P. Control System for Fixed-Wing Unmanned Aerial Vehicles: Automatic Tuning, Gain Scheduling, and Turbulence Mitigation. Ph.D. Thesis, RMIT University, Melbourne, Australia, 2018. Available online: https://researchrepository.rmit.edu.au/esploro/outputs/doctoral/Control-system-for-fixed-wing-unmanned-aerial-vehicles-automatic-tuning-gain-scheduling-and-turbulence-mitigation/9921864086901341 (accessed on 22 December 2022).
- Poksawat, P.; Wang, L.; Mohamed, A. Gain scheduled attitude control of fixed-wing UAV with automatic controller tuning. IEEE Trans. Control. Syst. Technol. 2017, 26, 1192–1203. [Google Scholar]
- Poksawat, P.; Wang, L.; Mohamed, A. Automatic tuning of attitude control system for fixed-wing unmanned aerial vehicles. IET Control. Theory Appl. 2016, 10, 2233–2242. [Google Scholar]
- Panta, A. Dynamics of leading-edge and trailing-edge control surfaces at low Reynolds number. Nat. Sci. Rep. 2022; in press. [Google Scholar]
- Sattar, A.; Wang, L.; Mohamed, A.; Panta, A.; Fisher, A. System Identification of Fixed-wing UAV with Multi-segment Control Surfaces. In Proceedings of the 2019 Australian & New Zealand Control Conference (ANZCC), Auckland, New Zealand, 27–29 November 2019. [Google Scholar]
- Panta, A.; Mohamed, A.; Marino, M.; Watkins, S.; Fisher, A. Unconventional control solutions for small fixed wing unmanned aircraft. Prog. Aerosp. Sci. 2018, 102, 122–135. [Google Scholar] [CrossRef]
- Gigacz, R.; Mohamed, A.; Poksawat, P.; Watkins, S.; Panta, A. Developing a Stable UAS for Operation in Turbulent Urban Environments. In Proceedings of the International Micro Air Vehicles Conference and Flight Competition 2017, Toulouse, France, 18–21 September 2017. [Google Scholar]
- Mohamed, A.; Clothier, R.; Watkins, S.; Sabatini, R.; Abdulrahim, M. Fixed-Wing MAV Attitude Stability in Atmospheric Turbulence PART 1: Suitability of Conventional Sensors. Prog. Aerosp. Sci. 2014, 70, 69–82. [Google Scholar]
- Mentzoni, F.; Ertesvåg, I.S. On turbulence criteria and model requirements for numerical simulation of turbulent flows above offshore helidecks. J. Wind. Eng. Ind. Aerodyn. 2015, 142, 164–172. [Google Scholar]
- Rowe, S.J.; Howson, D.; Turner, G. A turbulence criterion for safe helicopter operations to offshore installations. Aeronaut. J. 2006, 110, 749–758. [Google Scholar]
- Garcia-Magariño, A.; Bardera, R.; Sor, S.; Matias-Garcia, J.C. Flow Control Devices in Cities for Urban Air Mobility. In Proceedings of the AIAA AVIATION 2020 FORUM, Virtual, 15–19 June 2020. [Google Scholar]
- Heliport Design, in Advisory Circular. Federal Aviation Administration: Washington, DC, USA, 2023. Available online: https://www.faa.gov/documentLibrary/media/Advisory_Circular/AC_150_5390_2D_Heliports.pdf (accessed on 22 December 2022).
- Bassey, R. Vertiport Design. In Engineering Brief; Federal Aviation Administration: Washington, DC, USA, 2022. Available online: https://www.faa.gov/airports/engineering/engineering_briefs/engineering_brief_105_vertiport_design (accessed on 22 December 2022).
- City of London Corporation. In Wind Microclimate Guidlines for Developments in the City of London; City of London Corporation: London, UK; 2019. Available online: https://www.cityoflondon.gov.uk/services/planning/microclimate-guidelines (accessed on 22 December 2022).
- Prudden, S.; Fisher, A.; Mohamed, A.; Watkins, S. An anemometer for UAS-based atmospheric wind measurements. In Proceedings of the 17th Australian International Aerospace Congress (AIAC 2017), Melbourne, Australia, 26–28 February 2017. [Google Scholar]





| Parameter | Specification | |
|---|---|---|
| Delivery Drone | Advanced Air Mobility Vehicle | |
| MTOW | 4 kg | 1683 kg |
| Disk Loading | 14.14 kg/m2 | 35.68 kg/m2 |
| Configuration | Quadrotor | Octorotor |
| Rotor Size (diameter) | 0.3 m | 2.74 m |
| Flight Velocities | 5 ms−1, 15 ms−1 | 5 ms−1, 15 ms−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, A.; Marino, M.; Watkins, S.; Jaworski, J.; Jones, A. Gusts Encountered by Flying Vehicles in Proximity to Buildings. Drones 2023, 7, 22. https://doi.org/10.3390/drones7010022
Mohamed A, Marino M, Watkins S, Jaworski J, Jones A. Gusts Encountered by Flying Vehicles in Proximity to Buildings. Drones. 2023; 7(1):22. https://doi.org/10.3390/drones7010022
Chicago/Turabian StyleMohamed, Abdulghani, Matthew Marino, Simon Watkins, Justin Jaworski, and Anya Jones. 2023. "Gusts Encountered by Flying Vehicles in Proximity to Buildings" Drones 7, no. 1: 22. https://doi.org/10.3390/drones7010022
APA StyleMohamed, A., Marino, M., Watkins, S., Jaworski, J., & Jones, A. (2023). Gusts Encountered by Flying Vehicles in Proximity to Buildings. Drones, 7(1), 22. https://doi.org/10.3390/drones7010022







