Risk-Based UAV Corridor Capacity Analysis above a Populated Area

Abstract

To integrate unmanned aerial vehicles (UAVs) into the national airspace in a safe manner, a risk-based approach to the regulation of UAVs is adopted in many countries. Thus, the capacity to permit UAVs in urban airspace also needs to be evaluated in a risk-based sense. In this regard, this paper proposes a methodology to analyze the capacity of UAV corridors on the basis of third-party risk on the ground. By linking the collision rate of the corridor and the failure rates of UAVs with the number of fatalities on the ground, the capacity of the UAV corridor is derived to satisfy the target level of safety. To model the collision rate of UAVs in the corridor, the Reich collision risk model is utilized. Moreover, a ground risk map is generated to compute the third-party risk on the ground using the databases for Seoul, Korea. The results show that the failure rate of UAVs is the dominant factor for determining the capacity of the corridor, even if the number of corridors increases. The proposed methodology could be useful to manage the number of flights for applications where the UAV corridor is fixed and flight continues, such as package delivery.

1. Introduction

With the increase in the use of small, unmanned aircraft systems, the needs for their proper regulation and a traffic management system are increasing. Accordingly, efforts to develop a UAS (unmanned aircraft system) traffic management (UTM) system, including its operational concept and regulation, are continuing worldwide. In many countries, a risk-based approach is adopted as a baseline for the UAV (unmanned aerial vehicle) operational concept [1,2]. The risk-based approach means that UAV requirements, airspace design, and relevant UTM services depend on the associated risk of the operations. In January 2019, JARUS (Joint Authorities for Rulemaking on Unmanned Systems) published the Specific Operations Risk Assessment (SORA) guidelines to support the risk assessment of UAV operations [3]. In SORA, the requirements applied to UAV operations vary according to the determined ground risk and air risk levels for UAV operational approval.

In this regard, for UTM in Europe, named U-space, the airspace volume for UAV operation is divided into three types: X, Y, and Z [2]. The criteria for classification are the numbers of drone flights that are expected, the ground risk, the air risk, public acceptance factors, etc. Moreover, according to the volume type, the provision of UTM services is different as well as the access requirements for UAVs. A similar concept is also applied to UTM in the USA [1]. Furthermore, for U-space, the Demand and Capacity Optimization in U-Space (DACUS) project is in progress in order to properly manage the capacity of the airspace [4]. In air traffic management, capacity is linked to the capability of a human air traffic controller to manage aircraft within a certain volume of airspace; however, for UTM, capacity can be expressed as a function of risk-based and social indicators per a predefined volume of airspace by considering its operational concept [4]. Therefore, a new method for a DCB (demand and capacity balancing) technique is necessary for the development of UTM. In this regard, in 2021, Janisch et al., proposed a risk-based demand and capacity balancing concept for U-space by linking the collision risk and failure rates of UAV with the probability of causing harm to third parties as a part the DACUS project [5]. By limiting the number of UAV operations so that the third-party risk does not exceed the TLS (target level of safety), the balance between demand and capacity is managed.

In Korea, a prototype of a UTM system for small UAV operations under 150 m has been under development since April 2017. In keeping with the global trend, a quantitative risk evaluation technique to define the whole operational concept, including airspace volume and access requirements for a Korean UTM (K-UTM) system, is under development [6,7,8]. In our previous studies, we developed a ground risk map for a specific city in Korea and evaluated the operational ground risk for UAV trajectories and segmented the airspace volume on the basis of the resulting ground risk levels [6,7]. In addition, we derived the required navigation performance for the corridor by utilizing the ground risk map and the collision risk model for the corridor to satisfy the TLS [8]. Advancing our previous studies and motivated by the DACUS DCB concept, in this study, we propose a methodology for analyzing the capacity of a corridor—the maximum available traffic flow of sUAVs (small unmanned aerial vehicles)—based on third-party risk. To determine the maximum number of sUAV that can be flown in terms of third-party risk, various models representing the occurrence of events and their consequences in a risk scenario need to be specified. In this respect, a UAV ground risk model that represents the risk to entities of value (i.e., people and property) on the ground due to the operations of UAV was utilized.

There are many possible applications of UAVs, such as package delivery, surveillance, and search and rescue [9]. The proposed capacity analysis methodology could be useful to manage the total number of flights for applications where the UAV corridor is fixed and flight continues, for example, for the delivery of goods.

2. Related Work and Contribution

Examining the previous literature, there are many studies related to the ground risk model. The ground risk model can be deconstructed into a few subcomponent models: the event model, impact location model, exposure model, incident stress model, harm model, etc., as shown in Figure 1 [10].

First, regarding the event model, there are two primary events that cause UAVs to crash on the ground: failure of the UAV and a collision between UAVs in restricted airspace [5]. The failure model describes the uncertainty of the occurrence of failure in given conditions. This can be assumed from historical data and expert opinions, and in many previous studies, it was modeled as a constant failure rate or MTBF (mean time between failure) [6,7,10,11,12,13,14,15,16,17,18]. Regarding the mid-air collision model, it can be classified according to various airspace operations: free flight, structured flight, etc. [19]. For corridor-type operations, collision risk models are well developed for manned aviation, and efforts to apply them to UAVs are continuing [8,20,21,22]. The Reich model [23,24,25] has been used in manned aviation for several decades, and it is employed by the International Civil Aviation Organization in their airspace planning manual [26].

Second, the impact location model represents the location and size of the impact area due to a UAV crash. The ballistic descent model is frequently used for multirotor aircraft [6,7,8,11,12,13,15,27,28], and the gliding model is utilized for fixed-wing aircraft [12,13,14,15,29]. In addition, there are also studies that have used the 6 DOF (degree of freedom) model [16,30,31]. Moreover, the size of the impact area, also called the exposure area or lethal area, can be modeled on the basis of geometry, weight, etc. [10,17].

Third, the exposure model describes the uncertainty in the presence of an entity of value, in this study, a human being, at a given location and time. Mean population density [11,15,16,17,32], population behavior patterns [17], population density map [6,7,8,12,13], and car traffic data [6,7,8,14,27] are used to predict the presence of people at an area of impact.

Next, the incident stress model characterizes the magnitude of stress transferred to a human. The factors that can attenuate the magnitude of stress should be considered, for example, sheltering factors of buildings, cars, or trees. The sheltering effect can be implemented in various ways. Some studies use a sheltering factor table that categorizes the sheltering effect of each structure such as buildings, trees, and vehicles [6,7,8,13,15,32]. Weibel et al., explored the probability of penetrating a shelter according to UAV classes [18], and other works considered the amount of energy absorption among different materials [7,32,33]. Melnyk et al., assumed that the probability of people being exposed was approximately 30% when an aircraft collides with a building based on building casualty data [17]. Cour-Harbo also used a 30% probability of exposure in [12].

Finally, the harm model characterizes the probability of a fatality given an incident’s level of stress. In most studies, it is modeled as a function of impact kinetic energy [6,7,8,11,12,13,15,17,27,29,34,35]. Based on the literature review, a ground risk model can be developed by choosing the appropriate subcomponent models from various existing studies depending on the purpose and level of abbreviation.

Among the previous studies, Weibel et al., and Melnyk et al., derived the required MTBF or failure rate of UAVs to satisfy the target level of safety for third parties on the ground [17,18]. Cour-Harbo evaluated the probability of fatalities during UAV flights by considering four descent event types: ballistic descent, uncontrolled glide, parachute descent, and fly away [12]. Primatesta et al., developed the concept of the ground risk map and proposed a UAV path planning strategy based on Cour-Harbo’s work [13,36]. Additionally, Kim evaluated the third-party risk on the ground by utilizing real car traffic data when two UAVs collide above a road [27]. Furthermore, as mentioned above, as a part of the DACUS project, Janisch et al., introduced the DCB concept in which the capacity of the airspace is defined as the resulting ground risk as a result of failure and collisions in free-flight situations [5]. However, no studies have proposed the use of the DCB methodology for UAV corridors in a risk-based sense. In this regard, we propose a risk-based DCB methodology for UAV corridors to quantitatively evaluate the capacity of UAV corridors over a populated area, considering both the failure and collision rates. By linking the collision rate of the corridor and the failure rates of UAVs with the number of fatalities on the ground in the event of a UAV crash, the risk-based capacity of a UAV corridor can be derived to satisfy the target level of safety.

To evaluate the ground risk over a populated area, a conditional ground risk map, which is the ground risk conditioned by the occurrence of events, was generated using real databases that contain information on Seoul, Korea. The conditional risk represents the possible fatalities if a UAV was to crash to the ground. To model the existence of an entity of value, the population density, car traffic data, and information on the buildings of Seoul were utilized. By assuming the multicopter operations in the corridor, the ballistic descent model and weight-based impact area model were adopted to compute the impact locations and exposure areas. Furthermore, to consider the sheltering factor, the energy absorption and mortality rate of the building due to aircraft crashes were used. The models used in study are described in more detail in the following sections. Then, the corridor location (i.e., path of the UAV) is selected based on the conditional ground risk map. To model the occurrence of events, a constant failure rate was assumed. For the crash rate due to collisions, the Reich collision risk model used in manned aviation was utilized, because it has already been proven and widely used in many standards [26,37,38], including recent works on UAVs [8,20,21,22]. Finally, by linking these together, the capacity of the corridor was derived to satisfy the target level of safety. In addition, the dominant factor that determines the capacity of the corridor was also investigated, which, in this study, was the failure rate, even if the number of corridors increases.

In Section 3, the subcomponent models and the resulting conditional ground risk map of Seoul are described as well as the corridor configuration on the map. In Section 4, the risk-based corridor capacity analysis methodology and its result are presented. Finally, Section 5 summarizes the main conclusions of this research.

3. Conditional Ground Risk

The third-party risk on the ground caused by UAV operations can be expressed as follows:

$$N_{HH}=\left(N_{CO}+N_{failure}\right)\times N_{HH|fall}$$

(1)

where $N_{HH}$ is the number of fatalities per flight hour, and the subscript $HH$ refers to the harm to a human; $N_{CO}$ is the number of accidents per flight hour due to collision, and one collision is converted into two accidents; $N_{failure}$ is the number of UAV failures per flight hour; $N_{HH|fall}$ is the conditional ground risk (fatality/crash), because it is conditioned by the occurrence of failure and collision events. In Equation (1), it is assumed that the probability of a UAV crash is one when a collision or failure occurs, and it is also assumed that the failure event and collision event were mutually exclusive.

The concept for the generation of the conditional ground risk map is presented in Figure 2.

The conditional ground risk map can be generated using Equation (2), based on Weibel’s model, for each point on the map [18].

$$N_{HH|fall}\left(x_d,y_d\right)={\displaystyle \sum _{All grid}\left[P_{fall}\left(k\right)\times A_{\exp }\times \rho \left(k\right)\times \left(1-S\left(k\right)\right)\times P_{HH|impact}\right]}$$

(2)

where $\left(x_d,y_d\right)$ represents the initial descent point of the UAV; $P_{fall}$ is the probability that a UAV will fall on the grid, k; $A_{\exp }$ is the exposure area when a UAV crashes; $S$ is the sheltering factor, where one means perfect shelter, whereas zero means that there is no sheltering effect; $P_{HH|impact}$ is the probability of a fatality when a UAV impacts on a person. To calculate the ground risk for each point of descent of a UAV, the terms on the right side of Equation (2) should be determined. In addition, each term can be specified by choosing the proper subcomponent models from various existing studies depending on the purpose and level of abbreviation.

3.1. The Impact Location Model

In Equation (2), $P_{fall}$ and $A_{\exp }$ are determined using the impact location model.

First, to evaluate $P_{fall}$ (i.e., the probability that a UAV will fall on the specific grid), the UAV descent trajectory model needed to be determined. As mentioned in Section 2, the 6 DOF model, ballistic descent model, and gliding model can be used to compute the impact location. In some studies, several descent models were simultaneously considered for various types of UAVs such as fixed wing and multicopter [13]. It is reasonable if the airspace is operated at full mix. However, for corridor operation, we assumed that the UAV corridor was separately operated according to the UAV type because of its different performance characteristics such as average velocity, maximum turn rate, and hovering capability.

In this study, we considered a corridor for a multicopter-type UAV because of its advantage of having hovering capability compared to a fixed-wing type. Therefore, the ballistic descent model used in [6,7,8,11,12,13,27,28] was used as shown in Equation (3).

$$M\dot{\mathbf{V}}=M\mathbf{g}-c\left|\mathbf{V}\right|\mathbf{V}$$

(3)

where $M$ is the mass of the UAV; $\mathbf{V}$ is the velocity vector, both horizontal and vertical, of the UAV; $\mathbf{g}$ is the gravitational acceleration. $c=0.5{\rho }_{air}A{C}_D$, where ${\rho }_{air}$ is the air density; $A$ is the frontal area; $C_D$ is the drag coefficient. To assume the average weight, speed, and size of UAV in the corridor, an existing multicopter, Aurelia X6 pro drone, specification was referred to as shown in

Table 1. Assumed drone specifications.

Specification	Value
Weight (including batteries)	10 kg
Payload capability	5 kg
Maximum flight speed	15 m/s
Width × height	1.255 × 0.485 m
Width of core part	0.42 m

[39].

By using Equation (3), the maximum reachable horizontal distance and average kinetic energy were computed using the Monte Carlo simulation. Uncertainties were applied to the parameters to consider variations such as the payload weight and the angle of the body’s frame during a fall. In addition, in this study, the height of the corridor was designed to be 100 m, and the average speed of a UAV in the corridor was assumed to be 15 m/s. The resulting parameters used in the simulation are summarized in

Table 2. Parameters for the ballistic descent simulation.

Parameters	Value
Weight	$U\left(10, 15\right)$ kg
Frontal area	$N\left(0.2, 0.05\right)$ m2
Drag coefficient 1	$N\left(0.7, 0.2\right)$
Horizontal speed	$N\left(15, 3\right)$ m/s
Vertical speed	$N\left(0, 3\right)$ m/s
Height	$N\left(100, 5\right)$ m

¹ The drag coefficient was selected based on the values for the multicopter presented in [13].

.

In Table 2, $U\left(a,b\right)$ represents the uniform distribution between a and b; $N\left(m,\sigma \right)$ represents the Gaussian distribution with the mean ($m$) and standard deviation ($\sigma$). By using these parameter values, the maximum reachable horizontal distance was computed as 110 m, and the average kinetic energy at impact was calculated as 6700 J as shown in

Table 3. Resulting horizontal distance and kinetic energy.

Parameters	Value
Maximum horizontal distance	110 m
Average kinetic energy	6700 J

. The maximum reachable horizontal distance can also be simply assumed by applying the one-to-one rule used in determining the ground risk buffer in SORA [3]. For example, when a UAV is operated at a height of 100 m above the ground, then the ground risk buffer is determined to be the same as 100 m. This means that beyond the ground risk buffer, third parties on the ground are not affected by the UAV crash. In other words, third parties within this distance are affected by the vehicle crash.

Next, the position distribution inside the maximum reachable horizontal distance needed to be determined. In this study, we assumed that the impact location inside the horizontal distance was uniform because of the difficulty in estimating the exact location at the impact after the collision and failure. This means that there is no information on where the UAV will fall within the circle. If the exact impact location and kinetic energy are needed, a physics-based approach is necessary. However, according to the purpose of this study, to generate a conditional ground risk map of a city, this general approach at a statistical level is sufficient.

In this regard, the resulting 2D (two-dimensional) strike points on the ground are shown in Figure 3. The 2D distribution in Figure 3 was quantized by a 20 m by 20 m square to match the resolution of the map database.

Next, regarding the exposure area ($A_{\exp }$) representing the size of the area influenced by a UAV crash, also called the lethal area, various models exist: the geometric model, gliding model, weight-based model, etc. [10,17]. It was determined in a previous study that the weight-based method produces the best fit for the actual data [17]. Therefore, we used a weight-based equation to estimate the exposure area in this study, as shown in Equation (4) [27,40].

In addition, note that the exposure area was applied to outdoor and vehicle circumstances in this study. For vehicles, it was conservatively considered to be the same as the outdoor situation based on the results of the sheltering factor investigation, which are described in detail in Section 3.3. For indoor circumstances, the mortality rate of individuals inside buildings was applied rather than estimating the exposure area.

$$A_{\exp }\left({\mathrm{m}}^2\right)=0.220464\times M\left(\mathrm{kg}\right)$$

(4)

3.2. The Exposure Model

To account for the presence of humans in the grid, as shown in Figure 2, various databases that contained information on Seoul were utilized. Population and car traffic data were used to model the existence of people in specific locations. To estimate the number of people indoors and outdoors, the building-to-land ratio database was applied. The building structure code was used to calculate the sheltering factor for different types of buildings. Figure 4 shows the population, car traffic, building-to-land ratio, and the building structure code database for Seoul in November 2017.

Data on the population and building were downloaded from a platform operated by National Geographic Information Institute of Korea [41]. Car traffic data were provided by Korea Transport Institute [42]. The resolutions of the population, building-to-land ratio, and the building structure code were originally a 100 m grid, but we adjusted the resolution to a 20 m grid by assuming a uniform distribution inside the 100 m grid. The car traffic data were originally provided for each segmented road, and each road segment had its own ID as shown in

Table 4. Example of the car traffic data.

Car Traffic Data	Values
Road ID 1	55480752201
Car traffic for passenger vehicle	13,205.79 per day
Car traffic for bus	840.37 per day
Car traffic for truck	5928.26 per day
Average speed	90.39 km/h

¹ Geographic location of each road was provided in a shapefile.

. Car traffic data were given for each ID for a passenger vehicle, bus, and truck, and the unit for the car traffic data was the number of vehicles per day. Moreover, in the car traffic data, the average speeds of the vehicles were described. In addition, the average number of passengers per vehicle type, presented in [27], was used to compute the number of people on the road.

By using these data, the average number of people on the road can be computed as follows.

$$\begin{array}{l}Average number of people inside vehicle in specific road length\\ =car traffic / average speed\times road length \times average passengers for vehicle\end{array}$$

(5)

Using Equation (5), the number of people on each road was computed. Then, the data were converted to the 20 m grid value by computing the road length inside the grid to match the resolution of the population and building information data. For the data conversion, GIS (geographic information system) software QGIS (Quantum GIS) was used [43].

The building-to-land ratio data were used to assume the indoor/outdoor ratio of the population in the grid. For example, the building-to-land ratio was 70%, which means that 70% of the people were indoors and the remaining 30% outdoors. In the future, this can be refined by using the number of mobile phones connected to each base station of a mobile carrier.

The building construction code, shown in Figure 4d, was used for determining the sheltering factor of buildings, and it is explained in detail in the following section.

3.3. The Incident Stress Model

To model the sheltering factor of structures, such as buildings, vehicles, and trees, Primatesta et al., Zhang et al., and Guglieri et al., used the sheltering factor tabulated for each structure [13,15,32]. Kim et al., and Melnyk et al., considered the energy absorption of different materials based on DoD (Department of Defense) explosives studies [7,17,33], and Melnyk et al., also consider the mortality rate due to aircraft crashes and building collapses [17,44]. From these previous studies, in this study, we redefined the sheltering factor by using the building information in Seoul. For this, the amount of energy absorption due to the roof/wall material, as shown in the tables in page 75 in [33], and the building structure code database of Seoul, as shown in

Table 5. Building structure code.

Structure	Code	Percentage
Wood construction	51, 52	3%
Steel-framed/reinforced concrete construction	21, 22, 29, 41, 42, 49	67.85%
Steel-framed construction	31, 32, 33, 39	1.2%
Brick/block/stone/other masonry construction	11, 12, 13, 19	27.86%

, were utilized.

Based on the building structure code, shown in Figure 4d, it can be found that in Korea, the reinforced concrete structure buildings accounted for the largest number at 67.85%, followed by brick/block structure building at 27.86%. This is quite different from the United States. In the United States, wood structures account for 85.4% of buildings, steel structures 4.9%, and concrete structures 9.2% [17]. In addition, in an investigation on roof materials in major cities in Korea in 2010, it was found that reinforced concrete roofs occupied 66.34% of all roofs [45]. Moreover, it matched with the percentage of reinforced concrete structures presented in Table 5.

From the tables in page 75 in [33], it can be observed that the roof and wall types with reinforced concrete, 14″/4″ reinforced concrete for roofs and 14″/8″/6″ reinforced concrete for walls, have enough energy absorption capability to protect the people inside when involved in a collision with a UAV at 6700 J of energy. However, the other structures did not have sufficient energy absorption capability; thus, these buildings can be penetrated by falling UAVs. To predict the percentage of injured people when a UAV collides with a building other than reinforced concrete structures, the mortality rate for small aircraft presented in a RAND study was referred to in which the maximum mortality rate inside the building was 20% as shown in [44]. However, in the RAND study, a small aircraft was defined as an aircraft carrying fewer than 30 passengers, and this is quite an overly conservative value for a small UAV under 25 kg. Currently, due to the lack of relevant studies on UAVs, a 10% mortality rate was assumed to estimate the number of people injured inside buildings other than reinforced concrete structures. In addition, note that the maximum mortality rate due to the collapse of a building was 32% from DoD explosives studies [17,33]. Regarding automobiles, the sheltering factor was considered to be negligible for a 6700 J impact energy, even after the absorption of energy. As explained later, a 250 J impact can cause 100% fatality [11,34].

In summary, the sheltering effect used in this study is presented in

Table 6. Assumed sheltering factor for a 15 kg UAV.

Types of Shelter	Sheltering Factor
Reinforced concrete structure buildings	1
Other structured buildings	0.9
Automobiles	0
Outdoors	0

. The sheltering factor in Equation (2) was applied according to the different structures presented in Table 6, and because of the absence of information regarding the existence of trees in Seoul, the sheltering factor regarding trees is not considered here. Figure 5 shows the resulting sheltering factor map for Seoul in Korea.

3.4. The Harm Model

There are several studies on the probability of fatality due to kinetic energy [29,34,35]. Ball et al., presented the probability of skull fracture as a function of blunt criteria, which is computed by using the kinetic energy, thickness of skull, etc. [29]. Range Commanders Council and Shelley presented the probability of fatality as a function of kinetic energy [34,35]. From previous studies, it can be found that the probability of fatality is 100% when at least 250 J of kinetic energy is applied [11,34].

In this regard, for outdoor and automobile circumstances, the probability of fatality was considered to be one by considering a 6700 J kinetic energy of a UAV and the amount of energy absorption as shown in [33]. For indoor situations, 10% of people inside buildings other than reinforced concrete structures were exposed to damage. Anyone exposed to damage was deemed a casualty. Therefore, the probability of fatality was also assumed to be one in this case.

In summary, in this study, the probability of fatality was considered to be one for all cases for the reasons listed above.

$$P_{HH|impact}=1$$

(6)

3.5. Resulting Conditional Ground Risk Map and Conditional Risk of the Corridor

The resulting conditional ground risk map for Seoul is shown in Figure 6. The values for each grid represent the possible fatalities when a UAV falls to the ground.

A maximum of 0.1129 fatalities could occur according to the conditional ground risk map. Approximately 32% of the area of Seoul had a fatality probability of between 10⁻² and 10⁻¹, which is represented by the color orange in Figure 6, and approximately 35% of the area had a fatality probability of between 10⁻³ and 10⁻², which is represented by the color yellow. These two fatalities are most dominant values regarding Seoul.

Next, we assumed the arbitrary corridor location in Seoul as shown in Figure 7. The length of the corridor was approximately 5.4 km.

The designed corridor system had two corridors with opposite flight directions.

Table 7. Conditional ground risk of the corridors.

Conditional Ground Risk	Percentage of Corridor
0.1	43.34%
0.01	56.52%
0.001	0.14%
Total conditional ground risk: 0.049

shows the conditional ground risk of the selected corridor location. The conditional ground risk value was quantized to the power of 10 for convenience. For example, the values between 10⁻³ and 10⁻² were considered as 10⁻².

In this study, it was assumed that the drones were uniformly located in a longitudinal direction in the corridor. Therefore, approximately 43% of the drones were located in an area with a fatality of 0.1, and approximately 57% of drones were located in an area with a fatality of 0.01. In other words, an arbitrary drone in the corridor could cause 0.1 fatalities with a probability of 0.43 and 0.01 fatalities with the probability of 0.57. In this regard, by estimating the crash rate of drones in the corridor due to the event of failure and collision, the total ground risk could be investigated.

The conditional ground risk of the corridor in Equation (1) can be computed as follows:

$$N_{HH|fall}={\displaystyle \sum _i{N}_{HH|fall}\left(i\right)\times AR\left(i\right)}$$

(7)

In Equation (7), $i$ represents the index of conditional ground risk. For example, the corridor system with a conditional ground risk, as shown in Table 7, had three indexes. $N_{HH|fall}\left(i\right)$ is the conditional ground risk value of index $i$; $AR\left(i\right)$ is the area ratio for index $i$; with percentages of the corridor area at 0.4334, 0.5652, and 0.14 as shown in Table 7. Then, the total condition risk ($N_{HH|fall}$) was 0.049.

In this study, it was assumed that the average velocity, weight, size of the UAV, and traffic flow rates of each corridor were identical. Only the flight direction was opposite in the corridor system in Figure 7.

4. Risk-Based Airspace Capacity Analysis

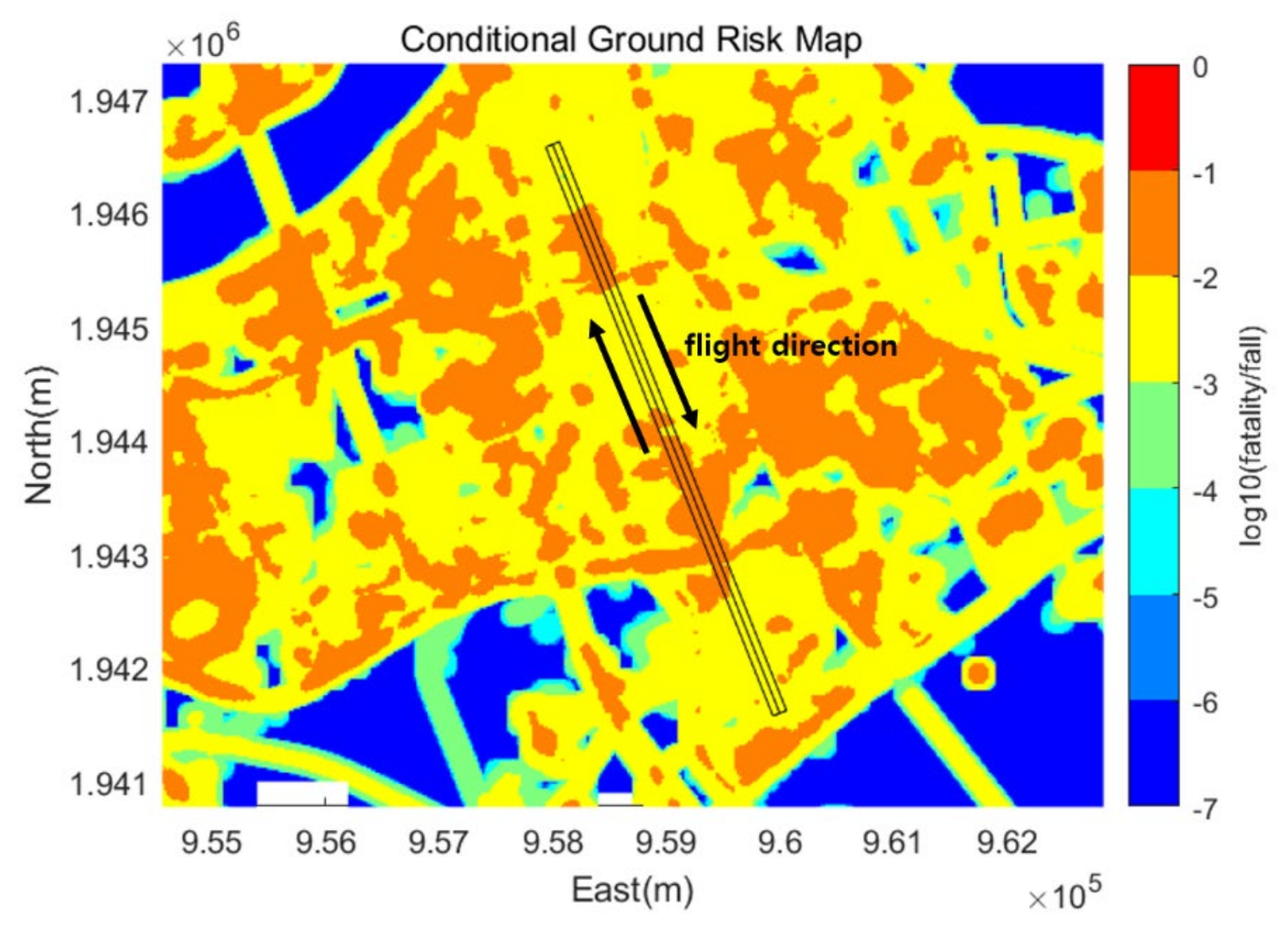
To investigate the capacity of the corridor in a risk-based sense, the collision rate ($N_{CO}$) and the failure rate ($N_{failure}$) in Equation (1) need to be formulated as a function of the traffic flow of the corridor. $N_{CO}$ and $N_{failure}$ can also be considered as the crash rate due to collisions and failures if it is assumed that the probability of a UAV crash is one when a collision or failure occurs.

4.1. Capacity Derivation Based on Failure Rate

The expected number of vehicles crashes on the ground due to failures can be easily calculated using the failure rate of UAV and the number of vehicles flown in the corridor. Regarding typical failure rates, values between 10⁻⁶ and 10⁻⁴ (number of failures/flight hour) are presented in the literature [10]. In this paper, two values for the failure rate were considered—10⁻⁶ and 10⁻⁵, because the failure rate of 10⁻⁴ is too large, such that even a single UAV could not satisfy the TLS, which was 10⁻⁶ (fatalities/flight hour) in this study [5].

Additionally, the total number of vehicles flown in the corridor can be computed by using the traffic flow as in Equation (8).

$$N_{UAS,corridor}=L\times m/V_x\times n$$

(8)

In Equation (8), $L$ is the length of the corridor; $m$ is the traffic flow rate of the corridor; $V_x$ is the average velocity of UAV in the corridor; and $n$ is the number of corridors. In this study, the traffic flow rate and the average velocity were the same along all corridors.

Then, the expected number of fallen UAVs due to failures per flight hour can be predicted as in Equation (9). In Equation (9), $FR$ is the failure rate (number of failures/flight hour) of UAVs.

$$N_{failure}=N_{UAS,corridor}\times FR$$

(9)

Finally, the ground risk caused by fallen UAVs due to failures can be calculated by applying the conditional ground risk of the corridor in Table 7. Among the $N_{failure}$ of the UAVs, approximately 43% produced a fatality of 0.1 and approximately 57% produced a fatality of 0.01. In this regard, the total ground risk caused by UAV failures can be evaluated using Equation (10).

$$N_{HH,failure}=N_{failure}\times N_{HH|fall}$$

(10)

4.2. Capacity Derivation Based on Collision Rate

To compute the expected number of vehicles that will crash on the ground due to a collision between UAVs in the corridor, the Reich collision risk model used in manned aviation was utilized. In the lateral/vertical Reich collision risk model, the course deviation error which is presented as RNP (Required Navigation Performance) in manned aviation is the major factor that affects the collision risk. Regarding the longitudinal collision risk model, collision risk was defined based on the longitudinal overlap of two consecutive aircrafts in a longitudinal direction during the position reporting period due to the position error and relative velocity. In this model, the lateral and vertical models do not account for air traffic controller intervention, while longitudinal models do. In the case of UAVs, the role of the air traffic controller is replaced by the UTM. Furthermore, the DAA (detect and avoid) capability of the UAV is not considered. If this kind of mitigation is applied, the collision risk can be decreased.

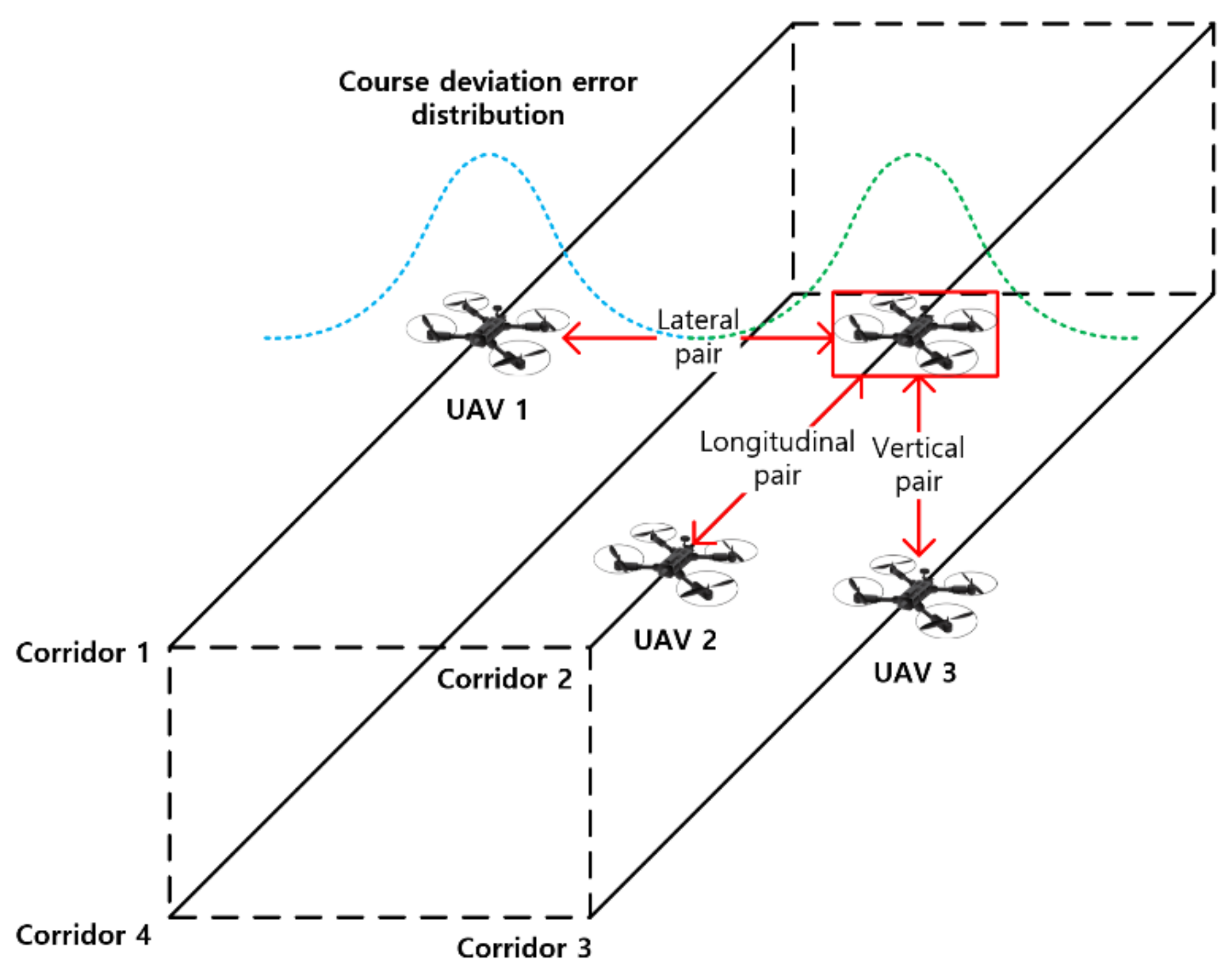
In the Reich model, the collision risk is evaluated by summing the collision risk of the pairs of all UAVs in three directions as shown in Figure 8.

$$N_{CO}=N_{ax}+N_{ay}+N_{az}$$

(11)

In addition, the total ground risk due to collisions can be calculated similar to the failure cases as in Equation (12).

$$N_{HH,CO}=N_{CO}\times N_{HH|fall}$$

(12)

In Equation (11), $N_{ax}$ is the collision risk for longitudinal pairs of UAV; $N_{ay}$ is the that in the lateral direction; and $N_{az}$ is the that in vertical direction.

The collision risk for all the lateral pairs of UAV was computed as follows [26,46]:

$$N_{ay}=P_y\left(S_y\right)P_z\left(0\right)\left[E_s\left(\frac{\left|\overline{\dot{x}}\right|}{2{\lambda }_x}+\frac{\left|\overline{\dot{y}}\right|}{2{\lambda }_y}+\frac{\left|\overline{\dot{z}}\right|}{2{\lambda }_z}\right)+E_o\left(\frac{2\left|V_x\right|}{2{\lambda }_x}+\frac{\left|\overline{\dot{y}}\right|}{2{\lambda }_y}+\frac{\left|\overline{\dot{z}}\right|}{2{\lambda }_z}\right)\right]$$

(13)

In Equation (13), $P_y\left(S_y\right)$ is the lateral overlap probability of two UAVs that are laterally separated by $S_y$; $P_z\left(0\right)$ is the vertical overlap probability of two UAVs at the same level; ${\lambda }_x$, ${\lambda }_y$, and ${\lambda }_z$ are the average of the longitudinal, lateral, and vertical sizes of the UAV; $V_x$ is the average speed of the UAV; $\left|\overline{\dot{x}}\right|$, $\left|\overline{\dot{y}}\right|$, and $\left|\overline{\dot{z}}\right|$ are the relative velocities of the two UAV in each direction; $E_s$ and $E_o$ are the same direction and opposite direction occupancies; ${\lambda }_x$, ${\lambda }_y$, ${\lambda }_z$, and $V_x$ were determined from Table 1, and $\left|\overline{\dot{x}}\right|$, $\left|\overline{\dot{y}}\right|$, and $\left|\overline{\dot{z}}\right|$ were determined by referring to a previous study [20].

The lateral overlap probability, $P_y\left(S_y\right)$, can be computed as follows [47]:

$$P_y\left(S_y\right)\approx 2{\lambda }_y{\displaystyle {\int }_{-\infty }^{\infty }{f}_y\left(y\right)f_y\left(y+S_y\right)dy}$$

(14)

In Equation (14), $f_y$ is the probability density of lateral navigation errors that can be written as follows using the double double exponential distribution (DDE) [22,26,47]:

$$f_y\left(y\right)=\left(1-\alpha \right)\frac{1}{2a_1}{e}^{-\left|\frac{y}{a_1}\right|}+\alpha \frac{1}{2a_2}{e}^{-\left|\frac{y}{a_2}\right|}$$

(15)

where $a_1$ and $a_2$ are the parameters for nominally and poorly navigating UAV; $a_1$ can be computed by using the RNP value representing 95% of the lateral positioning accuracy; $a_2$ is selected the same as with the lateral separation, $S_y$ [26,47]; and $\alpha$ is the weighting factor representing the percentage of UAVs that experience lateral navigation anomalies. In this study, the RNP value was determined based on the 95% position accuracy of the KASS (Korea Augmentation Satellite System), which is the SBAS (Satellite-Based Augmentation System) for Korea. The KASS is under development for APV (Approach with Vertical Guidance)-1 level performance, which is 16 m of 95% horizontal accuracy and 20 m of 95% vertical accuracy [48]. Note that in this study, the flight technical error was neglected in the RNP because it is known and continuously controlled to be small by a flight control computer which is presented at the submeter level for UAVs in the literature [49]. In addition, $\alpha$ was assumed to be 0.05, which is the conservative value in the case of manned aviation [47]. It means that 5% of UAVs experience a lateral navigation anomaly. In the literature, $\alpha$ is in the order of 10⁻⁴ in manned aviation [47].

The vertical overlap probability, $P_z\left(0\right)$, can be computed as follows [47]:

$$P_z\left(0\right)\approx 2{\lambda }_z{\displaystyle {\int }_{-\infty }^{\infty }{f}_z\left(z\right)f_z\left(z\right)dz}$$

(16)

In a previous study that aimed to apply the Reich collision risk model to UAV, the vertical overlap probability was extrapolated from the manned aviation data and computed as 0.0393 [20]. Moreover, we computed the vertical overlap probability by using double exponential distribution for $f_z$ with 20 m of 95% vertical positioning accuracy of the KASS. The resulting vertical overlap probability was computed as 0.0363, which was similar to the values in a previous study. Thus, in this study, we used 0.0363 as the vertical overlap probability.

The same direction and opposite direction occupancies $E_s$ and $E_o$ can be computed using Equation (17) by applying the steady-state flow model [47]. The occupancies for the lateral collision risk model were computed for the lateral pairs of UAV in Figure 8. Note that no distinction was made between the same and opposite direction traffic [24]. The occupancy in Equation (17) was computed for overlapping pairs rather than proximate pairs, which is convertible by matching with Equation (13) [46].

$$E=\frac{4{\lambda }_x}{V_x}\frac{{\displaystyle \sum _{all pairs of tracks}{m}_{i-1,j}{m}_{i,j}}}{{\displaystyle \sum m_{ij}}}$$

(17)

In Equation (17), $m$ represents the traffic flow rate of each corridor; $i$ is the corridor index in the lateral direction; and $j$ is the corridor index in the vertical direction. The corridor system considered in this study, as shown in Figure 7, had only one corridor in the vertical direction; therefore, in this case, the vertical corridor index $j$ can be neglected. In the lateral direction, there were two corridors. Thus, the denominator of Equation (17) can be calculated by summing the traffic flow rates of two corridors and the numerator is computed by multiplying the traffic flow rates of the corridors. Note that the same directional occupancy was zero in the case in Figure 7; only the opposite directional occupancy existed, because there was no corridor pair which had the same flight direction. As a result, the lateral collision risk can be linked with the traffic flow rate using the equations above.

In addition, the vertical collision risk for vertical pairs can be computed similarly as follows:

$$N_{az}=P_y\left(0\right)P_z\left(S_z\right)\left[E_s\left(\frac{\left|\overline{\dot{x}}\right|}{2{\lambda }_x}+\frac{\left|\overline{\dot{y}}\right|}{2{\lambda }_y}+\frac{\left|\overline{\dot{z}}\right|}{2{\lambda }_z}\right)+E_o\left(\frac{2\left|V_x\right|}{2{\lambda }_x}+\frac{\left|\overline{\dot{y}}\right|}{2{\lambda }_y}+\frac{\left|\overline{\dot{z}}\right|}{2{\lambda }_z}\right)\right]$$

(18)

Note that the occupancies are computed for the vertical pairs of UAVs in Figure 8. In this study, there were no UAV pairs in the vertical direction because only one corridor existed in the vertical direction. Therefore, the vertical collision risk was zero in this case.

Regarding the longitudinal collision risk, the model for computing the risk was different from the lateral and vertical directions, because its operational nature is that the aircraft is flying in the longitudinal direction and the assumption of air traffic controller intervention in the longitudinal direction which will be replaced by the UTM in the case of UAV. In the airspace planning manual published by ICAO, the longitudinal collision risk is defined on the basis of the probability of longitudinal overlap of two consecutive aircrafts in the longitudinal direction between the position reporting periods [26].

$$N_{az}={\mathsf{\Pi }}_x{P}_y\left(0\right)P_z\left(0\right)\left[\frac{\left|\overline{\dot{x}}\right|}{2{\lambda }_x}+\frac{\left|\overline{\dot{y}}\right|}{2{\lambda }_y}+\frac{\left|\overline{\dot{z}}\right|}{2{\lambda }_z}\right]$$

(19)

In Equation (19), ${\mathsf{\Pi }}_x$ represents the proportion of time that a typical UAV is in longitudinal overlap with another UAV assigned to the same track and flight level. In addition, the rest of the parameters are defined the same as with the lateral and vertical collision risk model.

${\mathsf{\Pi }}_x$ can be represented as follows [26]:

$${\mathsf{\Pi }}_x=\frac{4{\lambda }_x}{S_x}{\displaystyle {\int }_{s}w\left(s\right)U\left(s\right)ds}$$

(20)

where $w\left(s\right)$ is the probability density function of longitudinal separation, $s$, between consecutive pairs of UAVs in the longitudinal direction; $U\left(s\right)$ is the probability that longitudinal overlap occurs between times $t=0$ and $t=T$, given an initial nominal separation, $s$; $T$ is the position reporting period plus the air traffic controller intervention buffer; and $S_x$ is the longitudinal separation.

$w\left(s\right)$ can be modeled as follows:

$$w\left(s\right)=\left\{\begin{array}{cc}1\hspace{1em}& for s=S_x\\ 0\hspace{1em}& otherwise\end{array}\right.$$

(21)

This means that consecutive pairs of UAVs in the longitudinal direction are exactly separated at $S_x$. The ideal condition was assumed to compute the capacity of the corridor. In addition, in the traffic data of manned aviation, the actual separation was longer than the separation minima [50]. Thus, by choosing the probability density function of longitudinal separation, as in Equation (21), the conservative value for the longitudinal collision risk can be evaluated, because the longer the longitudinal separation, the smaller the probability of longitudinal overlap $U\left(s\right)$ between reporting periods.

$U\left(s\right)$ can be written as in Equation (22). This means that the probability of actual separation at $t=T$ is smaller than ${\lambda }_x$, when the estimated separation at $t=0$ is $s$ [26].

$$U\left(s\right)=P\left(S_{t=T}\le {\lambda }_x|{\widehat{S}}_{t=0}=s\right)$$

(22)

It can be formulated as follows by assuming the position error and relative velocity distribution in the longitudinal direction. The detailed derivation process can be found in [50].

$$\begin{array}{l}U\left(s\right)=\frac{2k^4{T}^4}{4{\left(\lambda -kT\right)}^2\left(\lambda +kT\right)}{e}^{-\left(s-{\lambda }_x\right)/\left(kT\right)}\\ \hspace{1em}\hspace{1em}+\frac{2{\lambda }^2\left({\lambda }^2-2k^2{T}^2\right)+\lambda \left({\lambda }^2-k^2{T}^2\right)\left(s-{\lambda }_x\right)}{2{\left(\lambda -kT\right)}^2{\left(\lambda +kT\right)}^2}{e}^{-\left(s-{\lambda }_x\right)/\lambda }\end{array}$$

(23)

where $\lambda$ is the shape parameter for the probability density function of the longitudinal navigation error of the UAV. In this study, $\lambda$ was determined from the 95% horizontal accuracy of the KASS. It was modeled using the double exponential (DE) distribution as follows [26,50]:

$$g\left(x\right)=\frac{1}{2\lambda }{e}^{\left(-\frac{\left|x\right|}{\lambda }\right)}$$

(24)

Note that, because of the non-simultaneous nature of the position reports of pairs of aircraft, the position of one of the aircrafts in a pair should be extrapolated forward in time to coincide with the reporting time of the other aircraft. Thus, the probability density function of the longitudinal position error of one of the aircraft in a pair is expressed as the sum of two DE random variables; one of the DE random variables represents the horizontal position error of the KASS and another DE random variable represents the extrapolation error [26]. However, if we assume that the position was extrapolated using GPS (global positioning system) velocity, which is a cm/s level in the literature [51], and the reporting period of UAV is less than few seconds, then the extrapolation error can be neglected. Therefore, in this study, a single DE distribution function was used to model the longitudinal position error of UAVs.

Moreover, $k$ is the shape parameter for the probability density function of the relative velocity in the longitudinal direction. In the literature, it was also modeled using the DE distribution as follows [50]:

$${\varphi }_x\left(v\right)=\frac{1}{2k}{e}^{\left(-\frac{\left|v\right|}{k}\right)}$$

(25)

For $k$, the average longitudinal relative velocity is presented as 1.0289 m/s in a previous study [20]; thus, the three values of 95% relative velocity were simulated as 1, 3, and 5 m/s. In the DE distribution, the shape parameter can be computed by dividing the 95% value by 2.996.

Finally, the longitudinal collision risk can be linked with the traffic flow rate as follows:

$$S_x=V_x/m$$

(26)

Note that, in manned aviation, the position reporting update rate is much longer than the UAV, for example, 15 or 30 min. However, in the case of UAVs, the reporting period is expected to be very short, such as few seconds. In the literature, it is already mentioned that the longitudinal technical collision risk with high update rate will be very small [46]. It was also confirmed from the simulation results of this study. The longitudinal collision risk was found to be negligible with a less than 10 s reporting period. As a result, it was found that for a high position update rate condition, the lateral and vertical collision risks dominated the total collision risk. It will be quantitatively described in the next section.

4.3. Capacity Analysis Result for the UAV Corridor

Finally, the ground risk due to collisions and failures can be evaluated using Equations (10) and (12). The target level of safety for third parties on the ground was selected as 10⁻⁶ (fatalities/flight hour) [5]. In addition, the conditional ground risk $N_{HH|fall}$ was computed as 0.049 in Section 3.5.

We considered two cases of failure rates, as shown in

Table 8. Failure rate of UAVs.

Case	Failure Rate (Number of Failures/Flight Hour)
1	10−5
2	10−6

, and the parameters used in the lateral and longitudinal collision risks are presented in

Table 9. Parameters for the lateral collision risk evaluation.

Parameter	Description	Value
$a_1$	Shape parameter of the DE (double exponential) distribution of the nominal navigation error, computed from the 95% horizontal accuracy of the KASS (Korea Augmentation Satellite System) (16 m)	5.3405 m
$a_2$	Shape parameter of the DE distribution of the abnormal navigation error, assumed the same as $S_y$ 1	50 m
$\alpha$	Weighting factor representing the percentage of UAVs (unmanned aerial vehicles) that experience lateral navigation anomalies	0.05
${\lambda }_x$	Size of the UAV in the longitudinal direction 2	1.255 m
${\lambda }_y$	Size of the UAV in the lateral direction 2	1.255 m
${\lambda }_z$	Size of the UAV in the vertical direction 2	0.485 m
$\left|\overline{\dot{x}}\right|$	Relative velocity among UAVs in the longitudinal direction 3	1.0289 m/s
$\left|\overline{\dot{y}}\right|$	Relative velocity among UAVs in the lateral direction 3	1.0289 m/s
$\left|\overline{\dot{z}}\right|$	Relative velocity among UAVs in the vertical direction 3	0.0772 m/s
$P_z\left(0\right)$	Probability of two UAVs nominally at the same level in vertical overlap, computed from the DE distribution by using 20 m of 95% vertical positioning accuracy of the KASS	0.0363
$S_y$	Lateral separation	50 m
$V_x$	Average velocity of the UAV 2	15 m/s

¹$a_2$ is selected as $S_y$ by referring to [26,45]. ² This is from Table 1. ³ Relative velocity determined by referring to [20].

and

Table 10. Parameters for longitudinal collision risk evaluation ¹.

Parameter	Description	Value
$\lambda$	Shape parameter of the DE distribution of the longitudinal navigation error, computed from the 95% horizontal accuracy of the KASS (16 m)	5.3405 m
$k$	Shape parameter of the DE distribution of the relative velocity of UAVs in the longitudinal direction, three values of 95% relative velocity were assumed: 1, 3, and 5 m/s	0.3338 m/s 1.0013 m/s 1.6689 m/s
$P_y\left(0\right)$	Probability of lateral overlap of UAVs nominally flying on the same track, computed from the DE distribution by using 16 m of 95% horizontal positioning accuracy of the KASS	0.1175

¹ The same parameters as in Table 9 were omitted.

.

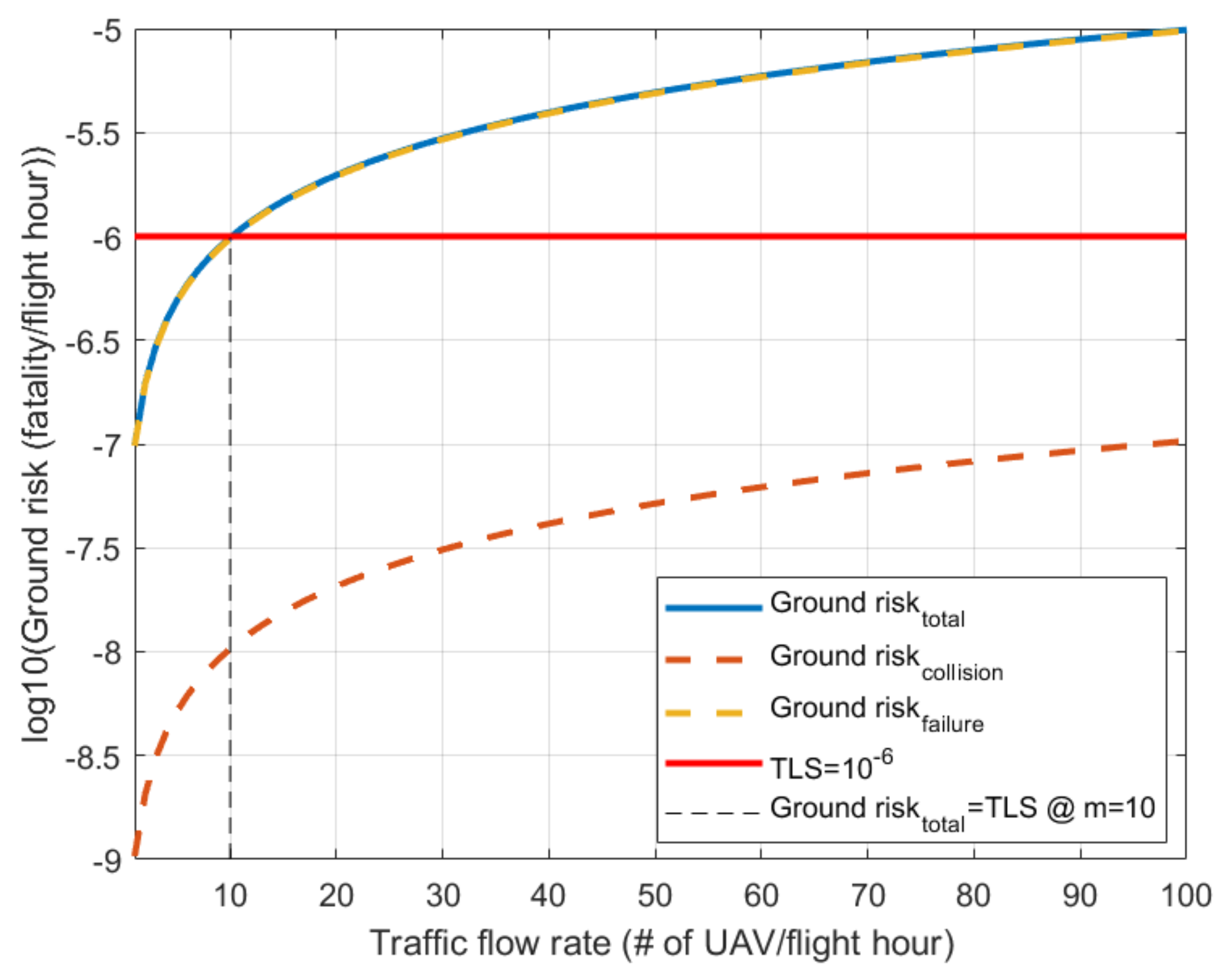
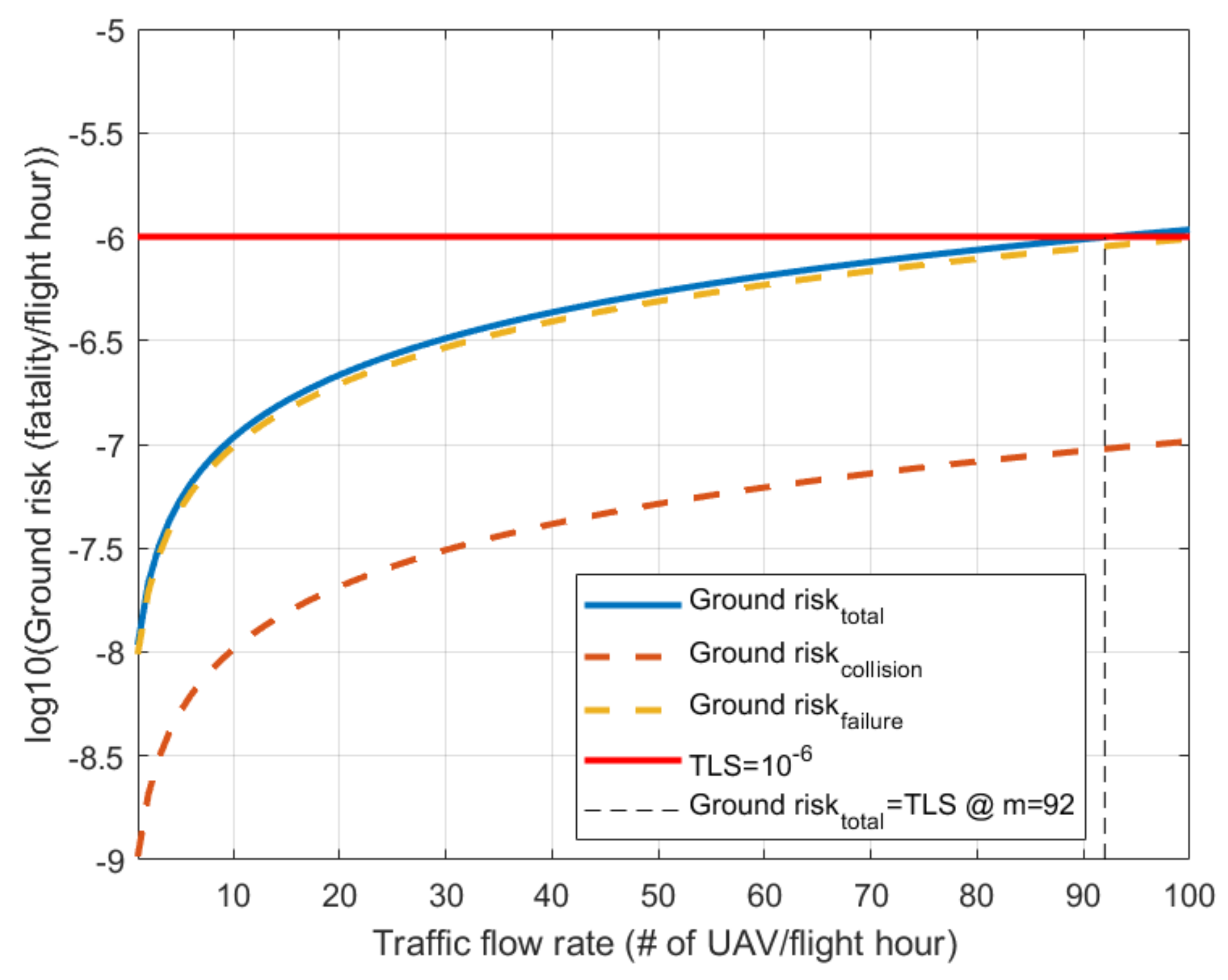
Figure 9 and Figure 10 show the resulting total ground risk due to failure and collision of UAVs. Figure 9 is the result of case 1 in Table 8 in which the failure rate was assumed as 10⁻⁵. Similarly, Figure 10 is the result of case 2 in Table 8 with a failure rate of 10⁻⁶. In Figure 9 and Figure 10, the total ground risks are evaluated by combining the ground risk due to failure and collision. In this regard, the maximum flow rate of the corridor can be evaluated to satisfy TLS. Note that only the lateral collision risk is considered in the results in Figure 9 and Figure 10, because the longitudinal collision risk is negligible, and the vertical collision risk is zero.

For case 1, 10 is the number of UAVs that can be flown in the corridor per hour. In addition, for case 2, 92 is the number of UAVs that can be flown per hour. For convenience, we rounded off the traffic flow rate to the integer value. As a result, the maximum flow rates for both cases are summarized in

Table 11. Capacity of the corridor.

Case	Maximum Traffic Flow (No. of UAV/Flight Hour)
1	10
2	92

.

From Figure 9 and Figure 10, it can be seen that the capacity of the corridor was dominated by the failure rate of UAVs rather than the collision risk. In case 1, the ground risk due to failure was 100 times larger than the ground risk due to collision. In addition, in case 2, the difference was 10 times. If the larger value of the failure rate was used, this difference would increase. Therefore, it can be known from the above results that the failure rate of UAVs is the most important factor for evaluating the third-party risk on the ground.

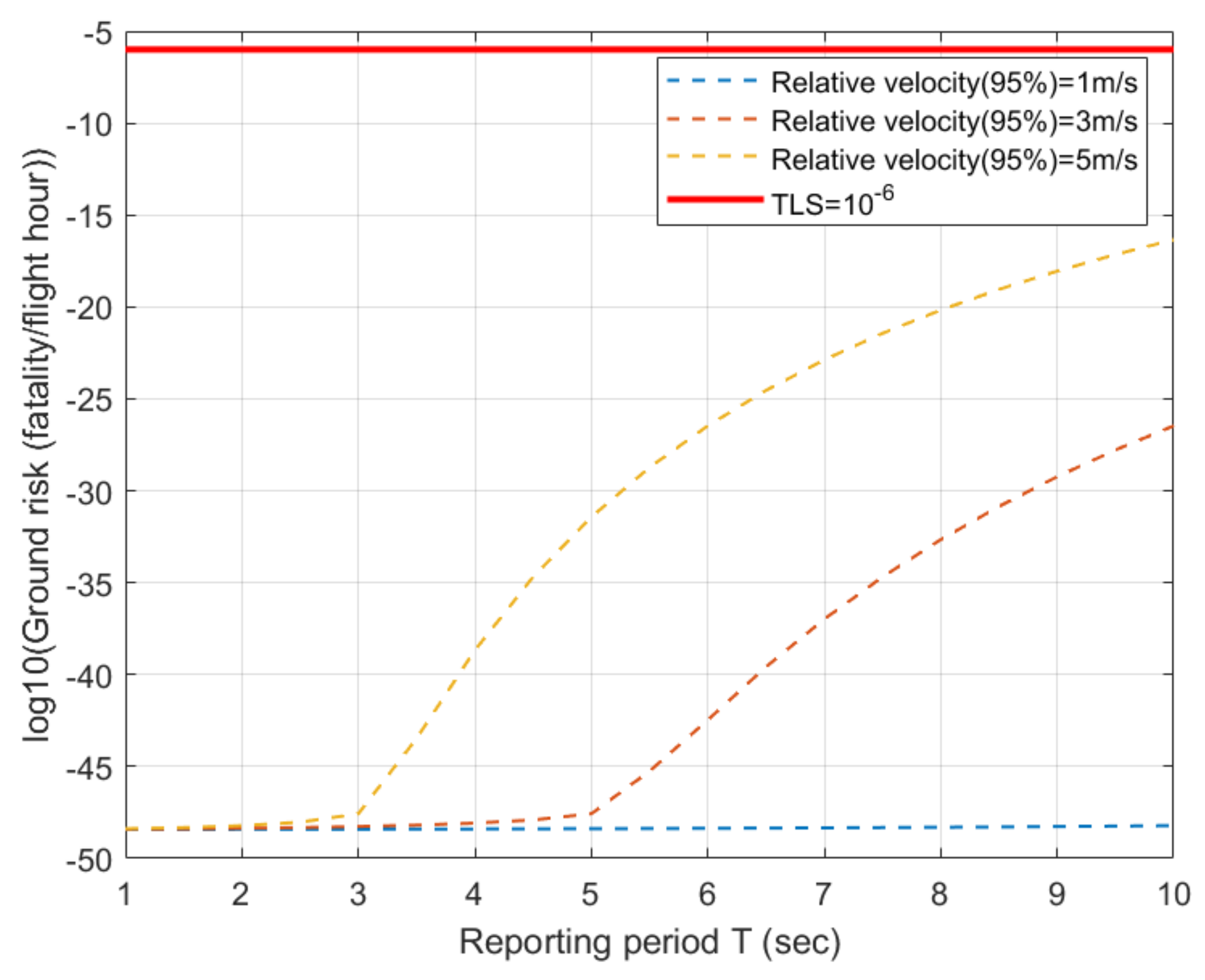
On the other hand, the ground risk due to longitudinal collisions was also investigated by applying the longitudinal separation of case 2. By using Equation (26), the longitudinal separation can be computed as 587 m. The longitudinal separation was larger in case 1; thus, the longitudinal collision risk would be smaller. Figure 11 shows the ground risk due to the longitudinal collision risk. The three values of relative velocity were assumed as in Table 10. For all three values, the ground risks due to the longitudinal collision risk were very small. The maximum value at $T=10 \mathrm{s}$ and 5 m/s of 95% relative velocity is 2.5661 × 10⁻¹⁹, which is negligible compared with the ground risk due to the lateral collision risk in Figure 9 and Figure 10. This was because of the high position reporting rate of UAVs.

In addition, we investigated the result when number of corridors increased laterally in the case of $FR={10}^{-6}$. The conditional ground risk was held the same as 0.049. By increasing the number of corridors, the ground risk due to failures would increase by considering Equation (8). In addition, the ground risk due to collisions would increase because the occupancy presented in Equation (17) would increase. If we assume that the corridor was added laterally and the flight direction between two consecutive corridors is opposite and the traffic flow rates of all corridors were identical, then the occupancy in Equation (17) can be written as follows:

$$E_o=\frac{4{\lambda }_x}{V_x}\frac{\left(n-1\right)\times m^2}{n\times m}$$

(27)

Note that the same directional occupancy is zero because the occupancy is evaluated for two consecutive corridor pairs. For this case, every consecutive pair of corridors has an opposite flight direction.

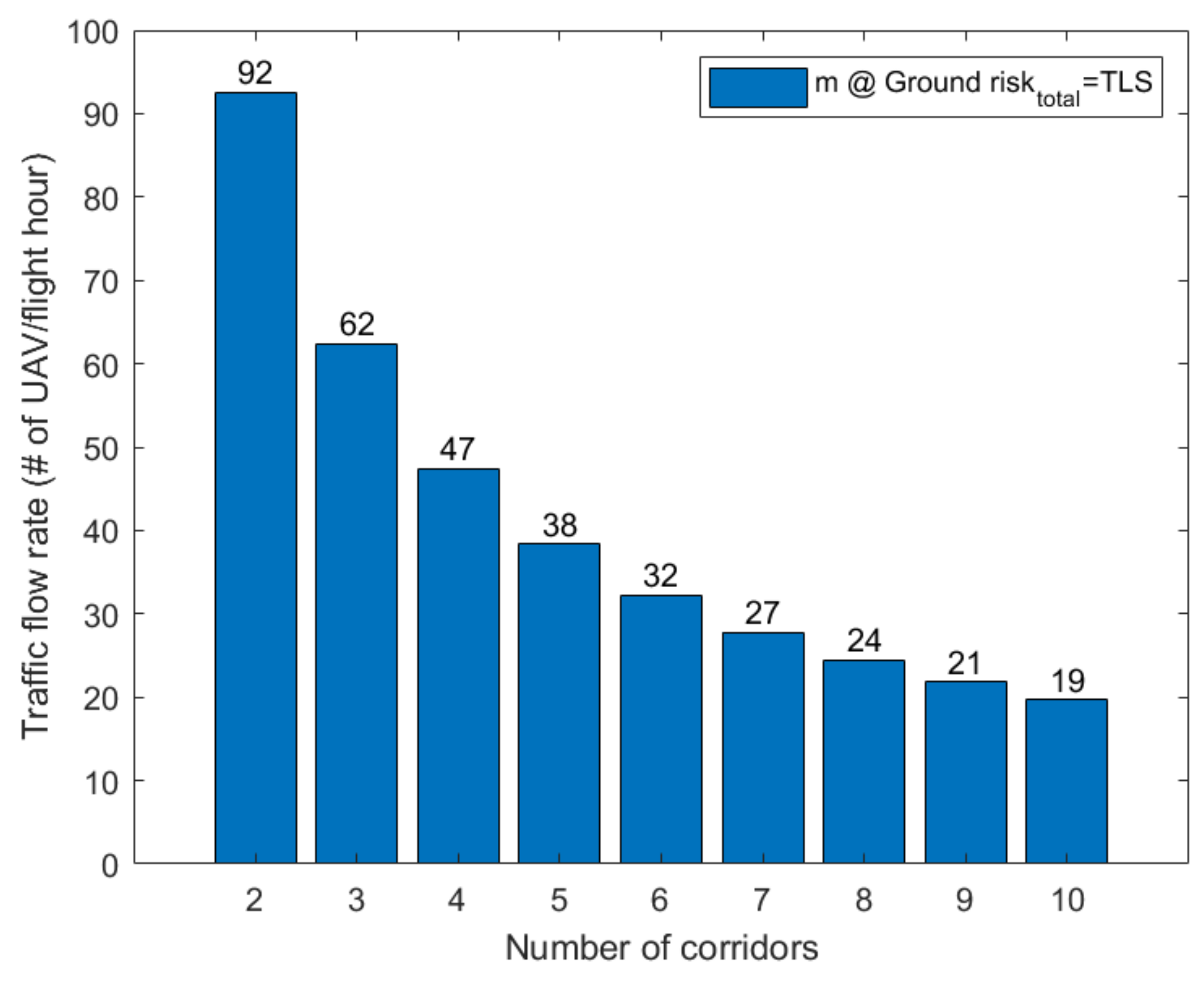
Figure 12 shows the ground risk composition when the total ground risk was equal to TLS in the case of $FR={10}^{-6}$. It was found that the ground risk due to the failure rate became more dominant as the number of corridors increased. A similar result can be expected when the number of corridors increases in the vertical direction. Figure 13 shows the maximum traffic flow rate according to the number of corridors. As expected, as the number of corridors increased, the capacity of the corridor decreased.

In summary, we found that the failure rate of UAVs is the major factor contributing to the ground risk even if the number of corridors increases. This is because the ground risk due to failures is proportional to the number of corridors, $n$, whereas the ground risk due to collisions increased as a function of $n-1/n$.

5. Conclusions

This paper proposed a risk-based capacity analysis methodology by combining the conditional ground risk and the crash rate due to the failure rate and collisions of UAVs. The conditional ground risk map was generated by choosing the appropriate subcomponent models of the ground risk model in the previous studies. In addition, real databases containing information regarding Seoul, the population density, car traffic density, building-to-land ratio, and the building structure code were utilized. To analyze the conditional ground risk of the corridor, the arbitrary corridor location was selected, and the resulting conditional ground risk was 0.049 fatalities/crash. This means that an average of 0.049 fatalities occur when an arbitrary UAV in the corridor crashes on the ground.

To evaluate the crash rate due to failures and collisions as a function of traffic flow rate of the corridor, the Reich collision risk model used in manned aviation was applied to compute crash rate due to collision and the fallen UAVs due to failure can be computed by using a simple equation. As a result, the maximum traffic flow rate of the corridor can be derived by combining these together. From the result, we found that the failure rate of UAV was the dominant factor when deciding the capacity of the corridor. In addition, it was also found that the longitudinal collision risk was negligible in the case of UAVs in which the position reporting period was very short, such as less than a few seconds.

Furthermore, the effect of the increase in the corridor was investigated, and it was determined that as the number of corridors increases, the ground risk due to the failure rate becomes more dominant. Therefore, to manage the third-party risk due to the operations in the corridor, the failure rate of UAVs should be specified and properly proved to fly in the corridor. In addition, it can be predicted that the collision risk will decrease more if the UAV is equipped with a DAA system. Then, this will make the failure rate a more important factor. The proposed risk-based capacity analysis method did not consider the above mitigations; thus, it can be a conservative starting point for determining the capacity of the corridor. Furthermore, it can be difficult to quantitatively evaluate the amount of mitigation due to the DAA system. To increase the capacity of the corridor, equipment, such as a parachute, can be a preferable option, because it can reduce the kinetic energy of fallen UAVs effectively for both cases of failure and collision.

The novelty of this work lies in the fact that we proposed a method for the quantitative evaluation of the maximum possible number of flights in a UAV corridor based on the third-party risk on the ground. This has not yet been suggested in previous studies. Therefore, the proposed capacity analysis methodology could be useful for managing the total number of flights for applications in which a UAV corridor is fixed and flight continues, such as for the delivery of goods.

Note that the collision risk model used in this work was originally developed for manned aviation. In this model, the lateral and vertical models do not account for air traffic controller intervention, while longitudinal models do. In the case of UAVs, the role of the air traffic controller is replaced by the UTM. Therefore, in the future, it is necessary to improve the collision risk model to account for the actual UTM separation service provision. Furthermore, other factors, such as noise pollution and the concurrent processing capability of the UTM system, are also needed to analyze and determine the final capacity of the corridor.