Rapid Evaluation Model of Endurance Performance and Its Application for Agricultural UAVs
Abstract
:1. Introduction
2. Materials and Methods
2.1. UAV Load Distribution Characteristics
2.2. Power Distribution Characteristics of Electric Quadrotors
2.2.1. Module Power Data Measurement
2.2.2. Module Output Power Function Fitting
2.2.3. Static Energy Consumption Module
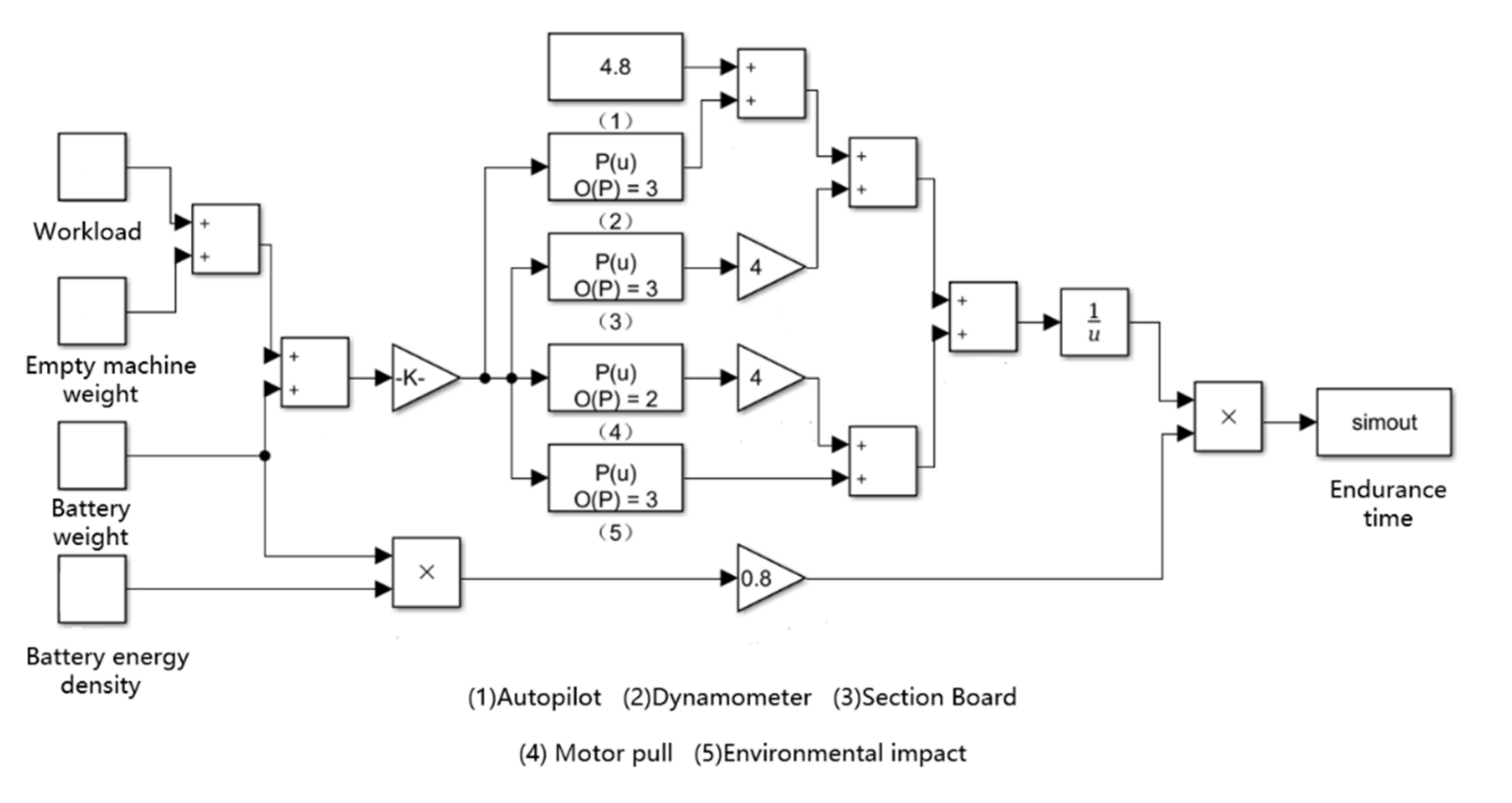
2.3. Endurance Evaluation Model of Agricultural UAVs
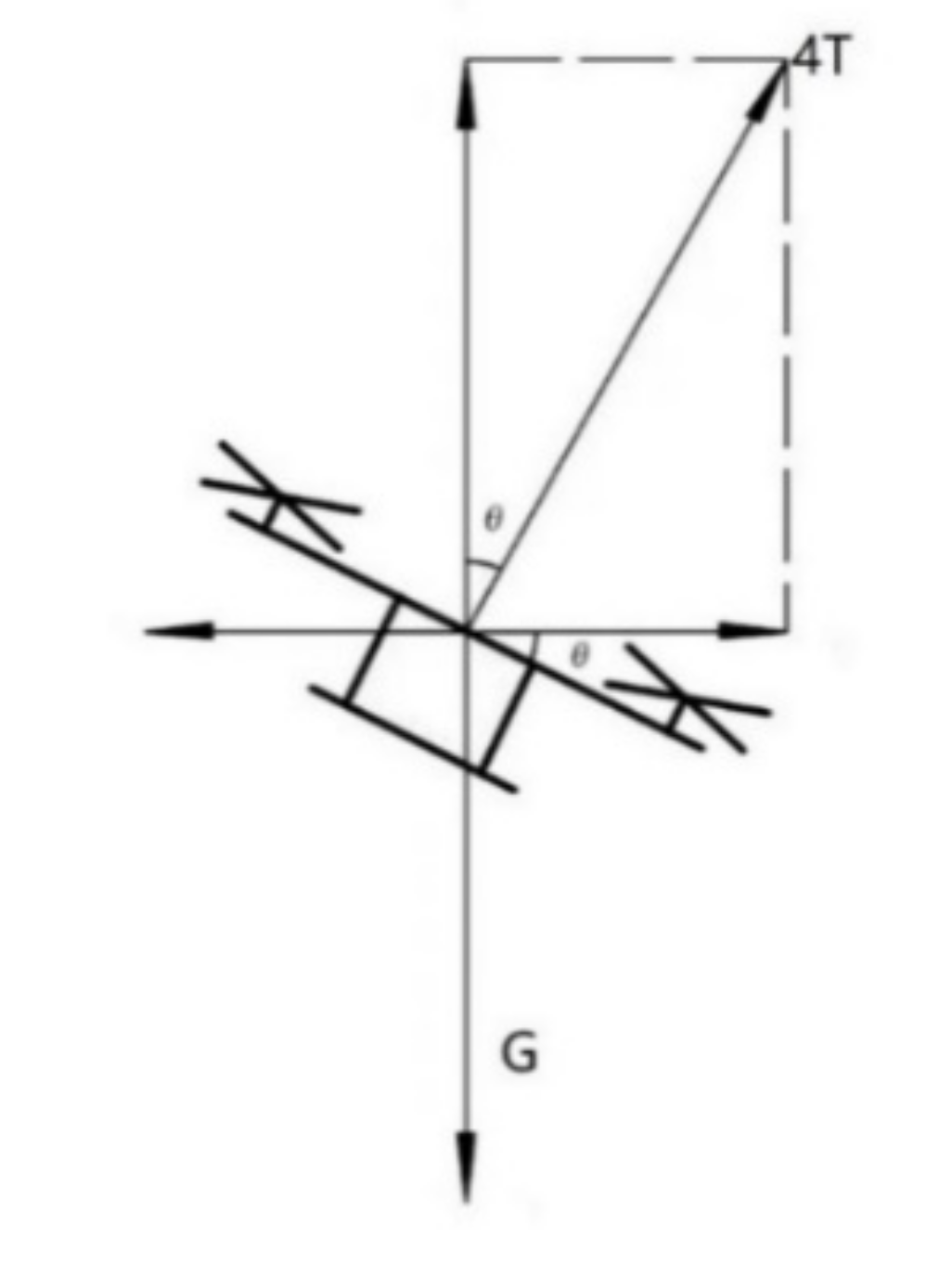
2.3.1. Theoretical Analysis of the Evaluation Model
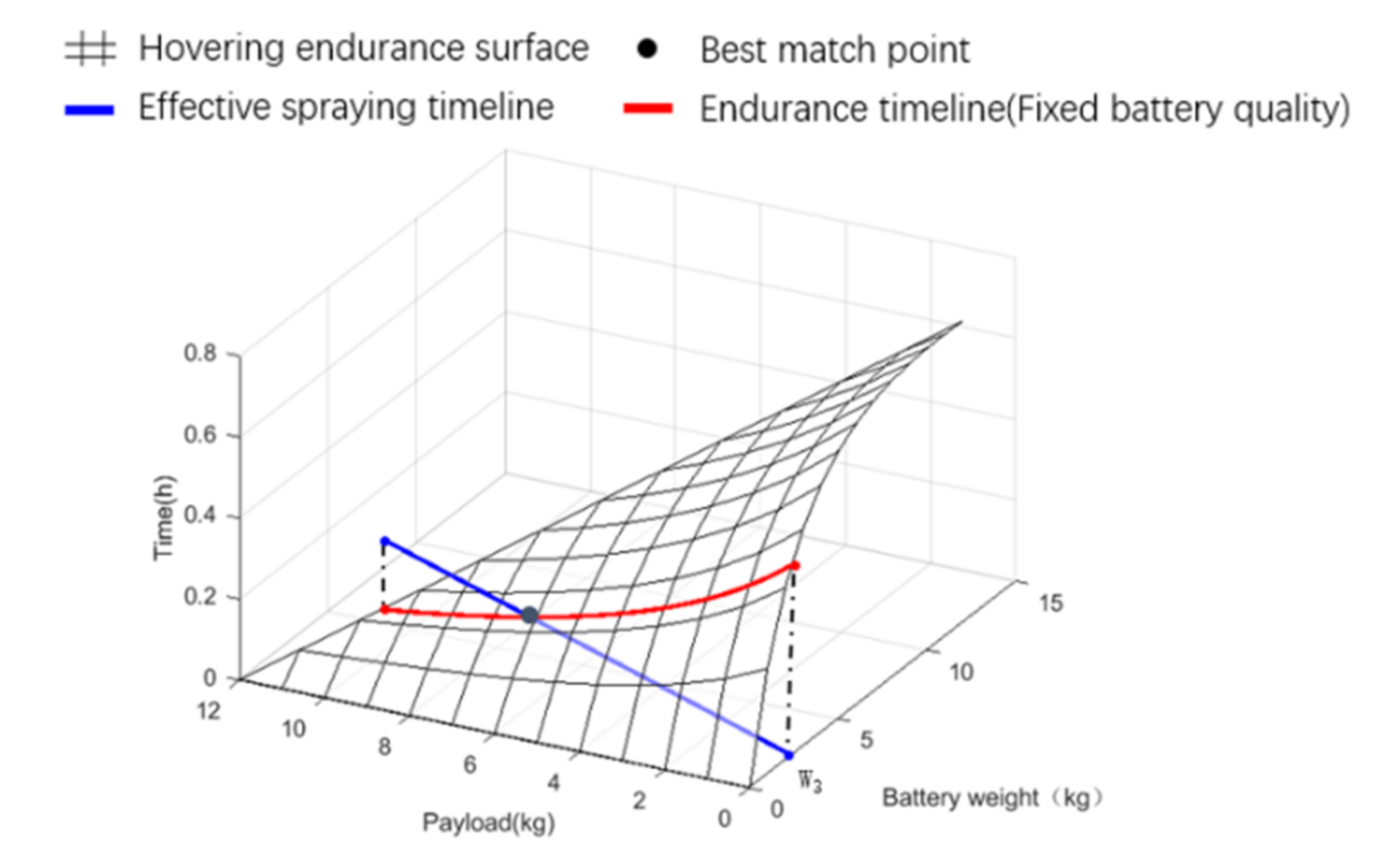
2.3.2. Endurance Evaluation Model
2.3.3. Model Calculation Results
3. Model Validation
3.1. Calculation Method of Equivalent Endurance
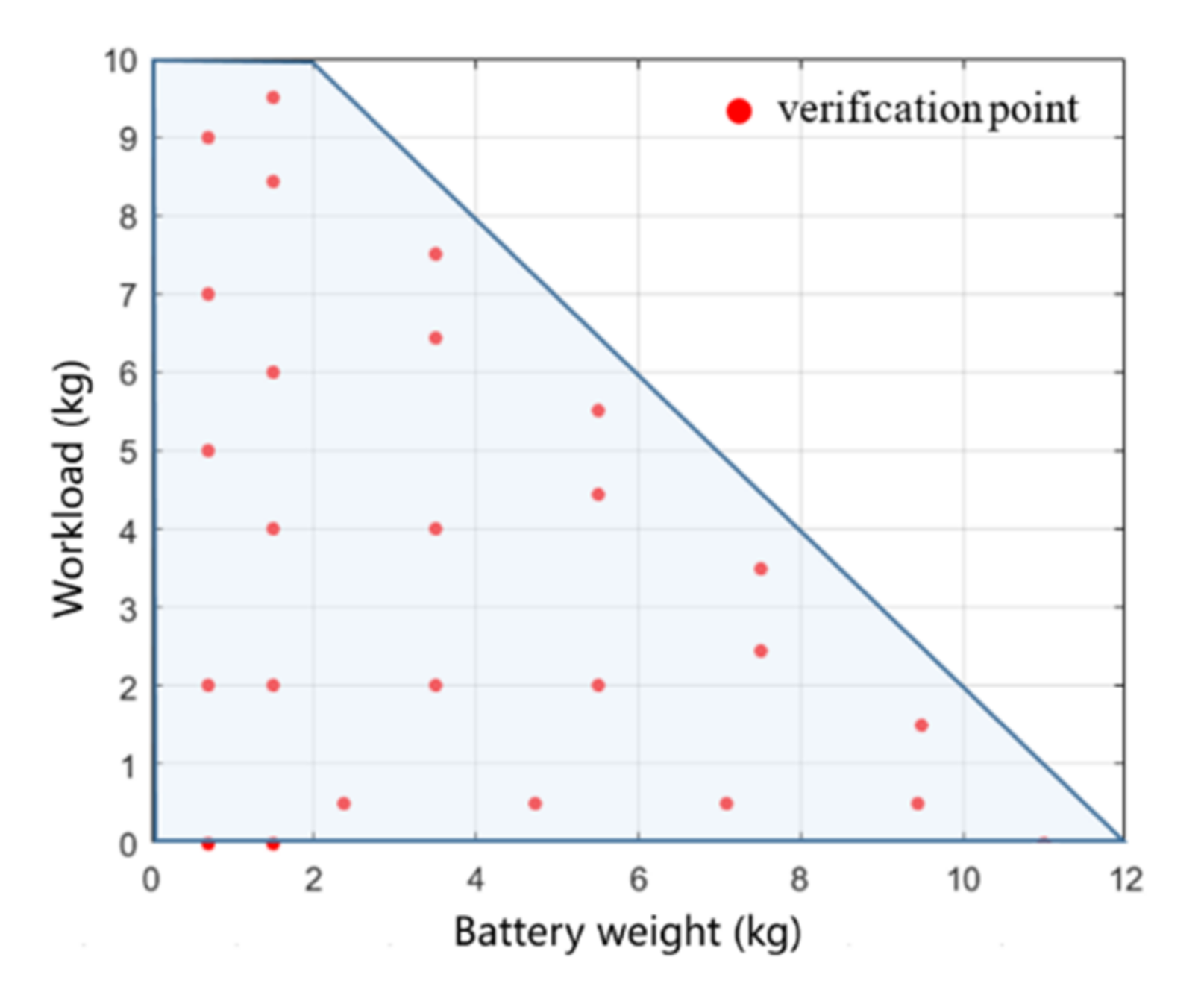
3.2. Distribution of Verification Points on the Endurance Surface
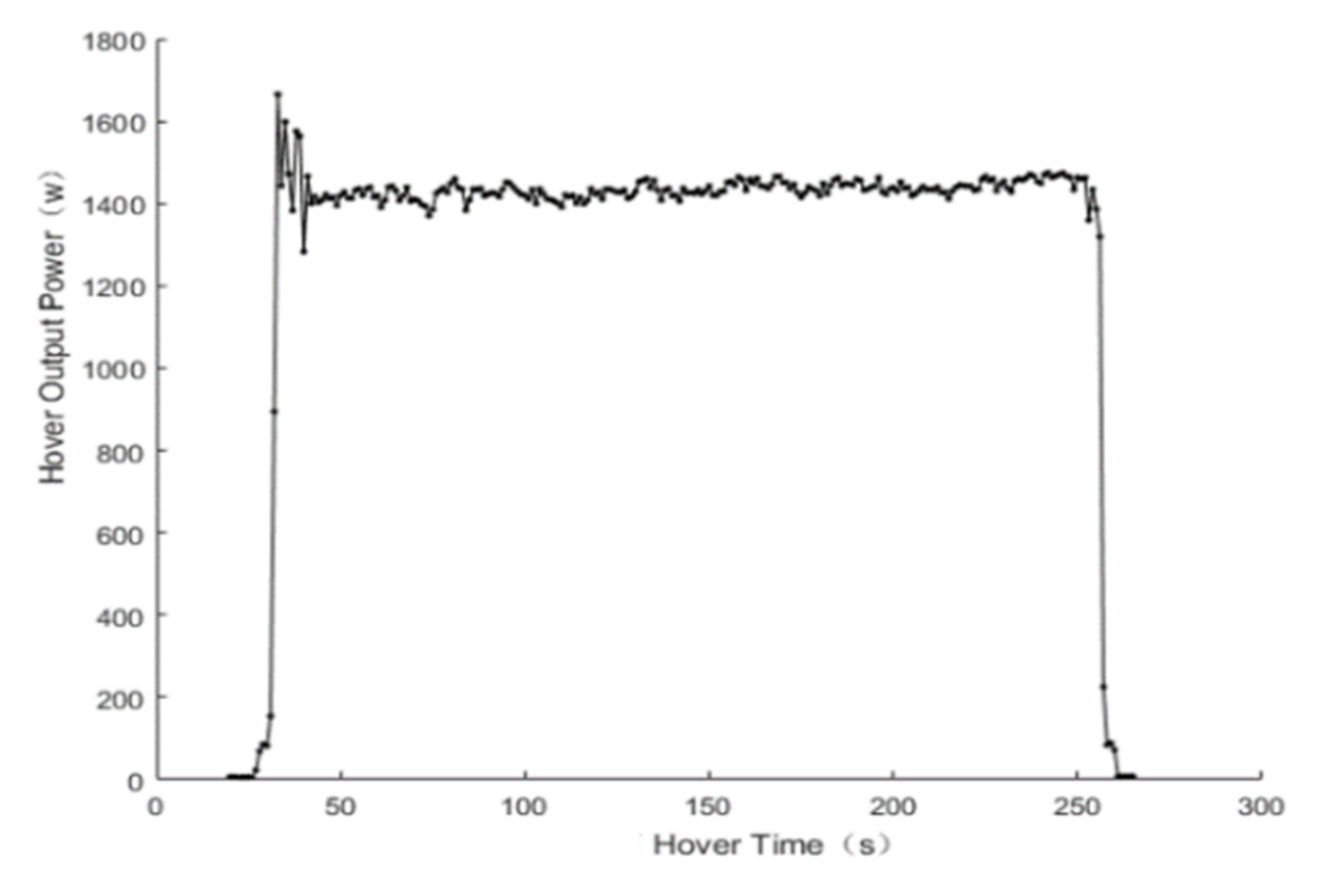
3.3. Verification Point Endurance Test
4. Results and Discussion
4.1. Verification of Experimental Results
4.2. Error Analysis
4.3. Model Application
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guang, B.; Xin, S.; Shuang, C.; Wen, Q. Multiple UAV Cooperative Trajectory Planning Based on Gauss Pseudospectral Method. J. Astronaut. 2014, 35, 10–22. [Google Scholar] [CrossRef]
- Zhang, D.; Lan, Y.; Chen, L.; Wang, X.; Liang, D. Current Status and Future Trends of Agricultural Aerial Spraying Technology in China. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2014, 45, 53–59. [Google Scholar]
- Zhang, B.; Zhai, C.; Li, H.; Han, S. Development Status Analysis of Precision Pesticide Application Techniques and Equipments. J. Agric. Mech. Res. 2016, 4, 1–5. [Google Scholar]
- Tang, W.; Song, B.; Cao, Y.; Yang, W. Preliminary Design Method for Miniature Electric-Powered Vertical Take-off and Landing Unmanned Airial Vehicle and Effects of Special Parameters. Acta Aeronaut. Astronaut. Sin. 2017, 38, 120–133. [Google Scholar] [CrossRef]
- Pei, Y. Analysis of the Mechanical Characteristics of the Transmission System of a Heavy-Duty Four-Rotor UAV; Shenyang University of Technology: Shengyang, China, 2019. [Google Scholar]
- Zhang, D.; Li, J.; Wang, Y. Development Status and Trends of High-Altitude and Long-Endurance UAVs. In Proceedings of the 2014 (Fifth) China UAV Conference, Beijing, China, 9 July 2014. [Google Scholar]
- Zhou, Z.; Ming, R.; Zang, Y.; He, X.; Luo, X.; Lan, Y. Development Status and Countermeasures of Agricultural Aviation in China. Trans. Chin. Soc. Agric. Eng. 2017, 33, 1–13. [Google Scholar] [CrossRef]
- He, X. Improving Severe Draggling Actuality of Plant Protection Machinery and Its Application Techniques. Trans. Chin. Soc. Agric. Eng. 2004, 20, 13–15. [Google Scholar] [CrossRef]
- Xie, C.; Duan, Y.; Xu, W.; Zhang, H.; Li, X. A Low-Cost Neutral Zinc–Iron Flow Battery with High Energy Density for Stationary Energy Storage. Angew. Chem. 2017, 129, 15149–15153. [Google Scholar] [CrossRef]
- Zeng, H.; Wang, Y.; Zhang, Z. Mathematical Derivation and Analysis of Factors Affecting the Performance of Permanent Magnet Brushless DC Motors. J. Liaoning Univ. Technol. Nat. Sci. Ed. 2020, 40, 29–32. [Google Scholar]
- Lian, H.; Zhang, C.; Li, G. Overview of the Performance of Long-Endurance Multi-Rotor Drones. Proceedings of OSEC First Ordnance Engineering Conference, Chongqing, China, 15–16 September 2017. [Google Scholar]
- Guo, Y.; Yuan, H.; He, X. Development Status and Prospect Analysis of My Country’s Agricultural Aviation Plant Protection. China Plant Prot. Guide 2014, 34, 78–82. [Google Scholar]
- Thibbotuwawa, A.; Nielsen, P.; Zbigniew, B.; Bocewicz, G. Energy Consumption in Unmanned Aerial Vehicles: A Review of Energy Consumption Models and Their Relation to the UAV Routing. In Information Systems Architecture and Technology: Proceedings of 39th International Conference on Information Systems Architecture and Technology—ISAT 2018; Świątek, J., Borzemski, L., Wilimowska, Z., Eds.; Springer International Publishing: Cham, Swizterland, 2019; pp. 173–184. [Google Scholar]
- Liu, Z.; Sengupta, R.; Kurzhanskiy, A. A Power Consumption Model for Multi-Rotor Small Unmanned Aircraft Systems. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Zhuhai, China, 27–29 October 2017; pp. 310–315. [Google Scholar]
- Traub, L.W. Validation of Endurance Estimates for Battery Powered UAVs. Aeronaut. J. 2013, 117, 1155–1166. [Google Scholar] [CrossRef]
- Tang, W.; Song, B.; Cao, Y. The Overall Design Method of Micro Electric Vertical Take-off and Landing UAV and the Influence of Special Parameters. Acta Aeronaut. Sin. 2017, 30, 115–128. [Google Scholar]
- An, S.; Liu, X.; Hou, K. Establishment of the Dynamic Model of the Electric Power System of a Slight UAV. J. Harbin Univ. Sci. Technol. 2020, 3, 33–39. [Google Scholar]
- Jin, J.; Zhu, Y.; Zeng, S. Research on the Endurance of Small Multi-Rotor Drones. Comput. Knowl. Technol. 2017, 13, 197–199. [Google Scholar]
- Liu, F.; Ma, X. Research for Improving the Endurance Performance of Minitype Electric-Powered UAV. Flight Dyn. 2010, 5, 13–15. [Google Scholar] [CrossRef]
- Lu, J.; Cen, H. The Application Status and Problems of Small Drones in Agricultural Plant Protection. Use Maint. Agric. Mach. 2014, 5, 123. [Google Scholar]
- Liu, S.; Li, Q.; Lu, N. A Method for Estimating the Endurance of Micro Electric Drones. In Proceedings of the 26th China Control and Decision Conference, Zhangjiajie, China, 31 May–2 June 2014. [Google Scholar]
- Lin, J.; Lan, Y.; Ouyang, F.; Li, J.; Chen, P. Construction and Experimental Verification of Power Consumption Model for Multi Rotor Agricultural UAV. J. Agric. Mech. Res. 2020, 42, 149–155. [Google Scholar]
- Zhu, X.; Zhu, J.; Wang, J.; Gan, Z.; Meng, C. Experimental Study on Long Cycling Performance of NCM523 Lithium-Ion Batteries and Optimization of Charge-Discharge Strategy. J. Therm. Sci. 2020, 29, 1180–1192. [Google Scholar] [CrossRef]
- High Temperature Operation Battery Maintenance of Plant Protection Drone. Agric. Mach. 2020, 873, 56.
- Li, J.; Zhan, Y.; Ou, Y.; Li, Y.; Lan, Y. Rotor Spacing Optimization and Energy Consumption Test of a Multi-Wing Single-Arm Tandem Electric UAV. Trans. Chin. Soc. Agric. Eng. 2019, 35, 87–95. [Google Scholar]
- Azaceta, E.; García, S.; Leonet, O.; Beltrán, M.; Gómez, I.; Chuvilin, A.; Mainar, A.R.; Blazquez, J.A.; Knez, M. Particle Atomic Layer Deposition as an Effective Way to Enhance Li-S Battery Energy Density. Mater. Today Energy 2020, 18, 100567. [Google Scholar] [CrossRef]
- Li, J.; Zhou, Z.; Lan, Y.; Hu, L.; Zang, Y.; Liu, A.; Luo, X.; Zhang, T. Distribution of Canopy Wind Field in Pollination Operation of Rotary-Wing UAV. Trans. Chin. Soc. Agric. Eng. 2015, 31, 85–94. [Google Scholar]
- Li, J.; Luo, H.; Zhu, C.; Li, Y.; Tang, F. Research and Implementation of Combination Algorithms about UAV Spraying Planning Based on Energy Optimization. Trans. Chin. Soc. Agric. Mach. 2019, 50, 106–115. [Google Scholar]
- Xu, B.; Chen, L.; Tan, Y.; Xu, M. Study on the Minimum Energy Trajectory Planning Algorithm for Plant Protection Drones with Multiple Sorties. Trans. Chin. Soc. Agric. Mach. 2015, 46, 43–49. [Google Scholar]
- Fan, Y.; Shen, K.; Wang, D.; Zhai, C.; Zhang, H. Optimal Path Planning of Energy Consumption for UAV Mountain Operations Based on Simulated Annealing. Algorithm Trans. Chin. Soc. Agric. Mach. 2020, 51, 34–41. [Google Scholar]
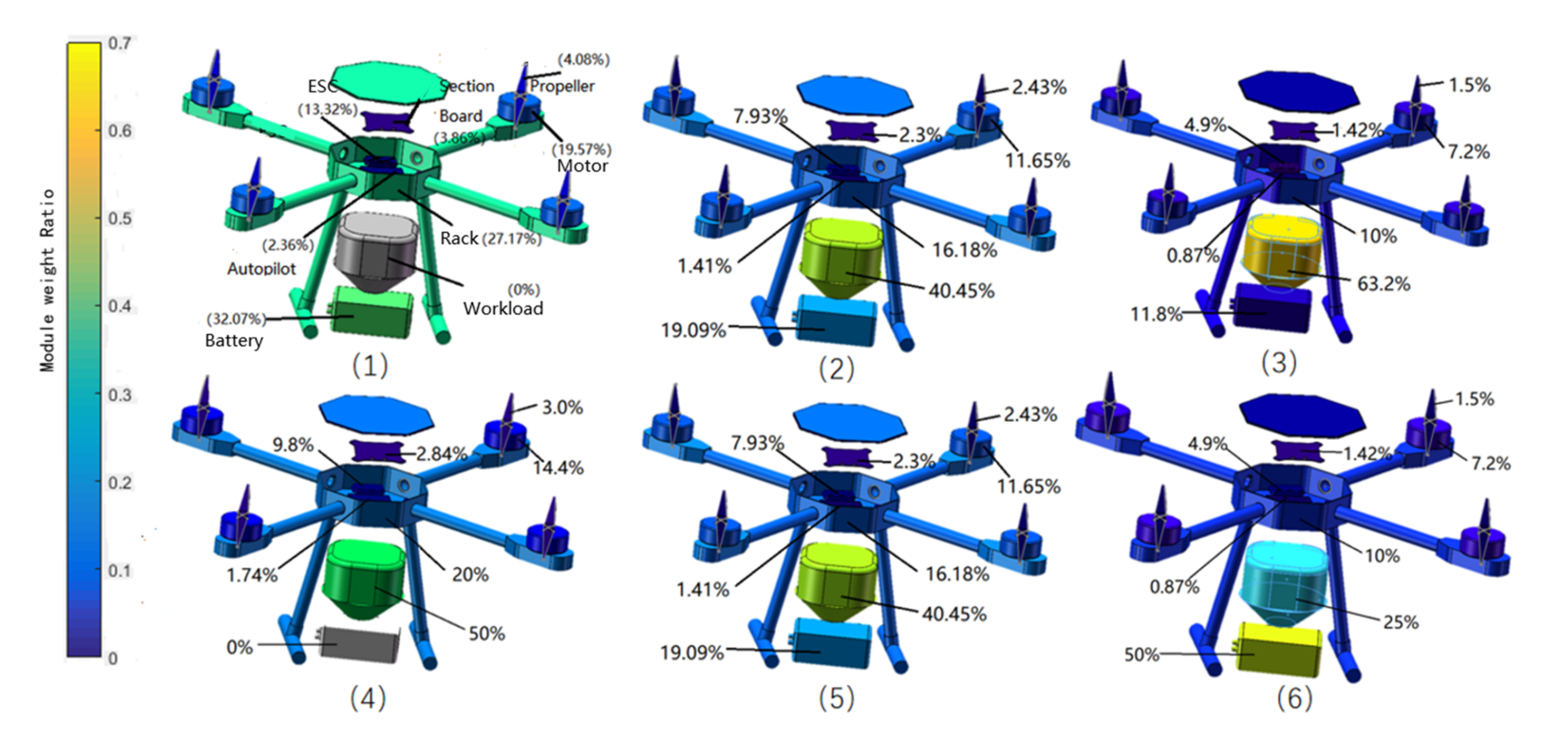




| Model/Parameter | Rack | Motor | ESC | Propeller | Section Board | Empty Weight | Maximum Weight | Standard Payload |
| AX-1000 | Sunnysky 6215/350 kV | Hobbywing 80 A/120 A MAX | Sunnysky 22 inch/22 × 6.6 | EFT-V3/12S200A | 5 kg | 17 kg | 5 kg |
| Main Equipment | Type | Precision | Power Supply Form |
|---|---|---|---|
| DC power power | LP220DE | Voltage regulation error: ≤0.01% + 2 mA | AC 220 V ± 10% |
| Motor test bench | LY-30 | Tension sensor: ≤0.05% ± 10 g | AC 220 V |
| Voltage sensor: ≤1.0% | |||
| current sensor: ≤1.0% + 0.1 A | |||
| Dynamometer | ZFT8 | Power sensor: ≤0.01% | DC 4.5 V–150 V |
| Motor Pull (kg) | Pull Curve (w) | Section Board (w) | Dynamometer (w) | Environmental Impact (w) |
|---|---|---|---|---|
| 1.90 | 179.00/92.53% | 6.38/3.30% | 2.77/0.36% | 29.55/3.82% |
| 2.27 | 230.00/92.78% | 6.64/2.68% | 3.08/0.31% | 41.97/4.23% |
| 2.70 | 294.00/92.14% | 6.64/2.68% | 3.08/0.31% | 41.97/4.23% |
| 3.16 | 362.00/91.27% | 8.11/2.04% | 3.48/0.22% | 102.50/6.46% |
| 3.57 | 441.00/91.05% | 9.26/1.91% | 3.80/0.20% | 132.50/6.84% |
| 4.03 | 523.00/90.92% | 11.55/2.01% | 4.47/0.19% | 158.30/6.88% |
| 4.45 | 605.00/91.18% | 15.42/2.32% | 5.14/0.19% | 167.20/6.30% |
| 4.84 | 692.00/91.79% | 17.31/2.30% | 6.11/0.20% | 172.30/5.71% |
| Battery Brand | Capacity (mah) | Weight (kg) | Total Energy (wh) | Energy Density (wh/kg) |
|---|---|---|---|---|
| Kudian | 16,000 | 2.7 | 555.2 | 205.6 |
| DJI MG1 | 12,000 | 1.85 | 366.4 | 198.05 |
| XAG P20 | 16,000 | 4.53 | 850 | 187.64 |
| DJI T16 | 17,500 | 4.75 | 906 | 190.84 |
| Battery Weight (kg) | Payload (kg) | Test #2 (h) | Test #1 (h) | Test #3 (h) | Model Calculation Results (h) | Average Error Rate |
|---|---|---|---|---|---|---|
| 0.70 | 0 | 0.203 | 0.203 | 0.202 | 0.203 | 0.164 |
| 0.70 | 2.00 | 0.137 | 0.135 | 0.135 | 0.136 | 0.499% |
| 0.70 | 5.00 | 0.088 | 0.090 | 0.086 | 0.088 | 0.309% |
| 0.70 | 7.00 | 0.070 | 0.072 | 0.070 | 0.072 | 1.458% |
| 0.70 | 9.00 | 0.056 | 0.058 | 0.055 | 0.058 | 2.695% |
| 1.50 | 0 | 0.366 | 0.368 | 0.364 | 0.366 | 0.039% |
| 1.50 | 2.00 | 0.256 | 0.255 | 0.253 | 0.256 | 0.577% |
| 1.50 | 4.00 | 0.194 | 0.195 | 0.191 | 0.194 | 0.309% |
| 1.50 | 6.00 | 0.150 | 0.152 | 0.154 | 0.154 | 1.487% |
| 1.50 | 8.44 | 0.115 | 0.116 | 0.115 | 0.118 | 2.678% |
| 1.50 | 9.50 | 0.104 | 0.104 | 0.106 | 0.107 | 2.306% |
| 2.36 | 0.50 | 0.452 | 0.449 | 0.450 | 0.449 | 0.668% |
| 3.50 | 2.00 | 0.454 | 0.452 | 0.451 | 0.454 | 0.331% |
| 3.50 | 4.00 | 0.350 | 0.352 | 0.350 | 0.356 | 1.458% |
| 3.50 | 6.44 | 0.268 | 0.268 | 0.269 | 0.276 | 2.703% |
| 3.50 | 7.50 | 0.244 | 0.244 | 0.242 | 0.249 | 2.293% |
| 4.72 | 0.50 | 0.633 | 0.635 | 0.632 | 0.634 | 0.063% |
| 5.50 | 2.00 | 0.550 | 0.552 | 0.550 | 0.559 | 1.427% |
| 5.50 | 4.44 | 0.421 | 0.423 | 0.420 | 0.433 | 2.686% |
| 5.50 | 5.50 | 0.383 | 0.385 | 0.383 | 0.392 | 2.289% |
| 7.08 | 0.50 | 0.706 | 0.702 | 0.703 | 0.709 | 0.786% |
| 7.50 | 2.44 | 0.575 | 0.577 | 0.577 | 0.592 | 2.695% |
| 7.50 | 3.50 | 0.522 | 0.524 | 0.524 | 0.535 | 2.306% |
| 9.44 | 0.50 | 0.723 | 0.725 | 0.723 | 0.743 | 2.690% |
| 9.50 | 1.50 | 0.662 | 0.660 | 0.662 | 0.677 | 2.301% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Long, B.; Wu, H.; Hu, X.; Wei, X.; Zhang, Z.; Chai, L.; Xie, J.; Mei, H. Rapid Evaluation Model of Endurance Performance and Its Application for Agricultural UAVs. Drones 2022, 6, 186. https://doi.org/10.3390/drones6080186
Li J, Long B, Wu H, Hu X, Wei X, Zhang Z, Chai L, Xie J, Mei H. Rapid Evaluation Model of Endurance Performance and Its Application for Agricultural UAVs. Drones. 2022; 6(8):186. https://doi.org/10.3390/drones6080186
Chicago/Turabian StyleLi, Jiyu, Bo Long, Han Wu, Xiaodan Hu, Xu Wei, Zhixun Zhang, Lin Chai, Jindian Xie, and Huilan Mei. 2022. "Rapid Evaluation Model of Endurance Performance and Its Application for Agricultural UAVs" Drones 6, no. 8: 186. https://doi.org/10.3390/drones6080186
APA StyleLi, J., Long, B., Wu, H., Hu, X., Wei, X., Zhang, Z., Chai, L., Xie, J., & Mei, H. (2022). Rapid Evaluation Model of Endurance Performance and Its Application for Agricultural UAVs. Drones, 6(8), 186. https://doi.org/10.3390/drones6080186







