How Big Is That Manta Ray? A Novel and Non-Invasive Method for Measuring Reef Manta Rays Using Small Drones
Abstract
:1. Introduction
2. Materials and Methods
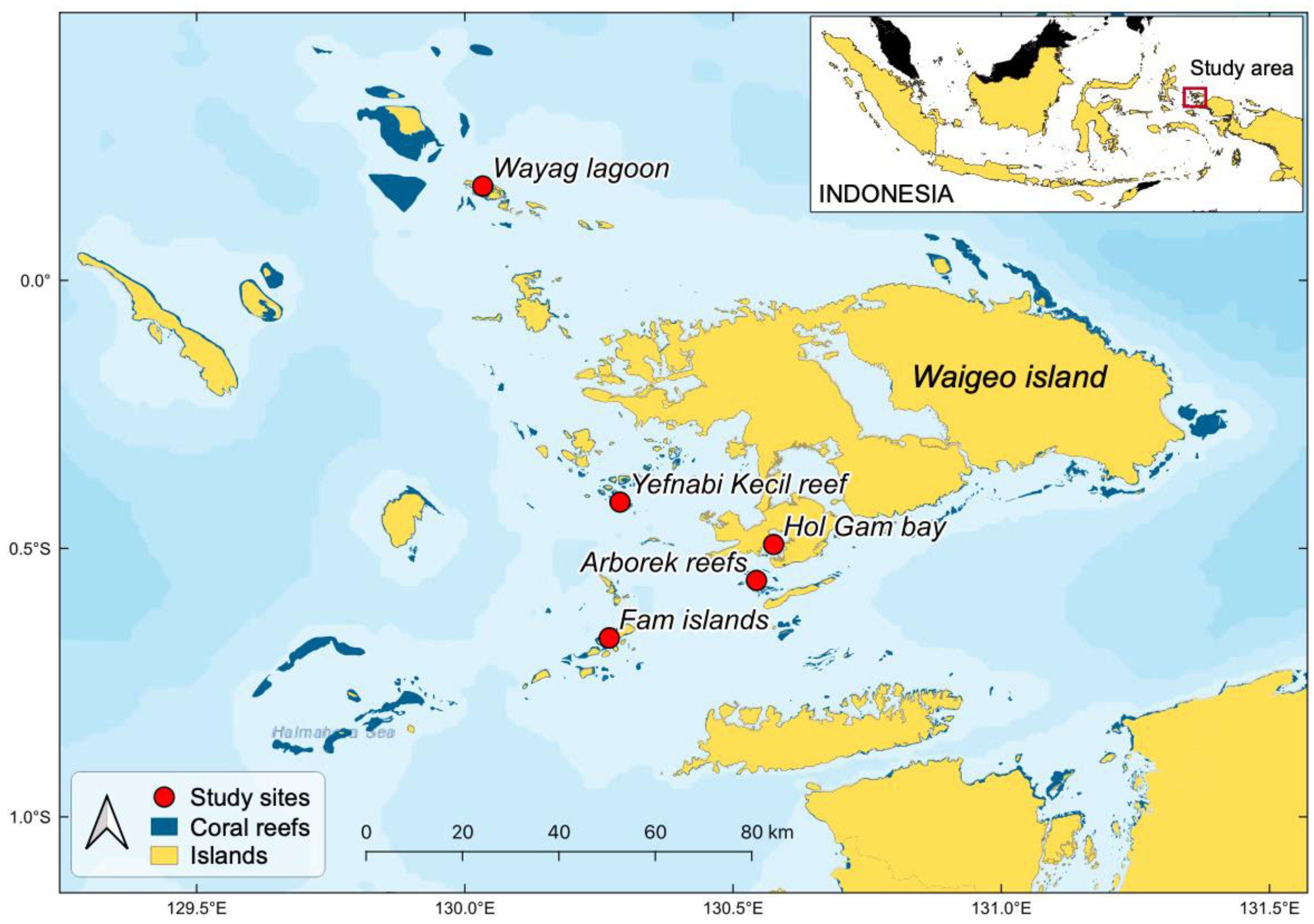
2.1. Study Area
2.2. Data Collection
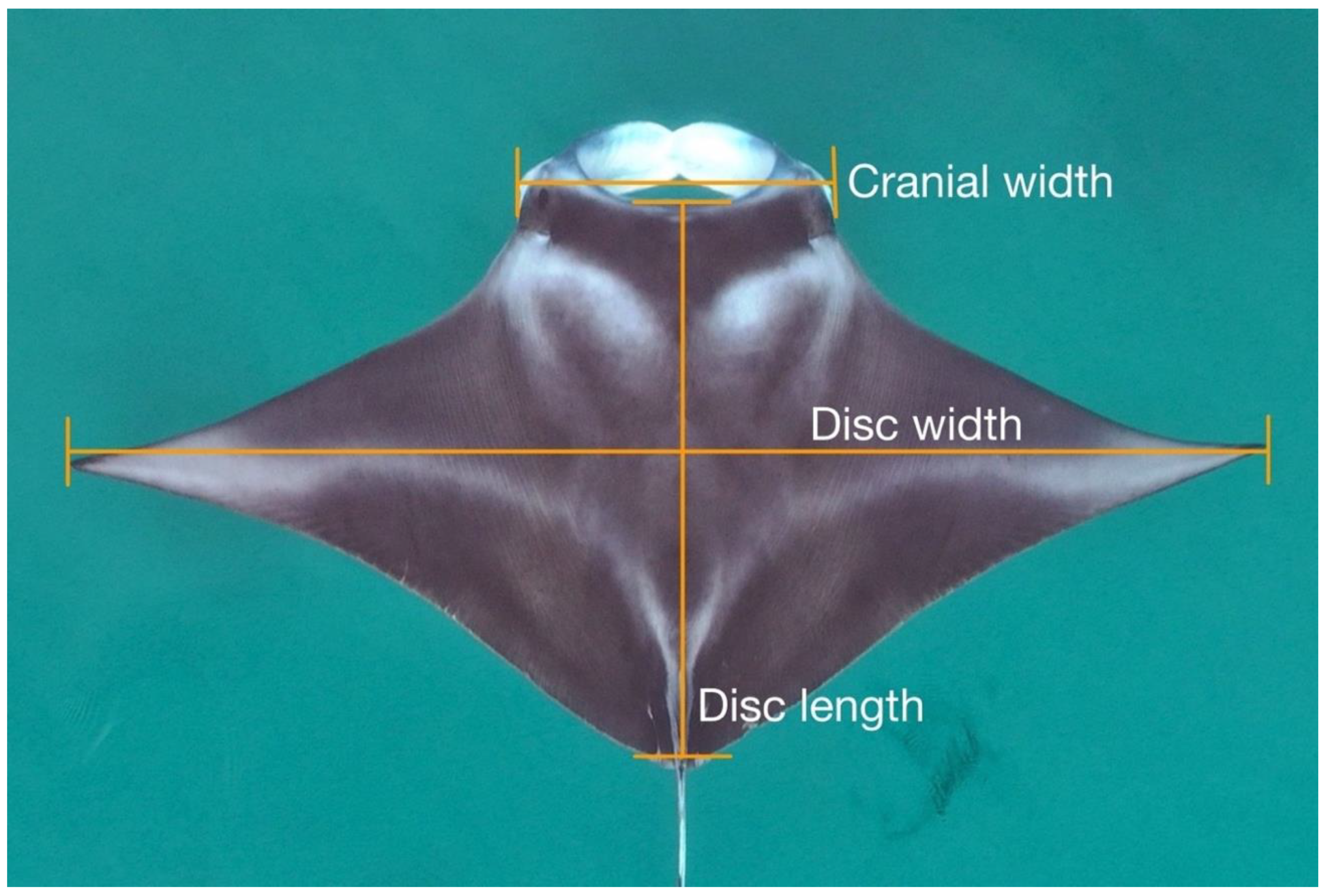
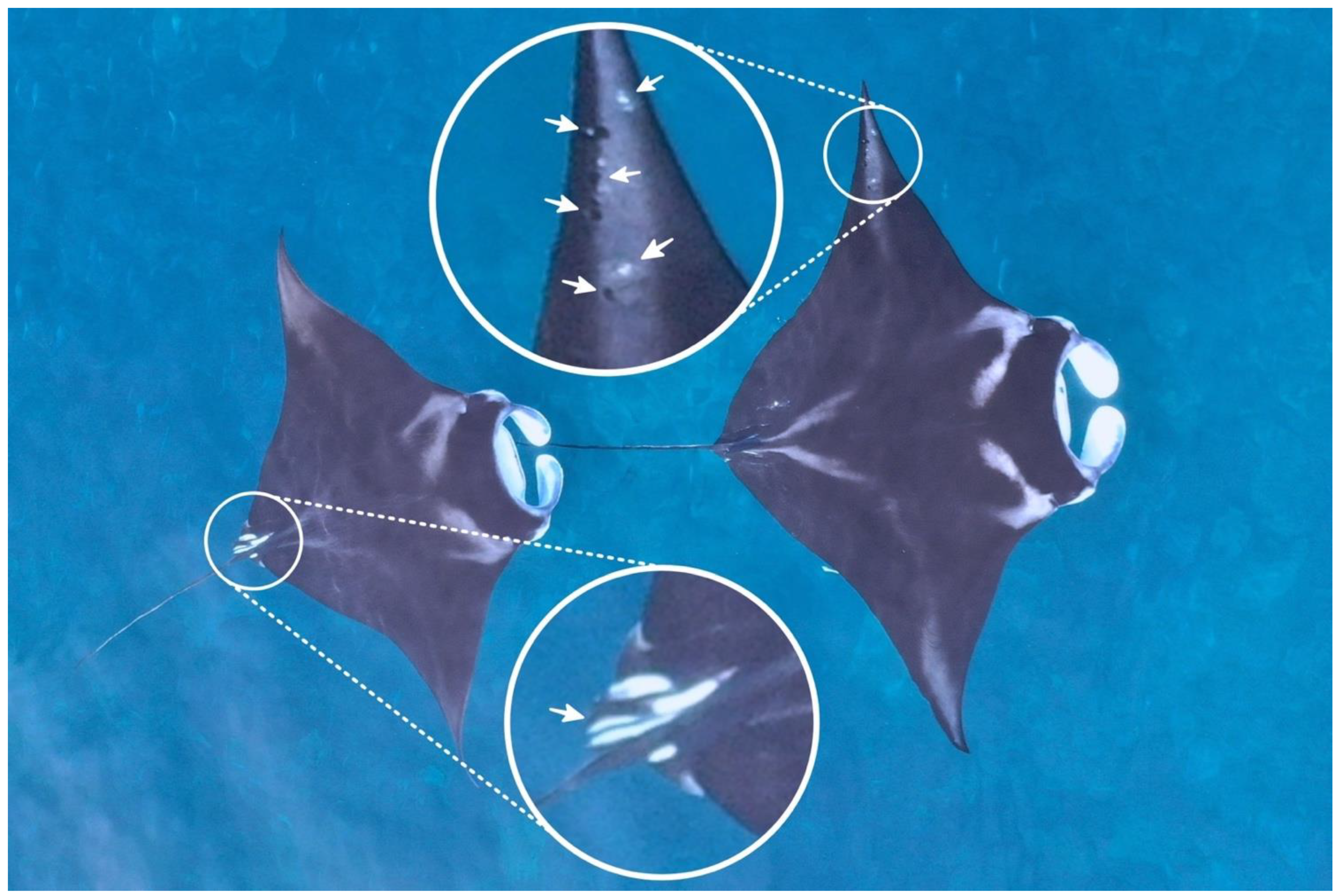
2.3. Image Processing and Measurements
2.4. Demographic Parameters
2.5. Statistical Analysis
3. Results
3.1. Measurement Summary, Accuracy, and Precision
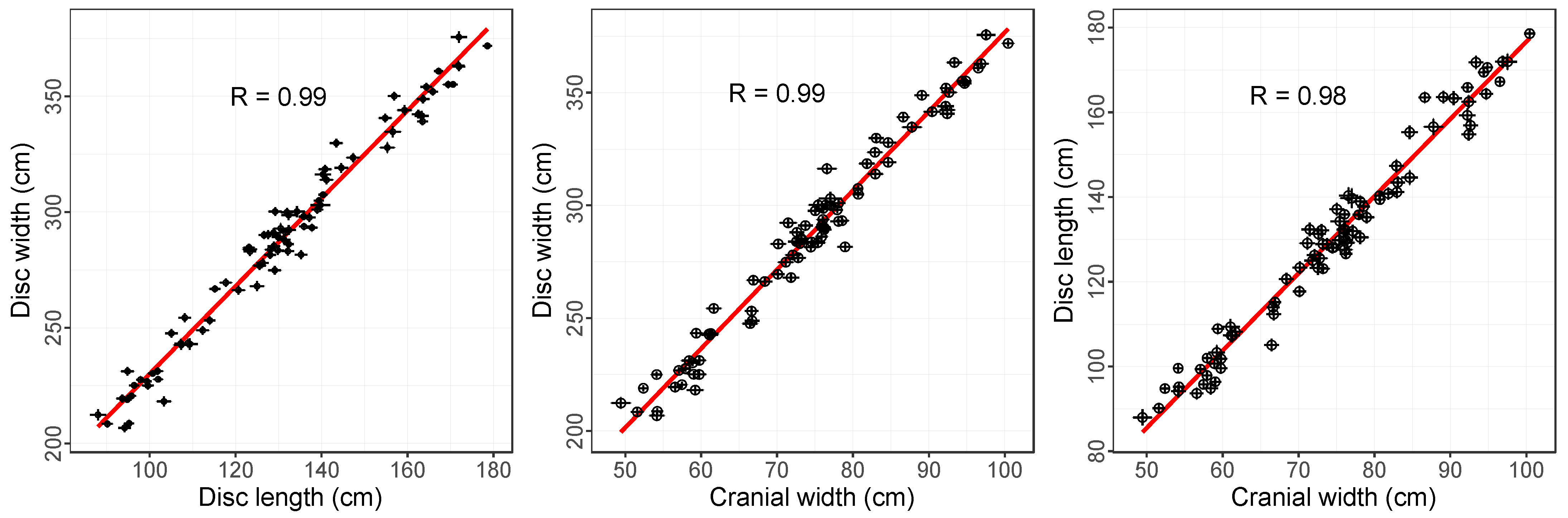
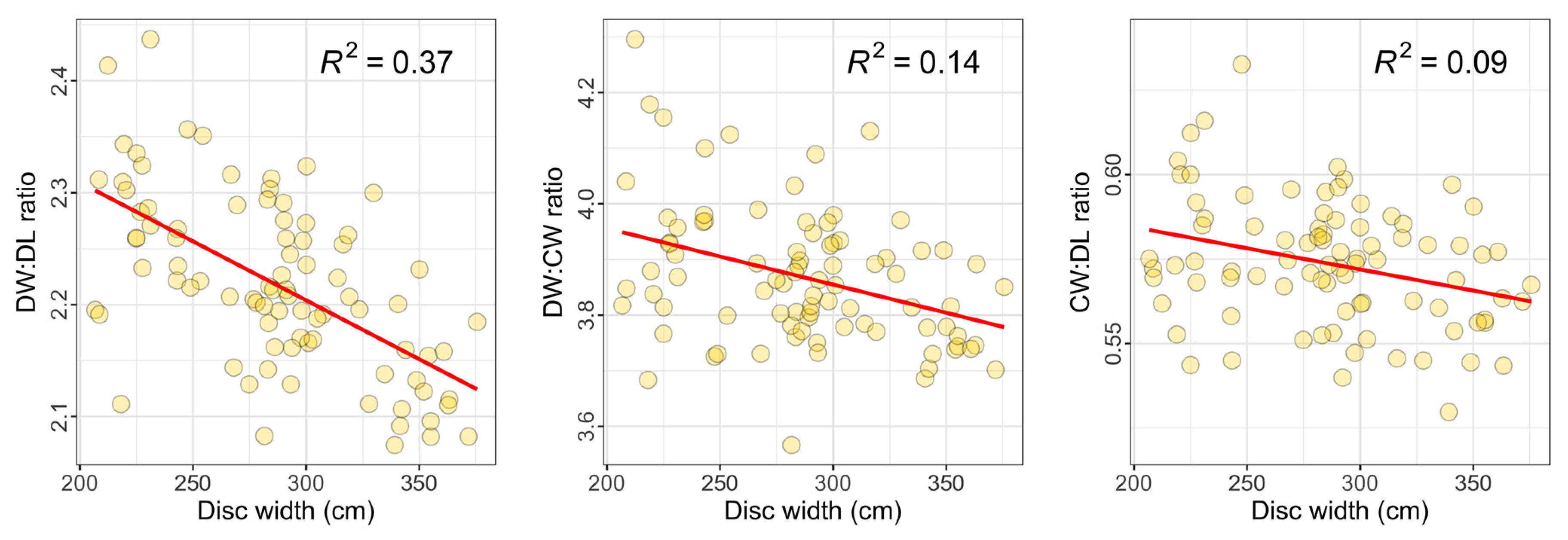
3.2. Relationships between Measured Dimensions
3.3. Using the Model to Predict Unmeasured DW from Other Measured Dimensions
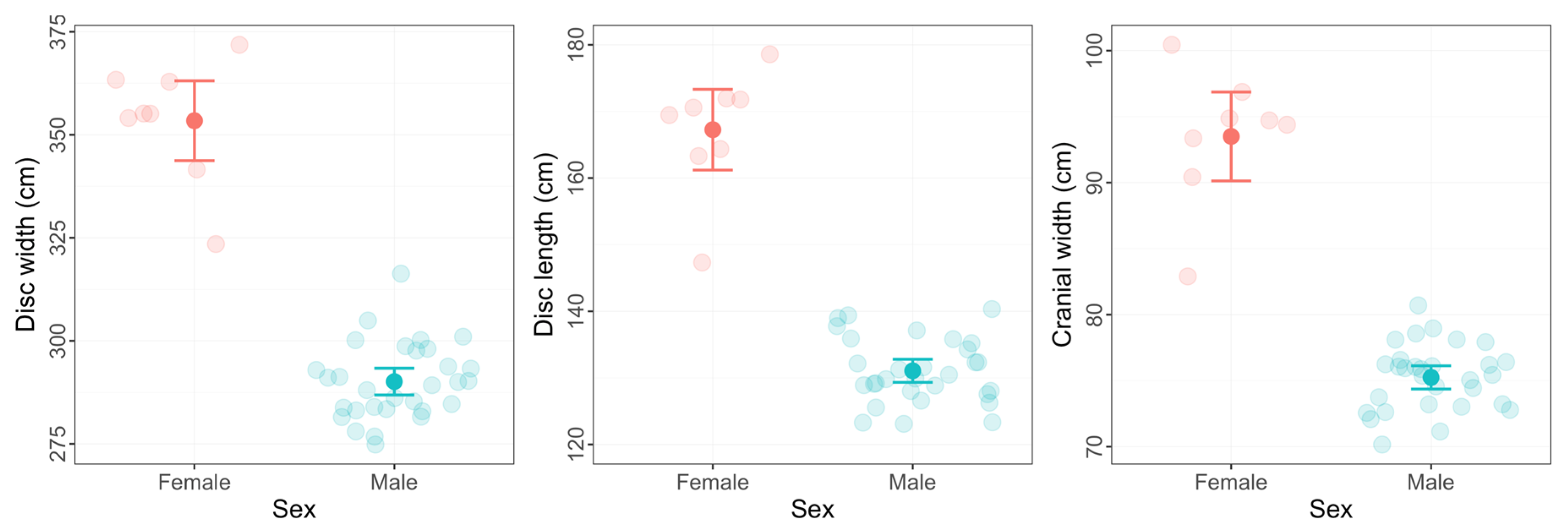
3.4. Size at Maturity and Evidence of Sexual Dimorphism
4. Discussion
4.1. Accuracy and Measurement Methods
4.2. Allometric Growth, Size at Maturity and Sexual Dimorphism
4.3. Limitations of the Methodology
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. True Measurements
Appendix A.2. Measurement Error
Appendix A.3. Model Parameters
- , where contains the underlying population means of the morphometric dimensions for the th group;
- , where contains the underlying population standard deviations of the morphometric dimensions for the th group;
- , where contains underlying population correlations between all pairs of morphometric dimensions;
- containing underlying standard deviations of the measurement errors for each of the dimensions; and
- containing underlying correlations between measurement errors of all morphometric dimensions.
Appendix A.4. Relationships between Dimensions
Appendix A.5. Parameter Estimation
References
- Christiansen, F.; Dujon, A.M.; Sprogis, K.R.; Arnould, J.P.; Bejder, L. Noninvasive unmanned aerial vehicle provides estimates of the energetic cost of reproduction in humpback whales. Ecosphere 2016, 7, e01468. [Google Scholar] [CrossRef]
- Gray, P.C.; Bierlich, K.C.; Mantell, S.A.; Friedlaender, A.S.; Goldbogen, J.A.; Johnston, D.W. Drones and convolutional neural networks facilitate automated and accurate cetacean species identification and photogrammetry. Methods Ecol. Evol. 2019, 10, 1490–1500. [Google Scholar] [CrossRef]
- Perryman, W.L.; Lynn, M.S. Identification of geographic forms common dolphin (Delphinus delphis) from aerial photogrammetry. Mar. Mamm. Sci. 1993, 9, 119–137. [Google Scholar] [CrossRef]
- Rogers, T.D.; Cambiè, G.; Kaiser, M.J. Determination of size, sex and maturity stage of free swimming catsharks using laser photogrammetry. Mar. Biol. 2017, 164, 213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deakos, M.H. Paired-laser photogrammetry as a simple and accurate system for measuring the body size of free-ranging manta rays Manta alfredi. Aquat. Biol. 2010, 10, 1–10. [Google Scholar] [CrossRef]
- Gaudioso, V.; Sanz-Ablanedo, E.; Lomillos, J.M.; Alonso, M.E.; Javares-Morillo, L.; Rodríguez, P. “Photozoometer”: A new photogrammetric system for obtaining morphometric measurements of elusive animals. Livest. Sci. 2014, 165, 147–156. [Google Scholar] [CrossRef]
- Schenk, T. Introduction to Photogrammetry; The Ohio State University: Columbus, OH, USA, 2005; Volume 106, p. 95. [Google Scholar]
- Bräger, S.; Chong, A.; Dawson, S.; Slooten, E.; Würsig, B. A combined stereo-photogrammetry and underwater-video system to study group composition of dolphins. Helgol. Mar. Res. 1999, 53, 122–128. [Google Scholar] [CrossRef] [Green Version]
- Jeffreys, G.; Rowat, D.; Marshall, H.; Brooks, K. The development of robust morphometric indices from accurate and precise measurements of free-swimming whale sharks using laser photogrammetry. Mar. Biol. Assoc. UK 2013, 93, 309–320. [Google Scholar] [CrossRef]
- Menesatti, P.; Costa, C.; Antonucci, F.; Steri, R.; Pallottino, F.; Catillo, G. A low-cost stereovision system to estimate size and weight of live sheep. Comput. Electron. Agric. 2014, 103, 33–38. [Google Scholar] [CrossRef]
- Marshall, A.; Barreto, R.; Carlson, J.; Fernando, D.; Fordham, S.; Francis, M.P.; Herman, K.; Jabado, R.W.; Liu, K.M.; Pacoureau, N.; et al. Mobula alfredi. In The IUCN Red List of Threatened Species 2019: e.T195459A68632178; 2019; Available online: https://dx.doi.org/10.2305/IUCN.UK.2019-3.RLTS.T195459A68632178.en (accessed on 9 April 2021).
- Stevens, G.M.W. Conservation and Population Ecology of Manta Rays in the Maldives. Ph.D. Dissertation, University of York, York, UK, 2016. [Google Scholar]
- Rambahiniarison, J.M.; Lamoste, M.J.; Rohner, C.A.; Murray, R.; Snow, S.; Labaja, J.; Araujo, G.; Ponzo, A. Life history, growth, and reproductive biology of four mobulid species in the Bohol Sea, Philippines. Front. Mar. Sci. 2018, 5, 269. [Google Scholar] [CrossRef] [Green Version]
- Peel, L.R.; Stevens, G.M.W.; Daly, R.; Daly, C.A.K.; Lea, J.S.E.; Clarke, C.R.; Collin, S.P.; Meekan, M.G. Movement and residency patterns of reef manta rays Mobula alfredi in the Amirante Islands, Seychelles. Mar. Ecol. Prog. Ser. 2019, 621, 169–184. [Google Scholar] [CrossRef]
- Notarbartolo Di Sciara, G. A revisionary study of the genus Mobula Rafinesque, 1810 (Chondrichthyes: Mobulidae) with the description of a new species. Zool. J. Linn. Soc. 1987, 91, 1–91. [Google Scholar] [CrossRef]
- Marshall, A.D.; Bennett, M.B. Reproductive ecology of the reef manta ray Manta alfredi in southern Mozambique. J. Fish Biol. 2010, 77, 169–190. [Google Scholar] [CrossRef]
- Sequeira, A.M.; Thums, M.; Brooks, K.; Meekan, M.G. Error and bias in size estimates of whale sharks: Implications for understanding demography. R. Soc. Open Sci. 2016, 3, 150668. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Couturier, L.I.E.; Dudgeon, C.L.; Pollock, K.H.; Jaine, F.R.A.; Bennett, M.B.; Townsend, K.A.; Weeks, S.J.; Richardson, A.J. Population dynamics of the reef manta ray Manta alfredi in eastern Australia. Coral Reefs 2014, 33, 329–342. [Google Scholar] [CrossRef] [Green Version]
- Letessier, T.B.; Juhel, J.-B.; Vigliola, L.; Meeuwig, J.J. Low-cost small action cameras in stereo generates accurate underwater measurements of fish. J. Exp. Mar. Biol. Ecol. 2015, 466, 120–126. [Google Scholar] [CrossRef]
- Harvey, E.; Fletcher, D.; Shortis, M. Estimation of reef fish length by divers and by stereo-video: A first comparison of the accuracy and precision in the field on living fish under operational conditions. Fish. Res. 2002, 57, 255–265. [Google Scholar] [CrossRef]
- Delacy, C.R.; Olsen, A.; Howey, L.A.; Chapman, D.D.; Brooks, E.J.; Bond, M.E. Affordable and accurate stereo-video system for measuring dimensions underwater: A case study using oceanic whitetip sharks Carcharhinus longimanus. Mar. Ecol. Prog. Ser. 2017, 574, 75–84. [Google Scholar] [CrossRef]
- Murray, A.; Garrud, E.; Ender, I.; Lee-Brooks, K.; Atkins, R.; Lynam, R.; Arnold, K.; Roberts, C.; Hawkins, J.; Stevens, G. Protecting the million-dollar mantas; creating an evidence-based code of conduct for manta ray tourism interactions. J. Ecotourism 2020, 19, 132–147. [Google Scholar] [CrossRef]
- Francis, M.P. Morphometric minefields—Towards a measurement standard for chondrichthyan fishes. Environ. Biol. Fishes 2006, 77, 407–421. [Google Scholar] [CrossRef]
- Marshall, A.D.; Pierce, S.J.; Bennett, M.B. Morphological measurements of manta rays (Manta birostris) with a description of a foetus from the east coast of Southern Africa. Zootaxa 2008, 1717, 24–30. [Google Scholar] [CrossRef]
- Last, P.; Naylor, G.; Séret, B.; White, W.; de Carvalho, M.; Stehmann, M. Rays of the World; CSIRO Publishing: Melbourne, Australia, 2016. [Google Scholar]
- Johnston, D.W. Unoccupied aircraft systems in marine science and conservation. Ann. Rev. Mar. Sci. 2019, 11, 439–463. [Google Scholar] [CrossRef] [Green Version]
- Landeo-Yauri, S.S.; Ramos, E.A.; Castelblanco-Martínez, D.N.; Niño-Torres, C.A.; Searle, L. Using small drones to photo-identify Antillean manatees: A novel method for monitoring an endangered marine mammal in the Caribbean Sea. Endanger. Species Res. 2020, 41, 79–90. [Google Scholar] [CrossRef] [Green Version]
- Lyons, M.B.; Brandis, K.J.; Murray, N.J.; Wilshire, J.H.; McCann, J.A.; Kingsford, R.T.; Callaghan, C.T. Monitoring large and complex wildlife aggregations with drones. Methods Ecol. Evol. 2019, 10, 1024–1035. [Google Scholar] [CrossRef] [Green Version]
- Schofield, G.; Esteban, N.; Katselidis, K.A.; Hays, G.C. Drones for research on sea turtles and other marine vertebrates—A review. Biol. Conserv. 2019, 238, 108214. [Google Scholar] [CrossRef]
- Torres, L.G.; Nieukirk, S.L.; Lemos, L.; Chandler, T.E. Drone up! Quantifying whale behavior from a new perspective improves observational capacity. Front. Mar. Sci. 2018, 5, 319. [Google Scholar] [CrossRef] [Green Version]
- Burnett, J.D.; Lemos, L.; Barlow, D.; Wing, M.G.; Chandler, T.; Torres, L.G. Estimating morphometric attributes of baleen whales with photogrammetry from small UASs: A case study with blue and gray whales. Mar. Mamm. Sci. 2019, 35, 108–139. [Google Scholar] [CrossRef] [Green Version]
- Christiansen, F.; Vivier, F.; Charlton, C.; Ward, R.; Amerson, A.; Burnell, S.; Bejder, L. Maternal body size and condition determine calf growth rates in southern right whales. Mar. Ecol. Prog. Ser. 2018, 592, 267–281. [Google Scholar] [CrossRef] [Green Version]
- Dawson, S.M.; Bowman, M.H.; Leunissen, E.; Sirguey, P. Inexpensive aerial photogrammetry for studies of whales and large marine animals. Front. Mar. Sci. 2017, 4, 366. [Google Scholar] [CrossRef] [Green Version]
- Bierlich, K.; Schick, R.; Hewitt, J.; Dale, J.; Goldbogen, J.; Friedlaender, A.; Johnston, D. Bayesian approach for predicting photogrammetric uncertainty in morphometric measurements derived from drones. Mar. Ecol. Prog. Ser. 2021, 673, 193–210. [Google Scholar] [CrossRef]
- Eurostat. Glossary of Statistical Terms: True Value. Available online: https://stats.oecd.org/glossary/detail.asp?ID=4557 (accessed on 21 October 2021).
- Beale, C.S.; Stewart, J.D.; Setyawan, E.; Sianipar, A.B.; Erdmann, M.V. Population dynamics of oceanic manta rays (Mobula birostris) in the Raja Ampat Archipelago, West Papua, Indonesia, and the impacts of the El Niño–Southern Oscillation on their movement ecology. Divers. Distrib. 2019, 25, 1472–1487. [Google Scholar] [CrossRef] [Green Version]
- Setyawan, E.; Erdmann, M.V.; Lewis, S.A.; Mambrasar, R.; Hasan, A.W.; Templeton, S.; Beale, C.S.; Sianipar, A.B.; Shidqi, R.; Heuschkel, H.; et al. Natural history of manta rays in the Bird’s Head Seascape, Indonesia, with an analysis of the demography and spatial ecology of Mobula alfredi (Elasmobranchii: Mobulidae). J. Ocean Sci. Found. 2020, 36, 49–83. [Google Scholar] [CrossRef]
- Setyawan, E.; Erdmann, M.; Gunadharma, N.; Gunawan, T.; Hasan, A.; Izuan, M.; Kasmidi, M.; Lamatenggo, Y.; Lewis, S.; Maulana, N.; et al. A holistic approach to manta ray conservation in the Papuan Bird’s Head Seascape: Resounding success, ongoing challenges. Mar. Policy 2022, 137, 104953. [Google Scholar] [CrossRef]
- Setyawan, E.; Sianipar, A.B.; Erdmann, M.V.; Fischer, A.M.; Haddy, J.A.; Beale, C.S.; Lewis, S.A.; Mambrasar, R. Site fidelity and movement patterns of reef manta rays (Mobula alfredi): Mobulidae using passive acoustic telemetry in northern Raja Ampat, Indonesia. Nat. Conserv. Res. 2018, 3, 17–31. [Google Scholar] [CrossRef] [Green Version]
- Brown, D.; Christian, W.; Hanson, R.M. Tracker: Video Analysis and Modeling Tool (Version 6.0.1). 2021. Available online: https://physlets.org/tracker/ (accessed on 1 March 2021).
- Bolker, B.M.; Brooks, M.E.; Clark, C.J.; Geange, S.W.; Poulsen, J.R.; Stevens, M.H.H.; White, J.-S.S. Generalized linear mixed models: A practical guide for ecology and evolution. Trends Ecol. Evol. 2009, 24, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Zuur, A.F.; Ieno, E.N.; Walker, N.J.; Saveliev, A.A.; Smith, G.M. Mixed Effects Models and Extensions in Ecology with R; Springer: New York, NY, USA, 2009; Volume 574. [Google Scholar]
- Ihaka, R.; Gentleman, R. R: A language for data analysis and graphics. J. Comput. Graph. Stat. 1996, 5, 299–314. [Google Scholar] [CrossRef]
- Riedel, R.; Caskey, L.M.; Hurlbert, S.H. Length-weight relations and growth rates of dominant fishes of the Salton Sea: Implications for predation by fish-eating birds. Lake Reserv. Manag. 2007, 23, 528–535. [Google Scholar] [CrossRef] [Green Version]
- Oleksyn, S.; Tosetto, L.; Raoult, V.; Joyce, K.E.; Williamson, J.E. Going batty: The challenges and opportunities of using drones to monitor the behaviour and habitat use of rays. Drones 2021, 5, 12. [Google Scholar] [CrossRef]
- Butcher, P.A.; Colefax, A.P.; Gorkin, R.A.; Kajiura, S.M.; López, N.A.; Mourier, J.; Purcell, C.R.; Skomal, G.B.; Tucker, J.P.; Walsh, A.J.; et al. The drone revolution of shark science: A review. Drones 2021, 5, 8. [Google Scholar] [CrossRef]
- Pate, J.H.; Marshall, A.D. Urban manta rays: Potential manta ray nursery habitat along a highly developed Florida coastline. Endanger. Species Res. 2020, 43, 51–64. [Google Scholar] [CrossRef]
- Oleksyn, S.; Tosetto, L.; Raoult, V.; Williamson, J.E. Drone-based tracking of the fine-scale movement of a coastal stingray (Bathytoshia brevicaudata). Remote Sens. 2021, 13, 40. [Google Scholar] [CrossRef]
- Durban, J.W.; Moore, M.J.; Chiang, G.; Hickmott, L.S.; Bocconcelli, A.; Howes, G.; Bahamonde, P.A.; Perryman, W.L.; LeRoi, D.J. Photogrammetry of blue whales with an unmanned hexacopter. Mar. Mamm. Sci. 2016, 32, 1510–1515. [Google Scholar] [CrossRef]
- Sabatini, A.M.; Genovese, V. A sensor fusion method for tracking vertical velocity and height based on Inertial and barometric altimeter measurements. Sensors 2014, 14, 13324–13347. [Google Scholar] [CrossRef]
- Wei, S.; Dan, G.; Chen, H. Altitude data fusion utilising differential measurement and complementary filter. IET Sci. Meas. Technol. 2016, 10, 874–879. [Google Scholar] [CrossRef]
- Kashiwagi, T. Conservation Biology and Genetics of the Largest Living Rays: Manta Rays. Ph.D. Dissertation, The University of Queensland, Brisbane, Australia, 2014. [Google Scholar]
- Kashiwagi, T.; Ito, T.; Sato, F. Occurrences of reef manta ray, Manta alfredi, and giant manta ray, M. birostris, in Japan, examined by photographic records. Rep. Jpn. Soc. Elasmobranch Stud. 2010, 46, 20–27. [Google Scholar]
- Cortés, E. Life History Patterns and Correlations in Sharks. Rev. Fish. Sci. 2000, 8, 299–344. [Google Scholar] [CrossRef]
- Hussey, N.E.; Wintner, S.P.; Dudley, S.F.J.; Cliff, G.; Cocks, D.T.; Aaron MacNeil, M. Maternal investment and size-specific reproductive output in carcharhinid sharks. J. Anim. Ecol. 2010, 79, 184–193. [Google Scholar] [CrossRef] [PubMed]
- Marshall, A.D.; Pierce, S.J. The use and abuse of photographic identification in sharks and rays. J. Fish Biol. 2012, 80, 1361–1379. [Google Scholar] [CrossRef] [PubMed]
- Setyawan, E.; Duffy, C.A.; Erdmann, M.V.; Green, L.; Tindale, S. First insights into the spatial ecology of endangered Mobula birostris in Aotearoa. In Proceedings of the New Zealand Marine Sciences Society Conference, Tauranga, New Zealand, 5–8 July 2021. [Google Scholar]
- Kristensen, K.; Nielsen, A.; Berg, C.W.; Skaug, H.; Bell, B.M. TMB: Automatic differentiation and Laplace approximation. J. Stat. Softw. 2016, 70, 21. [Google Scholar] [CrossRef]



| Demographic Group | Model Parameters | Estimates | Standard Error (SE) | 95% CIs | |
|---|---|---|---|---|---|
| Lower | Upper | ||||
| All manta rays combined (n = 86) | 286.5 | 4.87 | 277.0 | 296.1 | |
| 129.8 | 2.54 | 124.8 | 134.7 | ||
| 74.3 | 1.37 | 71.6 | 77.0 | ||
| 45.1 | 3.44 | 38.4 | 51.9 | ||
| 23.5 | 1.79 | 20.0 | 27.0 | ||
| 12.7 | 0.97 | 10.8 | 14.6 | ||
| 0.99 | 0.003 | 0.982 | 0.993 | ||
| 0.99 | 0.003 | 0.980 | 0.991 | ||
| 0.98 | 0.004 | 0.977 | 0.991 | ||
| 2.16 | 0.07 | 2.01 | 2.30 | ||
| 1.69 | 0.06 | 1.58 | 1.80 | ||
| 1.13 | 0.04 | 1.06 | 1.21 | ||
| Sexually mature males (n = 30) | 290.1 | 1.7 | 286.9 | 293.4 | |
| 131.1 | 0.9 | 129.3 | 132.8 | ||
| 75.2 | 0.4 | 74.4 | 76.1 | ||
| 9.0 | 1.2 | 6.7 | 11.3 | ||
| 4.8 | 0.6 | 3.5 | 6.0 | ||
| 2.4 | 0.3 | 1.8 | 3.0 | ||
| Sexually mature females (n = 8) | 353.4 | 4.9 | 343.7 | 363.1 | |
| 167.3 | 3.1 | 161.2 | 173.3 | ||
| 93.5 | 1.7 | 90.1 | 96.9 | ||
| 13.9 | 3.5 | 7.1 | 20.8 | ||
| 8.7 | 2.2 | 4.4 | 13.0 | ||
| 4.8 | 1.2 | 2.4 | 7.2 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Setyawan, E.; Stevenson, B.C.; Izuan, M.; Constantine, R.; Erdmann, M.V. How Big Is That Manta Ray? A Novel and Non-Invasive Method for Measuring Reef Manta Rays Using Small Drones. Drones 2022, 6, 63. https://doi.org/10.3390/drones6030063
Setyawan E, Stevenson BC, Izuan M, Constantine R, Erdmann MV. How Big Is That Manta Ray? A Novel and Non-Invasive Method for Measuring Reef Manta Rays Using Small Drones. Drones. 2022; 6(3):63. https://doi.org/10.3390/drones6030063
Chicago/Turabian StyleSetyawan, Edy, Ben C. Stevenson, Muhamad Izuan, Rochelle Constantine, and Mark V. Erdmann. 2022. "How Big Is That Manta Ray? A Novel and Non-Invasive Method for Measuring Reef Manta Rays Using Small Drones" Drones 6, no. 3: 63. https://doi.org/10.3390/drones6030063
APA StyleSetyawan, E., Stevenson, B. C., Izuan, M., Constantine, R., & Erdmann, M. V. (2022). How Big Is That Manta Ray? A Novel and Non-Invasive Method for Measuring Reef Manta Rays Using Small Drones. Drones, 6(3), 63. https://doi.org/10.3390/drones6030063







