Parallel Multiobjective Multiverse Optimizer for Path Planning of Unmanned Aerial Vehicles in a Dynamic Environment with Moving Obstacles
Abstract
1. Introduction
2. Related Work
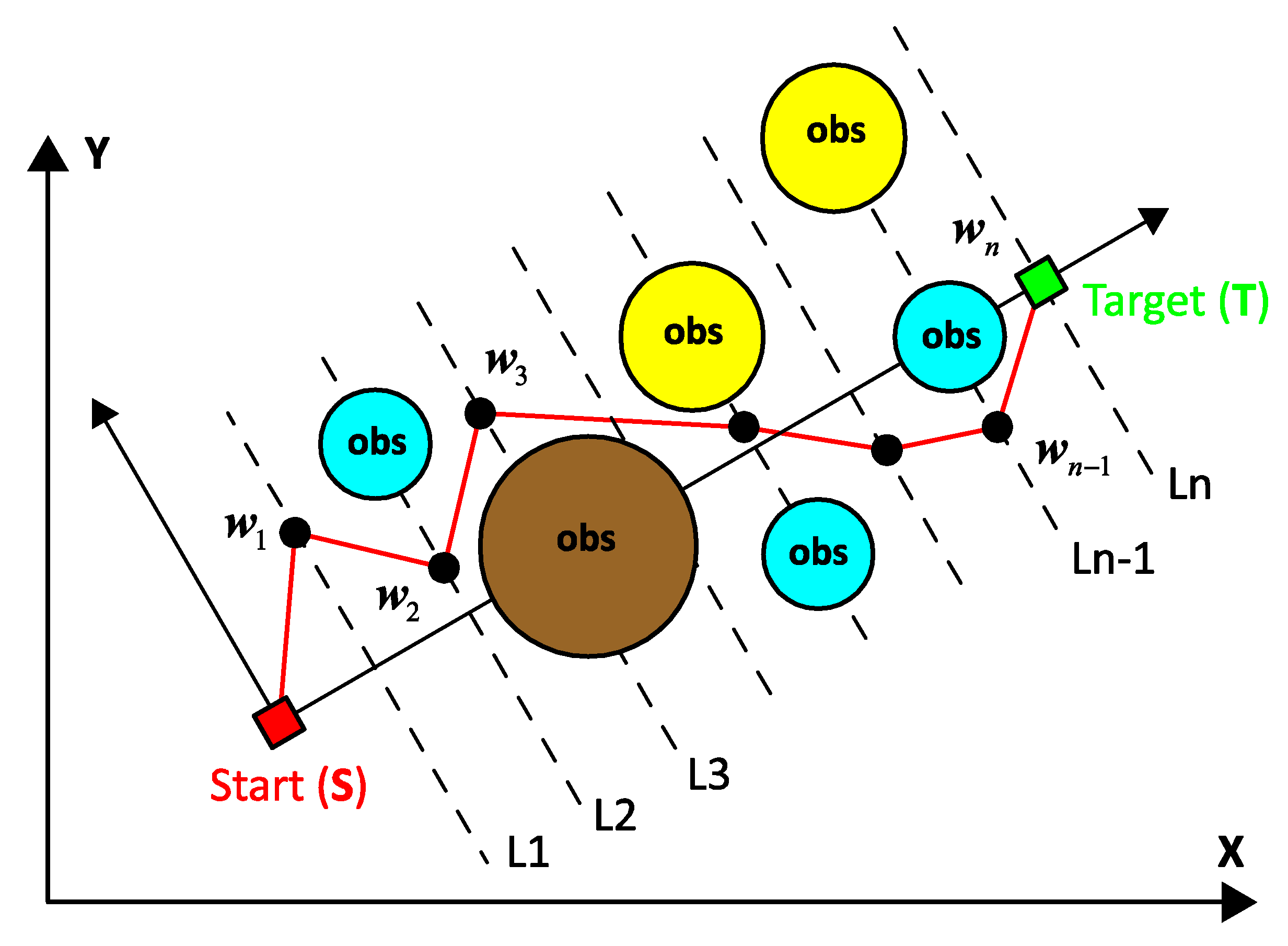
3. Path Planning Problem Formulation
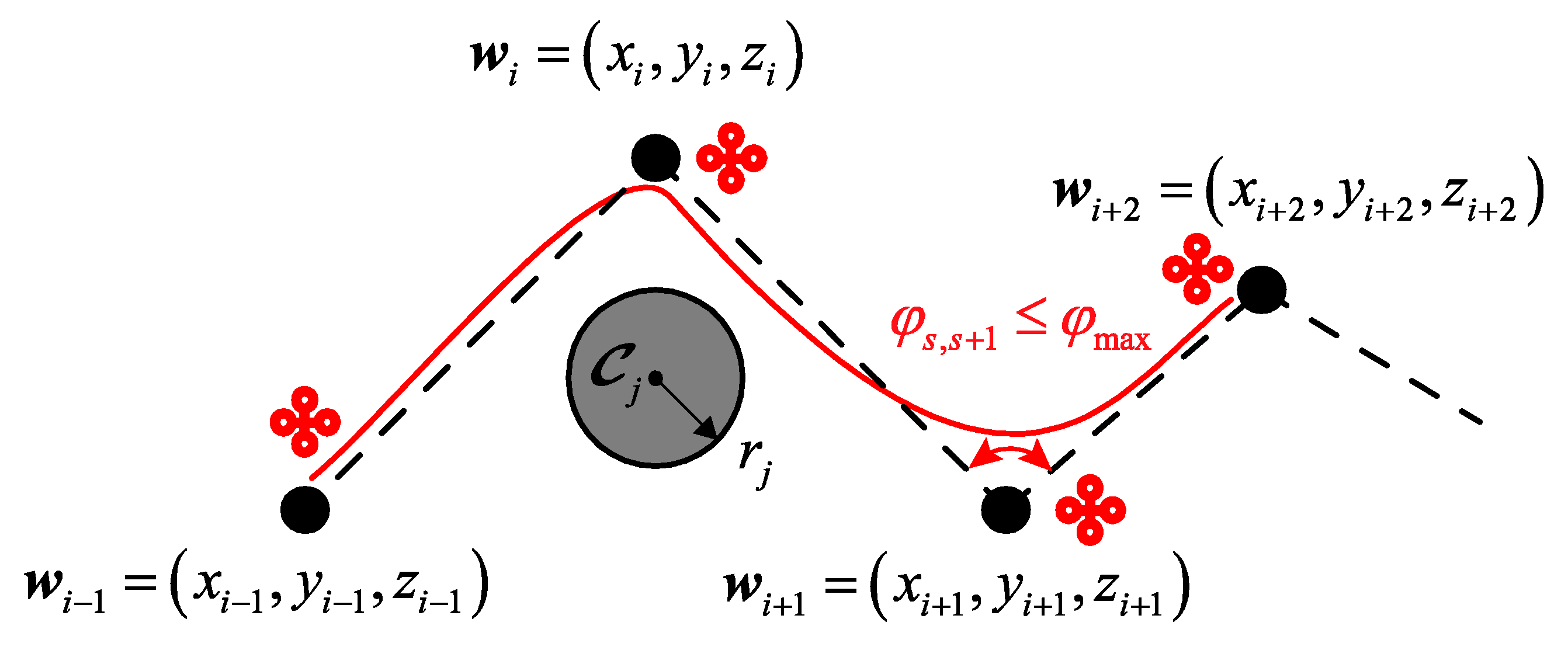
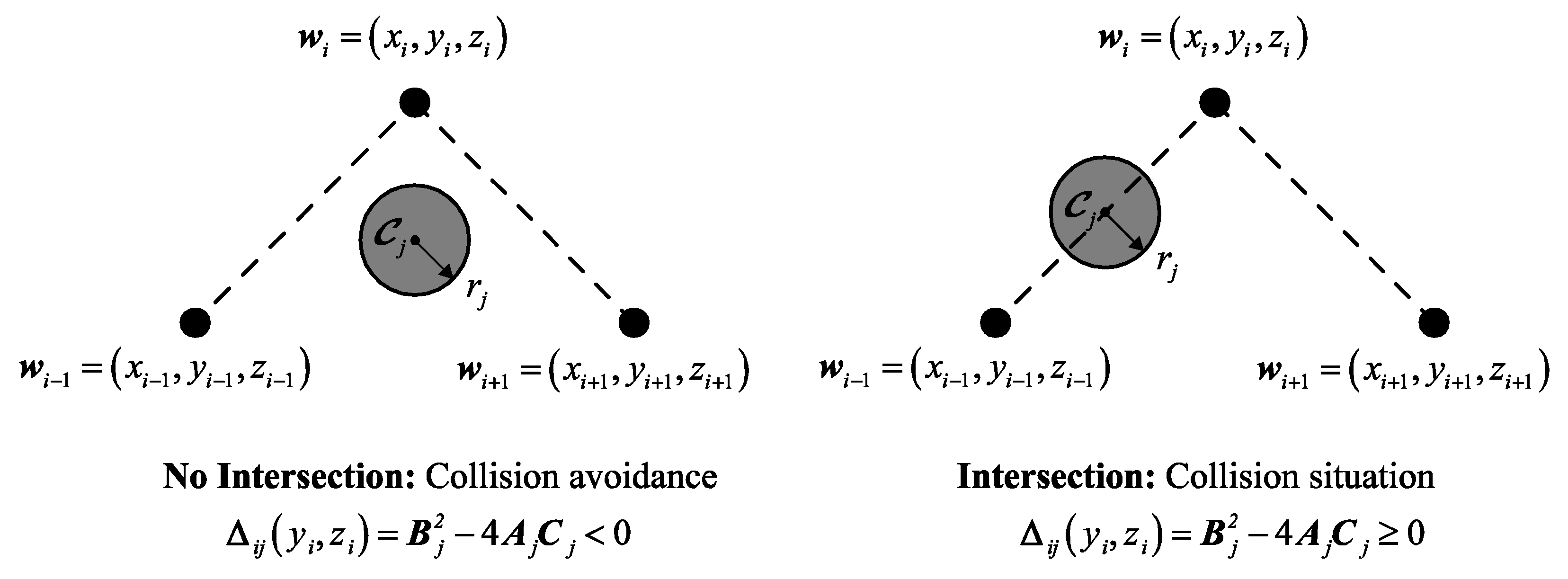
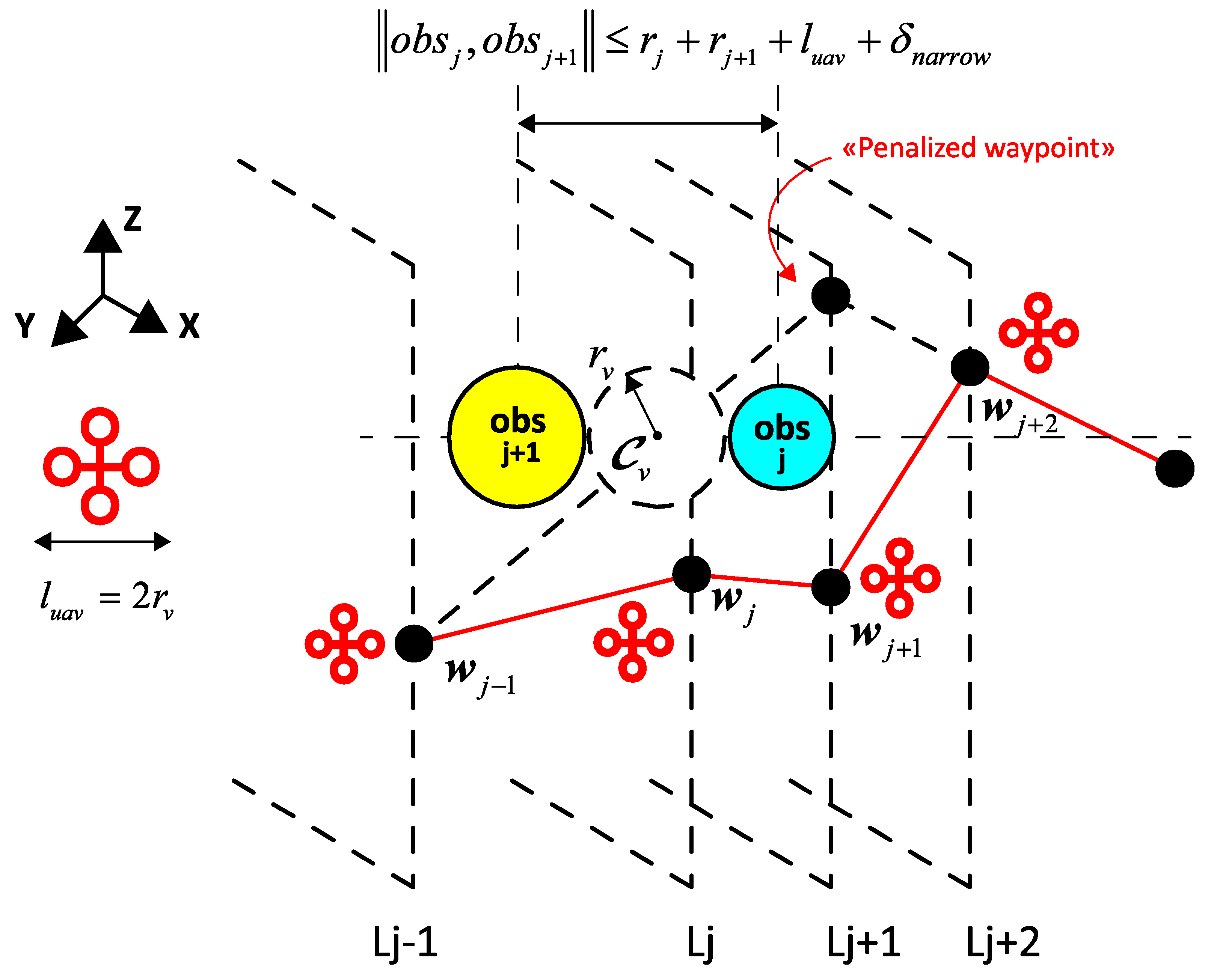
3.1. Dynamic Environment Modeling
3.2. Multiobjective Optimization Problem Formulation
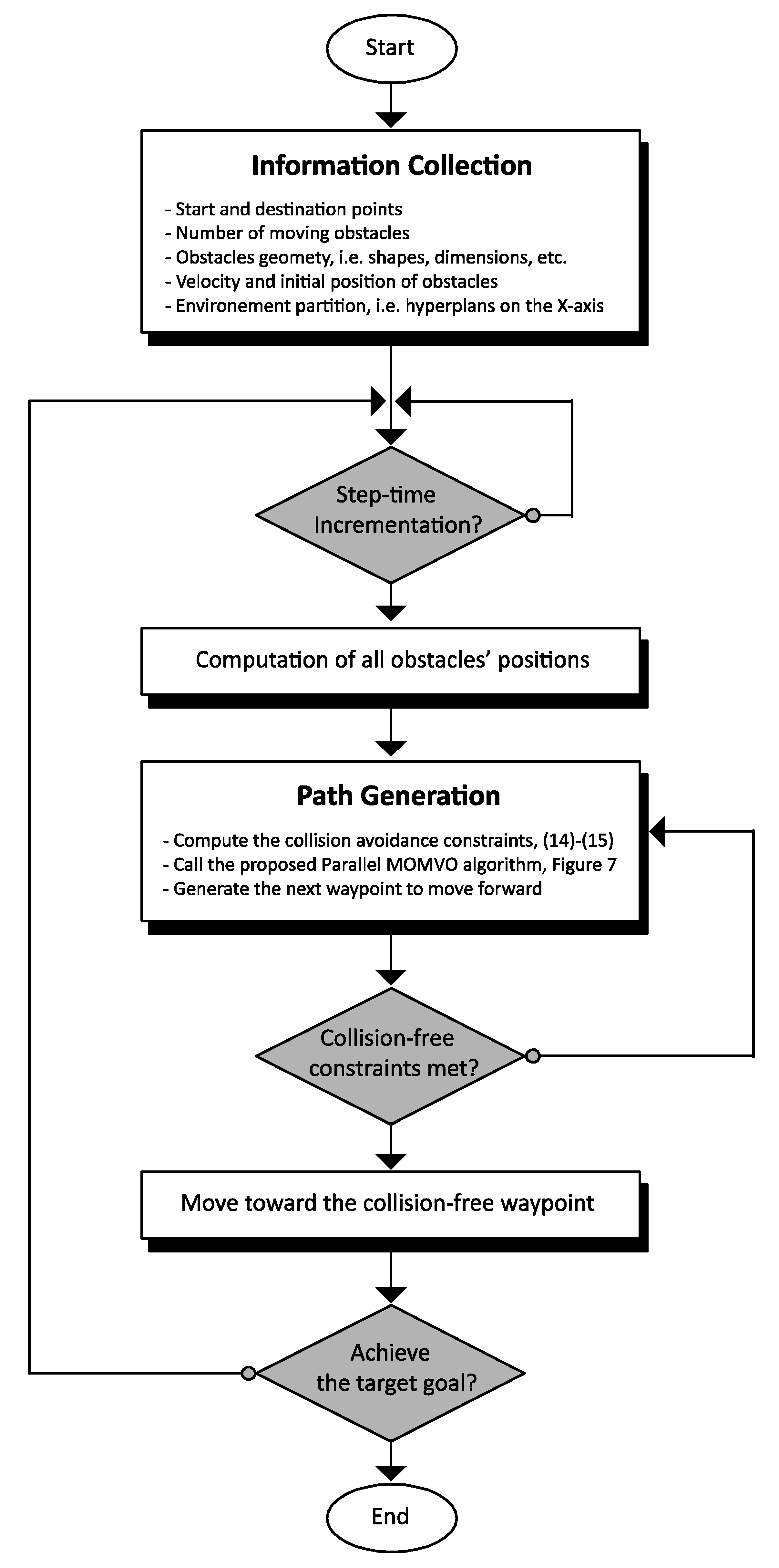
3.3. Proposed Path Planning Strategy
4. Parallel Optimization Algorithm
4.1. Multiobjective Multiverse Optimizer
| Algorithm 1: MOMVO |
|
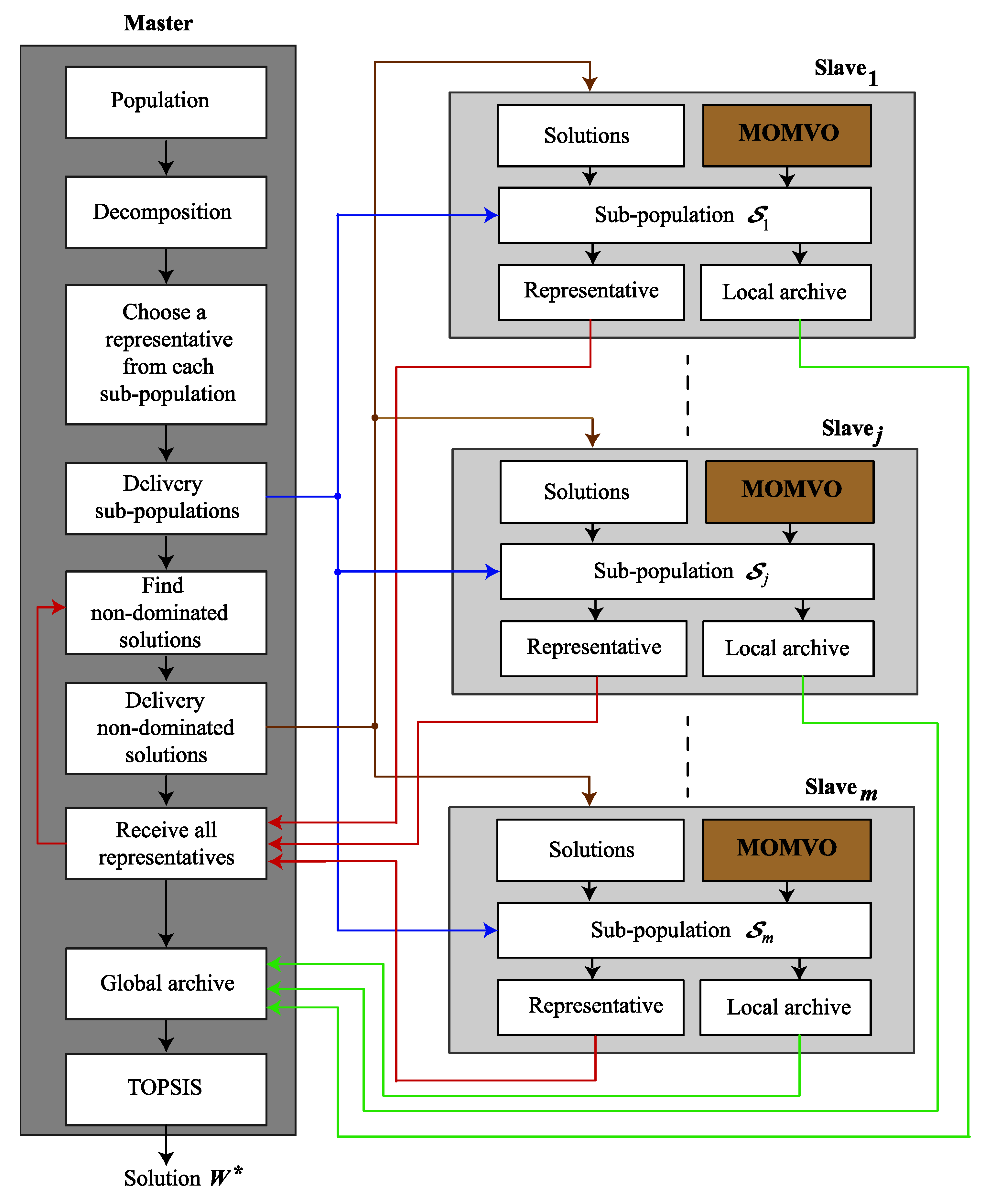
4.2. Parallelization of the MOMVO Algorithm
| Algorithm 2: PMOMVO |
| Master process |
|
| Slave [j] process |
|
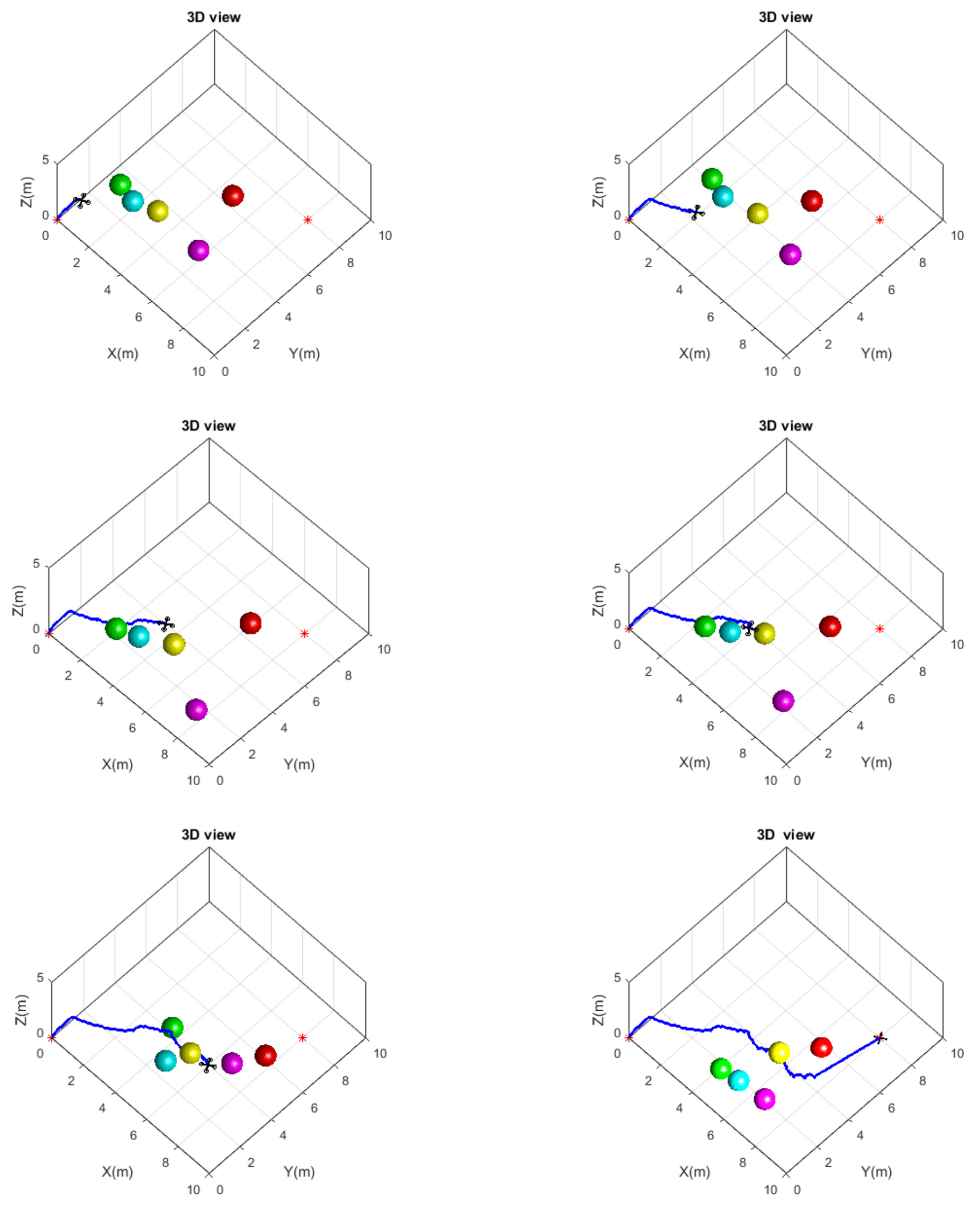
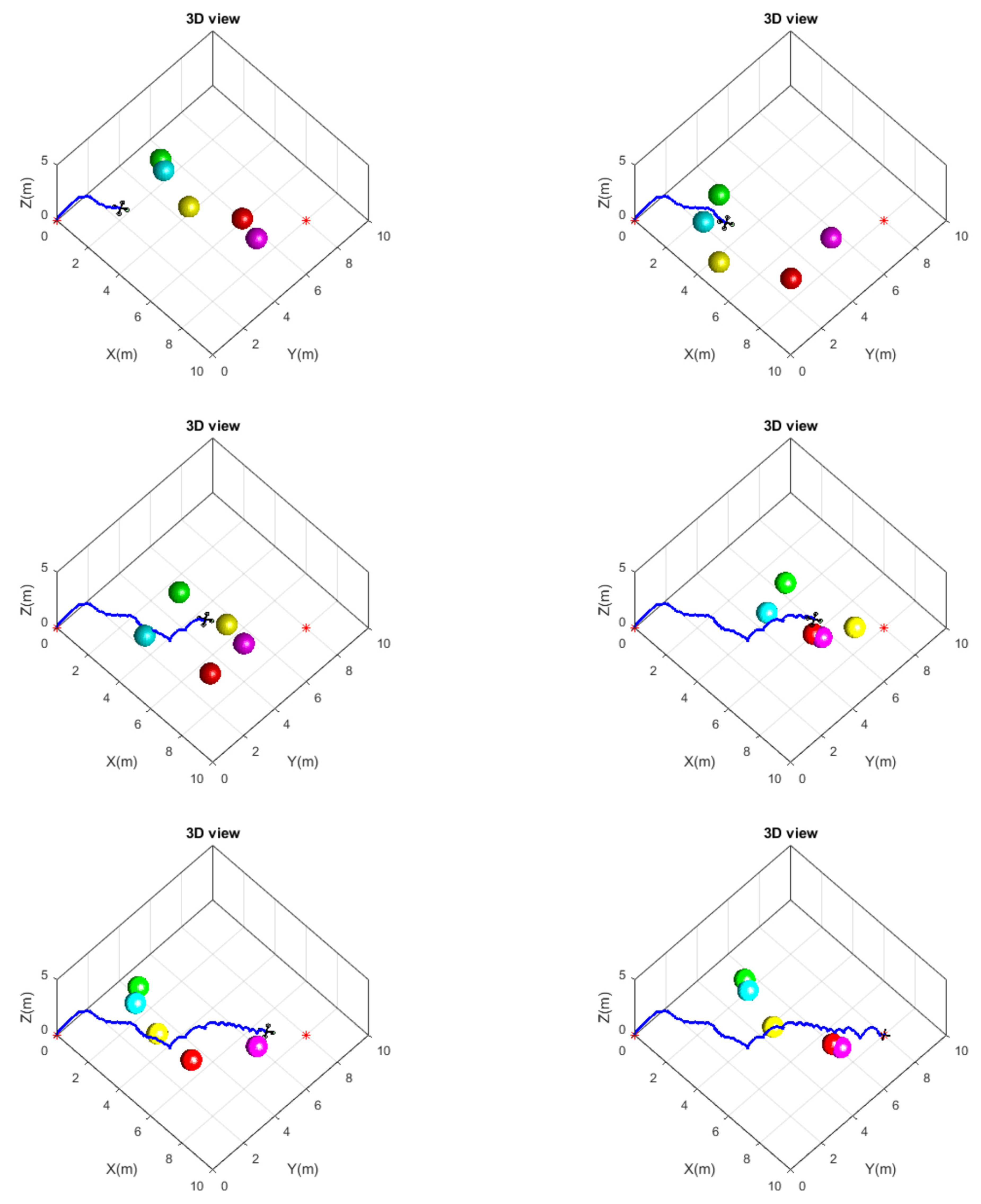
5. Simulation Results and Discussion
5.1. Software Environment for Parallel Computing
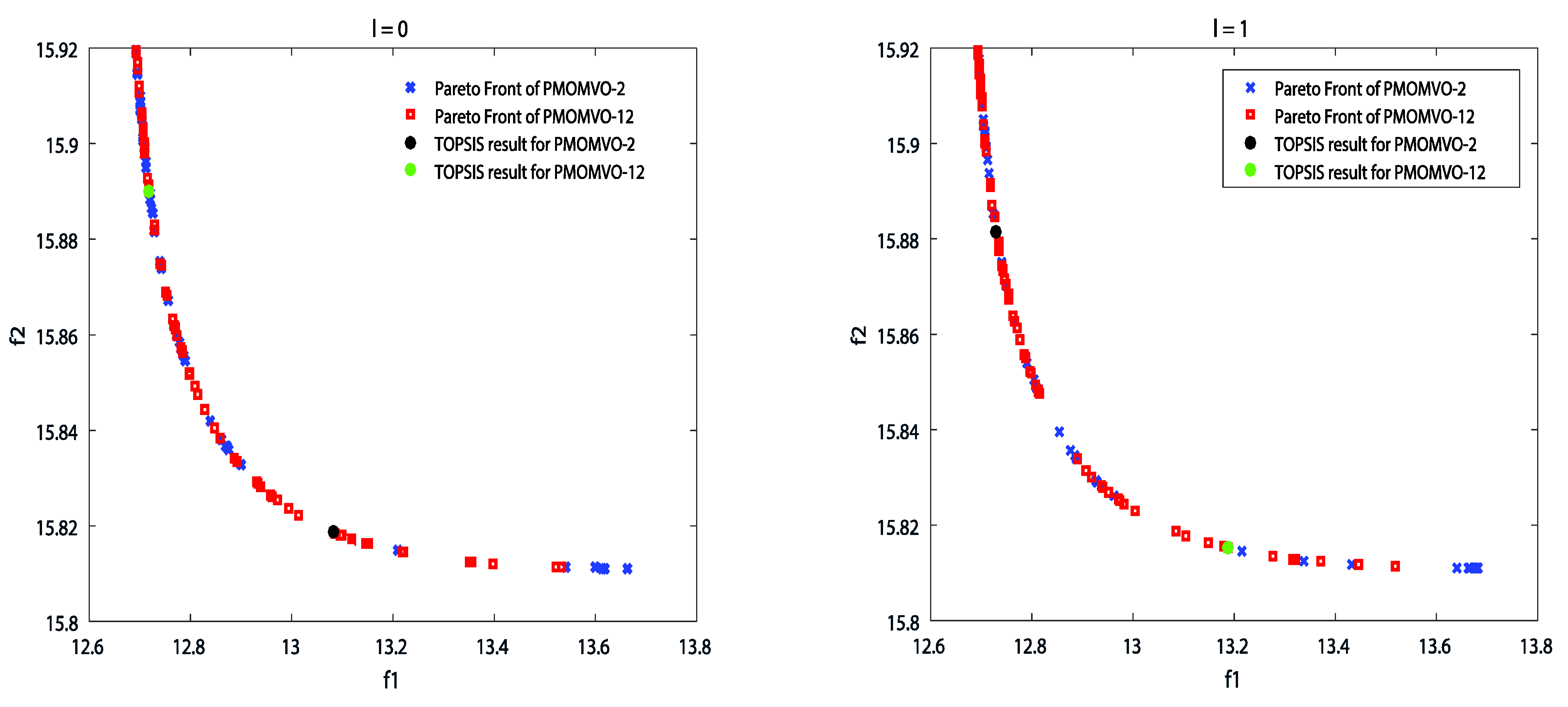
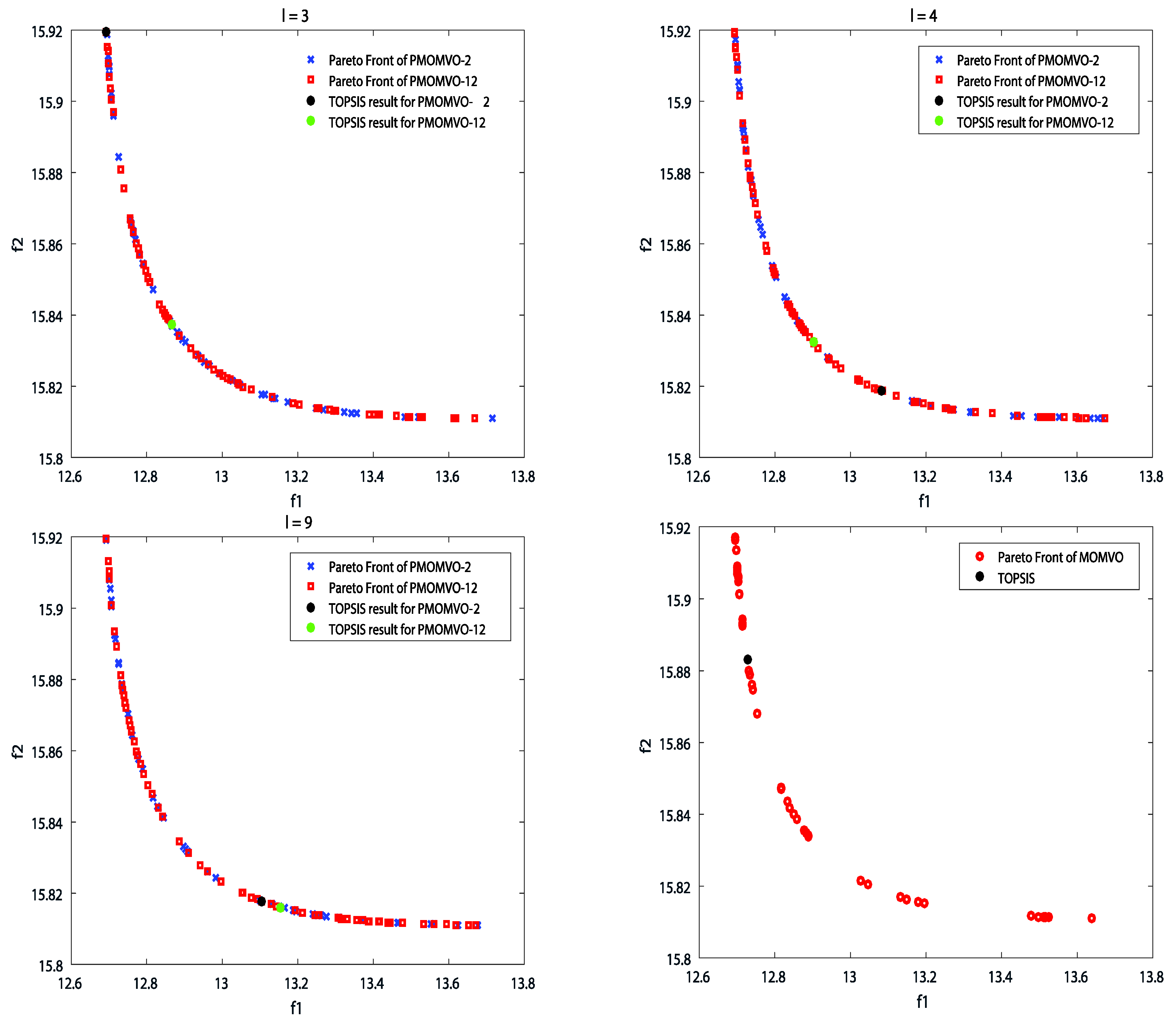
5.2. Numerical Experimentations and ANOVA Tests
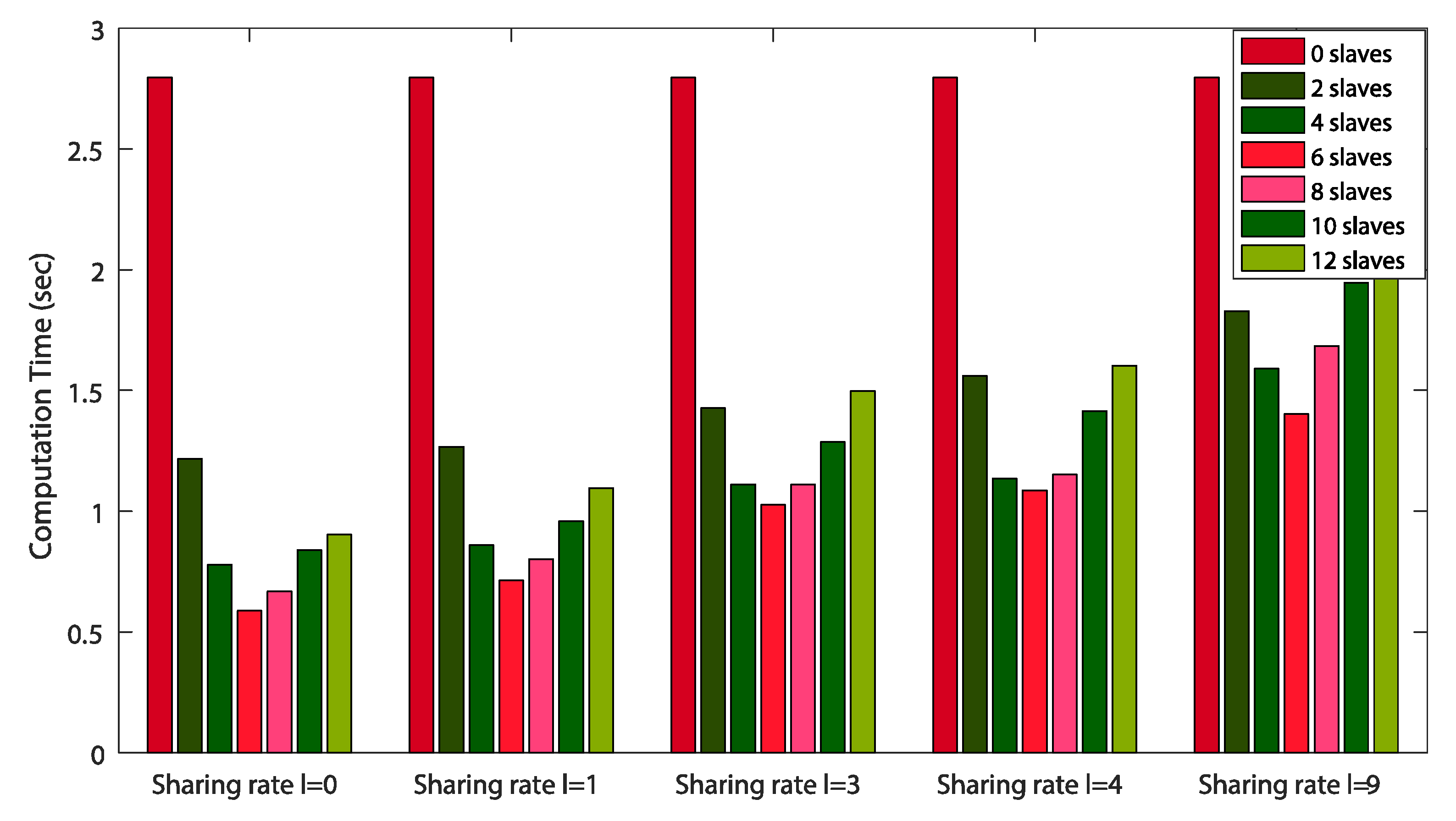
5.3. Computation Tims Analysis and Comparison
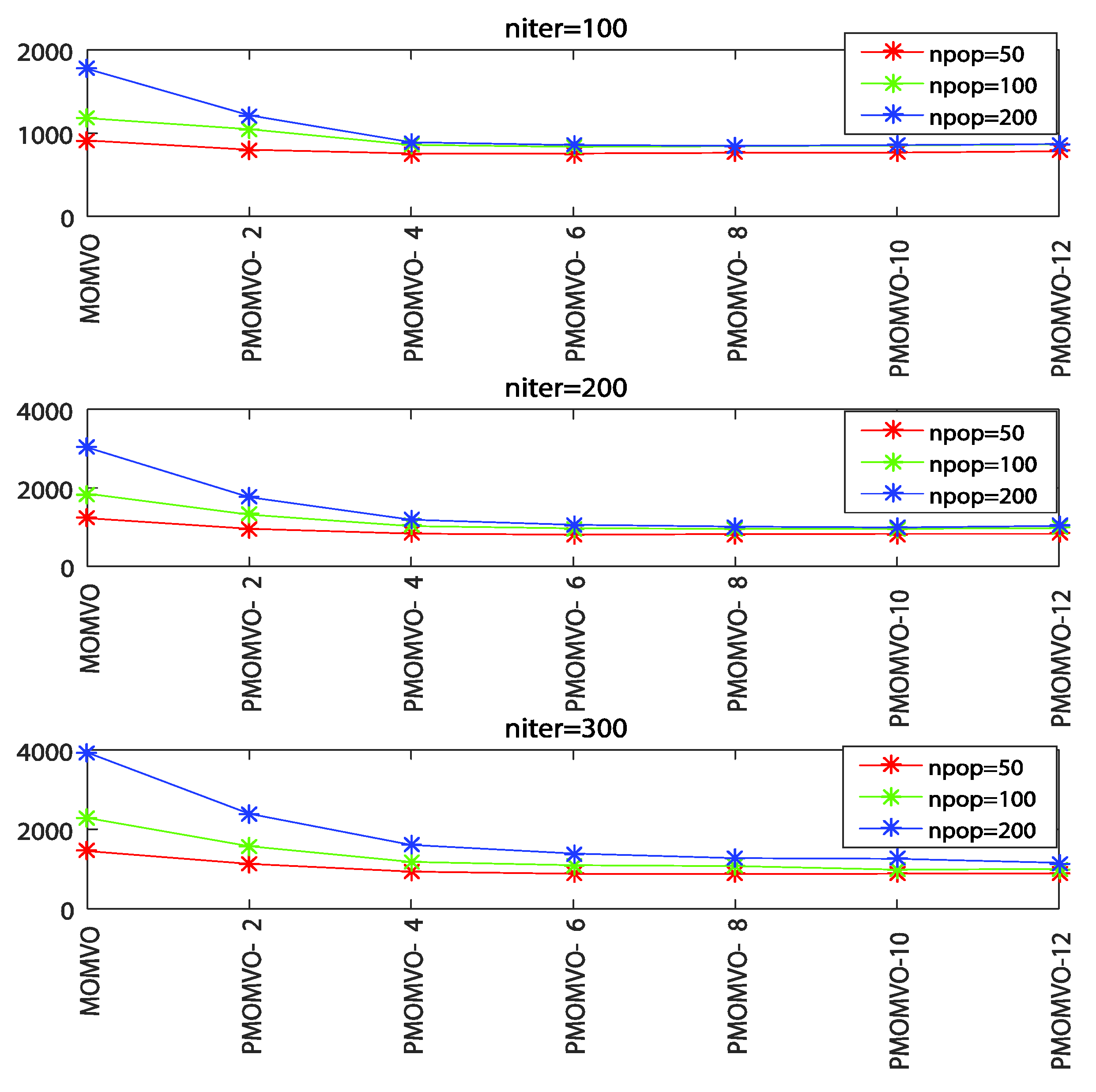
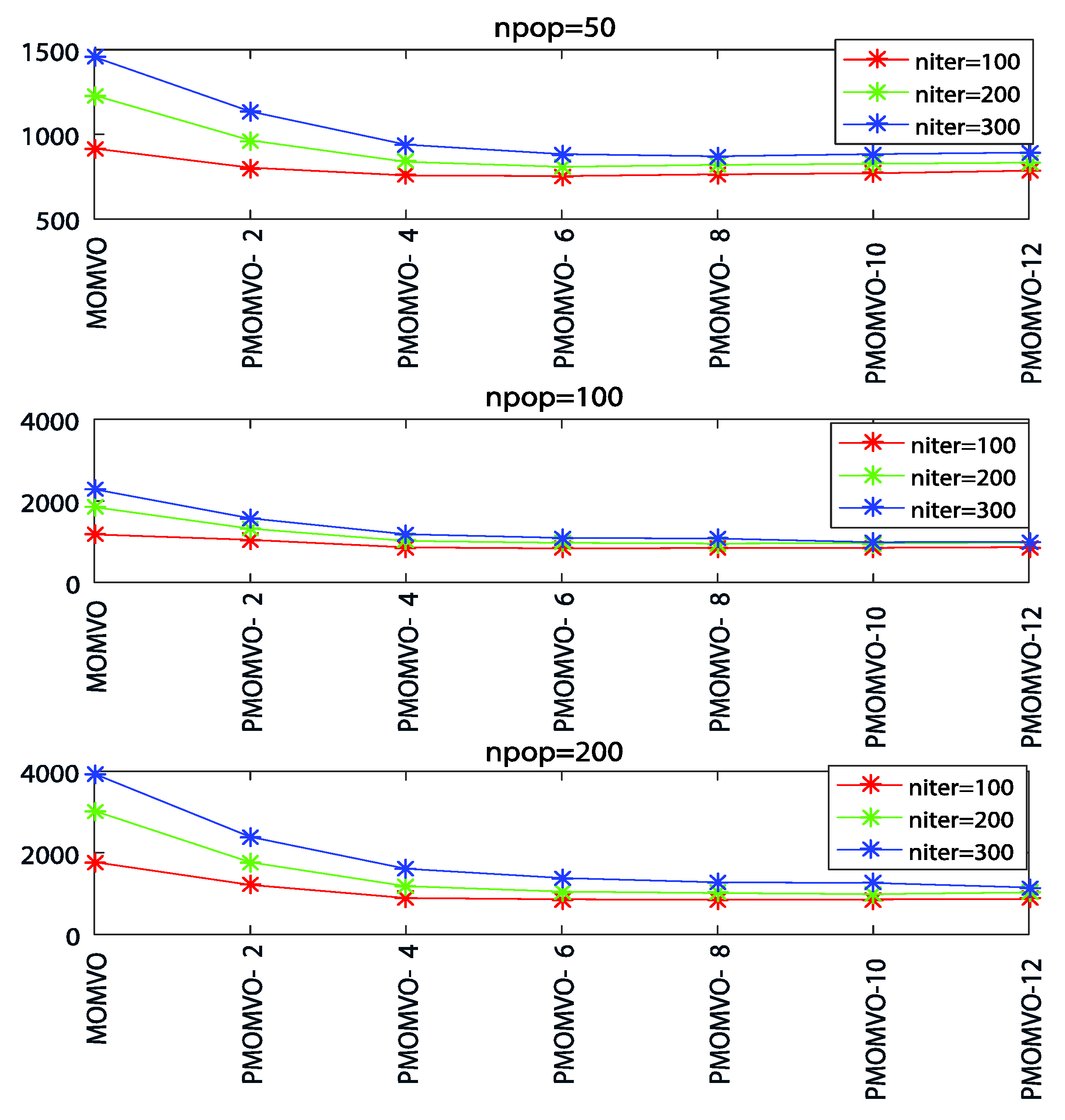
5.4. Parameters Sensitivity Analysis
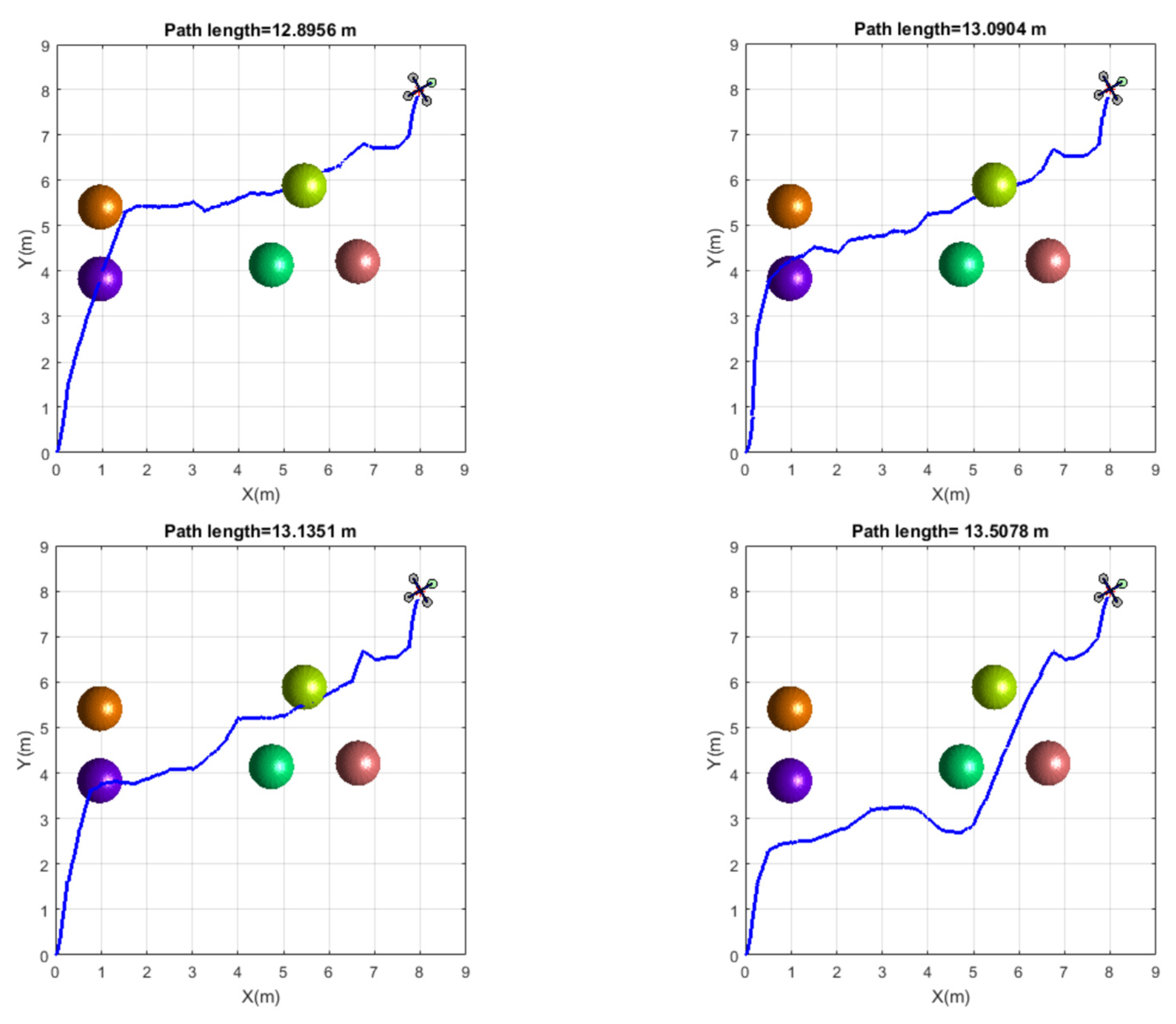
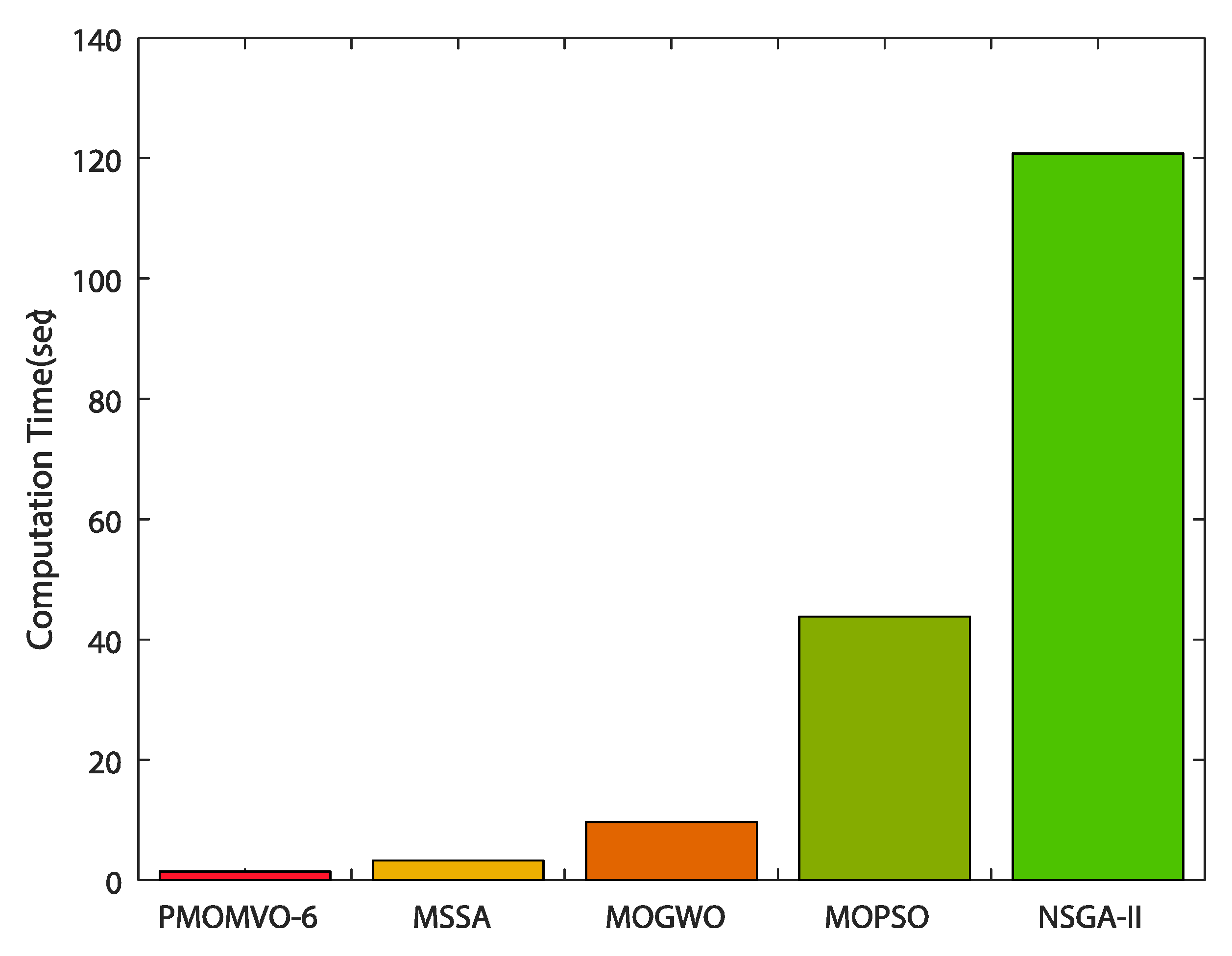
5.5. Comparison with Other Metaheuristics Algorithms
- − MSSA [55]: without control parameters (parameters-free algorithm).
- − MOGWO [56]: grid inflation 0.1, number of grids per dimension 10, leader selection pressure 4, and extra repository member selection pressure 2.
- − NSGA-II [57]: crossover probability 0.7, mutation probability 0.4, and mutation rate 0.02.
- − MOPSO [58]: social and cognitive parameters 2, grid inflation 0.1, leader selection pressure parameter 2, and number of grids per dimension 7.
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mohsan, S.A.H.; Khan, M.A.; Noor, F.; Ullah, I.; Alsharif, M.H. Towards the unmanned aerial vehicles (UAVs): A comprehensive review. Drones 2022, 6, 147. [Google Scholar] [CrossRef]
- Abro, G.E.M.; Zulkifli, S.A.B.M.; Masood, R.J.; Asirvadam, V.S.; Louati, A. Comprehensive review of UAV detection, security, and communication advancements to prevent threats. Drones 2022, 6, 284. [Google Scholar] [CrossRef]
- Yasin, J.N.; Mohamed, S.A.S.; Haghbayan, M.-H.; Heikkonen, J.; Tenhunen, H.; PLoSila, J. Unmanned aerial vehicles (UAVs): Collision avoidance systems and approaches. IEEE Access 2020, 8, 105139–105155. [Google Scholar] [CrossRef]
- Huang, S.; Teo, R.S.H.; Tan, K.K. Collision avoidance of multi unmanned aerial vehicles: A review. Annu. Rev. Control 2019, 48, 147–164. [Google Scholar] [CrossRef]
- Mohanan, M.G.; Salgoankar, A. A survey of robotic motion planning in dynamic environments. Robot. Auton. Syst. 2018, 100, 171–185. [Google Scholar] [CrossRef]
- Jones, M.R.; Djahel, S.; Welsh, K. Path-planning for unmanned aerial vehicles with environment complexity considerations: A survey. ACM Comput. Surv. 2022. [Google Scholar] [CrossRef]
- Aggarwal, S.; Kumar, N. Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges. Comput. Commun. 2019, 149, 270–299. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, M.; Yin, L. Dynamic path planning of the UAV avoiding static and moving obstacles. J. Intell. Robot. Syst. 2020, 99, 909–931. [Google Scholar] [CrossRef]
- Gan, X.; Wu, Y.; Liu, P.; Wang, Q. Dynamic Collision Avoidance Zone Modeling Method Based on UAV Emergency Collision Avoidance Trajectory. In Proceedings of the 2020 IEEE International Conference on Artificial Intelligence and Information Systems, Dalian, China, 20–22 March 2020. [Google Scholar]
- Wei, R.; Xu, Z.; Zhang, Q.; Zhou, K.; Ni, T. Analysis and Application to Collision Avoidance Stability of Cognitive UAV. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference, Xiamen, China, 10–12 August 2018. [Google Scholar]
- Corraro, F.; Corraro, G.; Cuciniello, G.; Garbarino, L. Unmanned aircraft collision detection and avoidance for dealing with multiple hazards. Aerospace 2022, 9, 190. [Google Scholar] [CrossRef]
- Lihua, Z.; Xianghong, C.; Fuh-Gwo, Y. A 3D collision avoidance strategy for UAV with physical constraints. Measurement 2015, 77, 40–49. [Google Scholar] [CrossRef]
- Blasi, L.; D’Amato, E.; Mattei, M.; Notaro, I. Path planning and real-time collision avoidance based on the essential visibility graph. Appl. Sci. 2020, 10, 5613. [Google Scholar] [CrossRef]
- Ma, R.; Ma, W.; Chen, X.; Li, J. Real-Time Obstacle Avoidance for Fixed-Wing Vehicles in Complex Environment. In Proceedings of the IEEE Chinese Guidance, Navigation and Control Conference, Nanjing, China, 12–14 August 2016. [Google Scholar]
- Lu, L.; Zong, C.; Lei, X.; Chen, B.; Zhao, P. Fixed-wing UAV path planning in a dynamic environment via dynamic RRT algorithm. In Mechanism and Machine Science; Asian MMS CCMMS, Lecture Notes in Electrical Engineering; Zhang, X., Wang, N., Huang, Y., Eds.; Springer: Singapore, 2017; Volume 408, pp. 271–282. [Google Scholar]
- Zu, W.; Fan, G.; Gao, Y.; Ma, Y.; Zhang, H.; Zeng, H. Multi-UAVs Cooperative Path Planning Method Based on Improved RRT Algorithm. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation, Changchun, China, 5–8 August 2018. [Google Scholar]
- Israr, A.; Ali, Z.A.; Alkhammash, E.H.; Jussila, J.J. Optimization methods applied to motion planning of unmanned aerial vehicles: A review. Drones 2022, 6, 126. [Google Scholar] [CrossRef]
- Huang, C.; Lan, Y.; Liu, Y.; Zhou, W.; Pei, H.; Yang, L.; Cheng, Y.; Hao, Y.; Peng, Y. A new dynamic path planning approach for unmanned aerial vehicles. Complexity 2018, 2018, 8420294. [Google Scholar] [CrossRef]
- Ge, F.; Li, K.; Han, Y.; Xu, W.; Wang, Y. Path planning of UAV for oilfield inspections in a three-dimensional dynamic environment with moving obstacles based on an improved pigeon-inspired optimization algorithm. Appl. Intell. 2020, 50, 2800–2817. [Google Scholar] [CrossRef]
- Zhang, B.; Duan, H. Three-dimensional path planning for uninhabited combat aerial vehicle based on predator-prey pigeon-inspired optimization in dynamic environment. IEEE ACM Trans. Comput. Biol. Bioinform. 2017, 14, 97–107. [Google Scholar] [CrossRef]
- Tian, G.; Zhang, L.; Bai, X.; Wang, B. Real-time Dynamic Track Planning of Multi-UAV Formation Based on Improved Artificial Bee Colony Algorithm. In Proceedings of the 37th Chinese Control Conference, Wuhan, China, 25–27 July 2018. [Google Scholar]
- Zajac, S.; Huber, S. Objectives and methods in multi-objective routing problems: A survey and classification scheme. Eur. J. Oper. Res. 2020, 290, 1–25. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.-W.; Zhang, J.-H. Robot path planning in uncertain environment using multi-objective particle swarm optimization. Neurocomputing 2013, 103, 172–185. [Google Scholar] [CrossRef]
- Jarray, R.; Al-Dhaifallah, M.; Rezk, H.; Bouallègue, S. Path planning of quadrotors in a dynamic environment using a multi-criteria multi-verse optimizer. Comput. Mater. Contin. 2021, 69, 2159–2180. [Google Scholar]
- Jarray, R.; Bouallègue, S. Multi-criteria path planning of unmanned aerial vehicles through a combined multi-verse and decision-making methods. Int. J. Sci. Res. Eng. Technol. 2021, 15, 1–8. [Google Scholar]
- Jarray, R.; Bouallègue, S. Multi-verse algorithm-based approach for multi-criteria path planning of unmanned aerial vehicles. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 324–334. [Google Scholar] [CrossRef]
- Paikray, H.K.; Das, P.K.; Panda, S. Optimal path planning of multi-robot in dynamic environment using hybridization of meta-heuristic algorithm. Int. J. Intell. Robot. Appl. 2022, 6, 625–667. [Google Scholar] [CrossRef]
- Manikandan, K.; Sriramulu, R. Optimized path planning strategy to enhance security under swarm of unmanned aerial vehicles. Drones 2022, 6, 336. [Google Scholar] [CrossRef]
- Alqarni, M.A.; Saleem, S.; Alkatheiri, M.S.; Chauhdary, S.H. Optimized path planning of drones for efficient logistics using turning point with evolutionary techniques. J. Electron. Imaging 2022, 31, 061819. [Google Scholar] [CrossRef]
- Mughal, U.A.; Ahmad, I.; Pawase, C.J.; Chang, K. UAVs path planning by particle swarm optimization based on visual-SLAM algorithm. In Intelligent Unmanned Air Vehicles Communications for Public Safety Networks; Kaleem, Z., Ahmad, I., Duong, T.Q., Eds.; Springer: Singapore, 2022; pp. 169–197. [Google Scholar]
- Shin, J.-J.; Bang, H. UAV path planning under dynamic threats using an improved PSO algorithm. Int. J. Aerosp. Eng. 2020, 2020, 8820284. [Google Scholar] [CrossRef]
- Jarray, R.; Al-Dhaifallah, M.; Rezk, H.; Bouallègue, S. Parallel cooperative co-evolutionary grey wolf optimizer for path planning problem of unmanned aerial vehicles. Sensors 2022, 22, 1826. [Google Scholar] [CrossRef]
- Hijazi, N.M.; Faris, H.; Aljarah, I. A parallel metaheuristic approach for ensemble feature selection based on multi-core architectures. Expert Syst. Appl. 2021, 182, 115290. [Google Scholar] [CrossRef]
- El Baz, D.; Fakih, B.; Sanchez Nigenda, R.; Boyer, V. Parallel best-first search algorithms for planning problems on multi-core processors. J. Supercomput. 2022, 78, 3122–3151. [Google Scholar] [CrossRef]
- Deng, H.; Yeh, C.H.; Willis, R.J. Inter-company comparison using modified TOPSIS with objective weights. Comput. Oper. Res. 2000, 27, 963–973. [Google Scholar] [CrossRef]
- Chen, X.; Chen, X. The UAV Dynamic Path Planning Algorithm Research Based on Voronoï Diagram. In Proceedings of the 26th Chinese Control and Decision Conference, Changsha, China, 31 May–2 June 2014. [Google Scholar]
- Budiyanto, A.; Cahyadi, A.; Adji, T.B.; Wahyunggoro, O. UAV Obstacle Avoidance Using Potential Field Under Dynamic Environment. In Proceedings of the 2015 International Conference on Control, Electronics, Renewable Energy and Communications, Bandung, Indonesia, 27–29 August 2015. [Google Scholar]
- Chen, S.; Yang, Z.; Liu, Z.; Jin, H. An improved artificial potential field based path planning algorithm for unmanned aerial vehicle in dynamic environments. In Proceedings of the 2017 International Conference on Security, Pattern Analysis, and Cybernetics, Shenzhen, China, 15–17 December 2017. [Google Scholar]
- Geng, L.; Zhang, Y.F.; Wang, J.; Fuh, J.Y.H.; Teo, S.H. Cooperative mission planning with multiple UAVs in realistic environments. Unmanned Syst. 2014, 2, 73–86. [Google Scholar] [CrossRef]
- Maurović, I.; Seder, M.; Lenac, K.; Petrović, I. Path planning for active SLAM based on the D* algorithm with negative edge weights. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 1321–1331. [Google Scholar] [CrossRef]
- Kim, H.; Jeong, J.; Kim, N.; Kang, B. A Study on 3D Optimal Path Planning for Quadcopter UAV Based on D* Lite. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems, Atlanta, GA, USA, 11–14 June 2019. [Google Scholar]
- Wang, J.; Li, Y.; Li, R.; Chen, H.; Chu, K. Trajectory planning for UAV navigation in dynamic environments with matrix alignment Dijkstra. Soft Comput. 2022, 26, 12599–12610. [Google Scholar] [CrossRef]
- Wang, M.; Voos, H. Safer UAV Piloting: A Robust Sense-and-Avoid Solution for Remotely Piloted Quadrotor UAVs in Complex Environments. In Proceedings of the 19th International Conference on Advanced Robotics, Belo Horizonte, Brazil, 2–6 December 2019. [Google Scholar]
- Yan, C.; Xiang, X.; Wang, C. Towards real-time path planning through deep reinforcement learning for a UAV in dynamic environments. J. Intell. Robot. Syst. 2019, 98, 297–309. [Google Scholar] [CrossRef]
- Xie, R.; Meng, Z.; Wang, L.; Li, H.; Wang, K.; Wu, Z. Unmanned aerial vehicle path planning algorithm based on deep reinforcement learning in large-scale and dynamic environments. IEEE Access 2021, 9, 24884–24900. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, Y. UAV path planning based on multilayer reinforcement learning technique. IEEE Access 2021, 9, 59486–59497. [Google Scholar] [CrossRef]
- Vieira, D.A.G.; Adriano, R.L.S.; Krähenbühl, L.; Vasconcelos, J.A. Handling constraints as objectives in a multi-objective genetic based algorithm. J. Microw. Optoelectron. Electromagn. Appl. 2002, 2, 50–58. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Mirjalili, S.; Jangir, P.; Mirjalili, S.Z.; Saremi, S.; Trivedi, I.N. Optimization of problems with multiple objectives using the multi-verse optimization algorithm. Knowl.-Based Syst. 2017, 134, 50–71. [Google Scholar] [CrossRef]
- MathWorks Inc. Parallel Computing ToolboxTM—User’s Guide. Available online: https://ch.mathworks.com/help/pdf_doc/parallel-computing/index.html (accessed on 20 November 2021).
- Zitzler, E.; Thiele, L. Multi-objective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of multi-objective evolutionary algorithms: Empirical results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef]
- Collette, Y.; Patrick, S. Three new metrics to measure the convergence of metaheuristics towards the Pareto frontier and the aesthetic of a set of solutions in bi-objective optimization. Comput. Oper. Res. 2005, 32, 773–792. [Google Scholar] [CrossRef]
- Pereira, D.G.; Afonso, A.; Medeiros, F.M. Overview of Friedman’s test and post-hoc analysis. Commun. Stat.-Simul. Comput. 2014, 44, 2636–2653. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; dos, S. Coelho, L. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Coello Coello, C.A.; Toscano Pulido, G.; Salazar Lechuga, M. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
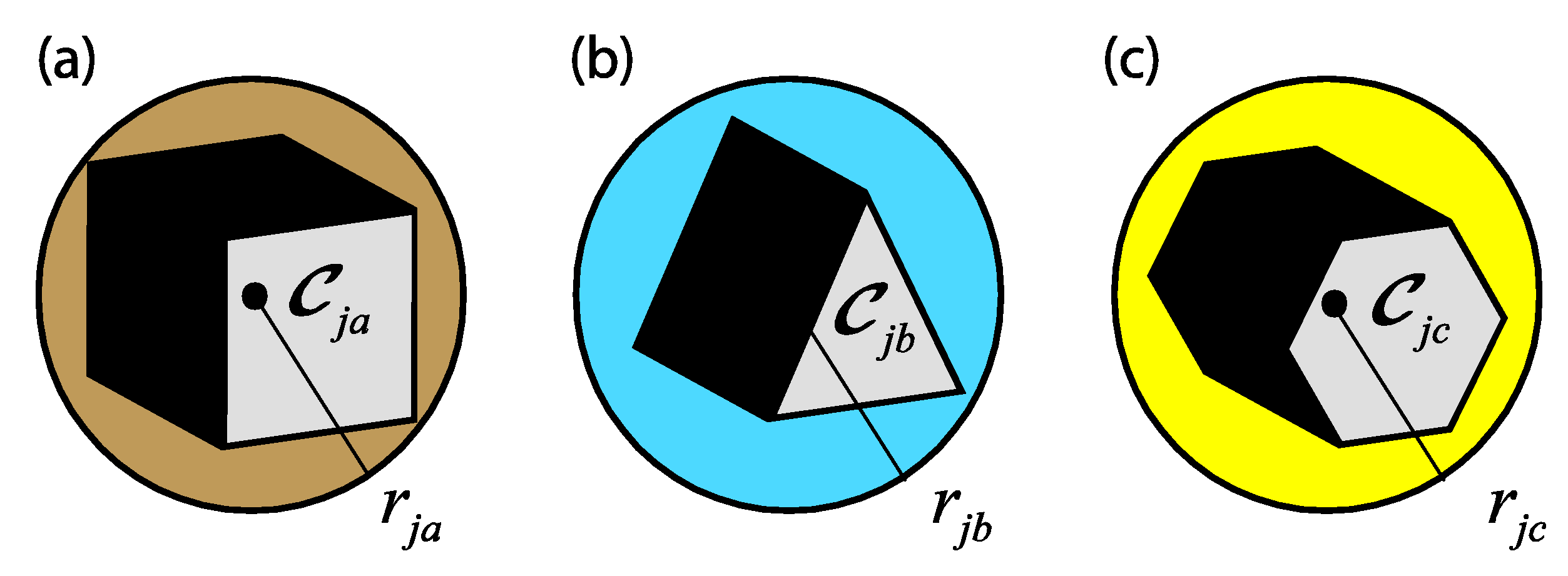


| Classes | Year | Literature | Description of the Main Topic and Used Technique |
|---|---|---|---|
| Sampling-based algorithms | 2014 | [36] | A Voronoï-diagram-based algorithm proposed for UAV path planning in a dynamic environment. |
| 2015 | [37] | An Artificial Potential Field (APF) algorithm using the attractive potential field to achieve goals and the repulsive potential field to avoid both static and dynamic obstacles. | |
| 2016 | [14] | A Rapidly exploring Random Tree (RRT) algorithm employed for fixed-wing UAV path planning in a dynamic environment. | |
| 2016 | [15] | A Dynamic RRT (DRRT) technique applied to solve fixed-wing UAV path planning problems in dynamic 3D environments. | |
| 2017 | [38] | An Improved APF (IAPF)-based method proposed to solve UAV trajectory planning problems in a dynamic environment. | |
| 2018 | [16] | An Improved RRT (IRRT)-based technique investigated to generate paths for multiple UAVs in real-time scenarios with the presence of unknown pop-up obstacles. | |
| Node-based algorithms | 2014 | [39] | An A-star (A*) algorithm used to obtain the shortest feasible flying path for a UAV. |
| 2017 | [40] | A D-star (D*) algorithm proposed to find the shortest path for mobile robots in highly dynamic environments. | |
| 2019 | [41] | A variant D* Lite of D* algorithm applied to solve the 3D path planning problem for quadrotor-types of UAVs. | |
| 2022 | [42] | A Matrix Alignment Dijkstra (MAD)-based technique proposed to make drones safely move in dynamic environments. | |
| Mathematical-based algorithms | 2019 | [43] | A planning strategy based on a nonlinear control system using an optimization-based avoidance strategy with account of sensor characteristics and an emergency evaluation policy. |
| Machine learning-based algorithms | 2019 | [44] | A Reinforcement Learning (RL)-based technique proposed to solve the UAV path planning problem based on global situation information. |
| 2021 | [45] | A Deep Reinforcement Learning (DRL) approach investigated path planning problems in complex and dynamic environments using local information and relative distance. | |
| 2021 | [46] | A Multilayer Reinforcement Learning (MRL) algorithm using a neural network with two layers proposed to collect both global and local information for navigation in dynamic environments. | |
| Metaheuristics-based algorithms | 2021 | [24,25,26] | A Multicriteria Multiverse Optimizer (MOMVO) associated with the TOPSIS technique proposed for path planning problems in a 3D environment with moving obstacles and threats. |
| 2022 | [27] | An Improved Particle Swarm Optimization (IPSO) and Arithmetic Optimization Algorithm (AOA)-based hybrid planner for the path planning of multiple robots in a dynamic environment. | |
| 2022 | [28] | A Resilient UAV Path Optimization Algorithm (RUPOA) as a new planning algorithm proposed to achieve safe path planning for UAVs under uncertain dynamic environments. | |
| 2022 | [29] | An Evolutionary PSO (EPSO) algorithm used to solve the drone path planning problem in a dynamic environment. | |
| 2022 | [30] | An Improved PSO (IPSO)-based algorithm employed for a visual-SLAM-based planning strategy to optimize the paths for multi-UAVs in a dynamic environment. |
| Scenarios | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Moving obstacles | 5 | 9 | 12 | 15 | 20 |
| Starting point [m] | [0, 0, 0] | [1, 2, 0] | [1, 2, 0] | [2, 4, 0] | [0, 0, 0] |
| Target point [m] | [9, 8, 0] | [10, 10, 0] | [13, 10, 0] | [16, 13, 0] | [16, 15, 0] |
| Initial positions [m] | [5 5 2], [3 3 2], [5 3 1], [2 1 1], [6 2 2] | [1 3 1], [3 5 1], [4 4 3], [5 5 4], [7 3 4], [8 2 1], [9 5 2], [10 8 1], [9 9 1] | [2 3 1], [2 4 1], [4 3 2], [5 3 3], [5 5 2], [6 4 1], [7 7 2], [7 3 4], [8 6 3], [10 8 2], [9 2 1], [12 9 2] | [1 3 1], [2 5 2], [2 4 3], [2 7 1], [3 2 1], [3 3 3], [4 1 2], [4 5 4], [6 7 1], [7 2 2], [8 5 2], [10 8 3], [6 12 2], [13 1 2], [15 11 3] | [2 5 1], [15 13 1], [4 2 1], [13 9 4], [10 7 2], [14 12 1], [6 2 3], [4 12 1], [14 2 4], [9 10 2], [7 12 1], [12 10 5], [8 1 2], [8 8 1], [9 14 2] [5 3 1], [10 3 2], [8 14 1], [14 2 3], [12 8 2] |
| Motion speeds [m/s] | [4 −2 1], [2 −2 −2], [4 2 2], [2 2 2], [−2 2 −2] | [2 1 1], [3- 3 1], [4 1 −2], [2 1 1], [−1 −2 2], [0.5 1 −1], [1 −1 2], [1 −1 1], [1 2 1] | [−1 3 −1], [−1 1 1], [2 2 1], [1 2 4], [0.2 1 3], [1 −1 1], [2 1 2], [−1 2 2], [1 2 1], [3 0.5 2], [2 −1 1], [3 1 1] | [1 2 1], [−2 1 1], [3 −1 3], [2 1 2], [−1 3 1], [1 2 −2], [2 −1 2], [4 1 2], [3 2 1], [0.5 2 −2], [1 −2 1], [1 2 3], [1 2 0.5], [0.5 −1 1], [−1 2 2] | [1 3 1], [3 −1 1], [4 1 3], [2 2 4], [−1 3 1], [2 1 1], [3 1 2], [1 3 −2], [1 1 1], [2 −0.5 2], [1 1 2], [1 2 1], [2 2 −2], [1 −2 1], [1 1 2], [1 −2 −1], [1 2 −1], [2 1 1], [1 −1 2], [−1 1 2] |
| Algorithms | Sharing Rates of Better Pareto Solutions | |||||
|---|---|---|---|---|---|---|
| MOMVO () | Best | 0.0915 | - | - | - | - |
| Mean | 0.0838 | - | - | - | - | |
| Worst | 0.0654 | - | - | - | - | |
| STD | 0.0153 | - | - | - | - | |
| PMOMVO-2 | Best | 0.0956 | 0.0964 | 0.0974 | 0.0987 | 0.0991 |
| Mean | 0.0803 | 0.0848 | 0.0860 | 0.0883 | 0.0912 | |
| Worst | 0.0687 | 0.0689 | 0.0715 | 0.0754 | 0.0853 | |
| STD | 0.0131 | 0.0135 | 0.0129 | 0.0115 | 0.0069 | |
| PMOMVO-4 | Best | 0.0964 | 0.0973 | 0.0989 | 0.0993 | 0.0995 |
| Mean | 0.0810 | 0.0869 | 0.0879 | 0.0898 | 0.0923 | |
| Worst | 0.0691 | 0.0695 | 0.0725 | 0.0758 | 0.0864 | |
| STD | 0.0138 | 0.0137 | 0.0131 | 0.0119 | 0.0066 | |
| PMOMVO-6 | Best | 0.0976 | 0.0986 | 0.0991 | 0.0997 | 0.1003 |
| Mean | 0.0816 | 0.0870 | 0.0889 | 0.0904 | 0.0950 | |
| Worst | 0.0721 | 0.0736 | 0.0754 | 0.0810 | 0.0839 | |
| STD | 0.0130 | 0.0124 | 0.0117 | 0.0093 | 0.0082 | |
| PMOMVO-8 | Best | 0.0981 | 0.0989 | 0.0992 | 0.0999 | 0.1014 |
| Mean | 0.0821 | 0.0880 | 0.0897 | 0.0929 | 0.0961 | |
| Worst | 0.0732 | 0.0740 | 0.0714 | 0.0823 | 0.0845 | |
| STD | 0.0128 | 0.0120 | 0.0140 | 0.0088 | 0.0082 | |
| PMOMVO-10 | Best | 0.0991 | 0.0994 | 0.0997 | 0.1045 | 0.1063 |
| Mean | 0.0933 | 0.0908 | 0.0942 | 0.0964 | 0.0989 | |
| Worst | 0.0756 | 0.0784 | 0.0792 | 0.0841 | 0.0859 | |
| STD | 0.0120 | 0.0103 | 0.0105 | 0.0102 | 0.0101 | |
| PMOMVO-12 | Best | 0.0995 | 0.0996 | 0.0998 | 0.1054 | 0.1084 |
| Mean | 0.0966 | 0.0946 | 0.0961 | 0.0978 | 0.0996 | |
| Worst | 0.0755 | 0.0786 | 0.0806 | 0.0845 | 0.0862 | |
| STD | 0.0130 | 0.0112 | 0.0103 | 0.0105 | 0.0110 | |
| Algorithms | Sharing Rates of Better Pareto Solutions | |||||
|---|---|---|---|---|---|---|
| MOMVO () | Best | 0.9685 | - | - | - | - |
| Mean | 0.9482 | - | - | - | - | |
| Worst | 0.9041 | - | - | - | - | |
| STD | 0.0336 | - | - | - | - | |
| PMOMVO-2 | Best | 0.9710 | 0.9796 | 0.9886 | 0.9891 | 0.9943 |
| Mean | 0.9550 | 0.9751 | 0.9874 | 0.9883 | 0.9886 | |
| Worst | 0.9413 | 0.9614 | 0.9712 | 0.9745 | 0.9813 | |
| STD | 0.0148 | 0.0099 | 0.0098 | 0.0080 | 0.0065 | |
| PMOMVO-4 | Best | 0.9723 | 0.9822 | 0.9889 | 0.9894 | 0.9954 |
| Mean | 0.9628 | 0.9765 | 0.9882 | 0.9884 | 0.9887 | |
| Worst | 0.9465 | 0.9652 | 0.9723 | 0.9765 | 0.9824 | |
| STD | 0.0135 | 0.0089 | 0.0094 | 0.0071 | 0.0062 | |
| PMOMVO-6 | Best | 0.9821 | 0.9836 | 0.9891 | 0.9926 | 0.9969 |
| Mean | 0.9708 | 0.9787 | 0.9885 | 0.9894 | 0.9897 | |
| Worst | 0.9563 | 0.9663 | 0.9754 | 0.9782 | 0.9839 | |
| STD | 0.0130 | 0.0089 | 0.0076 | 0.0075 | 0.0064 | |
| PMOMVO-8 | Best | 0.9841 | 0.9856 | 0.9894 | 0.9952 | 0.9986 |
| Mean | 0.9735 | 0.9793 | 0.9887 | 0.9912 | 0.9933 | |
| Worst | 0.9587 | 0.9681 | 0.9768 | 0.9863 | 0.9881 | |
| STD | 0.0129 | 0.0088 | 0.0072 | 0.0046 | 0.0053 | |
| PMOMVO-10 | Best | 0.9863 | 0.9874 | 0.9897 | 0.9965 | 1.0034 |
| Mean | 0.9812 | 0.9796 | 0.9895 | 0.9931 | 0.9957 | |
| Worst | 0.9621 | 0.9685 | 0.9771 | 0.9881 | 0.9892 | |
| STD | 0.0127 | 0.0094 | 0.0071 | 0.0045 | 0.0067 | |
| PMOMVO-12 | Best | 0.9876 | 0.9886 | 0.9902 | 1.0005 | 1.0123 |
| Mean | 0.9845 | 0.9804 | 0.9898 | 0.9957 | 0.9989 | |
| Worst | 0.9665 | 0.9714 | 0.9785 | 0.9898 | 0.9901 | |
| STD | 0.0113 | 0.0087 | 0.0067 | 0.0053 | 0.0110 | |
| Algorithms | Sharing Rates of Better Pareto Solutions | |||||
|---|---|---|---|---|---|---|
| MOMVO () | Best | 9.6741 | - | - | - | - |
| Mean | 14.7315 | - | - | - | - | |
| Worst | 20.3641 | - | - | - | - | |
| STD | 5.8492 | - | - | - | - | |
| PMOMVO-2 | Best | 9.9874 | 8.9631 | 6.9654 | 6.1234 | 4.1231 |
| Mean | 16.7786 | 12.5560 | 9.5141 | 7.2783 | 5.6696 | |
| Worst | 21.6521 | 15.8652 | 12.4264 | 11.3698 | 7.2541 | |
| STD | 5.8589 | 3.4520 | 2.7825 | 2.7552 | 1.5695 | |
| PMOMVO-4 | Best | 9.8841 | 8.7431 | 6.7412 | 5.8419 | 3.9841 |
| Mean | 14.0749 | 11.3203 | 8.7722 | 7.4904 | 4.1613 | |
| Worst | 18.3652 | 15.5874 | 11.3210 | 10.2143 | 6.1432 | |
| STD | 4.2452 | 3.4582 | 2.2923 | 2.2023 | 1.1974 | |
| PMOMVO-6 | Best | 9.7436 | 8.5961 | 6.6321 | 5.1231 | 3.4561 |
| Mean | 13.3927 | 10.9666 | 8.1799 | 6.1541 | 3.9961 | |
| Worst | 17.6354 | 13.8741 | 11.0362 | 9.4563 | 5.8741 | |
| STD | 3.9485 | 2.6423 | 2.2353 | 2.2614 | 1.2682 | |
| PMOMVO-8 | Best | 9.5896 | 8.2541 | 6.1536 | 4.8236 | 3.3987 |
| Mean | 13.1597 | 9.8244 | 7.0997 | 5.8765 | 3.8388 | |
| Worst | 16.5413 | 12.8741 | 10.8413 | 8.1243 | 5.3243 | |
| STD | 3.4723 | 2.3482 | 2.4723 | 1.6856 | 1.0088 | |
| PMOMVO-10 | Best | 9.4132 | 7.1245 | 5.4563 | 4.6874 | 3.1716 |
| Mean | 12.0952 | 8.8336 | 6.7727 | 5.2175 | 3.7988 | |
| Worst | 14.1452 | 10.2365 | 8.8741 | 7.6584 | 5.1413 | |
| STD | 2.3728 | 1.5569 | 1.7241 | 1.5823 | 1.0068 | |
| PMOMVO-12 | Best | 8.7413 | 6.5741 | 5.2416 | 4.2478 | 2.6746 |
| Mean | 11.7824 | 7.6079 | 6.1369 | 5.0861 | 3.7444 | |
| Worst | 13.4713 | 9.9541 | 8.5542 | 7.2365 | 5.0321 | |
| STD | 2.3968 | 1.7319 | 1.7136 | 1.5402 | 1.1804 | |
| Algorithms | Scenarios | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| MOMVO | Best | 1.0204 | 1.0271 | 1.0163 | 1.0069 | 1.0206 |
| Mean | 1.0321 | 1.0301 | 1.0273 | 1.0119 | 1.0378 | |
| Worst | 1.0898 | 1.0710 | 1.0354 | 1.0175 | 1.0422 | |
| STD | 0.3352 | 0.2982 | 0.1376 | 0.0893 | 0.2447 | |
| PMOMVO-2 | Best | 1.0094 | 1.0100 | 1.0164 | 1.0046 | 1.0205 |
| Mean | 1.0225 | 1.0214 | 1.0230 | 1.0085 | 1.0344 | |
| Worst | 1.0344 | 1.0338 | 1.0293 | 1.0129 | 1.0376 | |
| STD | 0.1423 | 0.1485 | 0.0913 | 0.0673 | 0.1985 | |
| PMOMVO-4 | Best | 1.0086 | 1.0081 | 1.0105 | 1.0033 | 1.0148 |
| Mean | 1.0180 | 1.0162 | 1.0153 | 1.0059 | 1.0205 | |
| Worst | 1.0253 | 1.0254 | 1.0232 | 1.0099 | 1.0251 | |
| STD | 0.1002 | 0.1042 | 0.0910 | 0.0563 | 0.1125 | |
| PMOMVO-6 | Best | 1.0079 | 1.0072 | 1.0101 | 1.0027 | 1.0146 |
| Mean | 1.0160 | 1.0144 | 1.0162 | 1.0054 | 1.0202 | |
| Worst | 1.0236 | 1.0223 | 1.0211 | 1.0086 | 1.0241 | |
| STD | 0.0913 | 0.0912 | 0.0781 | 0.0496 | 0.1046 | |
| PMOMVO-8 | Best | 1.0074 | 1.0065 | 1.0084 | 1.0024 | 1.0145 |
| Mean | 1.0144 | 1.0131 | 1.0140 | 1.0045 | 1.0203 | |
| Worst | 1.0219 | 1.0204 | 1.0175 | 1.0076 | 1.0240 | |
| STD | 0.0858 | 0.0825 | 0.0661 | 0.0426 | 0.1036 | |
| PMOMVO-10 | Best | 1.0071 | 1.0065 | 1.0078 | 1.0022 | 1.0143 |
| Mean | 1.0149 | 1.0110 | 1.0128 | 1.0048 | 1.0199 | |
| Worst | 1.0205 | 1.0191 | 1.0155 | 1.0070 | 1.0236 | |
| STD | 0.0832 | 0.0759 | 0.0549 | 0.0414 | 0.1029 | |
| PMOMVO-12 | Best | 1.0065 | 1.0057 | 1.0067 | 1.0015 | 1.0141 |
| Mean | 1.0137 | 1.0121 | 1.0112 | 1.0051 | 1.0203 | |
| Worst | 1.0197 | 1.0190 | 1.0141 | 1.0063 | 1.0235 | |
| STD | 0.0765 | 0.0783 | 0.0526 | 0.0401 | 0.1032 | |
| Algorithms | Scenarios | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| MOMVO | Best | 451.6952 | 491.3265 | 736.3214 | 828.9541 | 898.2541 |
| Mean | 462.8974 | 504.5230 | 745.9852 | 839.8741 | 915.5800 | |
| Worst | 471.2563 | 515.6932 | 752.6541 | 847.9852 | 930.6589 | |
| STD | 8.7587 | 11.1254 | 8.2263 | 9.5062 | 10.2123 | |
| PMOMVO-2 | Best | 404.3652 | 435.6523 | 668.3621 | 748.8741 | 794.2654 |
| Mean | 412.6981 | 441.6321 | 674.9852 | 756.9612 | 801.5542 | |
| Worst | 420.1234 | 447.6521 | 680.6311 | 761.6325 | 810.5461 | |
| STD | 6.7824 | 5.9524 | 6.1874 | 6.4525 | 7.1256 | |
| PMOMVO-4 | Best | 398.8741 | 417.8541 | 642.9874 | 708.2145 | 751.2541 |
| Mean | 406.8741 | 425.6952 | 648.7412 | 714.8963 | 757.2601 | |
| Worst | 411.6541 | 430.6541 | 654.6512 | 721.3241 | 765.2541 | |
| STD | 6.3685 | 5.9214 | 5.8326 | 6.5552 | 6.0395 | |
| PMOMVO-6 | Best | 391.5231 | 413.1782 | 638.6321 | 704.6411 | 748.9852 |
| Mean | 397.8214 | 419.8523 | 643.9852 | 709.8521 | 753.9252 | |
| Worst | 404.5241 | 424.3251 | 648.1243 | 714.9874 | 760.4123 | |
| STD | 5.5208 | 5.0833 | 4.7214 | 5.1732 | 5.0820 | |
| PMOMVO-8 | Best | 398.8741 | 420.8745 | 643.6521 | 711.9881 | 757.1635 |
| Mean | 406.7741 | 426.8741 | 649.8521 | 717.9852 | 763.5603 | |
| Worst | 412.8562 | 432.6523 | 656.3214 | 725.6521 | 771.2143 | |
| STD | 6.0185 | 5.8742 | 6.1524 | 6.8701 | 5.5258 | |
| PMOMVO-10 | Best | 403.5241 | 425.8541 | 644.3251 | 714.9663 | 763.1423 |
| Mean | 414.6892 | 431.6541 | 651.6598 | 722.5871 | 768.6741 | |
| Worst | 421.9852 | 438.5241 | 657.9874 | 729.9631 | 776.4512 | |
| STD | 7.1979 | 6.3512 | 6.3576 | 7.1254 | 5.6589 | |
| PMOMVO-12 | Best | 407.6352 | 428.2441 | 649.8741 | 722.8810 | 778.5412 |
| Mean | 418.4756 | 435.9874 | 656.9871 | 729.8741 | 784.3506 | |
| Worst | 425.7412 | 443.3652 | 662.8741 | 738.6954 | 792.1423 | |
| STD | 8.1256 | 7.5287 | 6.5586 | 7.5253 | 6.5266 | |
| Scenarios | Ranks’ Sum. | |||||
|---|---|---|---|---|---|---|
| Algorithms | 1 | 2 | 3 | 4 | 5 | |
| MOMVO | 7 | 7 | 7 | 7 | 7 | 35 |
| PMOMVO-2 | 6 | 6 | 6 | 6 | 6 | 30 |
| PMOMVO-4 | 5 | 5 | 4 | 5 | 5 | 24 |
| PMOMVO-6 | 4 | 4 | 5 | 4 | 3 | 20 |
| PMOMVO-8 | 2 | 3 | 3 | 1 | 4 | 13 |
| PMOMVO-10 | 3 | 1 | 2 | 2 | 2 | 10 |
| PMOMVO-12 | 1 | 2 | 1 | 3 | 1 | 8 |
| Scenarios | Ranks’ Sum. | |||||
|---|---|---|---|---|---|---|
| Algorithms | 1 | 2 | 3 | 4 | 5 | |
| MOMVO | 7 | 7 | 7 | 7 | 7 | 35 |
| PMOMVO-2 | 4 | 6 | 6 | 6 | 6 | 28 |
| PMOMVO-4 | 3 | 2 | 2 | 2 | 2 | 11 |
| PMOMVO-6 | 1 | 1 | 1 | 1 | 1 | 5 |
| PMOMVO-8 | 2 | 3 | 3 | 3 | 3 | 14 |
| PMOMVO-10 | 5 | 4 | 4 | 4 | 4 | 21 |
| PMOMVO-12 | 6 | 5 | 5 | 5 | 5 | 26 |
| PMOMVO-2 | PMOMVO-4 | PMOMVO-6 | PMOMVO-8 | PMOMVO-10 | PMOMVO-12 | |
|---|---|---|---|---|---|---|
| MOMVO | 5 | 11 | 15 | 22 | 25 | 27 |
| PMOMVO-2 | - | 6 | 10 | 17 | 20 | 22 |
| PMOMVO-4 | - | - | 4 | 11 | 14 | 16 |
| PMOMVO-6 | - | - | - | 7 | 10 | 12 |
| PMOMVO-8 | - | - | - | - | 3 | 5 |
| PMOMVO-10 | - | - | - | - | - | 2 |
| PMOMVO-2 | PMOMVO-4 | PMOMVO-6 | PMOMVO-8 | PMOMVO-10 | PMOMVO-12 | |
|---|---|---|---|---|---|---|
| MOMVO | 7 | 24 | 30 | 21 | 14 | 9 |
| PMOMVO-2 | - | 17 | 23 | 14 | 7 | 2 |
| PMOMVO-4 | - | - | 6 | 3 | 10 | 15 |
| PMOMVO-6 | - | - | - | 9 | 16 | 21 |
| PMOMVO-8 | - | - | - | - | 7 | 12 |
| PMOMVO-10 | - | - | - | - | - | 5 |
| Instance | Starting | Destination | Moving Obstacles’ Position [m] | Moving Obstacles’ Speed [m/s] |
|---|---|---|---|---|
| 1 | [0, 0, 0] | [8, 8, 0] | [5 5 1], [3 3 2], [5 3 1], [1.5 2.5 1], [1 1 1.5] | [4 −2 1], [2 −2 −2], [4 2 2], [1 1 1.5], [1 1 1] |
| 2 | [0, 0, 0] | [8, 8, 0] | [5 6 1], [3 3 1], [6 2 1], [2 2 1], [1 2 1] | [1 2 1], [1 −1 −1], [1 2 2], [1 1 1], [1 2 1] |
| 3 | [0, 0, 0] | [8, 8, 0] | [5 2 1], [3 1 1], [7 5 1], [1.5 1.5 1], [1 3 1] | [2 −1 1], [1 2 −1], [1 −2 1], [1 1 1], [1 −1 1] |
| Max- Iter. | Pop. Size | Variants of PMOMVO Algorithm | ||||||
|---|---|---|---|---|---|---|---|---|
| MOMVO | PMOMVO -2 | PMOMVO -4 | PMOMVO -6 | PMOMVO -8 | PMOMVO -10 | PMOMVO -12 | ||
| 100 | 50 | 22.7612 | 22.6852 | 22.3812 | 22.3755 | 22.3712 | 22.3674 | 22.3665 |
| 100 | 22.7521 | 22.5720 | 22.3805 | 22.3721 | 22.3645 | 22.3514 | 22.3465 | |
| 200 | 22.7132 | 22.5123 | 22.3751 | 22.3698 | 22.3612 | 22.3475 | 22.3308 | |
| 200 | 50 | 22.7574 | 22.6584 | 22.3798 | 22.3562 | 22.3478 | 22.3452 | 22.3398 |
| 100 | 22.7414 | 22.4652 | 22.3674 | 22.3462 | 22.3365 | 22.3325 | 22.3274 | |
| 200 | 22.6852 | 22.4036 | 22.3433 | 22.3241 | 22.3054 | 22.2974 | 22.2912 | |
| 300 | 50 | 22.7354 | 22.6136 | 22.3569 | 22.3287 | 22.3165 | 22.3126 | 22.2975 |
| 100 | 22.7058 | 22.4352 | 22.3171 | 22.3084 | 22.2987 | 22.2841 | 22.2798 | |
| 200 | 22.6123 | 22.3852 | 22.2893 | 22.2871 | 22.2846 | 22.2785 | 22.2672 | |
| Max- Iter. | Pop. Size | Variants of PMOMVO Algorithm | ||||||
|---|---|---|---|---|---|---|---|---|
| MOMVO | PMOMVO -2 | PMOMVO -4 | PMOMVO -6 | PMOMVO -8 | PMOMVO -10 | PMOMVO -12 | ||
| 100 | 50 | 915.5800 | 801.5542 | 757.2601 | 753.9252 | 763.5603 | 768.6741 | 784.3506 |
| 100 | 1178.8686 | 1049.3154 | 860.4351 | 836.8540 | 844.4646 | 852.6669 | 866.7345 | |
| 200 | 1772.3200 | 1214.5412 | 889.7868 | 856.2145 | 849.5713 | 857.1243 | 871.3265 | |
| 200 | 50 | 1230.2829 | 963.9214 | 837.9456 | 808.5869 | 819.6385 | 825.8947 | 830.4514 |
| 100 | 1849.4532 | 1322.0424 | 1024.7202 | 972.8741 | 958.6206 | 961.8273 | 977.5868 | |
| 200 | 3031.1316 | 1765.5321 | 1187.2541 | 1056.4123 | 1016.5471 | 992.2146 | 1031.2314 | |
| 300 | 50 | 1456.9254 | 1134.0631 | 938.2590 | 882.8192 | 870.1821 | 881.6050 | 892.7623 |
| 100 | 2286.0306 | 1572.8265 | 1181.4831 | 1098.2651 | 1077.8859 | 989.3251 | 998.2514 | |
| 200 | 3937.7016 | 2394.2541 | 1611.0361 | 1388.4576 | 1280.5775 | 1262.2143 | 1154.2651 | |
| Algorithms | Performance Criteria | ||
|---|---|---|---|
| Path Length SLR (m) | Flight Time FT (s) | ||
| MSSA | Best | 22.721 | 837.40 |
| Mean | 23.391 | 844.29 | |
| Worst | 24.414 | 856.35 | |
| STD | 0.1587 | 6.7255 | |
| MOGWO | Best | 23.654 | 1154.2 |
| Mean | 24.980 | 1248.7 | |
| Worst | 25.547 | 1549.7 | |
| STD | 0.2342 | 7.4924 | |
| NSGA-II | Best | 21.204 | 8150.1 |
| Mean | 22.865 | 8247.3 | |
| Worst | 23.481 | 8892.2 | |
| STD | 0.2871 | 8.2456 | |
| MOPSO | Best | 32.987 | 3194.7 |
| Mean | 35.281 | 3398.5 | |
| Worst | 37.242 | 4009.2 | |
| STD | 0.3733 | 6.62 | |
| PMOMVO-6 | Best | 22.251 | 748.9852 |
| Mean | 22.374 | 753.9252 | |
| Worst | 22.4602 | 760.4123 | |
| STD | 0.1046 | 5.0820 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jarray, R.; Bouallègue, S.; Rezk, H.; Al-Dhaifallah, M. Parallel Multiobjective Multiverse Optimizer for Path Planning of Unmanned Aerial Vehicles in a Dynamic Environment with Moving Obstacles. Drones 2022, 6, 385. https://doi.org/10.3390/drones6120385
Jarray R, Bouallègue S, Rezk H, Al-Dhaifallah M. Parallel Multiobjective Multiverse Optimizer for Path Planning of Unmanned Aerial Vehicles in a Dynamic Environment with Moving Obstacles. Drones. 2022; 6(12):385. https://doi.org/10.3390/drones6120385
Chicago/Turabian StyleJarray, Raja, Soufiene Bouallègue, Hegazy Rezk, and Mujahed Al-Dhaifallah. 2022. "Parallel Multiobjective Multiverse Optimizer for Path Planning of Unmanned Aerial Vehicles in a Dynamic Environment with Moving Obstacles" Drones 6, no. 12: 385. https://doi.org/10.3390/drones6120385
APA StyleJarray, R., Bouallègue, S., Rezk, H., & Al-Dhaifallah, M. (2022). Parallel Multiobjective Multiverse Optimizer for Path Planning of Unmanned Aerial Vehicles in a Dynamic Environment with Moving Obstacles. Drones, 6(12), 385. https://doi.org/10.3390/drones6120385









