Globally Attractive Hyperbolic Control for the Robust Flight of an Actively Tilting Quadrotor
Abstract
1. Introduction
1.1. Literature Review about Control of Actively Tilting Quadrotors
1.2. Problem Statement and Proposed Solution
1.3. Contributions of the Work
- The proposed hyperbolic control is inspired by some related works that have been successfully applied to other types of robotic systems [3]. To the best of the authors’ knowledge, this is the first time that a hyperbolic controller has been applied to the field of UAVs.
- Different from some texts, this paper presents a theoretically sound controller. Moreover, the allocation technique is included, which places this paper within a reduced set of published manuscripts that include both aspects.
- To the best of the authors’ knowledge, this is the first time that a robust model-free controller is implemented in an actively tilting quadrotor whose behaviour is almost identical to an actual UAV, which is possible due to the utilization of a physics-engine-based simulation approach.
2. Mathematical Preliminaries
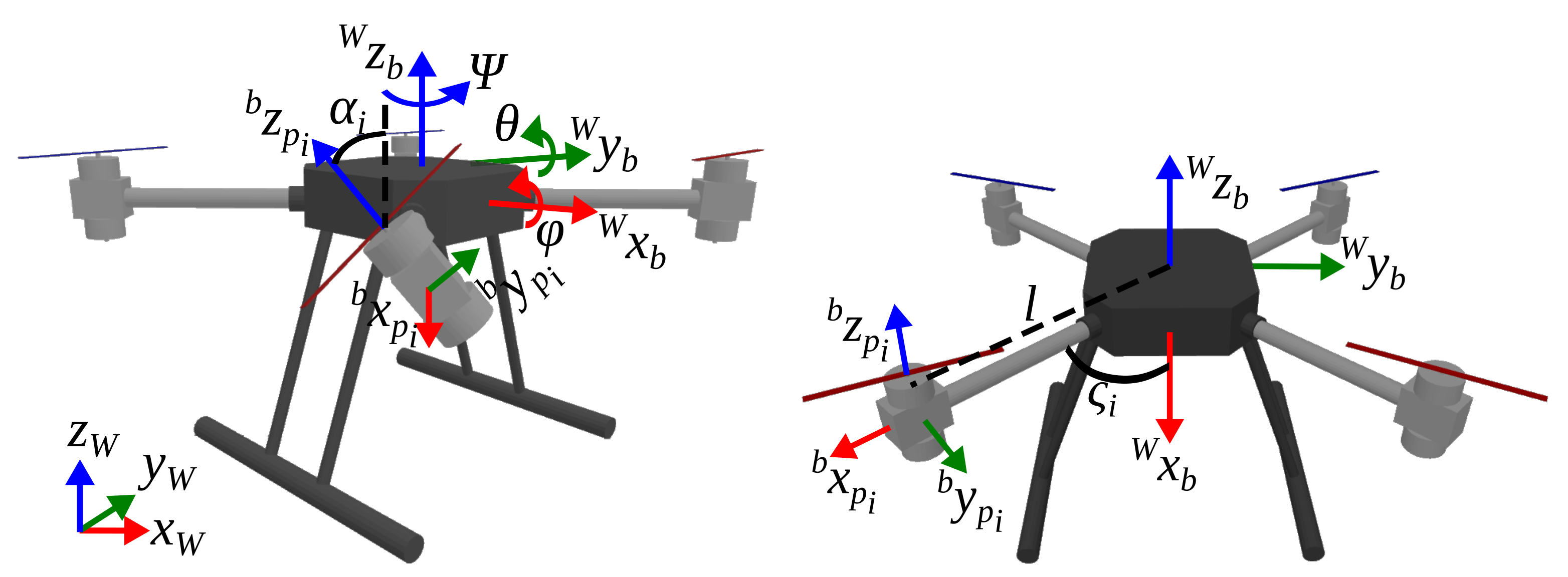
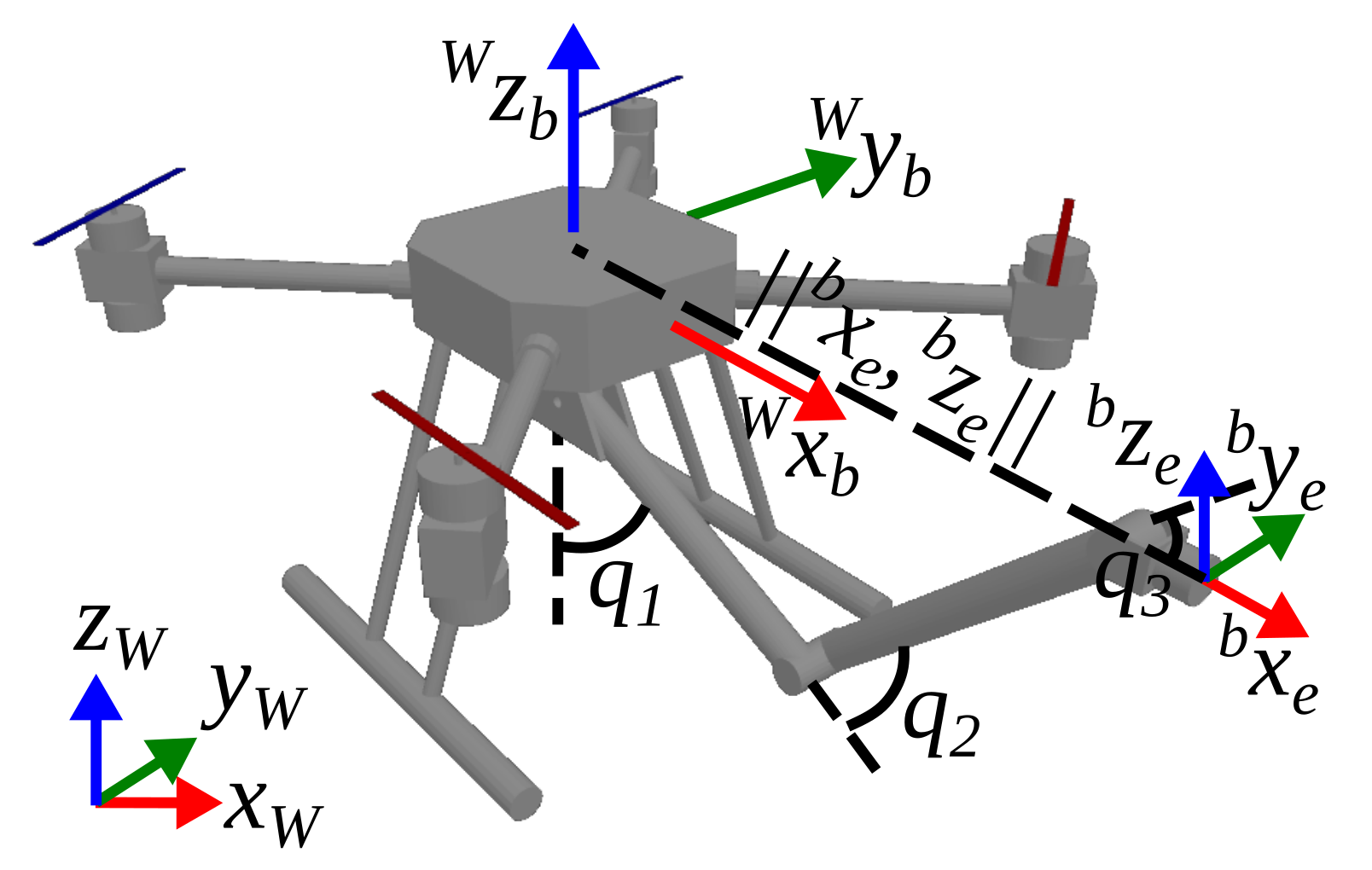
3. Dynamics of Actively Tilting Quadrotor
Properties and Assumptions of the Actively Tilting Quadrotor Dynamics
4. Hyperbolic Control for Robust Flight
4.1. Globally Attractive Ultimate Boundedness
4.2. Control Allocation
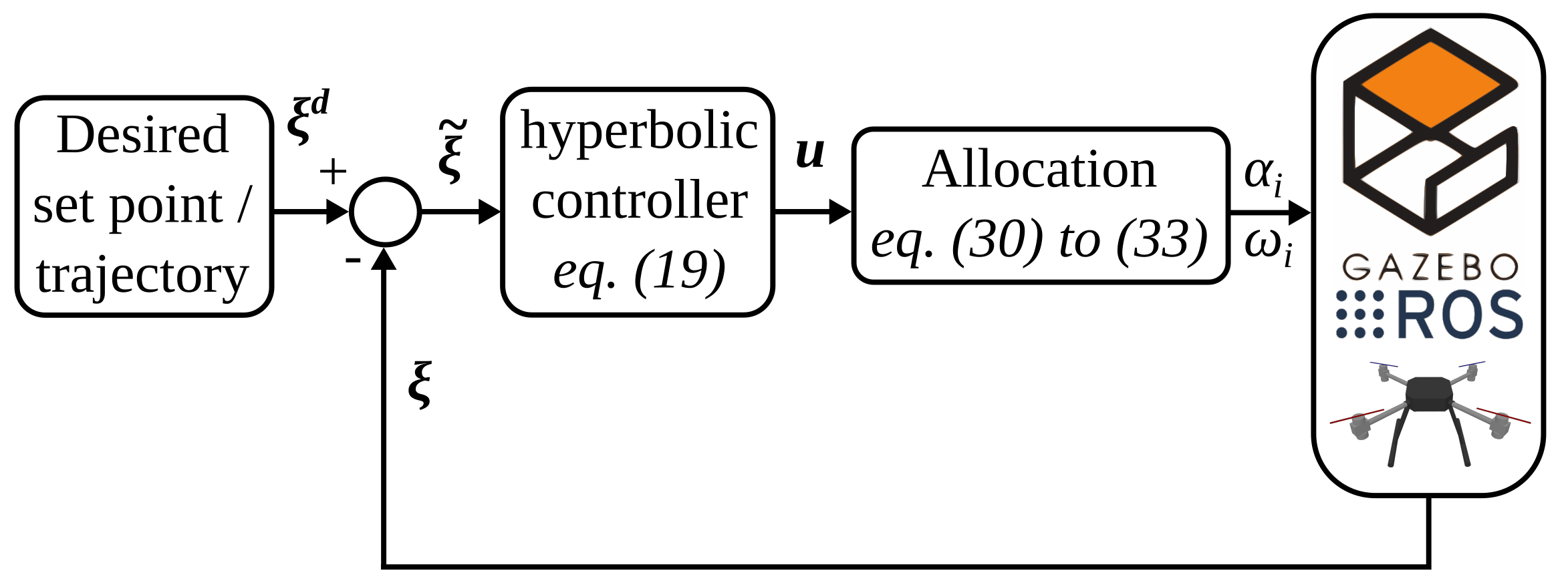
5. Physics-Engine-Based Simulation Results
5.1. Implementation of the Controller
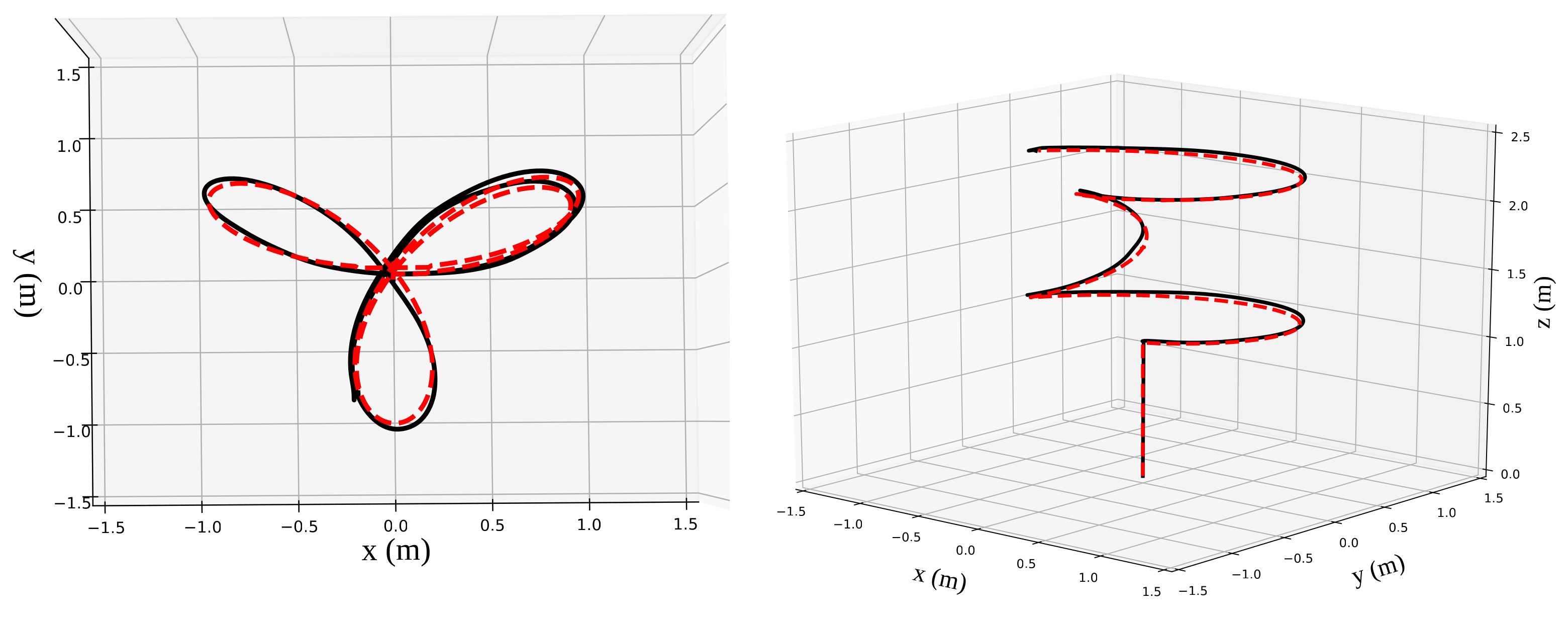
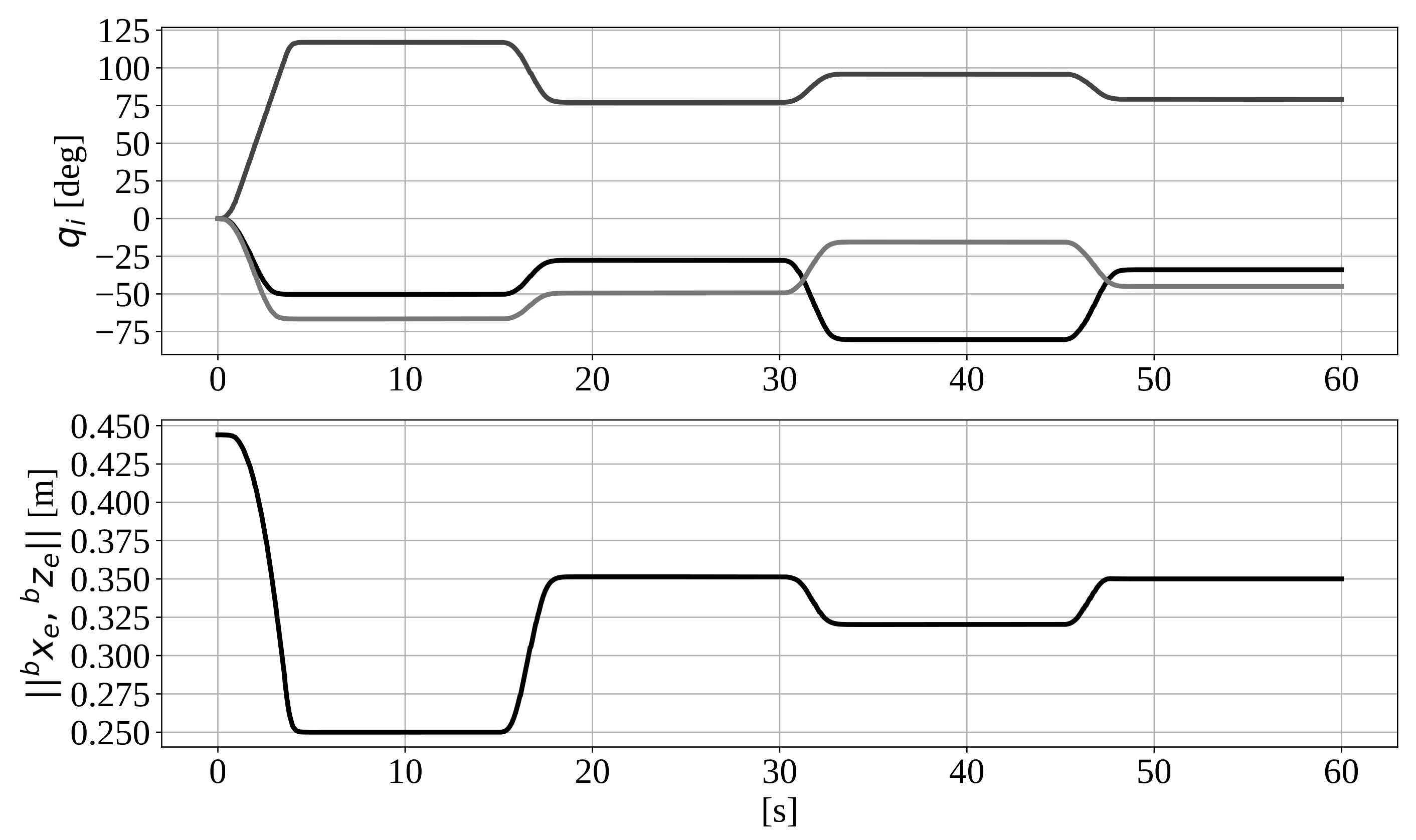
5.2. Tracking
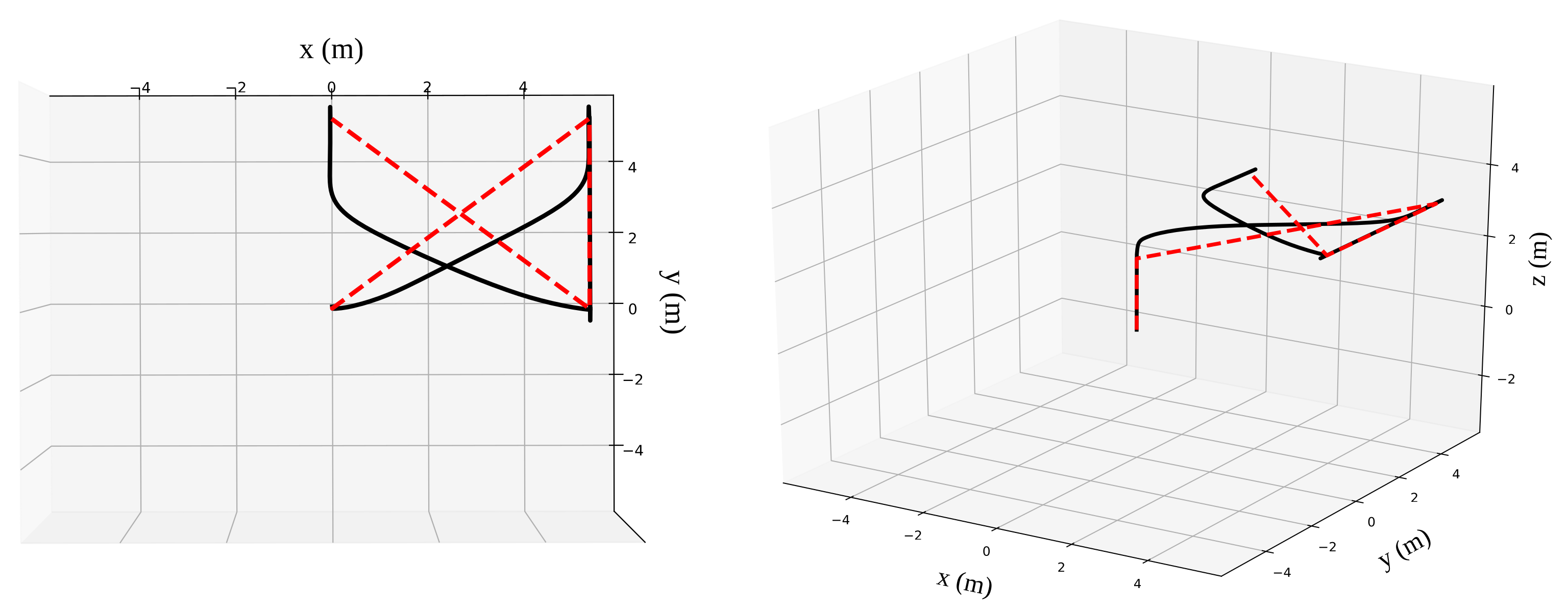
5.3. Regulation towards Far Set Points
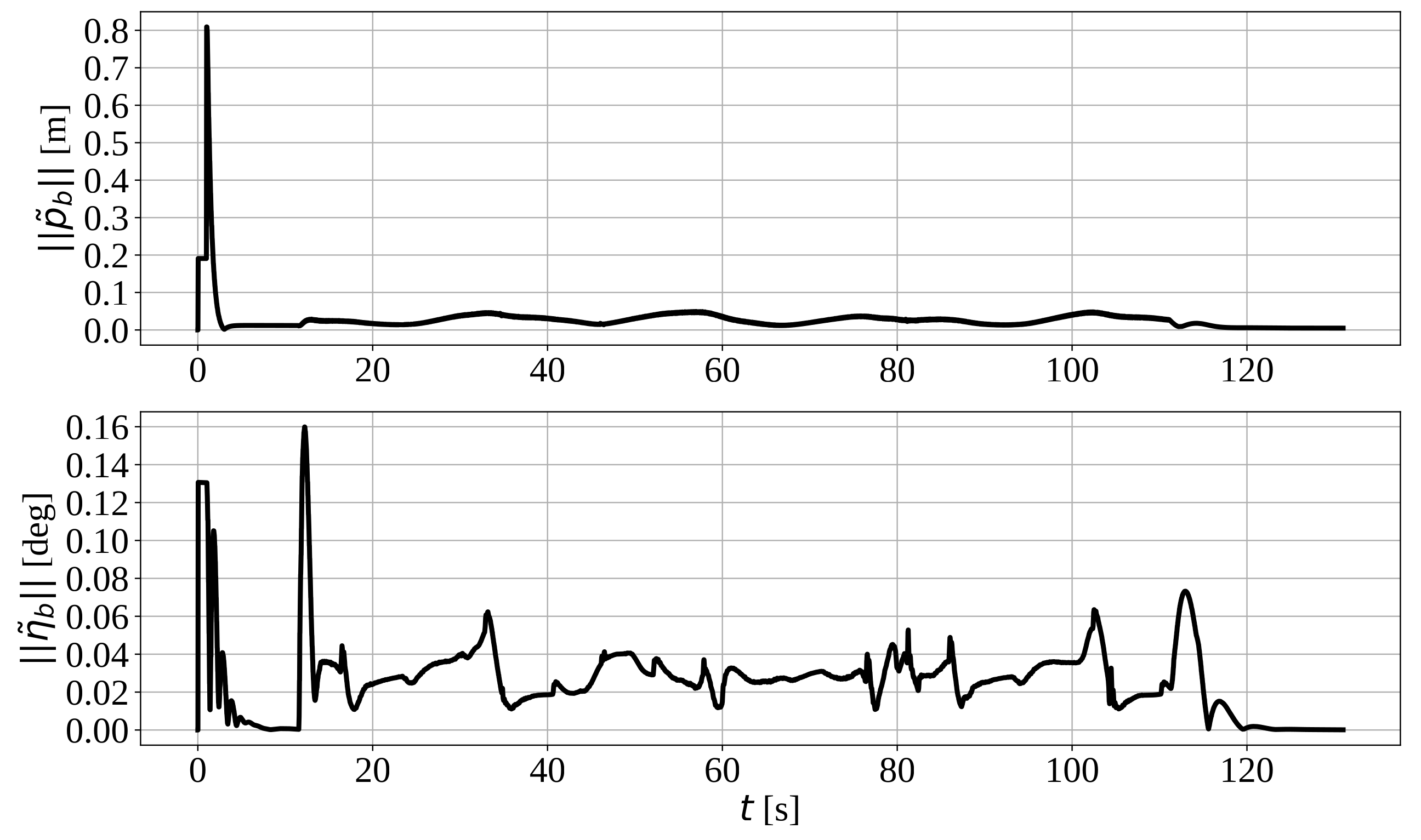
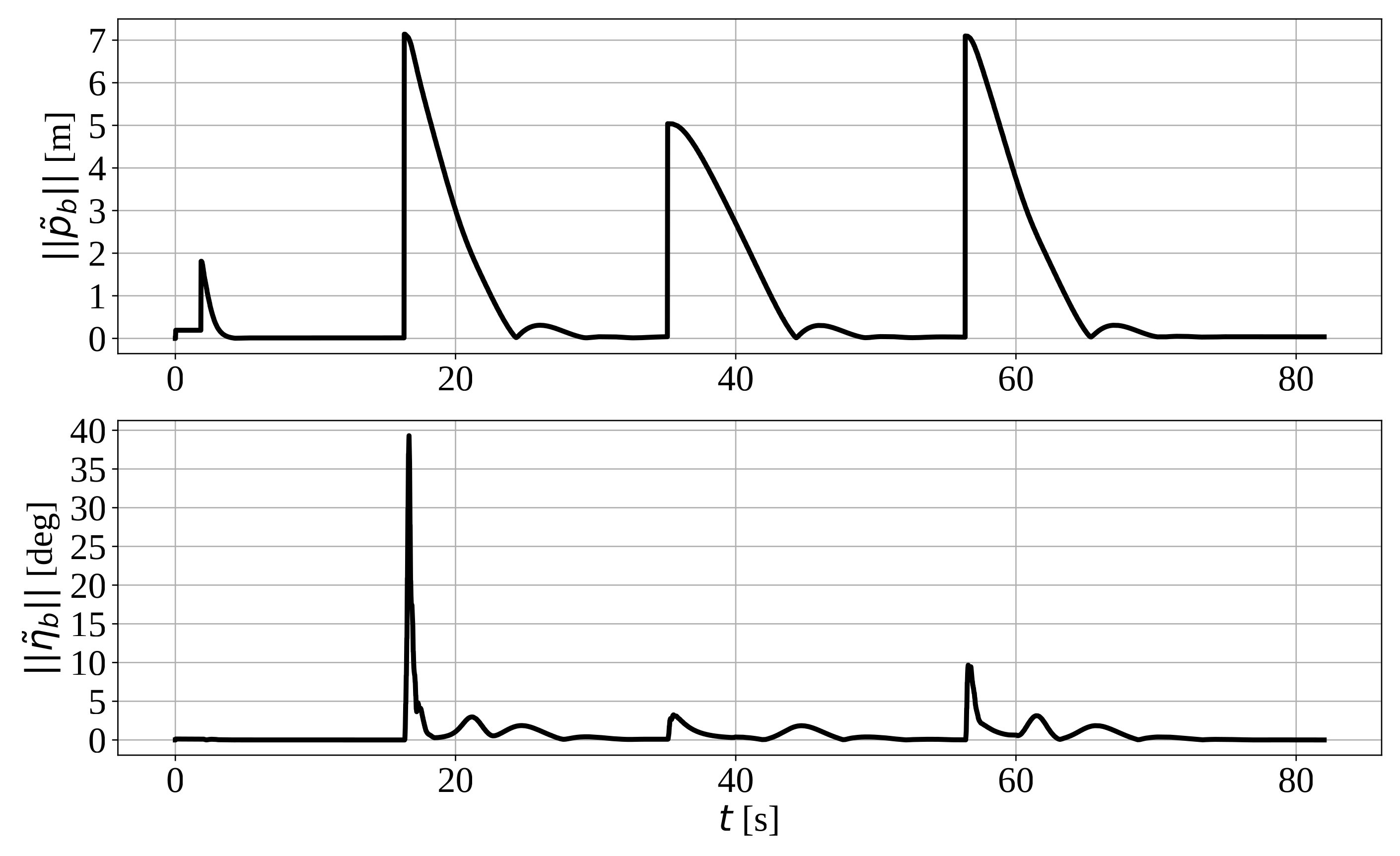
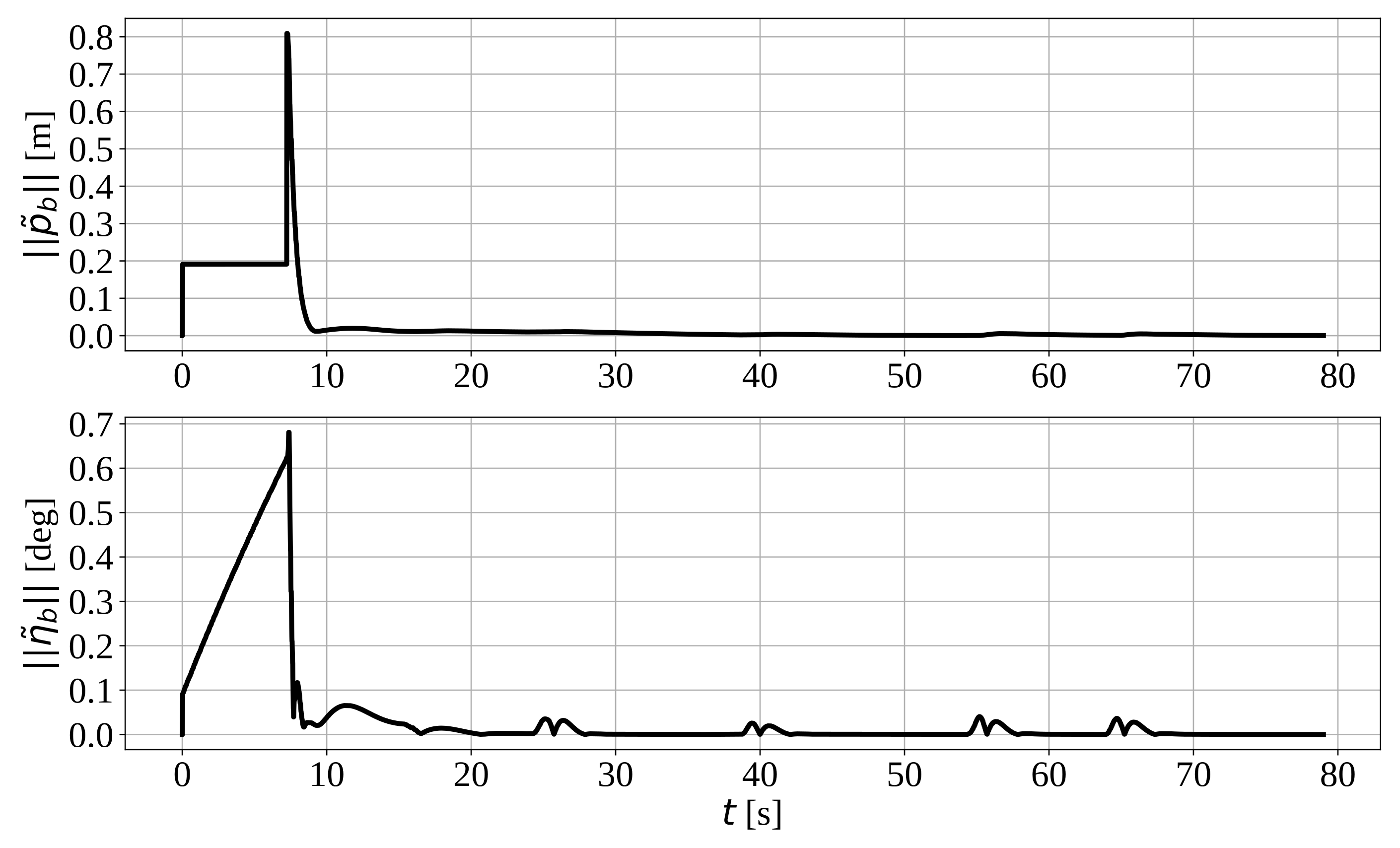
5.4. Robustness against Disturbances
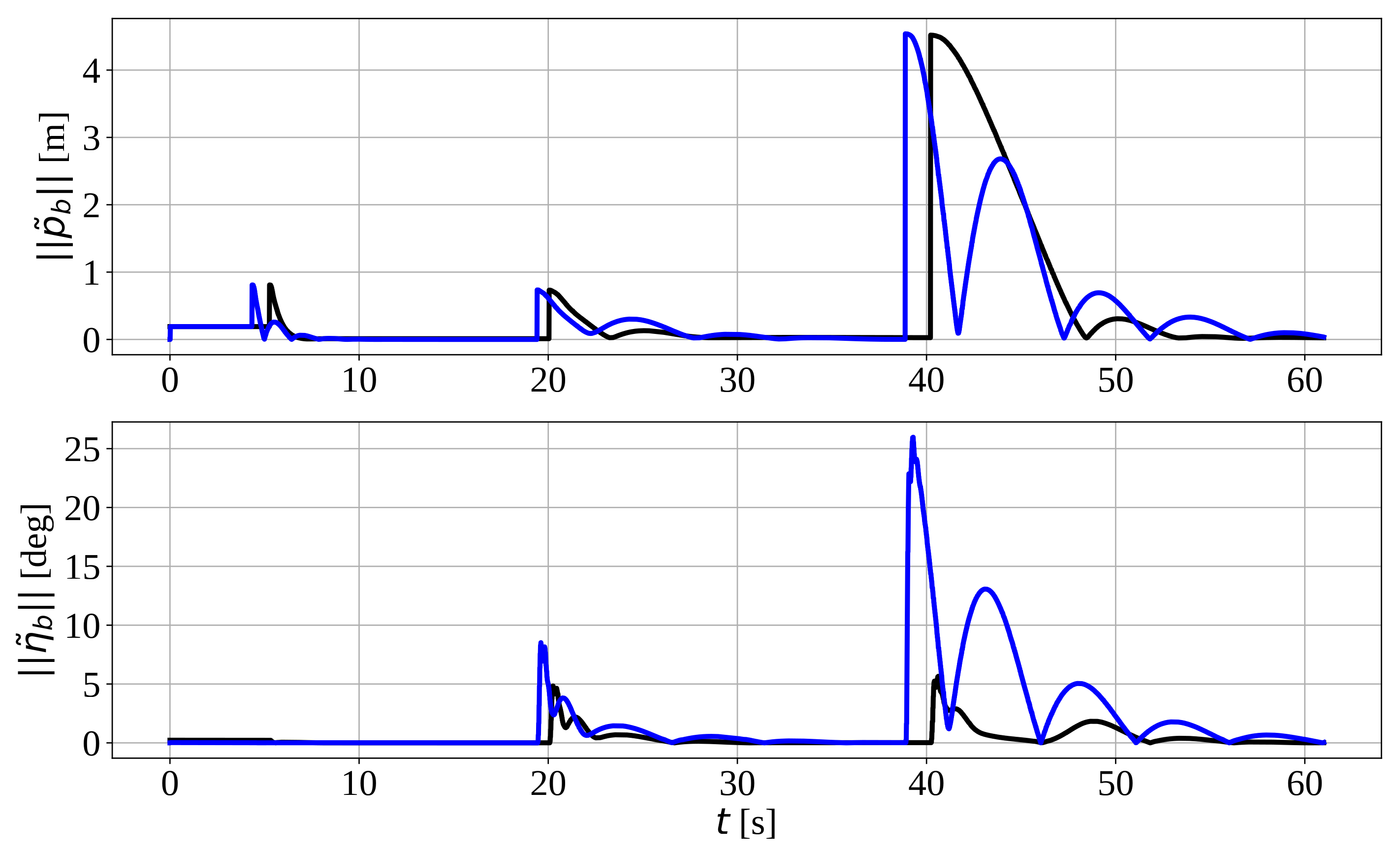
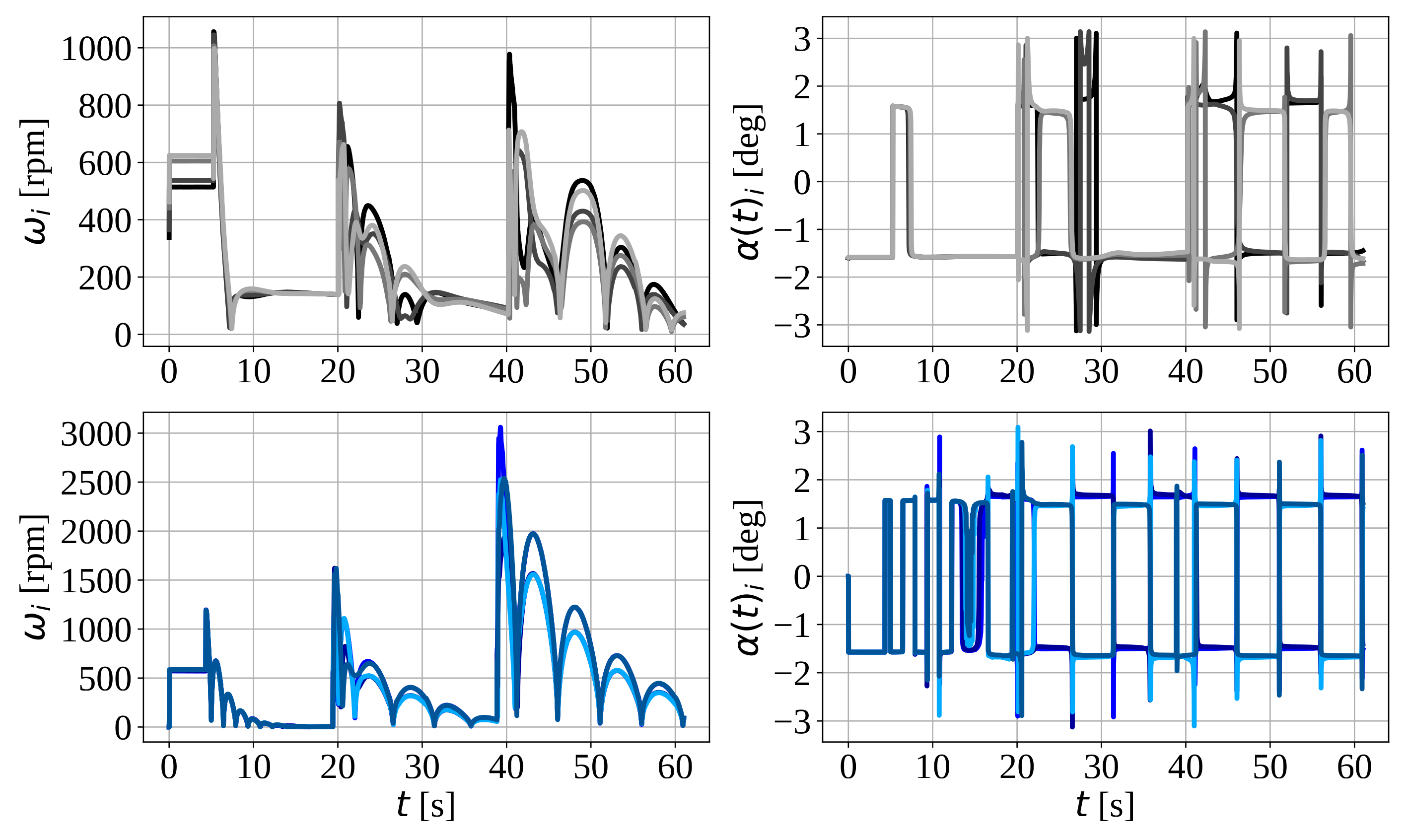
5.5. Comparative Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rashad, R.; Goerres, J.; Aarts, R.; Engelen, J.B.; Stramigioli, S. Fully actuated multirotor UAVs: A literature review. IEEE Robot. Autom. Mag. 2020, 27, 97–107. [Google Scholar] [CrossRef]
- Papachristos, C.; Alexis, K.; Tzes, A. Efficient force exertion for aerial robotic manipulation: Exploiting the thrust-vectoring authority of a tri-tiltrotor uav. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 4500–4505. [Google Scholar]
- Reyes-Cortes, F.; Felix-Beltran, O.; Cid-Monjaraz, J.; Alonso-Aruffo, G. A family of hyperbolic-type control schemes for robot manipulators. Kybernetika 2019, 55, 561–585. [Google Scholar] [CrossRef]
- Nemati, A.; Kumar, M. Non-linear control of tilting-quadcopter using feedback linearization based motion control. In Proceedings of the Dynamic Systems and Control Conference, San Antonio, TX, USA, 22–24 October 2014; Volume 46209, p. V003T48A005. [Google Scholar]
- Kumar, R.; Nemati, A.; Kumar, M.; Sharma, R.; Cohen, K.; Cazaurang, F. Tilting-rotor quadcopter for aggressive flight maneuvers using differential flatness based flight controller. In Proceedings of the Dynamic Systems and Control Conference, Tysons Corner, VA, USA, 11–13 October 2017; Volume 58295, p. V003T39A006. [Google Scholar]
- Kumar, R.; Bhargavapuri, M.; Deshpande, A.M.; Sridhar, S.; Cohen, K.; Kumar, M. Quaternion feedback based autonomous control of a quadcopter uav with thrust vectoring rotors. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 3828–3833. [Google Scholar]
- Ryll, M.; Bülthoff, H.H.; Giordano, P.R. A novel overactuated quadrotor unmanned aerial vehicle: Modeling, control, and experimental validation. IEEE Trans. Control Syst. Technol. 2014, 23, 540–556. [Google Scholar] [CrossRef]
- Invernizzi, D.; Giurato, M.; Gattazzo, P.; Lovera, M. Full pose tracking for a tilt-arm quadrotor UAV. In Proceedings of the 2018 IEEE Conference on Control Technology and Applications (CCTA), Copenhagen, Denmark, 21–24 August 2018; pp. 159–164. [Google Scholar]
- Offermann, A.; Castillo, P.; De Miras, J. Nonlinear model and control validation of a tilting quadcopter. In Proceedings of the 2020 28th Mediterranean Conference on Control and Automation (MED), Saint-Raphaël, France, 15–18 September 2020; pp. 50–55. [Google Scholar]
- Alkamachi, A.; Ercelebi, E. H∞ control of an overactuated tilt rotors quadcopter. J. Cent. South Univ. 2018, 25, 586–599. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Duan, D. Manipulation strategy of tilt quad rotor based on active disturbance rejection control. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2020, 234, 573–584. [Google Scholar] [CrossRef]
- Ji, R.; Li, D.; Ma, J. Adaptive Second-Order Fast Nonsingular Terminal Sliding Mode Control for a Tilting Quadcopter. In Proceedings of the 2022 13th Asian Control Conference (ASCC), Jeju, Korea, 4–7 May 2022; pp. 403–408. [Google Scholar]
- Sridhar, S.; Kumar, R.; Radmanesh, M.; Kumar, M. Non-linear sliding mode control of a tilting-rotor quadcopter. In Proceedings of the Dynamic Systems and Control Conference, Tysons Corner, VA, USA, 11–13 October 2017; Volume 58271, p. V001T09A007. [Google Scholar]
- Nikhilraj, A.; Simha, H.; Priyadarshan, H. Modeling and Control of port dynamics of a tilt-rotor quadcopter. IFAC-PapersOnLine 2022, 55, 746–751. [Google Scholar] [CrossRef]
- Ji, R.; Ma, J.; Ge, S.S.; Ji, R. Adaptive second-order sliding mode control for a tilting quadcopter with input saturations. IFAC-PapersOnLine 2020, 53, 3910–3915. [Google Scholar] [CrossRef]
- Lu, K.; Yang, Z.; Liao, L.; Jiang, Y.; Xu, C.; Xu, H.; Zhang, Q. Extended state observer-based robust control of an omnidirectional quadrotor with tiltable rotors. Trans. Inst. Meas. Control 2021, 43, 1143–1155. [Google Scholar] [CrossRef]
- Ruggiero, F.; Cacace, J.; Sadeghian, H.; Lippiello, V. Passivity-based control of VToL UAVs with a momentum-based estimator of external wrench and unmodeled dynamics. Robot. Auton. Syst. 2015, 72, 139–151. [Google Scholar] [CrossRef]
- Santibáñez, V.; Kelly, R. Strict Lyapunov functions for control of robot manipulators. Automatica 1997, 33, 675–682. [Google Scholar] [CrossRef]
- Rajappa, S.; Ryll, M.; Bülthoff, H.H.; Franchi, A. Modeling, control and design optimization for a fully-actuated hexarotor aerial vehicle with tilted propellers. In Proceedings of the 2015 IEEE international conference on robotics and automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4006–4013. [Google Scholar]
- Suarez, A.; Vega, V.M.; Fernandez, M.; Heredia, G.; Ollero, A. Benchmarks for aerial manipulation. IEEE Robot. Autom. Lett. 2020, 5, 2650–2657. [Google Scholar] [CrossRef]
- Goodarzi, F.; Lee, D.; Lee, T. Geometric nonlinear PID control of a quadrotor UAV on SE (3). In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 3845–3850. [Google Scholar]
| Gains | Value |
|---|---|
| diag | |
| diag | |
| diag |
| Parameter | Value |
|---|---|
| l | 0.183847763 |
| 8.54858 | |
| 1.75e |
| Parameter | Value |
|---|---|
| m | 5 kg |
| diag kg | |
| g | 9.81 m/ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orozco Soto, S.M.; Ruggiero, F.; Lippiello, V. Globally Attractive Hyperbolic Control for the Robust Flight of an Actively Tilting Quadrotor. Drones 2022, 6, 373. https://doi.org/10.3390/drones6120373
Orozco Soto SM, Ruggiero F, Lippiello V. Globally Attractive Hyperbolic Control for the Robust Flight of an Actively Tilting Quadrotor. Drones. 2022; 6(12):373. https://doi.org/10.3390/drones6120373
Chicago/Turabian StyleOrozco Soto, Santos Miguel, Fabio Ruggiero, and Vincenzo Lippiello. 2022. "Globally Attractive Hyperbolic Control for the Robust Flight of an Actively Tilting Quadrotor" Drones 6, no. 12: 373. https://doi.org/10.3390/drones6120373
APA StyleOrozco Soto, S. M., Ruggiero, F., & Lippiello, V. (2022). Globally Attractive Hyperbolic Control for the Robust Flight of an Actively Tilting Quadrotor. Drones, 6(12), 373. https://doi.org/10.3390/drones6120373







