Behavior Prediction Based Trust Evaluation for Adaptive Consensus of Quadrotors

Abstract

Without proper treatment, a malfunctional quadrotor may bring severe consequences, e.g., becoming out of control, to the whole swarm. To tackle this problem, we develop a trust evaluations based consensus protocol. Specifically, each quadrotor in the swarm communicates with its connected neighbors, exchanging behavior predictions. By comparing the predicted and the actual behaviors of its neighbor regarding a pre-defined tolerance, each quadrotor assigns trust values to determine potentially legitimate or malfunctional companions. On this basis, an online adaptive controller adjusts each weight in the protocol corresponding to the trust evaluations designed before. We prove that, within proper tolerance, it is almost sure that the legitimate quadrotors can identify the malfunctional quadrotors through trust evaluations and ameliorate their effects on the whole system. Almost surely, the legitimate quadrotors can converge to their center in a finite time. We verify our method through MATLAB and GAZEBO. In particular, with our proposed method, the swarm system discussed in this paper is able to reach position and velocity consensus in the presence of malfunctional quadrotors.

1. Introduction

Quadrotors have been a topic of particular interest in recent years. They have been widely used in military, industry, and disaster rescuing, owing to their low cost, small size, and autonomous navigation capabilities. Compared with a single quadrotor, a swarm with distributed multi-agent systems can provide better robustness. To establish a well-performed swarm, the distributed consensus is a basic but crucial problem.

Distributed consensus has been widely discussed for a long time. Many works have been conducted on both the consensus itself and the application of distributed consensus. Ref. [1] provides a new algorithm that deals with link failures and channel noise. Ref. [2] discusses the topic of filtering in sensor networks. Ref. [3] provides a new time-discrete algorithm for wireless sensor networks. Refs. [4,5] investigate the consensus problem for second-order multi-agent systems. In addition, Ref. [6] proposes a relative position measurement method to reach consensus. Ref. [7] discusses the convergent speed of consensus.

However, many of these Algorithms mentioned above are based on the assumption that all agents are legitimate ones, but they are vulnerable when there are malfunctional agents occur in the system discussed in Refs. [8,9,10], which leads to the problem of resilient consensus. Resilient consensus refers to consensus in a case, where agents become malfunctional due to either physical faulty or communication failure. As malfunction can be found in many multi-agent systems such as autonomous vehicles, delivery drones, or partners in security and defense as described in Refs. [11,12,13], the resilient consensus has become a very important problem worthy of investigation.

To deal with resilient consensus, many theories and control protocols have been proposed. Ref. [14] provides a consensus protocol that enables a system of n asynchronous processes, some of them malfunctional, to reach an agreement. This article has improved the t-resilient protocol to t < n/3. Refs. [9,15] conclude a basic result that well-behaving agents can always agree upon a parameter if and only if the number of malfunctional agents is less than 1/2 of the network connectivity. Grounded on the previous knowledge, Ref. [16] proposes a distributed function calculation iterative method to overcome the weakness brought by malfunctional agents. Ref. [15] focus on local strategies that provide resilience to faults and compromised nodes. Ref. [17] proposes DP-MSR Algorithm to reach resilient consensus. Refs. [18,19] consider trust evaluation applications in consensus protocols. Ref. [20] has further successfully proved that their protocol is useful even if t = n/2 and it emphasized the interagent trust. However, much of the research is based on the hypothesis that the malfunctional agents will directly broadcast their abnormal behavior to others without detection or observation from others and these consensus protocols are simplified and not suitable for quadrotor systems.

For real quadrotors discussed in this paper, such a hypothesis is not suitable and we need to formulate a method to detect such abnormal behavior of malfunctional quadrotors. Ref. [21] chooses to utilize visual techniques to detect faulty robots but with a strictly demanding requirement that robots should be within close range, typically 50 cm. To overcome this limitation, Ref. [22] focuses on the expected behavior of other agents offline to predict other’s possible failure. However, if the other robot faces a sudden fault after broadcasting a health status, it will not be able to react in time. To reach in-time reactions, Ref. [23] analyzes the coordination data and the signal strength of neighboring agents to detect failure. However, the noise was not taken into consideration. Refs. [24,25] eliminate noise and detect failure using the PCA-EWMA method, but may lose features in data or lead to misleading indications by increasing false alarms and missed detections, and yet they might not perform well in time response situations. Therefore, Therefore, this article mainly deals with the sudden and severe situations that one quadrotor may encounter such as collisions with obstacles in Section 5.2, which could possibly lead to sensor failure or even system failure. In addition, the possible malicious attacks [20] may also be taken into our consideration. Under these situations, we need a novel method that based on trust evaluations between quadrotors in order to improve the robustness of the whole swarm system.

Therefore, motivated by existing research [20], our work extends the trust value evaluation method to an online adaptive controller which is designed for multiple quadrotors systems. Specifically, each quadrotor in the swarm will monitor its nearby quadrotors. Based on the collected information, a trust value is assigned to each connected nearby quadrotor depending on whether the latter is within or out of the established tolerance, and therefore, the trust matrix is formed as trust evaluations for the whole swarm system. On this basis, an adaptive controller will adjust the weight according to the trust matrix. Finally, simulations are performed to verify the feasibility and expandability of our proposed method.

The main contributions of this work are of three aspects: (1) Based on the proposed trust value evaluation method, legitimate quadrotors are able to identify the malfunctional quadrotor. (2) Based on the proposed trust value evaluation method and the adaptive consensus protocol, legitimate quadrotors are able to converge to the correct position and maintain velocity consensus in the presence of malfunctional quadrotors. (3) Based on the proposed trust value evaluation method, the swarm system can outperform the single-quadrotor detecting method in terms of robustness and accuracy.

This article is addressed as the following: in Section 1, we introduce the background of consensus and related works; in Section 1, we introduce the model and consensus protocol we use; in Section 3, we analyze the properties of our adaptive consensus protocols; in Section 4, we briefly illustrate a simple 2-D plane simulation utilizing the method we proposed in Section 2; in Section 5, we discuss multiple quadrotors system in realistic situations. Section 6 concludes the paper.

2. Problem Description

We consider the problem of trust evaluations for the swarm system consensus protocol, where malfunctional quadrotors exist. We firstly establish a general mathmatic frame [18,19,20] to describe the problem. The quadrotors in the system communicate with each other over a network, which in this case, is represented by an undirected graph $\mathit{G}=(\mathit{V},\mathit{E})$, where $\mathit{V}=\{1,\cdots ,N\}$ indicates the set of node indices for agents and $\mathit{E}\in \mathit{V}\times \mathit{V}$ indicates the set of undirected edges in this graph. We use $\{i,j\}$ to denote the edge connecting quadrotors i and j. Since it’s an undirected graph, once quadrotor i views quadrotor j as its neighbor, j also recognizes i as its neighbor. Therefore, we donate the neighbors of i as a set ${\mathcal{N}}_i=\left\{j\right|i,j\in \mathit{E}\}$. With the graph $\mathit{G}$, we introduce the trust matrix $W\left(t\right)$ and we associate time-varying trust values $W_{ij}\left(t\right),i,j\in \mathit{V}$, which captures the value of trust i to j, in another word, to which extent, quadrotor i views quadrotor j as a legitimate quadrotor. Additionally, the matrix $W\left(t\right)$ need not be symmetric. We next define $N\left(t\right)$ as a time-varying weight matrix and use $N_{ij}\left(t\right)$ to donate the $i{j}^{th}$ entry of the weight matrix, which can be later derived from the trust matrix $W\left(t\right)$. Note that $N\left(t\right)$ must have nonnegative entries, and will have positive entry $N_{ij}\left(t\right)$ only if quadrotor i and j are connected and i views j as a trusted neighbor. We consider the case where a subset of nodes with indices denoted by the set $\mathcal{M}$, $\mathcal{M}$∈V, is either malicious or malfunctional and, thus, does not reliably follow the order in the consensus protocol. The set $\mathcal{M}$ is assumed to be unknown, with cardinality |$\mathcal{M}$|. At the same time, a quadrotor that is not malicious or malfunctional is termed legitimate, and the set of legitimate quadrotors is denoted $\mathcal{L}$, $\mathcal{L}$, with cardinality |$\mathcal{L}$|.

In what follows, we use $\mathbf{0}$ to denote the zero matrix, where the dimension of $\mathbf{0}$ is to be understood from the context. A nonnegative matrix is row-stochastic if the sum of its entries in every row is equal to 1, and it is row-substochastic if the sum of its entries in every row is equal to or less than 1. We use $\mathbf{1}$ to denote the vector with all entries equal to 1. Given a vector $\mathit{X}$, we use ${\mathit{X}}_i$ or ${\left[\mathit{X}\right]}_i$ (when $\mathit{X}$ has a subscript) to denote its ith entry. A similar notation is used for the entries of a matrix.

2.1. Model

We are concerned with the problem of consensus in a two-dimensional XY-plane, where each legitimate quadrotor updates its value by the following general and widely-used equations for all time t:

$$\mathit{X}(t+1)=\mathit{X}\left(t\right)+\mathit{V}\left(t\right)$$

(1)

$$\mathit{V}(t+1)=\mathit{V}\left(t\right)+\mathbf{U}\left(t\right)$$

(2)

where $\mathit{X}\left(t\right)$ represents the position of quadrotors at time t, $\mathit{V}\left(t\right)$ indicates the velocity of quadrotors at time t and $\mathit{U}\left(t\right)$ stands for the acceleration of quadrotors at time t, which is the control input in the simulation and swarm system discussed later as well. All three symbols mentioned above are n-dimensional vectors, in which n represents the number of quadrotors discussed in this article. Remark that for the 2D-plane distributed system that will be discussed later in this article, we assume that each quadrotor will maintain its own attitude. Therefore, we only need to separate the vector into two directions X and Y.

Besides, for the $\mathit{U}\left(t\right)$ mentioned above. We choose the following equations [26] as the consensus protocol:

$$\begin{array}{cc}\hfill {\mathit{u}}_i\left(t\right)& =-p_0{\mathit{v}}_i\left(t\right)+p_1\sum _{j\in {\mathit{N}}_i\left(t\right)}{a}_{ij}[{\mathit{x}}_j\left(t\right)-{\mathit{x}}_i\left(t\right)]\hfill \\ \hfill & +p_2\sum _{j\in {\mathit{N}}_i\left(t\right)}{a}_{ij}[{\mathit{v}}_j\left(t\right)-{\mathit{v}}_i\left(t\right)]\hfill \end{array}$$

(3)

where $a_{ij}$ comes from $N\left(t\right)$, $i\in \mathit{V}$. We donate the $N_0\left(t\right)$ as the original weight matrix that contains the initial weights of every quadrotor to their neighbors. $p_0$, $p_1$ and $p_2$ are user-defined parameters, which illustrate the control gain. Unlike Refs. [18,20], the consensus protocol we choose here is a more typical and more general second-order consensus protocol and suitable for swarm systems discussed in this paper.

 Definition 1 

(Malfunctional quadrotors:). Quadrotor i is said to be malfunctional if it does not follow the consensus protocol rule in $\left(1\right)\left(2\right)\left(3\right)$ to update its value ${\mathit{x}}_i\left(t\right)$ after some time t. To be more specific, we refer Malfunctional quadrotors to those which may deviate from the original calculated route whether resulting from communication failure, collision or hardware fault.

Let $\mathit{X}\left(t\right)$∈$R^n$ denote the vector of values ${\mathit{x}}_i\left(t\right)$∈ R for all the quadrotors at time t.

Suppose that

$$\mathsf{\Phi }\left(t\right)={({\mathit{x}}_1\left(t\right),{\mathit{V}}_1\left(t\right)\dots {\mathit{x}}_n\left(t\right),{\mathit{v}}_n\left(t\right))}^T$$

(4)

$$E=\left[\begin{array}{cc}1& 1\\ 0& 1-p_0\end{array}\right]F=\left[\begin{array}{cc}0& 0\\ p_1& p_2\end{array}\right]$$

(5)

Without loss of generality, we assume that the quadrotor indices are ordered in such a way that the vector $\mathsf{\Phi }\left(t\right)$ can be separated into two components: the first part of representing the legitimate quadrotors’ values ${\mathsf{\Phi }}_{\mathcal{L}}\left(t\right)$, the second part of the component representing the malfunctional quadrotors’ values ${\mathsf{\Phi }}_{\mathcal{M}}\left(t\right)$. In this way, the consensus dynamics become the following forms:

$$\left[\begin{array}{c}{\mathsf{\Phi }}_{\mathcal{L}}(t+1)\\ {\mathsf{\Phi }}_{\mathcal{M}}(t+1)\end{array}\right]=\left[\begin{array}{cc}{\mathsf{\Lambda }}_{\mathcal{L}}\left(t\right)& {\mathsf{\Lambda }}_{\mathcal{M}}\left(t\right)\\ \mathsf{\Theta }& \mathsf{\Omega }\end{array}\right]\left[\begin{array}{c}{\mathsf{\Phi }}_{\mathcal{L}}\left(t\right)\\ {\mathsf{\Phi }}_{\mathcal{M}}\left(t\right)\end{array}\right]$$

(6)

In addition, ${\mathsf{\Lambda }}_{\mathcal{L}}\left(t\right)$ and ${\mathsf{\Lambda }}_{\mathcal{M}}\left(t\right)$ are defined as follows:

$${\mathsf{\Lambda }}_{\mathcal{L}}\left(t\right)={\mathit{I}}_{|}\mathcal{L}|\otimes E-\left({\mathit{L}}_{|}\mathcal{L}\right|\left(t\right)-{\mathit{N}}_{\mathcal{L}}\left(t\right))\otimes F$$

(7)

$${\mathsf{\Lambda }}_{\mathcal{M}}\left(t\right)=\mathbf{0}-({\mathit{L}}_{\left|\mathcal{L}\right|\times \left|\mathcal{M}\right|}\left(t\right)-{\mathit{N}}_{\mathcal{M}}\left(t\right))\otimes F$$

(8)

where ${\mathit{N}}_{\mathcal{L}}\left(t\right)\in R^{\left|\mathcal{L}\right|\times \left|\mathcal{L}\right|}$ is the matrix multiplying the state component corresponding to the legitimate quadrotors’ values, and ${\mathit{N}}_{\mathcal{M}}\left(t\right)\in R^{\left|\mathcal{L}\right|\times \left|\mathcal{M}\right|}$ is the matrix multiplying the state component corresponding to the malfunctional quadrotors’ values. ${\mathit{I}}_n$ is defined as the identity matrix. The symbol ⊗ represents the Kronecker multiplication. ${\mathit{L}}_{|}\mathcal{L}|\left(t\right)$ and ${\mathit{L}}_{\left|\mathcal{L}\right|\times \left|\mathcal{M}\right|}\left(t\right)$ are the specific area of the Laplacian matrix of graph G. The matrices $\mathsf{\Theta }\left(t\right)$ and $\mathsf{\Omega }\left(t\right)$ dictate the dynamics of the malfunctional quadrotors’ values, which will not be necessary to give specific formulas.

 Definition 2 

(Trust evaluation $w_{ij}\left(t\right)$:). For every $i\in \mathcal{L}$ and $j\in {\mathcal{N}}_i$, the parameter $w_{ij}$ represents to which extent the quadrotor i views quadrotor j as a trustworthy neighbor at a certain time t.

We assume the availability of such observations $w_{ij}$ (t) throughout this article. In the next section, we will discuss how to determine $w_{ij}$ through quadrotors’ communication systems.

In this article, we assume that $w_{ij}\left(t\right)>0$ indicates quadrotor j is temporarily regarded as a trusted(legitimate) neighbor by quadrotor i at time t and vice versa. Note that $w_{ij}\left(t\right)$ = 0 means at time t, quadrotor j’s role is ambiguous to quadrotor i, which will not play a role in the iteration Equations (3) and (6).

Our ultimate goal is to reach convergence under the influence of malfunctions and design available observations of trust. Toward this target, our first priority is to decide which information should be sent through networks. By $\left(1\right)$ and $\left(2\right)$, we need the location of quadrotor i and the location of $j\in {\mathcal{N}}_i$ at time t to determine the velocity and the expected location at time $t+1$. In addition, for the determination of $w_{ij}$, we need the predicted speed of quadrotor i and the location of $j\in {\mathcal{N}}_i$ at the time t.

2.2. Noise

When it comes to the real system, whether we use drones or vehicles, there must be unmodeled factors such as friction, magnetic field, and data lagging, which may lead to the deviation between the actual movement and the computational one. Therefore, we set up noise equations that simulate the real environment as follows:

$${\mathit{x}}_{it,noise}=K_0\times {\alpha }_{it,x}+\frac{1}{2}CrhoS{V}^2$$

(9)

where ${\mathit{x}}_{it,noise}$ indicates the instability of location caused by noise. ${\alpha }_{it,x}$ is an arbitrary variable that has uniform distribution with a certain interval that the user can set up. In addition, $K_0$ is also a user-decided parameter that reduces or enlarges the influence of noise depending on the requirement of the real system. For simplicity, we assume that for both directions of every quadrotor, the parameter is the same $\alpha$. In addition, the second term is the basic wind disturbances, where C is the air drag coefficient, $\rho$ is the density of air and S is the windward area. Noise is important in this article as it gives a hint on how to determine the trust matrix. In addition, we include the term in the later simulations to serve as disturbances that the swarm system could possibly encounter in reality.

When taking noise into consideration, the iteration Formulas $\left(1\right)$ and $\left(2\right)$ evolve into the following modified equations:

$${\mathit{X}}_{ref,i}(t+1)={\mathit{X}}_{ref,i}\left(t\right)+{\mathit{V}}_i\left(t\right)+{\mathit{X}}_{it,noise}$$

(10)

where ${\mathit{X}}_{ref,i}\left(t\right)$ stands for the actuals position of quadrotors at time t.

2.3. The Trust Matrix and the Weight Matrix

In this subsection, firstly, we will discuss the methods to determine the trust matrix, which is obtained from the communication of quadrotors. After that, we directly derive the weight matrix.

Let ${\mathit{d}}_{(i,j)}\left(t\right)$ be the difference between the distance of quadrotor i and j and that after iteration (1) and (6) has been conducted, which can be written as:

$${\mathit{d}}_{(i,j)}\left(t\right)=|{\mathit{x}}_i\left(t\right)-{\mathit{x}}_j\left(t\right)-({\mathit{x}}_{ref,i}\left(t\right)-{\mathit{x}}_{ref,j}\left(t\right))|$$

(11)

See that the computed ${\mathit{x}}_i\left(t\right)$ and the actual movement ${\mathit{x}}_{ref,i}\left(t\right)$, are directly obtained by computing the following equations:

$$\mathsf{\Phi }\left(t\right)=(\prod _{t=0}^{t-1}\left[\begin{array}{cc}{\mathsf{\Lambda }}_{\mathcal{L}}\left(t\right)& {\mathsf{\Lambda }}_{\mathcal{M}}\left(t\right)\\ \mathsf{\Theta }& \mathsf{\Omega }\end{array}\right])\mathsf{\Phi }\left(0\right)$$

(12)

So we consider the trust matrix entry ${\mathit{w}}_{i,j}\left(t\right)$ of $\mathit{W}\left(t\right)$ as follows:

$${\mathit{w}}_{i,j}\left(t\right)=\left\{\begin{array}{c}{\mathit{w}}_{i,j}(t-1)+\beta ;\mathrm{if}{\mathit{d}}_{(i,j)}\left(t\right)\le \zeta \left(\alpha \right)\hfill \\ {\mathit{w}}_{i,j}(t-1)-\beta ;\mathrm{if}{\mathit{d}}_{(i,j)}\left(t\right)>\zeta \left(\alpha \right)\hfill \end{array}\right.$$

(13)

where $\beta$ is a trust value changing constant and, the equation represents the overall trust of i to j considering the information gathered from $t=0$ to $t=t$. In addition, $\zeta \left(\alpha \right)$ indicates the tolerance of error that will affect trust values. The equation provides some tolerance for a quadrotor to judge its neighbor. It will not simply classify a neighboring quadrotor as a legitimate or a malfunctional one based on one prediction as the trust value must go below zero to change its neighbor’s status from legitimate to malfunctional. It views the overall performance of its neighbors so as to resist certain extent of false prediction that the disturbances may generate in the process.

We now define a time-dependent trusted neighborhood for each quadrotor i as $T_i(t+1)=\{j\in {\mathcal{N}}_i:W_{i,j}(t+1)\ge 0\}$. This is the set of neighbors that legitimate quadrotor i identifies as its legitimate neighbors at time $t+1$. Denote $N_{wi}(t+1)=max\{\kappa ,|T_i(t+1)|+1\}\ge 1$ for all $i\in \mathcal{L}$ where, $\kappa$ >0 can be thought of as a parameter limiting the maximum influence that the neighbors of quadrotor i are allowed to have on quadrotor i’s update values (i.e., a value of $\kappa$ approaching infinity would preclude neighbors from influencing quadrotor i’s updated values). Using these quantities, we define the weight matrix $N\left(t\right)$ by choosing its entries $N_{ij}\left(t\right)$ as follows: for every $i\in \mathcal{L},j\in {\mathcal{N}}_i$, we have

$${\mathit{N}}_{i,j}(t+1)=\left\{\begin{array}{c}\frac{1}{{\mathit{N}}_{wi}(t+1)};\mathrm{if}j\in T_i\hfill \\ 0;\mathrm{if}j\notin T_i\cup \left\{i\right\}\hfill \\ 1-\sum _{m\in {\mathit{N}}_i}{\mathit{N}}_{im}\left(t\right),\mathrm{if}i=j\hfill \end{array}\right.$$

(14)

In this case, we do not consider the difference of weight between cooperative ones for simplicity, which might be improved in the future.

3. Analysis

 Proposition 1. 

There exists a finite time instant $T_f<0$ such that $N_{\mathcal{L}}\left(k\right)={\overline{N}}_{\mathcal{L}}$ for all $k\ge T_f$ almost surely when $\zeta \left(\alpha \right)$ and β are chosen properly.

Proof. 

Let $M={\sum }_1^t{\mathbf{w}}_{i,j}\left(t\right)$, then by Chernoff-Hoeffding Inequality [27] TH1.1, we have the following:

$$\mathbf{Pr}\left[\right|M-\mathit{E}\left(M\right)>\eta ]\le 2exp\left(\frac{-2{\eta }^2}{{\sum }_{k=1}^t{\mathsf{\Delta }}_k^2}\right)$$

(15)

where $\mathsf{\Delta }=2\beta$, $\eta \in (0,1/2)$. By the linearity of the expectation, we have $\mathit{E}\left(M\right)={\sum }_{k=1}^t\mathit{E}\left(w_{i,j}\left(k\right)\right)$. In addition, $\mathit{E}\left(W_{i,j}\left(k\right)\right)$ can be illustrated by the following equations:

$$\begin{array}{cc}\hfill \mathit{E}\left[w_{i,j}\left(k\right)\right]& ={\int }_0^{\zeta \left(\alpha \right)}\frac{\zeta \left(\alpha \right)}{2\sqrt{2}{k}_0\alpha }\times \beta d\alpha \hfill \\ & +{\int }_{\zeta \left(\alpha \right)}^{2\sqrt{2}{k}_0\alpha }\frac{2\sqrt{2}{k}_0\alpha -\zeta \left(\alpha \right)}{2\sqrt{2}{k}_0\alpha }\times (-\beta )d\alpha \hfill \end{array}$$

(16)

for every $k>0$ and every $i\in \mathcal{L}$, $j\in {\mathcal{N}}_i\cap \mathcal{L}$.

$$\begin{array}{cc}\hfill \mathit{E}\left[w_{i,j}\left(k\right)\right]& ={\int }_0^{\zeta \left(\alpha \right)}\frac{\zeta \left(\alpha \right)}{2\sqrt{2}{k}_0\alpha }\times \beta d\alpha \hfill \\ & +{\int }_{\zeta \left(\alpha \right)}^{+\infty }\frac{2\sqrt{2}{k}_0\alpha -\zeta \left(\alpha \right)}{2\sqrt{2}{k}_0\alpha }\times (-\beta )d\alpha \hfill \end{array}$$

(17)

for every $k>0$ and every $i\in \mathcal{L}$, $j\in {\mathcal{N}}_i\cap \mathcal{M}$.

The two equations above indicate to which extent the M reaches to $\mathit{E}\left(M\right)$ as time t increases. In other words, when we choose proper $\zeta \left(\alpha \right)$ and $\beta$, that M in (14) reaches $E\left(M\right)>0$ for every $i\in \mathcal{L}$, $j\in {\mathcal{N}}_i\cap \mathcal{L}$ and reaches $E\left(M\right)<0$ for every $i\in \mathcal{L}$, $j\in {\mathcal{N}}_i\cap \mathcal{M}$ occurs at a finite time almost surely by Borel–Cantelli Lemma. Thus, there exists a (random) finite time $T_f>0$ such that $N_{\mathcal{L}}\left(k\right)={\overline{N}}_{\mathcal{L}}$ for all $k\ge T_f$ almost surely.    □

In addition, we will give out an explicit example in the next section to prove there is such proper $\zeta \left(\alpha \right)$ and $\beta$.

Next, we will state the convergence of legitimate agents’ values. In particular, we use the decomposition ${\mathit{x}}_{\mathcal{L}}\left(t\right)={\mathit{x}}_{\mathcal{L}}^{\prime }\left(t\right)+{\mathit{X}}_{\mathcal{M}}^{\prime }\left(t\right)$ of the legitimate quadrotor states [see(4)] to formulate the following propositions.

 Lemma 1 

([26,28]). Let $H=p_2/p_1$, $d_{max}$ be the max eigenvalue of graph $\mathcal{G}$, then under the following conditions:

$$\frac{1+(1-Hp0)}{H}>p_2{d}_{max},1<Hand{p}_{0}H>1.$$

(18)

The matrix in (6) is a stochastic matrix.

 Proposition 2 

(Convergence of legitimate quadrotors’ values). Let ${\mathit{x}}_{\mathcal{L}}\left(0\right)$ be the vector of the initial value of legitimate agents. We have the following equations:

$${\mathit{x}}_{\mathcal{L}}^{\infty }=(\prod _{t=0}^{\infty }{\mathsf{\Lambda }}_{\mathcal{L}}\left(t\right)){\mathit{x}}_{\mathcal{L}}\left(0\right)$$

(19)

Proof. 

By Proposition 1, there exists a finite time instant $T_f<0$ such that $N_{\mathcal{L}}\left(k\right)={\overline{N}}_{\mathcal{L}}$ for all $k\ge T_f$ almost surely. Thus, by Lemma 1 there exists a finite time instant $T_f<0$ such that ${\mathsf{\Lambda }}_{\mathcal{L}}\left(t\right)={\overline{\mathsf{\Lambda }}}_{\mathcal{L}}$ directly from the definition in (6). In addition, by Perron–Frobenius theorem, we have

$$\underset{t\to +\infty }{lim}{\mathsf{\Lambda }}_L\left(t\right)=\mathbf{1}v$$

where v is a a stochastic column vector.

Therefore, we have the following equations:

$$\begin{array}{cc}\hfill {\mathit{x}}_{\mathcal{L}}^{\infty }\left(T_0\right)& =(\prod _{t=0}^{\infty }{\mathsf{\Lambda }}_{\mathcal{L}}\left(t\right)){\mathit{x}}_{\mathcal{L}}\left(0\right)\hfill \\ \hfill & =(\prod _{t=T_f}^{\infty }{\mathsf{\Lambda }}_{\mathcal{L}}\left(t\right))(\prod _{t=0}^{t=T_f-1}{\mathsf{\Lambda }}_{\mathcal{L}}\left(t\right)){\mathit{x}}_{\mathcal{L}}\left(0\right)\hfill \\ \hfill & =\mathbf{1}v(\prod _{t=0}^{t=T_f-1}{\mathsf{\Lambda }}_{\mathcal{L}}\left(t\right)){\mathit{x}}_{\mathcal{L}}\left(0\right)\hfill \end{array}$$

(20)

where $({\displaystyle \prod _{t=0}^{t=T_f-1}}{\mathsf{\Lambda }}_{\mathcal{L}}\left(t\right)){\mathit{x}}_{\mathcal{L}}\left(0\right)$ is a specific finite vector. Thus, Proposition 2 has been proved.    □

 Proposition 3 

(Convergence of malfunctional quadrotors’ values). Consider ${\varphi }_M^{\infty }$ defined by

$${\varphi }_{\mathcal{M}}^{\infty }=\sum _{k=0}^{\infty }(\prod _{t=k+1}^{\infty }{\mathsf{\Lambda }}_{\mathcal{L}}\left(t\right)){\mathsf{\Lambda }}_{\mathcal{M}}\left(k\right){\mathit{x}}_{\mathcal{M}}\left(k\right)$$

(21)

Then, the entries of this vector are all the same almost surely.

Proof. 

By Proposition 1 and Lemma 1, this imply $N_{\mathcal{M}}\left(k\right)=0$ and ${\mathsf{\Lambda }}_{\mathcal{M}}\left(k\right)=0$ for all $k\ge T_f$ almost surely.

Therefore, we have the following equations:

$$\begin{array}{cc}\hfill {\varphi }_{\mathcal{M}}^{\infty }& =\sum _{k=0}^{\infty }(\prod _{t=k+1}^{\infty }{\mathsf{\Lambda }}_{\mathcal{L}}\left(t\right)){\mathsf{\Lambda }}_{\mathcal{M}}\left(k\right){\mathit{x}}_{\mathcal{M}}\left(k\right)\hfill \\ \hfill & =\sum _{k=0}^{T_f-1}(\prod _{t=k+1}^{\infty }{\mathsf{\Lambda }}_{\mathcal{L}}\left(t\right)){\mathsf{\Lambda }}_{\mathcal{M}}\left(k\right){\mathit{x}}_{\mathcal{M}}\left(k\right)\hfill \\ \hfill & =\mathbf{1}v[\sum _{k=0}^{T_f-1}(\prod _{t=k+1}^{max\{T_f,k+1\}-1}{\mathsf{\Lambda }}_{\mathcal{L}}\left(t\right)){\mathsf{\Lambda }}_{\mathcal{M}}\left(k\right){\mathit{x}}_{\mathcal{M}}\left(k\right)]\hfill \end{array}$$

(22)

for some finite $T_f$, indicating that all the coordinates of the vector ${\varphi }_{\mathcal{M}}^{\infty }$ are identical almost surely.    □

By the result of Propositions 2 and 3, we directly get the following result.

 Proposition 4. 

There exists, almost surely, a random variable $z\left(T_0\right)$ that the consensus algorithm converges almost surely,

$$\underset{t=0\to \infty }{lim}{\mathit{x}}_{\mathcal{L}}\left(t\right)=z\left(T_0\right)\mathbf{1}$$

(23)

Proof. 

The result is directly obtained from Propositions 2 and 3 and the statement that ${\mathit{x}}_{\mathcal{L}}\left(t\right)={\mathit{x}}_{\mathcal{L}}^{\prime }\left(t\right)+{\mathit{x}}_{\mathcal{M}}^{\prime }\left(t\right)$.    □

4. MATLAB Simulation

In this section, we evaluate the performance of convergence of legitimate quadrotors through MATLAB. For simplicity, we set the graph $\mathcal{G}$ as a fully connected graph, and consider a system with 30 quadrotors among which there are 15 malfunctional ones. The initial location X, Y of each quadrotor is randomly chosen and the malfunctional quadrotors are also randomly chosen in order to guarantee generality. In addition, we consider the two most common cases in that the malfunctional quadrotors cannot move or in a circular movement.

4.1. Static Situation

In the first case, we discuss the situation where malfunctional quadrotors are set as static ones, which means they will remain in their initial locations and hover during the whole simulation as if they fail to take off. We set $K_0=0.05$, the X and Y noise ${\alpha }_{it,x},{\alpha }_{it,y}\in [-0.5,0.5]$, tolerance $\zeta$($\alpha$) = 0.05, and we set the least trusted limitation $\kappa =9$. Besides, we set $[p_0,p_1,p_2]=[0.1,0.01,0.2]$ to fulfill the requirement of convergence theory.

We demonstrate the following 2D-time results and $XY$ properties:

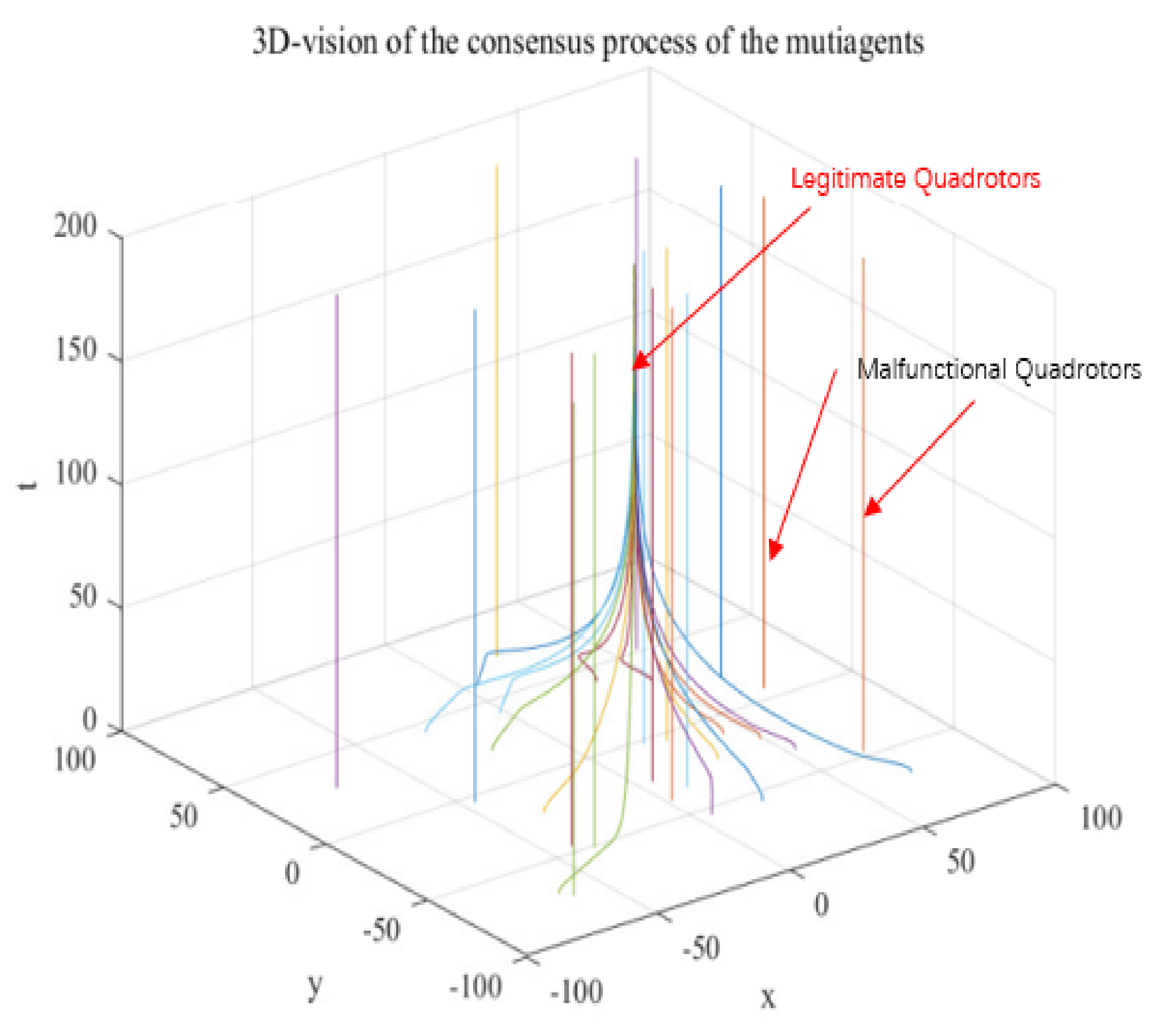
Figure 1 demonstrates the $XY$ movement with the time of all the quadrotors in the swarm system. As mentioned in the previous conditions, the malfunctional agents won’t move so it remains in their initial positions. The legitimate ones successfully reach their consensus.

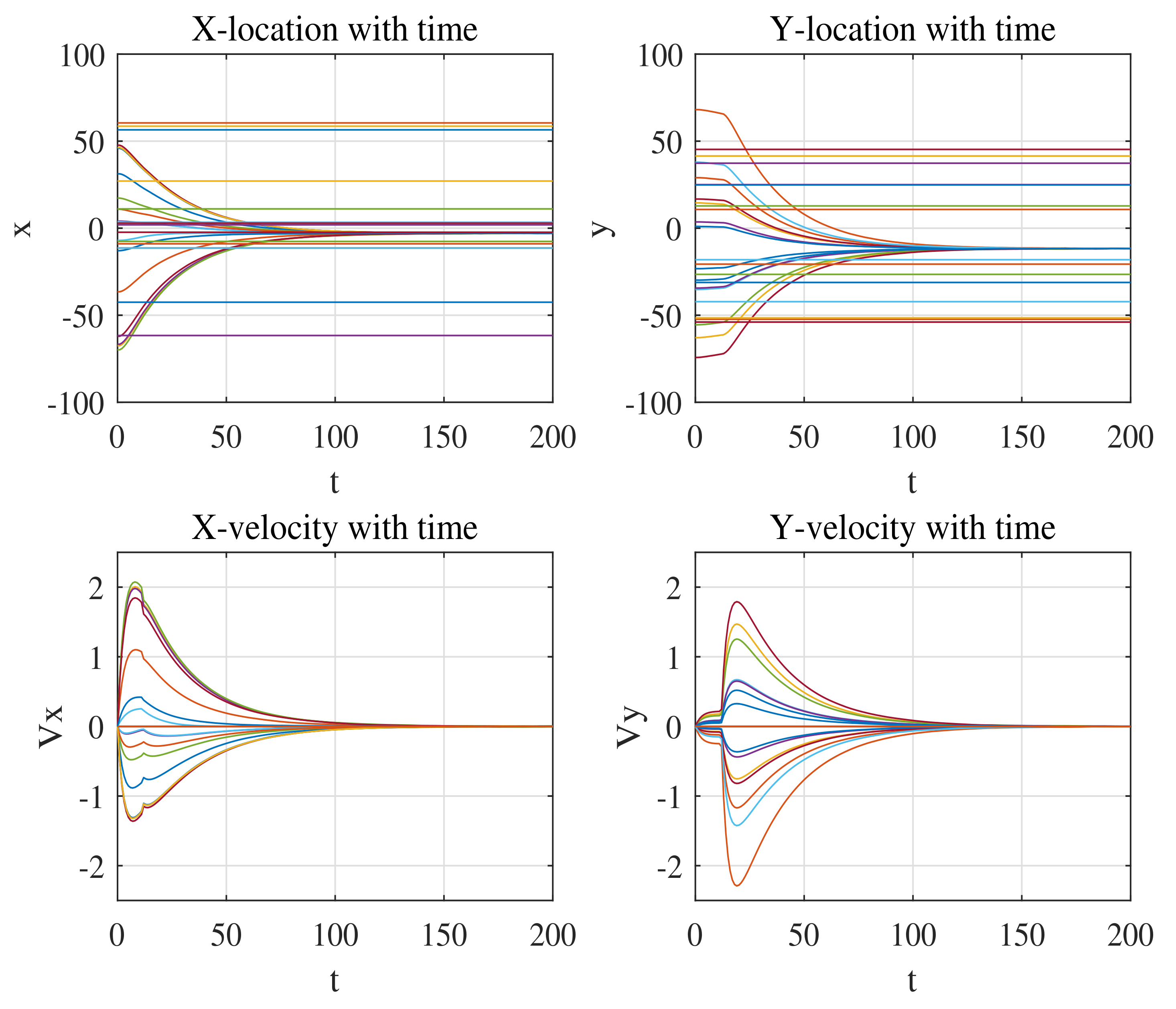
Figure 2 demonstrates the velocity and location of agents with time. As can be seen, the X and Y position converges and their velocities reach zero in the end, which fulfills the consensus requirement.

4.2. Movement Situation

In the second case, we discuss the situation where malfunctional quadrotors are set as moving ones, they will start a circular movement with radius $r_0=\sqrt{(x_i^2+y_i^2)}$ and the center is located at $(x,y)=(0,0)$. We set $K_0=0.05$, the noise ${\alpha }_{it,x},{\alpha }_{it,y}\in [-0.5,0.5]$, tolerance $\zeta$($\alpha$) = 0.05. In addition, we design $\kappa =9$. $[p_0,p_1,p_2]=[0.1,0.01,0.2]$.

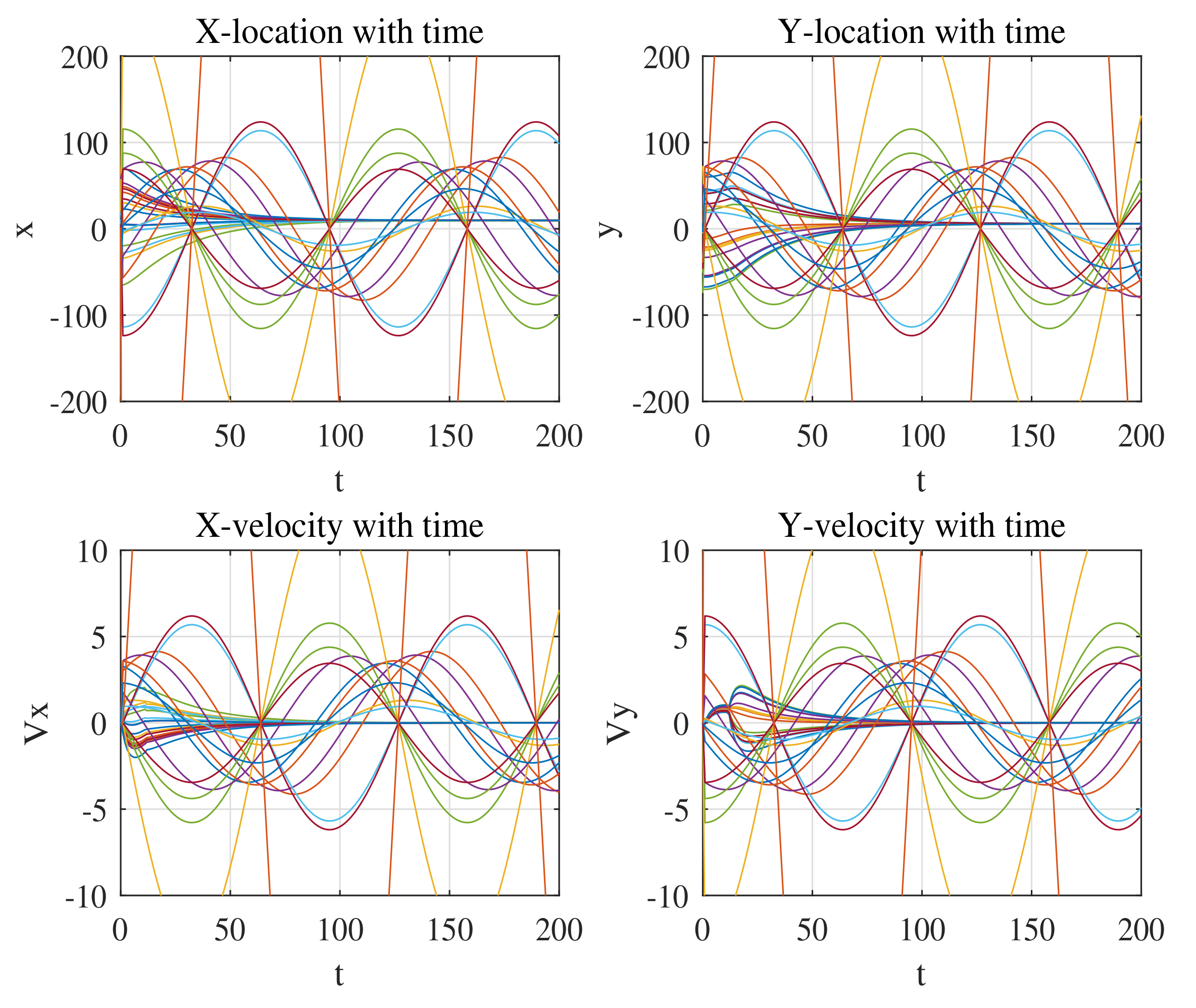
Figure 3 and Figure 4 demonstrate the situation that the malfunctional quadrotors rotate around the origin with the radius of their original distance with it. It’s clearly showed on the graph that the actual trajectory of each quadrotor and their correspondent speeds and positions. Judging from the graphs, we conclude that even if the malfunctional ones are moving in circles, it will not affect the consensus of the legitimate ones, and they will converge to their center, which proves the robustness of our method.

5. Gazebo Simulation

In this section, we apply our theory to the quadrotor swarm in Gazebo. We consider the four-quadrotor-situation where one of them is out of control. In the first case, the malfunctional quadrotor will hover at the original place after taking off, and in the second case will hit the obstacles. We firstly provide a pseudocode of our proposed scheme (Algorithm 1).

Algorithm 1 online adapative controller weight

Input:  Initial location of each quadrotor  Output:  Next-step Trust and Weight 1: functionTrustevaluation($x_j\left(t\right),u_j\left(t\right)$) 2:     while not reach consensus do 3:         if Quadrotor j fall within the tolerance of predicted location then $w_{i,j}(t+1)=w_{i,j}\left(t\right)+\beta$ 4:         else$w_{i,j}(t+1)=w_{i,j}\left(t\right)-\beta$ 5:         end if 6:         if 7:            $w_{i,j}(t+1)\leftarrow 0$ then $n_{i,j}(t+1)=0$ 8:         end if 9:     end while 10: end function

Each quadrotor will examine its relationship with its neighbours utilizing the above algorithm at each step, which means that they will online adapt the weight asigned to each other in the proposed protocol. As result, they will be able to distinguish the malfunctional quadrotors and eliminate their impacts on the whole robotic system.

5.1. Position Consensus

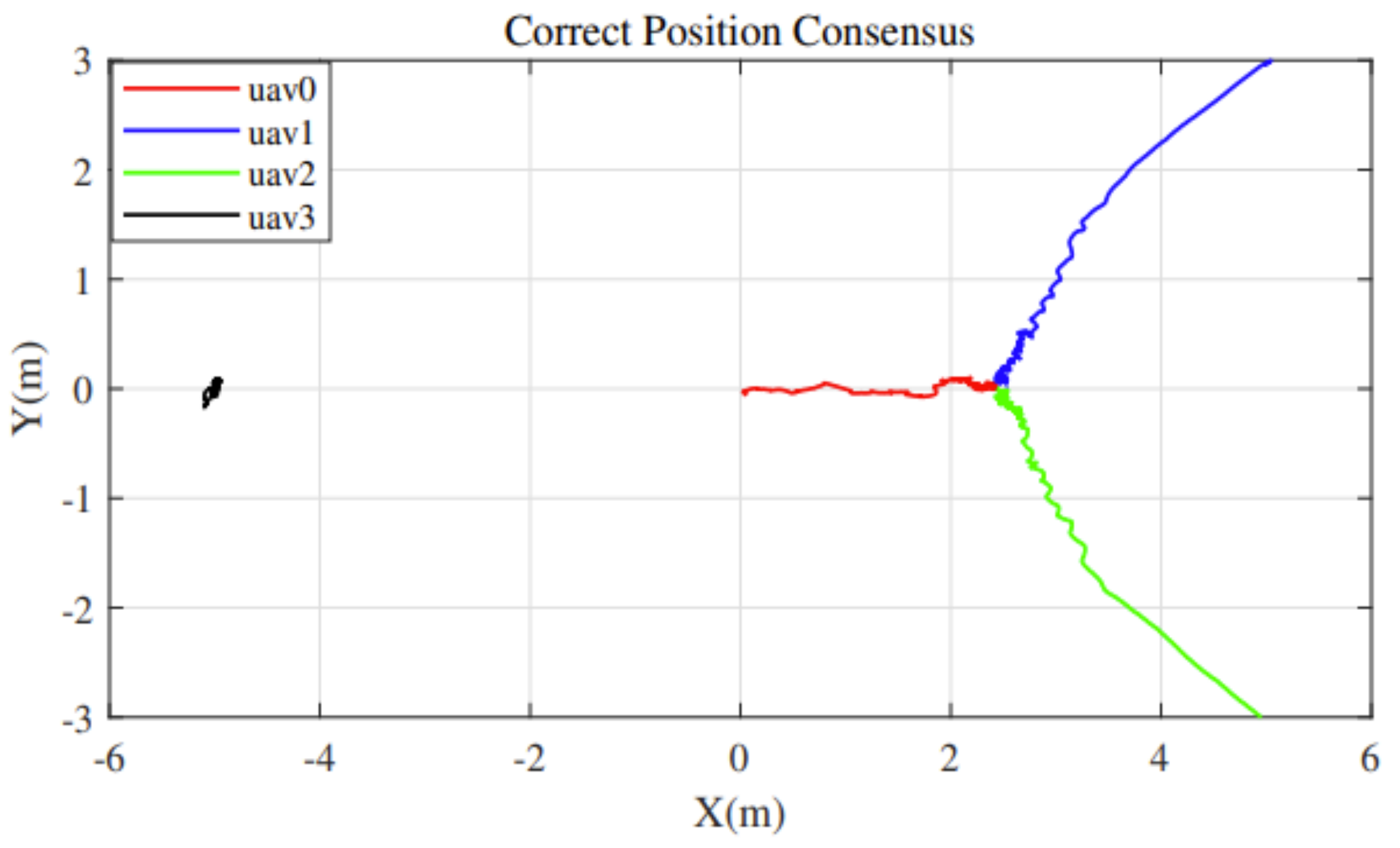
In this subsection, we consider the case where one of the four quadrotors hovers at the original place during the experiment. The location of the four quadrotors are $(5,3),(0,0),(5,-3),\mathrm{and}(-5,0)$ separately as shown in Figure 5. The quadrotor at $(-5,0)$ is designed as the malfunctional one. The four quadrotors are set in offboard mode and act upon our consensus protocol after they reach different heights in order to avoid Z-direction collision.

In the Figure 6, we present the actual movement of the four quadrotors with time under the adaptive consensus protocol. As the malfunctional quadrotor will hover at its original place after it takes off, its trust value will continue going down because its location prediction doesn’t match with its movement. The legitimate quadrotors are able to identify the malfunctional one to eliminate its effect on the whole swarm system by setting its weight to zero in the consensus protocol. Eventually, the legitimate quadrotors reach their center nearly at $X=2.48,Y=0.02$.

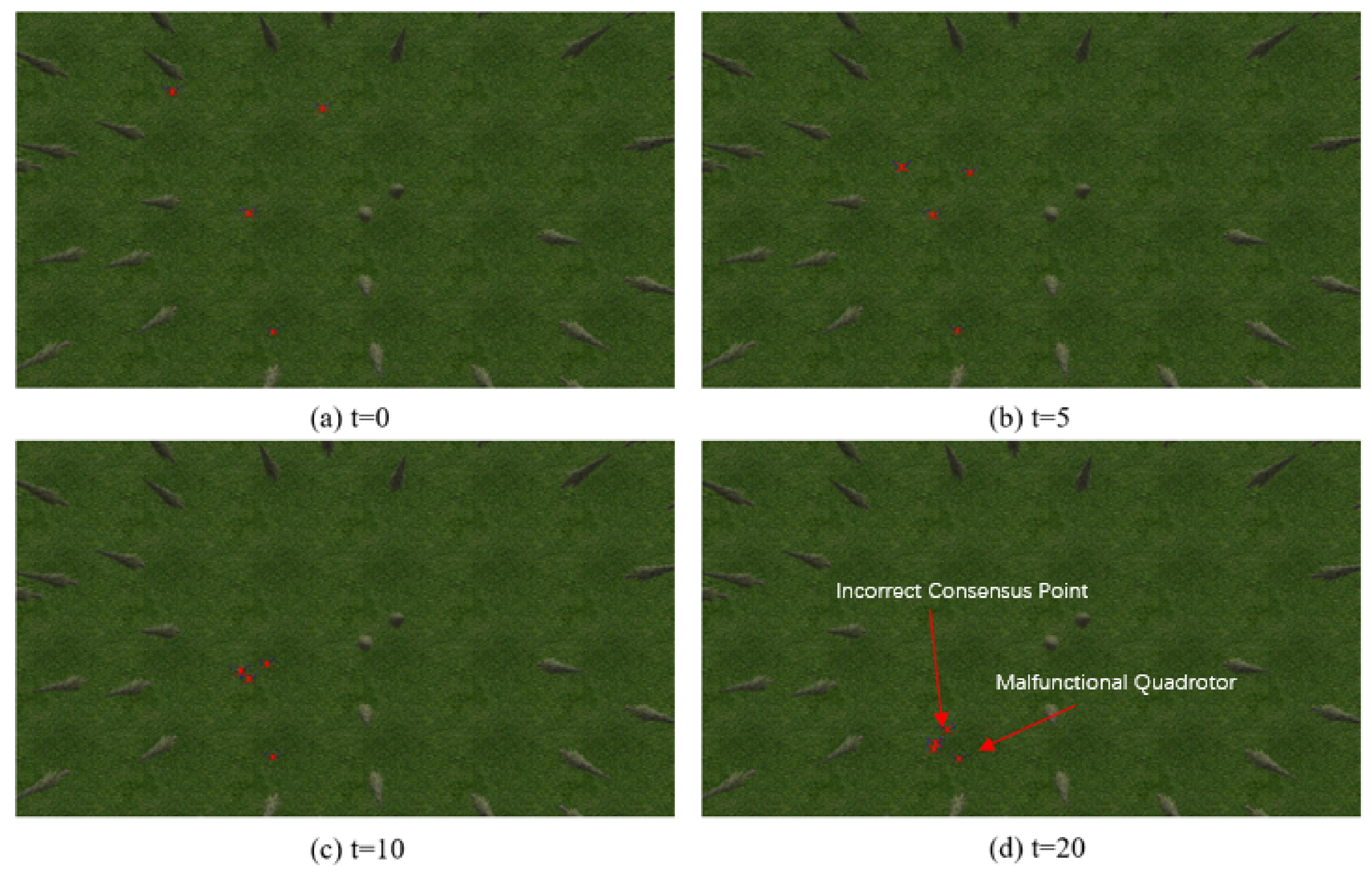
We next present the actual trajectory of the four quadrotors under the proposed protocol through the rosbag record in Figure 7. The black one which was designed as a malfunctional one will hover at the original place. In addition, the other three will reach their center, not affected by the malfunctional one which in this case is UAV3.

We next present the comparison test. We use the normal consensus protocol that each quadrotor assigns the same weight to its connected neighbors and they will not change weight during the experiment.

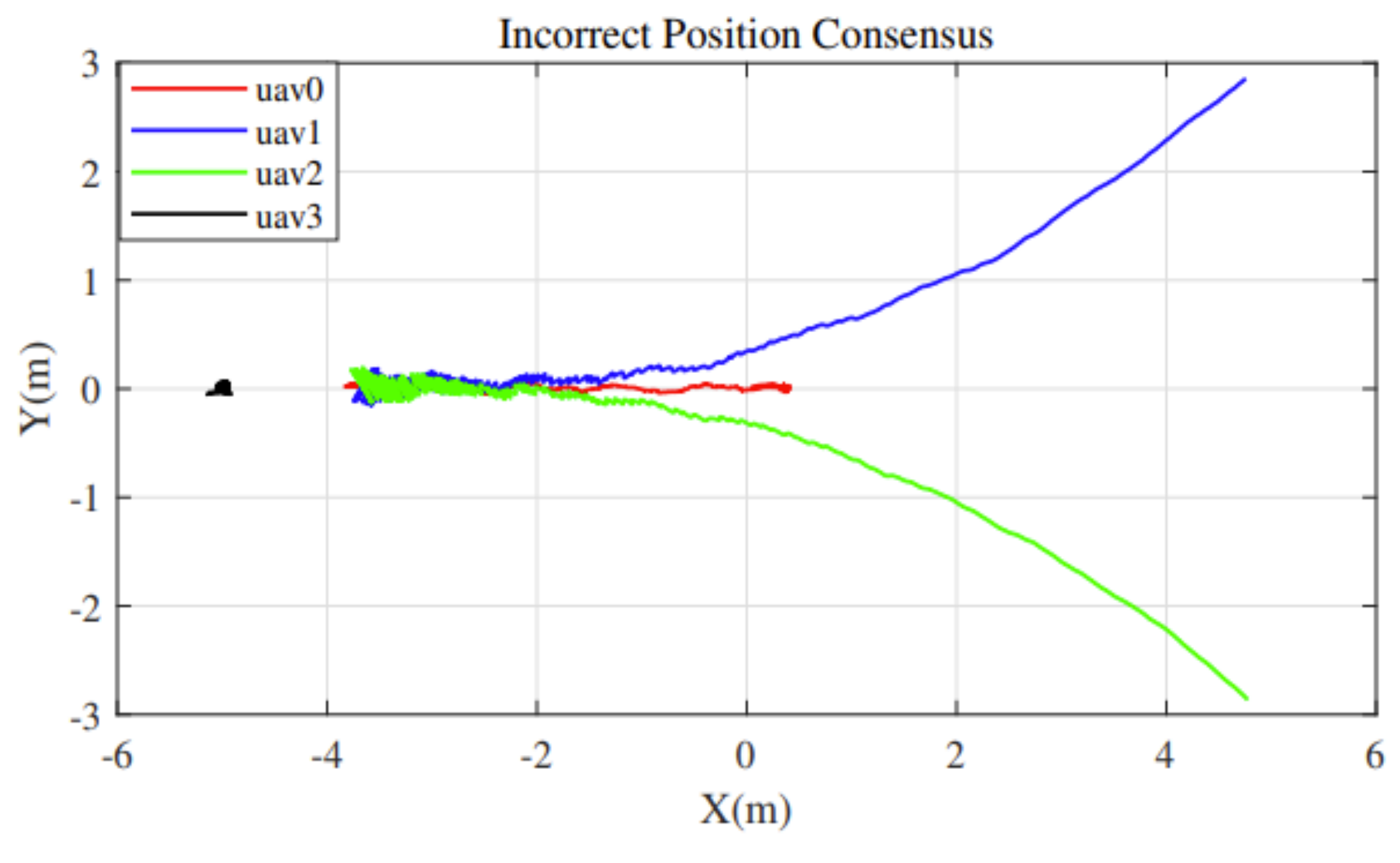
We can see from the Figure 8 that if the presence of the malfunctional quadrotor is not taken into consideration or the swarm system fail to identify the malfunctional one. The remaining three legitimate quadrotors will be severely affected as they mistakenly classify the malfunctional quadrotor as a trustworthy one. As the weight of the malfunctional quadrotors is not zero, others will try to reach consensus with it, leading to deviation. However, the swarm system will gradually fly towards $(-5,0)$, exactly the place where the malfunctional one is hovering.

We also present the actual trajectory of the four quadrotors under normal consensus protocol through the rosbag record. Figure 9 clearly shows that with the malfunctional quadrotor UAV3 hovering at $(-5,0)$, the remaining three legitimate quadrotors drift to UAV3’s location, indicating the severe consequence the misclassification brings about.

Notice that UAV0 whose original location is $(0,0)$ will first move forward due to two quadrotors locating ahead of it, and then drift backward to the malfunctional UAV3.

Compared with the actual movement under adaptive consensus, in which the true consensus point should be near the center of the three legitimate quadrotors’ original spawn location, that is $(2.5,0)$, the normal consensus leads to severe deviation.

In this case, our protocol gives out only a $0.8\%$ relative error at X-location, which is quite acceptable when considering a physical swarm system. While the comparison test gives out a relative error of $250.4\%$, which is unacceptable. This numerically demonstrates the improvement of our method.

5.2. Velocity Consensus

In this section, we extend our theory to velocity consensus and a more typical case will be discussed. We consider a four quadrotors swarm system that tries to fly through a forest while maintaining velocity consensus, and unfortunately, one of the quadrotors hit the tree and is trapped on the branches. Based on the same adaptive consensus protocol, we redesign the trust value and update the trust matrix based on the new function.

We list out the new trust design as the following equation:

$$\begin{array}{c}\hfill d_{i,j}\left(t\right)=\frac{1}{(X_i\left(t\right)-X_i(t-1))/V_i(t-1)+0.01}\times 0.5\\ \hfill +\frac{1}{(X_j\left(t\right)-X_j(t-1))/V_j(t-1)+0.01}\times 0.5\end{array}$$

(24)

Notice that the trust function is designed specifically for our experiment. When the malfunctional occurs, i.e., the quadrotor hit the obstacle, the movement of it per second will be very close to zeros, and when we place the measurement in the denominator, the reciprocal will be very large. As result, it can tell the difference between those which are still functioning and the one which hit the trees. Besides, the extra value $0.01$ is specialized for the situation when the movement is zero. And with its strong relation with $\beta$, the greater the $d_{i,j}\left(t\right)$ will lead to a faster descent in trust value, guaranteeing the quick response to the collision.

We provide the result by MATLAB and GAZEBO separately. In addition, the UAV3 is designed as the one will hit trees after flying for a while:

We set the swarm flying along the X-direction and maintain a lozenge formation. Y-direction velocity and position are not considered in the simulation. We can observe from the Figure 10 that with the unexpected malfunction at $t=20$, the X-velocity of UAV3 will become zero and resulting in the velocity decrease of the other three legitimate quadrotors. With our proposed trust values based consensus protocol, the remaining three are able to identify the malfunctional quadrotors, restore their velocity and reach velocity consensus.

We next present the GAZEBO simulation to illustrate a more realistic case.

As can be seen from the graphics, at $t=5$, UAV3 hit the trees and fell to the ground. The three legitimate quadrotors would slow down as they were lowering the trust values, but eventually, they identified the malfunctional quadrotor and disconnected from it. As result, they were able to continue their flying and maintained their consensus, even if the fourth one hit the tree and stopped moving, which indicates the effectiveness of our proposed method (Figure 11).

6. Conclusions

This work considers the problem of quadrotor swarm consensus in the presence of malfunctional quadrotors. Specifically, we propose a consensus protocol based on the trust value evaluation of each quadrotor’s neighboring quadrotors. We show that with the proper trust value design and the proposed consensus protocol:

(1) Correct classification of malfunctional and legitimate quadrotors can be achieved. The legitimate quadrotors can avoid potential risks by eliminating the effect of the malfunctional quadrotor.

(2) Almost sure that the remaining legitimate quadrotors are able to reach convergence even when malfunctional quadrotors occur.

(3) The deviation of the converged limit is much more improved than the one with a simple protocol not taking trust into consideration, which is acceptable and can be applied in physical swarms system.

Additionally, we show that our performance can be applied to a wide range of situations, such as velocity consensus, with different designed trust values and will guarantee more accuracy with more information observed. Taken together, these results point to the inherent value of quantifying and exploiting trust between quadrotors for consensus. Furthermore, with the theoretical derivations and mathematical proofs to guarantee the feasibility of our method and the certain noises to simulate the possible disturbance in reality, we believe that the tests in reality which we are currently working on will still be promising, such as the simulations as they have much in similarity such as gravity, collisions and sensors. All in all, we believe that the proposed method and framework of this article hold promise for a wide range of different purpose swarm systems.