Trajectory Tracking of UAVs Using Sigmoid Tracking Differentiator and Variable Gain Finite-Time Extended State Observer
Abstract
1. Introduction
- Combining improved sigmoid function and sliding mode terminal attractor, the improved sigmoid TD is proposed. The ISTD could not only accelerate global convergence, but also reduce the chattering of high-frequency noise. The stability of ISTD is proved theoretically, and the frequency characteristic analysis provides a theoretical basis for the subsequent parameters design.
- A variable gain finite-time ESO is proposed to weaken the “peak phenomenon”. With the aid of the finite-time stability theory, the proposed VGFESO can also achieve estimate performance and asymptotic stability in a finite time.
- The novel ADRC scheme based on ISTD, VGFESO, and STWSMC achieves high precision for quadrotor trajectory tracking. The results demonstrate that the proposed controller could converge in finite time and has higher tracking accuracy when compared to robust adaptive nonsingular fast terminal sliding-mode control (RANFTSMC) [7] and novel ADRC (NADRC) [39].
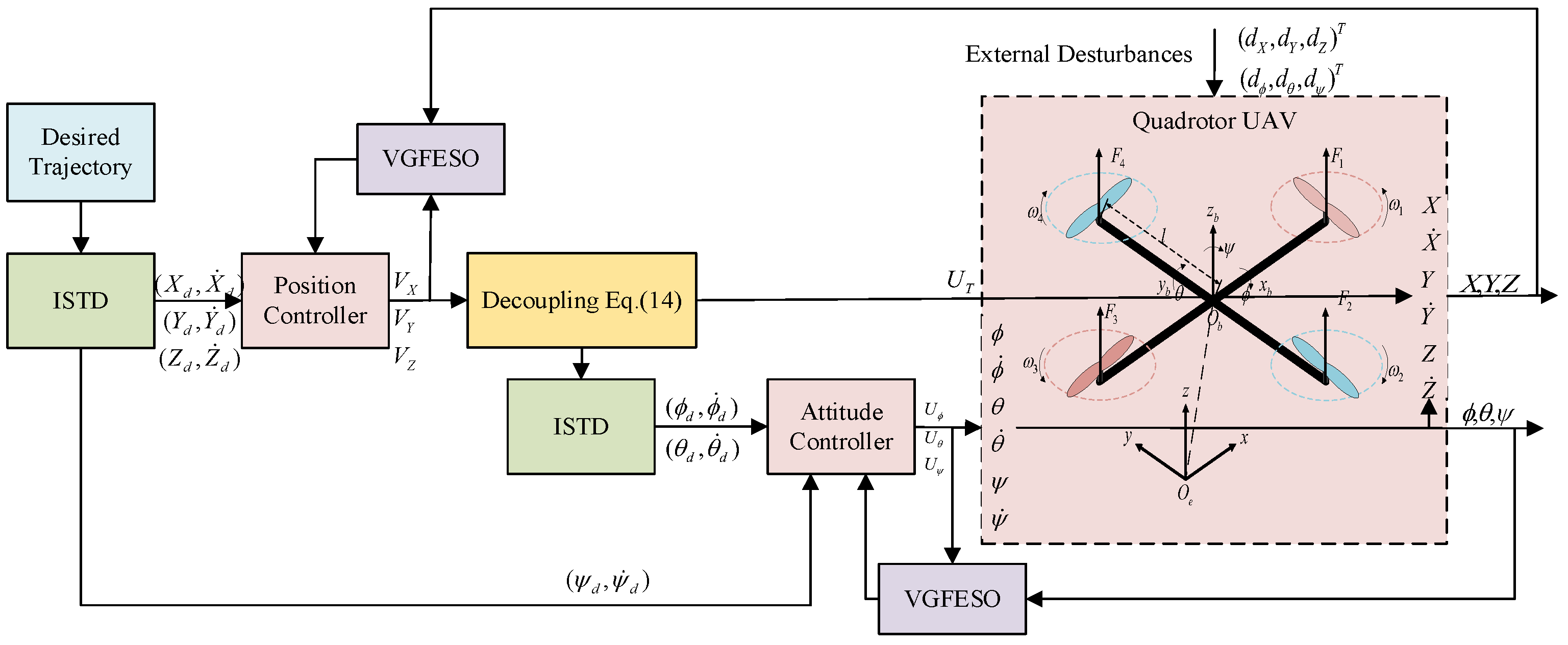
2. Dynamic Model Description
3. Improved ADRC Scheme
3.1. Preliminaries
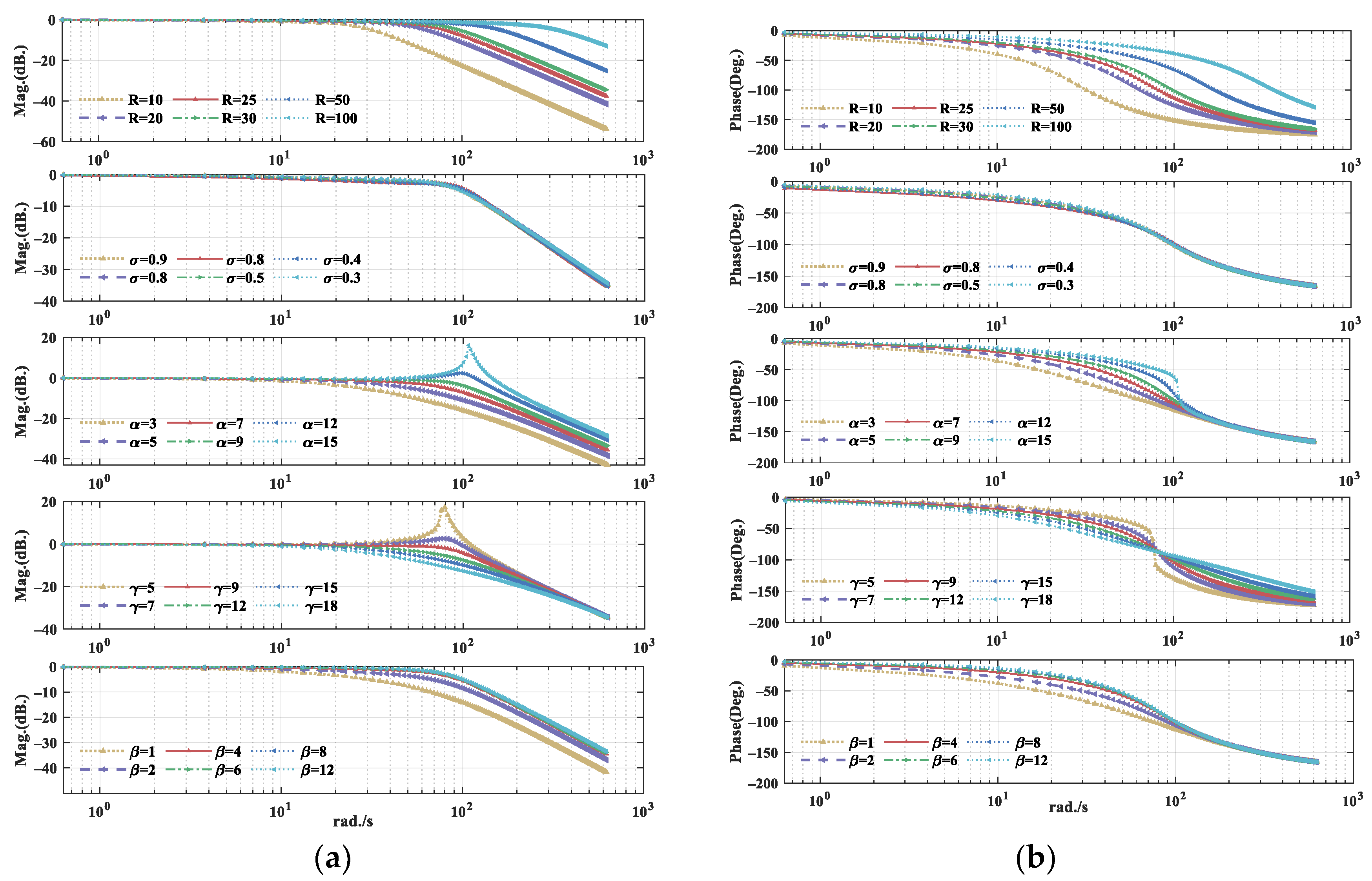
3.2. ISTD Design and Analysis
3.3. VGFESO Design and Stability Proof
3.4. Nonlinear Controller Design
4. Results and Discussion
4.1. Effect of the ISTD Parameter
4.2. Compared Simulation Results of Different TDs
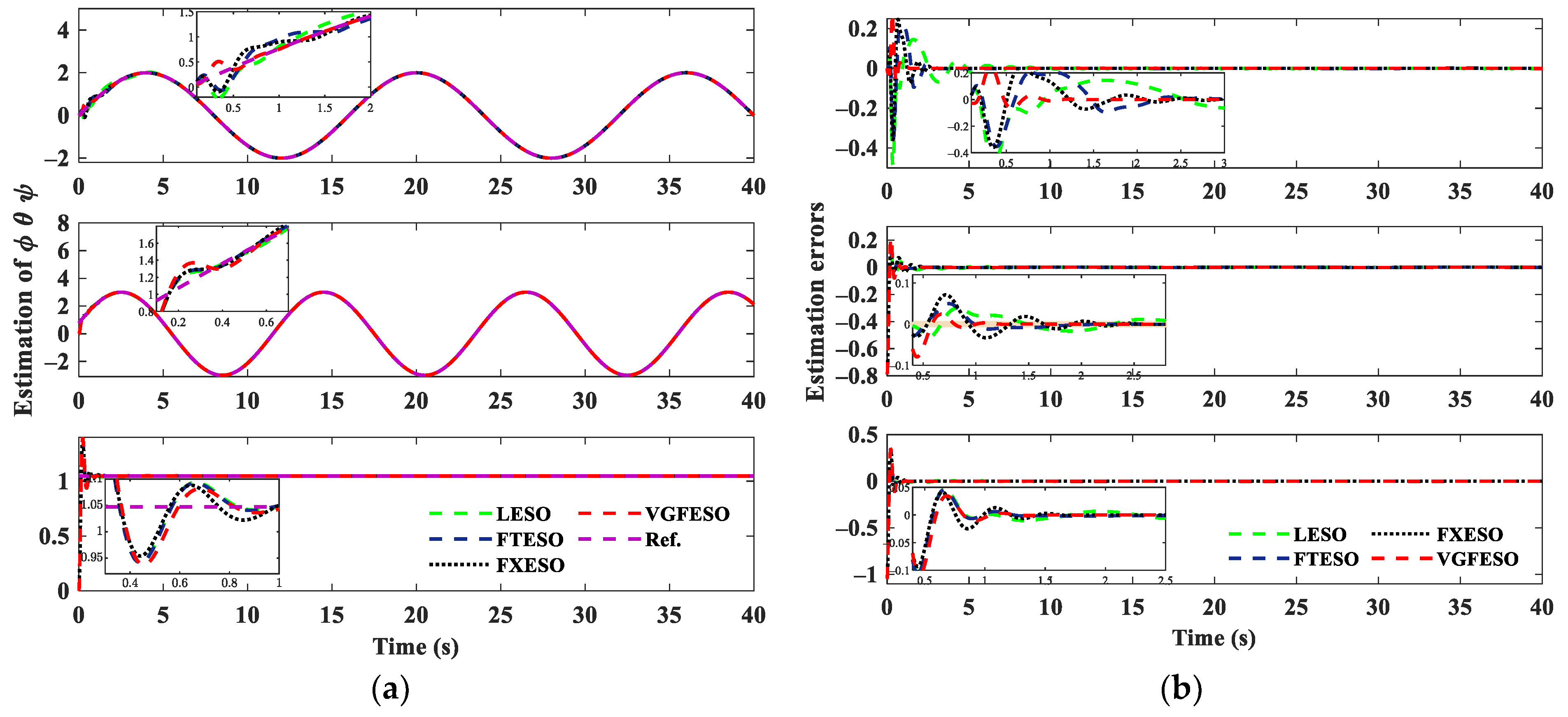
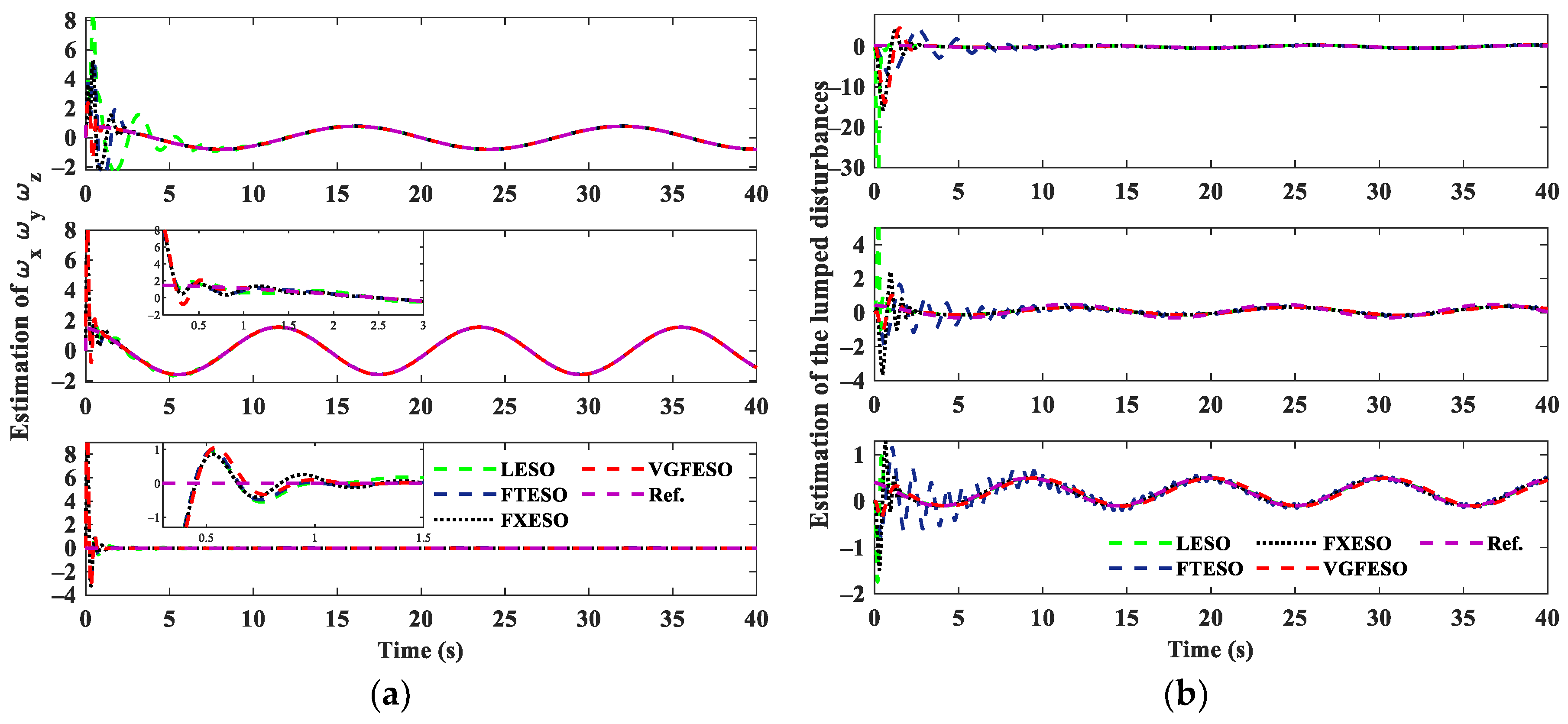
4.3. Comperated Performance with Different ESOs
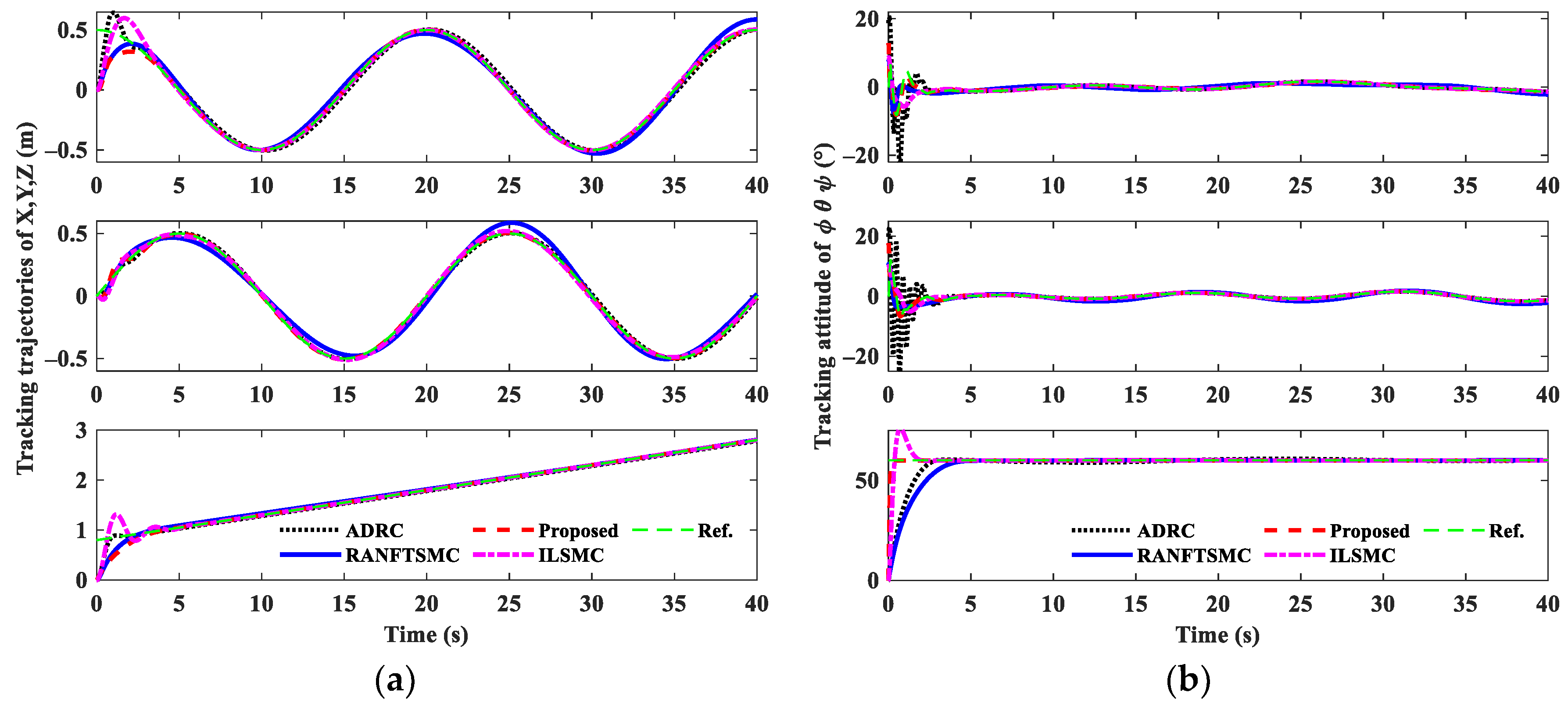
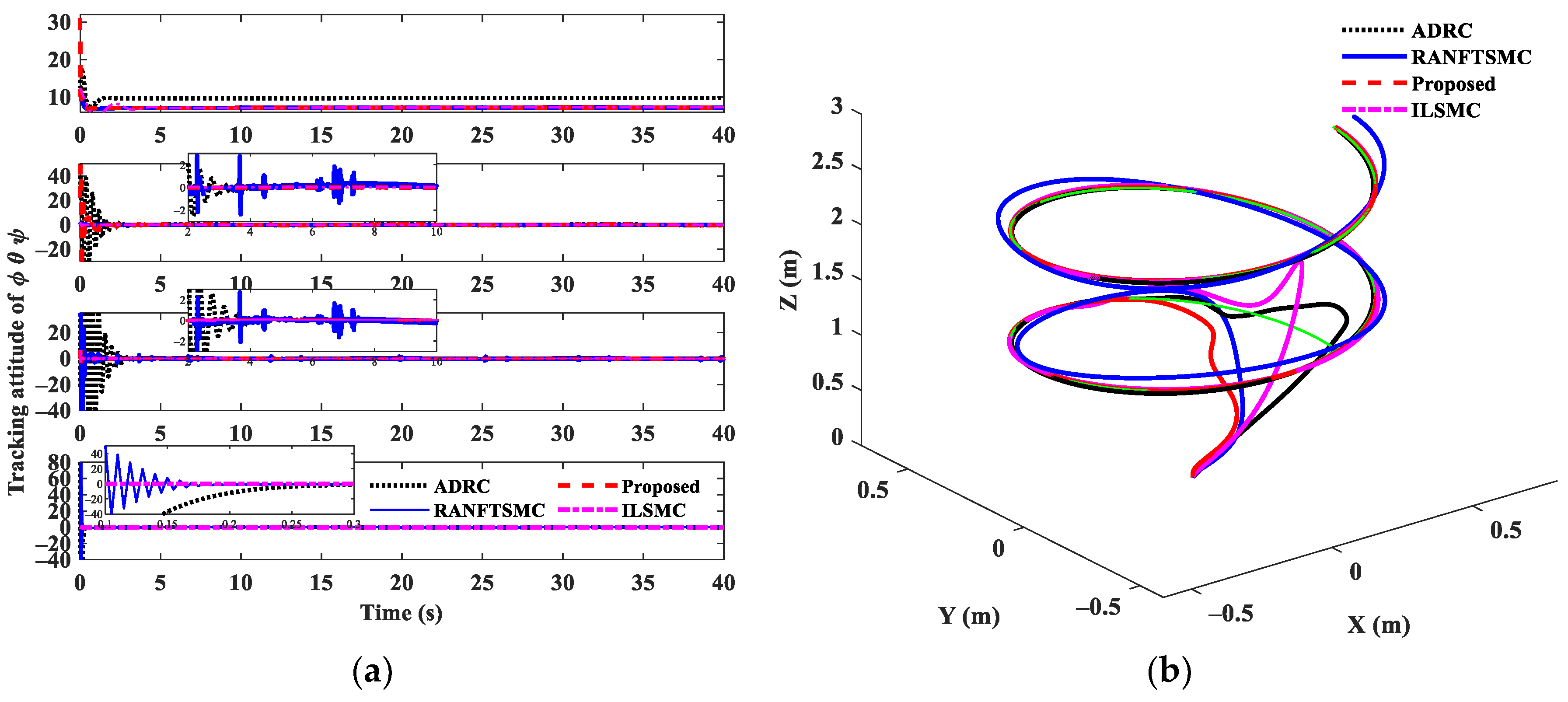
4.4. Trajectory Tracking Control Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hassanalian, M.; Abdelkefi, A. Classifications, applications, and design challenges of drones: A review. Prog. Aeosp. Sci. 2017, 91, 99–131. [Google Scholar] [CrossRef]
- Mahmud, I.; Cho, Y. Detection avoidance and priority-aware target tracking for UAV group reconnaissance operations. J. Intell. Robot. Syst. 2018, 92, 381–392. [Google Scholar] [CrossRef]
- Zhao, N.; Lu, W.; Sheng, M.; Chen, Y.; Tang, J.; Yu, F.R.; Wong, K.-K. UAV-assisted emergency networks in disasters. IEEE Wirel. Commun. 2019, 26, 45–51. [Google Scholar] [CrossRef]
- Mehndiratta, M.; Kayacan, E. A constrained instantaneous learning approach for aerial package delivery robots: Onboard implementation and experimental results. Auton. Robot. 2019, 43, 2209–2228. [Google Scholar] [CrossRef]
- Hao, M.; Zhao, W.; Qin, L.; Mao, P.; Qiu, X.; Xu, L.; Xiong, Y.J.; Ran, Y.; Qiu, G. A methodology to determine the optimal quadrat size for desert vegetation surveying based on unmanned aerial vehicle (UAV) RGB photography. Int. J. Remote Sens. 2020, 42, 84–105. [Google Scholar] [CrossRef]
- Zang, Y.; Zang, Y.; Zhou, Z.; Gu, X.; Jiang, R.; Kong, L.; He, X.; Luo, X.; Lan, Y. Design and anti-sway performance testing of pesticide tanks in spraying UAVs. Int. J. Agric. Biol. Eng. 2019, 12, 10–16. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Robust adaptive nonsingular fast terminal sliding-mode tracking control for an uncertain quadrotor UAV subjected to disturbances. ISA Trans. 2020, 99, 290–304. [Google Scholar] [CrossRef]
- Li, B.; Gong, W.; Yang, Y.; Xiao, B.; Ran, D. Appointed Fixed Time Observer-Based Sliding Mode Control for a Quadrotor UAV Under External Disturbances. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 290–303. [Google Scholar] [CrossRef]
- Miranda-Colorado, R.; Aguilar, L. Robust PID control of quadrotors with power reduction analysis. ISA Trans. 2020, 98, 47–62. [Google Scholar] [CrossRef]
- Wang, S.; Polyakov, A.; Zheng, G. Quadrotor stabilization under time and space constraints using implicit PID controller. J. Frankl. Inst.-Eng. Appl. Math. 2022, 359, 1505–1530. [Google Scholar] [CrossRef]
- Saif, A.; Aliyu, A.; Al Dhaifallah, M.; Elshafei, M. Decentralized backstepping control of a quadrotor with tilted-rotor under wind gusts. Int. J. Control Autom. Syst. 2018, 16, 2458–2472. [Google Scholar] [CrossRef]
- Liu, J.; Gai, W.; Zhang, J.; Li, Y. Nonlinear adaptive backstepping with ESO for the quadrotor trajectory tracking control in the multiple disturbances. Int. J. Control Autom. Syst. 2019, 17, 2754–2768. [Google Scholar] [CrossRef]
- Ijaz, S.; Chen, F.; Hamayun, M. A new actuator fault-tolerant control for Lipschitz nonlinear system using adaptive sliding mode control strategy. Int. J. Robust Nonlinear Control 2021, 31, 2305–2333. [Google Scholar] [CrossRef]
- Jiang, T.; Song, T.; Lin, D. Integral sliding mode based control for quadrotors with disturbances: Simulations and experiments. Int. J. Control Autom. Syst. 2019, 17, 1987–1998. [Google Scholar] [CrossRef]
- Najm, A.; Ibraheem, I. Altitude and Attitude Stabilization of UAV Quadrotor System using Improved Active Disturbance Rejection Control. Arab. J. Sci. Eng. 2020, 45, 1985–1999. [Google Scholar] [CrossRef]
- Han, J. Auto disturbances rejection controller and its applications. Control Decis. 1998, 13, 19–23. [Google Scholar]
- Han, J. From PID to Active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the American Control Conference 2003, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Guo, B.; Zhao, Z. On Convergence of the nonlinear active disturbance rejection control for MIMO systems. SIAM J. Control Optim. 2013, 51, 1727–1757. [Google Scholar] [CrossRef]
- Shao, X.; Liu, J.; Wang, H. Robust backstepping output feedback trajectory tracking for quadrotors via extended state observer and sigmoid tracking differentiator. Mech. Syst. Signal Process. 2018, 104, 631–647. [Google Scholar] [CrossRef]
- Mo, H.; Farid, G. Nonlinear and adaptive intelligent control techniques for quadrotor UAV—A survey. Asian J. Control 2018, 21, 989–1008. [Google Scholar] [CrossRef]
- Zhang, Q.; Fan, Y.; Mao, C. A gain design method for a linear extended state observer to improve robustness of deadbeat control. IEEE Trans. Energy Convers. 2020, 35, 2231–2239. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, B.; Yang, H.; Wang, Y. Finite-time tracking control for pneumatic servo system via extended state observer. IET Control Theory Appl. 2017, 11, 2808–2816. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, S.; Yan, Y. Fixed-time extended state observer-based trajectory tracking and point stabilization control for marine surface vessels with uncertainties and disturbances. Ocean. Eng. 2019, 186, 106109. [Google Scholar] [CrossRef]
- Zhao, Z.; Guo, B. On active disturbance rejection control for nonlinear systems using time-varying gain. Eur. J. Control 2015, 23, 62–70. [Google Scholar] [CrossRef]
- Tsai, S.; Chang, Y.; Lin, H.; Chang, L. Design and Implementation of Integral Backstepping Sliding Mode Control for Quadrotor Trajectory Tracking. Processes 2021, 9, 1951. [Google Scholar] [CrossRef]
- Wang, H.; Li, N.; Wang, Y.; Su, B. Backstepping sliding mode trajectory tracking via extended state observer for quadrotors with wind disturbance. Int. J. Control Autom. Syst. 2021, 19, 3273–3284. [Google Scholar] [CrossRef]
- Zhao, J.; Ding, X.; Jiang, B.; Jiang, G.; Xie, F. A novel control strategy for quadrotors with variable mass and external disturbance. Int. J. Robust Nonlinear Control 2021, 31, 8605–8631. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Robust adaptive backstepping fast terminal sliding mode controller for uncertain quadrotor UAV. Aerosp. Sci. Technol. 2019, 93, 105306. [Google Scholar] [CrossRef]
- Fu, X.; He, J. Robust Adaptive Sliding Mode Control Based on Iterative Learning for Quadrotor UAV. IETE J. Res. 2021. [Google Scholar] [CrossRef]
- Allahverdy, D.; Fakharian, A.; Menhaj, M.B. Back-Stepping Integral Sliding Mode Control with Iterative Learning Control Algorithm for Quadrotor UAVs. J. Electr. Eng. Technol. 2019, 14, 2539–2547. [Google Scholar] [CrossRef]
- Mofid, O.; Mobayen, S.; Wong, W.K. Adaptive terminal sliding mode control for attitude and position tracking control of quadrotor UAVs in the existence of external disturbance. IEEE Access 2020, 9, 3428–3440. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, Y.; Zhang, W. Integrated path planning and trajectory tracking control for quadrotor UAVs with obstacle avoidance in the presence of environmental and systematic uncertainties: Theory and experiment. Aerosp. Sci. Technol. 2022, 120, 107277. [Google Scholar] [CrossRef]
- Elmokadem, T.; Savkin, A.V. A method for autonomous collision-free navigation of a quadrotor UAV in unknown tunnel-like environments. Robotica 2022, 40, 835–861. [Google Scholar] [CrossRef]
- Zhao, G.; Chen, G.; Chen, J.; Hua, C. Finite-time control for image-based visual servoing of a quadrotor using nonsingular fast terminal siding mode. Int. J. Control Autom. Syst. 2020, 18, 2337–2348. [Google Scholar] [CrossRef]
- Eliker, K.; Zhang, W. Finite-time adaptive integral backstepping fast terminal sliding mode control application on quadrotor UAV. Int. J. Control. Autom. Syst. 2020, 18, 415–430. [Google Scholar] [CrossRef]
- Nie, Z.; Zhang, B.; Wang, Q.; Liu, R.; Luo, J. Adaptive active disturbance rejection control guaranteeing uniformly ultimate boundedness and simplicity. Int. J. Robust Nonlinear Control 2020, 30, 7278–7294. [Google Scholar] [CrossRef]
- Feng, H.; Guo, B. A new active disturbance rejection control to output feedback stabilization for a one-dimensional anti-stable wave equation with disturbance. IEEE Trans. Autom. Control. 2017, 62, 3774–3787. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Zhang, X.; Sun, Q.; Sun, M. A novel control scheme for quadrotor UAV based upon active disturbance rejection control. Aerosp. Sci. Technol. 2018, 79, 601–609. [Google Scholar] [CrossRef]
- Noordin, A.; Basri, M.A.M.; Mohamed, Z. Position and Attitude Tracking of MAV Quadrotor Using SMC-Based Adaptive PID Controller. Drones 2022, 6, 263. [Google Scholar] [CrossRef]
- Huang, S.R.; Yang, Y.N. Adaptive Neural-Network-Based Nonsingular Fast Terminal Sliding Mode Control for a Quadrotor with Dynamic Uncertainty. Drones 2022, 6, 206. [Google Scholar] [CrossRef]
- Liu, J.; Sun, M.; Chen, Z.; Sun, Q. Output feedback control for aircraft at high angle of attack based upon fixed-time extended state observer. Aerosp. Sci. Technol. 2019, 95, 105468. [Google Scholar] [CrossRef]
- Liu, J.; Sun, M.; Chen, Z.; Sun, Q. Super-twisting sliding mode control for aircraft at high angle of attack based on finite-time extended state observer. Nonlinear Dyn. 2020, 99, 2785–2799. [Google Scholar] [CrossRef]
- Pu, Z.; Yuan, R.; Yi, J.; Tan, X. A class of adaptive extended state observers for nonlinear disturbed systems. IEEE Trans. Ind. Electron. 2015, 62, 5858–5869. [Google Scholar] [CrossRef]
- Tian, B.; Cui, J.; Lu, H.; Liu, L.; Zong, Q. Attitude Control of UAVs Based on Event-Triggered Supertwisting Algorithm. IEEE Trans. Ind. Inform. 2021, 17, 1029–1038. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. Strict Lyapunov Functions for the Super-Twisting Algorithm. IEEE Trans. Autom. Control 2012, 57, 1035–1040. [Google Scholar] [CrossRef]
- Eliker, K.; Grouni, S.; Tadjine, M.; Zhang, W. Practical finite time adaptive robust flight control system for quad-copter UAVs. Aerosp. Sci. Technol. 2020, 98, 105708. [Google Scholar] [CrossRef]



| ESOs | Parameters |
|---|---|
| LESO | |
| FTESO | |
| FXESO | |
| VGFESO |
| States | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| LESO | 12.010 | 6.105 | 5.515 | 7.985 | 11.305 | 6.525 | 8.510 | 6.840 | 9.285 |
| FTESO | 3.120 | 2.430 | 1.725 | 4.910 | 6.775 | 2.945 | 2.685 | 2.100 | 5.150 |
| FXESO | 3.020 | 1.935 | 1.580 | 3.375 | 4.555 | 1.855 | 2.450 | 1.625 | 2.090 |
| VGFESO | 2.630 | 1.845 | 1.405 | 3.050 | 2.815 | 1.670 | 1.555 | 1.330 | 1.701 |
| Controllers | Parameters |
|---|---|
| ADRC | |
| RANFTSMC | |
| ILSMC | |
| Proposed |
| States | Sum | ||||||
|---|---|---|---|---|---|---|---|
| ADRC | 0.5441 | 0.1921 | 0.9744 | 0.0471 | 0.0216 | 0.0698 | 1.8491 |
| RANFTSMC | 0.1607 | 0.3506 | 0.7380 | 0.0430 | 0.2147 | 1.1411 | 2.6481 |
| ILSMC | 0.1510 | 0.4146 | 0.3043 | 0.0666 | 0.0202 | 0.1205 | 1.0872 |
| Proposed | 0.1002 | 0.3909 | 0.3434 | 0.0131 | 0.0153 | 0.0471 | 0.9100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Wang, L.; Ren, Y.; Li, Y. Trajectory Tracking of UAVs Using Sigmoid Tracking Differentiator and Variable Gain Finite-Time Extended State Observer. Drones 2022, 6, 350. https://doi.org/10.3390/drones6110350
Zhu W, Wang L, Ren Y, Li Y. Trajectory Tracking of UAVs Using Sigmoid Tracking Differentiator and Variable Gain Finite-Time Extended State Observer. Drones. 2022; 6(11):350. https://doi.org/10.3390/drones6110350
Chicago/Turabian StyleZhu, Wenxing, Lihui Wang, Yuan Ren, and Yong Li. 2022. "Trajectory Tracking of UAVs Using Sigmoid Tracking Differentiator and Variable Gain Finite-Time Extended State Observer" Drones 6, no. 11: 350. https://doi.org/10.3390/drones6110350
APA StyleZhu, W., Wang, L., Ren, Y., & Li, Y. (2022). Trajectory Tracking of UAVs Using Sigmoid Tracking Differentiator and Variable Gain Finite-Time Extended State Observer. Drones, 6(11), 350. https://doi.org/10.3390/drones6110350







