An Adaptive Control Framework for the Autonomous Aerobatic Maneuvers of Fixed-Wing Unmanned Aerial Vehicle
Abstract
1. Introduction
- Develop a control framework that integrates the reference generator and tracking controller for UAV maneuvers.
- Propose a quaternion-based inversion method to avoid the singularity during high angle maneuvers.
- Present a novel attitude controller, incorporating incremental dynamic inversion (INDI), neural network, and disturbance observer, which is able to alleviate the effects of up to model uncertainties and additive exogenous gusts in the aerobatic maneuvers.
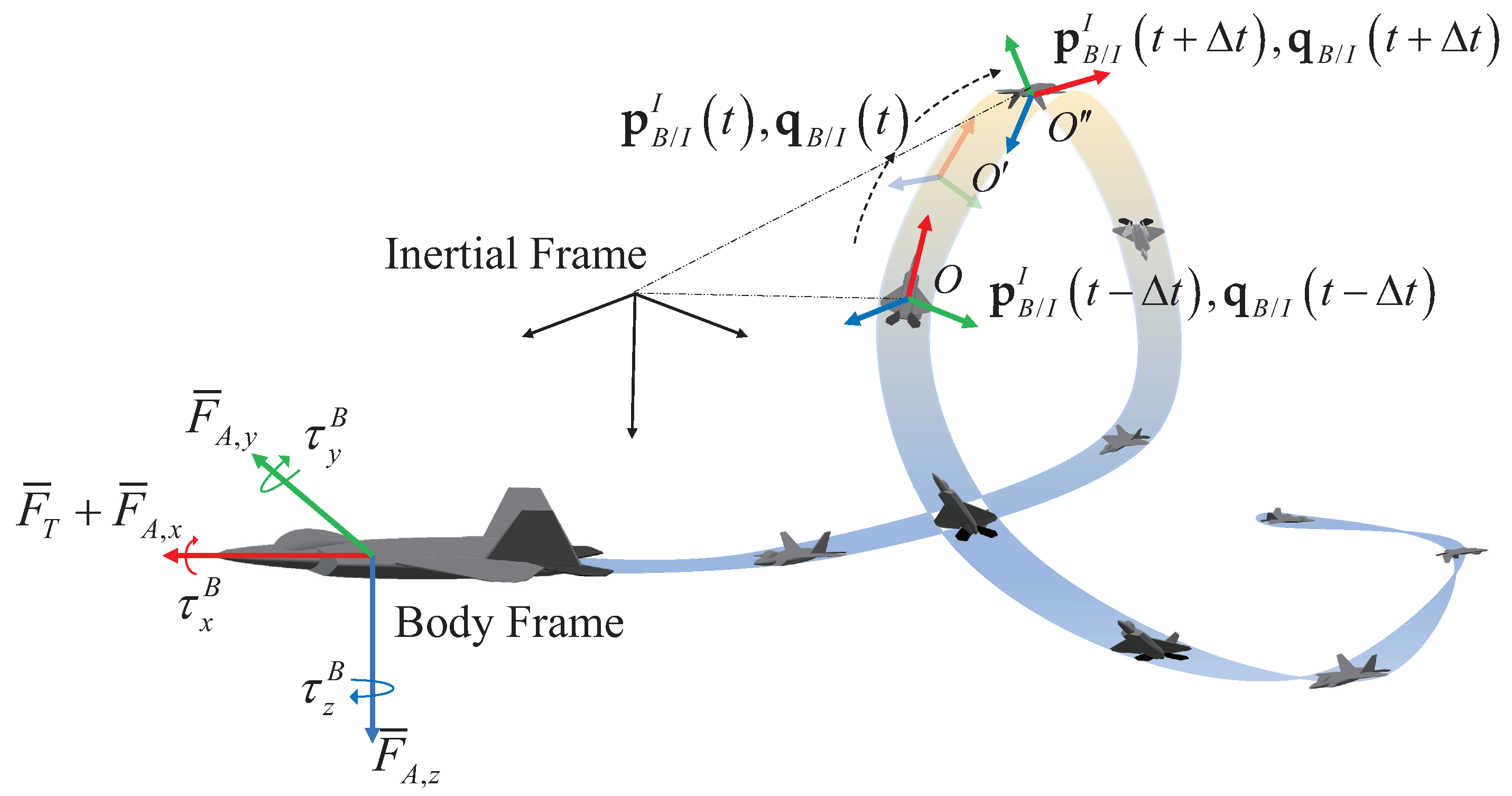
2. Preliminary
3. Disturbance Observer
3.1. Discrete-Time Disturbance Observer
3.2. Neural Network Estimation
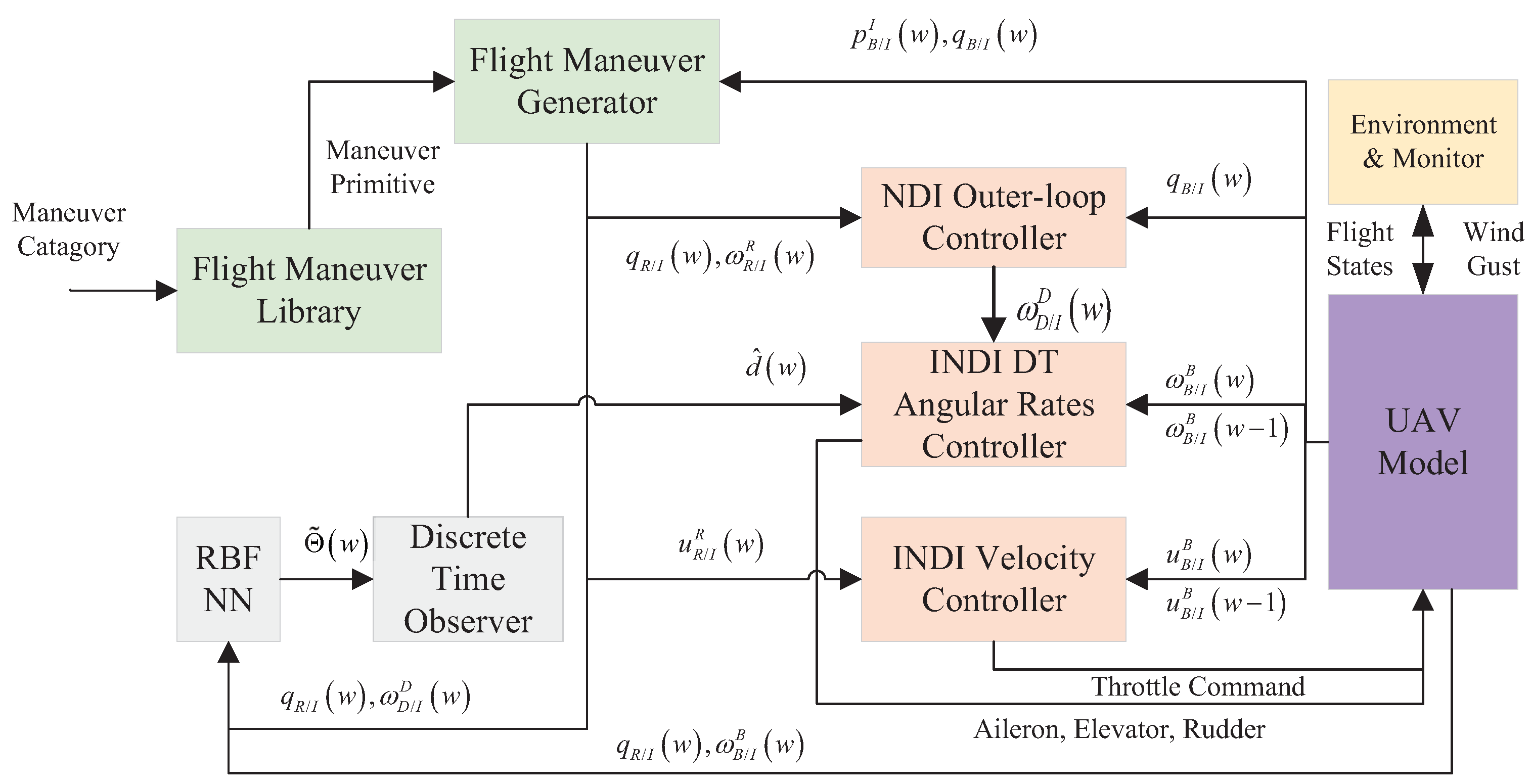
4. Controller Design
4.1. Incremental Velocity Tracking Control
4.2. Quaternion-Based NDI in Outer Loop
4.3. Adaptive Inner-Loop Controller
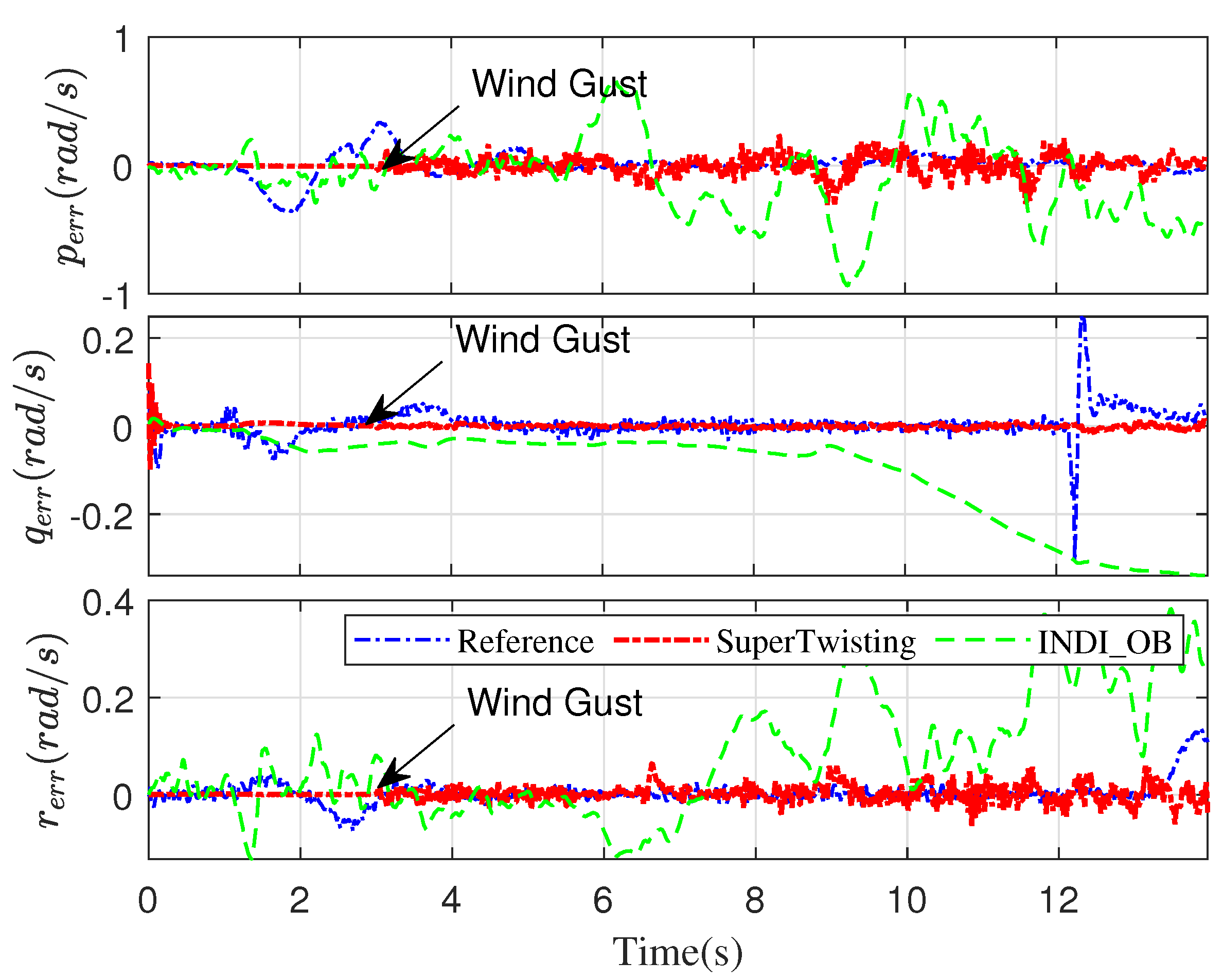
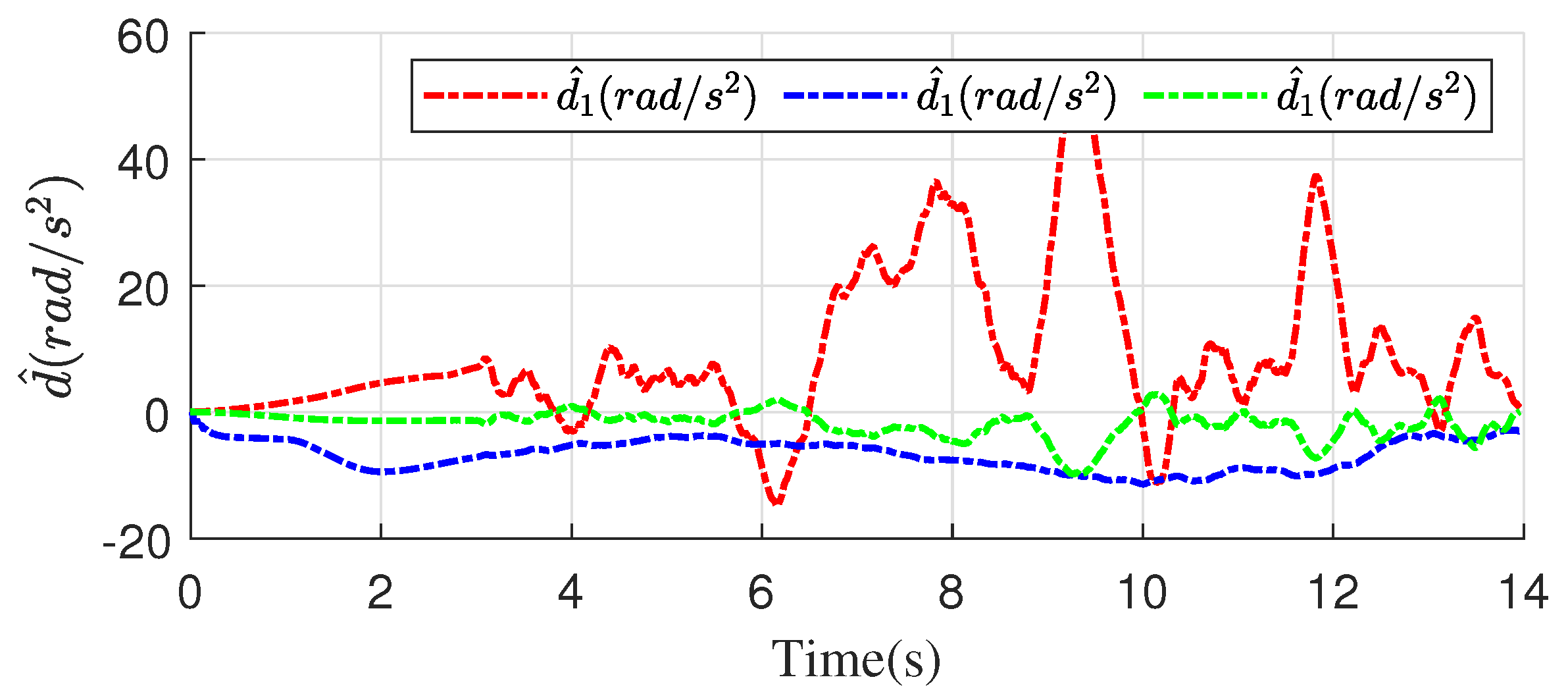
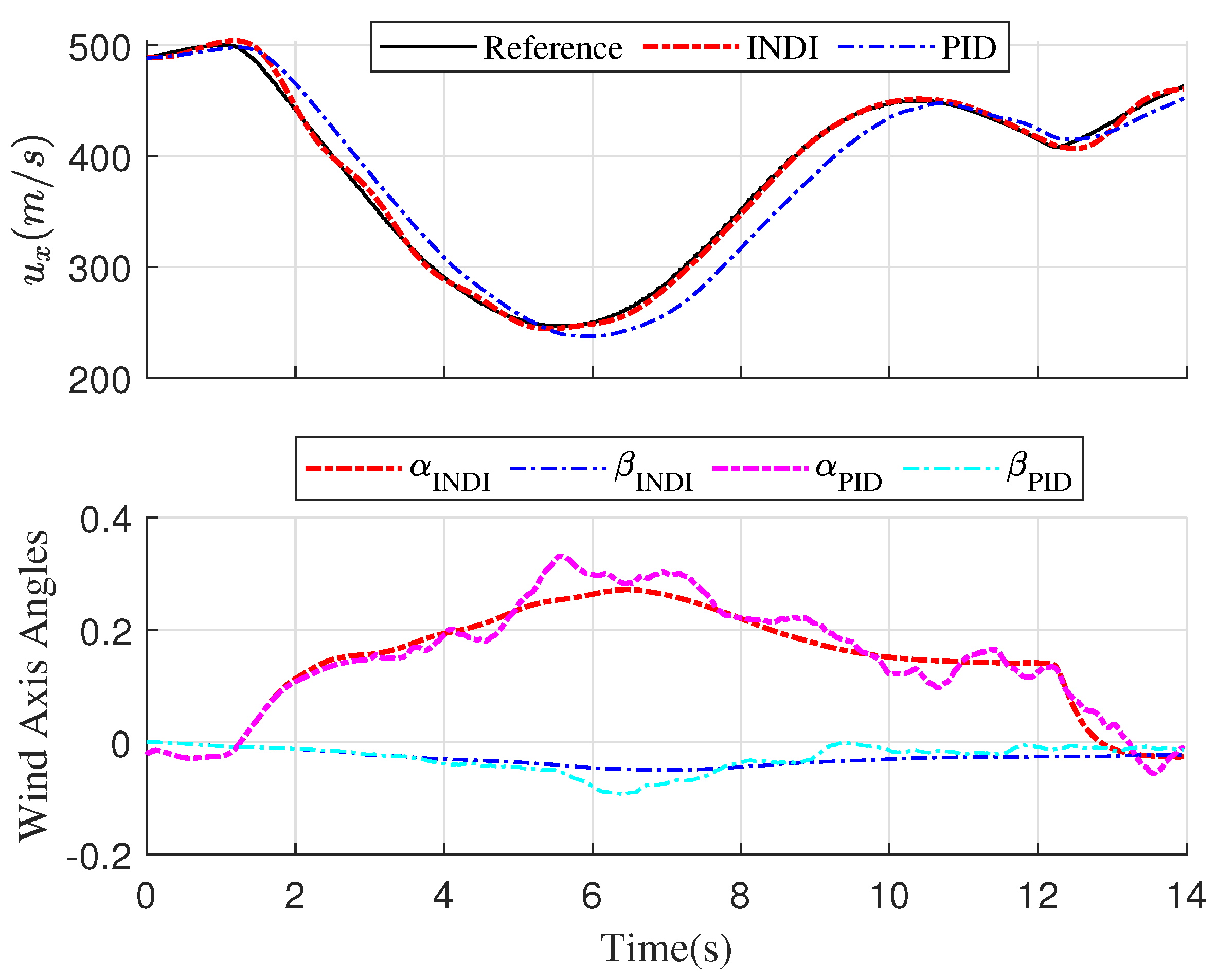
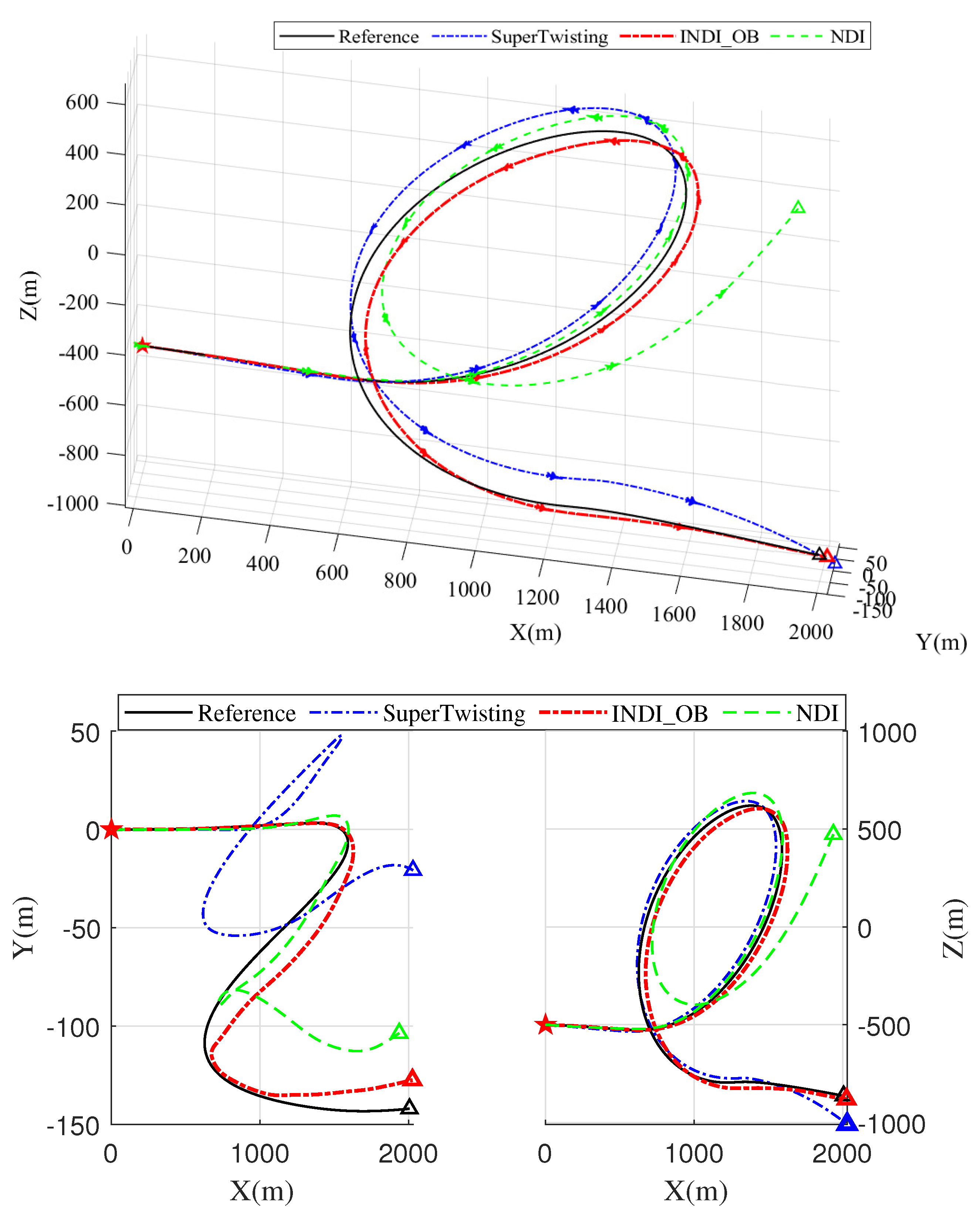
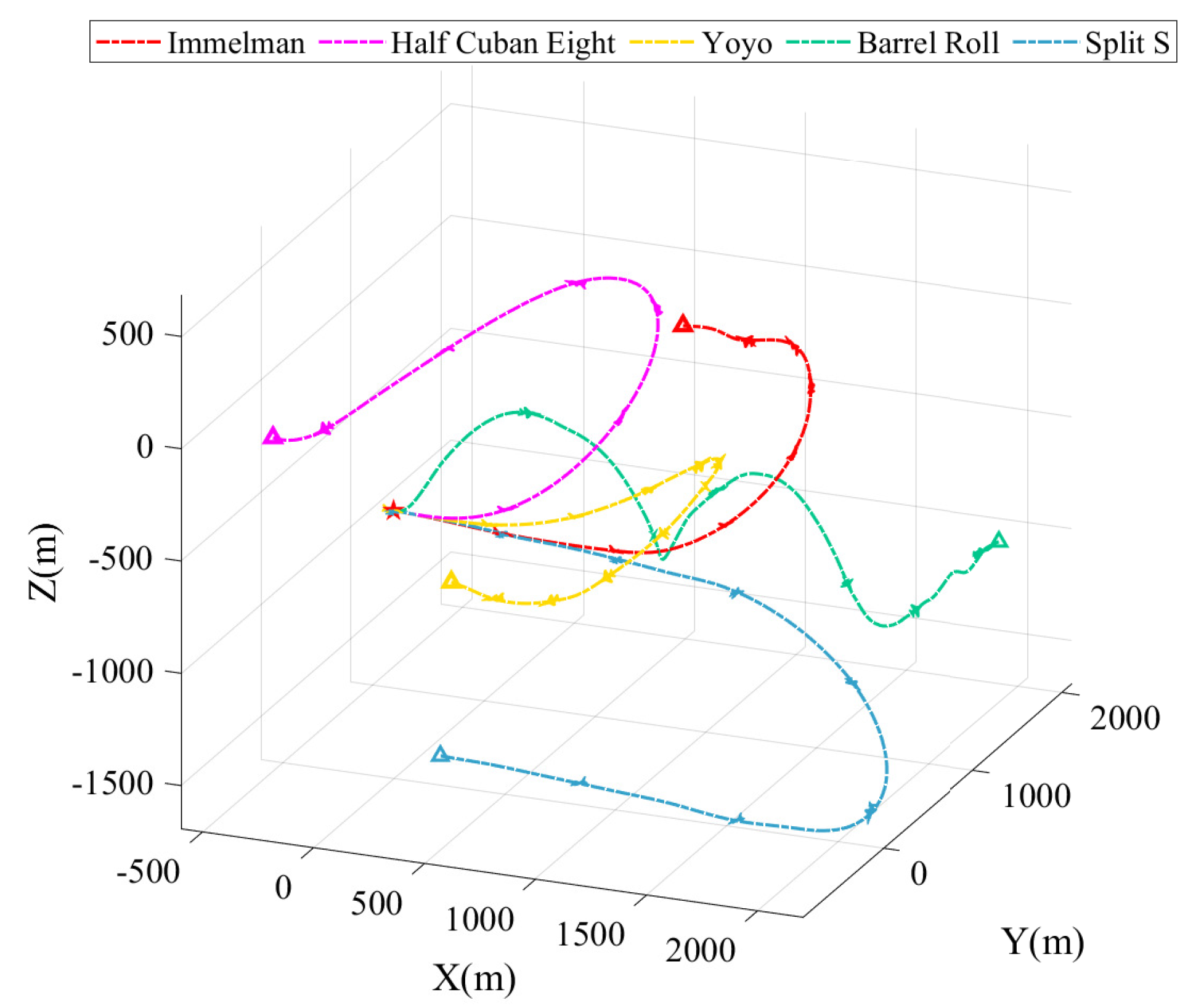
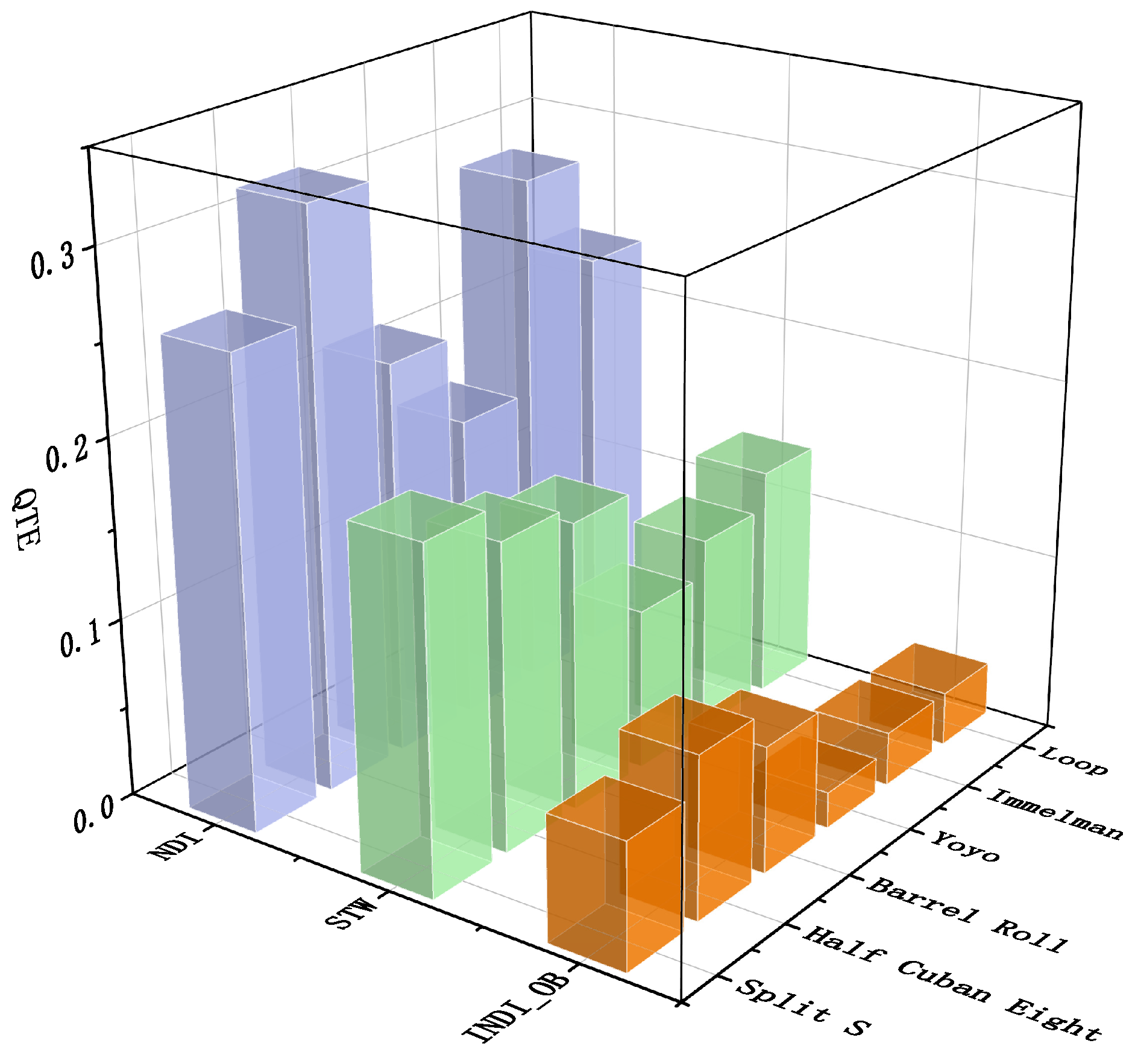
5. Evaluation
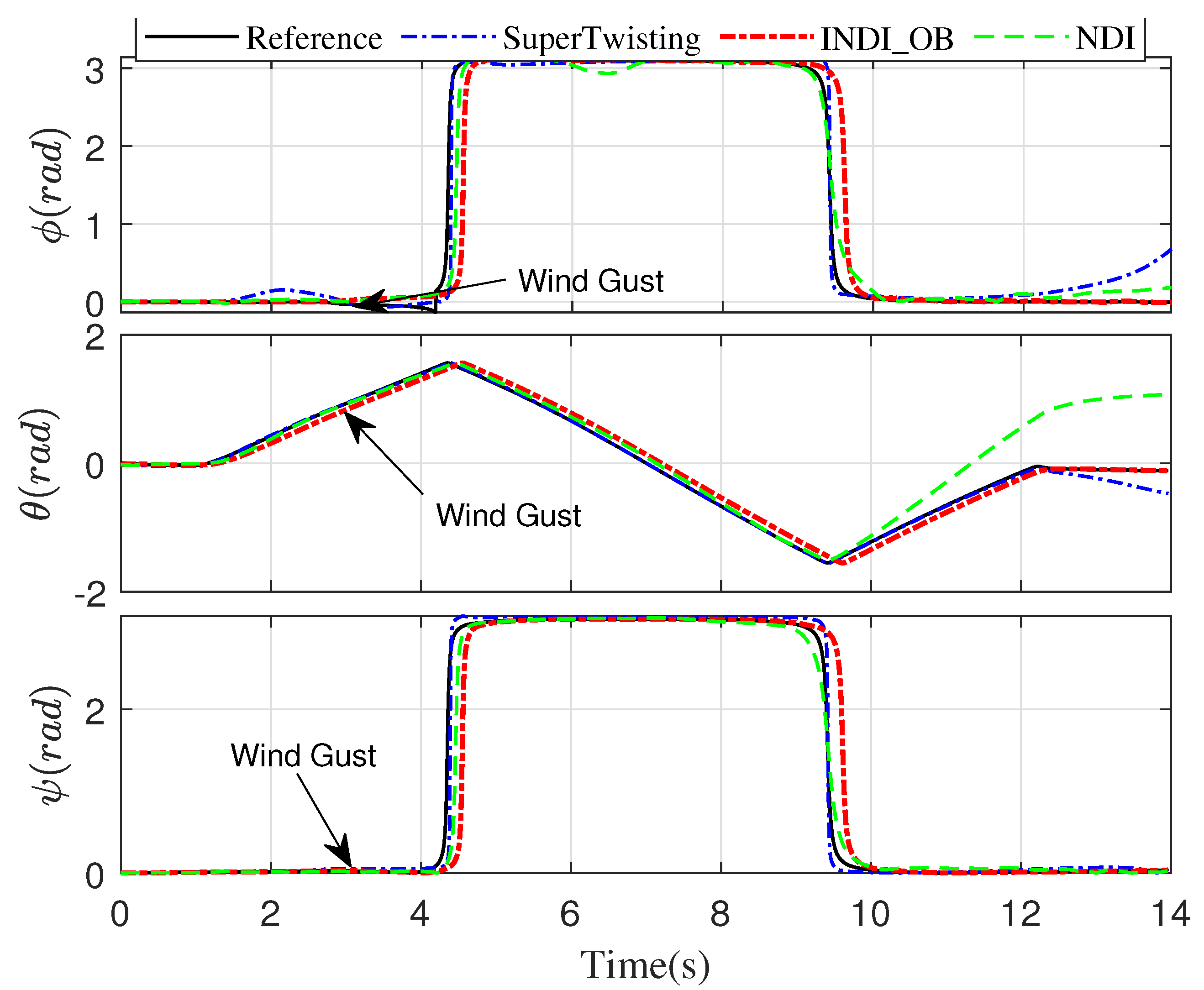
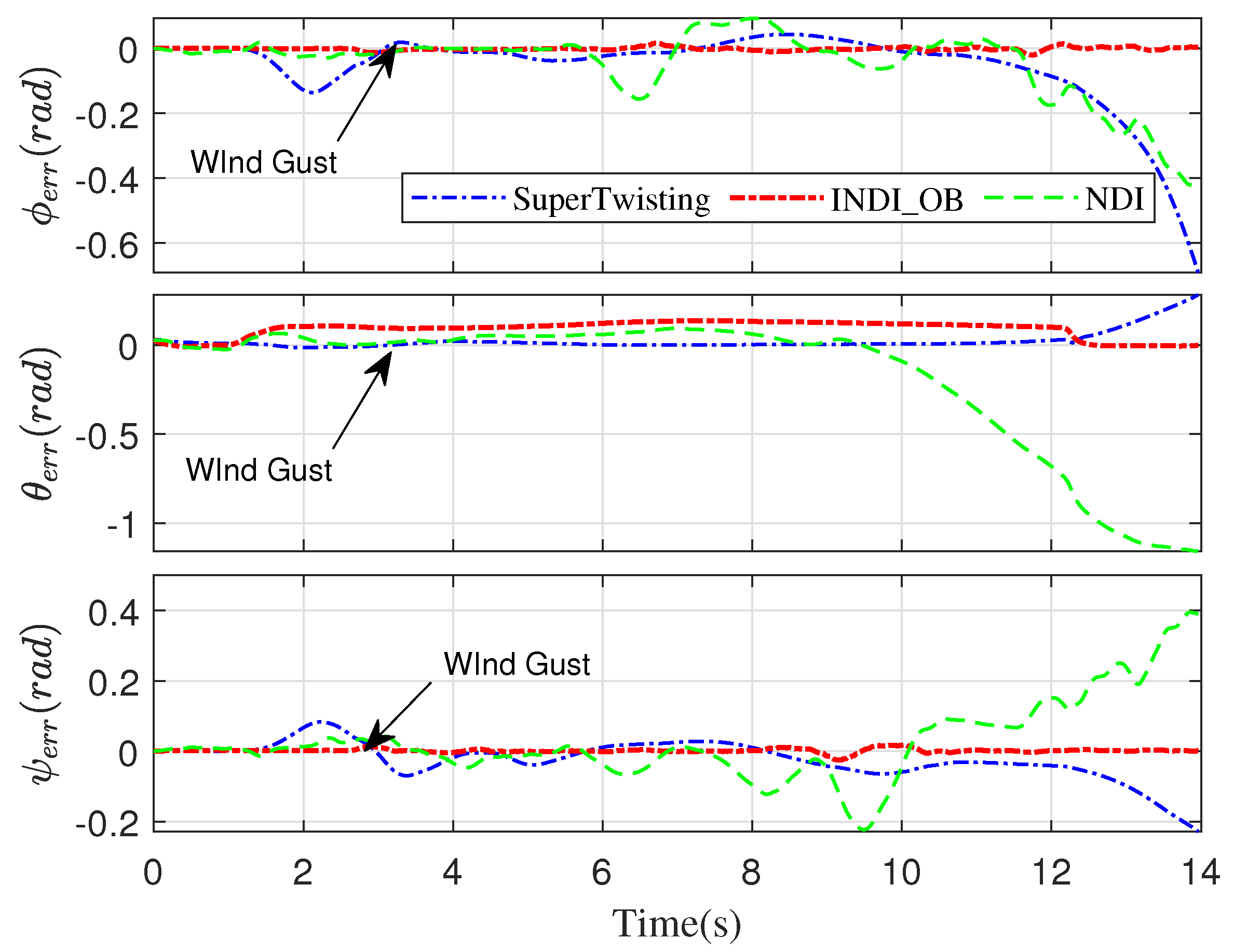
5.1. Numerical Simulations Setup
5.2. Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| INDI | Incremental nonlinear dynamic inversion |
| STW | Super-twisting |
| INFT_OB | Incremental finite time controller with observer |
| NDI | Nonlinear dynamic inversion |
Appendix A. Proof of Proposition 2
References
- Levin, J.M.; Paranjape, A.A.; Nahon, M. Agile maneuvering with a small fixed-wing unmanned aerial vehicle. Robot. Auton. Syst. 2019, 116, 148–161. [Google Scholar] [CrossRef]
- Kaufmann, E.; Loquercio, A.; Ranftl, R.; Müller, M.; Koltun, V.; Scaramuzza, D. Deep drone acrobatics. arXiv 2020, arXiv:2006.05768. [Google Scholar]
- Cao, S.; Wang, X.; Zhang, R.; Yu, H.; Shen, L. From Demonstration to Flight: Realization of Autonomous Aerobatic Maneuvers for Fast, Miniature Fixed-Wing UAVs. IEEE Robot. Autom. Lett. 2022, 7, 5771–5778. [Google Scholar] [CrossRef]
- Stevens, B.L.; Lewis, F.L.; Johnson, E.N. Aircraft Control and Simulation: Dynamics, Controls Design, and Autonomous Systems; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Boyd, S.; Barratt, C. Linear Controller Design: Limits of Performance; Technical Report; Stanford University: Stanford, CA, USA, 1991. [Google Scholar]
- Nguyen, L.T. Simulator Study of Stall/Post-Stall Characteristics of a Fighter Airplane with Relaxed Longitudinal Static Stability; National Aeronautics and Space Administration: Washington, DC, USA, 1979; Volume 12854. [Google Scholar]
- MacKunis, W.; Wilcox, Z.D.; Kaiser, M.K.; Dixon, W.E. Global adaptive output feedback tracking control of an unmanned aerial vehicle. IEEE Trans. Control Syst. Technol. 2010, 18, 1390–1397. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991; Volume 199. [Google Scholar]
- Reiner, J.; Balas, G.J.; Garrard, W.L. Flight control design using robust dynamic inversion and time-scale separation. Automatica 1996, 32, 1493–1504. [Google Scholar] [CrossRef]
- Da Costa, R.; Chu, Q.; Mulder, J. Reentry flight controller design using nonlinear dynamic inversion. J. Spacecr. Rocket. 2003, 40, 64–71. [Google Scholar] [CrossRef]
- Bacon, B.; Ostroff, A. Reconfigurable flight control using nonlinear dynamic inversion with a special accelerometer implementation. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Denver, CO, USA, 14–17 August 2000; p. 4565. [Google Scholar]
- Cao, S.; Wang, X.; Yu, H. Real-time Maneuver Command Generation and Tracking For a Miniature Fixed-Wing Drone with a Ducted-Fan Unit. In Proceedings of the 2021 60th IEEE Conference on Decision and Control (CDC), Austin, TX, USA, 14–17 December 2021; pp. 3591–3596. [Google Scholar]
- Sieberling, S.; Chu, Q.; Mulder, J. Robust flight control using incremental nonlinear dynamic inversion and angular acceleration prediction. J. Guid. Control Dyn. 2010, 33, 1732–1742. [Google Scholar] [CrossRef]
- Smeur, E.J.; Chu, Q.; de Croon, G.C. Adaptive incremental nonlinear dynamic inversion for attitude control of micro air vehicles. J. Guid. Control Dyn. 2015, 38, 450–461. [Google Scholar] [CrossRef]
- Wang, X.; Van Kampen, E.; Chu, Q.; De Breuker, R. Flexible Aircraft Gust Load Alleviation with Incremental Nonlinear Dynamic Inversion. J. Guid. Control Dyn. 2019, 42, 1–18. [Google Scholar] [CrossRef]
- Acquatella, P.; van Ekeren, W.; Chu, Q.P. PI (D) tuning for Flight Control Systems via Incremental Nonlinear Dynamic Inversion. IFAC-PapersOnLine 2017, 50, 8175–8180. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, T.; Yi, Y.; Wang, Q. Adaptive control of output feedback nonlinear systems with unmodeled dynamics and output constraint. J. Frankl. Inst. 2017, 354, 5176–5200. [Google Scholar] [CrossRef]
- Sharafian, A.; Bagheri, V.; Zhang, W. RBF neural network sliding mode consensus of multiagent systems with unknown dynamical model of leader-follower agents. Int. J. Control Autom. Syst. 2018, 16, 749–758. [Google Scholar] [CrossRef]
- Fei, J.; Lu, C. Adaptive Sliding Mode Control of Dynamic Systems Using Double Loop Recurrent Neural Network Structure. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1275–1286. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Shao, S.; Jiang, B. Adaptive Neural Control of Uncertain Nonlinear Systems Using Disturbance Observer. IEEE Trans. Cybern. 2017, 47, 3110–3123. [Google Scholar] [CrossRef]
- Razmi, H.; Afshinfar, S. Neural network-based adaptive sliding mode control design for position and attitude control of a quadrotor UAV. Aerosp. Sci. Technol. 2019, 91, 12–27. [Google Scholar] [CrossRef]
- Patan, K. Two stage neural network modelling for robust model predictive control. ISA Trans. 2018, 72, 56–65. [Google Scholar] [CrossRef]
- Li, X.J.; Yang, G.H. Neural-network-based adaptive decentralized fault-tolerant control for a class of interconnected nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2016, 29, 144–155. [Google Scholar] [CrossRef]
- Shastry, A.K.; Pattanaik, A.; Kothari, M. Neuro-adaptive augmented dynamic inversion controller for quadrotors. IFAC-PapersOnLine 2016, 49, 302–307. [Google Scholar] [CrossRef]
- Li, D.P.; Liu, Y.J.; Tong, S.; Chen, C.P.; Li, D.J. Neural networks-based adaptive control for nonlinear state constrained systems with input delay. IEEE Trans. Cybern. 2019, 49, 1249–1258. [Google Scholar] [CrossRef]
- Khaghani, M.; Skaloud, J. Assessment of VDM-based autonomous navigation of a UAV under operational conditions. Robot. Auton. Syst. 2018, 106, 152–164. [Google Scholar] [CrossRef]
- Hoffman, D.; Rehan, M.; MacKunis, W.; Reyhanoglu, M. Quaternion-based Robust Trajectory Tracking Control of a Quadrotor Hover System. Int. J. Control Autom. Syst. 2018, 16, 2575–2584. [Google Scholar] [CrossRef]
- Sonneveldt, L. Nonlinear F-16 Model Description; Delft University of Technology: Delft, The Netherlands, 2006. [Google Scholar]
- Wang, X.; Han, D.; Yu, C.; Zheng, Z. The geometric structure of unit dual quaternion with application in kinematic control. J. Math. Anal. Appl. 2012, 389, 1352–1364. [Google Scholar] [CrossRef]
- Wang, X.; Van Kampen, E.J.; Chu, Q.P.; Lu, P. Stability Analysis for Incremental Nonlinear Dynamic Inversion Control. In Proceedings of the 2018 AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, USA, 8–12 January 2018; p. 1115. [Google Scholar]
- Krüger, T.; Schnetter, P.; Placzek, R.; Vörsmann, P. Fault-tolerant nonlinear adaptive flight control using sliding mode online learning. Neural Netw. 2012, 32, 267–274. [Google Scholar] [CrossRef] [PubMed]
- Ramírez, J.C.H.; Nahon, M. A gravity-referenced moving frame for vehicle path following applications in 3d. IEEE Robot. Autom. Lett. 2021, 6, 4393–4400. [Google Scholar] [CrossRef]
- Shao, S.; Chen, M.; Zhang, Y. Adaptive discrete-time flight control using disturbance observer and neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3708–3721. [Google Scholar] [CrossRef]
- Bhardwaj, P.; Raab, S.A.; Zhang, J.; Holzapfel, F. Integrated Reference Model for a Tilt-rotor Vertical Take-off and Landing Transition UAV. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; p. 3479. [Google Scholar]
- Sonneveldt, L.; Chu, Q.; Mulder, J. Constrained adaptive backstepping flight control: Application to a nonlinear F-16/MATV model. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006; p. 6413. [Google Scholar]
- Raj, K.; Muthukumar, V.; Singh, S.N.; Lee, K.W. Finite-time sliding mode and super-twisting control of fighter aircraft. Aerosp. Sci. Technol. 2018, 82, 487–498. [Google Scholar] [CrossRef]
- Grauer, J.A.; Morelli, E.A. Generic global aerodynamic model for aircraft. J. Aircr. 2015, 52, 13–20. [Google Scholar] [CrossRef]
| Parameters | Mismatch |
|---|---|
| , , | |
| , , | |
| Mass, Gravity Center | |
| , , , |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, S.; Yu, H. An Adaptive Control Framework for the Autonomous Aerobatic Maneuvers of Fixed-Wing Unmanned Aerial Vehicle. Drones 2022, 6, 316. https://doi.org/10.3390/drones6110316
Cao S, Yu H. An Adaptive Control Framework for the Autonomous Aerobatic Maneuvers of Fixed-Wing Unmanned Aerial Vehicle. Drones. 2022; 6(11):316. https://doi.org/10.3390/drones6110316
Chicago/Turabian StyleCao, Su, and Huangchao Yu. 2022. "An Adaptive Control Framework for the Autonomous Aerobatic Maneuvers of Fixed-Wing Unmanned Aerial Vehicle" Drones 6, no. 11: 316. https://doi.org/10.3390/drones6110316
APA StyleCao, S., & Yu, H. (2022). An Adaptive Control Framework for the Autonomous Aerobatic Maneuvers of Fixed-Wing Unmanned Aerial Vehicle. Drones, 6(11), 316. https://doi.org/10.3390/drones6110316






