Abstract
This paper aims to describe the methodology used in the design and manufacture of a fixed-wing aircraft manufactured using additive techniques together with the implementation of technology based on solar panels. The main objective is increasing the autonomy and range of the UAV’s autonomous missions. Moreover, one of the main targets is to improve the capabilities of the aeronautical industry towards sustainable aircrafts and to acquire better mechanical properties owing to the use of additive technologies and new printing materials. Further, a lower environmental impact could be achieved through the use of renewable energies. Material extrusion (MEX) technology may be able to be used for the manufacture of stronger and lighter parts by using gyroids as the filling of the printed material. The paper proposes the use of minimal surfaces for the reinforcement of the UAV aircraft wings. This type of surface was never used because it is not possible to manufacture it using conventional techniques. The rapid growth of additive technologies led to many expectations for new design methodologies in the aeronautical industry. In this study, mechanical tests were carried out on specimens manufactured with different geometries to address the design and manufacture of a UAV as a demonstrator. In addition, to carry out the manufacture of the prototype, a 3D printer with a movable bench similar to a belt, that allows for the manufacture of parts without limitations in the Z axis, was tested. The parts manufactured with this technique can be structurally improved, and it is possible to avoid manufacturing multiple prints of small parts of the aircraft that will have to be glued later, decreasing the mechanical properties of the UAV. The conceptual design and manufacturing of a solar aircraft, SolarÍO, using additive technologies, is presented. A study of the most innovative 3D printers was carried out that allowed for the manufacture of parts with an infinite Z-axis and, in addition, a filler based on minimal surfaces (gyroids) was applied, which considerably increased the mechanical properties of the printed parts. Finally, it can be stated that in this article, the potential of the additive manufacturing as a new manufacturing process for small aircrafts and for the aeronautical sector in the future when new materials and more efficient additive manufacturing processes are already developed is demonstrated.
1. Introduction
Throughout the last decade, a diverse range of investigations was performed regarding additive manufacturing (AM) in the aerospace sector. AM is the process of creating an object by building it one layer at a time, it is the opposite of conventional subtractive manufacturing. Industry implementation of AM technologies increased continuously in recent years. This is due to the great design freedom and the continuous cost reduction [1,2]. The parts are fabricated directly from CAD files. Recently, AM expanded nearly to all the industrial activities, including aerospace, automotive, medical, pharmaceutical, and civil engineering sectors [3,4,5]. With the emergence of AM came the idea of printable UAVs enabling the production of a wide range of designs and geometries. Currently, this manufacturing technique is being used in aerospace to produce engine and turbine parts, as well as parts for cabin interiors [6]. A timeline of the inventions, development of AM techniques, and first applications towards engineering are shown in Figure 1.
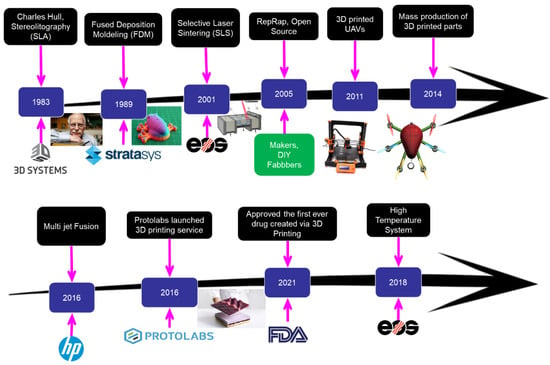
Figure 1.
Timeline invention of different 3D printing technologies.
AM techniques eliminate the need for tooling, then the manufacturing cost per unit for AM UAVs becomes relatively constant, as shown in Figure 2. On the other hand, the cost per unit for AM increases with the complexity, but the rate of increment is lower than the traditional manufacturing. Then, clearly the AM is a very competitive manufacturing process for a reduced number of units to be manufactured when the complexity of the part is high [7].
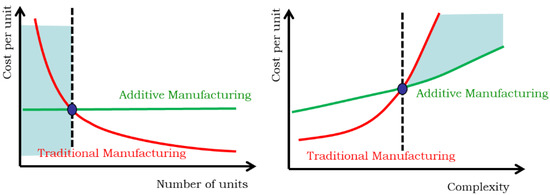
Figure 2.
Cost per unit vs quantity and complexity for traditional and additive manufacturing techniques.
This paper is structured as follows; a comprehensive review of literature is performed to identify advancements of AM for UAV manufacturing and the main advantages over conventional manufacturing methods. A proposal of materials and methods is described in Section 3. The minimal surfaces are used as an alternative to the wings infill and a mechanical study is performed in order to characterize its behavior. In Section 4, the design of the 3D printed UAV is proposed, and finally in Section 5, the main conclusions and future work are described. The material extrusion (MEX) manufacturing process is used in this work due to its ability to incorporate a wide range of materials. MEX is considered to be the most applicable AM technology. Table 1 lists the acronyms and abbreviations used in this paper.

Table 1.
Abbreviations/acronyms used.
2. Related Works
Although there are some size restrictions in AM due to its dependence on the size of 3D printers, printable parts are increasing as the size of print bays and the range of 3D printable material increases. In the UAV production segment, Aurora Flight Sciences [8], which develops and manufactures advanced unmanned systems and aerospace vehicles, were able to produce and fly a 62-inch wingspan aircraft whose components in the wings were manufactured entirely by AM. In addition, a project called Wing Design Methodology Validation—known as WINDY—which started in 2016, features an Airbus UK government partnership. The project is carrying out research into innovative approaches for the design of wings and the manufacturing processes used to produce them, as well as undertaking validation testing to demonstrate the effectiveness of a future application of load control on aircrafts to improve efficiency in flight [8]. The AM was also used for rotary wing configuration of the unmanned aerial vehicles (UAVs) [9,10]. In this case of study, solar-powered planes that take advantage of solar radiation to partially or completely power aircraft systems are involved. Solar panels can generate energy that recharges the battery during the day enough to keep the aircraft in the air throughout the night (perpetual flight) [11]. This continuous discharge–recharge cycle enables multi-day solar-powered flight and, from an energy perspective, leads to perpetual flight capability. Additionally, robotic technologies can provide the aircraft with an automatic and precise flight in terms of control and orientation, which means the flight time of the aircraft can be highly increased [12].
On the other hand, the development of new additive manufacturing technologies opens the door to new manufacturing processes previously unimaginable. Usually, aircraft wings are made of ribs that are placed in parallel, oriented in the direction of flight, and joined by stringers that are placed perpendicular to them. This method of arranging the internal structural elements of the aircraft wing was standard almost since the beginning of the aerospace sector; however, there are better techniques that would reduce the weight of the aircraft structure without compromising its structural strength [13]. This paper presents a proposal based on material extrusion (MEX) technology for manufacturing a small, unmanned aerial vehicle (UAV) with the aim of achieving perpetual solar flight [14,15]. Solar UAVs can use either solar energy exclusively as a power source or they can also be aided by a chemical battery [16]. Most solar UAVs require the use of a battery as a backup power source in order to fly. UAVs also can be classified according to the mission they are developed for:
- High flight/low flight: Solar UAVs can be designed for either low altitudes and long distances (LALE) or high altitudes and long distances (HALE). Since the density of the air is different depending on the height, at high altitudes’ energy consumption will be higher since the wings will generate less lift. HALE UAVs are much larger in size since they require a larger wing area and a greater number of solar panels; on the other hand, HALE UAVs are capable of storing large amounts of energy collected during the day, which can later be used to fly at night.
- Perpetual flight capacity: Depending on the energy consumption, the size of the battery, and the size of the solar panels, an aircraft may be able to perform perpetual flight. Aircrafts that do not have perpetual flight capabilities tend to be smaller, less complex, cheaper, and structurally more robust [17].
The quasi-static energy models used in solar UAVs, for example, those that can be seen in [6], usually ignore the kinetic energy of the actual aircraft and only model the electric energy of the batteries (); further, the height has a function of potential energy (). The two resulting equations of state are integrated to evaluate the energy fluxes and energy safety margins that a solar-powered UAV provides with respect to perpetual flight. These two equations combined model the evolution of the energy on the battery, which changes depending on the flight time because of the solar power that is received by the solar cells with the evolution of the flight altitude. The combined equation of state can be written as [18,19]:
where is the total energy of the battery, represents the energy losses during the charging process, describes the power delivered by the battery, is the total power delivered by the solar cells, represents the power consumed by the UAV systems, is the height, denotes the total weight of the aircraft, is the gravitational acceleration, the propeller efficiency, denotes the power consumed by the engine with a specific propeller, and finally, the represents the minimum power required to have a leveled flight.
The simulation of a UAV (which was performed taking into account that the battery mass is equal to 2.9 kg), in which the input power, the output power, and the energy in the battery are shown during a flight of approximately 2 days, is represented in Figure 3.
In this paper, a design of a solar UAV is proposed with the use of minimal surfaces in the manufacturing of the wings to improve its mechanical behavior and minimize its weight as much as possible [20].

Figure 3.
Energy balance of solar UAV.
3. Materials and Methods
3.1. Minimal Surfaces
Mathematically, a minimal surface is a surface that locally minimizes its area, and hence has zero mean curvature. Minimal surfaces are those considered to contain minimum potential energy and are the most stable [21]. A physical model to see the formation of a minimal surface can be made by dipping a wire frame into a soap solution, forming a soap film, which is a helicoid minimal surface, the boundary of which is the wire frame, as can be seen in Figure 4.

Figure 4.
Soap films and minimal surfaces.
The gyroid is a triply periodic minimal surface (TPMS), which is one of the most studied surfaces, and is used to create structures showing a characteristic robust mechanical performance. This minimal surface was first described by a NASA scientist. This surface seems to be the only known example of an intersection-free infinite periodic minimal surface which contains neither straight lines nor plane lines of curvature. The geometry of the gyroid surface unit cell and lattice is shown in Figure 5. Trigonometrically, the gyroid surface can be approximated by the equation: sin(x)cos(y) + sin(y)cos(z) + sin(z)cos(x) = 0. It was demonstrated that with sandwich panel structures with minimal surfaces, particularly gyroid, cores considerably lower material consumption while simultaneously maintaining mechanical properties [22]. Gyroids make MEX parts stronger and lighter.
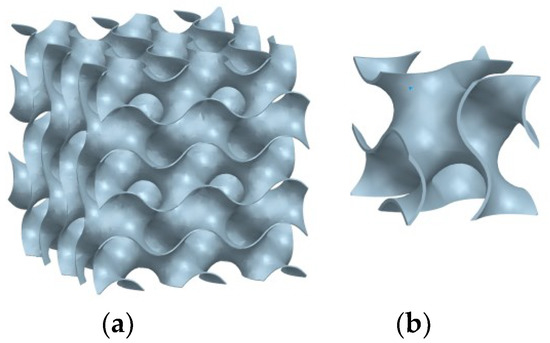
Figure 5.
Gyroid surface. (a) Repeated unit cell. (b) Unit cell.
Due to the complexity of this structure, it was designed by computational means, but was not able to be manufactured until the arrival of additive manufacturing. This method allows for accurate replication of the most sophisticated bio-inspired surfaces and structures, allowing them to reach their best mechanical properties. Some studies were performed to understand the mechanical properties of gyroid structures under bending forces, varying some of their principal parameters to analyze how their mechanical behavior is modified. One of the most influential parameters is the gyroid thickness, which results in an obvious stiffness increase with a deformation decrease due to a decrease in the porosity of the structure [23]. Further, the von Mises and shear stresses decrease when the gyroid thickness increases. Although a greater thickness usually implies better mechanical properties, the weight of the structure is increased. Therefore, when considering applications where light-weight structures are desired, a balance between mechanical behavior improvement and the weight should be found.
Furthermore, other studies were performed to analyze the behavior of gyroid cells under compressive loads, wherein the infill density was varied to study how this parameter affects the mechanical properties of the structure. Independently of the infill density, gyroid structures deform uniformly within the elastic region, but higher relative densities lead to a more uniform deformation. In addition, when the infill density is increased, the performance of structures under compressive forces is obviously improved. The advantages of using gyroid-like structures include their high stiffness and low maximum von Mises stress compared to other cell types, making them particularly suitable for use in lightweight components. Gyroid structures have two regions of localized deformation per unit cell, while other TPMS structures possess only one region per unit cell. In addition, unlike other TPMS lattices, gyroid-like structures possess axisymmetric stiffness, meaning that these structures will be able to withstand forces acting on the structure in many directions, and are therefore very suitable for applications where there are uncertainties about the magnitude and direction of the forces acting on the body.
3.2. Test Specimens Design and Manufacturing
To investigate the orthotropic properties of the extrusion-based AM, various mechanical tests, such as flexural and compressive tests, were conducted. Polylactic acid (PLA) was chosen to be used as the AM material; its characteristics are shown in Table 2.

Table 2.
Specifications of PLA material [24].
A gyroid lattice was generated using Matlab (The Math Works, R2020b) and imported separately into Ultimaker Cura 4.8.0, the program used to set up the test sample to be 3D printed, where Prusa i3 Mk3s (Prusa Research, Prague, Czech Republic) (Figure 6) was selected as the 3D printer. The test samples were set to contain a gyroid infill, and the density (λinfill) was varied to study how this affects the mechanical behavior of the structure. Hence λinfill depends on the case study. As the cuboid and the plates were imported as two separate models, the cuboid infill density was set to the specific percentage being studied, whilst the plates always had an infill density of 100%. In addition, the shell setting was used to modify the model wall thickness, by treating both models separately. The cuboid model was set to have no wall count for both the bottom and top layers. On the other hand, the plate model was set to have a wall count of 1 with a wall thickness of 0.8 mm. The printing settings used with the Prusa i3 Mk3 are shown in Table 3.

Figure 6.
Specimens set to be printed (a) and printed (b).

Table 3.
Print settings.
Another variable that was studied along with the infill density was the printing filament angle. To study this, the Blackbelt 3D printer (Blackbelt 3D B.V., Belfeld, The Netherlands) (Figure 7) was used, as it allows for printing under various nozzle angles. This is a continuous turning belt base printer that is able to produce series by printing individual models continuously or by producing very long parts. As this printer has the characteristic of infinite Z print, BlackBelt Cura 3.6.2 was used to slice the samples for this printer. This software is a version of Cura specially programmed for the Blackbelt printer. The main difference in the setup process is the explicit specification of the printing angle.

Figure 7.
The Blackbelt 3D printer and the specimens printed.
A parametric study was performed by changing different parameters in the setup to analyze the mechanical behavior of the structure with a gyroid pattern infill. The parameters chosen to study were the infill density (λinfill), the printing angle (θp), and the specimen thickness (th). Carbon-fiber-reinforced plastic (CFRP) inserts were considered in some cases. Carbon fiber is used in this study due to its excellent specific strength compared to that of the other continuous fibers. Mechanical characterization of the coupons was performed to obtain the mechanical properties required by the simulation [7,25]. The infill density and printing angle were modified by changing the printing settings for the two different 3D printers. The sample geometry had a length (l) of 140 mm, a width (b) of 30 mm, and a height (or thickness) (th) of 15 mm. These dimensions were kept constant along the whole experiment to ensure fair tests. Tests were performed under ISO 178:2019 standards [26] using an Instron 5967 (Illinois Tool Works Inc., Glenview, IL, USA) 30 kN load cell with a loading rate of 0.5 mm/s. The first test was performed by adjusting the printing settings in Ultimaker Cura with a gyroid infill pattern using an infill density of λinfill = 9.5%. Depending on the orientation the specimens had on the build plate, the gyroid was printed in one direction or another; therefore this was studied by printing 3 specimens in each direction, called X and Y, as shown in Figure 8. The second test involved the same principles as the first one, but this time with λinfill = 13%. Additionally at this stage, CFRP rods with a diameter of 1.5 mm were inserted into the structure through four different points of the specimen to investigate how the reinforcement of the external elements would affect the results. The CFRP rods were connected to the gyroid structure with epoxy glue and inserted through the longitudinal wholes generated by the gyroid infill pattern. The resulting test samples for the second test can be seen in Figure 9. Four specimens were printed in each direction, X and Y, and were tested with and without CFRP rods, with a total of sixteen specimens printed in this case.

Figure 8.
Specimen with gyroid in X direction (a). Specimen with gyroid in Y direction (b).

Figure 9.
3D printed specimens with gyroid in both directions - X direction (a) and Y direction (b) and inserted CFRP rods with a diameter of 1.5 mm and length of 150 mm. Dimensions (mm) of the CFRP rods locations are shown.
To perform the third test, the procedure was exactly the same as that for the second test. However, in this case, λinfill = 15%. Four specimens were printed in each direction, X and Y, and were tested with and without CFRP rods, with a total of 16 specimens therefore printed. The fourth test studied the variation in the printing angle, θp. In this case, the software BlackBelt Cura was used to specify the printing settings. Throughout the test, the parameters of all the specimens were kept constant, except for the printing angle, which was studied for θp = 15°, 25°, and 45°, as shown in Figure 10. The infill density of these specimens was 15%. The addition of CFRP rods supposed an increase in mass of 10.8%, high enough to be considered as a design factor.

Figure 10.
Specimens with different printing angles (θp): 15°, 25°, and 45°.
3.3. Flexural Test Analysis
A three-point bending flexural test was performed to simulate the main forces present during flight on an aircraft wing. The test method involved the use of a specified test fixture on a universal testing machine; the sample was placed on two supporting pins with a span distance (L) of separation between them (ISO 178:2019) (Figure 11). Then, a load descended that applied a desired force (F), deforming the specimen until a deflection settled. A span distance between both supports of L= 100 mm was set on the machine. To make it fair, all the tests were performed under the same conditions. In addition, 4 samples were examined for each configuration of test probe. These data will be used throughout this section to calculate the flexural stress and strain for each of the cases, allowing a comparison of these experimental results with those obtained by FE methods in the future.
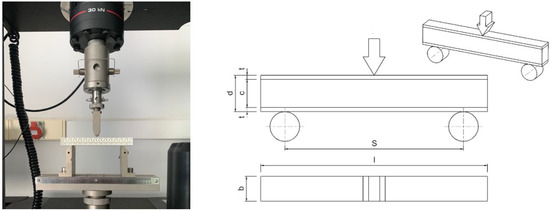
Figure 11.
Experiment setup with specimen in position, ready to be tested.
The total deformation includes the bending component δb and shear component δs., the deformation, δ, can be obtained as:
where: p is the applied load, l is the total length of the beam, is the equivalent flexural rigidity, is the equivalent shear rigidity, and B1 and B2 are constants of proportionality. The equivalent flexural and shear rigidity can be calculated as:
where is the Young´s modulus of the core, Ef is the Young´s modulus of the face sheets, is the shear modulus of the core [22].
The first test performed was for the samples with λinfill = 9.5% and θp = 0°. Average values were calculated from the results obtained for both directions of the gyroid infill, which are shown in Figure 12.
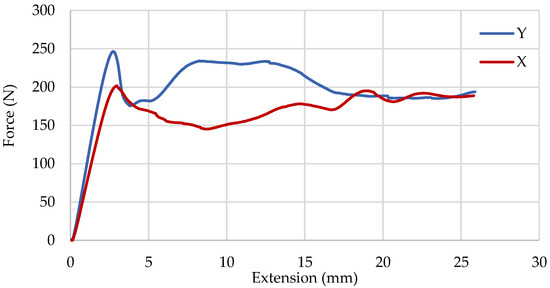
Figure 12.
Evolution of the bend extension of the specimen printed with an angle of 0°and infill density of 9.5% with an applied load.
Those specimens printed in the X direction reached their yield limit at a greater force, which means these specimens had a greater yield strength. Further, the deformation of the specimen at the elastic limit was approximately the same for both cases; it occurred at about 3.8 mm. From that point onwards, the specimens continued deforming without reaching the breaking point. This occurred due to the 0° printing direction, as the strength contribution from the filaments did not depend on the quality of the joint between the filaments. This printing angle represented the deposition of filaments along the principal stress lines which, as will be seen in this section, improved the anisotropic limitation of the conventional layer-based MEX.
In addition, flexural stress and strain were calculated, confirming their behavior. Further, the maximum flexural stress value (σf,max), which is the point where the specimen bears the maximum stress, and the maximum flexural strain value (ϵf,max), which is the maximum strain the specimen can bear before breaking, were calculated and are shown in Table 4. Therefore, these results suggest that this printing method could be quite appropriate for aircraft wings developed from additive manufacturing.

Table 4.
Results for λinfill = 9.5%.
In order to extrapolate the results obtained experimentally in the case of a real UAV wing manufactured by an additive manufacturing processes, the test samples had to be printed with an angle of θp = 90°. Therefore, the second test was performed over four samples printed with an infill density of 13% and a printing direction of 90°, tested for the gyroid in the X and Y direction. The mean and standard deviation of the results were plotted in the graph shown in Figure 13.
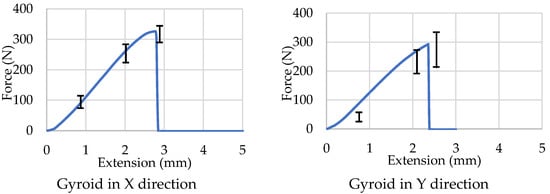
Figure 13.
Evolution of the bend extension of the specimen printed with an angle of 90° and infill density of 13% with an applied load.
It can be seen that the mechanical behavior of the specimens with the gyroid pattern printed in both directions was quite similar to that of the specimens that exhibited elastic behavior, until they suddenly broke with no plastic deformation. The average maximum load was approximately the same for X and Y cases, 261.3 N and 295.2 N, respectively. The samples exhibited high brittleness behavior, which is not the behavior desired for an aircraft wing, as wings should be flexible and show some elastic behavior—enough to allow for some wing buckling. Therefore, four CRFP rods were inserted per sample, keeping all parameters the same, to test their effect on the structure. The evolution of the bend extension of the specimen reinforced with CFRP rods and printed with an angle of 90° and infill density of 13% with an applied load is presented in Figure 14 and Table 5.
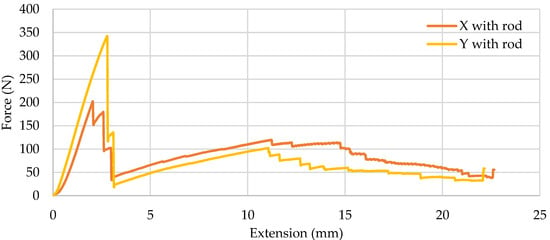
Figure 14.
Specimen reinforced with CFRP, angle of 90°, and infill density of 13%.

Table 5.
Results for λinfill = 13%.
The results show that there were differences on the maximum flexural stress, but these were not significant, and that the maximum flexural strain increased when the rods were introduced. This suggests that the addition of these rods slightly improved the mechanical behavior of the structure; however, this small improvement did not compensate for the addition of extra weight to the structure, so the use of rods inserted in this way should be discarded.
In addition, as four samples were tested for each case, the standard deviation of the maximum flexural stress was calculated, as shown in Table 4. Except for the case of the Y gyroid direction without rods, these values show that the variability of the data set is relatively low, as the standard deviation is relatively low. This means that the results obtained are quite precise and do not vary much from the mean value, making this quite representative. For the case of the Y gyroid direction without rods, more tests could be performed to obtained more reliable results.
The same test as before was performed for an infill density of 15% instead of 13%, without implementing the CRFP rods. This test allowed for a comparison of the results obtained for different infill densities. The mean and standard deviation of the results obtained for the fourth test were plotted in the graph shown in Figure 15. As seen in the results, the mechanical behavior of the specimens was very similar to that shown previously in the second test with an infill density of 13%, therefore reaching the same conclusions. Surprisingly, comparing both results, the average yield stress of the structure decreased as the infill density increased, but the average maximum strain increased. Nevertheless, again, this high brittleness behavior shown by the specimens printed in these conditions is not the desired behavior for an aircraft wing.
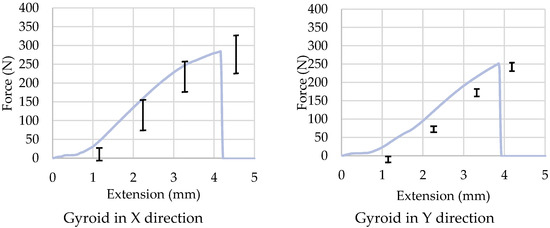
Figure 15.
Evolution of the bend extension of the specimen printed with an angle of 90° and infill density of 15% with an applied load, depending on the gyroid direction.
A parametric study was performed that varied the printing angles, leaving three cases for study, for angles of 15°, 25°, and 45°, and the average results for each printing angle were plotted, as shown in Figure 16. For the specimens printed with an angle of 15°, the results show a high yield strength. Nevertheless, the specimen did not break as the gyroid structure in the inside, together with the angle adopted by the PLA filaments in the printed piece, absorbed the load applied by deforming themselves, which resulted in an increasing in the extension.
When the printing angle of the specimens was increased to 25°, the average yield strength increased. However, in this case, from this point, the specimen started to deform plastically until it reached the breaking point around an extension of 25 mm, showing a high ductility, as it was able to absorb a lot of energy in the plastic region.
The last bending test performed was with samples of specimens printed with an angle of 45°. From the results, it can be said that there was an increase in the yield strength with respect to the previous cases. This means that an increase in the printing angle led to an increase in the yield strength of the structure. The breaking point was rapidly reached, at an extension of approximately 10 mm.
From Figure 16, it can be observed that initially the three cases showed very similar behavior; however, the greater the printing angle, the greater the load the structure was able to withstand before it started to deform and show plastic behavior; therefore, after this, it did not return to its original shape. This means that the maximum yield strength increased with increases in the printing angle. As an average, for the samples printed at an angle of 15°, the elastic limit was reached at approximately a force of 275 N and an extension of 3.7 mm, whilst for those printed at an angle of 25°, the elastic point appeared at 282 N and 3.9 mm, and for the samples printed at 45°, these values were 304 N and 3.8 mm.
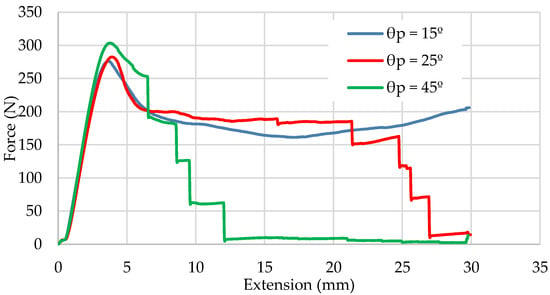
Figure 16.
Evolution of the bend deformation of the specimen, printed at different degrees, with an applied load.
On the other hand, analyzing Figure 16, it can be seen how those samples printed at lower angles were able to withstand forces for a longer period before breaking by deforming themselves, or even without breaking, as was the case for the samples printed at 15°. In these cases, the structure was able to absorb greater quantities of energy in the elastic region. This suggests that for greater printing angles, the breaking point of the structure will be reached earlier, and therefore will deform less before breaking.
The results in Table 5 show a clear trend: σf,max increased when θp increased, whilst ϵf,max decreased when θp increased. The differences in ϵf,max with variations in θp were much more significant than those for σf,max. This shows that the optimal printing angle is the one which approximates 0°, because the deposition of filaments along the principal stress lines improves the anisotropic limitation of the conventional layer-based MEX, but this may require more forming material. Therefore, the smaller the angle, the greater the deformation of the structure before it collapsed, withstanding very similar maximum loads in each case.
Moreover, the calculation of the standard deviation for each case shown in Table 6 suggests results are relatively precise and the actual mean could be used as a representative value.

Table 6.
Results for variations in θp.
After the analysis performed from the results obtained for the bending tests, some conclusions can be made regarding the optimization of the mechanical properties of a wing with a gyroid infill. Firstly, it is preferable to print the gyroid pattern in the Y direction when a conventional printer is used. When considering a Z-infinite printer applied to a wing structure, the best mechanical properties are obtained with smaller printing angles. Finally, the infill density should be as high as possible, and the weight of the structure should not be compromised, as with greater infill densities, the best mechanical properties, applicable to wings, are obtained.
3.4. Compression Test Analysis
Compression tests are used to determine the behavior of a material under applied crushing loads and are typically conducted by applying compressive pressure to a test specimen (usually of either a cuboid or cylindrical geometry) using plates or specialized fixtures on a universal testing machine. To proceed with the test, the sample is placed in between the two plates that distribute the applied load across the entire surface area of two opposite faces of the test sample, and then the plates are pushed together by a universal test machine, causing the sample to flatten.
The purpose of performing this test is to understand the mechanical behavior of the sample under compressive forces by measuring fundamental variables, such as strain, stress, and deformation. An analysis of the results obtained for these parameters, together with the values of a specific material, will allow for determining the suitability of the material test for specific applications. These materials tested often need to have a great load-bearing capacity under compressive forces, for which it is crucial their integrity and ability to maintain their shape without plastically deforming are sustained. There are different types of compression tests, including the top load test, which was performed in this case. In the following subsections, the experiment setup, as well as the results obtained, will be further explained. To evaluate the mechanical compressive behavior of the specimens, the tests were performed, as stated before, with a universal material electromechanical testing machine, at standard conditions (atmospheric pressure of 1 atm and temperature of 20 °C). The machine was set with the compression plates available in the laboratory, which were specific to the testing machine being used, and was mounted as shown in Figure 17. All the tests were performed under the same conditions, with a maximum compression of 20 mm. In addition, to ensure a reliable test, four samples were tested for each configuration of the test probe.
In this case, the specimens designed for the experiment used the same principles as those used to design the specimens for the bending test. First, a cuboid was designed, and then two plates were placed on the top and bottom of the structure, and a gyroid infill was developed on the inside of the structure. However, in this case, the lengths of the specimens were different, leaving the following dimensions: l= 70 mm, b= 30 mm, and d= 15 mm. After performing the compression tests, the universal material electromechanical testing machine stored all the relevant data measured from the tests in raw Excel documents, which were used to plot the specific graphs for each case study. Then, these plotted graphs were used to analyze the results obtained.

Figure 17.
Compression test setup with specimen between plates.
The first test performed was for those samples where the variations in the infill density were studied under compressive forces for λinfill = 9.5%, λinfill = 13%, and λinfill = 15%. It can be seen that the specimens underwent a deformation with a similar pattern for different infill densities, reaching a small peak at the start where the elastic region ended. Then, the specimens started to deform plastically, reaching a point where the infill gyroid structure was fully collapsed at about 9 mm of deformation, and the load applied tended to infinity with nearly no deformation. However, this last part was cut from the graph, as it is not valuable to the purpose of the research; the plot was kept between the range of values that could be reached during a real situation [27].
Comparing the average results obtained for each infill density (Figure 18), surprisingly, it can be seen that the specimens with the highest yield strength were those with λinfill = 13%, whilst those specimens with λinfill = 9.5% were the least strong. This graph shows that the specimens with λinfill = 13% had the highest maximum compressive stress, but those specimens with λinfill = 15% had the highest strain before the structure showed plastic deformation.
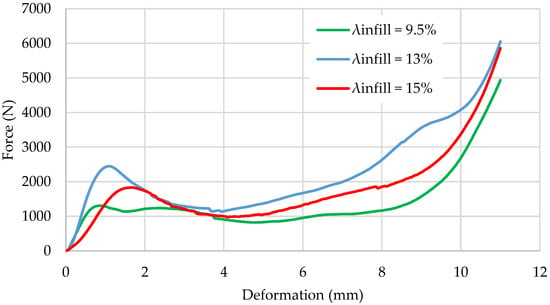
Figure 18.
Comparison of the evolution of the displacement of the specimen with a force applied for different infill densities.
As was demonstrated, the infill density plays an important role in the mechanical behavior of the structure under compressive forces, as with an increase in the infill density, the structure becomes stronger and stiffer, but it will increase its weight considerably. Therefore, as this will be applied to the case of an aircraft wing where weight must be minimized, a commitment between the strength required under compressive forces and the weight of the structure should be obtained.
Next, how the thickness of the structure affects its compressive behavior was studied. For this, the test was carried out using a specimen of the following dimensions: l = 15 mm, b = 20 mm and h = 25 mm. The specimens used in this case were manufactured with a Blackbelt 3D printer and were therefore printed with the filaments placed in a non-horizontal plane. This means that this test also enabled us to study how the printing angle affects the mechanical behavior of the structure. For each thickness, four samples were tested, and average values were calculated, as shown in Figure 19. The deformation was 12 mm for each coupon.
The specimens underwent a deformation with a similar pattern for different thicknesses, reaching a small peak at the start where the elastic region ended. Then, the specimens started to deform plastically, reaching a point where the infill gyroid structure was fully collapsed and the load applied tended to infinity with nearly no deformation. For the case of h = 25 mm, after a deformation of nearly 15 mm, the structure did not reach this irreversible point, and it was observed during the test that the structure partially recovered its shape once the load was removed.
Analyzing Figure 19, it can be observed where the elastic limit occurred in each case. For the specimens with h = 15 mm, this point occurred at a deformation of about e = 0.9 mm and with a force applied of F = 890 N. For the case of h = 20 mm, the elastic limit was reached around e = 0.8 mm and F = 720 N. For the case of h = 25 mm, the elastic limit was reached around e = 0.75 mm and F = 530 N. Interestingly, comparing in Figure 19 the average results obtained for each thickness, it can be seen that the initial deformation slope was practically identical; however, the yield point peak was reached at a lower displacement and a lower force applied for the thicker specimens. This means that, when the thickness of the structure is increased, the structure will start to deform plastically at lower loads and with a smaller deformation. Even though from this point onwards the structure deforms plastically, it will still be able to return partially to its original shape and size.
Applying this to the case of an aircraft wing, these results suggest that the thickest parts of the wings will deform more easily, i.e., they will deform with a lower compressive force applied, but will be able to partially recover their shape once these forces are removed. Additionally, the thinner parts of the wing will be able to withstand greater compressive forces, deforming elastically in the process.
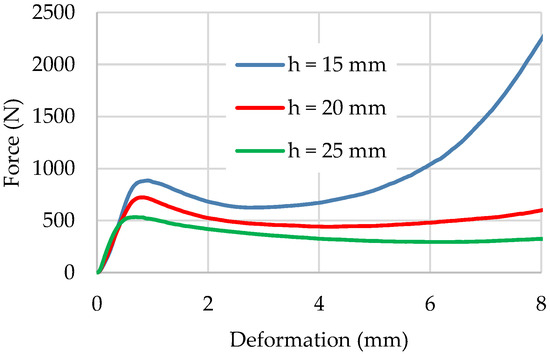
Figure 19.
Comparison of the evolution of the displacement of the specimen with a force applied for different thicknesses.
Furthermore, the last factor that was analyzed under compressive forces was the election of the additive manufacturing system. By comparing the results obtained for specimens with the same thickness (h = 15 mm) in Figure 18 and Figure 19 it can be clearly seen that specimens printed with a conventional printer have a greater deformation before the yield point, which is reached with the application of a greater load. Therefore, these structures seem to be stronger under compressive forces. In addition, structures printed with the conventional 3D printer collapse entirely after a greater deformation. This means that, generally, it is preferable to manufacture structures with a conventional 3D printer, rather than with an infinite Z printer, which places filaments on a certain angle, as those structures should be able to withstand great compressive forces, as was demonstrated.
4. Results
The design proposal aims to develop a solar fixed-wing aircraft manufactured using additive techniques. It seeks to improve the sustainability of small UAVs. The main solar parameters used in this work are shown in the table (Table 7).

Table 7.
SolarÍO main solar parameters [14].
The wings, with a wingspan of 3,096 mm, will be subdivided into two half wings so that they come together to facilitate the transport and assembly of the internal components of the wing. The main parameters of the plane proposal are shown in Table 8. The design of the SolarÍO UAV is shown in Figure 20 and Figure 21.
For the initial design of the SolarÍO, some points were taken into account in order to establish the best model for the mission. Initially, a design with a huge fuselage was proposed, nevertheless, although it is true that a big cavity could make the task of packing all the components inside the aircraft in a simple way easier, this would lead the design to one with more weight, creating the necessity of having to further reinforce the wings, leading to even more weight. Moreover, a bigger fuselage will be less aerodynamic, generating more drag. A glider with a NACA 4412 airfoil design with a V-tail in order to reduce parasitic drag was the one chosen, not only because its reduced weight will make it easier to deal with the structural weight hold by the wings, but also because it will reduce power needed to keep the aircraft in flight.
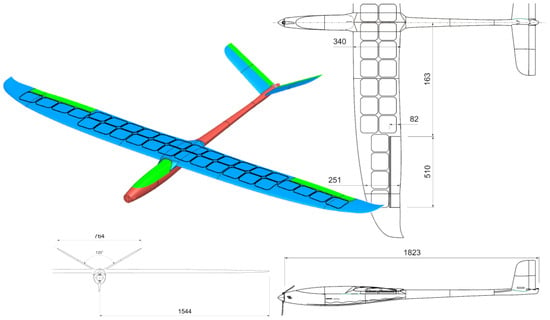
Figure 20.
UAV solar plane, SolarÍO (1/2).
The wings will be reinforced by a circular carbon fiber rod that runs along the span of the wing, providing greater structural strength to the aircraft. In this way, bending of the wings, which could result in damage to the solar panels on the wing surface, will be avoided as much as possible. Regarding the tail, a V design was chosen. As can be seen in Figure 20, the design closely resembles a glider plane. These types of non-powered aircraft generate very little drag since they must be able to glide, maximizing the flight time and, consequently, the flight distance.
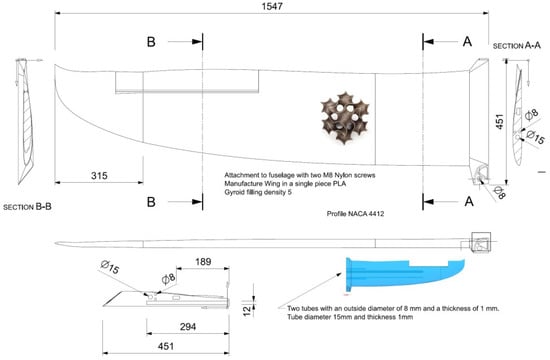
Figure 21.
UAV solar plane, SolarÍO (2/2).

Table 8.
SolarÍO main specifications.
Table 8.
SolarÍO main specifications.
| Parameter | Value |
|---|---|
| Wingspan (m) | 3.096 |
| Chord (m) | 0.305 |
| Total mass (kg) | 3 |
| Battery weight (kg) | 0.415 |
| Flight speed (m·s−1) | 8.6 (cruise) |
The conclusion drawn by the study performed on the wings of the SolarÍO was that the filling of the printed pieces with a minimal surface was the most optimal. Specifically, the gyroid surfaces were selected as fillers for both the wings of the aircraft and for certain parts of the fuselage. This surface maximizes the ratio of mechanical strength to surface (and, therefore, to weight). As already indicated above, its use is very limited due to the technical difficulty of its manufacture. With the introduction of additive manufacturing, the great potential of these surfaces can be appreciated for all types of parts, especially in the metalworking, aerospace, and automotive sectors [28,29].
Although it is possible to model the gyroid structure inside the wing with CAD/CAM/CAE software, the finite element study of the entire wing is not possible without simplifying its geometry. An attempt was made to carry out the study in smaller pieces, such as test tubes, but the calculation time and the number of nodes necessary to carry out a complete study is not feasible. A mechanical model was adjusted that simulates the behavior of parts manufactured with gyroid infill structures. To obtain this model, the results presented in previous sections on the study of specimens with different thicknesses were used. The material model for mechanical simulation was incorporated into finite element mechanical simulation software (Siemens NX v1988). The NACA 4412 airfoil was chosen since its drag and lift coefficients are relatively low.
The wings are reinforced with two tubular rods with an external diameter of 8 mm and a thickness of 1 mm. The other rod is a tube with a diameter of 15 mm and a thickness of 1 mm. In both cases they are made of high modulus carbon fiber whose mechanical characteristics are described in [14]. The numerical simulation of the mechanical behavior is shown in Figure 22. The finite element analysis (FEA) model has five meshes, one tetrahedral (four nodes) of size 15 mm and four one-dimensional meshes that model each of the tubes that reinforce the wing. The tetrahedron mesh is formed by a total of 135,381 nodes and 81,426 elements. The results do not change significantly with lower element size. It is considered that the wing works with a fixation in its central end and that it has a uniformly distributed load on the wing surface of 5 kg in each wing. This load is considered to be much higher compared to the one that will withdraw the wing under normal conditions. It is calculated with a safety index of 2.5, considering that the most critical moment of the flight is the impact with the ground at the time of landing.
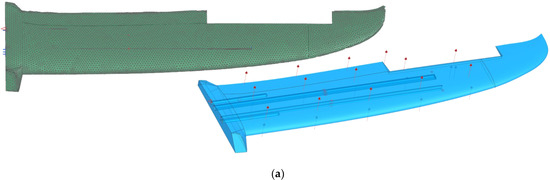
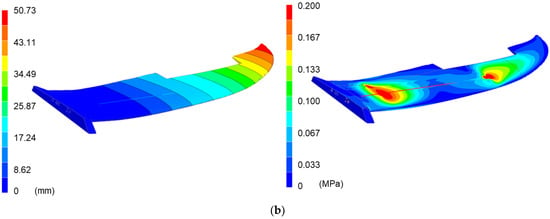
Figure 22.
Wing finite element mesh and applied loads (a). Wing displacement and von Mises stress; mm and MPa (b).
Nowadays, UAV industries moved towards composite materials. As demonstrated in this section, it is possible to use additive manufacturing in the UAV industry. Thermoplastics, such as PLA, acrylonitrile butadiene styrene (ABS), and nylon are the most commonly used materials in the production of 3D printed UAVs. However, to date, AM cannot completely replace traditional composite materials. These materials combine numerous advantages (high strength, low weight, easy processing, etc.) for most of the parts. Composite materials have significant advantages over AM, however, thanks to the evolution of forming processes and the excellent properties of AM to optimize the component geometry, it is foreseeable that these two technologies could converge in the future. The contributions made by the company Markforged (Watertown, MA, USA) in the manufacture of long fiber carbon components with a thermoplastic matrix should be highlighted [25,30]. Extrusion-based techniques were modified to enable the extrusion of continuous fiber-reinforced thermoplastics. The wing design and manufacturing in this work have an excellent mechanical behavior in terms of the maximum stress levels for both flexural and compression tests. This primary structure was reinforced with two tubular rods with an external diameter of 8 mm and a thickness of 1 mm and a tube with diameter of 15 mm and a thickness of 1 mm. In both cases they are made of high modulus carbon fiber. The manufacture of this primary structure only with PLA and MEX technology is not possible at this moment due to the limitation in flexural stress of the PLA.
4.1. Solar Equipment
Regarding solar equipment, it should be noted that this is a very expensive part of the UAV. However, these components ensure that perpetual flight can be carried out. It is necessary to buy high-performance equipment, such as solar panels with high efficiency values that allow for achieving a sufficient voltage and intensity to save weight and energy. In this respect, the choice of solar panels is limited, especially by the dimensions they can have (above all, it is limited by the wing chord of the SolarÍO). Therefore, the solar panels must measure a maximum of 0.4 m high. The 3-cell Maxeon model [8] was chosen, whose characteristics are seen in Figure 23.
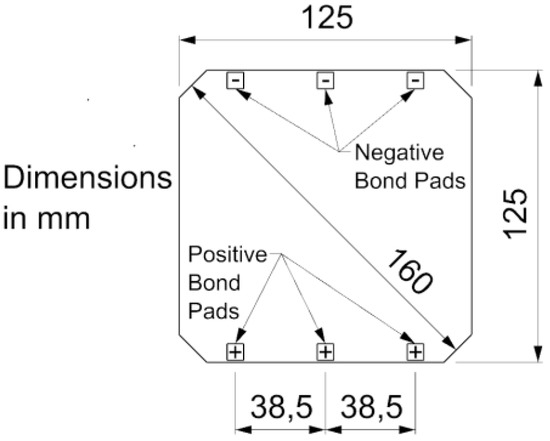
Figure 23.
Solar panel specifications.
Since the half wingspan of the SolarÍO is 1547 mm, it will be possible to place a total of 16 solar panels in each wing and, therefore, a total of 32 solar panels throughout the aircraft, which adds up to a total of 212 grams in solar panels, as can be seen in Figure 24.
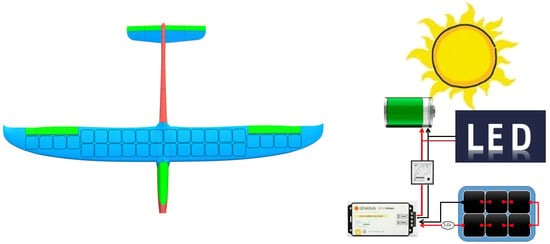
Figure 24.
Distribution of the solar panels along the wing of the SolarÍO.
During the plane mission, the point where the maximum power is achieved is variable. For this reason, it is important to use a device that monitors these data and defines the percentage of energy that is used to generate voltage and how much energy is used to generate current. The product of both (VxI) generates the maximum possible power and supplies the maximum amount of power to the aircraft’s propulsion system or battery. The maximum power point tracker (MPPT) regulator is commonly used with wind turbines and solar photovoltaic (PV) systems to maximize energy extraction in all conditions. Although it is applied mainly to solar energy, the principle is generally applied to sources with variable power: for example, optical and thermo-photovoltaic power transmission. The main problem addressed by the MPPT is that the efficiency of the transfer of energy from the solar cell depends on the amount of sunlight that falls on the solar panels, the angle of incidence of the solar light, the temperature of the solar panel and the characteristic electrical loads. The solar panels provided work at maximum efficiency at the maximum power point (MPP). MPPT devices are typically integrated into an electrical power converter system that provides voltage or current conversion, filtering, and regulation to drive various loads, including electrical networks, batteries, and motors. For this purpose, the commercial Genasun GV-10 Lithium 12.5 Volt MPPT regulator was selected. The scheme of the MPPT connections is described in Figure 25. Then, it is possible to obtain a performance even 60% greater than if the solar panels were connected directly to the electrical circuit of the UAV.
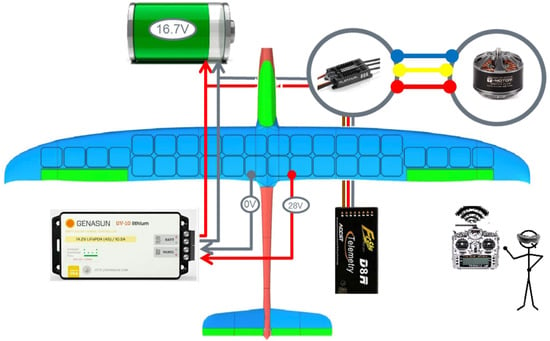
Figure 25.
Connecting the MPPT to the SolarÍO circuit.
4.2. Additive Manufacturing
The Blackbelt printer with a nozzle angle of 45 degrees was chosen. Blackbelt Cura is programmed and developed by Blackbelt 3D and provides a new environment to work with different deposition planes. There are many open problems associated with the non-planar deposition nozzles or 45-degree nozzles. Blackbelt Cura can set the gap between layers, but this distance will correspond only to the side surfaces of the pieces printed (ds); however, due to the printing angle, θp, at the top layer, the distance between filaments, dt, will be much greater. A simplification of this situation is illustrated in Figure 26 where it can be clearly seen how dt is greater than ds. This difference in distances will mean that the filaments in the layer at the top surface will be too separated to fuse together and will therefore not be able to create a compact robust structure. The phenomenon in Figure 26 should be considered, as it will affect the final results of the wings and fuselage printed with the Blackbelt printer.
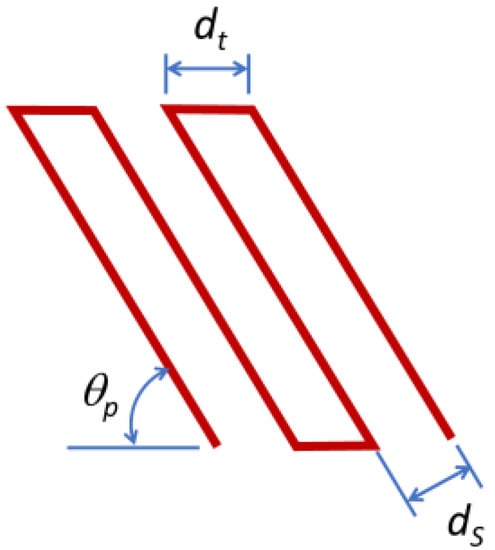
Figure 26.
Side view of the simplified situation of the error that occurred. Red lines represent the filaments.
A few trial-and-error tests were performed in Blackbelt Cura to understand this phenomenon better, and the conclusion reached was that there are three parameters mainly affecting dt: the printing angle (θp), the minimum distance between layers and the thickness of the layer. It was noticed that when the printing angle increased, due to Pythagoras’ theorem, df decreased. Additionally, when ds was decreased by decreasing the minimum distance between layers, dt decreased as well. In addition, when the thickness of the layer was increased, dt decreased.
Even though these fixtures will allow for a better printing result, where the structure is more robust, there are some disadvantages that should be considered. On the one hand, an increase in the printing angle will result in worse mechanical behavior from the wings, as was explained in previous sections. However, this effect on the mechanical behavior will not be critical, as the wings will still be able to perform properly under the distributed load bearded. On the other hand, a decrease in the minimum distance between layers means that the printer nozzle should make more passes, and therefore this will increase the printing time and the amount of material used. This will make the process more expensive, as well as increase the weight of the wings.
Considering the few disadvantages presented, the part was printed as described above. Its visualization in Blackbelt Cura can be seen in Figure 27 and the cross-section of the wing in Figure 28, which allows for a clear visualization of the gyroid infill. The fuselage to be printed and the partially printed fuselage can be seen in Figure 29. The results look much better than those obtained previously using a conventional 3D printing with the injection nozzle at 90º degrees.

Figure 27.
Visualization of the wing in Blackbelt Cura.
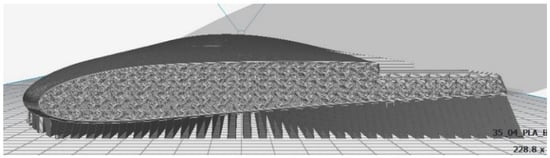
Figure 28.
Cross-section of the wing in Blackbelt Cura.

Figure 29.
Fuselage set to be printed (left) and printed (right) with the Blackbelt printer.
Finally, to be able to compare the structure obtained from conventional printing to a method consisting of 3D printing that uses an angle with infinite Z, the same wings were also printed with a conventional 3D printer. This wing was printed in different parts, which composed the whole wing, as conventional 3D printers print pieces upwards, and therefore they have a height limit that is established by the proper printer. In this case, as each wing had a height of 1 m, and the wing was printed in four parts, as shown in Figure 30 and Figure 31. These parts were joined together with an adhesive. Therefore, these joints will be critical bending stress points, which could fail more easily than a continuous structure, such as the wing manufactured with the Z-infinite printer, where the wing is printed as a whole part and there are no joints.

Figure 30.
Wing printed on Blackbelt 3D printer.

Figure 31.
Four parts of the wing on the conventional 3D printer.
5. Conclusions
In this paper, the conceptual design and manufacturing of a solar aircraft, SolarÍO, using additive technologies, was presented. Perpetual flight is possible in a lightweight aircraft and requires an aircraft with a wingspan of 5.6 m, an aspect ratio of 18.5, and a battery mass of 2.9 kg. A study of the most innovative 3D printers was carried out that allows for the manufacture of parts with an infinite Z-axis; in addition, a filler based on minimal surfaces (gyroids) was applied, which considerably increases the mechanical properties of the printed parts.
A minimal surface structure (gyroid) is used to maximize the mechanical properties and thus improve the stiffness/weight ratio of conventional structures. On the other hand, a 3D printing with a 45-degree nozzle was used to obtain more complex parts without support structures. Both, minimal surfaces and 45-degree 3D printing have obvious advantages, but also have drawbacks to be solved. With minimal structures, it is complex to integrate elements such us spars, actuators, or electrical connections. To optimize the mechanical properties, it is necessary to ensure that the core and the skin of the component are correctly bonded, for which pressure and temperature between the deposited material and the previous layer must be controlled. To improve this adhesion in hollow geometries, such as those of the aircraft wing, the use of the nozzle at 45 degrees is proposed. The main disadvantage of printing at 45 degrees is the internal stresses induced in the parts. There is a great lack of scientific knowledge about the behavior of these stresses, which in the case of large components can create nonconformities in the component. In the case of the parts manufactured in this work, the nozzles used are 0.4 mm in diameter and no shrinkage was observed. The proposal of this work achieves better results than the traditional MEX techniques, however, it was necessary to design the work to avoid the problems previously described. Fused granulate fabrication (FGF) pellet deposition equipment is proposed to manufacture larger components. FGF allows higher printing speeds and better interlayer adhesion.
After the analysis performed on the results obtained by the bending tests, it can be concluded that to optimize the mechanical properties of a wing with a gyroid infill, the following settings should be adjusted. Firstly, it is preferable to set up the greatest infill density possible without compromising the weight of the structure. Secondly, when manufacturing the wings with the conventional 3D printer, printing the gyroid infill in the Y direction will offer better mechanical properties, as demonstrated in the bending tests. When manufacturing the wings with a Z-infinite 3D printer, setting the lowest printing angle possible will result in the best mechanical properties of the structure under bending loads.
Moreover, after the analysis performed on the results obtained by the compression tests, further conclusions can be obtained regarding the mechanical behavior of the wings with a gyroid infill under compressive forces. Firstly, higher infill densities will mean, generally, a better mechanical performance, as a greater maximum strain is reached before the structure collapses. In addition, the thicker regions of the wings will deform more easily but will have a greater margin of deformation to partially recover their original shape once the compressive load is removed. On the other hand, the thinner regions will be able to withstand greater maximum stress but will take a lower deformation to behave plastically.
Furthermore, the 3D printer used was a factor that determined some characteristics of the wing’s mechanical behavior. Through the compression tests, it was shown that structures printed with the conventional 3D printer were able to withstand greater forces before collapsing, probably due to a better adhesion of the consecutive filaments. However, a wing manufactured with a conventional printer will exhibit more critical behavior under bending forces due to the discontinuities in its assembly, as it should be printed in four parts. These will join with an adhesive, which will fail more easily than a continuous structure, such as the wing manufactured with a Z-infinite printer. This paper demonstrates that AM offers new possibilities for rapid development of UAVs, reducing costs and time production.
Author Contributions
Conceptualization, C.G.-G. and P.C.-P.; methodology, C.G.-G. and P.C.-P.; software, C.G.-G.; validation, P.C.-P.; formal analysis, P.C.-P.; investigation, P.C.-P.; resources, J.A.G.-M.; writing—original draft preparation, C.G.-G., P.C.-P. and J.A.G.-M.; writing—review and editing, C.G.-G., P.C.-P. and J.A.G.-M.; funding acquisition, J.A.G.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received partial funding from the Government of Spain under the project PID2019-108807RB-I00 and Generalitat Valenciana under IDIFEDER/2021/040.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wohlers, T. Wohlers Report 2019: 3D Printing and Additive Manufacturing State of the Industry; Wohlers Associates, Inc.: Fort Collins, CO, USA, 2019; ISBN 978-0-9913332-5-7. [Google Scholar]
- Gibson, I.; Rosen, D.W.; Stucker, B. Additive Manufacturing Technologies; Springer: Boston, MA, USA, 2010. [Google Scholar] [CrossRef]
- Goh, G.D.; Agarwala, S.; Goh, G.L.; Dikshit, V.; Sing, S.L.; Yeong, W.Y. Additive manufacturing in unmanned aerial vehicles (UAVs): Challenges and potential. Aerosp. Sci. Technol. 2017, 63, 140–151. [Google Scholar] [CrossRef]
- Madla, C.M.; Trenfield, S.J.; Goyanes, A.; Gaisford, S.; Basit, A.W. 3D Printing Technologies, Implementation and Regulation: An Overview. In 3D Printing of Pharmaceuticals; Basit, A., Gaisford, S., Eds.; Springer: Cham, Switzerland, 2018; Volume 31. [Google Scholar] [CrossRef]
- Mulero-Pázmány, M.; Martínez-de Dios, J.R.; Popa-Lisseanu, A.G.; Gray, R.J.; Alarcón, F.; Sánchez-Bedoya, C.A.; Viguria, A.; Ibáñez, C.; Negro, J.J.; Ollero, A.; et al. Development of a Fixed-Wing Drone System for Aerial Insect Sampling. Drones 2022, 6, 189. [Google Scholar] [CrossRef]
- Leutenegger, S. Unmanned Solar Airplanes: Design and Algorithms for Efficient and Robust Autonomous Operation. PhD Thesis, ETH Zurich, Zurich, Switzerland, 2014. [Google Scholar] [CrossRef]
- Liu, J.; Huang, J.; Zhang, C.; Yu, H. Topology Optimization and Additive Manufacturing of Fiber-Reinforced UAV Components. In Proceedings of International Conference on Autonomous Unmanned Systems (ICAUS 2021); ICAUS 2021. Lecture Notes in Electrical Engineering; Wu, M., Niu, Y., Gu, M., Cheng, J., Eds.; Springer: Singapore, 2021; Volume 861. [Google Scholar] [CrossRef]
- Graves, P.; Riley, H.; Campbell, D.S.; Cottrell, D. Composite Structures Incorporating Additive Manufactured Elements. Patent Publication Number: 20190077098. 2019. Aurora Flight Sciences Corporation. Available online: https://sunpower.maxeon.com/int/solar-panel-products/maxeon-solar-cell-technology (accessed on 22 March 2020).
- Nvss, S.; Esakki, B.; Yang, L.-J.; Udayagiri, C.; Vepa, K.S. Design and Development of Unibody Quadcopter Structure Using Optimization and Additive Manufacturing Techniques. Designs 2022, 6, 8. [Google Scholar] [CrossRef]
- Kumar, A.; Sahdev, S.; Jha, A.; Gupta, A.K.; Samsher. Design and Development of an Unmanned Aerial Cargo Vehicle Using Additive Manufacturing. In Advances in Engineering Design; Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Chu, Y.; Ho, C.; Lee, Y.; Li, B. Development of a Solar-Powered Unmanned Aerial Vehicle for Extended Flight Endurance. Drones 2021, 5, 44. [Google Scholar] [CrossRef]
- Turk, I.; Obek, E.; Ekici, S.; Karakoc, T.H. A conceptual design of a solar powered UAV and assessment for continental climate flight conditions. Int. J. Green Energy 2022, 19, 638–648. [Google Scholar] [CrossRef]
- Li, K.; Wu, Y.; Bakar, A.; Wang, S.; Li, Y.; Wen, D. Energy System Optimization and Simulation for Low-Altitude Solar-Powered Unmanned Aerial Vehicles. Aerospace 2022, 9, 331. [Google Scholar] [CrossRef]
- García-Gascón, C. Design and fabrication of a fixed-wing solar UAV for autonomous mission. In Towards Printed Manufacturing in the Aeronautics Industry; (SolarÍO) Final Degree Aerospace Engineering Report; ETSID, Universitat Politècnica de Valencia: Valencia, Spain, 2021. [Google Scholar]
- Castelló, P. Application of Additive Manufacturing Techniques with Minimal Surfaces for the Development of a Fixed-Wing UAV; Final Degree Aerospace Engineering Report; ETSID, Universitat Politècnica de Valencia: Valencia, Spain, 2022. [Google Scholar]
- Oettershagen, P.; Melzer, A.; Mantel, T.; Rudin, K.; Lotz, R.; Siebenmann, D.; Leutenegger, S.; Alexis, K.; Siegwart, R. A solar-powered hand-launchable UAV for low-altitude multi-day continuous flight. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 3986–3993. [Google Scholar]
- Malaver, A.J.R.; Gonzalez, L.F.; Motta, N.; Villa, T.F. Design and flight testing of an integrated solar powered UAV and WSN for remote gas sensing. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 7–14 March 2015. [Google Scholar] [CrossRef]
- Rajendran, P.; Smith, H. Development of Design Methodology for a Small Solar-Powered Unmanned Aerial Vehicle. Int. J. Aerosp. Eng. 2018, 2018, 2820717. [Google Scholar] [CrossRef]
- Noth, A. Design of Solar Powered Airplanes for Continuous Flight. Ph.D. Thesis, ETH, Zurich, Switzerland, 2008. [Google Scholar]
- Rajendran, P.; Smith, H.; bin Masral., H. Modeling and simulation of solar irradiance and daylight duration for a high-power-output solar module system. Appl. Mech. Mater. 2014, 629, 475–480. [Google Scholar]
- López, F.J.; Martín, F. Complete minimal surfaces in R3. Publ. Mat. 2011, 43, 341–449. [Google Scholar] [CrossRef][Green Version]
- Lin, Z.-H.; Pan, J.-H.; Li, H.-Y. Mechanical Strength of Triply Periodic Minimal Surface Lattices Subjected to Three-Point Bending. Polymers 2022, 14, 2885. [Google Scholar] [CrossRef] [PubMed]
- Wallat, L.; Altschuh, P.; Reder, M.; Nestler, B.; Poehler, F. Computational Design and Characterisation of Gyroid Structures with Different Gradient Functions for Porosity Adjustment. Materials 2022, 15, 3730. [Google Scholar] [CrossRef] [PubMed]
- Prusa, J. Prusament PLA Technical Data Sheet; Prusa Polymers: Prague, Czech Republic, 2018; pp. 9–10. [Google Scholar]
- Goh, G.D.; Toh, W.; Yap, Y.L.; Ng, T.; Yeong, W.Y. Additively manufactured continuous carbon fiber-reinforced thermoplastic for topology optimized unmanned aerial vehicle structures. Compos. Part B Eng. 2021, 216, 108840. [Google Scholar] [CrossRef]
- International Organization for Standardization. Determination of Flexural Properties (ISO Standard No. 178:2019). 2019. Available online: https://www.iso.org/standard/70513.html (accessed on 21 August 2022).
- Sengsri, P.; Kaewunruen, S. Compression behaviour of an extremely lightweight structure with a gyroid core used for bridge bearings. Mater. Today 2022, 65, 1656–1659. [Google Scholar] [CrossRef]
- Madhavadas, V.; Srivastava, D.; Chadha, U.; Raj, S.A.; Thariq, M.; Syazwani, F.; Umaira, A. A review on metal additive manufacturing for intricately shaped aerospace components. CIRP J. Manuf. Sci. Technol. 2022, 39, 18–36. [Google Scholar] [CrossRef]
- Bacciaglia, A.; Ceruti, A.; Liverani, A. Towards Large Parts Manufacturing in Additive Technologies for Aerospace and Automotive applications. Procedia Comput. Sci. 2022, 200, 1113–1124. [Google Scholar] [CrossRef]
- Kim, H.; Oh, Y.; Hwang, J.; Young, S. High-performance continuous carbon fiber composite filament via solution process. J. Ind. Eng. Chem. 2022, 115, 466–475. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).