Fully Distributed Robust Formation Flying Control of Drones Swarm Based on Minimal Virtual Leader Information
Abstract
1. Introduction
- The reference path for each drone is a composite of the global flying path vector and the local formation vector. As a result, to achieve local trajectory tracking, the asymptotic internal model should cover the generating modes of both the global flying path vector and the local formation vector. To this end, the minimal polynomials associated with the global and local reference vectors are multiplied together to obtain an integrated internal model, which covers the generating modes of both the global and local reference vectors.
- The controllability of the matrix pair of the internal model is a prerequisite for synthesizing the dynamic state feedback control. For the time-invariant internal model, the matrix pair can take any form. Meanwhile, since the asymptotic internal model conceived in this paper is time-varying, we have adopted the canonical controllable form for the matrix pair of the asymptotic internal model so that the time-varying system matrices of the augmented closed-loop system associated with the time-varying asymptotic internal model is controllable for all the time being.
- In the design of the dynamic state feedback control, the control gains should be properly assigned so that all the eigenvalues of the nominal closed-loop system will be placed at pre-specified locations in the complex plane. Though it is easy to conduct this eigenvalue placement procedure for time-invariant matrix pair, the same calculation for time-varying matrix pair might not be straightforward if the time-varying matrix pair is merely stabilizable. To thoroughly address this issue, in this paper, we have proposed a novel adaptive gain assignment method by solving the real-time algebraic Riccati equation to stabilize the time-varying closed-loop system.
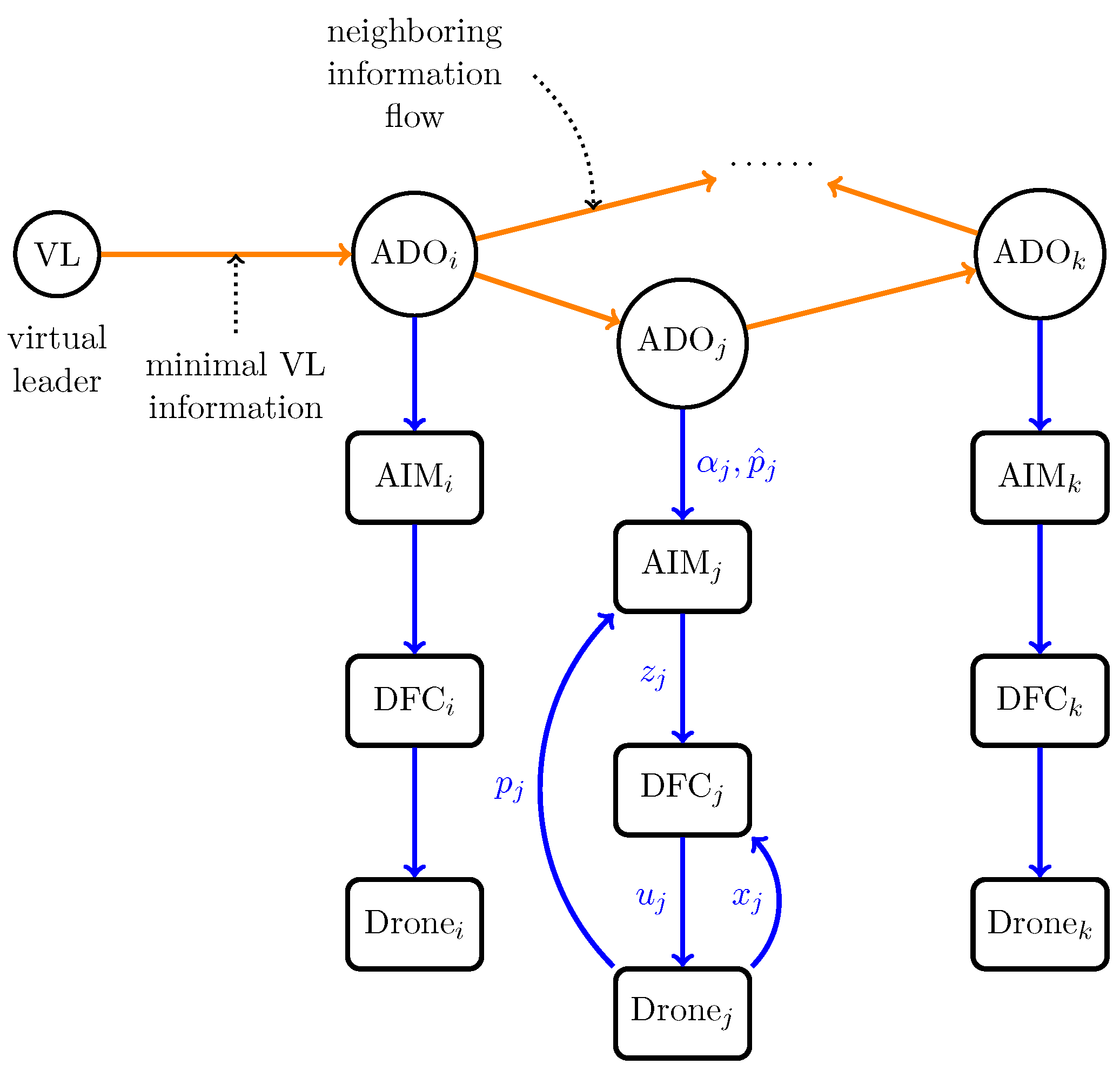
- The internal model approaches adopted in [27,31,32], and also in our previous work ([26], Chapter 10) required that full/partial information of the exosystem should be known to each individual in advance. Meanwhile, in this paper, the virtual leader which generates the global flying path vector is initially completely unknown to all the drones. The information of the virtual leader will be transmitted to each drone through the output feedback adaptive distributed observer proposed in [37]. Based on the estimated minimal polynomial of the system matrix of the virtual leader system, an asymptotic internal model is conceived to deal with system uncertainties.
- It is noteworthy that in [33,34,35,36], and also in our previous works ([26], Chapters 8 and 11) and [38], all the elements of the system matrices need to be recovered by various adaptive distributed observers. While, in this paper, by invoking the output-based adaptive distributed observer, much less system parameters need to be transmitted over the communication network, which drastically reduces the communication burden in comparison with the existing results.
- In [28,29,33,34,35,36,39,40], the individual models are free of parameter uncertainty. In contrast, in this paper, both the uncertain velocity damping matrix and the uncertain control gain matrix are taken into consideration for the second order drone models. To deal with system parameter uncertainties, we have resorted to the p-copy internal model approach [41], which is robust against moderate variations of system parameters around their nominal values.
2. Notation and Preliminary
- and are controllable.
- The minimal polynomial of divides the characteristic polynomial of .
3. Problem Description
4. Main Results
4.1. Design of the Output Based Adaptive Distributed Observer
4.2. Design of the Asymptotic Internal Model
4.3. Design of the Local Trajectory Tracking Controller
4.4. Stability Analysis
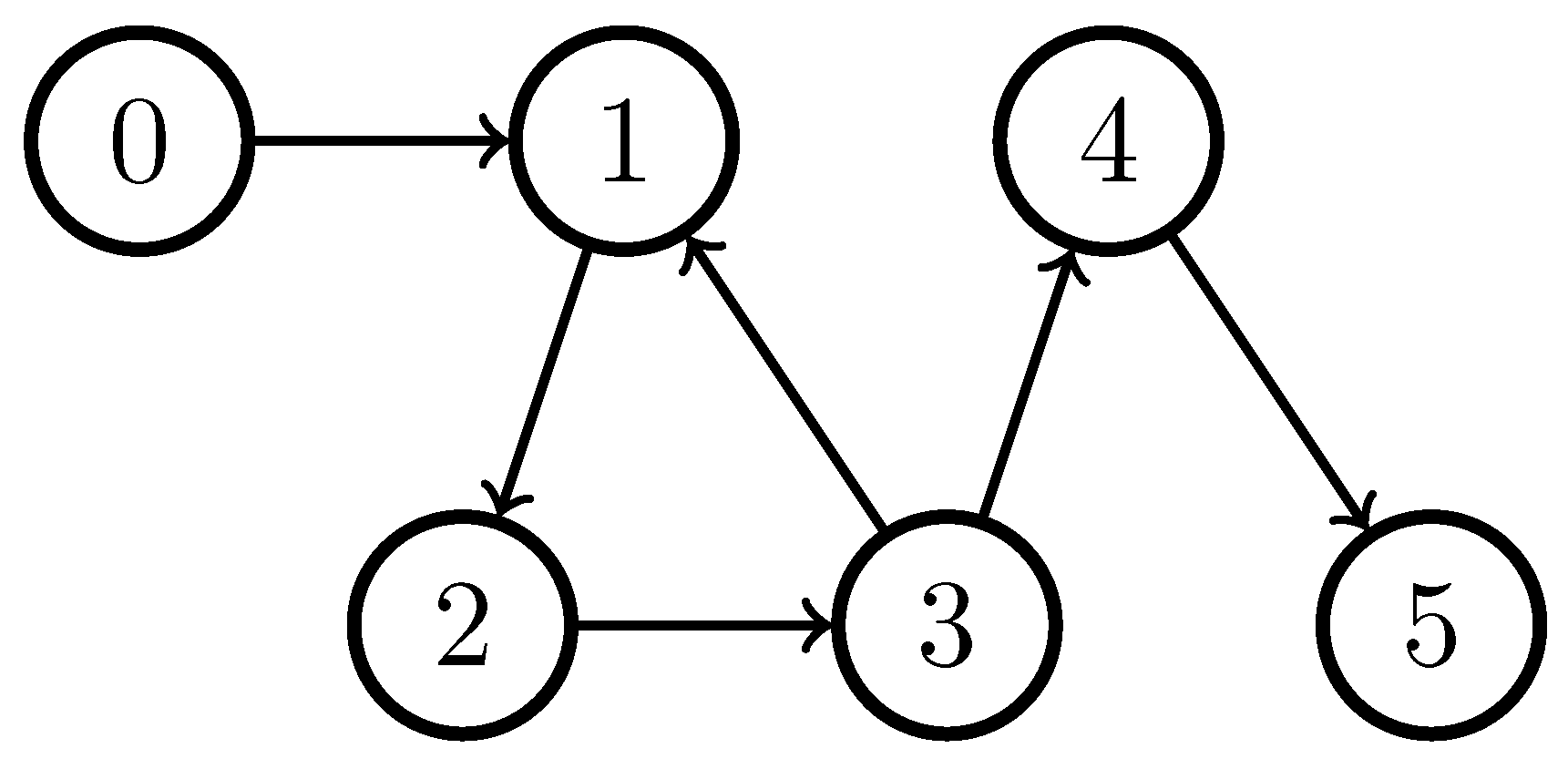
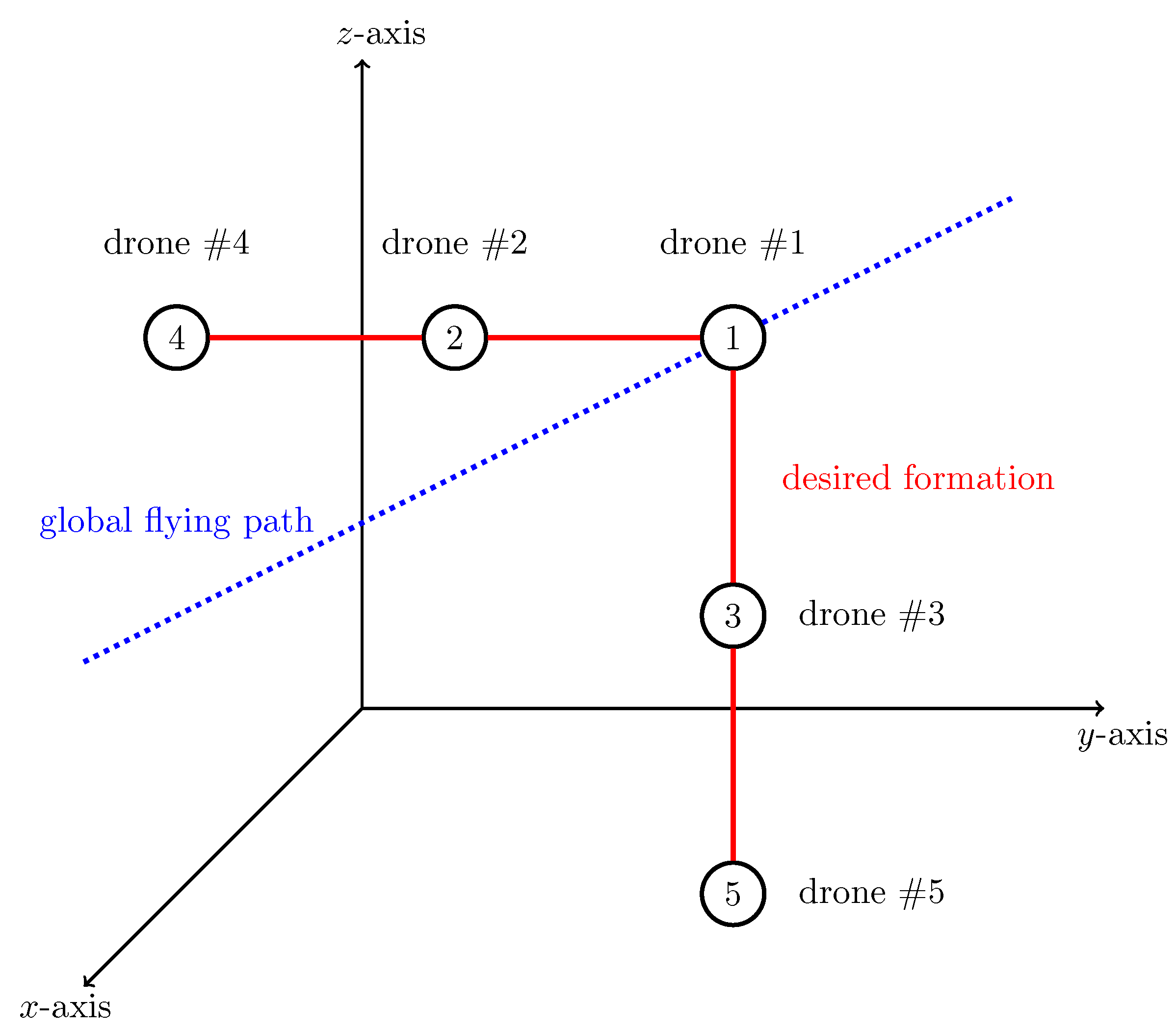
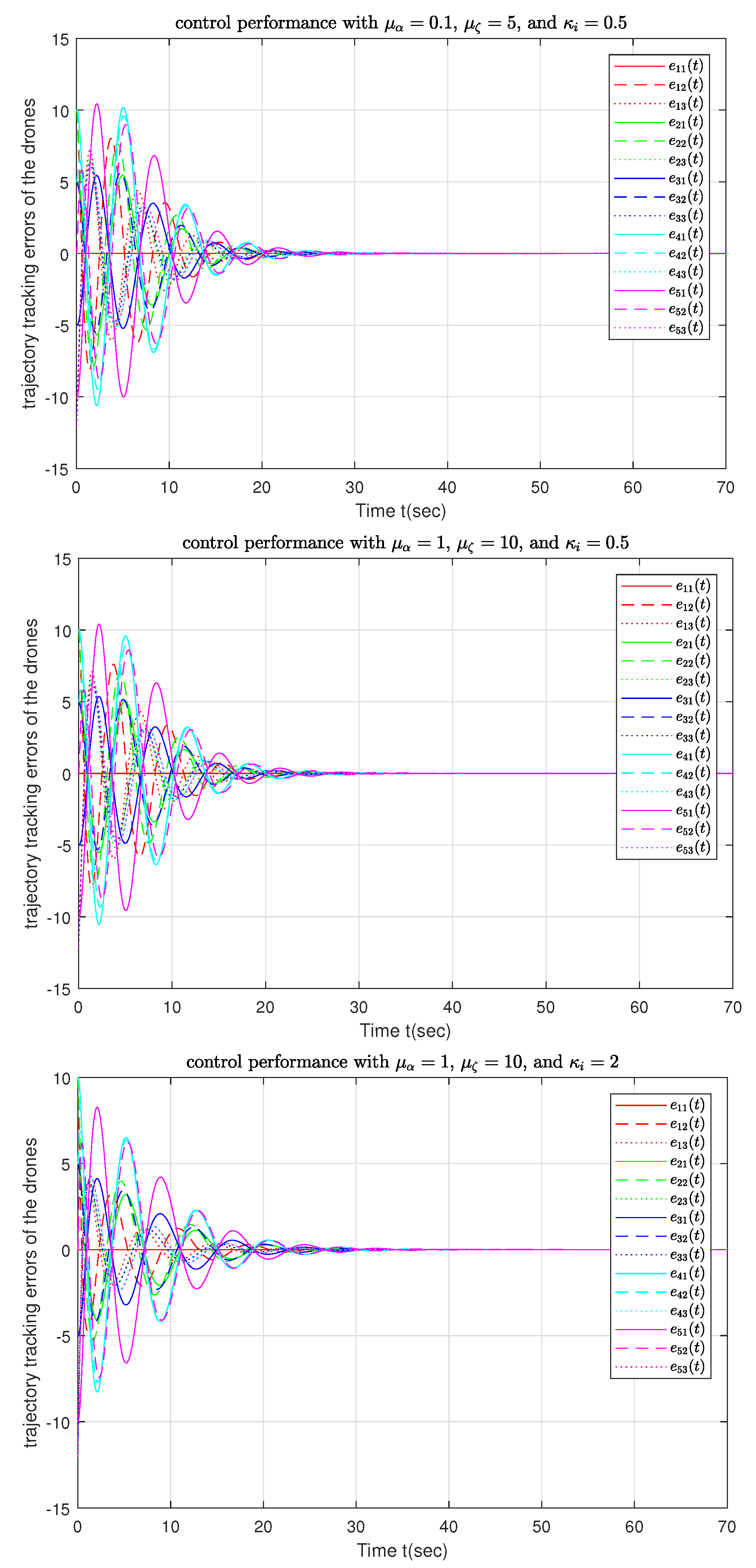
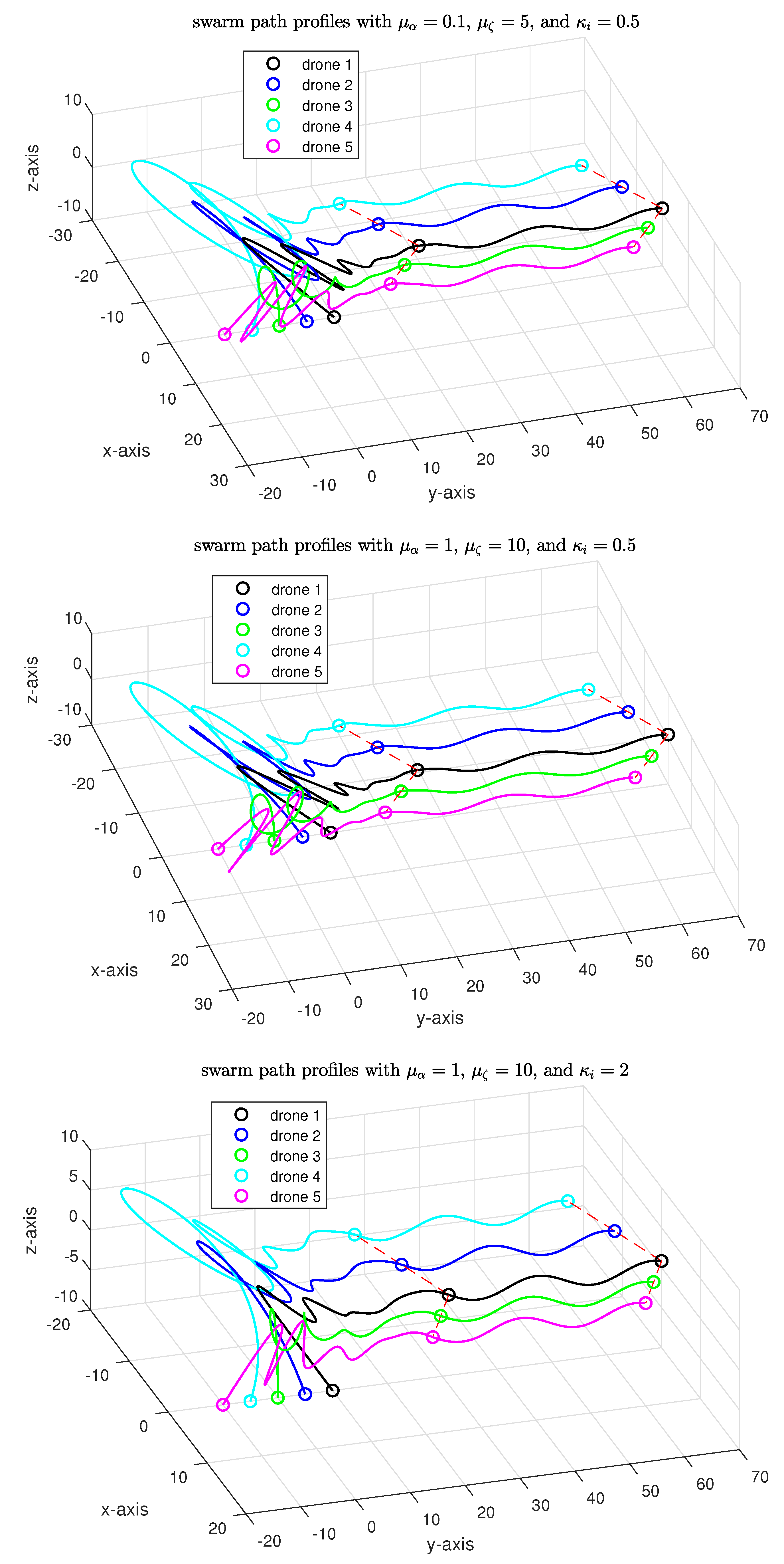
5. Numerical Simulations
- Gain Set 1: , , ,
- Gain Set 2: , , ,
- Gain Set 3: , ,
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bajec, I.L.; Heppner, F.H. Organized flight in birds. Anim. Behav. 2009, 78, 777–789. [Google Scholar] [CrossRef]
- Niwa, H.S. Self-organizing Dynamic Model of Fish Schooling. J. Theor. Biol. 1994, 171, 123–136. [Google Scholar] [CrossRef]
- Portugal, S. Lissaman, Shollenberger and formation flight in birds. J. Exp. Biol. 2016, 219, 2778–2780. [Google Scholar] [CrossRef][Green Version]
- Desai, J.; Ostrowski, J.; Kumar, V. Modeling and control of formations of nonholonomic mobile robots. IEEE Trans. Robot. Autom. 2001, 17, 905–908. [Google Scholar] [CrossRef]
- Shafiq, M.; Ali, Z.A.; Israr, A.; Alkhammash, E.H.; Hadjouni, M. A Multi-Colony Social Learning Approach for the Self-Organization of a Swarm of UAVs. Drones 2022, 6, 104. [Google Scholar] [CrossRef]
- Gao, Z.; Guo, G. Fixed-Time Leader-Follower Formation Control of Autonomous Underwater Vehicles With Event-Triggered Intermittent Communications. IEEE Access 2018, 6, 27902–27911. [Google Scholar] [CrossRef]
- Bai, H.; Wen, J.T. Cooperative Load Transport: A Formation-Control Perspective. IEEE Trans. Robot. 2010, 26, 742–750. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, K.; Jiang, Y.; Niu, S.; Yang, T.; Song, H. Communication Aware UAV Swarm Surveillance Based on Hierarchical Architecture. Drones 2021, 5, 33. [Google Scholar] [CrossRef]
- Nigam, N.; Bieniawski, S.; Kroo, I.; Vian, J. Control of Multiple UAVs for Persistent Surveillance: Algorithm and Flight Test Results. IEEE Trans. Control Syst. Technol. 2012, 20, 1236–1251. [Google Scholar] [CrossRef]
- Zheng, R.; Liu, Y.; Sun, D. Enclosing a target by nonholonomic mobile robots with bearing-only measurements. Automatica 2015, 53, 400–407. [Google Scholar] [CrossRef]
- Oh, K.K.; Park, M.C.; Ahn, H.S. A survey of multi-agent formation control. Automatica 2015, 53, 424–440. [Google Scholar] [CrossRef]
- Liu, Y.; Bucknall, R. A survey of formation control and motion planning of multiple unmanned vehicles. Robotica 2018, 36, 1019–1047. [Google Scholar] [CrossRef]
- Kamel, M.A.; Yu, X.; Zhang, Y. Formation control and coordination of multiple unmanned ground vehicles in normal and faulty situations: A review. Annu. Rev. Control 2020, 49, 128–144. [Google Scholar] [CrossRef]
- Balch, T.; Arkin, R. Behavior-based formation control for multirobot teams. IEEE Trans. Robot. Autom. 1998, 14, 926–939. [Google Scholar] [CrossRef]
- Lawton, J.; Beard, R.; Young, B. A decentralized approach to formation maneuvers. IEEE Trans. Robot. Autom. 2003, 19, 933–941. [Google Scholar] [CrossRef]
- Wang, C.; Wang, D.; Gu, M.; Huang, H.; Wang, Z.; Yuan, Y.; Zhu, X.; Wei, W.; Fan, Z. Bioinspired Environment Exploration Algorithm in Swarm Based on Levy Flight and Improved Artificial Potential Field. Drones 2022, 6, 122. [Google Scholar] [CrossRef]
- Tanner, H.; Pappas, G.; Kumar, V. Leader-to-formation stability. IEEE Trans. Robot. Autom. 2004, 20, 443–455. [Google Scholar] [CrossRef]
- Liang, X.; Liu, Y.H.; Wang, H.; Chen, W.; Xing, K.; Liu, T. Leader-Following Formation Tracking Control of Mobile Robots Without Direct Position Measurements. IEEE Trans. Autom. Control 2016, 61, 4131–4137. [Google Scholar] [CrossRef]
- Dong, X.; Yu, B.; Shi, Z.; Zhong, Y. Time-Varying Formation Control for Unmanned Aerial Vehicles: Theories and Applications. IEEE Trans. Control Syst. Technol. 2015, 23, 340–348. [Google Scholar] [CrossRef]
- Dong, X.; Hu, G. Time-varying formation control for general linear multi-agent systems with switching directed topologies. Automatica 2016, 73, 47–55. [Google Scholar] [CrossRef]
- Dong, X.; Hu, G. Time-Varying Formation Tracking for Linear Multiagent Systems with Multiple Leaders. IEEE Trans. Autom. Control 2017, 62, 3658–3664. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W.; Atkins, E.M. Information consensus in multivehicle cooperative control. IEEE Control Syst. Mag. 2007, 27, 71–82. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and Cooperation in Networked Multi-Agent Systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Cai, H.; Su, Y.; Huang, J. Cooperative Control of Multi-Agent Systems: Distributed-Observer and Distributed-Internal-Model Approaches; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Wang, X. Distributed formation output regulation of switching heterogeneous multi-agent systems. Int. J. Syst. Sci. 2013, 44, 2004–2014. [Google Scholar] [CrossRef]
- Hua, Y.; Dong, X.; Hu, G.; Li, Q.; Ren, Z. Distributed Time-Varying Output Formation Tracking for Heterogeneous Linear Multiagent Systems With a Nonautonomous Leader of Unknown Input. IEEE Trans. Autom. Control 2019, 64, 4292–4299. [Google Scholar] [CrossRef]
- Hua, Y.; Dong, X.; Li, Q.; Ren, Z. Distributed adaptive formation tracking for heterogeneous multiagent systems with multiple nonidentical leaders and without well-informed follower. Int. J. Robust Nonlinear Control 2020, 30, 2131–2151. [Google Scholar] [CrossRef]
- Song, W.; Feng, J.; Zhang, H.; Wang, W. Dynamic Event-Triggered Formation Control for Heterogeneous Multiagent Systems With Nonautonomous Leader Agent. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Chen, Z.; Liu, Z. Formation control for nonlinear multi-agent systems by robust output regulation. Neurocomputing 2014, 140, 114–120. [Google Scholar] [CrossRef]
- Huang, X.; Dong, J. Reliable Leader-to-Follower Formation Control of Multiagent Systems Under Communication Quantization and Attacks. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 89–99. [Google Scholar] [CrossRef]
- Li, W.; Zhang, H.; Ming, Z.; Wang, Y. Fully Distributed Event-Triggered Bipartite Formation Tracking Control for Heterogeneous Multi-Agent Systems on Signed Digraph. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 2181–2185. [Google Scholar] [CrossRef]
- Zhang, H.; Li, W.; Zhang, J.; Wang, Y.; Sun, J. Fully Distributed Dynamic Event-Triggered Bipartite Formation Tracking for Multiagent Systems With Multiple Nonautonomous Leaders. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.; Wen, G.; Peng, Z.; Huang, T.; Rahmani, A. Fully Distributed Dual-Terminal Event-Triggered Bipartite Output Containment Control of Heterogeneous Systems Under Actuator Faults. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 5518–5531. [Google Scholar] [CrossRef]
- Jiang, D.; Wen, G.; Peng, Z.; Wang, J.L.; Huang, T. Fully Distributed Pull-Based Event-Triggered Bipartite Fixed-Time Output Control of Heterogeneous Systems with an Active Leader. IEEE Trans. Cybern. 2022, 1–12. [Google Scholar] [CrossRef]
- Cai, H.; Huang, J. Output based adaptive distributed output observer for leader–follower multiagent systems. Automatica 2021, 125, 109413. [Google Scholar] [CrossRef]
- Cai, H.; Lewis, F.L.; Hu, G.; Huang, J. The adaptive distributed observer approach to the cooperative output regulation of linear multi-agent systems. Automatica 2017, 75, 299–305. [Google Scholar] [CrossRef]
- Yan, J.; Yu, Y.; Wang, X. Distance-Based Formation Control for Fixed-Wing UAVs with Input Constraints: A Low Gain Method. Drones 2022, 6, 159. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Park, D.; Ngoc, D.N.; Xuan-Mung, N.; Huynh, T.T.; Nguyen, T.N.; Hong, S.K. Quadrotor Formation Control via Terminal Sliding Mode Approach: Theory and Experiment Results. Drones 2022, 6, 172. [Google Scholar] [CrossRef]
- Huang, J. Nonlinear Output Regulation: Theory and Applications; SIAM: Philadelphia, PA, USA, 2004. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Li, W.; Cai, H. Fully Distributed Robust Formation Flying Control of Drones Swarm Based on Minimal Virtual Leader Information. Drones 2022, 6, 266. https://doi.org/10.3390/drones6100266
Gao H, Li W, Cai H. Fully Distributed Robust Formation Flying Control of Drones Swarm Based on Minimal Virtual Leader Information. Drones. 2022; 6(10):266. https://doi.org/10.3390/drones6100266
Chicago/Turabian StyleGao, Huanli, Wei Li, and He Cai. 2022. "Fully Distributed Robust Formation Flying Control of Drones Swarm Based on Minimal Virtual Leader Information" Drones 6, no. 10: 266. https://doi.org/10.3390/drones6100266
APA StyleGao, H., Li, W., & Cai, H. (2022). Fully Distributed Robust Formation Flying Control of Drones Swarm Based on Minimal Virtual Leader Information. Drones, 6(10), 266. https://doi.org/10.3390/drones6100266






