Occlusion-Aware UAV Path Planning for Reconnaissance and Surveillance

Abstract

Unmanned Aerial Vehicles (UAVs) have become necessary tools for a wide range of activities including but not limited to real-time monitoring, surveillance, reconnaissance, border patrol, search and rescue, civilian, scientific and military missions, etc. Their advantage is unprecedented and irreplaceable, especially in environments dangerous to humans, for example, in radiation or pollution-exposed areas. Two path-planning algorithms for reconnaissance and surveillance are proposed in this paper, which ensures every point on the target ground area can be seen at least once in a complete surveillance circle. Moreover, the geometrically complex environments with occlusions are considered in our research. Compared with many existing methods, we decompose this problem into a waypoint-determination problem and an instance of the traveling-salesman problem.

1. Introduction

The extensive use of Unmanned Aerial Vehicles (UAVs), also known as aerial drones, has recently jumped from military to hobby and professional applications [1]. Complete coverage has become a necessary function for activities including but not limited to border patrol [2,3], search and rescue [4,5], 3D reconstruction [6,7], infraction inspection [8], and surveillance and security [9,10,11,12], etc. In general, the coverage problem was first put forward over a 2D grid environment by [13]. We can classify this problem into two main categories based on vehicle movements. Static coverage focuses on the deployment of hovering UAVs to reconnoiter over certain terrains [14,15], while dynamic coverage addresses the reconnaissance and surveillance problem by moving UAVs [16,17].

A survey on computational-intelligence-based UAV path planning can be found in [18,19], which classifies UAV path-planning methods from the aspect of methodology, time domain, and space domain, respectively. In a common reconnaissance and surveillance scenario, a flying vehicle equipped with a downward-facing video camera with a certain visibility angle can monitor targets of interest on the ground, such as vehicles, humans, animals, etc. [20,21]. We can evaluate the quality of surveillance in terms of coverage and resolution [22]. In this case, the low altitude of the traveling path is preferred for a better resolution of the observed region of the terrain. One of the most significant technical challenges is to completely cover a given target area with the minimum number of drone waypoints, which requires every point on the target area to be seen at least once by the onboard camera during one complete surveillance circle. However, these two evaluation terms need to reach a suitable compromise to perform an ideal surveillance duty.

This paper presents two novel path-planning algorithms to address the aforementioned gaps. In contrast to the existing literature, our approach takes both UAV kinematics constraints and camera-sensing constraints into consideration. In the first algorithm, we consider the fixed-wing vehicle case, assuming the vehicle flies at a given altitude with constant speed and limited turning radius. This Dubins aircraft model is similar to those in paper [11,23,24]. We present a two-phase strategy to solve this surveillance problem. First, an easily implementable estimation algorithm is developed, and the minimum number and locations of waypoints are determined to provide the complete coverage of the target area. The second phase addresses the allocation of the achieved locations over one or more UAVs and creates the shortest paths to reconnoiter the corresponding area of interest. The Dubins paths consist of straight lines and arcs of the circle of a constant radius. To achieve this, regular triangular patterns and the clustered spiral-alternating method are implemented, respectively. Our second algorithm concerns the surveillance problem over geometrically complex environments with varying altitudes and occlusions, such as mountainous terrains and urban regions. In the first stage, the challenge is to find a set of camera locations called the vantage waypoint set to provide full coverage of the area of interest, which can be viewed as a 3D Art Gallery Problem using drones as the observers. In the second stage, one or several UAVs are determined to conduct the full coverage reconnaissance and surveillance duty along individual routes respecting their kinematic constraints in the optimization criterion (the shortest time possible). This variant of the combinatorial traveling-salesman problem is solved by introducing unsupervised learning and Bézier curves.

The rest of the paper is organized as follows. Section 2 presents our approach for the scenario where UAVs fly at a given altitude. Section 3 then presents the proposed algorithm for the case where UAVs can fly at different altitudes. Each of these sections starts with the addressed problem with the necessary background, followed by details of the proposed surveillance solution. The performance of the algorithms is then evaluated using computer simulations. Finally, Section 4 concludes the paper.

2. Surveillance Algorithm at a Given Altitude

This section provides a two-stage approach, which is similar to [11,22,25] but more realistic and efficient. In the first stage, we construct a set of waypoints to be visited by UAVs. The fundamental idea is to create a triangulation of the terrain. This triangulation contains several congruent equilateral triangles, and the length of the sides of the triangles depends on the visibility of UAVs. The second stage aims at producing the shortest smooth trajectory so that all the waypoints can be visited by UAVs. As we consider fixed-wing UAVs, the popular Dubins car model is used. Then, the constructed trajectory has several straight-line segments and arcs. In the following subsections, we first formally state the problem of interest and then present our approach in detail.

2.1. Problem Statement

Consider a surveillance problem over one or multiple disjoint surface areas. We have one or a fleet of fixed-wing UAVs. For simplicity, all the UAVs are identical. They fly at a constant speed v and their angular velocity is u. In this section, we assume that the UAVs fly at a given altitude. We describe the UAV motion by the following well-known Dubins car model [26], which is often used for aircraft, UAVs and missiles [27,28,29,30]:

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)& =v\left(t\right)cos\theta \left(t\right)\hfill \\ \hfill \dot{y}\left(t\right)& =v\left(t\right)sin\theta \left(t\right)\hfill \\ \hfill \dot{\theta }\left(t\right)& =u\left(t\right)\hfill \end{array}$$

(1)

where $\theta$ is the vehicle’s heading.

Let $(x_g,y_g)$ denote the Cartesian coordinates of a point on the ground. Let $z_g=F(x_g,y_g)$ be the perpendicular elevation of the point $(x_g,y_g)$ on the terrain. Moreover, let $\mathcal{G}$ denote a given Lebesgue measurable region [31] on the ground with zero elevation, i.e., $z_g=0$. In addition, this region $\mathcal{G}$ has piecewise boundary. Our goal is to survey the region $\mathcal{G}$ by one or more UAVs. Let $Z_{max}$ and $Z_{min}$ be the given constants representing the maximum and minimum altitudes of UAVs. Any vantage point $(x,y,z)$ must make the following constraints hold:

$$(x,y)\in \mathcal{G},z\in [Z_{min},Z_{max}],0<Z_{min}<Z_{max}.$$

(2)

Each UAV carries a fixed EO/IR camera, which is downward-facing to the ground with a certain visibility angle $0<\alpha <\pi$. The sensing process is based on pinhole perspective projection [32], and the quality of the resolution is influenced by both the distance to the object and the physical parameters. In particular, if we set the camera’s center as UAV’s position $(x,y,z)$, the UAV can only see points along the z axis with a limited angle of view, so that a cone-shaped field of view (FOV) with radius

$$R:=z·tan\left(\frac{\alpha }{2}\right)$$

(3)

is constructed (see Figure 1). A point is invisible if it falls out of the FOV.

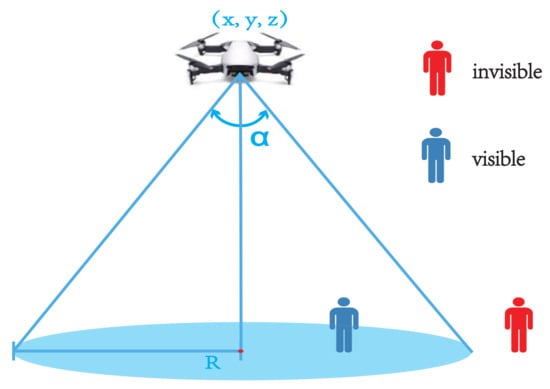
Figure 1. The visibility cone. Object within the FOV can be seen by the drone.

As aforementioned, a surveillance mission should deliver a coverage of the area of interest with a satisfactory resolution. Moreover, complete coverage means that every point of the region $\mathcal{G}$ is seen at least once in a complete surveillance circle of UAVs. One of the most significant technical challenges is how to completely cover the target region by the minimum number of waypoints. The visibility cone enlarges when the UAV flies higher, but the resolution of the onboard recording is worse. We can choose a certain altitude that can achieve the required resolution. Here, we select the lowest possible altitude z, i.e., $Z_{min}<z<Z_{max}$ for the best resolution. At this altitude, the generated waypoint set, which provides complete coverage of the target area with a resolution that cannot be further better, is preferred to conduct an ideal surveillance mission.

Definition 1.

The complete coverage means constraints (2) and (4) are satisfied and every point on the target area $\mathcal{G}$ can be seen at least once in a complete surveillance circle.

In the herein-addressed surveillance problem, we consider one waypoint location $p_i\in {\mathbb{R}}^3$ from vantage waypoint set

Let $P=\{p_1,...,p_n\}$ denote the set of the vantage waypoints. Here, $p_i\in {\mathbb{R}}^3$ is a vantage waypoint, which should be visited by a UAV. We assume that when a UAV is within $\delta$ distance from point $p_i$, a record such as the photo/video can be taken. Formally, when a UAV reaches any point $p_i^{*}$ satisfying $\left|\right|p_i^{*},p_i\left|\right|\le \delta$, where $\left|\right|·,·\left|\right|$ gives the standard Euclidean distance, we say the vantage point $p_i$ is visited successfully.

We need some more symbols to complete the problem statement. Let $q_{ij}$ denote the distance between waypoints i and j. Let $q_i$ be the minimum distance between a waypoint i and the terrain. For collision avoidance, the following constraints must be met:

$$q_{ij}\ge c_1,q_i\ge c_2$$

(4)

where $c_1>2\delta >0$ and $c_2>\delta >0$ are given safety margins.

With the above models, the problem of interest is to find the trajectory to visit the $\delta$-neighborhood of all assigned vantage points. Such a problem involves the optimization of the sequence of visits, which can be regarded as an instance of the well-known Dubins vehicle Traveling Salesman Problem (DTSP). As discussed earlier, the final trajectory for a UAV is a sequence of straight-line segments and circular arcs with the minimum radius that traverses the $\delta$-neighborhood of all the vantage points.

In DTSP, the shortest path between two configurations must be one of the six possible combinations: LSL, LSR, LRL, RSL, RSR, and RLR, where ’S’ means going straight and ’L’ and ’R’ denote left and right turn with the minimum turning radius, respectively, see Figure 2.

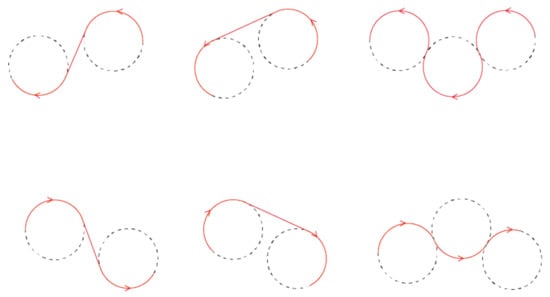
Figure 2. Six cases of Dubins curves.

2.2. Surveillance Algorithm

In this subsection, we present the proposed trajectory construction strategy. This strategy is based on a decomposition of the surveillance problem into a complete coverage problem and a DTSP. This strategy finds the waypoints to fully cover the area of interest first, and then plans trajectory along with these waypoints, such that the length of the path to visit all the waypoints is minimized.

2.2.1. Stage One: Waypoint Generation

In the first stage of the strategy, a method similar to [9] to estimate the minimal number of waypoint locations with coordinates on a given plane $z_p=z$ that is parallel to the ground is used. Then, the strategy finds the minimum altitude z to sense the achieved 2D coordinate.

The constructed triangulation consists of equilateral triangles, and the length of the side of all the triangles is $\sqrt{3}R$, where R is the radius of the vision-cone as defined in (3). We denote the direction of a side of a triangle with respect to a certain direction (such as the x-axis) as the angle of the triangle and we use $\lambda \in [0,\frac{\pi }{3})$ to represent this angle. Additionally, we denote $(x_0,y_0)$ as the coordinate of one of the vertices (see Figure 3a). Then, a triangulation can be represented by $\Delta (\lambda ,x_0,y_0)$. Moreover, in any triangle, the line segments connecting the center point, denoted by C, and the vertices divide the triangle into three congruent Voronoi cells. For instance, we use different colors to indicate these cells in Figure 3b. In an equilateral triangle with side length $\sqrt{3}R$, the distance between any two points in the same Voronoi cell is within R the radius of the FOV. It is obvious that the drone located at the same Voronoi cell to any point of the area of interest can cover at least this point of the area.

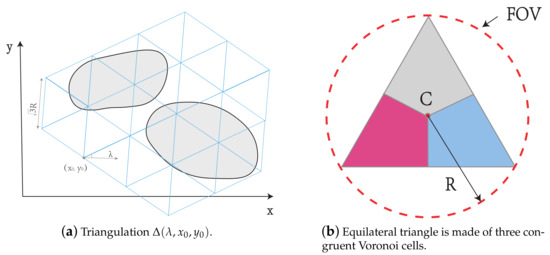
Figure 3. (a) Triangulation consists of equilateral triangles; (b) Congruent Voronoi cell.

Given similar environments in [9], the minimum number and the positions of waypoints are determined while decreasing the altitude z by 1 m each time from $z=Z_{min}=120$ m, and $\lambda ,x_0,y_0$ are randomly generated. Referring to the comparison results between [9,33], it is apparent that the method of [33] needs more waypoints than [9] to cover the same area at a similar altitude. So, the proposed method applies [9] for waypoint generation.

2.2.2. Stage Two: UAV Path Planning for Surveillance

We consider that the UAVs fly along Dubins paths. DTSP, as an extension of the Traveling Salesman Problem (TSP), assumes the salesman travels along the Dubins path, where the travel cost is proportional to length of the path [34]. The algorithms to derive the Dubins path can determine the shortest path connecting vantage waypoints generated in the first phase.

We briefly discuss two algorithms to address the DTSP problem, which are the alternating algorithm [34] and the spiral algorithm [25]. The alternating algorithm is an approximation algorithm to solve DTSP with given lower and upper bounds on solution quality. This algorithm computes the sequence of visits first uses the optimal solver for Euclidean TSP (ETSP) and then connects two waypoints by either an alternating straight-line and Dubins arc segments. The spiral algorithm is another popular DTSP surveillance algorithm. It links the chain of the convex hull of the given sets of waypoints. The shape of the resulting path resembles a spiral respecting the turning radius constraints.

When the waypoints are spare, i.e., when two waypoints are far enough with respect to the turning radius, the alternating algorithm computes the shortest path. By contrast, when the waypoints are dense, the spiral algorithm has been shown to be superior. In addition, the spiral algorithm is also more suitable for surveillance duty at low altitudes. The clustered spiral-alternating algorithm [35], which is actually a combination of the above two algorithms, is used in this paper to improve the effectiveness and efficiency of surveillance. To apply this algorithm we need to cluster the waypoints manually or by other methods. After clustering, waypoints in a cluster are dealt by the spiral algorithm. After this, the spiral paths for different clusters are combined, and the alternating line segments are replaced with Dubins segments to form the shortest path. From the observed result of total path length, the clustered spiral-alternating algorithm is always shorter than the original spiral algorithm in clusters. Compared to the alternating algorithm, the clustered spiral-alternating algorithm has fewer sharp turns.

The proposed scheme is also applicable when the target area consists of multiple disjointed areas (no overlaps). One of the most straightforward ways is to assign as many UAVs as the disjoint areas. The merits of the method include its simplicity, adaptability, and robustness against restricted communication among UAVs.

2.3. Simulation Results

In this section, computer simulation results are presented to demonstrate the effectiveness of the proposed approach.

2.3.1. Single-Area Surveillance

We first consider the vantage waypoints in a 700 × 900 m${}^2$ single area as shown in Figure 4a,b, which demonstrates the Voronoi diagram of the waypoints.

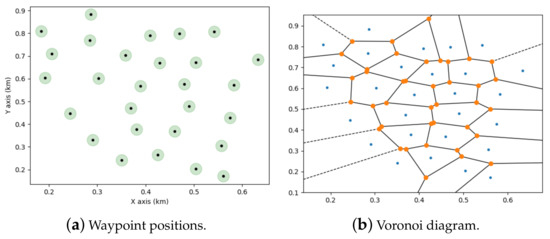
Figure 4. Single-area surveillance scenario.

Figure 5 shows the single UAV surveillance path generated by the spiral algorithm [34], the alternating algorithm [25], the genetic algorithm [17], Grey Wolf Optimizer (GWO) algorithm in [36], and the clustered spiral-alternating algorithm [35], respectively. We evaluated the selected clustered spiral-alternating algorithm with mentioned four algorithms in terms of path length and number of sharp turns. The path generated by clustered spiral-alternating algorithm Figure 5e is shorter than the spiral algorithm (SA) Figure 5a and Grey Wolf Optimizer (GWO) algorithm Figure 5c, and fewer sharp turns than the alternating algorithm (AA) Figure 5b and genetic algorithm (GA) Figure 5d. The straight-line segments and the Dubins segments are represented by yellow and red segments, respectively. The average execution times for the above methods are shown in Table 1. The average execution times for the above methods are shown in Table 1. The SA and AA are faster than the GWO, GA, and the proposed method. However, the proposed method has a far shorter path length than the SA method and fewer sharp turns than the AA method. The proposed method is available as an option when there is a tradeoff between the execution time and optimal path.

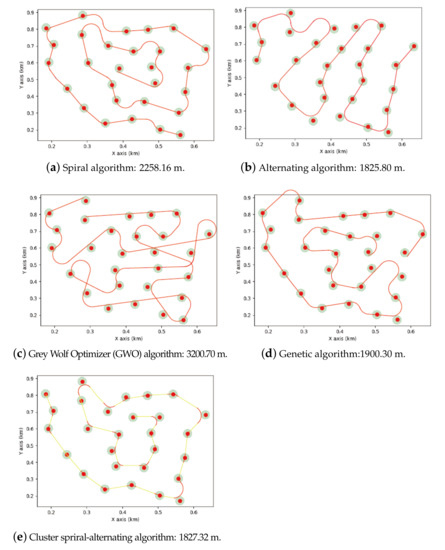
Figure 5. UAV surveillance trajectory—Single UAV.

Table 1. Average execution times (seconds) for the different algorithms.

Algorithm	Time (s)
SA	3.21
AA	3.69
GWO	16.14
GA	10.36
Proposed	4.84

2.3.2. Multiple Disjoint Areas Surveillance

The multiple disjoint surface area in a 600 × 600 m${}^2$ terrain is shown in Figure 6. In the first stage, the minimum number and position of the waypoints of our region of interest are generated and shown in Figure 6a, and the $\delta$-neighborhood of each individual vantage waypoint location is in Figure 6b. Then, the path is achieved using clustered spiral-alternating algorithm and Dubins curves. For our results in Figure 6c, two clusters are assigned to two UAVs, respectively. In addition, the coverage of the area of interest is achieved when both finish their surveillance circle. It makes the quick parallel surveillance possible and the subsequent task allocations simple.

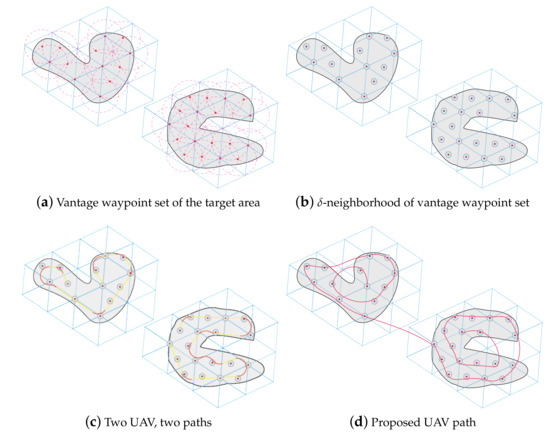
Figure 6. Proposed UAV surveillance in multiple disjoint surface area.

In the single UAV scenario, we can use only one drone to carry out the surveillance. With the consideration of computation efficiency, we decide to keep one obtained path and regenerate the other cluster’s path. The final surveillance planning with Dubins curves by the proposed algorithm shows in Figure 6d. The simulation result demonstrated the validation of the algorithm.

3. Surveillance Algorithm at Different Altitudes

This section considers a more challenging and realistic situation involving surveillance in geometrically complex environments, such as mountainous terrains and urban regions. Because the video camera can only see the points within its cone-shaped field of view (FOV), the FOV can be reduced when facing any kind of obstacle. Similar to our previous section, we address the mentioned problems separately, decoupling them into the waypoint-generation part and trajectory determination part.

3.1. Problem Statement

We consider the dynamic coverage problem in the target area, where UAVs keep flying through each pre-defined waypoint during surveillance and take video. The vehicle’s kinematic model at the point $p=(x,y,z)$ can be described as follows:

$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{z}\end{array}\right]=v\left[\begin{array}{c}cos\theta cos\psi \\ sin\theta cos\psi \\ sin\psi \end{array}\right]$$

(5)

where $\theta$ is the turning angle and $\psi$ is the pitch (climb/dive) angle. The state of our drone is $s=(p,\theta ,\psi )$.

Several assumptions described in the last section also apply to the model of the terrain. In the addressed reconnaissance and surveillance scenario, our UAV is equipped with a downward-facing video camera with a certain visibility angle. It can monitor the relatively small targets of interest on the ground with the required level of details within its FOV. Figure 7 is the onboard camera with a given visibility angle $0<\alpha <\pi$. The drone at $(x,y,z)$ can only see points $(x_g,y_g,z_g)$ that are inside the cone-shaped field of view (FOV) of radius on the target area

$$\begin{array}{cc}\hfill & R\left(z_g\right):=(z-z_g)·tan\left(\frac{\alpha }{2}\right),\hfill \\ \hfill & z>z_g.\hfill \end{array}$$

(6)

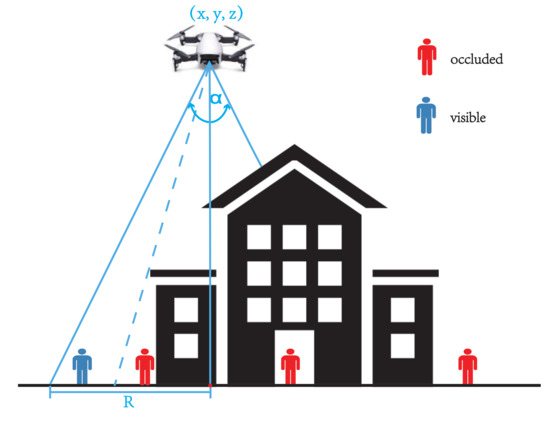
Figure 7. Occlusion effects on camera sensing.

The problem becomes to find the trajectory that goes through the $\delta$-neighborhood of all assigned vantage points, which take the optimization of the sequence of visits into account, i.e., a variant of the combinatorial traveling-salesman problem. The final trajectory is connected by a sequence of piecewise cubic Bézier curves that traverse the $\delta$-neighborhood of all assigned vantage points. A n degree Bézier curve can be parametrized as:

$$\mathsf{\Gamma }\left(t\right)=\sum _{i=0}^n{\mathbf{P}}_i{b}_{i,n}\left(t\right)$$

(7)

where ${\mathbf{P}}_i$ stands for the i-th control point, and $0\le t\le 1$. $b_{i,n}\left(t\right)$ is named the Bernstein polynomial and defined as follows:

$$b_{i,n}\left(t\right)=\left(\begin{array}{c}n\hfill \\ i\hfill \end{array}\right)t^i{(1-t)}^{n-i}$$

(8)

and $0\le t\le 1$. The binomial coefficient is given by

$$\left(\begin{array}{c}n\\ i\end{array}\right)=\frac{n!}{i!(n-i)!}$$

(9)

The used cubic Bézier curve is defined by four control points $({\mathbf{P}}_0,{\mathbf{P}}_1,{\mathbf{P}}_2,{\mathbf{P}}_3)$, and can be expanded as

$$\begin{array}{c}\hfill \mathsf{\Gamma }\left(t\right)={\mathbf{P}}_0{(1-t)}^3+3{\mathbf{P}}_{1}t{(1-t)}^2+3{\mathbf{P}}_2{t}^2(1-t)+{\mathbf{P}}_3{t}^3.\end{array}$$

(10)

As the final trajectory $\mathsf{\Gamma }$ is closed and smooth curve, which consists of n Bézier curves, two consecutive curves ${\mathsf{\Gamma }}_i$ and $\mathsf{\Gamma }j$ with control points $({\mathbf{P}}_0^i,{\mathbf{P}}_1^i,{\mathbf{P}}_2^i,{\mathbf{P}}_3^i)$ and $({\mathbf{P}}_0^j,{\mathbf{P}}_1^j,{\mathbf{P}}_2^j,{\mathbf{P}}_3^j)$ should be connected at the same endpoint:

$$\begin{array}{c}\hfill {\mathbf{P}}_3^i={\mathbf{P}}_0^j\end{array}$$

(11)

And the tangents ${\mathbf{t}}_a^i$ and ${\mathbf{t}}_b^i$ with length $\left|t_a^i\right|$ and $\left|t_b^i\right|$ of ${\mathsf{\Gamma }}_i$ and $\mathsf{\Gamma }j$ must point to the same direction to connect a sequence of Bézier curves into a smooth path:

$$\begin{array}{c}\hfill l_a^j{t}_b^i=l_b^i{t}_a^j\end{array}$$

(12)

where

$$\begin{array}{c}\hfill {\mathbf{t}}_a^i={\mathbf{P}}_1^i-{\mathbf{P}}_0^i,{\mathbf{t}}_b^i={\mathbf{P}}_3^i-{\mathbf{P}}_2^i,l_a^i=\left|t_a^i\right|,l_b^i=\left|t_b^i\right|.\end{array}$$

(13)

Compared with the constant speed Dubins, the multi-motor model can slow down turning and accelerate on fairly straight paths. For the UAV model, the multi-rotor UAV is preferred to the Dubins model with limited curvature. Therefore, the goal is to find the fastest traveling route for UAV under the limit of maximum speed and acceleration, instead of finding the shortest path under the limit of Dubins speed. In this case, this section does not consider minimizing the length of the track, but considers the expected travel time of the path.

3.2. Surveillance Algorithm

In this section, first, we try to find the vantage waypoint set that can completely cover the area of interest, and then search for a smooth trajectory along with these locations at different altitudes as quickly as possible, so as to minimize the completion time of visiting all the locations. We decompose the surveillance problem into a drone version of the 3D Art Gallery Problem and an instance of the combinatorial traveling-salesman problem.

3.2.1. Stage One: Vantage Waypoint Set Generation

The problem of finding the set of vantage waypoints can be regarded as a drone version of the 3D Art Gallery Problem. It has been proved to be NP-hard [37], and the approximation approach is always employed. In this section, we use a method similar to [38] to estimate the minimal number of the waypoints by method in [39], and the vantage waypoint set $P=\{p_1,\dots ,p_n\},p_i\in {\mathbb{R}}^3$ in two major steps. In the first step, the 2D coordinates $(x_i,y_i)$ of each vantage waypoints are determined. With the achieved 2D coordinates $(x_i,y_i)$, the optimal altitudes $z_i$ are in the second step.

We assumed the terrain $\mathcal{G}$ is a polygon with n vertices, and ${\mathcal{G}}_1,...,{\mathcal{G}}_i$ are obstacles inside $\mathcal{G}$ with $n_1,...,n_i$ vertices, respectively. Let ${\mathcal{E}}_1,...,{\mathcal{E}}_i$ be inside polygons of ${\mathcal{G}}_1,...,{\mathcal{G}}_i$, respectively. In addition, each ${\mathcal{E}}_i$ has same number of vertices $n_i$ as ${\mathcal{G}}_i$. We can consider ${\mathcal{E}}_i$ as and “top” face, and ${\mathcal{G}}_i$ as the corresponding “bottom” face of each obstacle polyhedron model. $\mathcal{P}$ is obtained from $\mathcal{G}$ without ${\mathcal{G}}_1,...,{\mathcal{G}}_i$, which is a non-convex polygon with i “holes”. Let $c>0$ be a given constant, we assume that the relative even area’s altitude $|z_g|\le c$, and $c+c_2\le Z_{min}$ holds. In addition, let ${\widehat{d}}_e:=max\left\{d_e,{\widehat{d}}_l\right\}$, $d_e$ is the maximum distance between $(x_i,y_i)$ to the corresponding vertices of ${\mathcal{E}}_i$, and b is the maximum altitude of the terrain points corresponding to the ${\mathcal{E}}_i$ and its side quadrilaterals. Let $d_l$ be the maximum length of the triangulation triangles sides whose vertex is one of the two end points. The developed Vantage Waypoint Set Generation algorithm can be found in Algorithm 1.

The number of waypoints in vantage waypoint set P is less than or equal to $\frac{n+2n_1+\cdots +2n_k+2k}{3}$, because the color with the minimum number of vertices will be selected after painting all vertices of the triangulation $\widehat{\mathcal{T}}$ by 3-coloring method (see from line 5–6 of Algorithm 1, vertices in $\widehat{\mathcal{T}}$ is $n+2n_1+\cdots +2n_k+2k$). For any waypoint $p_i=(x_i,y_i,z_i)$ generated by Algorithm 1, $(x_i,y_i)\in \mathcal{G}$ by line 2, and lines 9–12 guarantee $Z_{min}\le z_i\le Z_{max}$. As a result, (2) still hold. According to the construction (see line 1–4), every triangle of $\widehat{\mathcal{T}}$ can find a waypoint located at one of its vertices. Moreover, any point outside the obstacles ${\mathcal{G}}_1,...,{\mathcal{G}}_i$ falls in one of the triangles of triangulation $\mathcal{T}$, the drone located at one of the three vertices of this particular triangle can see this point with the altitude determined by line 10–12. Furthermore, for the“side” face of each obstacle, there exists a waypoint located at one of the four vertices with the altitude determined by line 10–11 can see any point of this “side” face. In addition, it is apparent that any point of a“top” face is visible to the drone located at the altitude determined by line 12. Consequently, the terrain $\mathcal{G}$ can be completely covered by $\frac{n+2n_1+\cdots +2n_k+2k}{3}$ waypoints or fewer.

Algorithm 1 Vantage Waypoint Set Generation

1: procedure STEP I 2:  Construct polygon $\mathcal{P}$ without “holes” by i non-intersect diagonals with $n+n_1+...+n_i+2i$ vertices 3:  Cut $\mathcal{P}$ into triangulation $\mathcal{T}$, whose vertices are $\mathcal{P}$’s, and sides are either $\mathcal{P}$’s or its diagonals. 4:  Build the dual graph of $\widehat{\mathcal{T}}$ by enlarging $\mathcal{T}$ by the vertices of ${\mathcal{E}}_i$ 5:  Paint the vertices of the triangulation $\widehat{\mathcal{T}}$ by 3-coloring method in [39] 6:  The minimum number of vertices subset of the three is selected as the 2D coordinates $(x_i,y_i)$ of the vantage waypoint set 7: end procedure 8: procedure Step II 9:  while $z_i\le Z_{max}$ do 10:   if $(x_i,y_i)$ is not a vertex of any polygons ${\mathcal{E}}_i,{\mathcal{G}}_i$then $$z_i:=max\left\{Z_{min},c+\frac{d_l}{tan\left(\frac{\alpha }{2}\right)}\right\}$$ 11:   else if $(x_i,y_i)$ is a vertex of some polygons ${\mathcal{E}}_i,{\mathcal{G}}_i$ then $$z_i:=max\left\{Z_{min},b+c_2+\frac{{\widehat{d}}_e}{tan\left(\frac{\alpha }{2}\right)}\right\}$$ 12:   else $$z_i:=max\left\{Z_{min},a+c_2+\frac{{\widehat{d}}_l}{tan\left(\frac{\alpha }{2}\right)}\right\}$$ 13:   end if 14:  end while 15: end procedure 16: return vantage waypoint set $P=\{p_1,\dots ,p_n\},p_i=(x_i,y_i,z_i)$

3.2.2. Stage Two: UAV Path Planning for Surveillance

As mentioned in the previous section, the final trajectory includes the $\delta$-neighborhood of the set of vantage waypoints to reduce the completion time. We do not directly tackle the coverage problems by visiting the neighborhoods. Regarding the kinematic constraints of the UAV, the variant of the combinatorial traveling-salesman problem is solved by introducing Self-Organizing Map (SOM) and Bézier curves.

As we assumed that the UAV will return to the initial location $p_1$ after the complete reconnaissance tour, $\delta =0$ for the initial location. With the vantage waypoint set $P=\{p_1,\dots ,p_n\},p_i\in {\mathbb{R}}^3$ generated above, and the given initial location $p_1$ and $\delta$, we can determine the final trajectory $\mathsf{\Gamma }$ as a sequence $\mathsf{\Sigma }=\left({\sigma }_1,\cdots ,{\sigma }_n\right)$ of Bézier curves ${\mathsf{\Gamma }}_i,1\le i\le n$. The final trajectory $\mathsf{\Gamma }=({\mathsf{\Gamma }}_{{\sigma }_1},\dots ,{\mathsf{\Gamma }}_{{\sigma }_n}),1\le {\sigma }_i\le n$, we need to minimize the estimation of the travel time $\mathbf{E}\left(\mathsf{\Gamma }\right)$, which can be determined from (10). To simplify the model, we employ the Model Predictive Controller (MPC) for path following, and the vertical and horizontal movements of the drone are individually considered. We denote $a_{ver}$, $v_{ver}$, $a_{hor}$, $v_{hor}$ as maximal vertical and horizontal accelerations and speeds, respectively. We also assume that the initial and final velocity of the drone is zero, so that the drone will start from the initial location $p_1$ with zero velocity and return back to it in the end. The estimation of the travel time $\mathbf{E}\left(\mathsf{\Gamma }\right)$ and the profile of the velocity can be computed by the method in [40] by maximum possible tangent acceleration $a_{tan}=\sqrt{a_{hor}^2-a_{rad}^2}$, $a_{rad}$ is the radial acceleration.

The adaptation can be considered to be a movement of the waypoint locations towards the alternate location $s_p$ and a new location of each adapted waypoint location $\nu$ becomes ${\nu }^{\prime }$ and it follows the standard SOM learning [41].

$${\nu }^{\prime }=\nu +\mu f(\sigma ,d)\left(s_p-\nu \right)$$

(14)

where $\mu$ is the learning rate, $\sigma$ is the learning gain, d is the distance of $\nu$ from the winner waypoint location ${\nu }^{*}$, and $f(\sigma ,d)$ is the neighboring function.

$$f(\sigma ,d)=\left\{\begin{array}{cc}{e}^{\frac{-d^2}{{\sigma }^2}}\hfill & \mathrm{for}d<0.2M\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(15)

where M is the current number of neurons in the SOM.

The surveillance planning algorithm will stop the adaptation if $i\le i_{max}$ or ${\nu }^{*}$ are negligibly close to their respective $s_p$, or all winner waypoint locations are inside the $\delta$-neighborhood of the respective initial waypoint location. Local Iterative Optimization (LIO) [42] is a procedure that optimizes the whole trajectory locally, e.g., it can consecutively optimize ${\theta }_i$, ${\psi }_i$, $l_a^i$, and $l_b^i$ in the loop with waypoint${\nu }_{i-1}$, ${\nu }_i$, and ${\nu }_{i+1}$. The reason (5) can optimize variables ${\theta }_i$, ${\psi }_i$, $l_a^i$ independently is tangent vector $t_a^i$ and $t_b^{i-1}$ implicitly satisfy the smooth constraint (12). $t_a^i$ and $t_b^{i-1}$ are related to the same waypoint ${\nu }_i$.

Otherwise, go to Step 3. An intersection of the straight-line segment $(s_p,p)$ with the sphere in ${\mathbb{R}}^3$ shaped $\delta$-neighborhood of p is used to determine the alternate location $s_p$ towards which the network is adapted instead of p to save the travel time.

We can easily extend the described mechanism into multiple UAV versions by two principal methods:

1

Once the surveillance path for single UAV is generated, we can distribute multiple UAVs travel along the same path as the single UAV, but with different initial position to avoid collisions. To avoid collisions, the initial deployment of UAVs must be coordinated with the drone’s velocity and the length of the path, by, for instance, evenly spacing the appropriate number of UAVs along the determined trajectory. Thereafter, each UAV can perform its surveillance duty independently without further coordination. This method can markedly reduce the surveillance circle or duration, and significantly increase the frequency and intensity of surveillance.

2

The vantage waypoint set can be partitioned into several subsets, and dedicated UAV(s) can traverse through each subset independently. In the case of multiple UAVs, we may use the aforementioned method to perform collision-free monitoring tasks.

We also analyze the complexity of the algorithm. In each learning epoch, the computational complexity depends on the number of waypoints n and the number of neurons in the SOM network M. Notice the SOM is a two-layered neural network, whose input layer is the locations of vantage waypoints $P=\{p_1,\dots ,p_n\},p_i\in {\mathbb{R}}^3$, and output layer is an array of adapted waypoint locations $\mathcal{N}=\{{\nu }_1,...,{\nu }_M\}$. As the algorithm regenerates the loop N with winner waypoints between $n-2n$ (see from line 8 of Algorithm 2), the complexity of the path-planning procedure is $O\left(n^2\right)$.

3.3. Simulation Results

To verify the effectiveness of the proposed algorithm, two simulation scenarios are given in this section. The target area is 20 m by 20 m terrain with $i=3$ random shaped obstacles are shown in Figure 8a, and the obstacles have $n_1=3,n_2=4,n_3=4$ vertices, respectively. The average execution times for the above methods are shown in Table 2, and the average velocities and coverage times for the different algorithms are shown in Table 3. Furthermore, the simulation is conducted with the following parameters in Table 4.

Algorithm 2 UAV Path-Planning Algorithm

1: Create the loop $\mathcal{N}$ with n waypoint locations around the initial location $p_1$ 2: Set the learning gain $\gamma =12.41n+0.6$, the learning rate $\mu =0.5$, and the gain decreasing rate $\eta =0.1$. Set the epoch counter $i=1$, $i_{max}=100$. 3: while the termination condition has not been reached do 4:  for $p\in \mathsf{\Pi }\left(P\right)$ do 5:   for each learning epoch do 6:    determine ${\nu }^{*}$ and $s_p$ 7:    Adapt ${\nu }^{*}$ and its neighbors towards $s_p$ using (7) 8:    remove all non-winner waypoint locations and perform LIO-based optimization of the trajectory 9:    Update learning parameters: $\gamma =(1-\eta )\gamma ,i=i+1$ 10:   end for 11:  end for 12: end for 13: return final trajectory $\mathsf{\Gamma }$

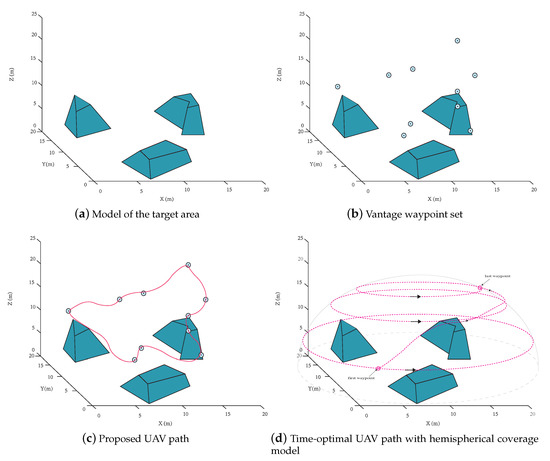
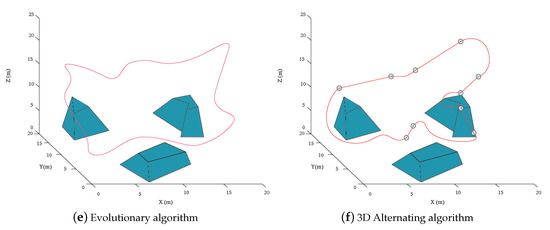
Figure 8. (a) the given environment, (b) the vantage waypoint set by the proposed method, UAV surveillance trajectory using (c) proposed strategy, (d) time-optimal strategy in [43], (e) evolutionary algorithm [44] and (f) 3D Alternating algorithm—Single UAV.

Table 2. Average execution times (seconds) for the different algorithms.

Algorithm	Single-Area Single UAV	Single-Area Multiple UAVs (Two UAVs, Two Paths)
TOS	3.48	4.53
3DAA	4.74	5.12
EA	5.30	5.91
Proposed	5.14	6.35

Table 3. Average velocity (meter/second) and coverage time (second) for the different algorithms.

Algorithm	Scenario	Average Velocity (m/s)	Minimum Coverage Time (s)
TOS	Single-Area Single UAV	6.5	22.2
	Single-Area Multiple UAVs (Three UAVs, three paths)	5.1	7.4
3DAA	Single-Area Single UAV	6.5	13.6
	Single-Area Multiple UAVs (Two UAVs, two paths)	6.5	8.7
EA	Single-Area Single UAV	6.6	12.5
	Single-Area Multiple UAVs (Two UAVs, two paths)	6.8	6.5
Proposed	Single-Area Single UAV	6.8	7.9
	Single-Area Multiple UAVs (Two UAVs, two paths)	6.8	4.2

Table 4. Simulation Parameters.

Camera
$\theta$	$H_{min}$	$c_1$	$c_2$	c
$\frac{\pi }{2}$	4 m	1 m	0.5 m	0.2 m
Mobility of UAV for proposed method				Mobility of UAV for time-optimal method
$a_{ver}$	$a_{hor}$	$v_{ver}$	$v_{hor}$	$a_z$	$v_z$	$v_f$
0.5 m/s${}^2$	1.2 m/s${}^2$	0.5 m/s	1.2 m/s	0.5 m/s${}^2$	0.5 m/s	1.2 m/s

3.3.1. Single-Area Single UAV

To confirm the performance of our monitoring strategy in a complex environment, we performed validation in the following scenario. First, we apply the proposed Vantage Waypoint Set Generation in step one to obtain the waypoint set that can fully cover the target area. Figure 8b shows the $\delta$-neighborhood of all 10 waypoint locations at different heights from 6.4 m to 23.3 m. Secondly, we compare the proposed UAV path with the three mentioned methods’ paths in terms of operation time and surveillance quality. In accordance with surveillance quality, we take the smoothness of the path, path length, and whether the uncovered area exits into consideration. Under the same velocity profiles as our proposed method, the time-optimal strategy (TOS) [43], evolutionary algorithm (EA) [44], and 3D Alternating algorithm (3DAA) then run under the same environment. The proposed algorithm (see Figure 8c) and evolutionary algorithm (see Figure 8e) are superior to the time-optimal surveillance path-planning algorithm (see Figure 8d) and 3D alternating algorithm see Figure 8f) in terms of operation time. The time-optimal surveillance path-planning algorithm is the most straightforward method and smoothest path among them. Nonetheless, it inevitably neglects the problems caused by occlusion, so we may need to apply the geometric calculation to calculate the uncovered part and deploy other unmanned aerial vehicles to cover it completely. On the other hand, the evolutionary algorithm has a longer path and more sharp turns.

3.3.2. Single-Area Multiple UAVs

In this scenario, multiple UAVs are being used for full coverage reconnaissance and surveillance missions. The same waypoint positions are shown in Figure 8b. Figure 9a shows two drones in different initial positions share the same route. Figure 9b shows the situation where each UAV has a separate track to cover part of the terrain. Moreover, when both complete their monitoring circle, the coverage of the region of interest is realized. In both scenarios, the duration of covering the region of interest is obviously increased, so the average time of covering any point between two continuous times is reduced by about $47\%$. In other words, the points of interest are monitored more often. We also deploy three UAVs to cover each individual obstacle as a comparison. However, the uncovered part due to the overlapping of the flight surfaces is inevitable. Another two methods are applied for two UAVs to conduct the surveillance duty in Figure 9d,e. In this case, the evolutionary algorithm generates a smoother path than the proposed one. However, the proposed algorithm still outperforms the 3D alternating algorithm with a shorter length and fewer sharp turns. Table 3 shows the average velocity and minimum coverage time in both scenarios. The proposed approach shown in Figure 8c has the minimum coverage time in the single UAV scenario, and Figure 9a has the minimum coverage time in the multiple UAV scenario. Table 2 shows the computational time of the simulation above. The time-optimal strategy and 3D alternating algorithm take less time to cover the target area than the other two methods because of the lower computation load. Moreover, the evolutionary algorithm compromises the surveillance quality with computation time.

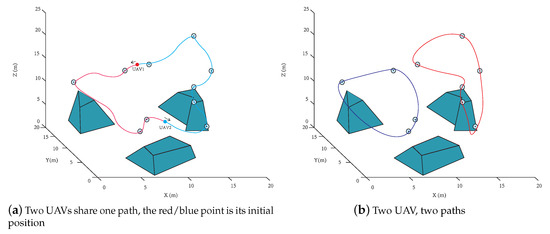
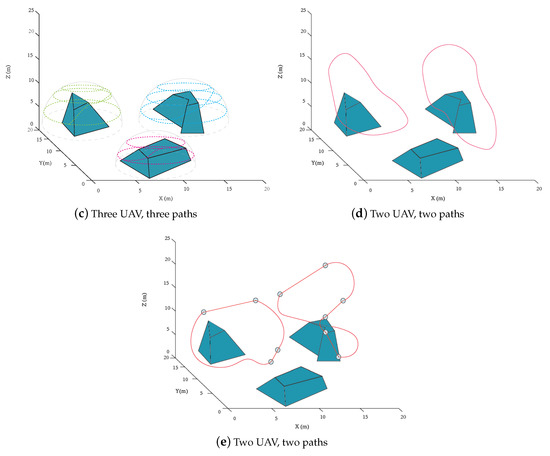
Figure 9. UAV surveillance trajectories using (a,b) proposed strategy and (c) time-optimal strategy in [43], (d) evolutionary algorithm [44], and (e) 3D alternating algorithm—Multiple UAVs.

4. Conclusions and Future Work

We consider the dynamic coverage problem over the target area, where UAVs keep flying through each pre-defined waypoint during surveillance and taking video. In the first part, we propose a two-stage strategy to cover the target area completely at a given height. We tackle this thorny problem by decomposing it into a variant of the waypoint-determination problem and an instance of the Dubins Traveling Salesman Problem. An asymptotically optimal waypoint-generation algorithm is proposed, in the sense that the number of waypoints is closing to the minimum number of the waypoints as the target area tends to infinity. In addition, the proposed method considers solving the Dubins Vehicle Traveling-Salesman Problem (DTSP) by introducing the clustering spiral alternation algorithm, thus its performance is guaranteed to be better or the same as the benchmark methods. Furthermore, the trajectory takes into account the kinematics constraints of the UAV.

In the second part, we consider the reconnaissance and surveillance of UAV flying in complex geometric environments, such as mountainous and urban areas. We propose a two-stage strategy to completely cover the target area with different heights. The main contribution of this paper includes providing a method to determine the minimum number of waypoints that need to be visited and drawing a track at a given height to monitor the area, as well as an occlusion-aware UAV monitoring strategy based on UAV kinematic constraints and obstacle occlusion. The operation time and surveillance quality including smoothness, path length, and whether the uncovered area exits are considered to compare the performance of the described approach with the state of the art. The unsupervised learning method Self-Organizing Map (SOM) and Bézier curves are used to generate a smooth and fast trajectory for the UAV. The proposed method achieves closer performance to the best performance among benchmarks. The performance and effectiveness of the two proposed algorithms have been confirmed by extensive computer simulations in different scenarios.

In the future research of occlusion-aware UAV surveillance, the change of the environment during the mission is an inevitable technical challenge to build an effective and efficient UAV surveillance system. For instance, drones should be able to change, adapt, modify and optimize paths to handle the occlusions by moving obstacles. It would be very interesting to modify the trajectories of the UAVs during the mission execution to avoid the occlusion effects by large moving objects.