1. Introduction
Much interest and research on drones, also known as Unmanned Aerial Vehicles, are attributed to the fact that drones do not require on-board pilots and road. Much research has been conducted in various fields such as healthcare delivery, border surveillance, damage assessment, and remote sensing [
1,
2,
3,
4]. In the aforementioned applications, the flight capability of drones to reach a remote area is mainly limited by the performance of the battery [
5,
6]. The limited flight duration per a fully charged battery on drones is revealed to be one of the major obstacles for the current drone technology to be practically useful in the above mentioned applications. The flight duration of drones is relatively short so that drones are required to return to a station or control center to exchange or recharge their batteries. This is inefficient and may not achieve a seamless flight mission over border areas requiring 24/7 operations [
7].
Some research efforts have been made to resolve this issue including high performance batteries [
8], autonomous battery swapping systems [
9], Stationary Wireless Charging Systems (SWCS) [
10,
11,
12,
13], in-flight charging (hovering mode) [
14], and Dynamic Wireless Charging Systems (DWCS) [
2]. The SWCS is a stationary pole, pad, or box type system that recharges a drone battery through wireless power transfer (WPT) methods while landing on its surface [
10], and the DWCS is a system similar to the electrified road (lane) for ground electric vehicles [
15], in which the drone battery can be recharged by flying (dynamic) over the WPT system which consists of multiple coiled lines [
2]. The DWCS presented in [
2] is practically feasible for implementation considering the related technologies that are currently being developed [
14].
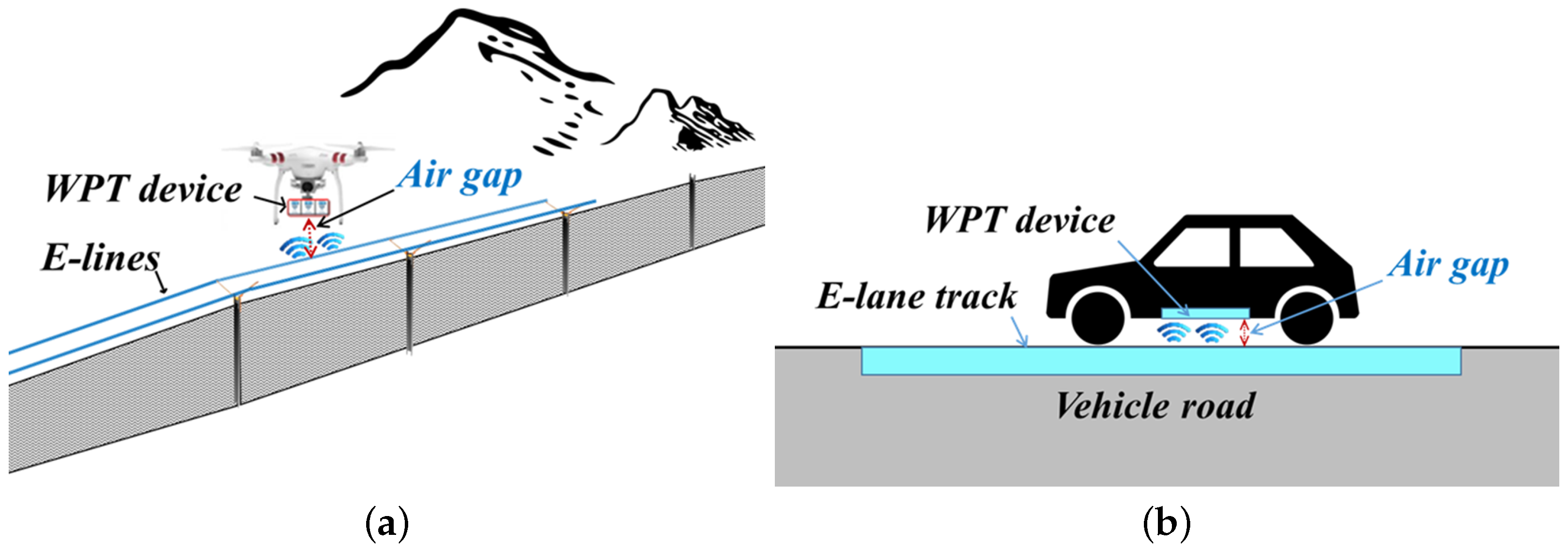
To increase the capacity (performance) of the battery, the size of the battery needs to be increased. However, this causes other problems. First, the weight of the drone increases due to the increase in battery size. This results in more battery consumption and/or reduction in payload. As a result, it may be hard to get the enhanced-effect of the big-sized battery. Second, the enhanced battery may require a longer charging time at stations. Lengthy charging times at stations can interfere with seamless or urgent flight missions. The three methods (high performance batteries, autonomous battery swapping systems, and SWCS) all need drones to return, land, or stop for battery replacement or charging. The DWCS method charges a drone battery using dynamic WPT similar to the SWCS; however, the DWCS differs from the SWCS in that it does not require landing/stopping of the drone [
2]. The main drawback of the DWCS, however, is an uncertain rate of the WPT. It may not guarantee a constant WPT rate due to the variability of the air gap, which is the distance between a drone and the DWCS (see
Figure 1a). It is important to keep a certain distance in order to achieve a desired rate of the WPT, but it is difficult for drones to keep a certain distance in DWCS. As shown in
Figure 1a, unlike ground electric vehicles (EVs) that keep a certain distance from the DWCS (Electrified lane:
E-lane) installed on the road through vehicle tires in contact with the road (
Figure 1b), a drone does not have a physical device or system that can keep a certain distance from the DWCS (Electrified lines:
E-lines [
2]). Thus, considering the drone’s physical features and the real flight environment (strong winds), the planned charging level after flying over the DWCS (
E-line systems) may not be attained due to the uncertainty in the WPT rate (efficiency) of the DWCS.
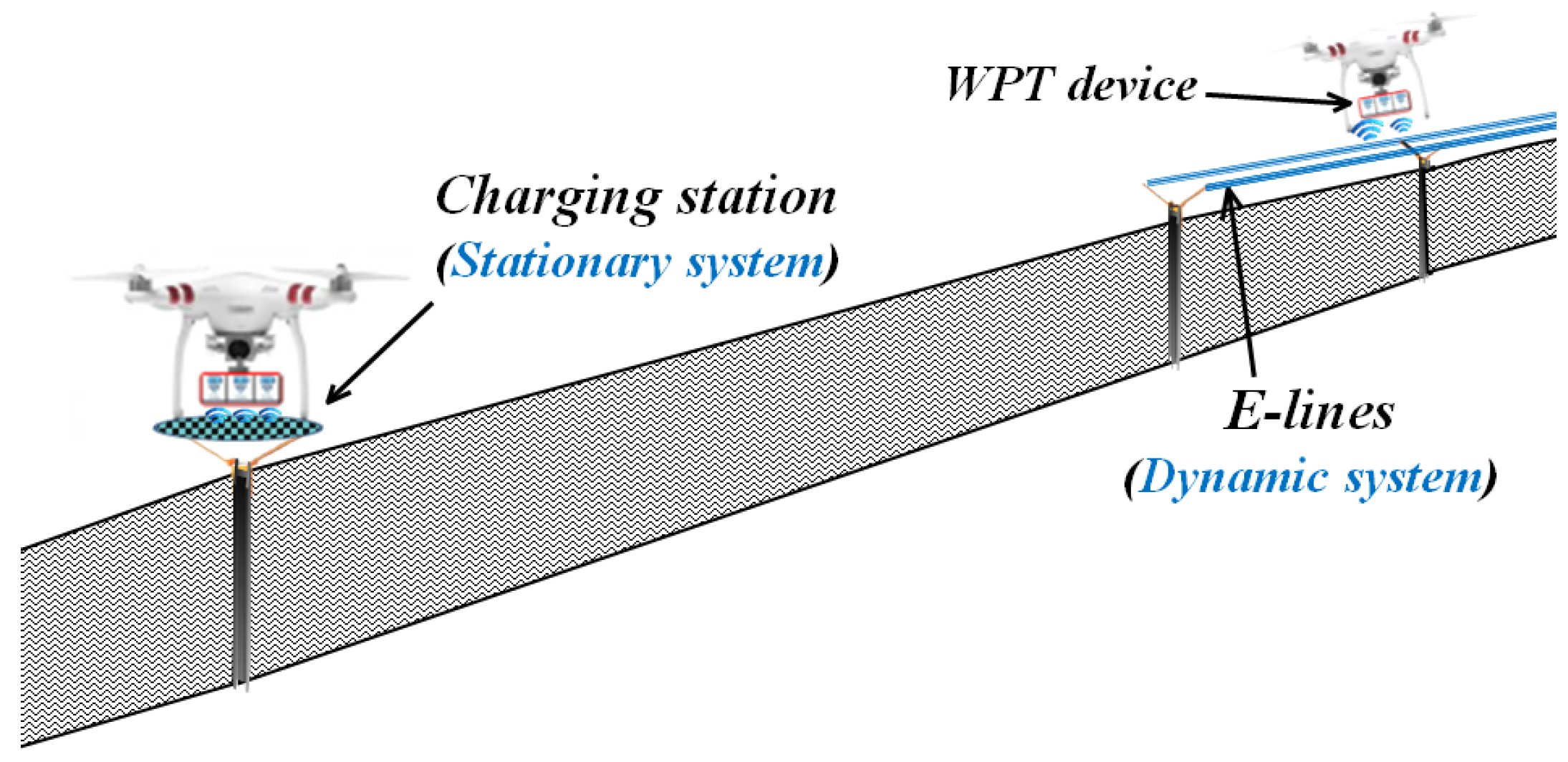
Therefore, this paper proposes a hybrid approach to overcome these issues on wireless charging systems. As shown in
Figure 2, the hybrid approach is to combine the strengths of both stationary and dynamic charging systems to extend the flight duration of drones in real time. If the DWCS cannot guarantee a sufficient charging efficiency, the SWCS can compensate for the insufficient amount of the WPT efficiency.
Using the hybrid approach of battery charging system, the primary goal of this paper is to determine how many systems (SWCS and DWCS) are needed and where they should be installed for drone-aided border surveillance.
The main contributions of this work to the existing body of literature are summarized as follows:
To extend the capability of drones using the proposed hybrid approach: By implementing the proposed hybrid approach, we can lengthen the flight duration per charge from the initial launching point.
To cope with the uncertainty in the DWCS and reduce the landing time of drones on the SWCS: The proposed hybrid approach can complement the major drawback of each wireless charging system.
To propose a mathematical model to determine optimal locations of the wireless charging systems so as to minimize the total cost of the hybrid system. Furthermore, the proposed model provides optimal drone flight paths including the time to land on the SWCS.
The rest of this paper is organized as follows.
Section 2 specifies the problem with assumptions applied in this work. A mathematical model is formulated for the problem in
Section 3. We illustrate the numerical results from a case study in
Section 4.
Section 5 contains concluding remarks with future research.
2. Problem Description
This paper proposes a new method to extend the flight capability of drones in real time. The new method is to combine two wireless charging methods (stationary wireless charging systems and dynamic wireless charging systems) into a hybrid mode. By utilizing both systems at the same time, we can mitigate the limitation of each method.
This work is to determine optimal installation and operating time of each system and an optimal flight path for drones while minimizing total operation and installation cost of the hybrid system. For a routine flight mission such as border patrol, drones are deployed to obtain information on suspicious objects. Rotary-wing drones are assumed in this paper. Unlike fixed-wing drones, the rotary-wing drones can be easily controlled to land on the SWCS. The installation cost of each system incurs once, the operation cost of each system incurs per utilization.
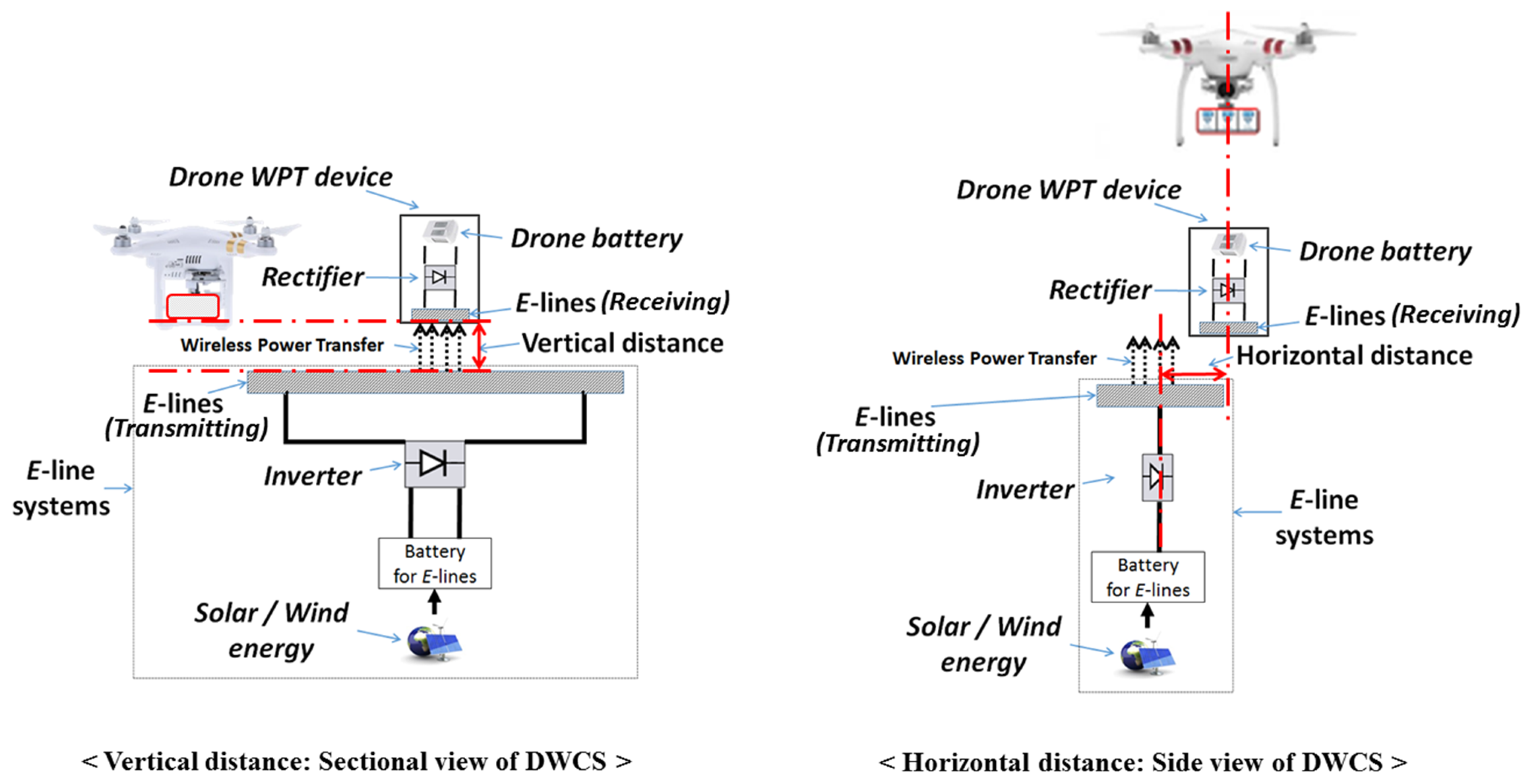
To delineate this uncertainty of the efficiency in the DWCS, we refer to the results from [
13]. They obtained the efficiency of a SWCS by varying the vertical and horizontal distances between a drone and a SWCS. As shown in
Figure 3, the vertical distance is the difference between the
E-lines, and the horizontal distance is the difference between the centers of the
E-lines. The stored electricity powered by renewable sources, such as wind and solar energy, is wirelessly transferred to a drone’s battery by magnetic resonant coupling methods [
11] through an inverter device embedded in the DWCS, transmitting
E-lines on the DWCS, receiving
E-lines under drone’s WPT device, and a rectifier device embedded in drone’s WPT device, successively. In this process, the efficiency of the WPT is affected by the vertical and horizontal distances [
16].
According to the results from [
13], the WPT efficiency in varying vertical distance slowly decreases with the increase of the vertical distance whereas the efficiency in varying horizontal distance decreases more sharply with the increase of the horizontal distance. There is a certain threshold in the distance where the efficiency converges to zero. The efficiency varies from zero to a maximum value according to the distance. However, it is currently not possible to get a reasonable relationship between the efficiency and the distances (varying both distances: vertical and horizontal) because there are many factors that affect the power transfer efficiency such as
E-line shape, size, turns, input-power, and frequency. The general trend is that the efficiency decreases as the distance (air gap) increases [
17,
18]. Moreover, the flight trajectory of the rotary-wing drone (the distance between a drone and a DWCS varied with flight) varies with flight environment. Hence, we assume that the variability of the air gap is equally distributed, and the power transfer efficiency in the DWCS (DCE) follows a uniform distribution. In addition, the flight speed of the drones is assumed constant for all flights.
Note that the two distances (vertical and horizontal) in the SWCS keep certain values to get a maximum efficiency while the drone lands on the SWCS. The SWCS has limited space to accommodate multiple drones at the same time. We assume that the value of efficiency of the SWCS is proportional to the landing time of drones on the SWCS. Moreover, the operation cost of the SWCS incurs proportionately to the number of drones landed on the SWCS as well as the time spent by drones on the SWCS. Other factors such as battery life degradation, weight of the WPT device, and payload in the process of the WPT are beyond the scope of this paper.
3. Mathematical Formulation Model
In this section, we propose a mathematical model to illustrate the hybrid approach for drones to extend its flight capability by charging wirelessly. The mathematical optimization model of the proposed method is expressed below:
The objective of this model (
1) is to minimize the total cost of the hybrid system including the installation and operation cost of the hybrid system (DWCS and SWCS) as well as the drone operation cost. The first term is the total operation cost of drones, the second term is the total cost associated with the DWCS, and the third term is the total cost associated with the SWCS. As described in
Section 2, the operation costs of the drones, DWCS, and SWCS incur proportionately to the amount of utilization of each one (the number of flights for a mission per given period:
m).
Constraints (
2) and (
3) ensure that a waypoint can be visited more than once by drones for the purpose of returning to a depot or visiting its first waypoint. The flow conservation of the drone flight is ensured by Constraint (
4). Constraint (
5) is utilized to make sure that the drone returns to the initial depot. Constraints (
6) and (
7) are to check whether a drone is utilized from an initial depot. Constraints (
8) and (
9) define the possible number of flights over the first flight segment (from the initial launching depot to the first visiting waypoint: outbound) and the last flight segment (from the last visiting waypoint to the initial launching depot: inbound), in which the number of possible flights (
or
) is mainly determined by the flight environment such as mountain, building, and non-flying zone. Constraint (
10) ensures to accomplish the flight mission of drones. The number of possible flights between waypoints (
) is determined by decision makers (flight purpose).
Considering flight environments such as mountain and wetland, some flight segments or waypoints may not be allowed to install the DWCS or the SWCS. To reflect this property of the flight environment, Constraints (
11)–(
13) are developed: Constraints (
11) and (
12) are for the installation possibility of the DWCS, and Constraint (
13) is for the installation possibility of the SWCS. Constraints (
14) and (
15) are to count the number of drones that land on the SWCS at the same time. As described in
Section 2, the operation cost of the SWCS incurs proportionately to the number of drones in recharging process. The charging level of the drone battery cannot exceed its maximum capacity (Constraint (
16)), and the maximum flight duration of the drone flight path is confined by Constraint (
17). Constraints (
18)–(
23) are to calculate the remaining battery duration whenever the drone arrives at the next waypoint. When the drone arrives at its first visiting waypoint from the launching point (depot), the amount of its remaining battery is determined by constraints (
18) and (
19). It is not necessary to consider the SWCS at the launching depot because the drone takes off with its fully charged battery from the launching point (
= 0). Constraints (
20) and (
21) are to define the remaining battery duration while the drone flies over between waypoints except the depot. The final remaining battery duration of the drone is determined by constraints (
22) and (
23). To prevent sub-tours, Constraint (
24) is implemented [
19,
20].
4. Numerical Experiments
In this section, we analyze a case study to show how the proposed mathematical model works. In
Section 4.1, the setup of the case study is explained in detail.
Section 4.2 shows the numerical results and analysis on the results.
Section 4.3 analyzes the results in terms of the one-time service time to complete the flight only once for the border surveillance. The mathematical optimization model is implemented in GAMS 25.1.1 [
21] and then solved by BARON 18.5.8 [
22]. All experiments are performed on a server running RedHat Linux 64-bit with an Intel Xeon processor and 16GB of RAM.
4.1. A Case Study
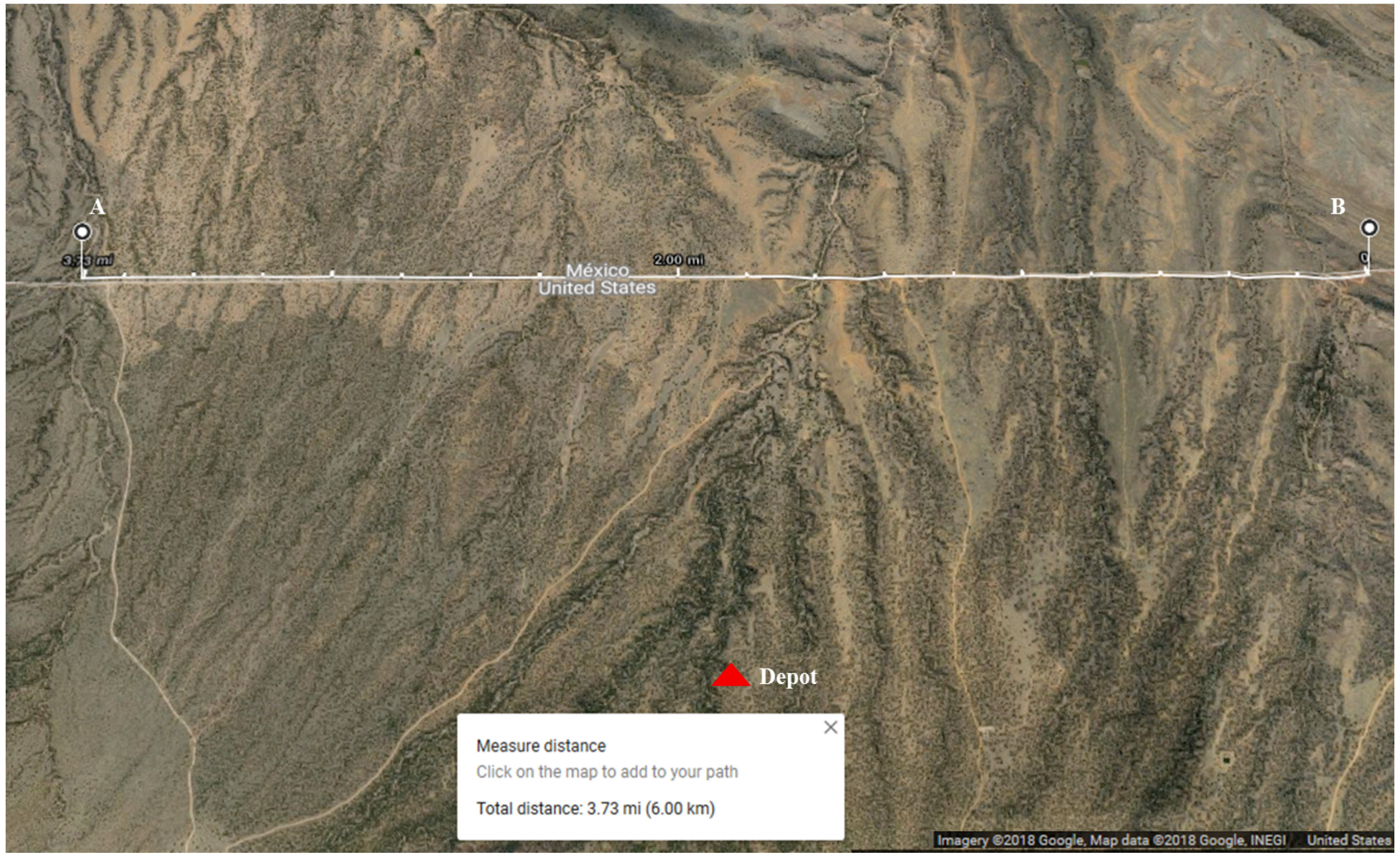
For the case study, we selected a part of the U.S. - Mexico border located in Arizona state in the U.S., having a length of 6 km (A-B) as shown in
Figure 4. Over this area, drones are required to conduct surveillance missions (routine flight mission) under the control of the center (Depot).
The parameters used in the case study are shown in
Table 1. In this case study, there are two types of drones to be utilized for surveillance missions. We assumed that the minimum installation length of the DWCS is 250 m, which is used as the unit length to get virtual waypoints between A and B. Hence, we get twenty-four flight segments (twenty-five waypoints) between A and B. Those waypoints are labeled as
to
. The efficiency of the DWCS follows a uniform distribution as described in
Section 2, in which we tested our proposed model with varying minimum values of the DCE (from 0.0 to 0.4: varying the interval). In the SWCS, the charging efficiency is assumed as 0.5 min per minute, and the capacity to accommodate drones is set as 1 (
= 1). In addition, the surveillance mission should be conducted 300 times per given period (
).
4.2. Numerical Results
The numerical results from the case study are shown in
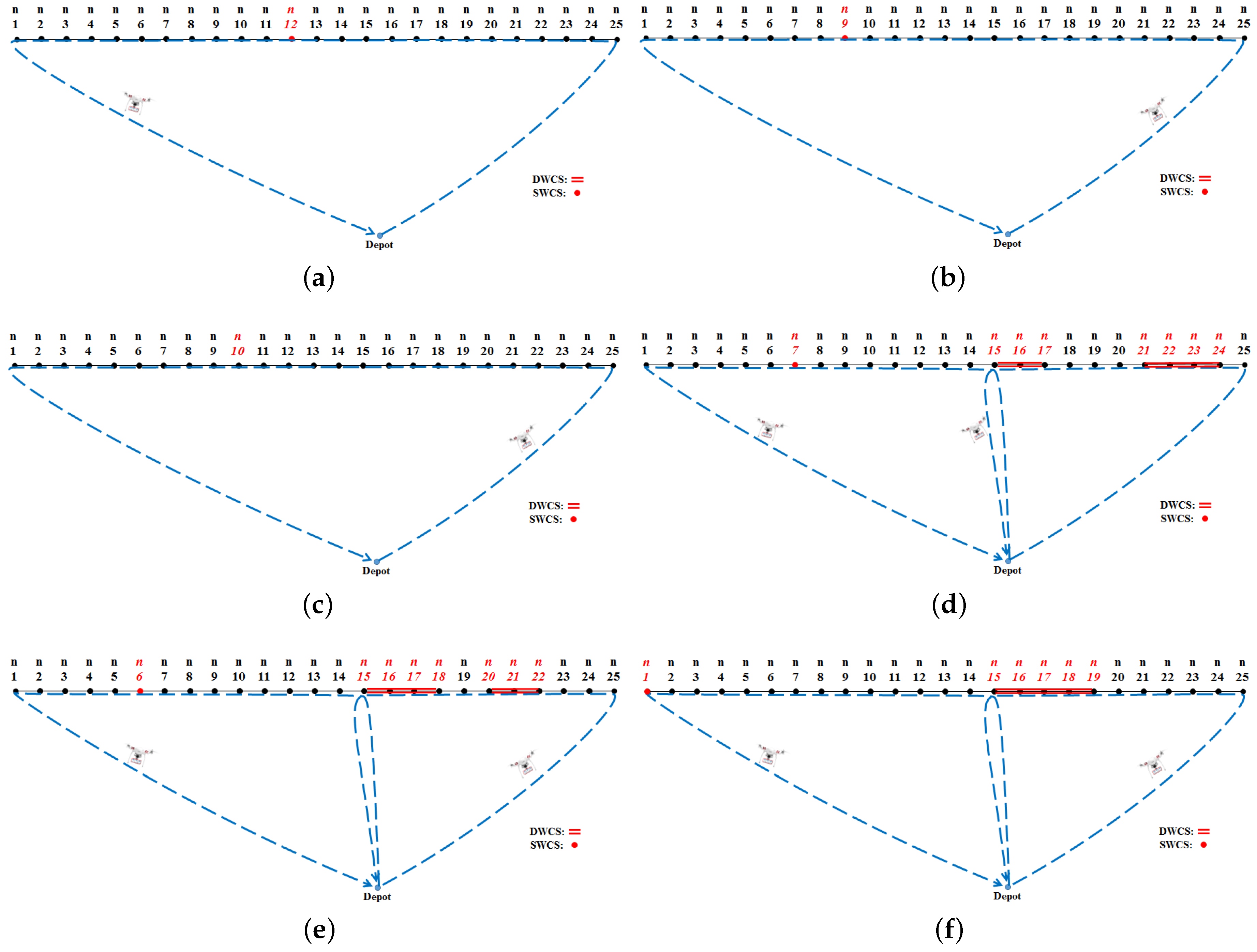
Table 2, and the optimal flight paths of drones are shown in
Figure 5. We also provided the result and an optimal flight path for drones with a constant value of DCE (Constant 0.5 min) to compare with the consequence of uncertain values of DCE.
When the value of the DCE follows a uniform distribution over the interval [0.0, 0.5], only the SWCS and one drone (Type I ) are needed to monitor the border area. The drone lands on the SWCS installed at waypoint 12 (
) and stops its flight for 58 min to recharge its battery. After that, the drone visits the remaining waypoints and returns to its initial launching waypoint (Depot). The total cost of conducting this mission over a given period (
) is
$27,400. This result is also shown when the value of the DCE follows a uniform distribution over the interval [0.1, 0.5] or [0.2, 0.5]. The difference between these results is the location of the SWCS installation. Depending on the location, the flight direction (clockwise or counter-clockwise) changes as shown in
Figure 5a–c.
However, when the value of the DCE follows a uniform distribution over the interval [0.3, 0.5] or [0.4, 0.5], it shows different results. First, under these intervals, both the DWCS and the SWCS are needed and two drones (Type I) are to be employed to patrol the border area. One of the two drones uses the DWCS while the other uses the SWCS to conduct a given mission as shown in
Figure 5d,e. The total length of the DWCS is 1.25 km, installed on the right side of the border (
Figure 5d,e. The drone that uses the SWCS lands for 22 min at the waypoint where the SWCS is installed. After charging its battery, the drone conducts the surveillance mission on the left side of the border. The total cost corresponding to these operations and installations is
$27,225, which is a decrease of 0.63% from the previous results (
$27,400 →
$27,225). In addition, if the DWCS ensures a constant DCE as planned (i.e., constant value: 0.5 min), we can reduce its installation length by 20% (1.25 km → 1.00 km) as shown in
Table 2. Accordingly, the cost of additional installation/operation of the DWCS to cope with the uncertainty in the DCE can be reduced (
$27,225 →
$26,900) while providing the surveillance mission with the same flight conditions in terms of the required number of drones and the landing time (
) (
Figure 5f).
From the results, this proposed method can lengthen the flight duration of the Type I drone (30 min → 32–59 min). Moreover, we can see that if the value of the DCE is maintained above a certain level, the time spent on the SWCS to recharge the drone battery is significantly reduced (58 min → 22 min). If the value of the DCE is not within a certain range, there is no need to utilize the DWCS. It means that we can get the benefits (reduced landing time and extended flight duration) of the hybrid system by ensuring a certain range of the DCE even though there is uncertainty in the DCE.
4.3. Analysis on One-Time Surveillance Flight
We analyzed the required time to finish a one-time surveillance mission, which is the time it takes for drones to take off from the Depot and return to the Depot, completing the flight mission only once. A surveillance mission in border areas should be a 24/7 operation [
7], so the required time for the one-time surveillance flight of drones is important if there is no other border surveillance system except drones to monitor a border area. Results under varying intervals of the DCE value are shown in
Table 3.
The required time to finish a one-time surveillance flight in the interval [0.0, 0.5], [0.1, 0.5], or [0.2, 0.5], is 117 min because only one drone is utilized to monitor the border area. The waypoints aside from the one where the SWCS is installed are not monitored by the drone for 117 min. These waypoints would be blind spots for 117 min if there is no other surveillance system. However, in the interval [0.3, 0.5] or [0.4, 0.5], the required time significantly reduces to 32 or 63 min. In these cases, two drones are assigned to the border area, so that the times spent by the two drones are 32 and 63 min, respectively. Hence, by ensuring a certain level of the DCE value, we can reduce the time that the border area is left uncontrolled. These results in
Table 3 show that the value of the DCE has an effect on the surveillance mission for this case study.
5. Conclusions
We proposed the hybrid approach to extend flight duration of drones flying over border areas. To deal with a short flight duration, uncertain charging efficiency of a dynamic wireless power transfer, and the need for landing or stopping of drones for recharging during flights, the hybrid approach has been proposed. The hybrid system consisted of two methods, DWCS and SWCS. One method compensated for the other’s drawback.
For this problem, we proposed the mathematical optimization model to decide optimal installation locations of the hybrid system and optimal flight paths for a surveillance mission on the border. Our case study suggested that the hybrid approach had benefits such as reducing landing time on the SWCS (58 min → 22 min) and uncontrolled time for most of the case study area (117 min → 32–63 min) if the efficiency of the DWCS is kept over a certain value (DCE: Uniform (0.2, 0.5)), and extending flight duration (30 min → 32–59 min).
As an extension of this work, one may include other distribution data for the value of the DCE and different flight speeds of drones when drones fly over the DWCS in a scaled down system.