Robust Optimal Consensus Control for Multi-Agent Systems with Disturbances

Highlights

What are the main findings?

• A novel improved nonlinear extended state observer (INESO) is designed to achieve real-time estimation of unknown disturbances in multi-agent systems (MASs), significantly enhancing system robustness through an effective compensation mechanism.
• A momentum-accelerated Actor–Critic network is developed that substantially improves convergence speed and suppresses unstable oscillations during multi-agent consensus.

What are the implications of the main findings?

• The proposed distributed optimal disturbance rejection control protocol provides a scalable solution for nonlinear MASs under unknown disturbances, overcoming the inherent trade-off between convergence rate and stability in existing methods.
• This framework establishes a reliable technical foundation for UAV swarm applications in search and rescue, logistics, and inspection missions, demonstrating improved cooperative stability in disturbed environments.

Abstract

The purpose of this article is to develop optimal control strategies for discrete-time multi-agent systems (DT-MASs) with unknown disturbances, with the goal of enhancing their consensus performance and disturbance rejection capabilities. Complex flight conditions, such as the scenario of multi-unmanned aerial vehicle (multi-UAV) maintaining consensus under strong wind gusts, pose significant challenges for MAS control. To address these challenges, this article develops an optimal controller for UAV-based MASs with unknown disturbances to reach consensus. First, a novel improved nonlinear extended state observer (INESO) is designed to estimate disturbances in real time, accompanied by a corresponding disturbance compensation scheme. Subsequently, the consensus error systems and cost functions are established based on the disturbance-free DT-MASs. Building on this, a policy iterative algorithm based on a momentum-accelerated Actor–Critic network is proposed for the disturbance-free DT-MASs to synthesize an optimal consensus controller, whose integration with the disturbance compensation scheme yields an optimal disturbance rejection controller for the disturbance-affected DT-MASs to achieve consensus control. Comparative quantitative analysis demonstrates significant performance improvements over a standard gradient Actor–Critic network: the proposed approach reduces convergence time by 12.8%, improves steady-state position accuracy by 22.7%, enhances orientation accuracy by 42.1%, and reduces overshoot by 22.7%. Finally, numerical simulations confirm the efficacy and superiority of the method.

1. Introduction

In recent years, growing research interest in cooperative control of multi-agent systems (MASs) has emerged, motivated by extensive applications in unmanned air vehicle (UAV) [1], aerospace robotics [2], autonomous vehicles [3], and smart grids [4]. As a cornerstone of cooperative control, consensus problems constitute a fundamental research focus, wherein control protocols ensure state agreement among agents [5,6,7,8]. Notably, the consensus problem of MASs is a comprehensive interdisciplinary field encompassing artificial intelligence [9], computer science [10], control theory [11], and communication technology [12]. However, it is insufficient for MASs to achieve consensus alone in practice, and practical objectives typically require simultaneous optimization of control costs, leading to optimal consensus control frameworks [13,14].

It is well established that optimal consensus control depends on solving the coupled Hamilton–Jacobi–Bellman (HJB) equations, which are generally intractable for analytical solutions [15,16]. Consequently, developing computationally feasible and efficient methods to overcome this challenge remains an open and significant research problem [17]. Fortunately, adaptive dynamic programming (ADP) [18,19,20] has received increasing attention as a powerful machine learning and optimization strategy for addressing the above-mentioned difficulties in the past several decades. This approach tackles optimal control problems forward-in-time assisted by approximators, such as neural networks (NNs). Within the existing literature on ADP control for nonlinear systems, policy iteration (PI) is extensively utilized and is typically implemented via Actor–Critic networks using standard gradient descent learning. An online adaptive PI algorithm in Vamvoudakis and Lewis [21] was developed to solve optimal control problems, utilizing the classic Actor–Critic framework with gradient descent-based learning, and rigorous proofs for stability and convergence were provided. Subsequently, a novel data-based adaptive dynamic programming method was developed in [22] to solve the optimal consensus tracking problem for discrete-time multi-agent systems (DT-MASs) with multiple time delays, which also relies on gradient descent-driven Actor–Critic networks to realize policy iteration. Building upon this line of work, ref. [23] introduced an event-triggered control scheme to alleviate communication burdens while retaining the gradient-based Actor–Critic design for policy learning. Notably, in the context of UAV swarm coordination, ADP-based approaches have shown significant promise. For instance, ref. [24] developed an ADP-based optimal formation control protocol for UAVs, enabling distributed learning without requiring precise system models. Similarly, online ADP algorithms have been proposed to solve the cooperative tracking control problem for multiple UAVs, achieving optimal performance through critic-only network design [25]. These studies demonstrate the potential of ADP in addressing the computational challenges of coupled HJB Equations for MASs, especially in complex platforms like UAVs. While these ADP approaches offer promising solutions for optimal consensus control, they face significant challenges when applied to practical MASs operating in disturbed environments. A critical limitation in existing ADP-based consensus control approaches is their inability to simultaneously achieve fast convergence and stable performance [26]. The standard gradient descent methods employed in Actor–Critic networks often result in either prolonged training times or oscillatory behavior, severely constraining their applicability in real-time multi-agent scenarios where both rapid consensus and operational stability are paramount.

Beyond these inherent challenges in ADP methods, practical implementations of MASs inevitably encounter unknown disturbances, which critically impede optimal consensus control [27,28,29]. This is particularly acute in UAV swarm applications, where agents are exposed to time-varying wind gusts, payload uncertainties, and complex aerodynamic interactions. For instance, ref. [30] investigated the impact of wind disturbances on UAV formation stability, while [31] addressed robust trajectory tracking for quadrotors under both model uncertainties and external disturbances. For dynamical systems subject to external disturbances, the robust control problem can be reformulated as an optimal control framework through proper selection of the cost function [32]. However, this method requires a priori knowledge of the disturbances bound, which may reduce the actual robustness. In [33], an enhanced ESO-based feedback control scheme was developed, specifically designed for multi-input multi-output (MIMO) systems to improve disturbance compensation. Building upon this foundation, the active disturbance rejection control (ADRC) method proposed in [34] utilizes an extended state observer (ESO) to simultaneously estimate both exogenous disturbances and system uncertainties. In [35], an ESO is designed for a single nonlinear system to simultaneously estimate system states and total disturbances, with real-time compensation achieved. The study in [36] addresses the tracking control problem for uncertain surface vessels (SVs) subject to external disturbances by proposing a disturbance observer (DO)-based optimal control scheme with ADP. An intelligent transportation system disturbance suppression method was proposed in [37], where the event-triggered observer was used to estimate the disturbances, and the upper bound of the disturbances was processed by the adaptive compensation law. This method avoided the Zeno behavior while ensuring the boundedness of the tracking error.

Despite significant advances in optimal consensus control, ADP frameworks, and ESO-based disturbance estimation for MASs, critical limitations persist in existing methodologies. First, Actor–Critic training strategies relying on standard gradient descent exhibit an inherent trade-off between convergence rate and stability, where low learning rates slow convergence while high learning rates induce destabilizing oscillations [21,23,38], which severely constrains the real-time control performance of MASs. Second, conventional observers, typically based on linear assumptions, may struggle to achieve rapid and accurate estimation when dealing with the complex, nonlinear, and time-varying disturbances commonly encountered in UAV swarms [37,39], such as wind gusts, thereby compromising disturbance rejection and degrading system performance. To holistically address these dual challenges, this article introduces an integrated solution framework. The principal innovations are summarized as follows:

• A novel improved nonlinear extended state observer (INESO) is designed to realize the real-time estimation of the unknown disturbances of DT-MASs. The unknown disturbances are effectively handled by a compensation mechanism, and the robustness of the systems is significantly improved.
• A momentum-accelerated Actor–Critic network is developed for DT-MASs to accelerate state convergence and suppress unstable behaviors. The problem of a slow convergence rate of the standard gradient descent method is effectively overcome by historical gradient information, and the state convergence time is shorter for DT-MASs to achieve stability.
• A distributed optimal disturbance rejection consensus control protocol is proposed for DT-MASs subject to unknown disturbances to reach consensus. Relying solely on local neighbor interactions, this protocol guarantees scalability to arbitrarily large-scale networks.

The remainder of this article is organized as follows. The preliminaries on graph theory and neural network are introduced in Section 2. The dynamics of DT-MASs under unknown disturbances and the definition of consensus, along with the underlying research motivation, are presented in Section 3. In Section 4, an INESO is designed to estimate the disturbances, and a momentum-accelerated Actor–Critic network and an optimal control protocol are proposed for DT-MASs to reach consensus. Simulations and discussions follow in Section 5 and Section 6. Finally, Section 7 concludes this work.

2. Preliminaries

2.1. Algebraic Graph Theory

The communication topology among agents is described by a directed graph $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{A})$, where $\mathcal{V}=\{1,2,\dots ,N\}$ is the node set, $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$ denotes the edge set, and $\mathcal{A}=\left[a_{ij}\right]\in {\mathbb{R}}^{N\times N}$ represents the weighted adjacency matrix, where $a_{ij}>0$ iff $(j,i)\in \mathcal{E}$, otherwise $a_{ij}=0$. Self-loops are excluded, i.e., $a_{ii}=0$. The neighbor set of node $i\in \mathcal{V}$ is ${\mathcal{N}}_i=\{j\mid (j,i)\in \mathcal{E}\}$, where agent j is a neighbor of agent i. The in-degree matrix $\mathcal{D}=diag\{d_1,\dots ,d_i,\dots ,d_N\}$ is defined by $d_i={\sum }_{j\in {\mathcal{N}}_i}{a}_{ij}$, yielding the Laplacian matrix $\mathcal{L}=\mathcal{D}-\mathcal{A}$. A directed graph is said to contain a spanning tree if there exists at least one node, called the root, from which there is a directed path to every other node. This structural feature is essential for ensuring global information propagation throughout MASs.

2.2. Neural Network

Neural network (NN) is widely recognized for their capability to universally approximate any continuous function $F\left(X\right)$:$R^n\to R^m$ with arbitrary accuracy over a compact subset $X\subset R^n$. The NN-based approximation of $F\left(X\right)$ can be expressed as

$$\begin{array}{c}\hfill F\left(X\right)=W^{T}S\left(X\right),\end{array}$$

(1)

where $W\in R^{p\times m}$ represents the weight matrix with p neurons, and $S\left(X\right)=[S_1\left(X\right)$, $S_2\left(X\right)$, …, $S_p{\left(X\right)]}^T\in R^p$ denotes the vector of Gaussian basis functions.

For the NN approximation (1), there exists an ideal weight matrix $W^{*}$, such that $F\left(X\right)$ can be reformulated as

$$\begin{array}{c}\hfill F\left(X\right)={W^{*}}^{T}S\left(X\right)+\delta \left(X\right),\end{array}$$

(2)

where $\delta \left(X\right)\in R^m$ is the approximation error satisfying $\parallel \delta \left(X\right)\parallel \le \vartheta$, and $\vartheta$ is a small positive constant.

The ideal weight matrix $W^{*}$, introduced solely for analytical purposes, is defined as the solution to the following optimization problem

$$\begin{array}{c}\hfill W^{*}:=arg\underset{W\in R^{p\times m}}{min}\left\{\underset{X\in \Omega }{sup}\parallel F\left(X\right)-W^{T}S\left(X\right)\parallel \right\},\end{array}$$

(3)

where ${sup}_{X\in \Omega }$ denotes the supremum of the approximation error over the compact set $\Omega$. This means that $W^{*}$ is chosen to minimize the worst-case approximation error across the entire operating region $\Omega$, ensuring uniform approximation performance.

3. Problem Formulation

3.1. Modeling Assumptions and Motivation

The multi-agent coordination problem in drone swarms is intrinsically rooted in three-dimensional space. However, to elucidate the core control mechanisms with enhanced clarity and prevent analytical interference from the holistic complexity of three-dimensional dynamics, this study strategically confines both system modeling and convergence analysis to a two-dimensional plane. This dimensional reduction transcends mere formal simplification, constituting a focused methodological approach that isolates motion space dimensions weakly correlated with collaborative consensus, thereby intensively investigating the pivotal scientific challenge of achieving state consensus under wind disturbance conditions. The rationale for this approach stems fundamentally from the dominance of horizontal lateral components in both planar coordinated dynamics among agents and wind disturbances. The design and verification within this two-dimensional framework facilitate thorough characterization of algorithmic performance at the theoretical stage, establishing a robust foundation for subsequent extension to three-dimensional space. Accordingly, the validity of this dimensionally reduced modeling paradigm is substantiated through the following two principal aspects:

• Application Context: The primary motivation stems from a broad category of real-world applications where drone swarms predominantly operate in planar configurations. A representative example is precision agriculture, where coordinated drone formations are deployed for monitoring vast croplands. In such missions, drones typically maintain a predetermined constant altitude to achieve uniform area coverage, thereby effectively constraining their operational space to an approximately horizontal plane. While minor altitude adjustments may occur, the core coordination tasks—formation maintenance, collision avoidance, and consensus on flight paths—remain fundamentally two-dimensional problems within the $(x,y)$ plane. Focusing on this plane enables the isolation and rigorous analysis of swarm responses to lateral wind disturbances, which constitute the primary source of trajectory deviations in outdoor environments.
• Methodological Rationale: This reduction from 3D to 2D represents an established and justified methodology in robotics and control theory for initial theoretical development. The 2D model preserves the fundamental challenges of multi-agent consensus, such as nonlinear dynamics and disturbance rejection, while significantly enhancing analytical clarity and reducing computational overhead in simulations [24]. It serves as a critical and necessary first step toward understanding the core principles of the proposed coordination algorithm before undertaking more complex 3D extensions. We explicitly acknowledge that a full 3D model, incorporating turbulent wind fields and vertical dynamics, remains the ultimate objective for real-world deployment. The insights gained from this 2D study will provide a solid foundation for such future work.

In conclusion, the 2D modeling paradigm adopted in this article is a deliberate and justified strategy to make a clear, verifiable, and significant contribution to the theory of robust cooperative control. It allows us to answer critical scientific questions with a level of rigor that would be severely compromised in a more complex setting. We explicitly acknowledge that the final goal is 3D deployment, and the results presented here constitute a vital and necessary step toward that ambitious objective. The subsequent discussion and future work sections will outline the specific pathway for this 3D extension, building directly upon the theoretical foundation established in this study.

3.2. System Dynamics

Assume that UAV-based DT-MASs comprise a disturbance-free leader and N followers subject to unknown disturbances, and that all UAVs are flying at the same altitude. Given these assumptions, the system can be modeled in a two-dimensional plane [24], and the dynamics of the i-th follower, which is also the i-th agent, can be governed by

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{x}_i(k+1)\\ y_i(k+1)\\ {\theta }_i(k+1)\end{array}\right]& =\left[\begin{array}{c}{x}_i\left(k\right)\\ y_i\left(k\right)\\ {\theta }_i\left(k\right)\end{array}\right]+\mathcal{T}\left[\begin{array}{cc}cos\left({\theta }_i\left(k\right)\right)& 0\\ sin\left({\theta }_i\left(k\right)\right)& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}{v}_i\left(k\right)+d_{i1}\left(k\right)\\ w_i\left(k\right)+d_{i2}\left(k\right)\end{array}\right],\hfill \end{array}$$

(4)

where the state vector of agent $i(i\in \mathcal{V})$ is defined by the vector $(x_i\left(k\right)$, $y_i\left(k\right)$, ${\theta }_i{\left(k\right))}^T\in R^3$, $\mathcal{T}$ is the sampling period, the control input vector is represented by $(v_i\left(k\right)$, $w_i{\left(k\right))}^T\in R^2$, and the unknown disturbances is denoted by $d_{i1}\left(k\right)\in R$ and $d_{i2}\left(k\right)\in R$. Specifically, $x_i\left(k\right)$ and $y_i\left(k\right)$ are the position coordinates representing the UAV’s location in the Cartesian plane, while ${\theta }_i\left(k\right)$ is the orientation angle denoting the UAV’s heading direction, measured counterclockwise from the positive x-axis. The control input $(v_i\left(k\right)$, $w_i{\left(k\right))}^T$ consists of $v_i\left(k\right)$, the linear velocity along the current heading direction ${\theta }_i\left(k\right)$, and $w_i\left(k\right)$, the angular velocity controlling the rate of orientation change. The terms $d_{i1}\left(k\right)$ and $d_{i2}\left(k\right)$ represent unknown but bounded input disturbances affecting the linear velocity and angular velocity channels, respectively, which may arise from environmental factors, model uncertainties, or external disturbances.

The operator ${\Lambda }_i\left(k\right)$ is defined as the transformation matrix that converts the control inputs from the UAV’s body-fixed frame to the global inertial frame. This matrix is constructed based on the current orientation angle ${\theta }_i\left(k\right)$ and has the specific form:

$${\Lambda }_i\left(k\right)=\left[\begin{array}{cc}cos\left({\theta }_i\left(k\right)\right)& 0\\ sin\left({\theta }_i\left(k\right)\right)& 0\\ 0& 1\end{array}\right].$$

The first column, containing $cos\left({\theta }_i\left(k\right)\right)$ and $sin\left({\theta }_i\left(k\right)\right)$, projects the linear velocity $v_i\left(k\right)$ onto the global x and y axes, respectively. The second column maps the angular velocity $w_i\left(k\right)$ directly to the orientation dynamics, as orientation is already defined in the global frame.

If $(x_i\left(k\right)$, $y_i\left(k\right)$, ${\theta }_i{\left(k\right))}^T$=$X_i\left(k\right)$, $(v_i\left(k\right)$, $w_i{\left(k\right))}^T$=$u_i\left(k\right)$, and $(d_{i1}\left(k\right)$, $d_{i2}{\left(k\right))}^T$=$d_i\left(k\right)$, then system (4) can be compactly expressed as

$$\begin{array}{cc}\hfill X_i(k+1)& =X_i\left(k\right)+\mathcal{T}{\Lambda }_i\left(k\right)(u_i\left(k\right)+d_i\left(k\right)),\hfill \end{array}$$

(5)

where ${\Lambda }_i\left(k\right)$ is the transformation matrix defined above. Similarly, the dynamics of the leader can be expressed as

$$\begin{array}{cc}\hfill X_0(k+1)& =X_0\left(k\right)+\mathcal{T}{\Lambda }_0\left(k\right)u_0\left(k\right),\hfill \end{array}$$

(6)

where $X_0\left(k\right)$ = $(x_0\left(k\right)$, $y_0\left(k\right)$, ${\theta }_0{\left(k\right))}^T\in R^3$, ${\Lambda }_0\left(k\right)$ is defined in the same manner as ${\Lambda }_i\left(k\right)$, and $u_0\left(k\right)$=$(v_0\left(k\right)$, $w_0{\left(k\right))}^T\in R^2$.

3.3. Control Object

In order to investigate the robust optimal consensus control of DT-MASs (5) and (6), the consensus error system for agent i is defined as

$$\begin{array}{c}\hfill {\epsilon }_i\left(k\right)=\sum _{j\in {\mathcal{N}}_i}{a}_{ij}(X_i\left(k\right)-X_j\left(k\right))+a_{i0}(X_i\left(k\right)-X_0\left(k\right)).\end{array}$$

(7)

In distributed control frameworks, each agent’s decision-making relies on both its own state information and that received from neighboring agents within the network. Consequently, for the DT-MASs described by (5) and (6), the performance index associated with agent i is influenced not only by its own control input $u_i\left(k\right)$ but also by the control input $u_j\left(k\right)$ of its neighbor j and the consensus error system ${\epsilon }_i\left(k\right)$. To capture this interdependence, the cost function for agent i is defined as

$$\begin{array}{cc}\hfill J_i({\epsilon }_i\left(k\right),u_i\left(k\right),u_j\left(k\right))=& \sum _{l=k}^{\infty }{\mu }^{(l-k)}{C}_i({\epsilon }_i\left(l\right),u_i\left(l\right),u_j\left(l\right))\hfill \\ \hfill =& \sum _{l=k}^{\infty }{\mu }^{(l-k)}({\epsilon }_i^T\left(l\right)S_{ii}{\epsilon }_i\left(l\right)+u_i^T\left(l\right)R_{ii}{u}_i\left(l\right)\hfill \\ \hfill & +\sum _{j\in {\mathcal{N}}_i}{u}_j^T\left(l\right)R_{ij}{u}_j\left(l\right)),\hfill \end{array}$$

(8)

where $C_i({\epsilon }_i\left(l\right),u_i\left(l\right),u_j\left(l\right))$ is the instantaneous cost founction at step l, $S_{ii}\ge 0$, $R_{ii}\ge 0$, and $R_{ij}\ge 0$ are all positive symmetric matrices, and $0<\mu \le 1$ is the discount factor.

The control objective is to design the control input $u_i\left(k\right)$, such that the cost function (8) is minimized while ensuring that the DT-MASs (5) and (6) satisfy the consensus condition, thereby achieving robust optimal consensus control. The consensus condition is given as

$$\begin{array}{c}\hfill \underset{k\to +\infty }{lim}∥X_i\left(k\right)-X_0\left(k\right)∥\le \varrho ,\forall i\in \mathcal{V},\end{array}$$

(9)

where $\varrho$ is an arbitrarily assigned nonnegative constant that represents the maximum allowable state error for the DT-MASs (5) and (6). The control input $u_i\left(k\right)$ can constitute an optimal consensus controller for the i-th agent when the DT-MASs (5) and (6) satisfy the consensus condition (9).

4. Main Results

This section first designs an INESO for real-time estimation of unknown disturbances and then constructs a disturbance compensation scheme. Subsequently, a momentum-accelerated Actor–Critic network is proposed for the disturbance-free DT-MASs to synthesize an optimal consensus controller, whose integration with the disturbance compensation scheme yields an optimal disturbance rejection controller for the disturbance-affected DT-MASs to achieve consensus control.

4.1. Improved Nonlinear Extended State Observer

To estimate the unknown disturbance $d_i\left(k\right)$, an INESO is designed as

$$\begin{array}{cc}\hfill {\widehat{X}}_i(k+1)& ={\widehat{X}}_i\left(k\right)+\mathcal{T}{\Lambda }_i\left(k\right)(u_i\left(k\right)+{\widehat{d}}_i\left(k\right))-\mathcal{T}{\alpha }_i{\Psi }_1({\xi }_i\left(k\right),{\varsigma }_i,{\gamma }_i,{\beta }_i),\hfill \\ \hfill {\widehat{d}}_i(k+1)& ={\widehat{d}}_i\left(k\right)-\mathcal{T}{\zeta }_i{\Lambda }_i^T\left(k\right){\Psi }_2({\xi }_i\left(k\right),{\lambda }_i,{\eta }_i,{\chi }_i),\hfill \end{array}$$

(10)

where

• ${\widehat{X}}_i\left(k\right)\in R^3$ is the estimate of $X_i\left(k\right)$;
• ${\widehat{d}}_i\left(k\right)\in R^2$ is the estimate of $d_i\left(k\right)$;
• ${\xi }_i\left(k\right)=X_i\left(k\right)-{\widehat{X}}_i\left(k\right)\in R^3$ is the state estimation error vector;
• ${\alpha }_i>0$, ${\zeta }_i>0$, $0<{\gamma }_i<1$, ${\beta }_i\ge 0$, $0<{\eta }_i<1$, ${\chi }_i\ge 0$ are tunable parameters;
• ${\varsigma }_i$ and ${\lambda }_i$ are arbitrarily small positive constants;
• ${\Psi }_1({\xi }_i\left(k\right),{\varsigma }_i,{\gamma }_i,{\beta }_i)\in R^3$ and ${\Psi }_2({\xi }_i\left(k\right),{\lambda }_i,{\eta }_i,{\chi }_i)\in R^3$ are nonlinear functions defined by

$$\begin{array}{cc}\hfill {\Psi }_1({\xi }_i\left(k\right),{\varsigma }_i,{\gamma }_i,{\beta }_i)& =\left\{\begin{array}{cc}(\parallel {\xi }_i\left(k\right){\parallel }^{{\gamma }_i-1}+{\beta }_i){\xi }_i\left(k\right),\hfill & \parallel {\xi }_i\left(k\right)\parallel >{\varsigma }_i,\hfill \\ ({\varsigma }_i^{-(1-{\gamma }_i)}+{\beta }_i){\xi }_i\left(k\right),\hfill & \parallel {\xi }_i\left(k\right)\parallel \le {\varsigma }_i,\hfill \end{array}\right.\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\Psi }_2({\xi }_i\left(k\right),{\lambda }_i,{\eta }_i,{\chi }_i)& =\left\{\begin{array}{cc}(\parallel {\xi }_i\left(k\right){\parallel }^{{\eta }_i-1}+{\chi }_i){\xi }_i\left(k\right),\hfill & \parallel {\xi }_i\left(k\right)\parallel >{\lambda }_i,\hfill \\ ({\lambda }_i^{-(1-{\eta }_i)}+{\chi }_i){\xi }_i\left(k\right),\hfill & \parallel {\xi }_i\left(k\right)\parallel \le {\lambda }_i.\hfill \end{array}\right.\hfill \end{array}$$

(12)

Theorem 1.

Consider the DT-MASs (5) equipped with the INESO (10). If the following conditions hold

(i) 

The disturbance difference $\Delta d_i\left(k\right)=d_i(k+1)-d_i\left(k\right)$ is bounded, i.e., there exists a positive constant ${\overline{d}}_i$ such that $\parallel \Delta d_i\left(k\right)\parallel \le {\overline{d}}_i$ for all k;

(ii) 

The parameters ${\alpha }_i$, ${\zeta }_i$, ${\varsigma }_i$, ${\gamma }_i$, ${\beta }_i$, ${\lambda }_i$, ${\eta }_i$, and ${\chi }_i$ are chosen such that the induced matrix norm (or spectral radius) of $A_{INESO}\left(k\right)$ satisfies

$$\begin{array}{c}\hfill \parallel A_{INESO}\left(k\right)\parallel \le \sigma <1,\mathrm{for}\mathrm{all}k,\end{array}$$

(13)

where σ is a positive constant,

$$\begin{array}{c}\hfill A_{INESO}\left(k\right)=\left[\begin{array}{cc}(1+\mathcal{T}{\alpha }_{i}h(\parallel {\xi }_i\left(k\right)\parallel \left)\right)I_{3\times 3}& \mathcal{T}{\Lambda }_i\left(k\right)\\ \mathcal{T}{\zeta }_{i}g(\parallel {\xi }_i\left(k\right)\parallel ){\Lambda }_i^T\left(k\right)& I_{2\times 2}\end{array}\right],\end{array}$$

(14)

$$\begin{array}{c}\hfill h(\parallel {\xi }_i\left(k\right)\parallel )=\left\{\begin{array}{cc}(\parallel {\xi }_i\left(k\right){\parallel }^{{\gamma }_i-1}+{\beta }_i),\hfill & \parallel {\xi }_i\left(k\right)\parallel >{\varsigma }_i,\hfill \\ ({\varsigma }_i^{-(1-{\gamma }_i)}+{\beta }_i),\hfill & \parallel {\xi }_i\left(k\right)\parallel \le {\varsigma }_i,\hfill \end{array}\right.\end{array}$$

and

$$\begin{array}{c}\hfill g(\parallel {\xi }_i\left(k\right)\parallel )=\left\{\begin{array}{cc}(\parallel {\xi }_i\left(k\right){\parallel }^{{\eta }_i-1}+{\chi }_i),\hfill & \parallel {\xi }_i\left(k\right)\parallel >{\lambda }_i,\hfill \\ ({\lambda }_i^{-(1-{\eta }_i)}+{\chi }_i),\hfill & \parallel {\xi }_i\left(k\right)\parallel \le {\lambda }_i,\hfill \end{array}\right.\end{array}$$

• then the estimation error ${\Gamma }_i\left(k\right)={[{\xi }_i{\left(k\right)}^T,{\phi }_i{\left(k\right)}^T]}^T={[{(X_i\left(k\right)-{\widehat{X}}_i\left(k\right))}^T,{(d_i\left(k\right)-{\widehat{d}}_i\left(k\right))}^T]}^T$ is uniformly ultimately bounded. Moreover, there exists a finite time step K such that for all $k>K$, the estimation error is bounded by $\parallel {\Gamma }_i\left(k\right)\parallel \le {\kappa }_i$, where the ultimate bound ${\kappa }_i$ is given by

$$\begin{array}{c}\hfill {\kappa }_i={\displaystyle \frac{{\overline{d}}_i}{1-\sigma }}.\end{array}$$

(15)

Proof. 

From the system dynamics (5) and the INESO (10), the state estimation error

$$\begin{array}{cc}\hfill {\xi }_i(k+1)& =X_i(k+1)-{\widehat{X}}_i(k+1)\hfill \\ \hfill & =[X_i\left(k\right)+\mathcal{T}{\Lambda }_i\left(k\right)(u_i\left(k\right)+d_i\left(k\right))]\hfill \\ \hfill & -[{\widehat{X}}_i\left(k\right)+\mathcal{T}{\Lambda }_i\left(k\right)(u_i\left(k\right)+{\widehat{d}}_i\left(k\right))-\mathcal{T}{\alpha }_i{\Psi }_1({\xi }_i\left(k\right),{\varsigma }_i,{\gamma }_i,{\beta }_i)]\hfill \\ \hfill & ={\xi }_i\left(k\right)+\mathcal{T}{\Lambda }_i\left(k\right){\phi }_i\left(k\right)+\mathcal{T}{\alpha }_i{\Psi }_1({\xi }_i\left(k\right),{\varsigma }_i,{\gamma }_i,{\beta }_i),\hfill \end{array}$$

(16)

where ${\phi }_i\left(k\right)=d_i\left(k\right)-{\widehat{d}}_i\left(k\right)\in R^2$.

Note that based on the definition of ${\Psi }_1({\xi }_i\left(k\right),{\varsigma }_i,{\gamma }_i,{\beta }_i)$, one can obtain

$$\begin{array}{c}\hfill {\Psi }_1({\xi }_i\left(k\right),{\varsigma }_i,{\gamma }_i,{\beta }_i)=h(\parallel {\xi }_i\left(k\right)\parallel ){\xi }_i\left(k\right),\end{array}$$

(17)

where $h(\parallel {\xi }_i\left(k\right)\parallel )$ is defined in Theorem 1. Therefore, Equation (16) can be rewritten as

$$\begin{array}{cc}\hfill {\xi }_i(k+1)& ={\xi }_i\left(k\right)+\mathcal{T}{\Lambda }_i\left(k\right){\phi }_i\left(k\right)+\mathcal{T}{\alpha }_{i}h(\parallel {\xi }_i\left(k\right)\parallel ){\xi }_i\left(k\right)\hfill \\ \hfill & =(1+\mathcal{T}{\alpha }_{i}h(\parallel {\xi }_i\left(k\right)\parallel \left)\right)I_3{\xi }_i\left(k\right)+\mathcal{T}{\Lambda }_i\left(k\right){\phi }_i\left(k\right).\hfill \end{array}$$

(18)

Furthermore, the disturbance estimation error

$$\begin{array}{cc}\hfill {\phi }_i(k+1)& =d_i(k+1)-{\widehat{d}}_i(k+1)\hfill \\ \hfill & =[d_i\left(k\right)+\Delta d_i\left(k\right)]-[{\widehat{d}}_i\left(k\right)-\mathcal{T}{\zeta }_i{\Lambda }_i^T\left(k\right){\Psi }_2({\xi }_i\left(k\right),{\lambda }_i,{\eta }_i,{\chi }_i)]\hfill \\ \hfill & ={\phi }_i\left(k\right)+\Delta d_i\left(k\right)+\mathcal{T}{\zeta }_i{\Lambda }_i^T\left(k\right){\Psi }_2({\xi }_i\left(k\right),{\lambda }_i,{\eta }_i,{\chi }_i).\hfill \end{array}$$

(19)

Based on the definition of ${\Psi }_2({\xi }_i\left(k\right),{\lambda }_i,{\eta }_i,{\chi }_i)$, one can get

$$\begin{array}{c}\hfill {\Psi }_2({\xi }_i\left(k\right),{\lambda }_i,{\eta }_i,{\chi }_i)=g(\parallel {\xi }_i\left(k\right)\parallel ){\xi }_i\left(k\right),\end{array}$$

(20)

where $g(\parallel {\xi }_i\left(k\right)\parallel )$ is defined in Theorem 1. Therefore, Equation (19) can be rewritten as

$$\begin{array}{c}\hfill {\phi }_i(k+1)=\mathcal{T}{\zeta }_{i}g(\parallel {\xi }_i\left(k\right)\parallel ){\Lambda }_i^T\left(k\right){\xi }_i\left(k\right)+{\phi }_i\left(k\right)+\Delta d_i\left(k\right).\end{array}$$

(21)

Combining Equations (18) and (21), the dynamics of the estimation error ${\Gamma }_i\left(k\right)$ can be written as

$$\begin{array}{c}\hfill {\Gamma }_i(k+1)=A_{INESO}\left(k\right){\Gamma }_i\left(k\right)+\left[\begin{array}{c}{0}_{3\times 1}\\ \Delta d_i\left(k\right)\end{array}\right],\end{array}$$

(22)

where $A_{INESO}\left(k\right)$ is defined as in (14).

Taking the norm on both sides of (22), and applying the triangle inequality and the sub-multiplicative property of the induced norm yields

$$\begin{array}{c}\hfill \parallel {\Gamma }_i(k+1)\parallel \le \parallel A_{INESO}\left(k\right)\parallel \parallel {\Gamma }_i\left(k\right)\parallel +\parallel \Delta d_i\left(k\right)\parallel .\end{array}$$

(23)

Since $\parallel A_{INESO}\left(k\right)\parallel \le \sigma <1$ and $\parallel \Delta d_i\left(k\right)\parallel \le {\overline{d}}_i$, then

$$\begin{array}{c}\hfill \parallel {\Gamma }_i(k+1)\parallel \le \sigma \parallel {\Gamma }_i\left(k\right)\parallel +{\overline{d}}_i.\end{array}$$

(24)

This is a stable linear difference inequality. Solving it recursively leads to

$$\begin{array}{cc}\hfill \parallel {\Gamma }_i\left(k\right)\parallel & \le {\sigma }^k\parallel {\Gamma }_i\left(0\right)\parallel +{\overline{d}}_i\sum _{l=0}^{k-1}{\sigma }^l\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & \le {\sigma }^k\parallel {\Gamma }_i\left(0\right)\parallel +{\displaystyle \frac{{\overline{d}}_i}{1-\sigma }}.\hfill \end{array}$$

(26)

As $k\to \infty$, the first term ${\sigma }^k\parallel {\Gamma }_i\left(0\right)\parallel \to 0$ due to $\sigma <1$. Therefore, for any $\varphi >0$, there exists a positive integer K such that for all $k>K$, the estimation error ${\Gamma }_i\left(k\right)$ is uniformly ultimately bounded by

$$\begin{array}{c}\hfill \parallel {\Gamma }_i\left(k\right)\parallel \le {\displaystyle \frac{{\overline{d}}_i}{1-\sigma }}+\varphi .\end{array}$$

(27)

Moreover, from the above inequality, a global and explicit bound for all k is also available, confirming that $\parallel {\Gamma }_i\left(k\right)\parallel$ does not exceed the finite constant ${\kappa }_i={\displaystyle \frac{{\overline{d}}_i}{1-\sigma }}$. This completes the proof.    □

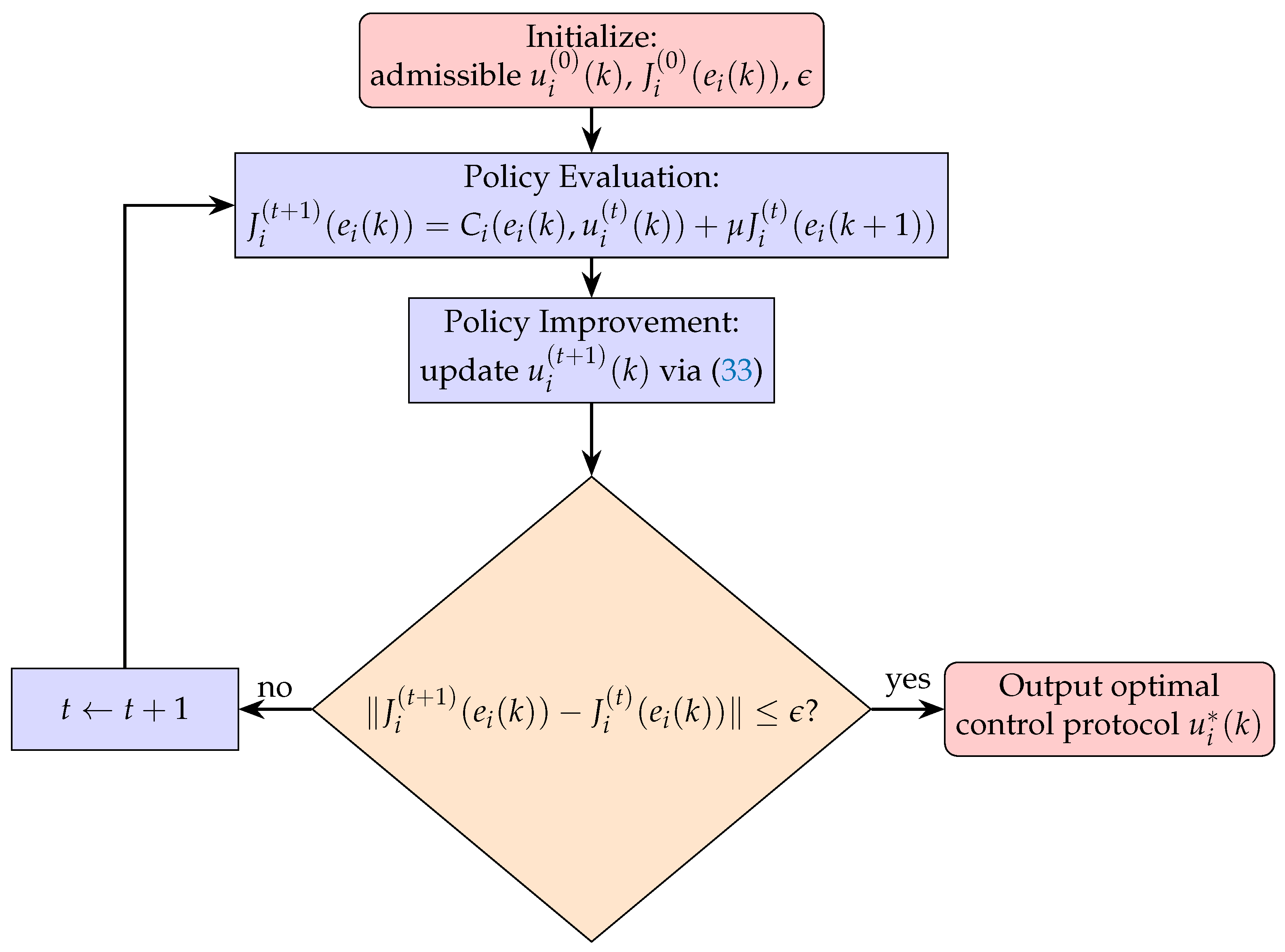
4.2. Optimal Consensus Control

Based on the system (5), consider the disturbance-free dynamics of the i-th follower, which can be expressed as

$$\begin{array}{cc}\hfill X_i(k+1)& =X_i\left(k\right)+\mathcal{T}{\Lambda }_i\left(k\right)u_i\left(k\right),\hfill \end{array}$$

(28)

and the consensus error system for the i-th follower is represented as

$$\begin{array}{c}\hfill e_i\left(k\right)=\sum _{j\in {\mathcal{N}}_i}{a}_{ij}(X_i\left(k\right)-X_j\left(k\right))+a_{i0}(X_i\left(k\right)-X_0\left(k\right)).\end{array}$$

(29)

To achieve distributed optimal consensus, each follower minimizes a cost function, which is

$$\begin{array}{cc}\hfill J_i(e_i\left(k\right),u_i\left(k\right),u_j\left(k\right))=& \sum _{l=k}^{\infty }{\mu }^{(l-k)}(C_i(e_i\left(l\right),u_i\left(l\right),u_j\left(l\right))\hfill \\ \hfill =& \sum _{l=k}^{\infty }{\mu }^{(l-k)}(e_i^T\left(l\right)S_{ii}{e}_i\left(l\right)+u_i^T\left(l\right)R_{ii}{u}_i\left(l\right)\hfill \\ \hfill & +\sum _{j\in {\mathcal{N}}_i}{u}_j^T\left(l\right)R_{ij}{u}_j\left(l\right)).\hfill \end{array}$$

(30)

For simplicity, let $J_i(e_i\left(k\right)$, $u_i\left(k\right)$, $u_j\left(k\right))$=$J_i\left(e_i\left(k\right)\right)$ and $C_i(e_i\left(k\right)$, $u_i\left(k\right)$, $u_j\left(k\right))$=$C_i(e_i\left(k\right)$, $u_i\left(k\right))$. The cost function then satisfies the Bellman equation

$$\begin{array}{c}\hfill J_i\left(e_i\left(k\right)\right)=C_i(e_i\left(k\right),u_i\left(k\right))+\mu J_i\left(e_i(k+1)\right),\end{array}$$

(31)

and the optimal cost function $J_i^{*}\left(e_i\left(k\right)\right)$ obeys the HJB Equation

$$\begin{array}{c}\hfill J_i^{*}\left(e_i\left(k\right)\right)=\underset{u_i\left(k\right)}{min}\{C_i(e_i\left(k\right),u_i\left(k\right))+\mu J_i^{*}\left(e_i(k+1)\right)\}.\end{array}$$

(32)

By differentiating (32) with respect to $u_i\left(k\right)$, the optimal control protocol of the i-th follower is derived as

$$\begin{array}{c}\hfill u_i^{*}\left(k\right)=-{\displaystyle \frac{\mu \mathcal{T}}{2}}(d_i+a_{i0})R_{ii}^{-1}{\Lambda }_i^T\left(k\right){\displaystyle \frac{\partial J_i^{*}\left(e_i(k+1)\right)}{\partial e_i(k+1)}},\end{array}$$

(33)

whose PI algorithm flow can be obtained in Algorithm 1, and the overall execution flow of the proposed policy iteration scheme is visualized in Figure 1.

After obtaining ${\widehat{d}}_i\left(k\right)$ and $u_i^{*}\left(k\right)$, the optimal disturbance rejection consensus control protocol for system (5) is designed as

$$\begin{array}{c}\hfill u_i\left(k\right)=u_i^{*}\left(k\right)-{\widehat{d}}_i\left(k\right).\end{array}$$

(34)

Remark 1.

The cost function (30) is designed to achieve optimal consensus by balancing the trade-off between consensus error and control effort. Specifically, the first term $e_i^T\left(l\right)S_{ii}{e}_i\left(l\right)$ penalizes the consensus error, encouraging the follower agents to synchronize their states with the leader and neighbors. The second term $u_i^T\left(l\right)R_{ii}{u}_i\left(l\right)$ penalizes the control effort of the i-th follower, preventing excessive control input. The third term ${\sum }_{j\in {\mathcal{N}}_i}{u}_j^T\left(l\right)R_{ij}{u}_j\left(l\right)$ accounts for the control efforts of neighboring agents, which reflects the cooperative nature of MASs.

The weighting matrices $S_{ii}$, $R_{ii}$, and $R_{ij}$ are chosen as positive definite symmetric matrices based on the following assumptions: (1) $S_{ii}$ emphasizes the importance of state consensus, where larger values lead to faster convergence but potentially higher control costs; (2) $R_{ii}$ regulates the control effort of agent i, with larger values resulting in more conservative control actions; (3) $R_{ij}$ influences the cooperative behavior by considering neighbors’ control costs, promoting energy-efficient coordination.

The discount factor μ ($0<\mu \le 1$) ensures the convergence of the infinite-horizon cost function and determines the relative importance of future costs. A value closer to 1 places more emphasis on long-term performance, while smaller values focus on immediate costs. This cost function formulation directly influences the optimal consensus control process through the HJB Equation (32), where the minimization of (30) leads to the optimal control protocol (33) that achieves consensus while optimizing the defined performance criteria.

Algorithm 1 Policy Iteration Algorithm for Optimal Consensus Control

1: Initialization: 2:    Let $u_i^{\left(0\right)}\left(k\right)$ be an arbitrary admissible control policy 3:    Let $J_i^{\left(0\right)}\left(e_i\left(k\right)\right)$ be an initial cost function 4:    Set iteration index $t\leftarrow 0$ 5:    Select convergence tolerance $ϵ>0$ 6: Procedure: 7: Step 1: Policy Evaluation 8:    Update the cost function: 9:    $J_i^{(t+1)}\left(e_i\left(k\right)\right)\leftarrow C_i(e_i\left(k\right),u_i^{\left(t\right)}\left(k\right))+\mu J_i^{\left(t\right)}\left(e_i(k+1)\right)$ 10: Step 2: Policy Improvement 11:    Update the control policy: 12:    $u_i^{(t+1)}\left(k\right)\leftarrow -{\displaystyle \frac{\mu \mathcal{T}}{2}}(d_i+a_{i0})R_{ii}^{-1}{\Lambda }_i^T\left(k\right){\displaystyle \frac{\partial J_i^{\left(t\right)}\left(e_i(k+1)\right)}{\partial e_i(k+1)}}$ 13: Step 3: Convergence Check 14:    Compute error: $\Delta \leftarrow \parallel J_i^{(t+1)}\left(e_i\left(k\right)\right)-J_i^{\left(t\right)}\left(e_i\left(k\right)\right)\parallel$ 15:    If $\Delta \le ϵ$, then: 16:       Set $u_i^{*}\left(k\right)\leftarrow u_i^{(t+1)}\left(k\right)$ 17:       break 18:    Else: 19:       $t\leftarrow t+1$ 20:       Return to Step 1 21: Output: Optimal control protocol $u_i^{*}\left(k\right)$

4.3. Momentum-Accelerated Actor–Critic Network

A closed-form solution to the HJB Equation (32) remains analytically challenging. To address this, an Actor–Critic framework based on ADP is developed to approximate its solution.

An critic network (CN) is used to approximate $J_i\left(e_i\left(k\right)\right)$, that is

$$\begin{array}{c}\hfill {\widehat{J}}_i\left(k\right)={\widehat{W}}_{ci}^T{\varphi }_{ci}\left(z_{ci}\left(k\right)\right),\end{array}$$

(35)

where ${\widehat{J}}_i\left(k\right)$ is the estimated value of $J_i\left(e_i\left(k\right)\right)$, $z_{ci}\left(k\right)$ is an input vector of the CN, ${\varphi }_{ci}\left(z_{ci}\left(k\right)\right)$ denotes the activation function, and ${\widehat{W}}_{ci}^T$ denotes the weight matrix.

Therefore, the estimation error of (31) of the CN is represented as

$$\begin{array}{c}\hfill e_{ci}\left(k\right)={\widehat{J}}_i\left(k\right)-J_i\left(e_i\left(k\right)\right),\end{array}$$

(36)

and

$$\begin{array}{c}\hfill E_{ci}\left(k\right)={\displaystyle \frac{1}{2}}{e}_{ci}^T\left(k\right)e_{ci}\left(k\right).\end{array}$$

(37)

In order to accelerate the convergence of the weight matrix ${\widehat{W}}_{ci}^T$ of the CN, a momentum term is incorporated to update ${\widehat{W}}_{ci}^T$ based on a standard gradient descent method. Consequently, the iterative update rule of ${\widehat{W}}_{ci}^T$ is as follows:

$$\begin{array}{cc}\hfill {\widehat{W}}_{ci}^{T^{(t+1)}}& ={\widehat{W}}_{ci}^{T^{\left(t\right)}}-{\rho }_{ci}{\displaystyle \frac{\partial E_{ci}\left(k\right)}{\partial e_{ci}\left(k\right)}}{\displaystyle \frac{\partial e_{ci}\left(k\right)}{\partial {\widehat{J}}_i\left(k\right)}}{\displaystyle \frac{\partial {\widehat{J}}_i\left(k\right)}{\partial {\widehat{W}}_{ci}}}-{\rho }_{ci}{\displaystyle \frac{\partial E_{ci}(k-1)}{\partial {\widehat{W}}_{ci}}}\hfill \\ \hfill & ={\widehat{W}}_{ci}^{T^{\left(t\right)}}-{\rho }_{ci}{e}_{ci}\left(k\right){\varphi }_{ci}^T\left(z_{ci}\left(k\right)\right)-{\rho }_{ci}{e}_{ci}(k-1){\varphi }_{ci}^T\left(z_{ci}(k-1)\right),\hfill \end{array}$$

(38)

where $\partial E_{ci}(k-1)/\partial {\widehat{W}}_{ci}$ is the momentum term, and ${\rho }_{ci}$ is the learning rate of the CN.

An actor network (AN) is used to approximate $u_i^{*}\left(k\right)$, that is

$$\begin{array}{c}\hfill {\widehat{u}}_i\left(k\right)={\widehat{W}}_{ai}^T{\varphi }_{ai}\left(z_{ai}\left(k\right)\right),\end{array}$$

(39)

where ${\widehat{u}}_i\left(k\right)$ is the estimated value of $u_i^{*}\left(k\right)$, $z_{ai}\left(k\right)$ is an input vector of the AN, ${\varphi }_{ai}\left(z_{ai}\left(k\right)\right)$ denotes the activation function, and ${\widehat{W}}_{ai}^T$ is the weight matrix.

On the basis of (35), (33) is expressed as

$$\begin{array}{c}\hfill u_i^{*}\left(k\right)=-{\displaystyle \frac{\mu \mathcal{T}}{2}}(d_i+a_{i0})R_{ii}^{-1}{\Lambda }_i^T\left(k\right){\widehat{W}}_{ci}^T{\displaystyle \frac{\partial {\varphi }_{ci}\left(z_{ci}(k+1)\right)}{\partial e_i(k+1)}}.\end{array}$$

(40)

If the estimation error of (40) of the AN is defined as

$$\begin{array}{c}\hfill e_{ai}\left(k\right)={\widehat{u}}_i\left(k\right)-u_i^{*}\left(k\right),\end{array}$$

(41)

and

$$\begin{array}{c}\hfill E_{ai}\left(k\right)={\displaystyle \frac{1}{2}}{e}_{ai}^T\left(k\right)e_{ai}\left(k\right),\end{array}$$

(42)

then the iterative update rule of ${\widehat{W}}_{ai}^T$ is as follows:

$$\begin{array}{cc}\hfill {\widehat{W}}_{ai}^{T^{(t+1)}}& ={\widehat{W}}_{ai}^{T^{\left(t\right)}}-{\rho }_{ai}{\displaystyle \frac{\partial E_{ai}\left(k\right)}{\partial e_{ai}\left(k\right)}}{\displaystyle \frac{\partial e_{ai}\left(k\right)}{\partial {\widehat{u}}_i\left(k\right)}}{\displaystyle \frac{\partial {\widehat{u}}_i\left(k\right)}{\partial {\widehat{W}}_{ai}}}-{\rho }_{ai}{\displaystyle \frac{\partial E_{ai}(k-1)}{\partial {\widehat{W}}_{ai}}}\hfill \\ \hfill & ={\widehat{W}}_{ai}^{T^{\left(t\right)}}-{\rho }_{ai}{e}_{ai}\left(k\right){\varphi }_{ai}^T\left(z_{ai}\left(k\right)\right)-{\rho }_{ai}{e}_{ai}(k-1){\varphi }_{ai}^T\left(z_{ai}(k-1)\right),\hfill \end{array}$$

(43)

where ${\rho }_{ai}$ is the learning rate of the AN.

These weight update rules ensure that the critic and actor networks converge to accurately approximate $J_i^{*}\left(e_i\left(k\right)\right)$ and $u_i^{*}\left(k\right)$. Based on the derivation above, the optimal control protocol (33) is obtained, and the final control protocol (34) is consequently derived. By substituting the control protocol (34) into the system (5), the original system (5) is transformed into the disturbance-free system (28).

4.4. Opitimal Consensus Analysis

Theorem 2.

For agent i, if $J_i^{*}\left(e_i\left(k\right)\right)$ satisfies the coupled HJB Equation (32), then $e_i\left(k\right)$ is asymptotically stable, which implies that the DT-MASs (6) and (28) under the control protocol (33) can achieve optimal consensus, and the DT-MASs (5) and (6) under the control protocol (34) can reach optimal consensus.

Proof. 

According to (32), one has

$$\begin{array}{c}\hfill J_i^{*}\left(e_i\left(k\right)\right)-\mu J_i^{*}\left(e_i(k+1)\right)=C_i(e_i\left(k\right),u_i^{*}\left(k\right)),\end{array}$$

(44)

and

$$\begin{array}{c}\hfill {\mu }^k{J}_i^{*}\left(e_i\left(k\right)\right)-{\mu }^{k+1}{J}_i^{*}\left(e_i(k+1)\right)={\mu }^k{C}_i(e_i\left(k\right),u_i^{*}\left(k\right)).\end{array}$$

(45)

Define the difference of the Lyapunov function candidate as

$$\begin{array}{c}\hfill \Delta \left({\mu }^k{J}_i^{*}\left(e_i\left(k\right)\right)\right)={\mu }^{k+1}{J}_i^{*}\left(e_i(k+1)\right)-{\mu }^k{J}_i^{*}\left(e_i\left(k\right)\right).\end{array}$$

(46)

According to (45), (46) can be rewritten as

$$\begin{array}{c}\hfill \Delta \left({\mu }^k{J}_i^{*}\left(e_i\left(k\right)\right)\right)=-{\mu }^k{C}_i(e_i\left(k\right),u_i^{*}\left(k\right))\le 0,\end{array}$$

(47)

which implies that $e_i\left(k\right)$ is asymptotically stable, satisfying ${lim}_{k\to \infty }{e}_i\left(k\right)=0$, and the DT-MASs (6) and (28) can achieve optimal consensus. This indicates that the DT-MASs (5) and (6) can reach optimal consensus under the control protocol (34). This completes the proof. □

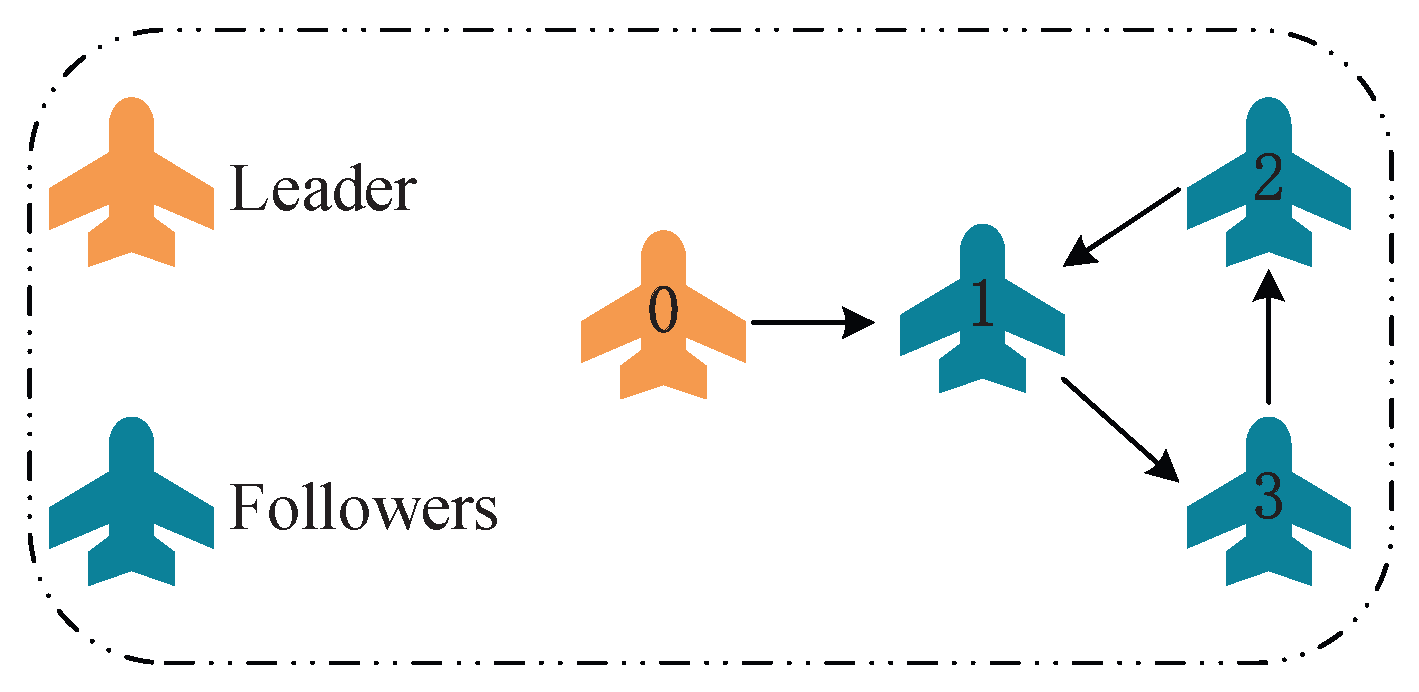
5. Simulation Results

This section provides a numerical example to validate the effectiveness of the proposed momentum-accelerated Actor–Critic network-based control method. The validation is conducted on UAV-based DT-MASs, which are given by Equations (5) and (6), with the control objective of achieving optimal consensus. The considered DT-MAS comprises one leader and three follower UAVs, whose directed communication topology is illustrated in Figure 2.

According to Figure 2, choose $a_{10}$ = 1, $a_{12}$ = $a_{23}$ = $a_{31}$ = 1, and the rest of the communication weights are 0. The initial states of the DT-MASs (5) and (6) are set as $X_1\left(0\right)$ = $(-1$, $0.5$, ${0)}^T$, $X_2\left(0\right)$ = $(0$, $-1$, ${-\pi /4)}^T$, $X_3\left(0\right)$ = $(1$, $-0.5$, ${-\pi /6)}^T$, and $X_0\left(0\right)$ = $(2$, 1, ${\pi /3)}^T$. The sampling period $\mathcal{T}$ is given as 0.005 s. The control input of the leader is $u_0\left(k\right)$ = $(0.5$, ${0.05)}^T$.

The parameters of the INESO (10) are configured as ${\alpha }_i=1.5$, ${\zeta }_i=100$, ${\gamma }_i$ = $0.1$, ${\varsigma }_i$ = $0.5$, ${\lambda }_i$ = $0.1$, ${\beta }_i=0.1$, ${\chi }_i=0.1$, and ${\eta }_i$ = $0.01$, where $i\in \{1,2,3\}$. The parameters of cost function (30) are set as $S_{ii}$ = $I_{3\times 3}$, and $R_{ii}$ = $R_{ij}$ = $I_{2\times 2}$, and $\mu$ is set as $0.99$. The learning rate ${\rho }_{ci}$ = ${\rho }_{ai}$ = $0.1$, and the activation functions of the CN and AN are respectively designed as ${\varphi }_{ci}\left(z_{ci}\left(k\right)\right)={(e_{i1}^2,e_{i2}^2,e_{i3}^2,e_{i1}{e}_{i2},e_{i1}{e}_{i3},e_{i2}{e}_{i3})}^T$ and ${\varphi }_{ai}\left(z_{ai}\left(k\right)\right)=e_i^T$, where $i\in \{1,2,3\}$. The disturbances are defined as $d_{i1}\left(k\right)$ = $3sin\left(0.0025k\right)+1$ and $d_{i2}\left(k\right)$ = $e^{sin\left(0.0025k\right)}+0.5cos\left(0.0025k\right)+0.5$, where $i\in \{1,2,3\}$.

Remark 2.

The selection of these specific disturbance functions is physically motivated and reflects realistic operational scenarios for UAV swarms. The sinusoidal component $3sin\left(0.0025k\right)+1$ represents periodic wind gusts and atmospheric turbulence commonly encountered during UAV flight operations, where the amplitude and frequency parameters capture typical wind disturbance characteristics. The exponential term $e^{sin\left(0.0025k\right)}$ + $0.5cos\left(0.0025k\right)+0.5$ models the nonlinear and transient disturbance effects, such as sudden wind shear or gust fronts that exhibit rapid onset and decay patterns. This combined disturbance profile effectively captures the complex, time-varying nature of environmental disturbances that multi-UAV systems encounter in practical applications, providing a comprehensive test scenario that challenges both the estimation accuracy of the INESO and the compensation capability of the proposed control scheme. Such disturbance models are widely adopted in the literature for evaluating the robustness of UAV control systems under realistic operating conditions.

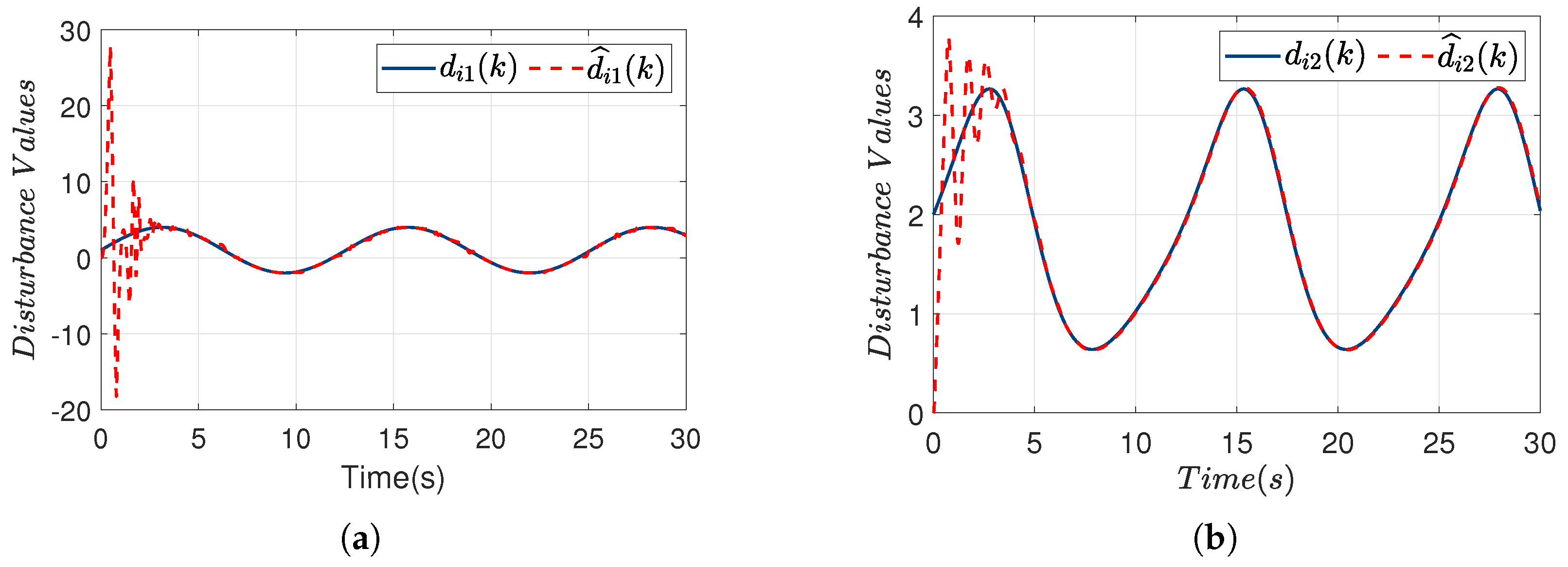
5.1. Simulations for INESO

This subsection validates the estimation performance of the INESO (10) under the prescribed complex disturbance scenario. To focus on evaluating the observer’s inherent estimation performance for the disturbances and to streamline the analysis, all follower UAVs are subjected to the same disturbances described above.

Figure 3 shows the trajectories of the actual disturbances $d_i\left(k\right)$ and their estimates ${\widehat{d}}_i\left(k\right)$ provided by the INESO (10). The close match between the two, for both disturbance components, demonstrates the observer’s high estimation accuracy and rapid convergence.

To quantitatively validate the advantages of the proposed INESO (10), a comparative analysis with a conventional LESO is conducted. The conventional LESO is designed as follows:

$$\begin{array}{cc}\hfill {\widehat{X}}_{i-lin}(k+1)& ={\widehat{X}}_{i-lin}\left(k\right)+\mathcal{T}{\Lambda }_i\left(k\right)(u_i\left(k\right)+{\widehat{d}}_{i-lin}\left(k\right))-\mathcal{T}{\alpha }_{i-lin}{\xi }_{i-lin}\left(k\right),\hfill \\ \hfill {\widehat{d}}_{i-lin}(k+1)& ={\widehat{d}}_{i-lin}\left(k\right)-\mathcal{T}{\zeta }_{i-lin}{\Lambda }_i^T\left(k\right){\xi }_{i-lin}\left(k\right),\hfill \end{array}$$

(48)

where ${\xi }_{i-lin}\left(k\right)=X_i\left(k\right)-{\widehat{X}}_{i-lin}\left(k\right)$, ${\alpha }_{i-lin}={\alpha }_i=1.5$, ${\zeta }_{i-lin}={\zeta }_i=100$, and the remaining parameters are the same as the INESO (10).

Figure 4 presents the performance comparison of the disturbance estimation between the proposed INESO and the conventional LESO for UAV1 under identical disturbance conditions. The quantitative comparison metrics are summarized in

Table 1. Quantitative comparison between the proposed INESO and the conventional LESO.

Performance Metric	LESO	INESO	Improvement
Mean Squared Error	0.041	0.028	46.4%
Maximum Estimation Error	0.072	0.050	44.0%
Steady-State Error	0.046	0.031	48.4%
Convergence Time (s)	4.95	2.84	42.6%

.

The comparative results demonstrate three key advantages of the proposed INESO:

• Enhanced Nonlinear Disturbance Estimation: The nonlinear functions ${\Psi }_1({\xi }_i\left(k\right),{\varsigma }_i,{\gamma }_i,{\beta }_i)$ and ${\Psi }_2({\xi }_i\left(k\right),{\lambda }_i,{\eta }_i,{\chi }_i)$ enable adaptive gain adjustment based on estimation error magnitude. For large errors ($\parallel {\xi }_i\left(k\right)\parallel >{\varsigma }_i$), the nonlinear term $\parallel {\xi }_i{\left(k\right)\parallel }^{{\gamma }_i-1}$ provides aggressive correction, while for small errors, the linearized term ensures smooth convergence with almost no overshoot.
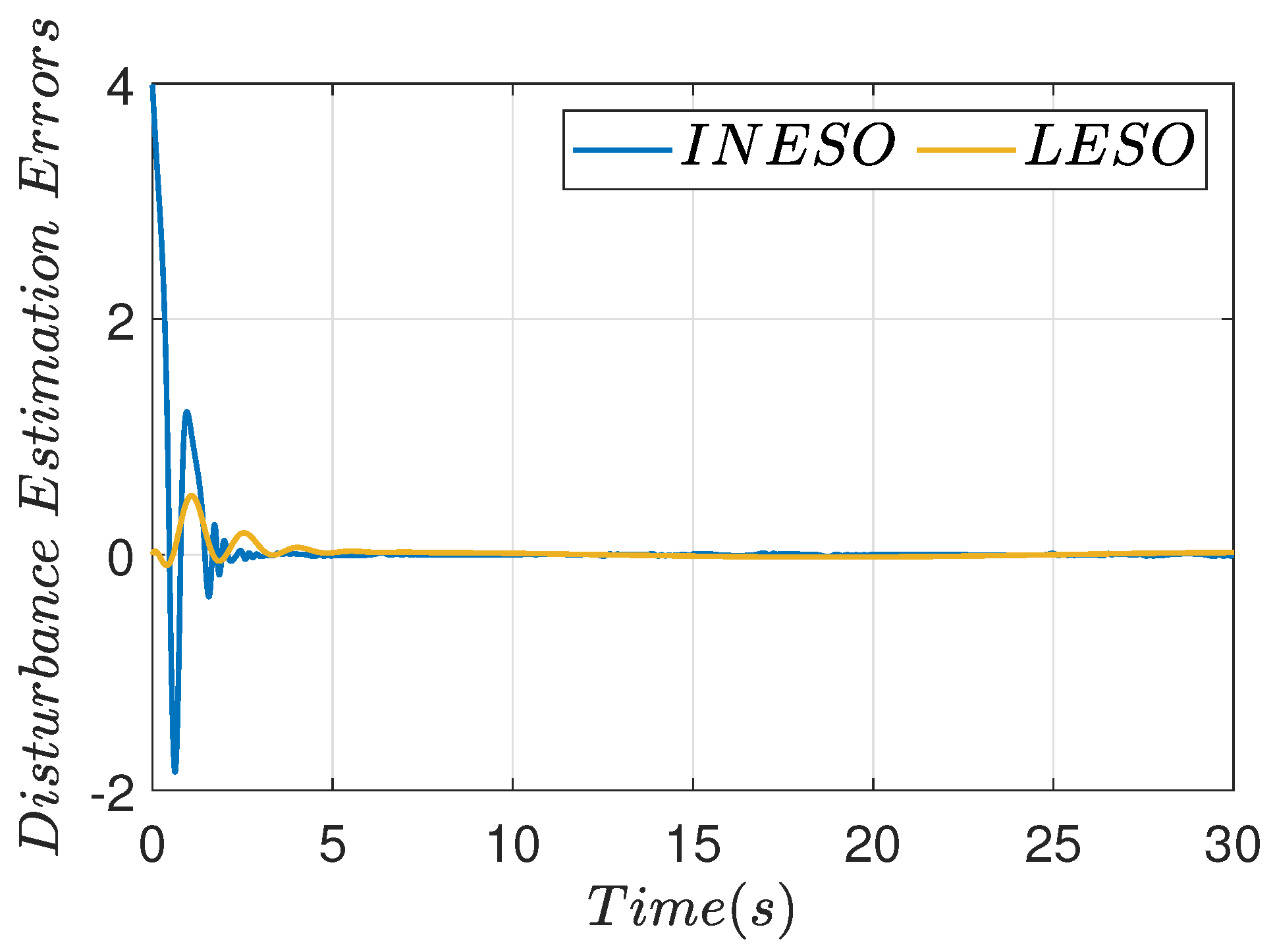
• Superior Estimation Accuracy: As shown in Table 1, the INESO demonstrates significant improvements over the conventional LESO across multiple key estimation accuracy metrics. The mean squared error is reduced by 46.4%, indicating a substantial decrease in overall estimation bias. The maximum estimation error is reduced by 44.0%, showcasing enhanced robustness against abrupt or large disturbances. Furthermore, the steady-state error is decreased by 48.4%, reflecting the INESO’s ability to achieve more precise disturbance tracking in equilibrium states. This comprehensive enhancement in accuracy directly strengthens the control system’s disturbance rejection and tracking performance, providing a reliable foundation for precise control in high-order, nonlinear, or strongly disturbed environments.
• Faster Convergence Speed: The 42.6% reduction in convergence time (from 4.95 s to 2.84 s) indicates that the INESO achieves stable and accurate disturbance estimates more rapidly. This accelerated convergence enhances the overall responsiveness of the control system, allowing it to compensate for disturbances in a timelier manner, which is crucial for maintaining system stability and convergence performance under dynamic conditions.

These quantitative results substantiate the mechanistic innovation of the proposed INESO in addressing the limitations of the conventional LESO for MASs operating under disturbance conditions.

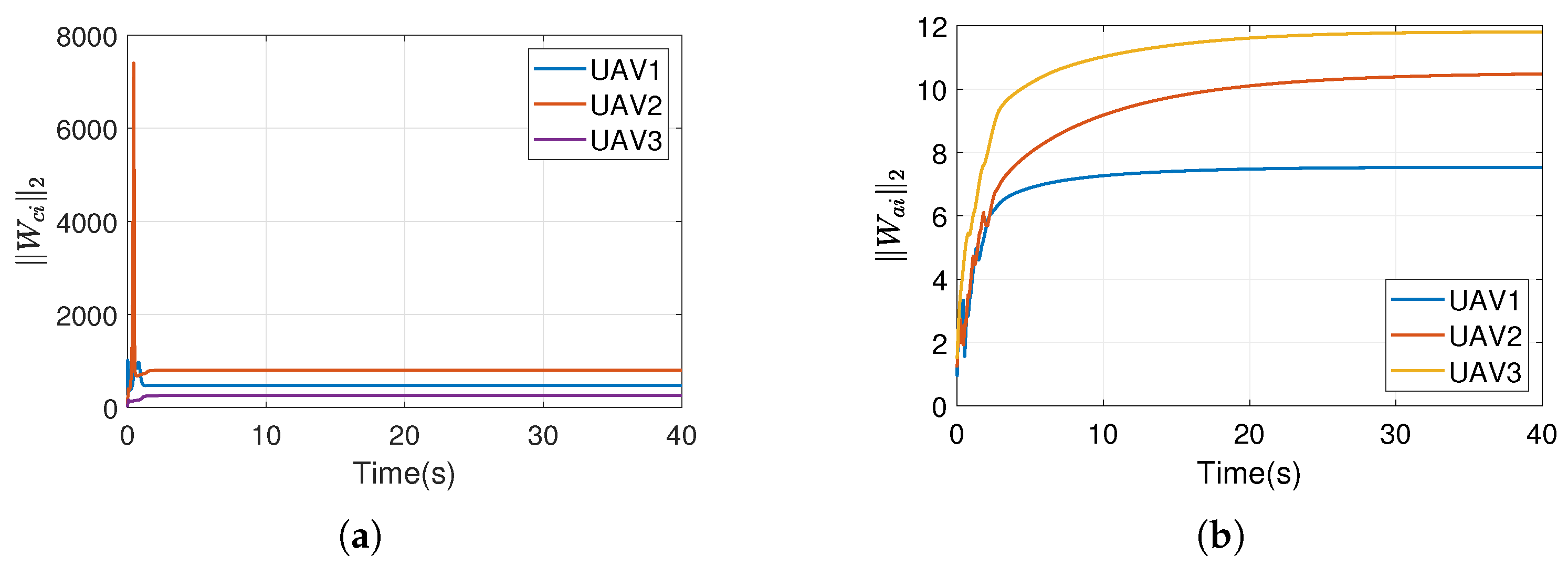
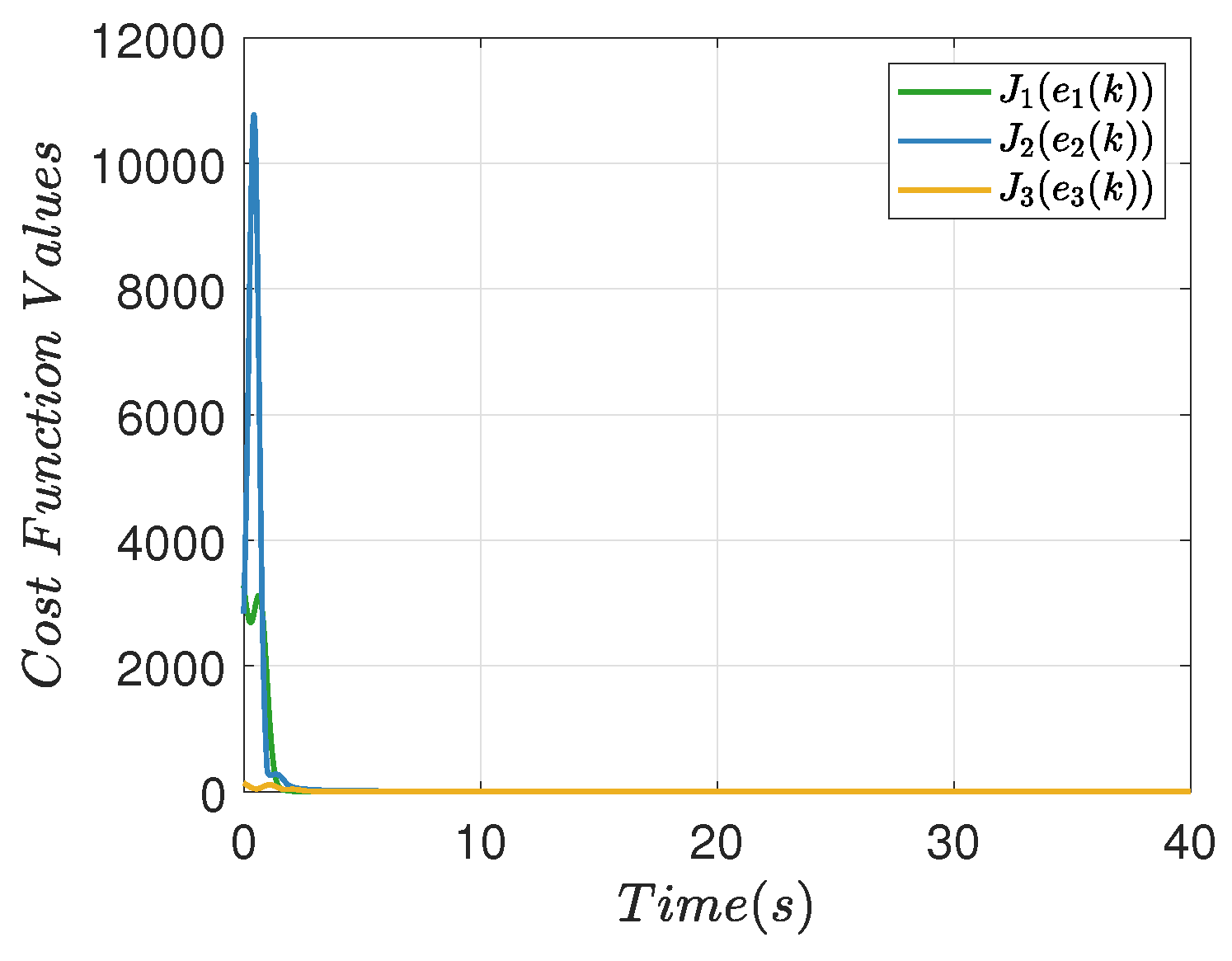
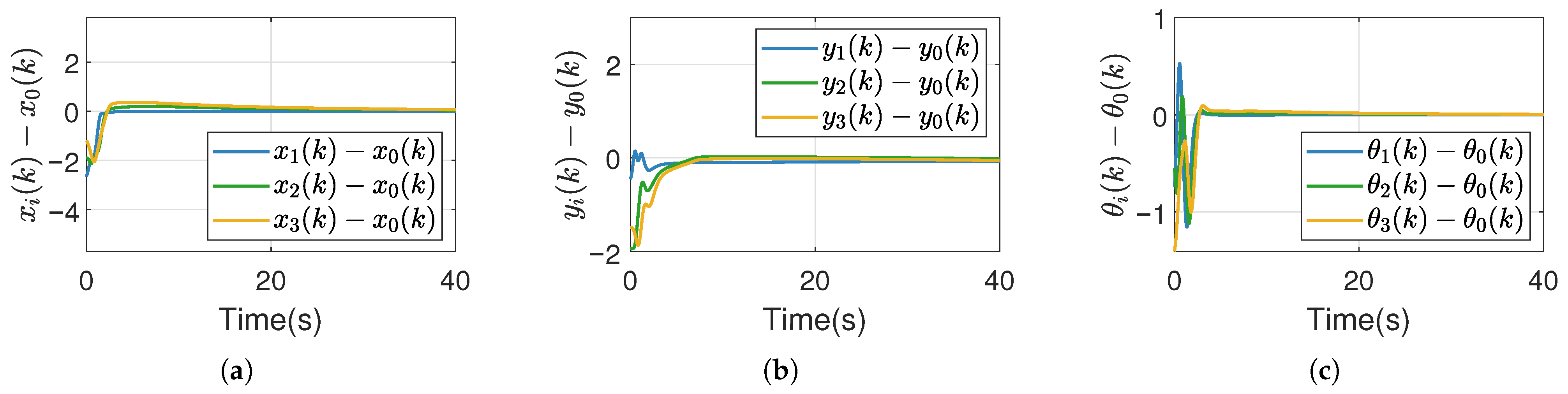
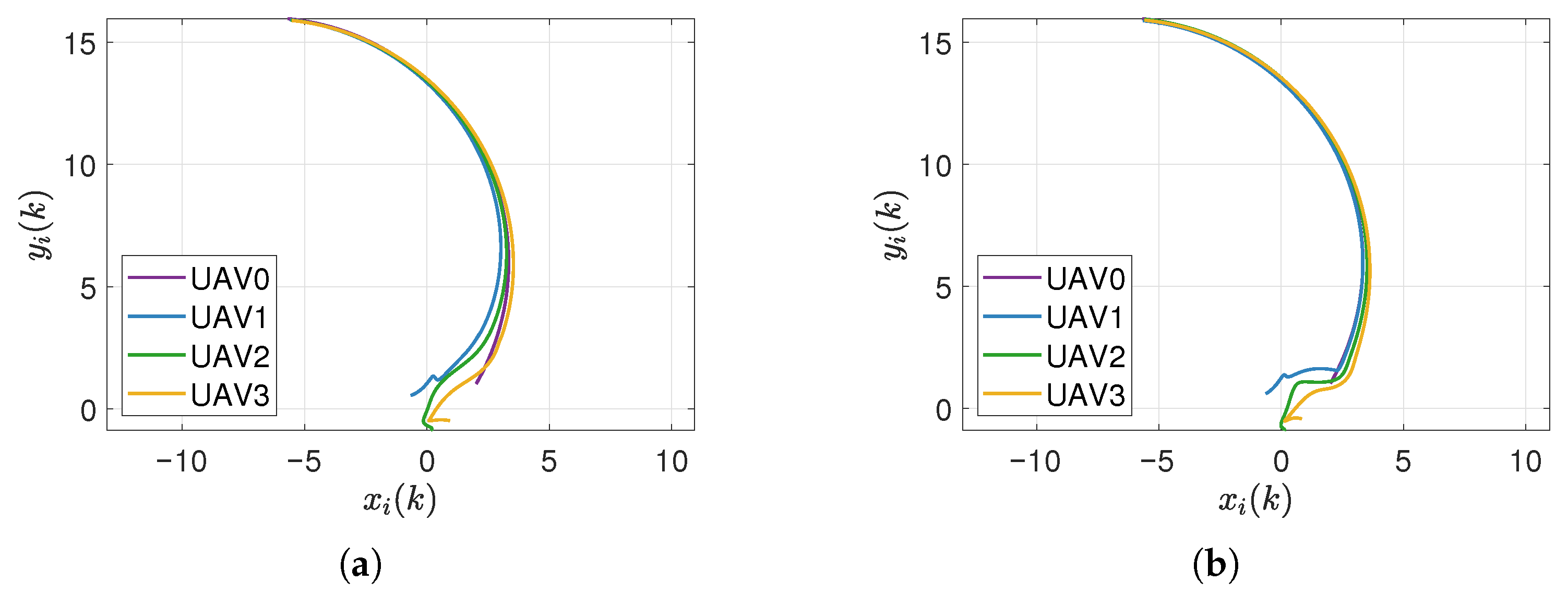
5.2. Simulations for Momentum-Accelerated Actor-Critic Network and Optimal Consensus

Figure 5 illustrates the weight norm curves of the CN and the AN for all followers, indicating that the norm of each network’s weights asymptotically stabilizes to an equilibrium value, confirming the convergence of the learning parameters.

To further validate the optimization performance of the proposed control strategy, Figure 6 presents the convergence curves of the cost function $J_i\left(e_i\left(k\right)\right)$ for each follower agent. All cost functions exhibit a consistent decreasing trend and converge to near-zero values, demonstrating the effectiveness of the momentum-accelerated Actor-Critic network in minimizing the cost function defined in (30). The rapid and smooth descent of the cost curves reflects the accelerated learning capability of the proposed method.

The trajectories of the state errors $x_i\left(k\right)-x_0\left(k\right)$, $y_i\left(k\right)-y_0\left(k\right)$, and ${\theta }_i\left(k\right)-{\theta }_0\left(k\right)$ for all agents are shown in Figure 7. It is observed that all error trajectories converge asymptotically to zero. This result verifies that, despite the presence of external disturbances, the DT-MASs (5) and (6) achieve robust optimal consensus through the integrated control strategy based on the designed INESO and the momentum-accelerated Actor–Critic network. The fast and smooth convergence of the errors further demonstrates that the proposed method not only optimizes transient performance but also ensures closed-loop system stability and enhances robustness in the face of system uncertainties and external disturbances.

To evaluate the advantage of the proposed acceleration technique, a comparative study is conducted under identical parameters. Figure 8 displays the 2D state trajectories of the systems based on the standard gradient Actor–Critic network and the momentum-accelerated one. A clear observation is that the momentum-accelerated network exhibits a significantly faster convergence rate, underscoring the effectiveness and superiority of the proposed method.

In order to further clarify the superiority of the proposed momentum-accelerated Actor–Critic network compared with the standard gradient algorithm, this article makes a quantitative statistical analysis of its convergence performance.

Table 2. Performance comparison between the standard gradient Actor–Critic network (SGACN) and the momentum-accelerated Actor–Critic network (MAACN).

Average Performance Metric	SGACN	MAACN	Improvement
convergence time (s)	22.13	19.30	12.8%
Convergence steps	4426	3860	12.8%
Steady-state position error (m)	0.075	0.058	22.7%
Steady-state orientation error (rad)	0.038	0.022	42.1%
Overshoot percentage	12.3%	9.5%	22.7%

summarizes the key performance metrics obtained from extensive simulations.

The statistical analysis clearly demonstrates the superior performance of the momentum-accelerated approach across all metrics. The convergence time was reduced by 12.8%, from 22.13 s with the standard method to 19.30 s with the momentum-accelerated network. This improvement is attributed to the incorporation of historical gradient information, which enables more stable and efficient weight updates during the learning process.

Furthermore, the momentum-accelerated network has achieved significantly better steady-state performance, with steady-state position and orientation errors reduced by 22.7% and 42.1%, respectively. The overshoot percentage, which indicates the transient response quality, was reduced by 22.7%, demonstrating enhanced stability during the convergence process. These statistical results substantiate the visual observations in Figure 8 and provide the quantitative evidence of the performance gains achieved by the proposed momentum-accelerated Actor–Critic network.

Simulation results demonstrate that the proposed INESO can accurately estimate complex disturbances, showing significant improvements in estimation error and convergence time compared to the conventional LESO. Meanwhile, the momentum-accelerated Actor–Critic network effectively enhances the learning speed and consensus performance of DT-MASs, achieving faster and more stable optimal consensus control. Overall, the integrated control strategy exhibits good robustness and optimization capability in the presence of external disturbances.

6. Discussion

This article presents an optimal disturbance rejection control protocol for achieving consensus in nonlinear MASs under unknown disturbances. Compared to existing methods [21,22,33], the proposed momentum-accelerated Actor–Critic framework significantly accelerates the convergence to consensus. Integrated with an extended state observer, the approach further enhances the system’s capability to suppress external disturbances, highlighting its potential value for practical applications.

It is important to acknowledge several challenges for the real-world deployment of this protocol. First, at the communication level, issues such as network latency, packet loss, and dynamic topology changes must be addressed. Second, regarding motion control, dynamic characteristics not fully captured by the kinematic model—including actuator saturation, aerodynamic coupling effects, and inertial forces—require further consideration. Third, computational constraints of embedded platforms, including real-time processing requirements and memory limitations, must be satisfied.

A primary limitation of the current work lies in its validation within a two-dimensional environment. Real-world UAV swarms operate in three-dimensional space, and wind disturbances exhibit complex spatial characteristics. Although the simplified 2D model serves as a crucial step for verifying the core algorithms and establishing a theoretical foundation, future work should extend the framework in the following aspects to improve physical realism: extension to 3D operational environments with full spatial dynamics; incorporation of vertical wind components and their effects on altitude control; development of 3D consensus protocols accounting for full positional and attitude coordination; and validation using more realistic three-dimensional turbulence models.

Nevertheless, the fundamental contributions of this work—the nonlinear extended state observer and the momentum-accelerated Actor–Critic network—remain applicable to 3D scenarios. The principles of disturbance estimation and compensation can be directly extended to three dimensions, and the ADP framework naturally accommodates higher-dimensional state spaces. Subsequent research will focus on implementing the algorithm in three-dimensional environments and conducting experimental validation on real physical systems, such as multi-rotor UAV platforms, to further investigate its performance in tasks like multi-UAV trajectory tracking.

7. Conclusions

This article investigates the optimal consensus problem for MASs based on UAVs under unknown disturbances. An INESO is designed to accurately estimate disturbances, and a composite compensation strategy is introduced to significantly improve disturbance rejection performance. Moreover, a momentum-accelerated Actor–Critic network is proposed, which enhances convergence speed during consensus achievement. Simulation results confirm the effectiveness and robustness of the approach, demonstrating improved cooperative stability and mission performance of MASs in disturbed environments.

While the current study is conducted in a two-dimensional framework, it provides a reliable technical foundation for UAV swarm applications in areas such as search and rescue, logistics, and inspection. The core algorithmic contributions, including the nonlinear extended state observer and momentum-accelerated learning framework, establish essential building blocks for future extensions to three-dimensional operational environments.

Beyond UAV applications, the proposed control framework opens up new possibilities for coordinated decision-making in complex and dynamic multi-agent scenarios. By ADP with disturbance estimation, the strategy supports real-time task allocation and adaptive cooperative control. The method is general and scalable, making it applicable to a wide range of MAS coordination tasks beyond UAVs. Future work will focus on extending the framework to three-dimensional environments and addressing consensus control for highly nonlinear multi-UAV systems under strong disturbances, further bridging the gap between theoretical design and practical deployment.