Tilted Triangular Springs with Constant-Force Reaction ^†

Abstract

Guiding mechanisms are among the most elementary components of in-plane micro-electro-mechanical systems (MEMS). Usually, a spring is desired that is compliant in only one direction and stiff in other directions. We introduce triangular springs with a preset tilting angle. The tilting angle lowers the force reaction in the displacement direction and implements a constant-force reaction whereby the maximum selectivity of the tilted triangular spring is shifted to larger displacements. Thus, the tilted triangular springs can increase the lateral stability of comb-drive actuators. We show tilted triangular springs exhibiting constant forces in a deflection range of about 75 µm to 175 µm.

1. Introduction

Guiding mechanisms are among the most important components of microsystem technology as they enable the translational in-plane displacement of MEMS. This makes springs and guiding mechanisms suitable, e.g., for guiding electrostatic comb-drive actuators. To generate constant forces in microsystems, electrostatic actuators with closed-loop feedback control (e.g., realized by capacitive force sensors) are often used to control the actuator force in MEMS. An alternative to this is springs that achieve a constant-force reaction when applying an external force [1,2]. In our contribution to the field, we show the constant forces realized by a single compact tilted triangular spring.

2. Materials and Methods

A tilted triangular spring with a partially constant spring force is illustrated in Figure 1a. The properties of this spring are defined by the number of beams n, the beam length L, the thickness d, and the inclination angle α. The triangular spring achieves a constant-force reaction when designing the spring with a preset initial tilting angle β as an additional degree of freedom. Springs with constant force feature a stiffness k_x in displacement direction, that approaches 0 N/m in the constant-force range (CFR). As shown in Figure 1b, the CFR arises with proceeding displacement of the spring. Figure 1c shows a fabricated comb-drive actuator with tilted triangular springs and an integrated force sensor. The chips were manufactured by a dicing-free SOI process. The force sensor allows us to experimentally characterize the spring force by the measuring setup shown in Figure 1d.

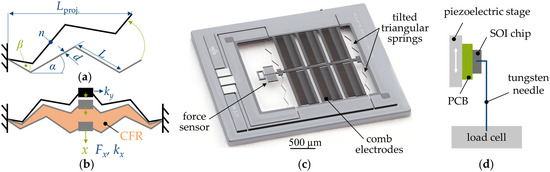
Figure 1. Tilted triangular spring. (a) Setup; (b) constant-force range (CFR) arising from the proceeding displacement; (c) fabricated SOI chip; (d) setup for experimental spring force reaction characterization.

3. Discussion

Figure 2a shows the simulated force reaction of a triangular spring for different preset tilting angles β. For tilting angles from 0° to 5°, the reaction force increases continuously. For tilting angles of 6° and 7°, the spring exhibits an approximate constant-force range (CFR); the force reaction shows local maxima and minima for β = 8° or higher for the selected geometry. Experimentally, an approximate constant-force range was obtained for a displacement of about 75 to 175 µm (Figure 2b).

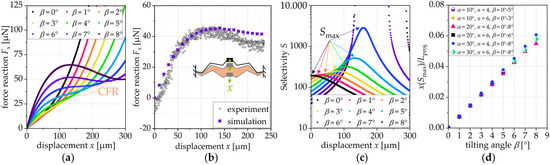
Figure 2. (a) Simulated force reaction F_x as a function of β; (b) simulated selectivity S as a function of β; (c) position of maximum selectivity x(S_max) depending on the projected length L_proj. of the tilted triangular spring; (d) experimental force reaction, for the experiment where L = 400 µm, α = 20°, n = 6, d = 5 µm/3.6 µm.

Apart from generating a constant force, tilted triangular springs exhibit a high level of selectivity as defined by the stiffness ratio between the y- and x- directions. With k_y being the stiffness orthogonal to the displacement, the tilted triangular spring exhibits a selectivity S (=k_y/k_x) shown in Figure 2c as a function of the tilting angle. With increasing tilting angle, the maximum selectivity S_max increases too. From there, the position of maximum selectivity x(S_max) shifts towards larger displacements. Figure 2d shows that the position of maximum selectivity normalized to the projected spring length L_proj. depends only on the tilting angle β and increases almost linearly with it. Consequently, a spring with a tilting angle of, e.g., β = 6°, reaches maximum selectivity at a deflection of about 4.5% of its projected length. The increase in selectivity is, e.g., important for the lateral instability of comb-drive actuators: a higher selectivity allows for a higher voltage at which lateral instability occurs [3]. The electrostatic comb-drive actuators shown in Figure 1c guided by these springs achieve voltage-dependent displacements of up to 56 µm at 28 V.