1. Introduction
Since their first appearances in the late 1990s, Radio Frequency Micro Electro-Mechanical System (RF-MEMS) switches have attracted the interest of the research community for their superior capabilities in terms of linearity, miniaturization, and wideband electrical performance [
1]. Their miniaturization, high isolation levels, and minimal losses have been shown to outclass RF switches based on Positive-Intrinsic-Negative (PIN) diodes and Field-Effect transistors (FETs); thus, their presence is increasing in the fields of satellite communications and radar and navigation systems [
2]. The same applies to the fields of mobile phones, interconnected consumer electronics, and house appliances framed in the Internet of Things (IoT) paradigm, which will contribute to the forecast Compound Annual Growth Rate (CAGR) of 7.07% for the global RF-MEMS market during the 2023–2028 period [
3]. Regarding devices relying on existing communication standards, such as mobile phones and IoT devices, the growing presence of RF-MEMS components or devices is due to the increasingly demanding features of the current 5G scenario. In fact, while the remarkable capabilities of RF-MEMS were not strictly necessary for devices operating in the 4G LTE environment, the huge amounts of connected devices, allocated frequency bands, and data rates of the 5G framework pose the need for their increasing presence in RF front ends [
4].
Among the different mechanisms employed in the actuation of the movable membrane of an RF-MEMS switch, the electrostatic one is the most common since it guarantees negligible power consumption. In fact, besides minimal leakage currents in the range of nA, electrostatic actuation does not rely on a flow of current, and it is generally characterized by a small switching time [
5]. This extends the employment of such RF-MEMS devices in handheld wireless devices, whose functioning is limited by the capacity of the batteries. The other possible mechanisms are the piezoelectric, electro-thermal, and electro-magnetic ones, which are often avoided because of drawbacks like parasitic and unwanted actuations and incompatibility with standard Complementary Metal–Oxide–Semiconductor (CMOS) fabrication [
6], higher power consumption and switching time, or thermal fatigue to the movable parts [
7]. The classification of RF-MEMS switches can be carried out on the basis of the movement of the membrane (vertical or lateral), on the basis of the established mechanical contact (metal-to-metal or metal-to-oxide), or on the basis of their electrical role (series or shunt connection), as examined in depth in many other reference texts [
5,
8].
A research challenge of constant interest in recent years has been that of devices characterized by a low actuation voltage (or “pull-in” voltage). There are many reasons behind this trend; in fact, devices with a low pull-in, in the order of 6.5 V, can use the same voltages of common circuitry and devices based on CMOS technology. In fact, most RF-MEMS devices in the literature are operated by voltages in the order of tens of volts, and step-up converters are required in order to integrate them into common circuits, increasing the footprint and complexity of the whole circuit [
9]. Low pull-in voltages also determine a reduced mechanical shock on the movable membrane during the actuation, which increases the lifetime of the devices [
10]. Therefore, using RF-MEMS devices with low pull-in voltages represents a solution that might be beneficial to the reliability of the device, surely improving the integrability, compactness, and cost of the final device.
From a designer’s point of view, different strategies can be followed to obtain low pull-in RF-MEMS switches, each of which is represented by numerous examples in recent works in the literature. Despite their practical drawbacks, piezoelectric, electro-thermal, and electro-magnetic mechanisms are particularly suitable for obtaining low actuation voltages. Within the piezoelectric context, the adoption of materials with high piezoelectric coefficients is permitted to achieve actuation voltages in the range of 2 V [
11] to 2.5 V [
12]. The electro-thermal device reported in [
13] features chevron lateral actuators driven by an 11 V source, while in [
14], the combination of driving and latching electro- thermal actuators allowed the authors to obtain a lateral actuation at 6 V. In the case of electro-magnetic devices, the proper dimensioning of the coil generating the magnetic field which triggers the collapse of the membrane allows the designer to achieve arbitrarily low pull-in voltages, such as 3 V [
15] or 4.3 V [
16].
Within the framework of electrostatic actuation, the most common strategy to reach reduced pull-in voltages is to combine the maximization of the “effective area” (the overlapping area between the fixed electrodes and the movable structure) with the design of a movable membrane characterized by a small spring constant [
6]. Structures with a low spring constant can be attained by elongated shapes (long straight membranes or beams) or by meandered, folded, or serpentine-shaped beams. While the choice of elongated structures may be problematic from the point of view of miniaturization, meandered beams represent a more viable solution. In fact, elongated membranes may determine an excessive footprint or aspect ratio for such basic switching components. As an example, the sole membrane employed in [
17] has a footprint of 1600 × 240 µm
2. Regarding the design of the beams, some examples can be traced in the recent literature, such as the fabricated samples described in [
18,
19], which are characterized by clamped–clamped structures with folded or convoluted beams and by the actuation voltages of 16 V and 5.8 V, respectively. Simulated clamped–clamped membranes with meandered and serpentine-shaped beams are reported in [
20,
21], featuring estimated pull-in voltages of 3.3 V and 2.5 V, respectively, while the simulated cantilever structures detailed in [
22,
23] displayed actuations at 9.1 V and 7.3 V.
In this paper, a class of clamped–clamped series ohmic switches with actuation voltages within the 4–8 V range is discussed in terms of design principles and measured electrical and electromechanical performances. The simulated electrical and electromechanical behaviors of the three variants of meandered beams were formerly reported in [
24], and in this paper, it will be compared to actual measurements performed on the first batch of recently fabricated samples and critically evaluated.
This paper is organized as follows: In
Section 2, the basic design principles regarding the discussed devices will be summarized, starting from the layout and from 3D models; in
Section 3, the outcomes of the recent electrical and electromechanical measurements will be displayed and assessed.
Section 4 concludes this paper with a summary of the considerations.
2. Design Principles
As visible in
Figure 1 and
Figure 2, the design of the proposed class of switches relies on a basic arrangement, characterized by uniform meanders, which is varied in order to achieve increasingly low pull-in voltages. Starting from the layout represented in
Figure 1a, it is possible to identify several crucial layers, namely the first layer of the fabrication process, the polycrystalline silicon, which composes the central buried electrodes and the lateral decoupling resistors. While the former, deployed under the drilled areas of the membrane, are meant to cause the collapse of the membrane, the latter avoid the flow of the RF signal towards the ground planes when the membrane is actuated. It is also possible to identify square pillars under the drilled areas of the membrane, which are intended to prevent the complete collapse of the membrane onto the underlying layer of silicon oxide, and the chance of stiction (missed release of the membrane when the bias of the electrodes is removed) in the case of charges trapped within the oxide. The pillars are composed by layers of polycrystalline silicon, multi-metal based on aluminum, and evaporated gold. The multi-metal layer is also employed to deploy the central and interrupted RF signal line, whose terminals are covered by rectangular contact pads of evaporated gold. Such areas will be the surfaces that make contact with the collapsed membrane, which is made by two layers of electroplated gold. While the first layer represents the actual structure of the central membrane, the second thicker layer is present just over the surfaces, which are meant to be stiffer (anchors, borders of the movable membrane). Additional details regarding the fabrication process at Fondazione Bruno Kessler (FBK) facilities can be found in [
25].
As noticeable in the 3D model of
Figure 1b, all of the layers below the one of evaporated gold are buried under silicon oxide (except the pillars). The footprint of the whole membrane is 780 × 270 µm
2, featuring a central rectangular plate of 380 × 170 µm
2 and beams shaped by uniform meanders of 50 µm by 25 µm (
a and
b in
Figure 1b) and characterized by a width of 10 µm. The second device, partially illustrated in
Figure 2a, is marked by non-uniform meandered beams, obtained by doubling the length of each terminal meander. In the third device, whose beam is depicted in
Figure 2b, the length of the terminal meander increased by up to four times its initial length, and the lateral dimension of the meanders slightly increased (
h in
Figure 2b) to maintain a minimum distance of 10 µm between the contact pads and the beams. All of the parameters reported in the abovementioned figures are specified in
Table 1.
3. Simulated and Measured Results
The following simulation results were obtained using the Finite Element Method (FEM). More specifically, Ansys HFSS was employed for the simulation of the electro-magnetic performances, while the Ansys Workbench was used for the electro-mechanical ones. The material properties considered in the following simulations are the ones of the gold used in the fabrication: a 19,300 kg/m3 density, a 98.5 GPa Young’s modulus, and a 0.22 Poisson’s ratio.
3.1. Electro-Mechanical Behavior
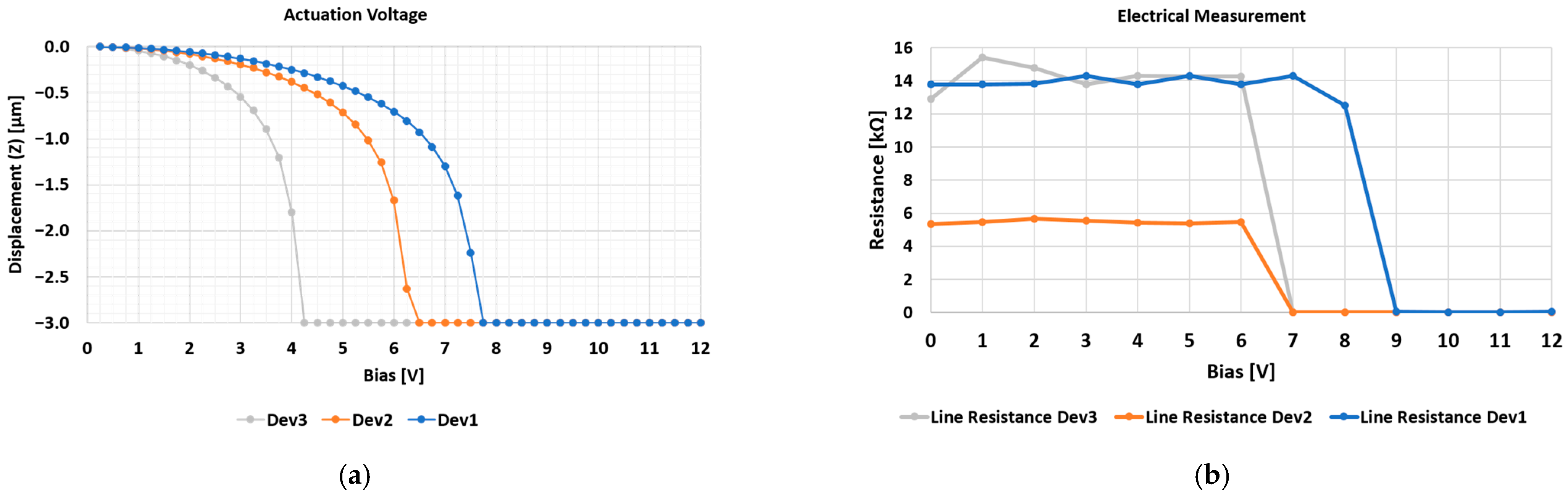
As reported in
Figure 3a, the simulated pull-in voltages of
Dev1,
Dev2, and
Dev3 correspond to 7.75 V, 6.5 V, and 4.25 V, respectively. The measurements represented by
Figure 3b were performed using a manual probe station equipped with micromanipulators and tips connected to two digital multimeters. The first multimeter, a Keithley 2430, provided the DC bias voltage and the ground reference to pads of the device under test (DUT), while the second one, a Keysight B2902A, maintained a limited voltage drop between the input and the output ends of the central RF signal line in order to measure the resistance of the line and the amount of flowing DC current. In fact, when the DC bias reaches the pull-in voltage, the collapse of the membrane will cause a sudden drop in the resistance (increase in DC current) measured along the RF line.
Under the premise that the DC bias has been provided by 1 V steps, the values displayed in
Figure 3b show a good agreement between the simulated and measured performances. In fact, while the measured pull-in voltages of
Dev3 and
Dev1 (9 V and 7 V) are slightly higher than the simulated ones (8 V and 5 V, respectively), the measured actuation of
Dev2 coincides with the expected one. The limited mismatch characterizing
Dev3 and
Dev1 switches can be attributed to the increased stiffness of their movable membranes due to the residual tensile stress induced during the fabrication process. In fact, the initial measurements displayed pull-in voltages exceeding the ones in
Figure 3b by 10–15 V. Most of the initial residual stress was released by means of a re-baking thermal treatment, during which the devices were kept at 200 °C for a couple of hours and then slowly cooled. The reported measurements were performed after.
3.2. Electro-Magnetic Behavior
The following characterization was achieved by means of a measurement setup composed of a Karl Suss PM5 probe station (KARL SUSS, Garching, Germany) equipped with two Karl Suss micromanipulators for DC tips and two RF/Microwave Ground-Signal-Ground (GSG) probes (Z50-X-GSG-200 model). The probes were connected to a proper 45 MHz–50 GHz Vector Network Analyzer (VNA), HP 8510C model.
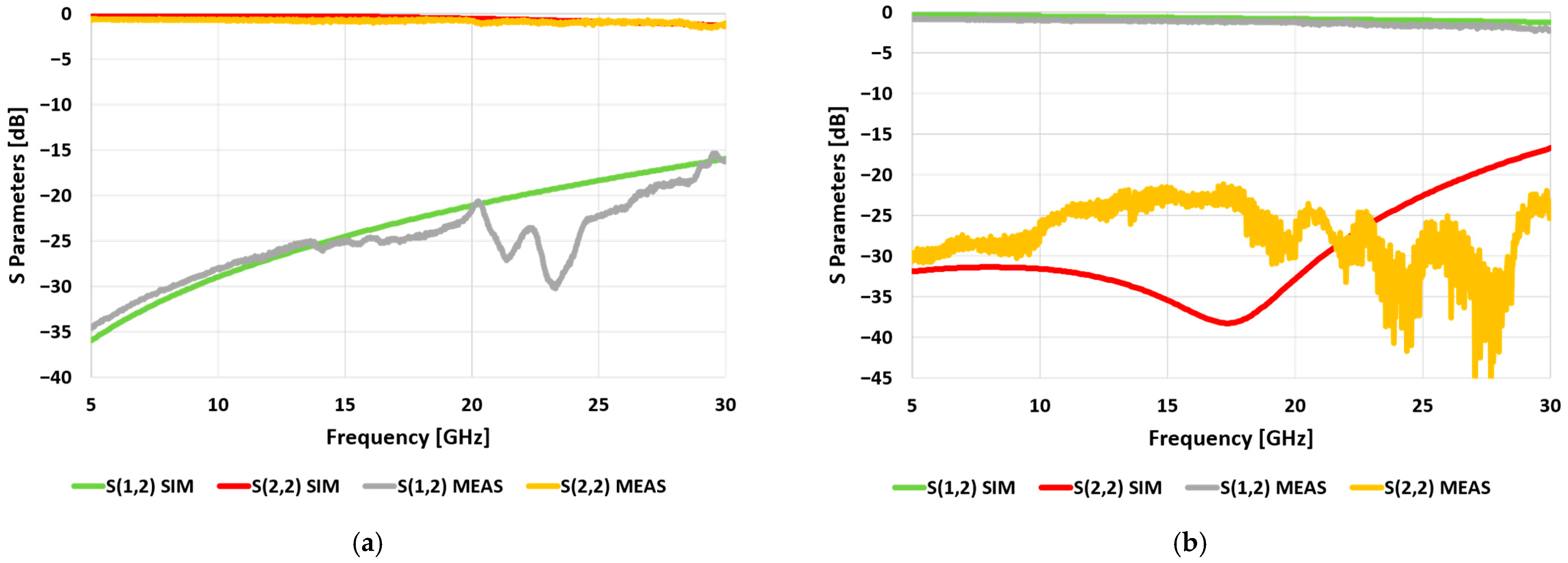
The outcomes of the performed characterization are reported in
Figure 4,
Figure 5 and
Figure 6, in which they are compared with the simulation results. From a general point of view, regarding the electrical behavior of
Dev1, in the following plots, the measured curves seem to be quite stable: contrary to the simulated curve, the measured return loss (S22 curve of each device in ON state) does not exceed the −21.3 dB along the entire considered frequency interval. In the OFF state (
Figure 4a), a remarkable agreement between the S22 curves is displayed, with a gap that never exceeds the 0.6 dB observable at 5 GHz. Also, in terms of insertion loss (S12 curve of each device in ON state), a substantial agreement is visible in
Figure 4b between the two curves, which are separated by a gap smaller than 0.95 dB along the entire measured interval. The measured insertion loss is smaller than −2 dB up to 29.2 GHz, and it reaches its maximum at 30 GHz (−2.17 dB). Regarding the isolation (S12 curve of each device in OFF state), in
Figure 4a, it is possible to notice that, while the measured curve approximates the simulated one up to 14 GHz, in the 14–29 GHz interval, it is generally even better, reaching the local minimum of −30 dB (at 23.3 GHz). Along the entire interval, the measured isolation is better than −15.5 dB (at 29.45 GHz). The only noisy curve is the one describing the return loss, which is also the one showing the most significant discrepancy with the simulation curves. In fact, it is possible to notice a non-negligible gap between the measured and simulated S22 curves of the ON state (
Figure 4b), with the measured one being greater in the 10–22 GHz range and reaching the maximum discrepancy of 16.93 dB at 17.19 GHz.
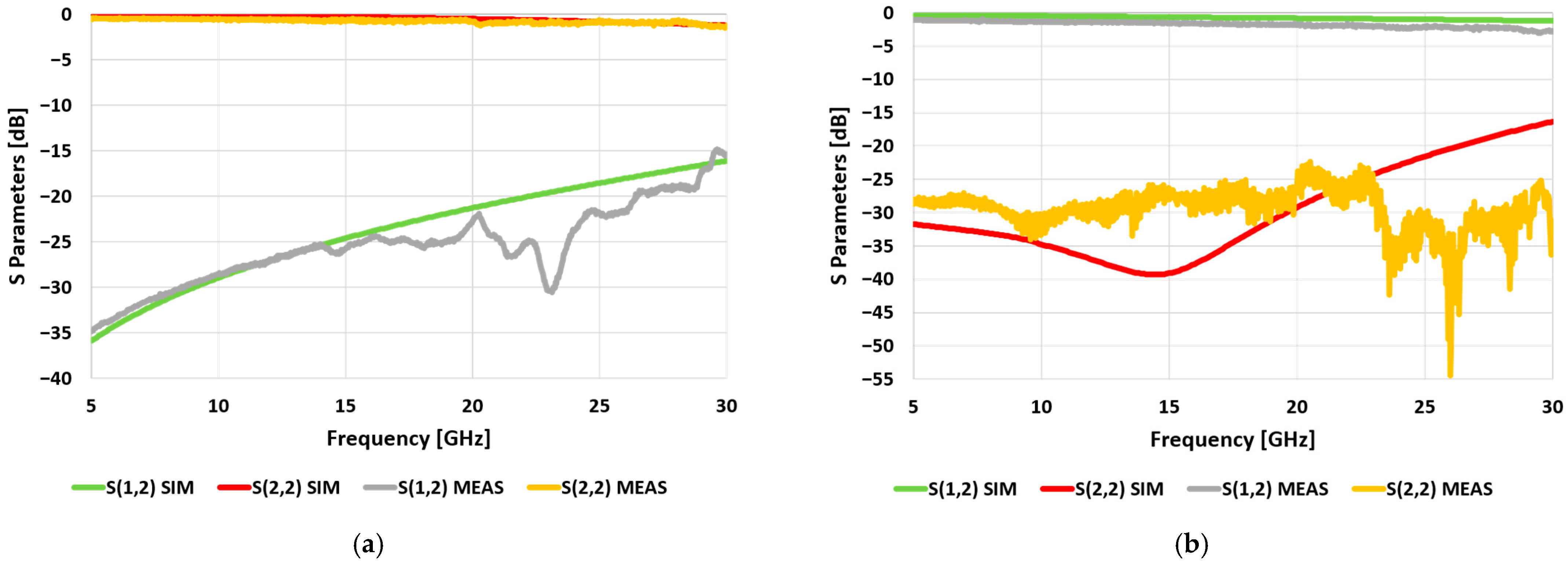
Compared to
Dev1, the S parameters of
Dev2 reported in
Figure 5a,b display a similar pattern. In fact, in this case, the measured return loss (S22) of
Figure 5b is higher than the simulated one along the central part (roughly from 10 to 22 GHz) of the frequency interval, and conversely to the simulated return loss, the measured one does not exceed −22.43 dB (reached at 20.53 GHz). Regarding the insertion loss (S12) curves of
Figure 5b, their discrepancy is smaller than 1.75 dB. While the minimum measured insertion loss is −3.02 dB (at 29.47 dB), it does not exceed the −2 dB threshold up to 22.8 GHz. The measured isolation (S12) of
Figure 5a is always below −14.86 dB (reached at 29.62 GHz), and it is better than the simulated one that ranges roughly from 14 to 29 GHz, with a local minimum of −30.52 dB at 23.13 GHz (−19.52 dB simulated value at the same frequency).
Concerning the performance of
Dev3, as reported in
Figure 6a,b, it is possible to notice that the measured return loss (S22) curve of
Figure 6b shows more limited oscillations, ranging from −20.22 dB (at 18.94 GHz) to −27.08 dB (at 28.22 GHz). The measured insertion loss (S12) curve of
Figure 6b shows a minimum of −3.35 dB (at 30 GHz), and it does not exceed −2 dB up to 15.7 GHz, with a rather constant discrepancy compared to the simulated curve, a discrepancy which is smaller than 1.88 dB along the entire interval. Following the pattern characterizing the previous devices, the measured isolation (S12) curve of
Figure 6a approximates the simulation curve at lower frequencies (roughly up to 12 GHz). In the subsequent portion of the considered spectrum, the measurement curve is generally better than the simulated one, and it reaches a minimum of −28.41 dB (at 23.56 GHz) and a maximum of −15.49 dB (at 30 GHz).
According to the reported measurements, the electromagnetic behavior of the considered devices is generally satisfying. In fact, among the three investigated devices along the 5–30 GHz interval, the return loss is always better than −20.22 dB, the insertion loss is better than −3.35 dB, and the isolation is better than −14.86 dB.