Abstract
In recent decades, natural hazards have caused major disasters in natural and man-made environments. Floods are one of the most devasting natural hazards, with high levels of mortality, destruction of infrastructure, and large financial losses. This study presents a methodological approach for flood risk management at lakes and adjacent areas that is based on the implementation of the EU Floods Directive (2007/60/EC) in Greece. Contemporary engineering approaches have been used for the estimation of the inflow hydrographs. The hydraulic–hydrodynamic simulations were implemented in the following order: (a) hydrologic modeling of lake tributaries and estimation flood flow inflow to the lake, (b) flood inundation modeling of lake tributaries, (c) simulation of the lake as a closed system, (d) simulation of the lake outflows to the adjacent areas, and (e) simulation of flood inundation of rural and urban areas adjacent to the lake. The hydrologic modeling was performed using the HEC-HMS model, and the hydraulic-hydrodynamic simulations were implemented with the use of the two-dimensional HEC-RAS model. The simulations were applied to three soil moisture conditions (dry, medium and wet) and three return periods (T = 50, T = 100 and T = 1000 years) and a methodology was followed for the flood inundation modeling in urban areas. Upper and lower estimates on water depths, flow velocities and inundation areas are estimated for all inflow hydrographs and for varying roughness coefficient values. The proposed methodology presents the necessary steps and the results for the assessment of flood risk management and mapping for lake and adjacent urban and rural areas. The methodology was applied to Lake Pamvotida in Epirus, Greece, Ioannina.
1. Introduction
Natural hazards have caused significant damages to natural and manmade environments during the last few decades. Floods are among the most destructive water-related hazards and lead to the loss of human lives, damage to infrastructure and economic losses [1]. According to the EM-DAT database, during the period 1900–2017 Greece experienced 26 major floods that caused 113 deaths, affected about 23,000 people and cost $2.0 billion [2].
The estimation and mapping of flood inundation areas and flood hazard in ungauged watersheds and basins is based on four components: (i) synthetic storm generator/estimator; (ii) hydrological modeling; (iii) hydraulic/hydrodynamic modeling, and (iv) application of geographical information systems. The estimation of synthetic storms is based on the Intensity–Duration–Frequency (IDF) curves with standard time profiles for constructing synthetic rainfall events of a certain probability. A method is used for extracting the excess rainfall and rainfall abstractions (losses); for example the SCS-CN method. Various methods have been used for transforming excess rainfall into runoff, such as the synthetic unit hydrograph method. The SCS-CN method, developed by the Soil Conservation Service [3] (currently referred to as Natural Resources Conservation Service, NRCS) is considered the prevailing modeling approach for ungauged basins. The flood inundation modeling and mapping and associated the flood risk could be assessed by using one-dimensional (1D) and two-dimensional (2D) hydraulic/hydrodynamic models (e.g., [4,5]). Under complex and composite flow conditions and wide flood plains, a 2D-modeling approach is generally suggested due to the provision of more accurate or realistic results [5,6].
An operational framework for flood inundation mapping in ungauged urban areas is proposed, developed and demonstrated in this paper. The framework is developed in the context of the implementation of the EU Floods Directive in Greece and is demonstrated for Lake Pamvotida, adjacent to Ioannina city. The framework is a tool to estimate and map flood inundation areas, and could be used for the application of design measures and policies for the protection of human life, property, and economic activities.
2. Materials and Methods
In this study, an integrated flood hazard modeling and mapping framework has been developed and implemented at ungauged urban, suburban and rural streams/catchments. The main goal is to highlight the possible disastrous effect of fluvial floods on human health, economic activities, cultural heritage, and the environment for three typical design return periods (T = 50, 100, 1000 years), according to the European Union Flood Directive 2007/60/EC and the respective Greek legislation. The single event-based deterministic approach is adopted, based on three modeling components: (i) a synthetic storm generator/estimator; (ii) a hydrological simulation model; and (iii) a hydraulic simulation model. The major assumption of the framework is that the flood hazard is connected to the determination of the input rainfall return period. Finally, the outcome of the framework is the flood hazard maps (for T = 50, 100, 1000 years) corresponding to the “average” hydrological scenario as well as two “extreme” scenarios, which allow providing lower and upper uncertainty bounds of the estimated flood quantities for each return period of interest. The proposed framework is described in the next paragraphs.
2.1. Synthetic Design Storm Estimator
A key assumption of the event-based approach is that the flood risk is determined in terms of return period, T, of the design rainfall (hyetograph). The latter represents the temporal evolution of a hypothetical storm event of a certain duration D and time resolution Δt, which corresponds to the given return period. In this study, we have investigated a number of rainfall scenarios, setting D = 24 h (which is about five times larger than the time of concentration of the basin) and Δt = 15 min. Moreover, following the semi-distributed approach, we assigned spatially-varying rainfall inputs across sub-basins, thus accounting for the heterogeneity of the storm regime over the study basin, which is due to climatic reasons as well as relief and orography effects.
The computational procedure for extracting design hyetographs across sub-basins comprised three steps: (a) estimation of partial rainfall depths for all temporal scales and return periods of interest, on the basis of spatially-averaged Intensity Duration Frequency (IDF) curves relationships; (b) derivation of a synthetic hyetograph, by placing the partial depths at specific time intervals across the given duration (i.e., 24 h); and (c) application of an empirical reduction formula, to transform point to areal estimations.
The IDF relationships could be described by the following equation, proposed by [7]:
where, i is the average rainfall intensity over a certain time scale (also referred to as duration) d, and a given return period T, as the ratio of a probability function, a(T), to a function of time scale, b(d). The nominator a(T) of Equation (1) is the mathematical expression of a Generalized Extreme Value (GEV) distribution for rainfall intensity over some threshold at any time scale. The parameters of Equation (1), η and θ were estimated from observed data and the shape parameter κ is initially obtained by fitting the GEV model to the maximum 24 h data and estimating its parameters by the L-moments method. For given parameters κ, η and θ, the L-moments method is employed to estimate the scale and location parameters, λ′ and ψ′, at each station. In order to extract the confidence intervals of rainfall estimations, a generalized Monte Carlo framework was applied, because there are no analytical formulas for the GEV distribution as made for most of distributions [8].
2.2. Hydrological Modeling
For each return period of interest (T = 50, 100, 1000 years), three scenarios (herein referred to as low, average and high) have been formulated, in order to account for joint rainfall and hydrological uncertainties. Specifically, the design rainfall estimation provided by the IDF relationship is assumed to correspond to the average scenario (or median 50%), while its 80% confidence limits, which are measures of rainfall uncertainty, correspond to the two extreme scenarios (e.g., low-20% and high-80%). The design hyetorgraphs have been produced by IDF curves using the Alternating Block Method (ABM) for return periods of T = 50 and 100 years, and the method of Worst Case Design Storm (WCDS) for the return period of T = 1000 years.
The hydrological uncertainty has been expressed in terms of three typical antecedent soil moisture conditions: Dry, moderate, and wet. The well-known SCS-CN approach developed by the Soil Conservation Service (SCS) [3] has been used for the estimation of excess rainfall. Three antecedent soil moisture conditions have been employed in each case, the dry (or low) represented by CNI, the moderate (or average) represented by CNII, and the wet (or high) represented by CNIII.
The transformation of the excess rainfall over the basin to flood hydrograph at the outlet junction is made by using the dimensionless curvilinear unit hydrograph approach of SCS of the HEC-HMS modeling system. The widely-used empirical Giandotti formula is used for the estimation of basin time of concentration, tc, given by:
where tc is the time of concentration (h), A is the basin area (km2), L is the length of the longest runoff distance across the basin (km), and Δz is the difference between the mean elevation of the basin and the outlet elevation (m). Its predictive capacity was by far superior with respect to other widely-used empirical formulas of the literature [9]. To account for the dependence of the response time of the basin against runoff, the following semi-empirical formula, which arises from the kinematic wave theory, is used. This is based on the consideration that tc is inversely proportional to the design rainfall, i.e.,:
where i(5) is the design rainfall intensity for return period Τ = 5 years, for which the time of concentration is estimated by the Giandotti formula, and i(Τ) is the intensity of any higher return period, T.
2.3. Hydraulic-Hydrodynamic Modeling
The two-dimensional (2D) HEC-RAS model is used for hydraulic/hydrodynamic flow simulation and flood routing within streams/rivers and lakes. The model has been developed by the Hydrologic Engineering Center (HEC) of United States Army Corps of Engineers [10] and has been applied in many studies for flood inundation modeling (e.g., [5,11]). Furthermore, a benchmark analysis based on the two dimensional modeling capabilities, conducted by the U.S. Army Corps of Engineers, proved that HEC-RAS performed extremely well compared to the leading 2D models [12].
The HEC-RAS 5.0.3 computational engine is based on the full 2D Saint-Venant equations or the 2D diffusive wave equations [10]. Shallow water equations are simplifications of the Navier-Stokes equations. The Diffusive Wave Approximation of the Shallow Water (DSW) equations can be derived through the combination of mass conservation and the two-dimensional form of the Diffusion Wave Approximation. The HEC-RAS 2D solver is using the sub-grid bathymetry approach [10].
One of the basic factors of input data uncertainty in flood inundation modeling and mapping, especially when 2D hydraulic hydrodynamic models are used, is the Digital Elevation Model (DEM) accuracy. The DEM estimation process involves several errors, especially in complex river and riverine areas, due to the topographical technique used. In this study, the DEM resolution used is 5m and has been provided by National Cadastre and Mapping Agency S.A. (NCMA). The raw data consist of the Digital Surface Model that includes canopy, manmade structures and other surface obstacles. First, the different DSMs derived from the 1:5000 aerial photos have been merged to a continue DSM. Then, the entire DSM has been processed to fill/sink the erroneous areas. Finally, the DSM has been re-corrected using typical elevation downgrading methods in order to create the DEM.
An important input data uncertainty factor in flood inundation modeling is the roughness coefficient and the parameterization process that follows. A typical approach for large scale applications that uses two-dimensional hydraulic models is the estimation of the roughness coefficient using CORINE land cover data and standard roughness coefficient tables (e.g., [13]). This approach has been used in this study. Moreover, based on the EU Flood Directive guides, the “upper” and “lower” boundaries of Manning’s roughness coefficient were estimated, as −50% and +50% of the average Manning’s roughness coefficient values, respectively. Furthermore, all hydraulic structures of the study area were detected using aerial photographs, a GIS database of the technical works, field observations, and information collected by several authorities. Then, based on hydraulic structures geometry data, the entire DEM has been modified in order to include the flood protection works and the geometry of all hydraulic structures.
Finally, flood inundation modeling and mapping at urban and suburban areas remains a big challenge due to the complexity of the entire system. One of the most important factors in flood inundation modeling in built-up areas is the representation of buildings within the 2D hydraulic-hydrodynamic model. In this study, the local increase of building block representation method with parallel adjustment of roughness coefficient is used for significant urban areas such as large cities, whereas the approach of building representation with the local rise of roughness coefficient value is applied for small settlements and villages.
Following the above methodology, three (3) hydrologic/hydraulic scenarios have been formulated and simulated for the reach of every basin/sub-basin, stream/river and lake in every return period, considering uncertainty. The first, low, scenario represents the dry antecedent soil moisture conditions (CNI); the design synthetic storm is estimated for the 20% confidence level of IDF curves using the ABM for the storm time distribution; and low Manning’s roughness coefficient (e.g., nlow = naverage – 0.5 × naverage). Accordingly, the average scenario represents average antecedent soil moisture conditions (CNII), the design storm is estimated by the median IDF curves (50%) using the ABM for the storm time distribution, and the estimated Manning’s roughness coefficient (naverage). The high scenario represents high antecedent soil moisture conditions (CNIII). The design storm is estimated for the 80% confidence level of IDF curves (80%) using the WCDS for the storm time distribution and high Manning’s roughness coefficient (e.g., nhigh = naverage + 0.5 × naverage). In total, nine scenarios were simulated for the three return periods (e.g., T = 50, 100, 1000 years).
3. Application and Results of the Modeling Framework: Lake Pamvotida Basin
The Lake Pamvotida Basin is a closed basin with an area of 340.78 km2, located in Epirus, a region in Northwestern Greece (Figure 1). Part of the basin’s runoff flows through small streams into Lake Pamvotida and a smaller portion of the runoff is diverted to the adjacent Kalama River basin to the northwest). The city of Ioannina is located at the middle of the western bank of the lake and it is the capital and largest city of the Ioannina regional unit and of the administrative region of Epirus. Its population is 112,486, according to 2011 census.
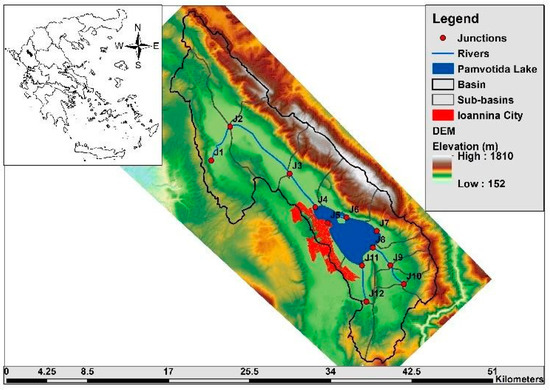
Figure 1.
Map of Lake Pamvotida Basin and modeling components (sub-basins, reaches, junctions).
The hydrological and hydraulic model of the basin consists of 15 sub-basins, 13 flow nodes, and 11 stream reaches. The basin is divided into two independent hydraulic sub-systems and the upstream sub-system consists of 10 sub-basins, which drain into the Lake Pamvotida. The downstream sub-system is divided into four (4) sub-basins (to the Northwest; Figure 1). The lake has five inflow nodes (i.e., J5, J6, J7, J8, J11) and it is modelled as an independent sub-basin (GR0514FL2009) and its runoff is concentrated in the node J4. When the stage of the lake increases above a certain threshold, a part of the stored volume overflows to the lower sub-system, which begins from node J4 and ends to node J1. The excess water is then diverted to the Kalama River basin through a canal. The formulation of the hydrological and hydraulic system is shown in Figure 1. In total, eight (8) stream reaches with total length of 46.7 km are located in the potential flood hazard zone and they have simulated for the routing of flood hydrographs and the estimation of flood hazard.
The two methodologies, outlined before, for rural and not significant settlements and for significant urban areas (e.g., Ioannina City) have been applied in the hydraulic simulations. The simulation results for inundated areas, water depth and maximum flow velocity are presented in Figure 2 (for T = 50 years) and Figure 3 (for T = 1000 years), respectively. The results indicate that the inundated area increases with the return period of the event and the depth of water is more sensitive than the water velocity.
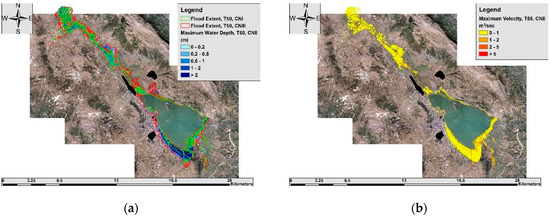
Figure 2.
Flood extent and maximum water depths of return period T = 50 years for all examined scenarios (a) and simulated maximum velocities (b) only for the average scenario.
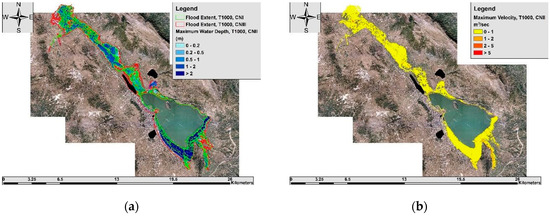
Figure 3.
Flood extent and maximum water depths of return period T = 1000 years for all examined scenarios (a) and simulated maximum velocities (b) only for the average scenario.
Results are quite diverse (Table 1), since the uncertainty bounds of all key flood quantities (peak flows, flood volumes, inundated areas, etc.) strongly overlap the risk expressed in terms of return period of rainfall. Special attention should be given to the developed methodology and its application only for specific return periods and hydrologic-hydraulic conditions due to the great variability in the peak discharge estimation. An ensemble of methods and scenarios should always be applied for engineering purposes, in order to choose the most appropriate technique in relation to the flood prone areas and proposed flood protection measures.

Table 1.
Total inundated area (km2) of Lake Pamvotida basin for all examined hydrologic and hydraulic scenarios at the selected return periods.
4. Conclusions
In this study, a methodological approach for implementing the EU Floods Directive 2007/60/EC in Greece is developed, with an emphasis on flood risk management in rural, urban and suburban areas, and on the Lake Pamvotida basin. The methodology is based on typical hydrological and flood inundation modeling and mapping techniques for ungauged catchments. Spatially distributed design hyetographs are applied for hydrologic and hydraulic 2D modeling of floods, taking into account parametric and structural uncertainty.
According to the flood extent values, it seems that the uncertainty induced in hydrological modeling, with respect to extreme rainfall estimation and antecedent soil moisture conditions, dominates against the return period. It should be emphasized that these two components are not the sole sources of uncertainty within rainfall-runoff transformations. This makes it essential to move to more rigorous methodological approaches (e.g., stochastic), instead of quantifying the flood risk on the basis of the return period of rainfall.
Author Contributions
G.P. performed the simulation and contributed to the writing of the paper, A.L. designed, organized and supervised the study and wrote the manuscript, and L.V. performed the analysis and presentation of the results and contributed to the writing of the paper.
Funding
This paper is part of the project “Management Plans of Flood Risks for River Basins in Thessaly, Western Sterea Hellas and Epirus Regions, Greece”, co-funded by the E.U. and the Greek Ministry of Energy and the Environment. This project constitutes the implementation of the EU Directive on Floods (E.C. 2007/60) in the above regions of Greece. The research presented in the paper is partially supported by this project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tsakiris, G. Flood risk assessment: Concepts, modelling, applications. Nat. Hazards Earth Syst. Sci. 2014, 14, 1361–1369. [Google Scholar] [CrossRef]
- Centre for Research on the Epidemiology of Disasters (CRED): Summarized Table of Natural Disasters in Greece from 1900 to 2017, EM-DAT: The CRED/OFDA International Disaster Database–www.emdat.be–Université Catholique de Louvain–Brussels–Belgium [online]. Available online: http://www.emdat.be (accessed on 12 January 2018).
- Soil Conservation Service (SCS). National Engineering Handbook; Section 4, Hydrology (NEH-4); U.S. Department of Agriculture: Washington, DC, USA, 1972.
- Aronica, G.; Bates, P.D.; Horritt, M.S. Assessing the uncertainty in distributed model predictions using observed binary pattern information within GLUE. Hydrol. Process. 2002, 16, 2001–2016. [Google Scholar] [CrossRef]
- Papaioannou, G.; Loukas, A.; Vasiliades, L.; Aronica, G.T. Flood inundation mapping sensitivity to riverine spatial resolution and modelling approach. Nat. Hazards 2016, 83, 117–132. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A mathematical framework for studying rainfall intensity-duration-frequency relationships. J. Hydrol. 1998, 206, 118–135. [Google Scholar] [CrossRef]
- Tyralis, H.; Koutsoyiannis, D.; Kozanis, S. An algorithm to construct Monte Carlo confidence intervals for an arbitrary function of probability distribution parameters. Comput. Stat. 2013, 28, 1501–1527. [Google Scholar] [CrossRef]
- Efstratiadis, A.; Koussis, A.D.; Koutsoyiannis, D.; Mamassis, N. Flood design recipes vs. reality: Can predictions for ungauged basins be trusted? Nat. Hazards Earth Syst. Sci. 2014, 14, 1417–1428. [Google Scholar] [CrossRef]
- Brunner, G. HEC-RAS River Analysis System: Hydraulic Reference Manual, Version 5.0. US Army Corps of Engineers–Hydrologic Engineering Center. 2016a, 1–538. Available online: http://www.hec.usace.army.mil/software/hec-ras/documentation/HEC-RAS%205.0%20Reference%20Manual.pdf (accessed on 12 January 2018).
- Dottori, F.; Di Baldassarre, G.; Todini, E. Detailed data is welcome, but with a pinch of salt: Accuracy, precision, and uncertainty in flood inundation modeling. Water Resour. Res. 2013, 49, 6079–6085. [Google Scholar] [CrossRef]
- Brunner, G. Benchmarking of the HEC-RAS Two-Dimensional Hydraulic Modeling Capabilities. US Army Corps of Engineers–Hydrologic Engineering Center. US Army Corps of Engineers—Hydrologic Engineering Center. 2016b, 1–116. Available online: http://www.hec.usace.army.mil/software/hec-ras/documentation/RD-51_Benchmarking_2D.pdf (accessed on 12 January 2018).
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).