Analyses of Monthly Discharges in Slovakia Using Hydrological Exploratory Methods †
Abstract
:1. Introduction
2. Materials and Methods
- A division of the time data series into two 30-year periods. The first period was from 1931 to 1960, and the second period was from 1986 to 2016.
- A division of the time data series into two halves; the first period was from 1931 to 1973, and the second period was from 1974 to 2016.
- A division of the time data series by an analysis of the residuals. The change-point of the summer and winter periods determines the division of the time data series (Table 2, the columns Qsum and Qwin). The summer period was defined as May to October and the winter period from November to April.
- A division of the time data series also by an analysis of the residuals. The change-point of the mean monthly discharge period determines the division of the time data series (Table 2, the last column Qm).
3. Results
3.1. The Analysis of the Residuals
3.2. Pettitt’s Test
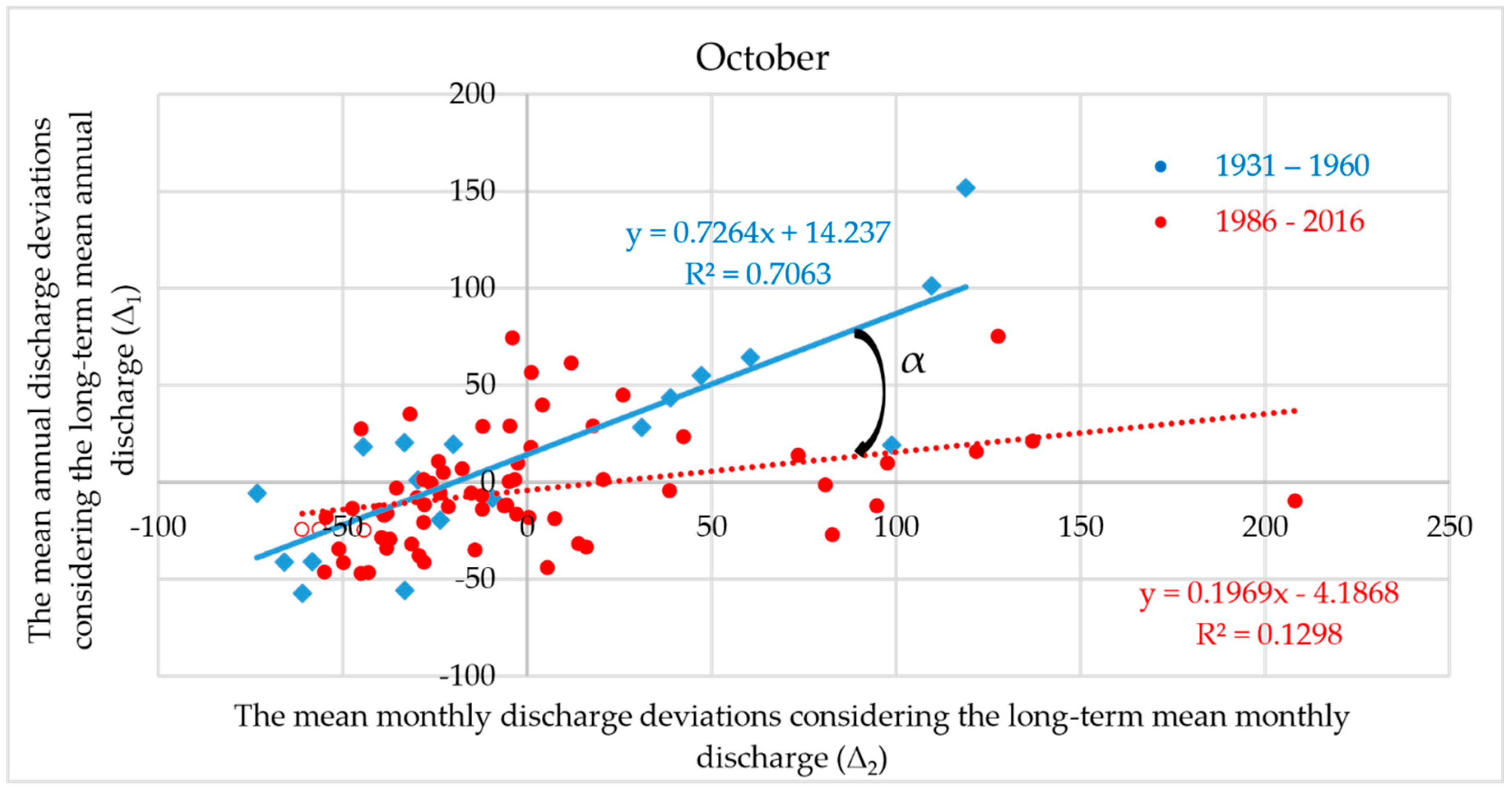
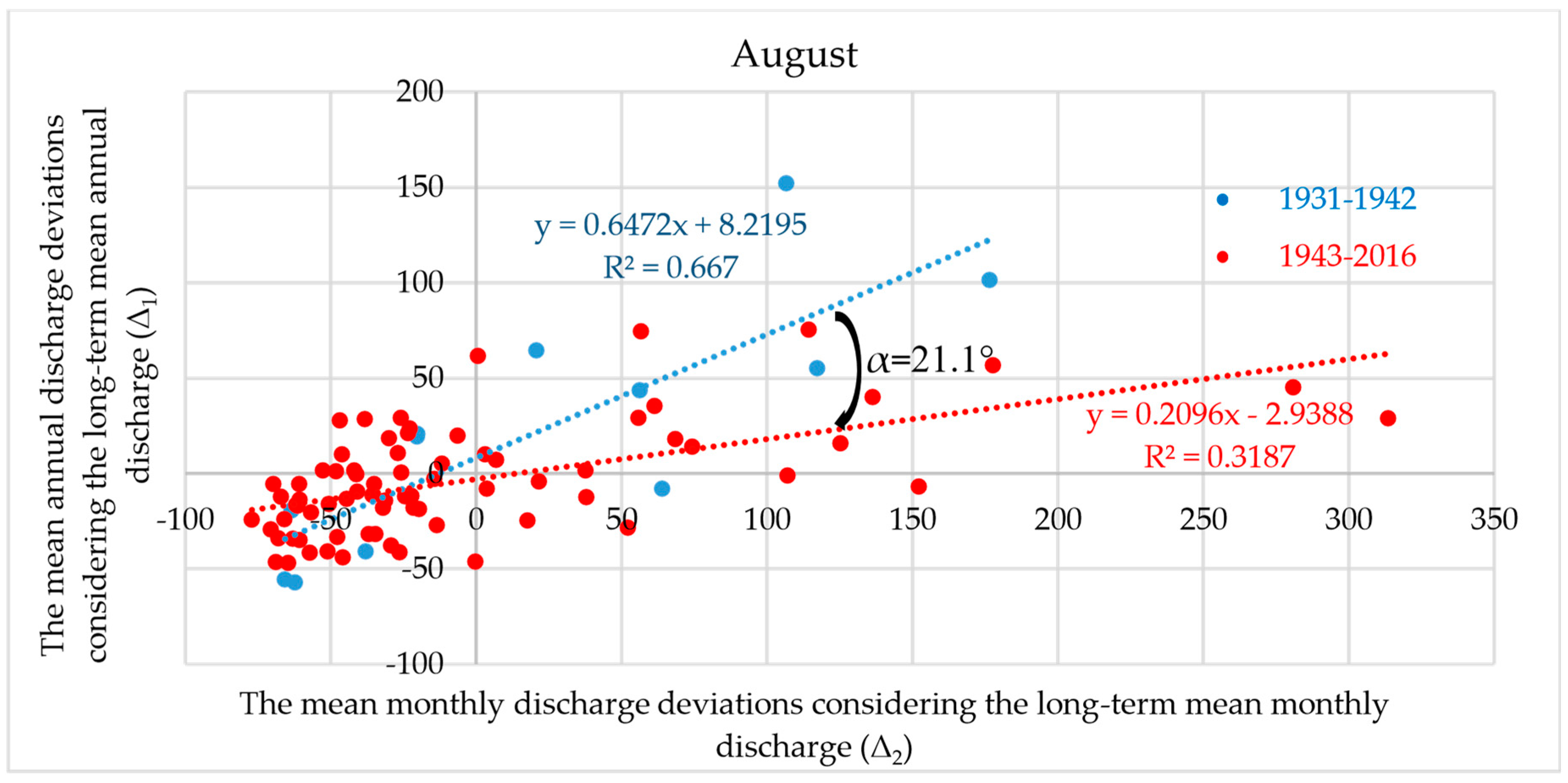
3.3. An Analysis of the Runoff Regime Changes by the Deviations
4. Discussion
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential Impacts of a Warming Climate on Water Availability in Snow-Dominated Regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Hlavcova, K.; Szolgay, J.; Kohnová, S.; Hlásny, T. Simulation of hydrological response to the future climate in the Hron River basin. J. Hydrol. Hydromech. 2008, 56, 163–175. [Google Scholar]
- Škvarenina, J.; Szolgay, J.; Šiška, B.; Lapin, M. (Eds.) The Climate Change and Landscape—Impacts of the Climate Change and Assessment of the Territorial Vulnerability in Slovakia in Water Resources Management, Forests and agriculture; Study XXV, Vol. XXII; The Slovak Bioclimatological Society: Zvolen, Slovakia, 2010; ISBN 978-80-228-2272-5. [Google Scholar]
- Implementation of Directive 2007/60/EC of the European Parliament and of the Council of 23 October 2007 on the Assessment and Management of Flood Risks. The Preliminary Flood Risk Assessment in the Bodrog Subbasin. Ministry of the Environment of the Slovak Republic. Dec. 2011, pp. 38–42. Available online: http://www.minzp.sk/sekcie/temyoblasti/voda/ochrana-pred-povodnami/manazment-povodnovych-rizik/ (accessed on 28 October 2018).
- Pettitt, A.N. A non-parametric approach to the change-point problem. J. Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Tegelhoffová, M.; Danáčová, M.; Szolgay, J. A spatial assessment of the indicator of hydrological regime changes. Acta Hydrologica Slovaca 2013, 14, 243–251. [Google Scholar]
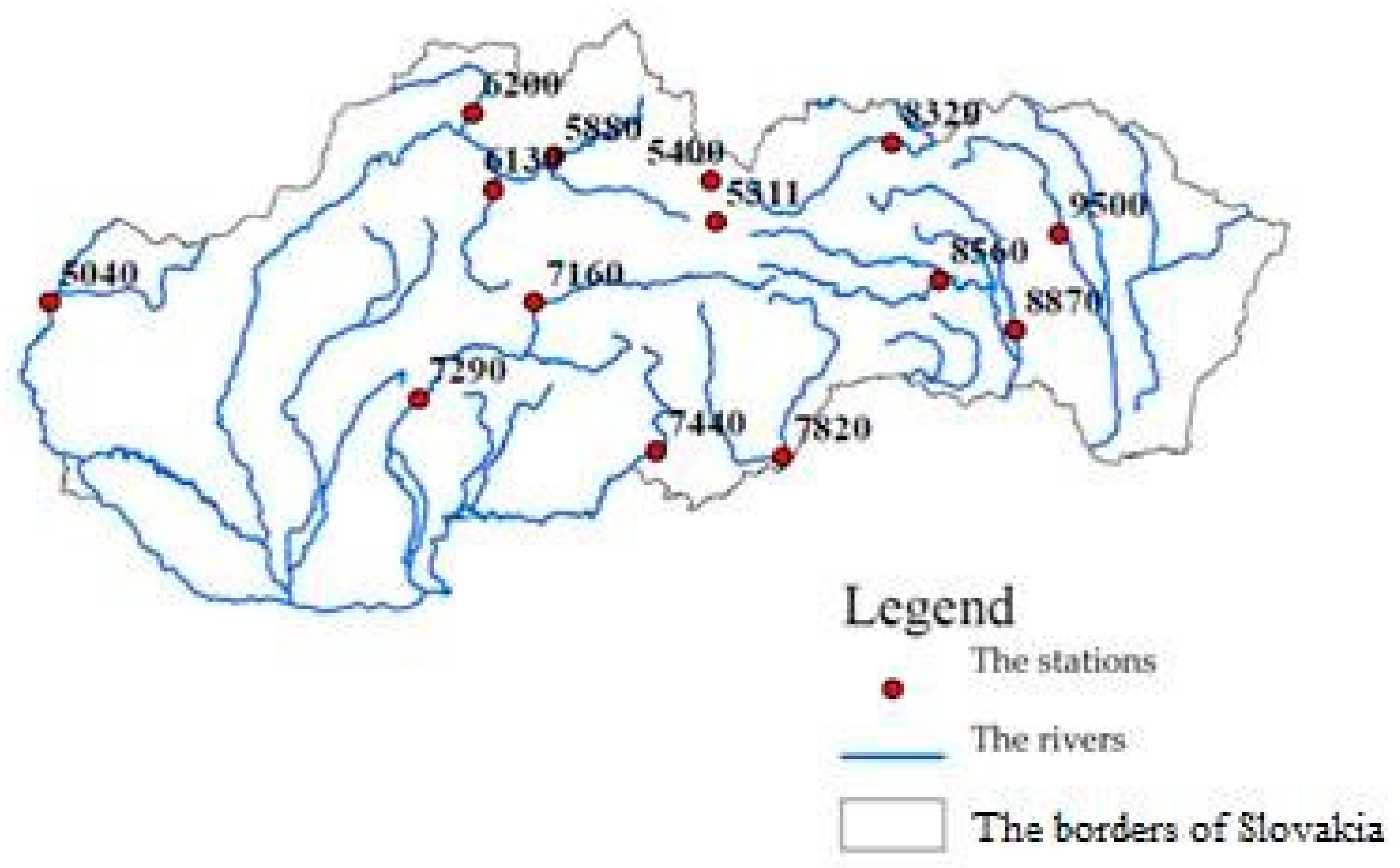
| Stage-Discharge Gauging Stations | The Rivers | Number of Station | Catchment Area (km2) |
|---|---|---|---|
| Moravský sv. Ján | Morava | 5040 | 24,129.30 |
| Čierny Váh | Čierny Váh | 5311 | 243.06 |
| Podbánské | Belá | 5400 | 93.49 |
| Dierová | Orava | 5880 | 1966.75 |
| Martin | Turiec | 6130 | 827.00 |
| Kysucké Nové Mesto | Kysuca | 6200 | 955.09 |
| Bánska Bystrica | Hron | 7160 | 1766.48 |
| Brehy | Hron | 7290 | 3821.38 |
| Holiša | Ipeľ | 7440 | 685.27 |
| Lenártovce | Slaná | 7820 | 1829.65 |
| Jaklovce | Hnilec | 8560 | 606.32 |
| Košické Olšany | Torysa | 8870 | 1298.30 |
| Hanušovce | Topľa | 9500 | 1050.03 |
| Chmelnica | Poprad | 8320 | 1262.41 |
| Stat. | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Qsu | Qwi | Qm |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5040 | 1974 | 1988 | 1948 | 1970 | 1987 | 1987 | 1952 | 1987 | 1941 | 1941 | 1952 | 1988 | 1942 | 1948 | 1948 |
| 5311 | 1953 | 1977 | 1983 | 1972 | 1979 | 1989 | 1975 | 1972 | 1984 | 1980 | 1952 | 1966 | 1979 | 1980 | 1980 |
| 5400 | 1947 | 1944 | 1953 | 1953 | 1974 | 2002 | 1985 | 1981 | 1975 | 1962 | 1952 | 1952 | 1964 | 1953 | 1981 |
| 5880 | 1954 | 1954 | 1951 | 1956 | 1986 | 1954 | 1993 | 1978 | 1941 | 1981 | 1952 | 1962 | 1945 | 1983 | 1949 |
| 6130 | 1974 | 1965 | 1951 | 1970 | 1972 | 1968 | 1966 | 1966 | 1941 | 1980 | 1952 | 1976 | 1966 | 1977 | 1967 |
| 6200 | 1973 | 1965 | 1976 | 1970 | 1938 | 1954 | 1975 | 1986 | 1941 | 1981 | 1952 | 1989 | 1987 | 1965 | 2002 |
| 7160 | 1953 | 1977 | 1981 | 1972 | 1996 | 1989 | 1966 | 1966 | 1941 | 1984 | 1952 | 1966 | 1985 | 1970 | 1981 |
| 7290 | 1953 | 1977 | 1983 | 1970 | 1987 | 1989 | 1966 | 1966 | 1941 | 1984 | 1952 | 1980 | 1985 | 1981 | 1981 |
| 7440 | 1982 | 1979 | 1970 | 1980 | 1942 | 1994 | 1952 | 1970 | 2009 | 1973 | 1952 | 1976 | 2009 | 1980 | 1981 |
| 7820 | 2008 | 1979 | 1941 | 1961 | 1969 | 1964 | 1952 | 1970 | 1944 | 1963 | 1952 | 1976 | 1953 | 1980 | 1980 |
| 8560 | 1953 | 1977 | 1945 | 1980 | 1945 | 1975 | 1960 | 1960 | 1941 | 1984 | 1952 | 1952 | 1955 | 1953 | 1955 |
| 8870 | 1953 | 1965 | 1945 | 1980 | 1974 | 2004 | 1996 | 1985 | 1941 | 1973 | 1952 | 1985 | 1969 | 1981 | 1945 |
| 9500 | 1953 | 1977 | 1986 | 1980 | 1973 | 1964 | 1996 | 1985 | 1941 | 1980 | 1980 | 1987 | 1969 | 1981 | 1981 |
| 8320 | 1975 | 1969 | 1946 | 1970 | 1982 | 1967 | 1996 | 1960 | 1941 | 1973 | 1952 | 1950 | 1949 | 1970 | 1949 |
| Stat. | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Qsum | Qwin | Qm |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5040 | 1973 | 1988 | 1948 | 1988 | 1997 | 1987 | 1987 | 1987 | 1954 | 1954 | 1981 | 1998 | 1987 | 1948 | 1988 |
| 5311 | 1953 | 1971 | 1983 | 1979 | 1996 | 1989 | 1975 | 1972 | 1980 | 1981 | 1952 | 1966 | 1980 | 1979 | 1980 |
| 5880 | 1954 | 1954 | 1951 | 1952 | 1986 | 1954 | 1993 | 1978 | 1941 | 1981 | 1950 | 1962 | 1945 | 1983 | 1949 |
| 5400 | 1947 | 1944 | 1944 | 1997 | 1974 | 2002 | 1985 | 1981 | 1941 | 1962 | 1952 | 1952 | 2002 | 1953 | 1981 |
| 6130 | 1992 | 2006 | 1998 | 1972 | 1987 | 1968 | 1972 | 1986 | 1942 | 1966 | 1966 | 1976 | 1966 | 1977 | 1967 |
| 7160 | 1983 | 1977 | 1983 | 1972 | 1996 | 1989 | 1975 | 1980 | 1981 | 1941 | 1952 | 1966 | 1980 | 1970 | 1980 |
| 6200 | 1973 | 1965 | 2009 | 1970 | 1938 | 1957 | 1982 | 1986 | 1941 | 1941 | 1952 | 1989 | 1987 | 1936 | 2002 |
| 7290 | 2000 | 1981 | 1983 | 1988 | 1987 | 1989 | 1972 | 1978 | 1981 | 1941 | 1952 | 1967 | 1985 | 1983 | 1985 |
| 7440 | 1982 | 1981 | 1970 | 1988 | 1991 | 1991 | 1952 | 1952 | 1950 | 1962 | 1980 | 1970 | 1950 | 1980 | 1980 |
| 7820 | 1983 | 1980 | 1941 | 1961 | 1964 | 1989 | 1975 | 1996 | 1980 | 1944 | 1945 | 1966 | 1950 | 1980 | 1980 |
| 8560 | 1983 | 1973 | 1955 | 1980 | 1991 | 1976 | 1960 | 1960 | 1955 | 1945 | 1952 | 1968 | 1980 | 1970 | 1980 |
| 8870 | 1953 | 2006 | 1986 | 2001 | 1969 | 1937 | 1996 | 1995 | 1941 | 1973 | 1945 | 1945 | 1969 | 1983 | 1945 |
| 9500 | 2004 | 2006 | 1986 | 2000 | 1969 | 1964 | 1952 | 1981 | 1996 | 1945 | 1981 | 1982 | 1969 | 1983 | 1981 |
| 8320 | 1961 | 1969 | 1971 | 1970 | 1936 | 1936 | 1996 | 1945 | 1941 | 1945 | 1952 | 1960 | 1949 | 1970 | 1949 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ďurigová, M.; Ballová, D.; Hlavčová, K. Analyses of Monthly Discharges in Slovakia Using Hydrological Exploratory Methods. Proceedings 2019, 7, 18. https://doi.org/10.3390/ECWS-3-05824
Ďurigová M, Ballová D, Hlavčová K. Analyses of Monthly Discharges in Slovakia Using Hydrological Exploratory Methods. Proceedings. 2019; 7(1):18. https://doi.org/10.3390/ECWS-3-05824
Chicago/Turabian StyleĎurigová, Mária, Dominika Ballová, and Kamila Hlavčová. 2019. "Analyses of Monthly Discharges in Slovakia Using Hydrological Exploratory Methods" Proceedings 7, no. 1: 18. https://doi.org/10.3390/ECWS-3-05824
APA StyleĎurigová, M., Ballová, D., & Hlavčová, K. (2019). Analyses of Monthly Discharges in Slovakia Using Hydrological Exploratory Methods. Proceedings, 7(1), 18. https://doi.org/10.3390/ECWS-3-05824




