A Low-Cost Miniature Electrohydrostatic Actuator †
Abstract
:1. Introduction
2. Materials and Methods
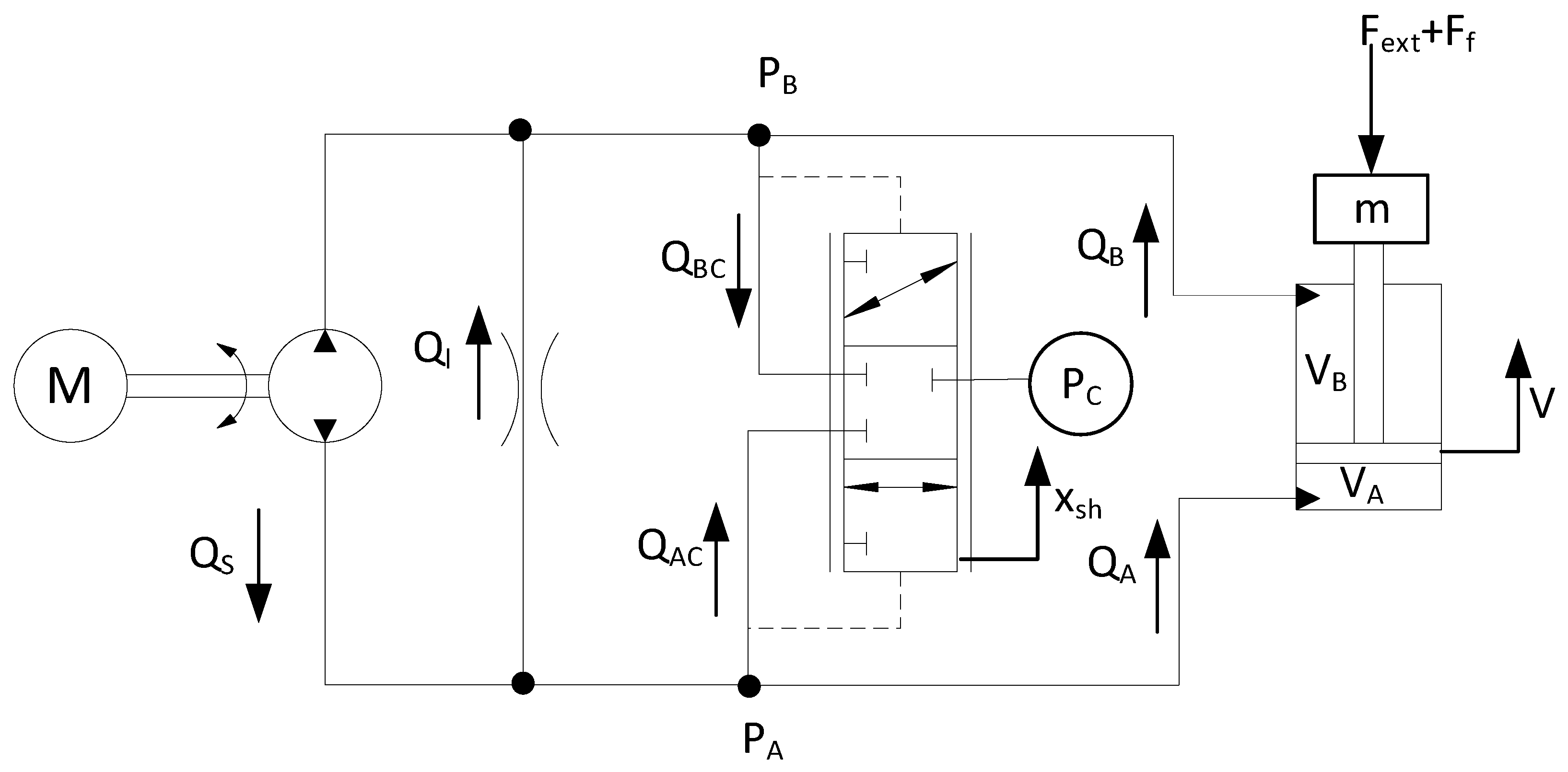
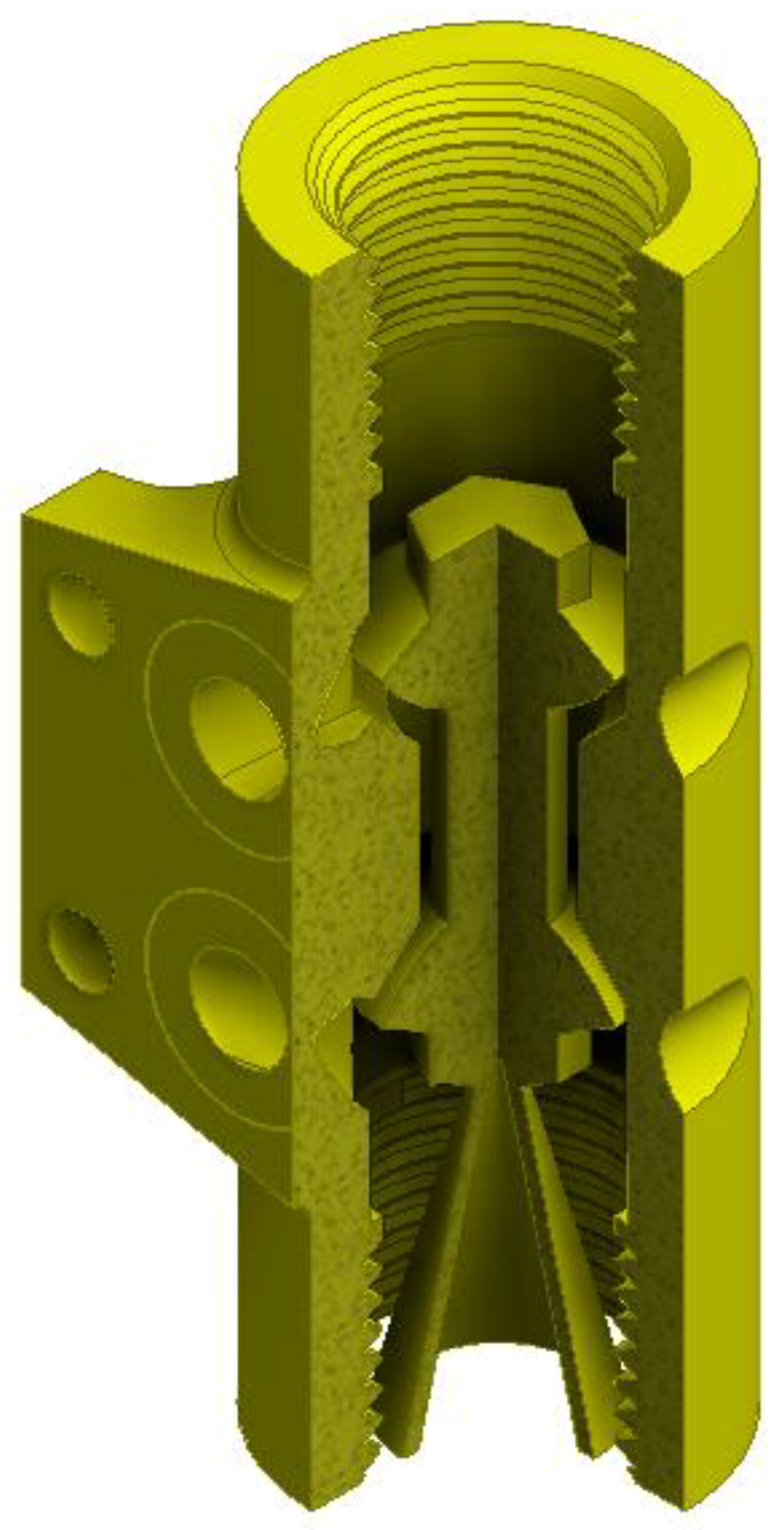
2.1. System Description
2.2. Dynamic Model
2.3. Controller
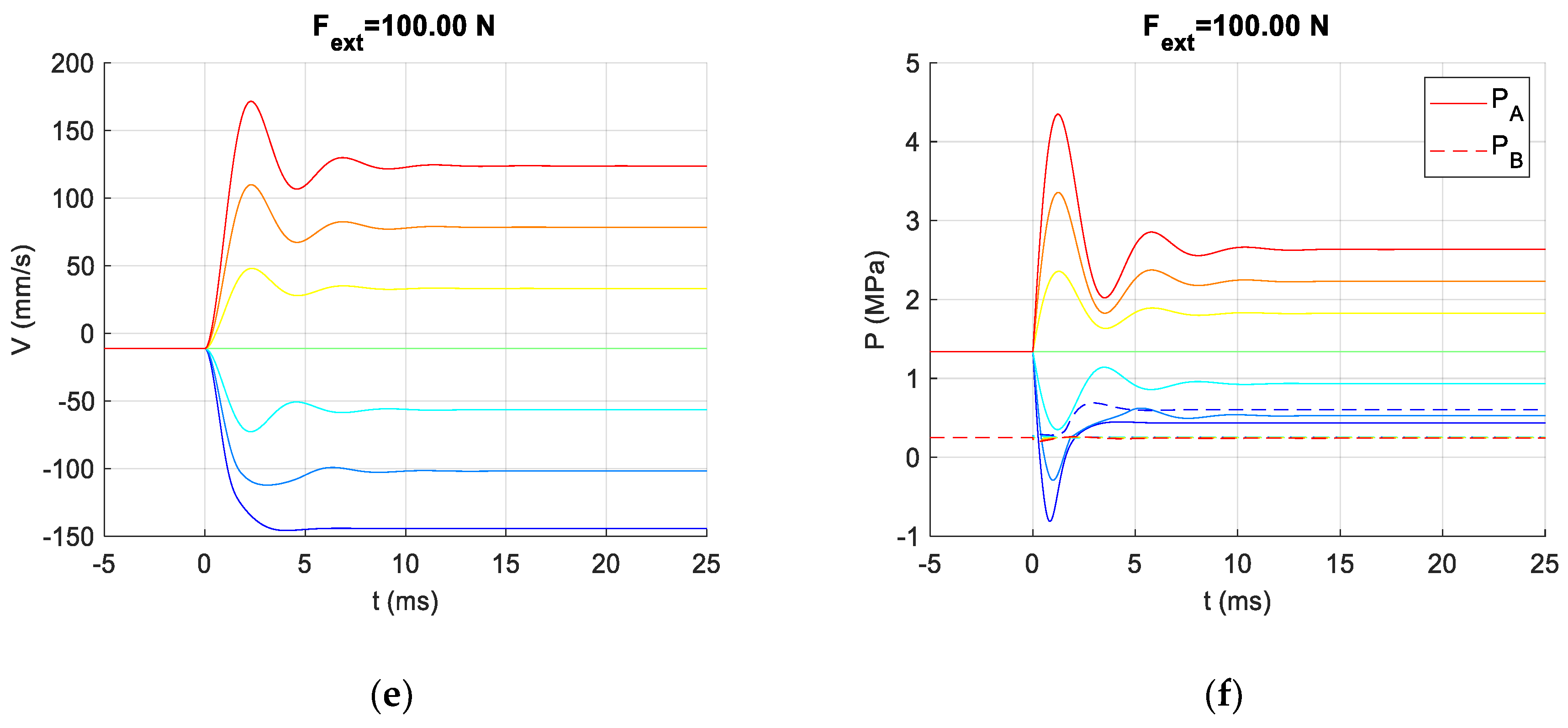
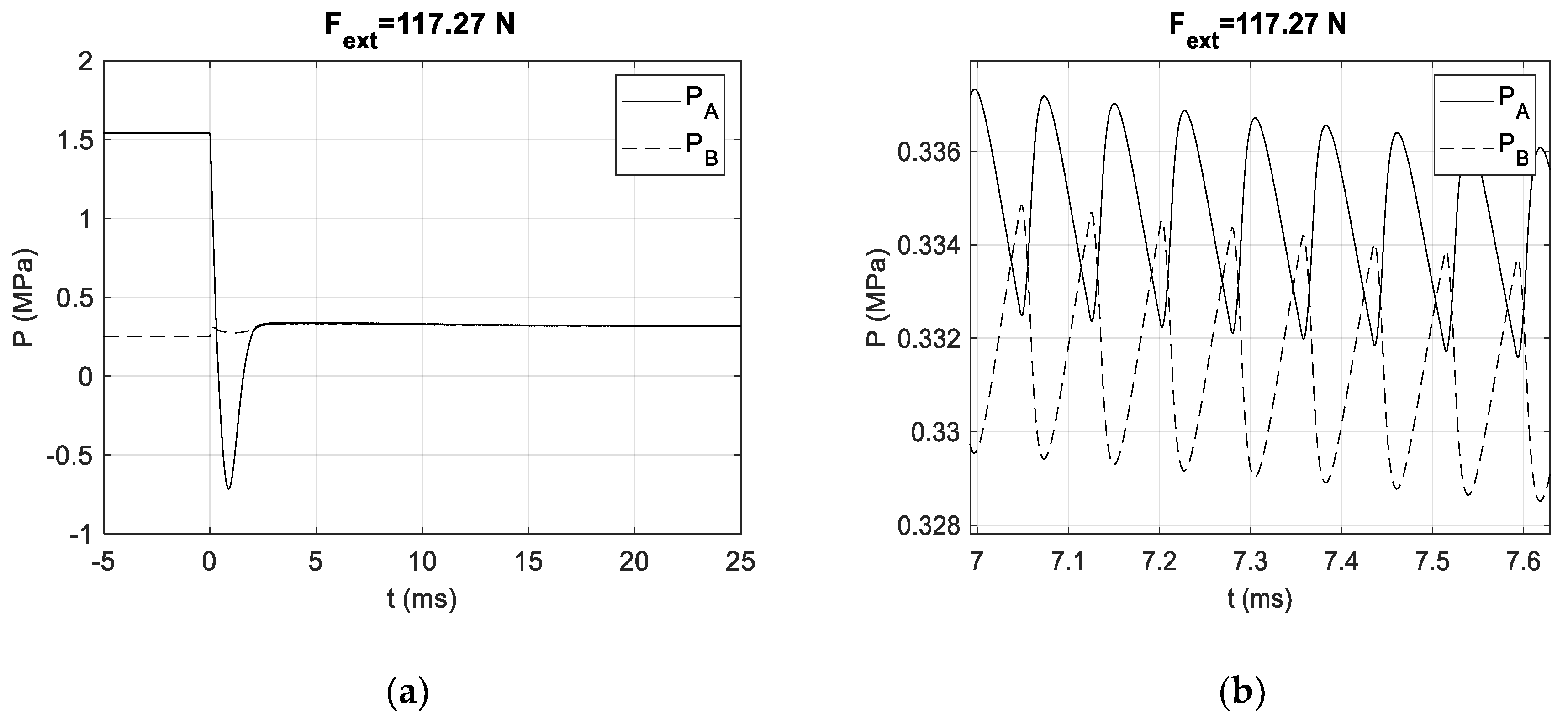
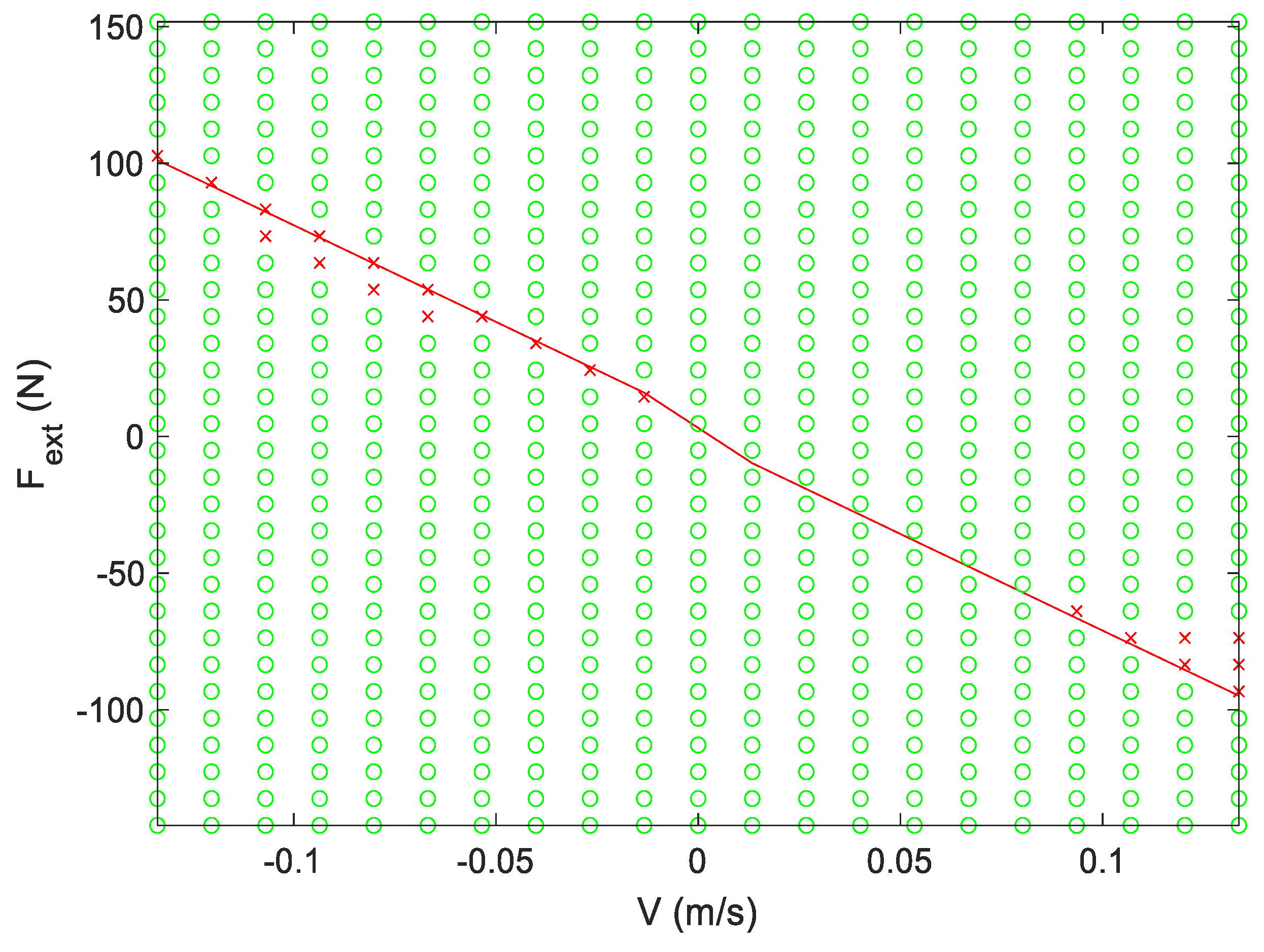
2.4. Simulation Studies
3. Results
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| EHA | Electrohydrostatic Actuator |
References
- Ketelsen, S.; Padovani, D.; Andersen, T.O.; Ebbesen, M.K.; Schmidt, L. Classification and Review of Pump-Controlled Differential Cylinder Drives. Energies 2019, 12, 1293. [Google Scholar] [CrossRef]
- Merritt, H.E. Hydraulic control systems. J. Wiley 1967. [Google Scholar] [CrossRef]
- Ketelsen, S.; Kolks, G.; Andersen, T.O.; Schmidt, L.; Weber, J. Bootstrap Reservoir Concepts for Electro-Hydraulic Compact Cylinder Drives. 12th International Fluid Power Conference (12. IFK), Dresden, 12–14 October 2020. [Google Scholar]
- Zhang, S.; A Minav, T.; Pietola, M. Decentralized Hydraulics for Micro Excavator. In Proceedings of the 13th International Modelica Conference, Regensburg, Germany, 4–6 March 2019. [Google Scholar] [CrossRef]
- Wiens, T.; Bitner, D. An Efficient, High Performance and Low-Cost Energy Recovering Hydrostatic Linear Actuator Concept. In BATH/ASME 2016 Symposium on Fluid Power and Motion Control; Univeristy of Bath: Bath, UK, 2016. [Google Scholar]
- Wiens, T. An efficient, compact and low-cost Dual Cylinder Hydrostatic Actuator (DCHA). Int. J. Fluid Power 2018, 19, 80–90. [Google Scholar] [CrossRef]
- Achten, P.J.; Palmberg, J.O. What a difference a hole makes: The commercial value of the Innas hydraulic transformer. In The Sixth Scandinavian International Conference on Fluid Power (Tampere, May 26-28 1999, Proceedings); University of Tampere: Tampere, Finland, 1999; pp. 873–886. [Google Scholar]
- Costa, G.K.; Sepehri, N. Four-Quadrant Analysis and System Design for Single-Rod Hydrostatic Actuators. J. Dyn. Syst. Meas. Control. 2018, 141, 021011. [Google Scholar] [CrossRef]
- Adams, C. A380: ‘More Electric’ Aircraft. Aviation Today, October 2001. [Google Scholar]
- Parker. Compact Electro-Hydraulic Actuator (EHA). 2020. Available online: https://www.parker.com/Literature/Hydraulic%20Pump%20Division/Oildyne%20EHA/Compact-EHA-Catalog-HY22-3101E-7-13.pdf (accessed on 16 November 2020).
- Actuonix Motion Devices. Miniature Linear Motion Series-L16. 2019. Available online: https://s3.amazonaws.com/actuonix/Actuonix+L16+Datasheet.pdf (accessed on 27 October 2020).
- Odrive Robotics. Odrive High Performance Motor Control. Available online: https://odriverobotics.com/ (accessed on 27 October 2020).
- Wiens, T.; Deibert, B. A Low-cost Miniature Electrohydrostatic Actuator System. Actutors 2020, 9, 130. [Google Scholar] [CrossRef]
- Bonchis, A.; Corke, P.I.; Rye, D.C. A pressure-based, velocity independent, friction model for asymmetric hydraulic cylinders. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No.99CH36288C), Detroit, Michigan, 10–15 May 1999. [Google Scholar] [CrossRef]
- Caliskan, H.; Balkan, T.; Platin, B.E. A Complete Analysis and a Novel Solution for Instability in Pump Controlled Asymmetric Actuators. J. Dyn. Syst. Meas. Control. 2015, 137, 091008. [Google Scholar] [CrossRef]
- Wang, L.; Book, W.J.; Huggins, J.D. A Hydraulic Circuit for Single Rod Cylinders. J. Dyn. Syst. Meas. Control. 2011, 134, 011019. [Google Scholar] [CrossRef]
- Wang, L.; Book, W.J. Using Leakage to Stabilize a Hydraulic Circuit for Pump Controlled Actuators. J. Dyn. Syst. Meas. Control. 2013, 135, 061007. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| 78.5 mm2 | |
| 66.0 mm2 | |
| 28.3 cP | |
| 1.0 GPa | |
| 2.50 × 104 N/(m/s)/(Pa s) | |
| 3.41 N | |
| 5.27 × 10−6 N/(m/s)/Pa | |
| 0.01 mm/s | |
| 1.25 kg | |
| 1.23 × 1012 Pa/(m3/s) | |
| 6.83 × 1014 Pa/(m3/s) | |
| 2.41 × 1012 Pa/(m3/s) | |
| 1.11 × 1011 Pa/(m3/s) | |
| 5.29 × 109 Pa/(m3/s) | |
| 50.3 mm2 | |
| 12.2 N/(m/s) | |
| 1.2 g | |
| 2 mm | |
| −2 mm | |
| 2.55 mL | |
| 2.24 mL | |
| 250 kPa | |
| 0.7 L/min |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wiens, T.; Deibert, B. A Low-Cost Miniature Electrohydrostatic Actuator. Proceedings 2020, 64, 35. https://doi.org/10.3390/IeCAT2020-08488
Wiens T, Deibert B. A Low-Cost Miniature Electrohydrostatic Actuator. Proceedings. 2020; 64(1):35. https://doi.org/10.3390/IeCAT2020-08488
Chicago/Turabian StyleWiens, Travis, and Brendan Deibert. 2020. "A Low-Cost Miniature Electrohydrostatic Actuator" Proceedings 64, no. 1: 35. https://doi.org/10.3390/IeCAT2020-08488
APA StyleWiens, T., & Deibert, B. (2020). A Low-Cost Miniature Electrohydrostatic Actuator. Proceedings, 64(1), 35. https://doi.org/10.3390/IeCAT2020-08488





