A Concept Design of an Adaptive Tendon Driven Mechanism for Active Soft Hand Orthosis ^†

Abstract

The Hands exert a vital role in the simplest to most complex daily tasks. Losing the ability to make hand movements, which is usually caused by spinal cord injury or stroke, dramatically impacts the quality of life. In order to counteract this problem, several assisting devices have been proposed, but they still present several usage limitations. The marketable orthoses are generally either the static type or over-expensive active orthosis that cannot perform the same degrees of freedom (DoF) that a hand can do. This paper presents a conceptual design of a tendon-driven mechanism for hand’s active orthosis. This study is a part of an effort to develop an effective and low-cost hand’s orthosis for people with hand paralysis. The tendon design proposed was thought to comply with some requisitions such as lightness and low volume, as well as fit with the biomechanical constraints of the hand joints to enable a comfortable use. The mechanism employs small cursors on the phalanges to allow the tendons to run on the dorsal side and by both sides of the fingers, allowing 2 DoF for each finger, and one extra tendon enlarges the hands’ adduction nuances. With this configuration, it is simple enough to execute the flexion and extension movements, which are the most used movements in daily actives, using one single DC actuator for one DoF to reduce manufacturing costs, or with more DC actuators to enable more natural hand coordination. This system of actuation is suitable to create soft exoskeletons for hands easily embedded into 3D printed parts, which could be merged over statics thermoplastic orthosis. The final orthosis design allows dexterous finger movements and force to grasp objects and perform tasks comfortably.

1. Introduction

In everyday activities such as eating, basic hygienic or interacting with other people, hands are essentials to our world perception. Mobility deficits in the upper limbs, especially in the hands, generate a negative life impact [1]. Stroke and spinal cord injuries (SCI) are common hand paralysis causes. According to the Brazilian Journal of Neuroscience [2], Brazil has more than 11,000 new cases of spinal cord injuries each year, this represents about 71 cases per million, 42% more than the U.S. A global report by the World Health Organization (WHO) [3] states that up to 500,000 SCI occur worldwide every year. Likewise, stroke is equally harmful, being the third source of disabilities in the world [4]. WHO reports conclude that the worse effects, difficulties in treatment and rehabilitation occur in low and middle-income countries [3,4]. Furthermore, the regional rehabilitation program of the Pan-American organization says the only 2% of the 85 million people with some disability have their rehabilitation necessities attended in Latin America [5].

Robotic solutions used in physiotherapy can perform treatments with similar results to those accomplished by physiotherapists when using traditional techniques, and once they can be programmed to execute exercises, this rehabilitation strategy saves therapists time, yielding attendance to more people [6,7,8,9,10].

Active upper limb orthoses are, in the vast majority, rigid exoskeletons (e.g., four-bar mechanisms) that perform a low Degree-of-Freedom (DoF). Although rigid exoskeletons can reach accurate movements, they are commonly bulky and heavy, making them inadequate to interact with small everyday objects. These concerns also apply to the power supply, for example, pneumatic actuators dramatically reduce mobility [11,12]. To properly perform daily live activities (DLA) with comfort for long periods, lightness and low-volume are fundamental characteristics. Soft exoskeletons that are based on light materials (e.g., fabric and polymeric materials) and actuators that do not restrict mobility become a good alternative [13].

The recent orthoses that were developed had had characteristics of low volume and lightness, but in view of a wide range of hand sizes, the correct fit has been a problem, requiring the development of a completely new device for different sizes. Furthermore, it leads to joint alignment problems and it is difficult to provide a customized solution for particular demands [12,14,15,16].

This paper presents a soft exoskeleton concept to address these shortcomings. The proposed mechanism was thought to be compact, lightweight and able to fit with different hand sizes. The number of DoFs can be expanded or simplified to reduce costs and capably reach multiple clinical demands. We expect this set can suitably perform DLA, providing comfort to the wearer for long periods of use.

2. Methods

The system was conceived to be embedded into a soft exoskeleton and powered by DC motors for physiotherapy sessions and DLA assistance. Hand anatomy inspired the device development to attend biomechanical constraints [13].

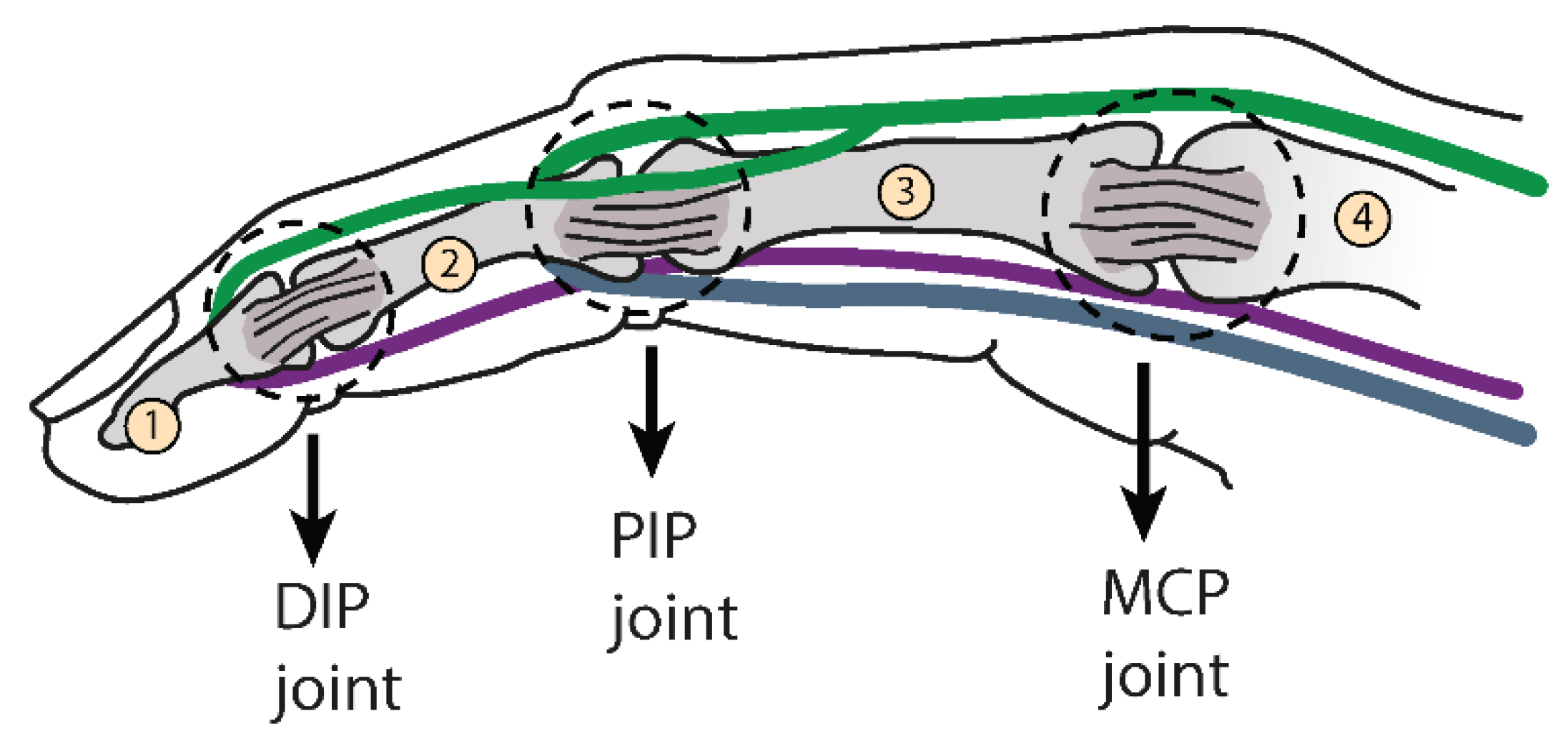
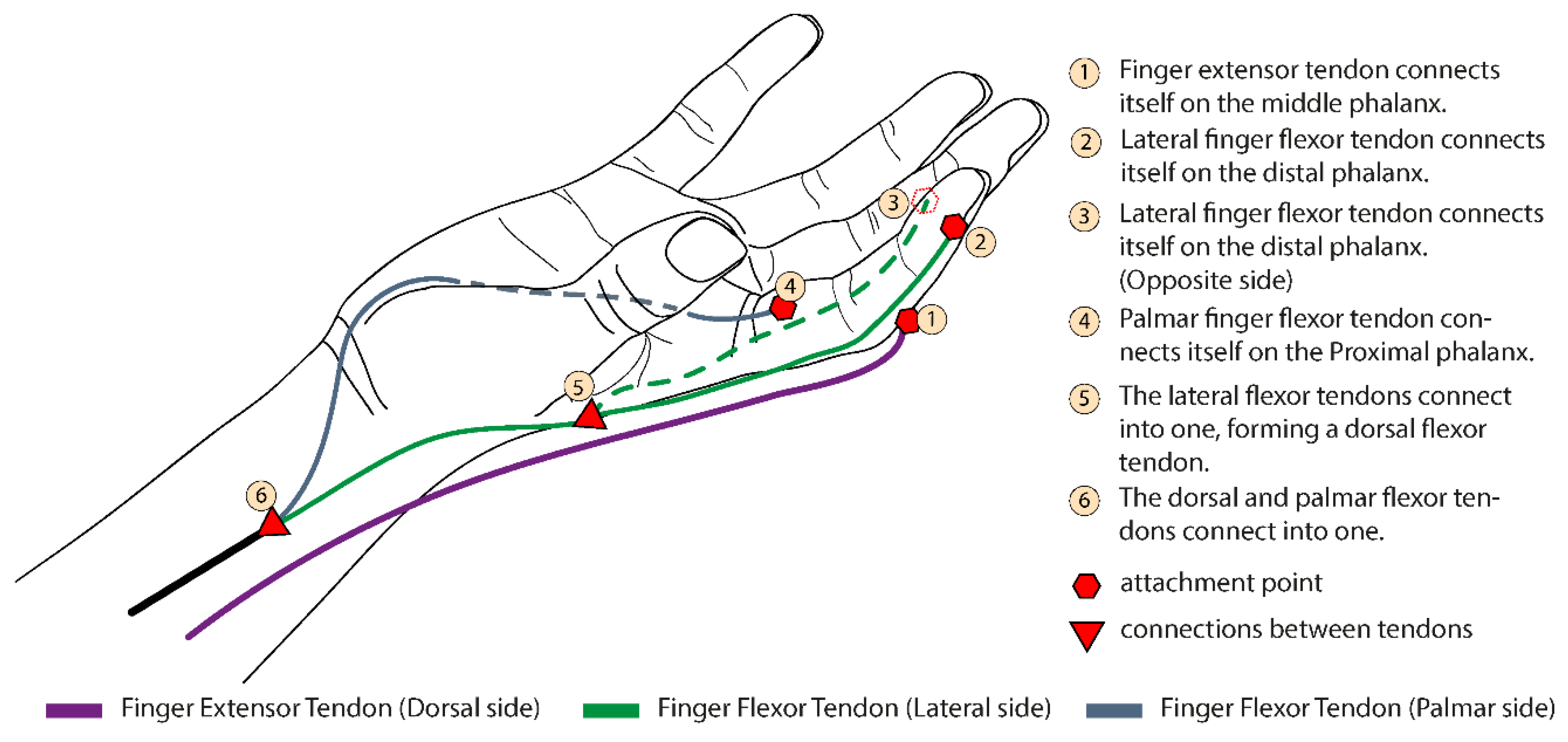
2.1. Biological Inspiration

The finger framework is composed of three distal, middle and proximal bones in a designated phalanx. They are connected by ligaments and driven by three tendons to perform extension/flexion movement, whereas the thumb has additional tendons to adduction/abduction motion [17]. Figure 1 shows this configuration. The tendon Extensor Digitorum Communis (EDC), was represented in green, this tendon connects to the middle and distal bones. Flexors tendons Digitorum Profundus (FDP) and Superficialis (FDS) were illustrated in purple and pale blue and they insert on distal and middle bones, respectively (FDP goes through FDS between a bifurcation).

This set up creates an angular interdependence constraint. It has been experimentally estimated that the angular relationships between the distal interphalangeal joint (DIP) and the proximal interphalangeal joint (PIP) are about ∆θ_distal = 1.5∆θproximal (joints shown in Figure 1) [12,17]. Exceeding the DIP-PIP ratio can cause discomfort, pain, and injury.

2.2. Concept

Figure 2 represents three artificial tendons, and their main points of attachment on the index finger.

The Extensor Artificial Tendon (EAT) (purple wire) runs on dorsal side and performs the EDC role inserting itself on middle phalanx. This attachment avoids the DIP joint’s curves outside of the palmar side when EAT has been stretched. For flexion, there are the Palmar Artificial Tendon (PAT) (pale blue wire) and Lateral Artificial Tendon (LAT) (green wire). The LAT is fixed on the distal phalanx and makes the finger retraction, beginning on both distal phalanx sides, and both wires connect themselves into one on the hand dorsal face. The palmar one inducts angular movement around the metacarpal joint (MCP) and is fixed on the proximal phalange. This tendon model indirectly stimulates the biological ones (The EAT stimulates EDC, LAT the FDP and FDS in a little, respecting the DIP-PIP correlation, and the PAT complies with the FDS tendon).

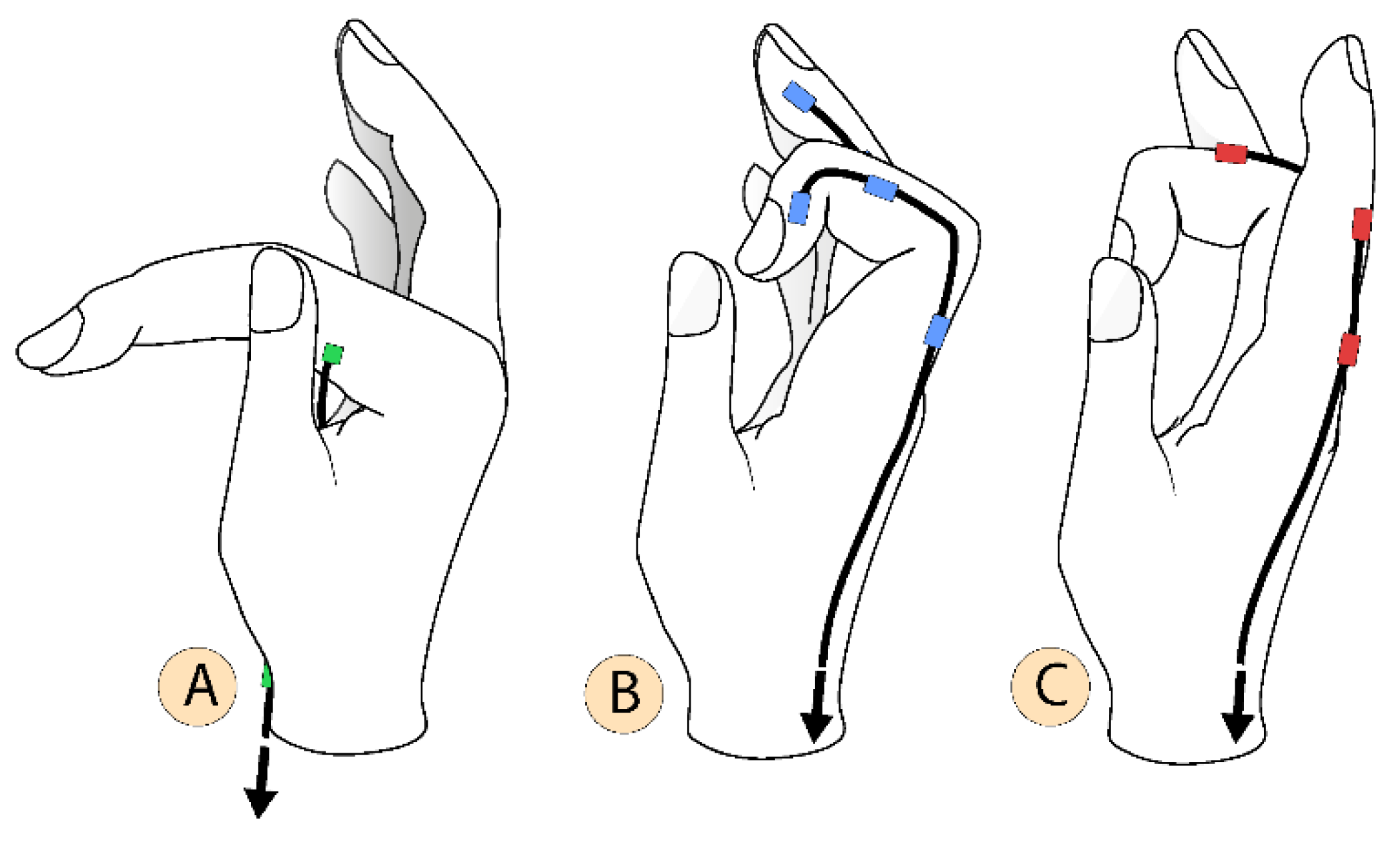
2.3. Multiple Configurations

This set can meet different rehabilitation and cost demands, through a simple idea, the linear dependence (LD) and the linear independence (LI) of the movements. Flexion and extension movements are linearly independent. Meanwhile, a hand flexion could be described as a linear combination of each finger flexion, as well as for the extension movements. For example, Figure 2 shows the cables on the index finger; the three wire ends of the flexion artificial tendons (two by LAT and one by PAT) are connected, thereby remaining two cables (one for extension and one for the flexion moves). Reproducing this on the other fingers (including thumb) will result in ten cables (five for the extension and five for the flexion moves), joining the extension cables each other, as well with flexion cables, making the LI hand movements be set, by the LD implementations, resulting in only two cables per hand. Both cables can be added in one DC motor to perform one LI movement at each rotation direction. This configuration has the lower-cost and 1 DoF, performing a “rigid grasp” move. On the other hand, joining some key wires with others create a customizable design suitable for specific needs. Figure 3 describes independent motions of the finger attributed to each artificial tendon. Different linear combinations of these movements, shown at Figure 3A,B create narrow or wide paths for grasp and describe 2 DoF per finger (by using 1 DC actuator per finger), including the thumb.

Driving up each cable that comprises LAT (Figure 3B) adds one unique movement to open wide the fingers, being useful to hold bulky objects. The implementation of these independent movements and the ones in Figure 3 makes the system have 4 DoF per finger. However, the arrangement with two degrees of freedom has a better cost-benefit, being suitable to grasp objects in DLA.

2.4. Prototype

There are many metric dimensions that need to be considered to properly define the correct shape of a hand orthosis. A unique design capable of fitting properly at many different hand sizes is hard to achieve. To face this shortcoming, a customizable design is proposed that could be easily modified for any specific hand size. To provide a proper fit and comfort to the wearer, a thermoplastic is applied to involve the wrist, forearm and hand base. This solution is widely used on static orthosis and shall be used to make the system base. Furthermore, 3D printed parts are employed at fingers, these elements have a ring shape and can be easily adapted to any finger size to allow tendons to run through the cursors. Other 3D cursors pieces are attached to the thermoplastic base to guide the wires. Varying the offset between these attachments is enough for a proper alignment. Figure 4 illustrates the proposed hand orthosis. The thimble and rings are expected to be 2.2 mm thick and have a 1.2 mm inner diameter. This construction strategy allows fast adjustments, enabling the quick implementation of new prototype versions.

3. Results and Discussion

Here a kinematic model is presented for the hand orthosis to assist in establishing the wire slacks and the resulting force applied by the fingers. The slacks’ information is important to adjust the amount of cable actuated by the DC motors. Thus, optimizing the thread lengths improves the actuation time. For this model, the connection points between the thimble and the first cursor piece outside of the fingers were considered. This region needs to be adjusted according to the different hands’ sizes. To do that, the wires were considered with inextensible, longitudinal symmetry of the fingers and neglected friction losses. Figure 5 and

Table 1. Description of kinematic parameters.

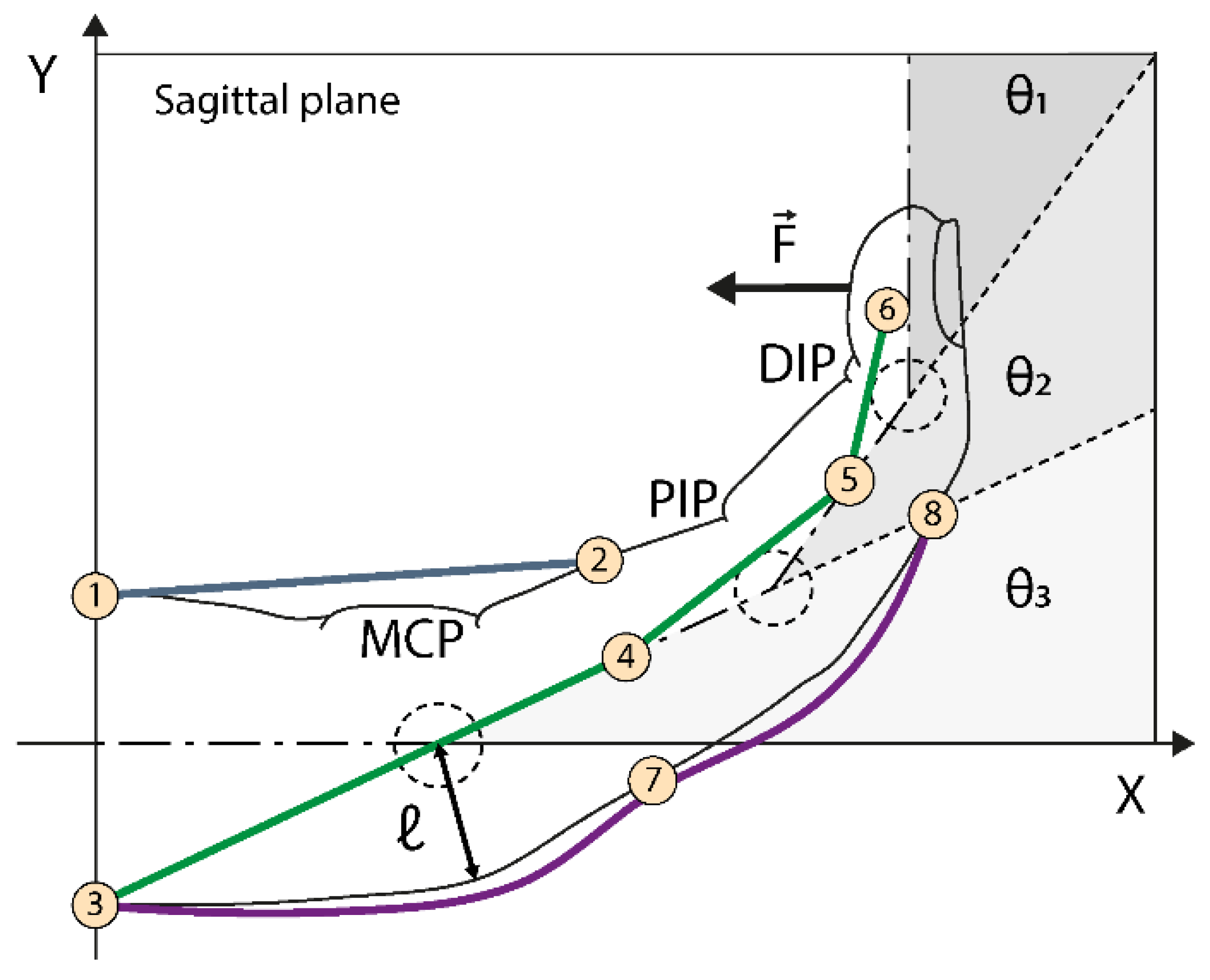
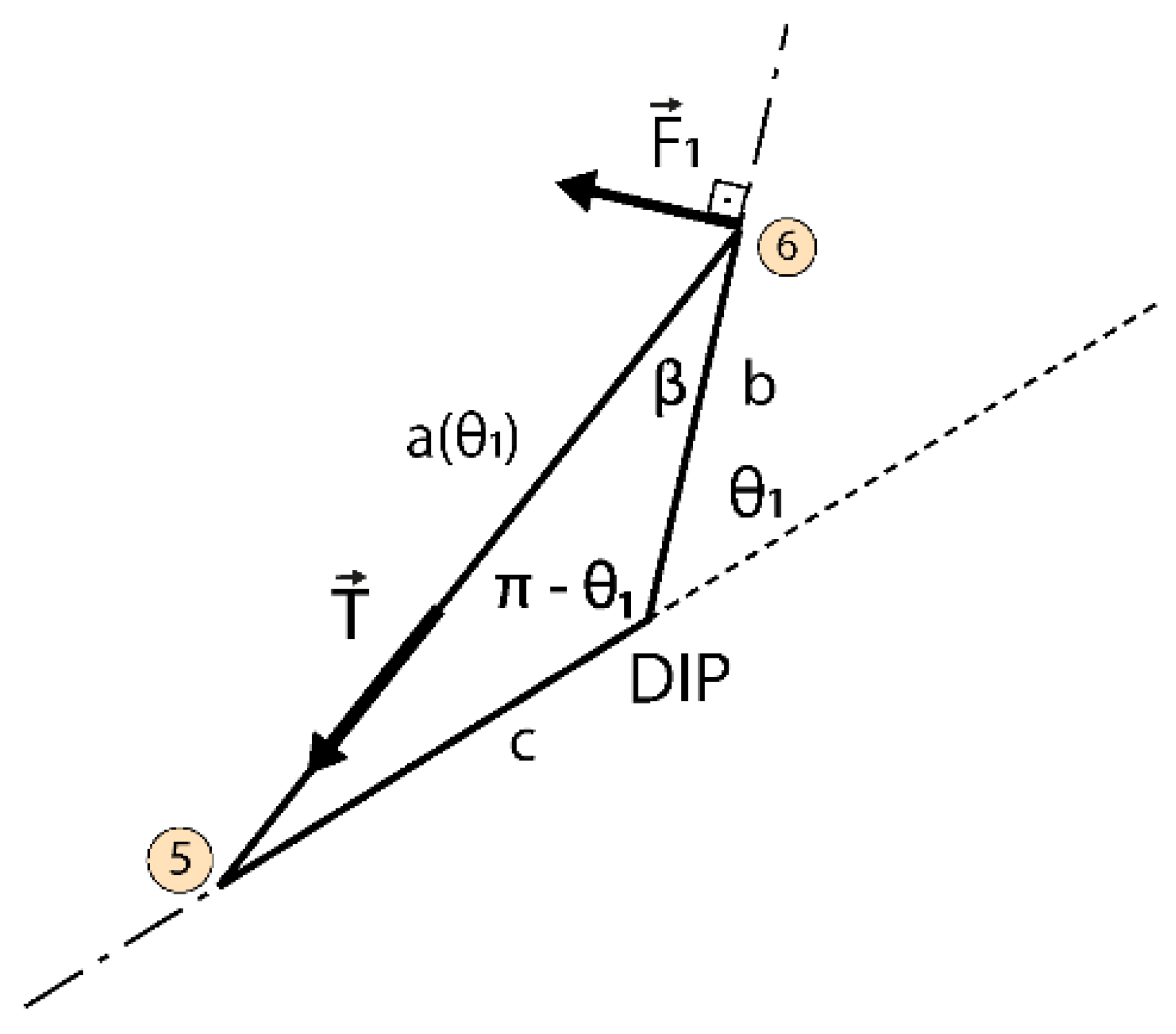
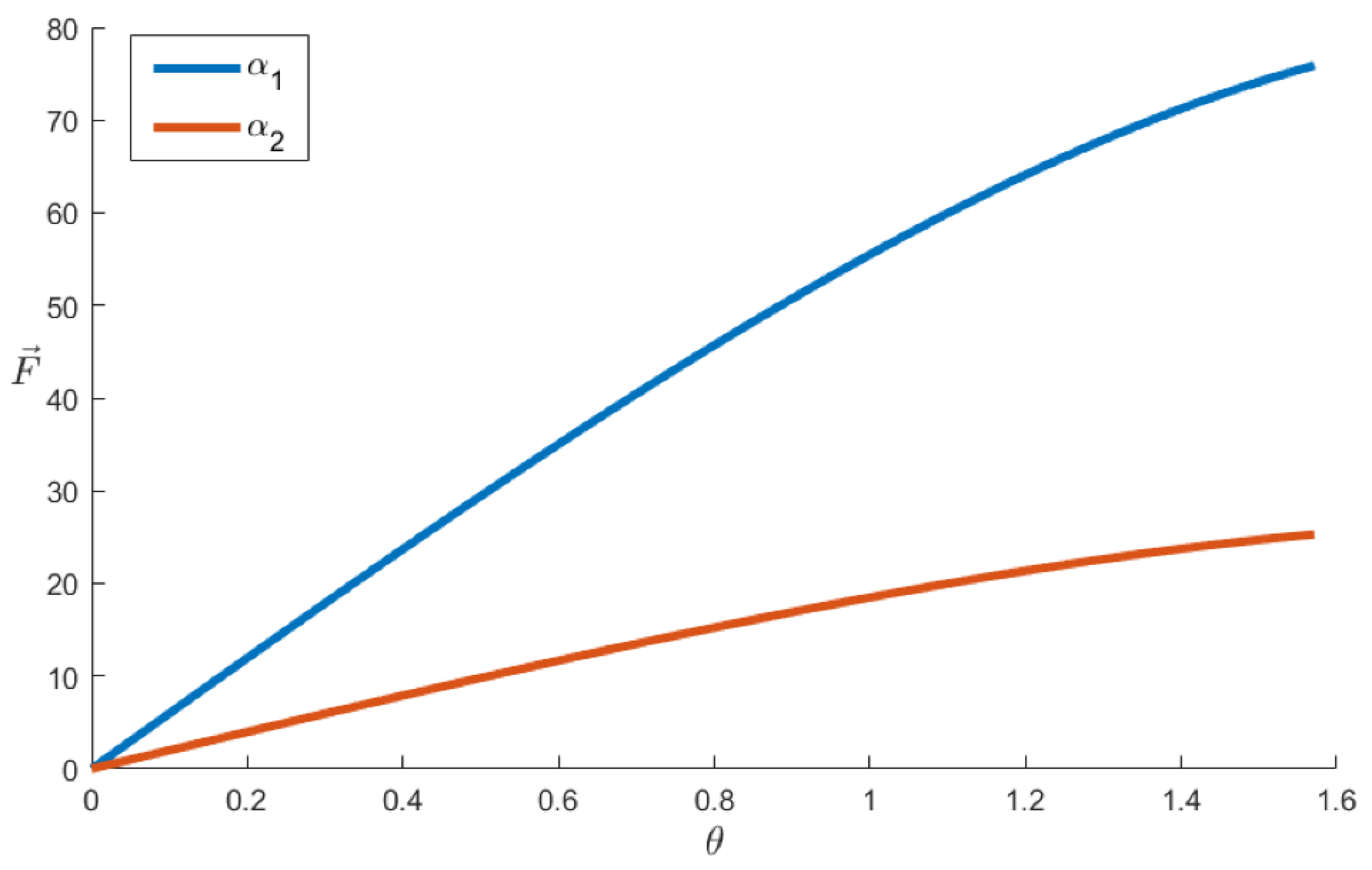
Parameters	Description
θ1, θ2, θ3	MCP, PIP, DIP joint angles
ℓ	curvature radius reference, has the average value between each length ℓ for each reference joint
$P_k \in \left[1, 8\right]; k \in \mathbb{N}$	wires connection points
δr	wire length at the reference position
δc	wire length at contraction position
δp	length to be wound on the pulley
PjMCP	MCP projected on the palmar side
$\overrightarrow{F}$	Normal force at the distal phalanx
$\overrightarrow{T}$	Thread tension

show the analyses parameters.

The reference position is defined for θ₁ = θ₂ = θ₃ = 0°, at this position, the hand longitudinal symmetry line coincides with the x-axis. The length measurements are made between the reference and the theta function positions.

Figure 5 shows eight connection points through which the cables pass. Points P₁–P₂ refer to the PAT, P₃ to P₆ to the LAT and P₃–P₇–P₈ to the EAT. For simplification sake, point 3 will be used to represent two particles, one belonging to the EAT and the other to the LAT. A scalar approach provides the lengths in the simplest way. For the EAT we have that:

$${\delta }_{r, \mathrm{EAT}}=\overline{P_3,P_7}+\overline{P_7,P_8}$$

(1)

$${\delta }_{c, \mathrm{EAT}}=\overline{P_3,P_7}+\overline{P_7,P_8}+\ell \left({\theta }_2+{\theta }_3\right)$$

(2)

$${\delta }_{p, \mathrm{EAT}}=\ell \left({\theta }_2+{\theta }_3\right)$$

(3)

For the palmar artificial tendon, we have:

$${\delta }_{r, \mathrm{PAT}}=\overline{P_1,P_2}$$

(4)

PAT in an arbitrary position is given by the cosine law:

$${\delta }_{c, \mathrm{PAT}}=\sqrt{{\left(\overline{P_1,P{j}_{MCP}}\right)}^2+{\left(\overline{P{j}_{MCP},P_2}\right)}^2-2\left(\overline{P_1,P{j}_{MCP}}\right)\left(\overline{P{j}_{MCP},P_2}\right)\cos \left(\pi -{\theta }_3\right)}$$

(5)

$${\delta }_{p, \mathrm{PAT}}=\left|{\delta }_{c, \mathrm{PAT}}-{\delta }_{r, \mathrm{PAT}}\right|$$

(6)

The same procedure is applied on LAT analysis:

$${\delta }_{r, \mathrm{LAT}}=\overline{P_3,P_4}+\overline{P_4,P_5}+\overline{P_5,P_6}$$

(7)

$${\delta }_{c, \mathrm{LAT}}={\displaystyle \sum }_{\zeta }\sqrt{{\left(\overline{P_i,k}\right)}^2+{\left(\overline{k,P_{i+1}}\right)}^2-2\left(\overline{P_i,k}\right)\left(\overline{k,P_{i+1}}\right)\cos \left(\pi -{\theta }_j\right)}$$

(8)

For (i, j, k) ∈ ζ; ζ = {(3, 3, MCP), (4, 2, PIP), (5, 1, DIP)}.

$${\delta }_{p, \mathrm{LAT}}=\left|{\delta }_{c, \mathrm{LAT}}-{\delta }_{r, \mathrm{LAT}}\right|$$

(9)

Although the MCP angular movement which is given by PAT communicates this one to the other phalanges, this resultant force is negligible. The resultant force will be provided by LAT wire tension, being perpendicular at the phalanx surface. $\overrightarrow{F}$ is shown in Figure 5 and it is a function of theta (θ₁) angle. The fingertip force ($\overrightarrow{F}$) is represented in Figure 6. To determine the fingertip force, β must be written as a function of θ₁.

$$\beta = {\sin }^{-1}\left[\frac{c}{a\left({\theta }_1\right)}\sin \left({\theta }_1\right)\right]$$

(10)

$$\overrightarrow{F}=\overrightarrow{T}\cos \left(\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.-\beta \right)$$

(11)

Equation (10) is provided by law of sines. As previously discussed, the parameters b and c (see Figure 6) are obtained through direct measurement and the wire length between P₅ and P₆ is a function of theta (a(θ₁)). The result reveals that the ring position impacts on the force optimization resulting from the system. To optimize the fingertip force, we should pay attention to the kinematic coefficient alpha (α) given by $\frac{c}{a\left({\theta }_1\right)}$ in the Equation (10). The resulted force will be higher for lower a(θ₁). Thus, to reduce a(θ₁) is necessary to reduce b and increase c as much as possible. To represent this effect graphically (Figure 7) we plot Equations (10) and (11) merge them, with a(θ₁) equal to the last term of Equation (8) replaced. These substitutions provide the plot equation of the Figure 7, Equation (12).

$$\overrightarrow{F}=\overrightarrow{T}\cos \left(\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.-{\sin }^{-1}\left[\underset{\alpha }{\underbrace{\frac{c}{\sqrt{{\left(\overline{P_5,DIP}\right)}^2+{\left(\overline{DIP,P_6}\right)}^2-2\left(\overline{P_5,DIP}\right)\left(\overline{DIP,P_6}\right)\cos \left(\pi -{\theta }_1\right)}}}}\sin \left({\theta }_1\right)\right]\right)$$

(12)

The graph was built considering $\overrightarrow{T}=80 N$ and θ ∈ [0,$\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.$] which is the range of a healthy dip phalanx [18]. The blue curve represents α₁ given by b = 0.5 mm and c = 1.5 mm (b and c are shown in Figure 6) having P₆ close to the DIP and P₅ close to PIP joint. The orange curve has the parameters swapped, representing α₂ with b = 1.5 mm and c = 0.5 mm.

4. Conclusions

In this paper, we presented a novel concept for hand orthosis, based on a soft exoskeleton approach for assistance in physiotherapy sessions and DLA for people with hand disabilities. The concept considered the biological constraints stimulating the natural tendons to comply with angular constraints. The proposed design allows for smooth coordination for the hands while giving power assistance to grasp objects and execute tasks. It is expected that when using thermoplastics and additive manufacturing, the resulting prototype achieves lightness, low volume, and a customized design. The variety of possibilities for DoF is an advantage of this design, as it is able to adapt to multiple rehabilitation and assistance demands. Thermoplastic moldability guarantees comfort, and adequate adjustments to the hands, forearms, and arms of different users. A kinematic model was considered to evaluate design parameters to develop the prototype. These data were useful to optimize the fingertip force as a function of orthosis positioning, and avoid points where the movements cannot be performed. We verified that the wire paths positioning has a strong impact on the resultant grasping force. In future works we intent to manufacture a prototype of the hand orthosis to evaluate friction losses and non modeled dynamics to develop the control system and the embedded electronics for experimental testing.