Coal and Biomass Co-Combustion: CFD Prediction of Velocity Field for Multi-Channel Burner in Cement Rotary Kiln †
Abstract
1. Introduction
2. Mathematical Models
2.1. Gas-Phase Governing Equations
2.2. Particle-Phase Governing Equations
3. Numerical Computation and Strategy
3.1. Geometry and Grid Description
3.2. Numerical Method and Boundary Condition
3.3. Case Study
4. Results and Discussion
5. Conclusions
References
- Ngadi, Z.; Lahlaouti, M.L. Impact of Using Alternative Fuels on Cement Rotary Kilns: Experimental Study and Modeling. Procedia Eng. 2017, 181, 777–784. [Google Scholar] [CrossRef]
- Guessab, A.; Aris, A.; Bounif, A. Simulation of turbulent piloted methane non-premixed flame based on combination of finite-rate/eddy-dissipation model. Mechanika 2013, 19, 657–664. [Google Scholar] [CrossRef][Green Version]
- Collazo, J.; Porteiro, J.; Míguez, J.L.; Granada, E.; Gómez, M.A. Numerical simulation of a small-scale biomass boiler. Energy Convers. Manag. 2012, 64, 87–96. [Google Scholar] [CrossRef]
- Yang, Y.B.; Newman, R.; Sharifi, V.; Swithenbank, J.; Ariss, J. Mathematical modelling of straw combustion in a 38 MWe power plant furnace and effect of operating conditions. Fuel 2007, 86, 129–142. [Google Scholar] [CrossRef]
- Djurović, D.; Nemoda, S.; Repić, B.; Dakić, D.; Adzić, M. Influence of biomass furnace volume change on flue gases burn out process. Renew. Energy 2015, 76, 1–6. [Google Scholar] [CrossRef]
- Tumsa, T.Z.; Chae, T.Y.; Yang, W.; Paneru, M.; Maier, J. Experimental study on combustion of torrefied palm kernel shell (PKS) in oxy-fuel environment. Int. J. Energy Res. 2019, 43, 7508–7516. [Google Scholar] [CrossRef]
- Ranade, V.V.; Gupta, D.F. Computational Modeling of Pulverized Coal Fired Boilers; CRC Press: Boca Raton, FL, USA, 2015; ISBN 9781482215359. [Google Scholar]
- ANSYS Fluent theory guide. In ANSYS Fluent Theory Guide 15.0; Ansys Inc.: Canonsbourg, PA, USA, 2013; p. 193.
- Cassol, F.; Brittes, R.; França, F.H.R.; Ezekoye, O.A. Application of the weighted-sum-of-gray-gases model for media composed of arbitrary concentrations of H2O, CO2 and soot. Int. J. Heat Mass Transf. 2014, 79, 796–806. [Google Scholar] [CrossRef]
- Spalding, D.B. Mixing and chemical reaction in steady confined turbulent flames. Symp. (Int.) Combust. 1971, 13, 649–657. [Google Scholar] [CrossRef]
- Rosin, P.; Rammler, E. The laws governing the fineness of powdered coal. J. Inst. Fuel 1933, 7, 29–36. [Google Scholar]
- Shuen, J.-S.; Chen, L.-D.; Faeth, G.M. Evaluation of a stochastic model of particle dispersion in a turbulent round jet. AIChE J. 1983, 29, 167–170. [Google Scholar] [CrossRef]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193. [Google Scholar] [CrossRef]
- Badzioch, S.; Hawksley, P.G.W. Kinetics of Thermal Decomposition of Pulverized Coal Particles. Ind. Eng. Chem. Process Des. Dev. 1970, 9, 521–530. [Google Scholar] [CrossRef]
- Baum, M.M.; Street, P.J. Predicting the Combustion Behaviour of Coal Particles. Combust. Sci. Technol. 1971, 3, 231–243. [Google Scholar] [CrossRef]
- Hiromi Ariyaratne, W.K.W.K.; Malagalage, A.; Melaaen, M.C.; André Tokheim, L. CFD Modeling of Meat and Bone Meal Combustion in a Rotary Cement Kiln. Int. J. Model. Optim. 2014, 4, 263–272. [Google Scholar] [CrossRef]
- Vaillancourt, P.A.; Yau, M.K. Review of Particle–Turbulence Interactions and Consequences for Cloud Physics. Bull. Am. Meteorol. Soc. 2000, 81, 285–298. [Google Scholar] [CrossRef]
- Yilmaz, H.; Cam, O.; Tangoz, S.; Yilmaz, I. Effect of different turbulence models on combustion and emission characteristics of hydrogen/air flames. Int. J. Hydrogen Energy 2017, 42, 25744–25755. [Google Scholar] [CrossRef]
- Chen, L.; Yong, S.Z.; Ghoniem, A.F. Oxy-fuel combustion of pulverized coal: Characterization, fundamentals, stabilization and CFD modeling. Prog. Energy Combust. Sci. 2012, 38, 156–214. [Google Scholar] [CrossRef]
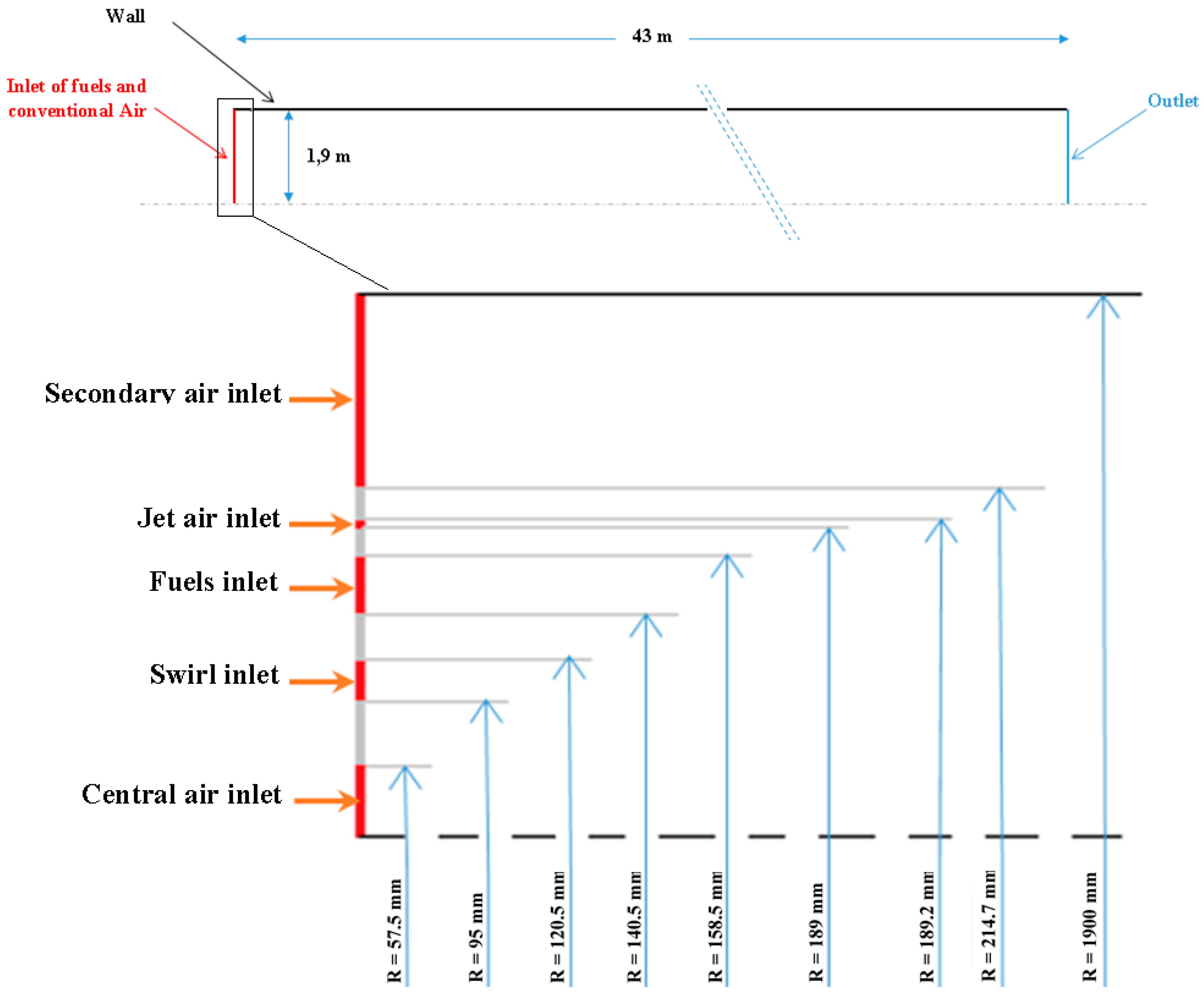
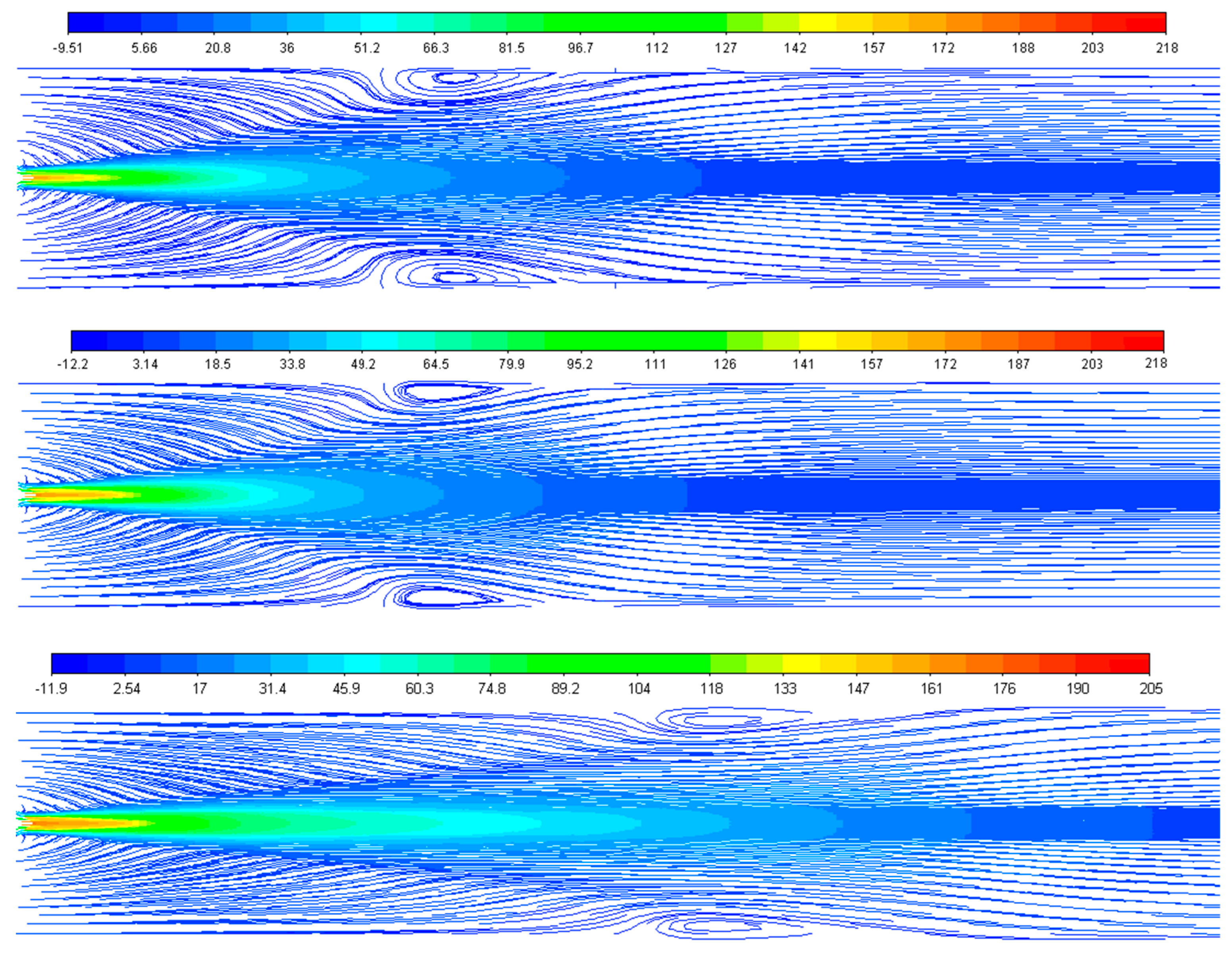

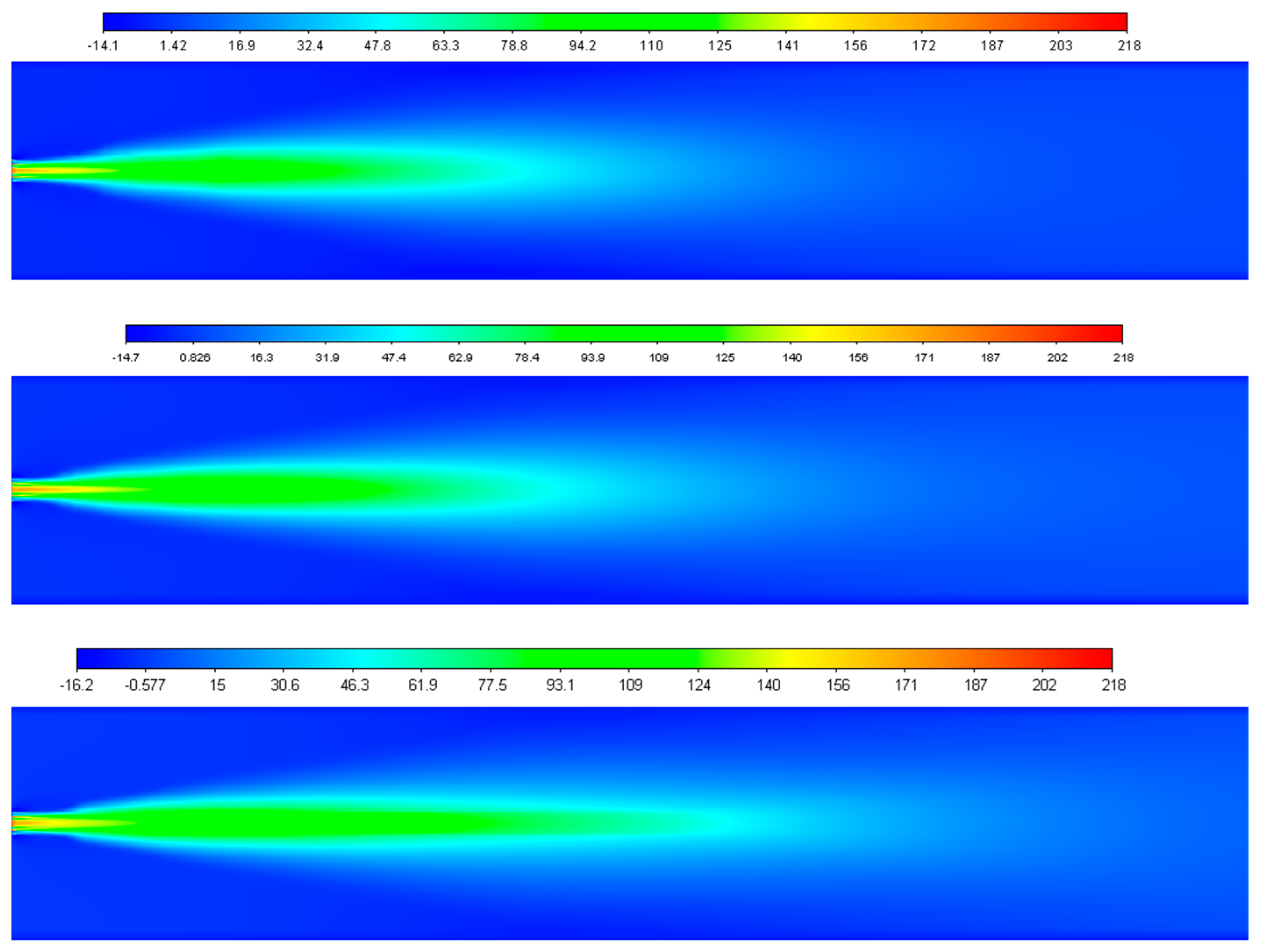
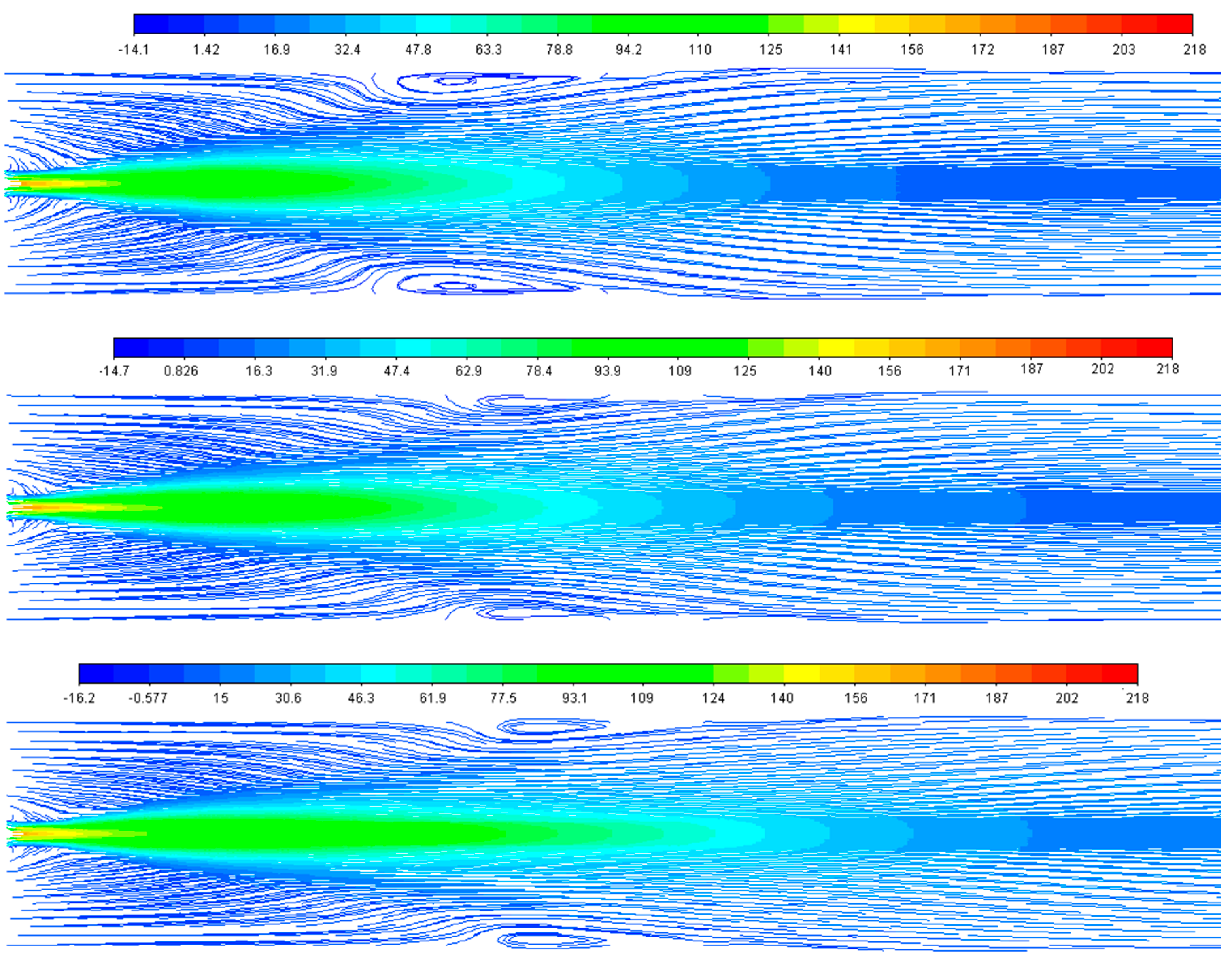
| Boundaries | Velocity m/s | Temperature °K |
|---|---|---|
| Secondary air inlet | 5 | 1126 |
| Jet air inlet | 218 | 500 |
| Fuels inlet | Transport air 30 Coal and AF 30 | 500 |
| Swirl inlet | Axial 212 Tangential 45 | 500 |
| Central air inlet | 200 | 500 |
| Case | Turbulence Model | Turbulence Chemistry Interaction Model | Discrete Phase Model (DPM) |
|---|---|---|---|
| 1 | STD | OFF | OFF |
| 2 | ON | ON | |
| 3 | RNG | OFF | OFF |
| 4 | ON | ON | |
| 5 | RKE | OFF | OFF |
| 6 | ON | ON |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ngadi, Z.; Lahlaouti, M.L. Coal and Biomass Co-Combustion: CFD Prediction of Velocity Field for Multi-Channel Burner in Cement Rotary Kiln. Proceedings 2020, 63, 18. https://doi.org/10.3390/proceedings2020063018
Ngadi Z, Lahlaouti ML. Coal and Biomass Co-Combustion: CFD Prediction of Velocity Field for Multi-Channel Burner in Cement Rotary Kiln. Proceedings. 2020; 63(1):18. https://doi.org/10.3390/proceedings2020063018
Chicago/Turabian StyleNgadi, Zakia, and Mohamed Lhassan Lahlaouti. 2020. "Coal and Biomass Co-Combustion: CFD Prediction of Velocity Field for Multi-Channel Burner in Cement Rotary Kiln" Proceedings 63, no. 1: 18. https://doi.org/10.3390/proceedings2020063018
APA StyleNgadi, Z., & Lahlaouti, M. L. (2020). Coal and Biomass Co-Combustion: CFD Prediction of Velocity Field for Multi-Channel Burner in Cement Rotary Kiln. Proceedings, 63(1), 18. https://doi.org/10.3390/proceedings2020063018





