Optimal Sizing of RF Integrated Inductors for Power Transfer of Implantable Biosensors †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Physical Model of Spiral Inductor
2.1.1. Equivalent Model
- Coupling capacity between the coils:
- Parasitic capacitance:
- Capacity of substrates:
- Resistance of the substrate:
2.1.2. Inductance Ls
2.1.3. Factor of Quality-Q
2.2. Differential Evolutionary Algorithm (DE)
Objective Function
- Maximize the quality factor Q which depends on the geometrical parameters of the inductor (N, W, S);
- We will introduce the cost function Qreq = 1/Q, it represents the desired quality factor, so the problem is transformed towards a minimization of Qreq, in order to maximize the quality factor Q;
- All this will be done by the following constraints that must be satisfied:
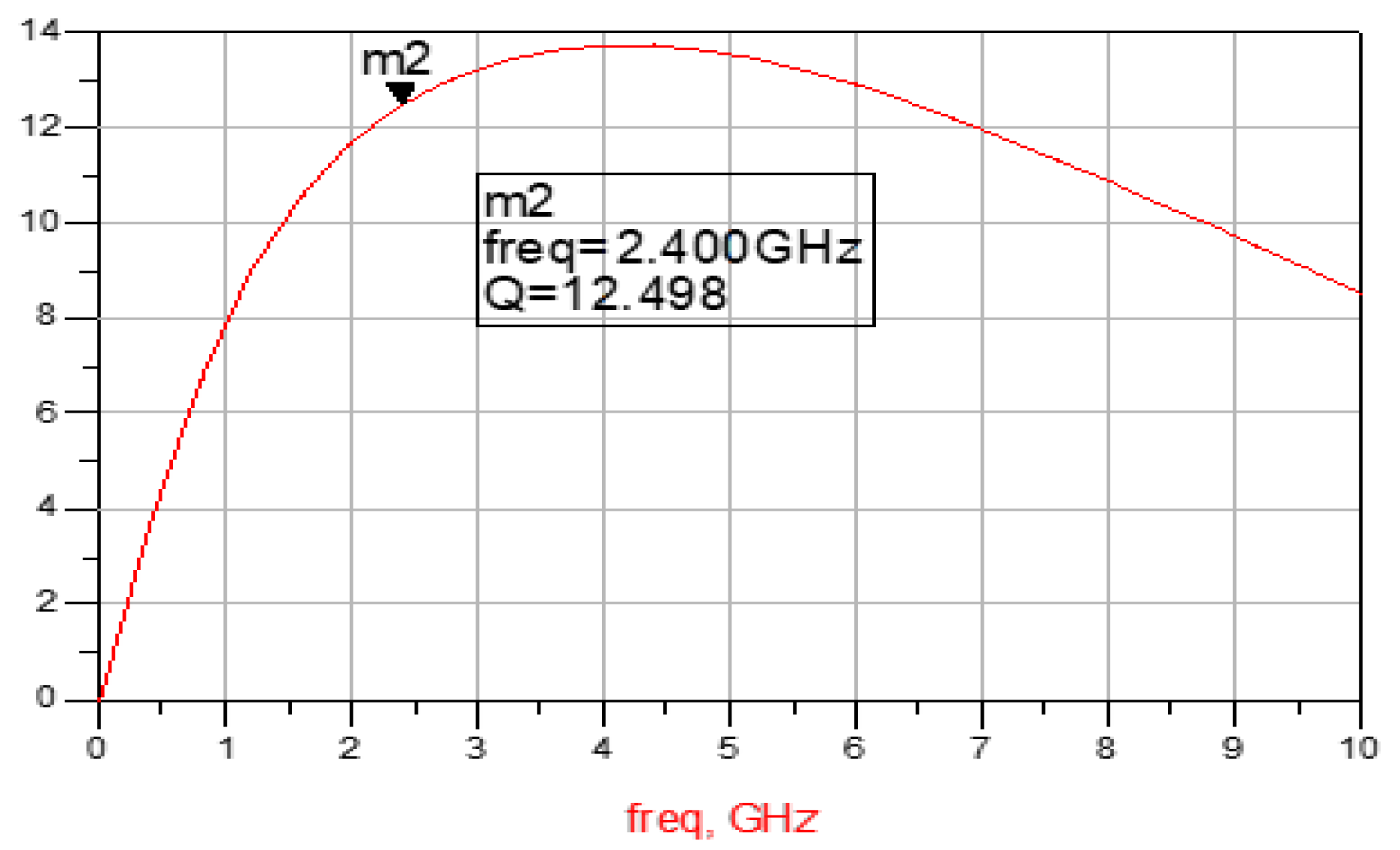
3. Results
4. Discussion
References
- Jeamsaksiri, W.; Mercha, A.; Ramos, J.; Linten, D.; Thijs, S.; Jenei, S.; Detcheverry, C.; Wambacq, P.; Velghe, R.; Decoutere, S. Integration of a 90 nm RF CMOS technology (200 GHz fmax—150 GHz fT NMOS) demonstrated on a 5 GHz LNA. In Proceedings of the 2004 Symposium on VLSI Technology, Honolulu, HI, USA, 15–17 June 2004; pp. 100–101. [Google Scholar]
- Chen, L.Y.; Benjamin, C.K.T.; Alex, L.C.; Gregor, S.; Victor, T.; Darren, J.L.; Philip, H.S.W.; Michael, V.M.; Bao, Z. Continuous wireless pressure monitoring and mapping with ultra-small passive sensors for health monitoring and critical care. Nat. Commun. 2014, 5, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Eom, K.; Jeong, J.; Lee, T.H.; Lee, S.E.; Jun, S.B.; Kim, S.J. Columnar transmitter based wireless power delivery system for implantable device in freely moving animals. In Proceedings of the Engineering in Medicine and Biology Society (EMBC), 2013 35th Annual International Conference of the IEEE, Osaka, Japan, 3–7 July 2013; pp. 1859–1862. [Google Scholar]
- Yue, C.P.; Ryu, C.; Lau, J.; Lee, T.H.; Wong, S.S. A Physical model for planar spiral inductors on silicon. In Proceedings of the IEEE International Electron Devices Meeting (IEDM) Technical Digest, San Francisco, CA, USA, 8–11 December 1996; pp. 155–158. [Google Scholar]
- Bouyghf, H.; Benhala, B.; Raihani, A. Analysis of the impact of metal thickness and geometric parameters on the quality factor-Q in integrated spiral inductors by means of artificial bee colony technique. Int. J. Electr. Comput. Eng. (IJECE) 2019, 9, 2918–2931. [Google Scholar] [CrossRef]
- Bouyghf, H.; Benhala, B.; Raihani, A. Artificial bee colony technique for a study of the influence of impact of metal thickness on the factor of quality-Q in integrated square spiral inductors. In Proceedings of the 4th International Conference on Optimization and Applications (ICOA 18), Mohammedia, Morocco, 26–27 April 2018. [Google Scholar]
- Mohan, S.S.; Hershenson, M.D.; Boyd, S.P.; Lee, T.H. Simple accurate expressions for planar spiral inductances. IEEE J. Solid State Circuits 1999, 34, 1419–1424. [Google Scholar] [CrossRef]
- Bryan, H.E. Printed inductors and capacitors. Tele-Tech. Electron. Ind. 1955, 14, 68. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]

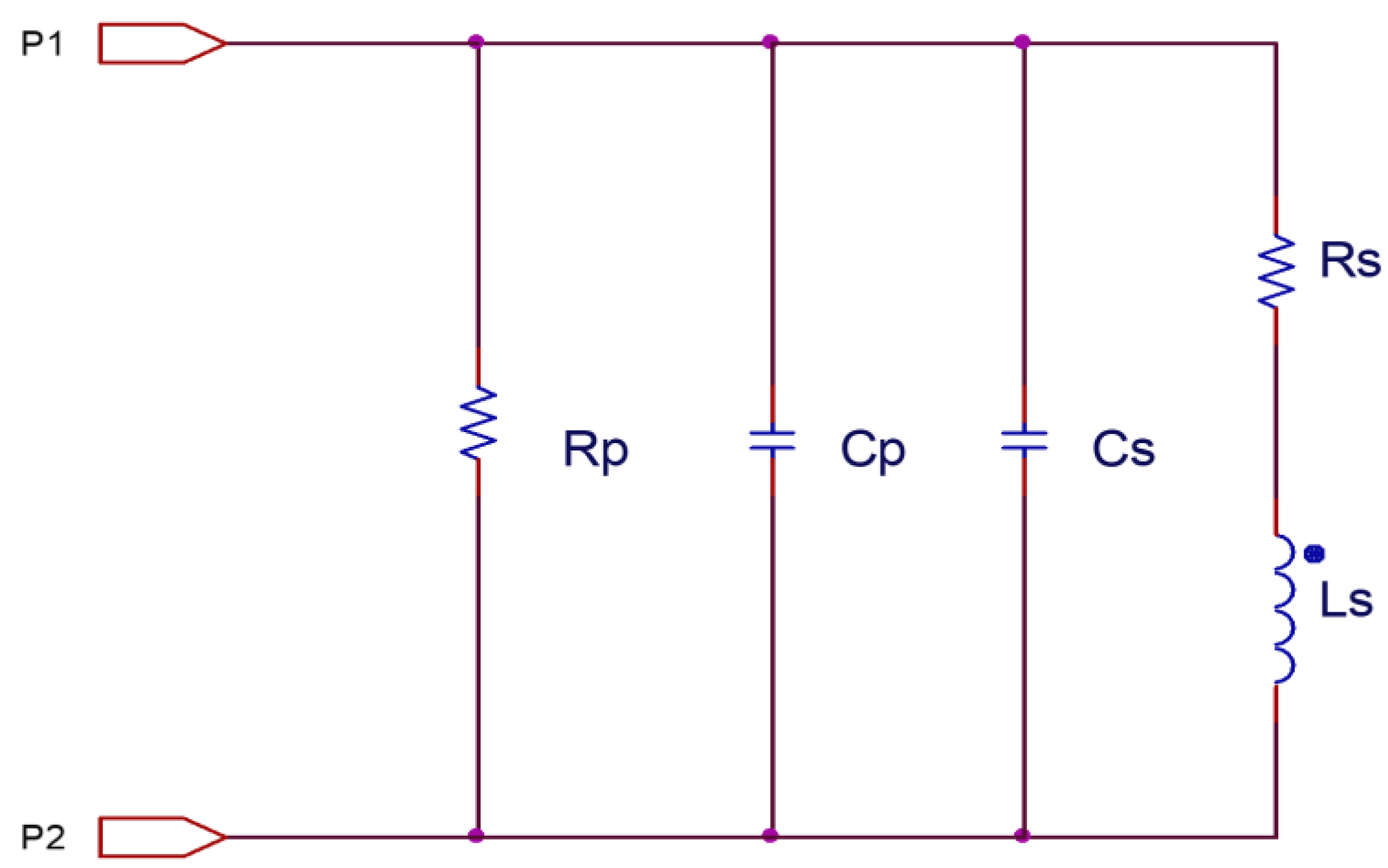
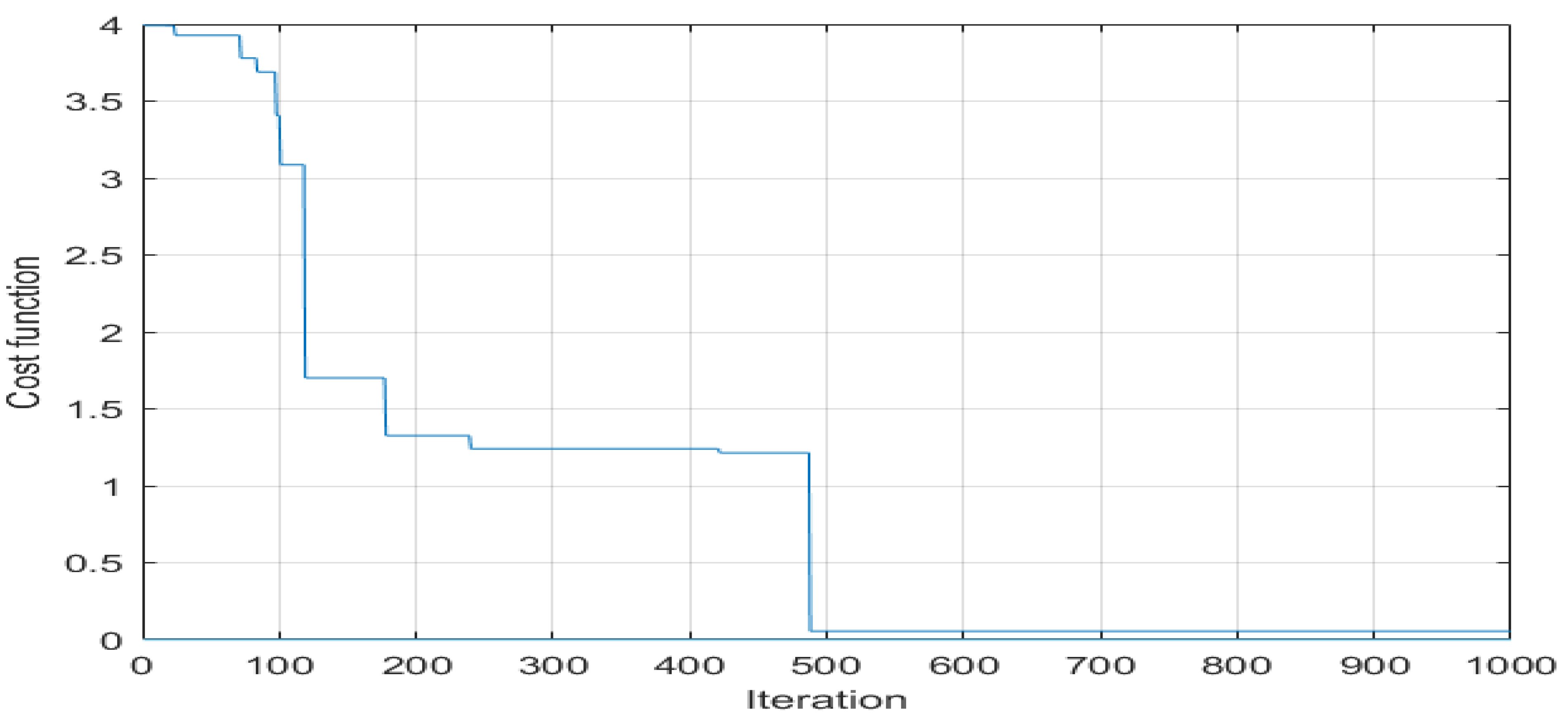
| Geometry | β | α1 | α2 | α3 | α4 | α5 |
|---|---|---|---|---|---|---|
| Octagonal | −1.21 | −0.163 | 2.43 | 1.75 | −0.049 |
| S (µm) | w (µm) | N | Dout (µm) | Lsreq (nH) | LDE (nH) | QDE |
|---|---|---|---|---|---|---|
| 4.56 | 13.62 | 3.21 | 223 | 4 | 3.95 | 13.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabiri, I.; Bouyghf, H.; Raihani, A. Optimal Sizing of RF Integrated Inductors for Power Transfer of Implantable Biosensors. Proceedings 2020, 60, 30. https://doi.org/10.3390/IECB2020-07053
Sabiri I, Bouyghf H, Raihani A. Optimal Sizing of RF Integrated Inductors for Power Transfer of Implantable Biosensors. Proceedings. 2020; 60(1):30. https://doi.org/10.3390/IECB2020-07053
Chicago/Turabian StyleSabiri, Issa, Hamid Bouyghf, and Abdelhadi Raihani. 2020. "Optimal Sizing of RF Integrated Inductors for Power Transfer of Implantable Biosensors" Proceedings 60, no. 1: 30. https://doi.org/10.3390/IECB2020-07053
APA StyleSabiri, I., Bouyghf, H., & Raihani, A. (2020). Optimal Sizing of RF Integrated Inductors for Power Transfer of Implantable Biosensors. Proceedings, 60(1), 30. https://doi.org/10.3390/IECB2020-07053





