Biocompatible Temperature Nanosensors Based on Titanium Dioxide †
Abstract
:1. Introduction
2. Materials and Methods
3. Results and discussion
3.1. Characterization of TiO2 through Raman Spectroscopy
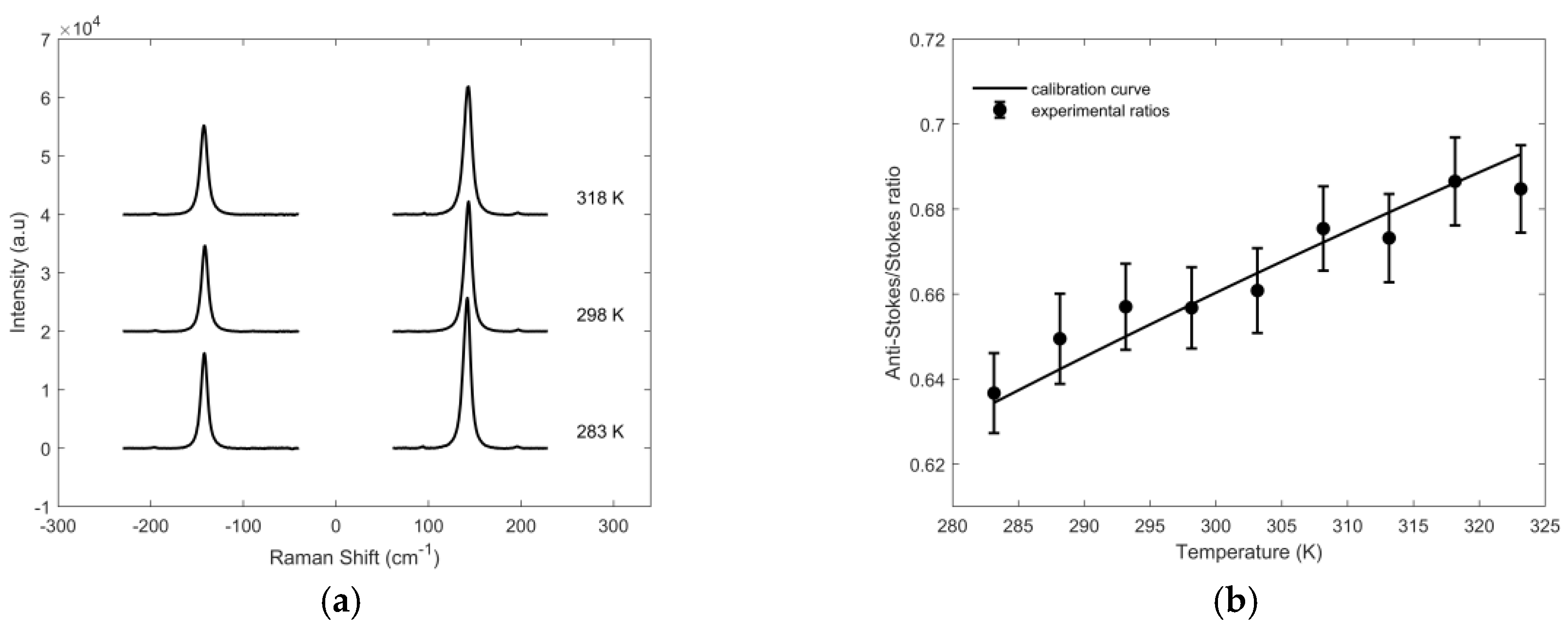
3.2. Temperature Determination
4. Conclusions
References
- Quintanilla, M.; Liz-Marzan, L.M. Guiding Rules for Selecting a Nanothermometer. Nano Today 2018, 19, 126–145. [Google Scholar] [CrossRef]
- Neumann, P.; Dolde, I.J.F.; Burk, C.; Reuter, R.; Waldherr, G.; Honert, J.; Wolf, T.; Brunner, A.; Shim, J.H.; Suter, D.; et al. Thermometry at the Nanoscale; The Royal Society of Chemistry: London, UK, 2019. [Google Scholar] [CrossRef]
- McCabe, K.M.; Hernandez, M. Molecular Thermometry. Pediatric Res. 2010, 67, 469–475. [Google Scholar] [CrossRef]
- Bai, T.; Gu, N. Micro/Nanoscale Thermometry for Cellular Thermal Sensing. Small 2016, 12, 4590–4610. [Google Scholar] [CrossRef] [PubMed]
- Uchiyama, S.; Gota, C.; Tsuji, T.; Inada, N. Intracellular temperature measurements with fluorescent polymeric thermometers. Chem. Commun. 2017, 53, 10976–10992. [Google Scholar] [CrossRef] [PubMed]
- McCreery, R.L. Raman Spectroscopy for Chemical Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar] [CrossRef]
- Griffiths, J.E.; Malyj, M. Stokes/Anti-Stokes Raman Vibrational Temperatures: Reference Materials, Standard Lamps, and Spectrophotometric Calibrations. Appl. Spectrosc. 1983, 37, 315–333. [Google Scholar] [CrossRef]
- Beechem, T.E.; Serrano, J.R. Raman Thermometry of Microdevices: Choosing a Method to Minimize Error. Spectroscopy 2011, 26, 36–44. [Google Scholar]
- Tuschel, D. Raman Thermometry: Understanding the Mathematics to Better Design Raman Measurements. Spectroscopy 2019, 34, 8–13. [Google Scholar]
- Serrano, J.R.; Phinney, L.M.; Kearney, S.P. Micro-Raman evaluation of polycrystalline silicon MEMS devices. MRS Online Proc. Libr. Arch. 2005, 890. [Google Scholar] [CrossRef]
- Beechem, T.; Christensen, A.; Graham, S.; Green, D. Micro-Raman thermometry in the presence of complex stresses in GaN devices. J. Appl. Phys. 2008, 103, 8. [Google Scholar] [CrossRef]
- Abel, M.R.; Graham, S.; Serrano, J.R.; Kearney, S.P.; Phinney, L.M. Raman thermometry of polysilicon microelectromechanical systems in the presence of an evolving stress. J. Heat Transf. Trans. ASME 2007, 129, 329–334. [Google Scholar] [CrossRef]
- Sarua, A.; Bullen, A.; Haynes, M.; Kuball, M. High-resolution Raman temperature measurements in GaAs p-HEMT multifinger devices. IEEE Trans. Electron Devices 2007, 54, 1838–1842. [Google Scholar] [CrossRef]
- Ahmad, I.; Kasisomayajula, V.; Holtz, M.; Berg, J.M.; Kurtz, S.R.; Tigges, C.P.; Allerman, A.A.; Baca, A.G. Self-heating study of an AlGaN/GaN-based heterostructure field-effect transistor using ultraviolet micro-Raman scattering. Appl. Phys. Lett. 2005, 86, 3. [Google Scholar] [CrossRef]
- Calizo, I.; Balandin, A.A.; Bao, W.; Miao, F.; Lau, C.N. Temperature dependence of the Raman spectra of graphene and graphene multilayers. Nano Lett. 2007, 7, 2645–2649. [Google Scholar] [CrossRef]
- Rassat, S.D.; Davis, E.J. Temperature-measurement of single levitated microparticles using Stokes anti-Stokes Raman intensity ratios. Appl. Spectrosc. 1994, 48, 1498–1505. [Google Scholar] [CrossRef]
- Lundt, N.; Kelly, S.T.; Rodel, T.; Remez, B.; Schwartzberg, A.M.; Ceballos, A.; Baldasseroni, C.; Anastasi, P.A.F.; Cox, M.; Hellman, F.; et al. High spatial resolution Raman thermometry analysis of TiO2 microparticles. Rev. Sci. Instrum. 2013, 84, 7. [Google Scholar] [CrossRef]
- Gallardo, J.J.; Navas, J.; Zorrilla, D.; Alcantara, R.; Valor, D.; Fernandez-Lorenzo, C.; Martin-Calleja, J. Micro-Raman Spectroscopy for the Determination of Local Temperature Increases in TiO2 Thin Films due to the Effect of Radiation. Appl. Spectrosc. 2016, 70, 1128–1136. [Google Scholar] [CrossRef] [PubMed]
- Peral, J.; Domenech, X.; Ollis, D.F. Heterogeneous photocatalysis for purification, decontamination and deodorization of air. J. Chem. Technol. Biotechnol. 1997, 70, 117–140. [Google Scholar] [CrossRef]
- Giarola, M.; Sanson, A.; Monti, F.; Mariotto, G.; Bettinelli, M.; Speghini, A.; Salviulo, G. Vibrational dynamics of anatase TiO2: Polarized Raman spectroscopy and ab initio calculations. Phys. Rev. B 2010, 81, 7. [Google Scholar] [CrossRef]
- Yin, Z.F.; Wu, L.; Yang, H.G.; Su, Y.H. Recent progress in biomedical applications of titanium dioxide. Phys. Chem. Chem. Phys. 2013, 15, 4844–4858. [Google Scholar] [CrossRef]
- Pascual, J.; Camassel, J.; Mathieu, H. Resolved Quadrupolar Transition in TiO2. Phys. Rev. Lett. 1977, 39, 1490–1493. [Google Scholar] [CrossRef]
- Fujishima, A.; Honda, K. Electrochemical Photolysis of Water at a Semiconductor Electrode. Nature 1972, 238, 37–38. [Google Scholar] [CrossRef] [PubMed]
- Michael, G. The Artificial Leaf, Molecular Photovoltaics Achieve Efficient Generation of Electricity from Sunlight. Comments Inorg. Chem. 2006, 12, 93–111. [Google Scholar] [CrossRef]
- Ohsaka, T.; Izumi, F.; Fujiki, Y. Raman spectrum of anatase, TiO2. J. Raman Spectrosc. 1978, 7, 321–324. [Google Scholar] [CrossRef]
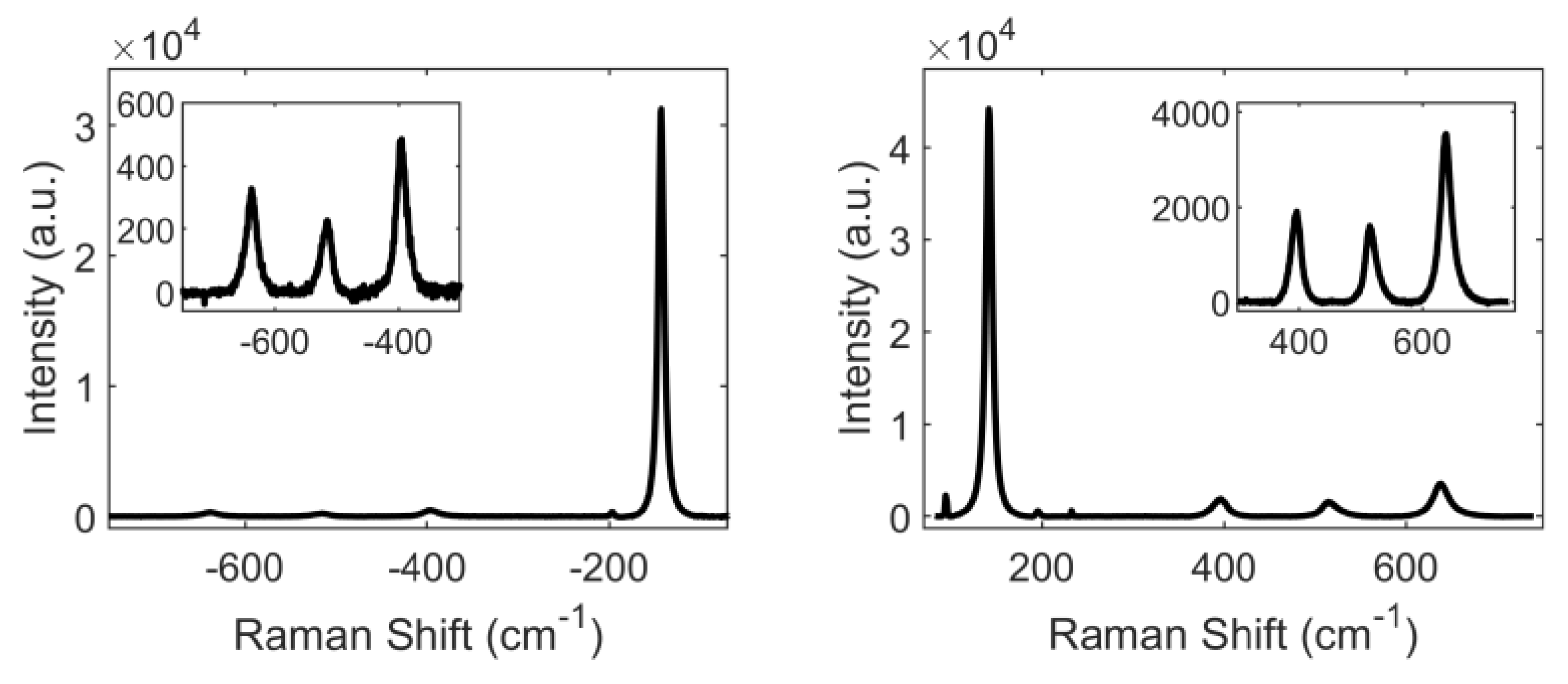
| Symmetry | Experimental (cm−1) | Literature [20] (cm−1) |
|---|---|---|
| Eg | 143 | 143 |
| Eg | 197 | 198 |
| B1g | 397 | 395 |
| B1g | 515 | 512 |
| A1g | 518 | |
| Eg | 640 | 639 |
| Excitation Wavelength (nm) | Anti-Stokes/Stokes Ratio | Raw Temperature (K) | Calibration Constant | Sample Temperature (K) |
|---|---|---|---|---|
| 514.5 | 0.5231 | 292 | 0.979 ± 0.006 | 301 |
| 568.2 | 0.5120 | 281 | 0.964 ± 0.007 | 296 |
| 647.1 | 0.6569 | 425 | 1.22 ± 0.01 | 298 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zani, V.; Pedron, D.; Pilot, R.; Signorini, R. Biocompatible Temperature Nanosensors Based on Titanium Dioxide. Proceedings 2020, 60, 16. https://doi.org/10.3390/IECB2020-07086
Zani V, Pedron D, Pilot R, Signorini R. Biocompatible Temperature Nanosensors Based on Titanium Dioxide. Proceedings. 2020; 60(1):16. https://doi.org/10.3390/IECB2020-07086
Chicago/Turabian StyleZani, Veronica, Danilo Pedron, Roberto Pilot, and Raffaella Signorini. 2020. "Biocompatible Temperature Nanosensors Based on Titanium Dioxide" Proceedings 60, no. 1: 16. https://doi.org/10.3390/IECB2020-07086
APA StyleZani, V., Pedron, D., Pilot, R., & Signorini, R. (2020). Biocompatible Temperature Nanosensors Based on Titanium Dioxide. Proceedings, 60(1), 16. https://doi.org/10.3390/IECB2020-07086







