2. The Entropy Production Due to Heat Exchange
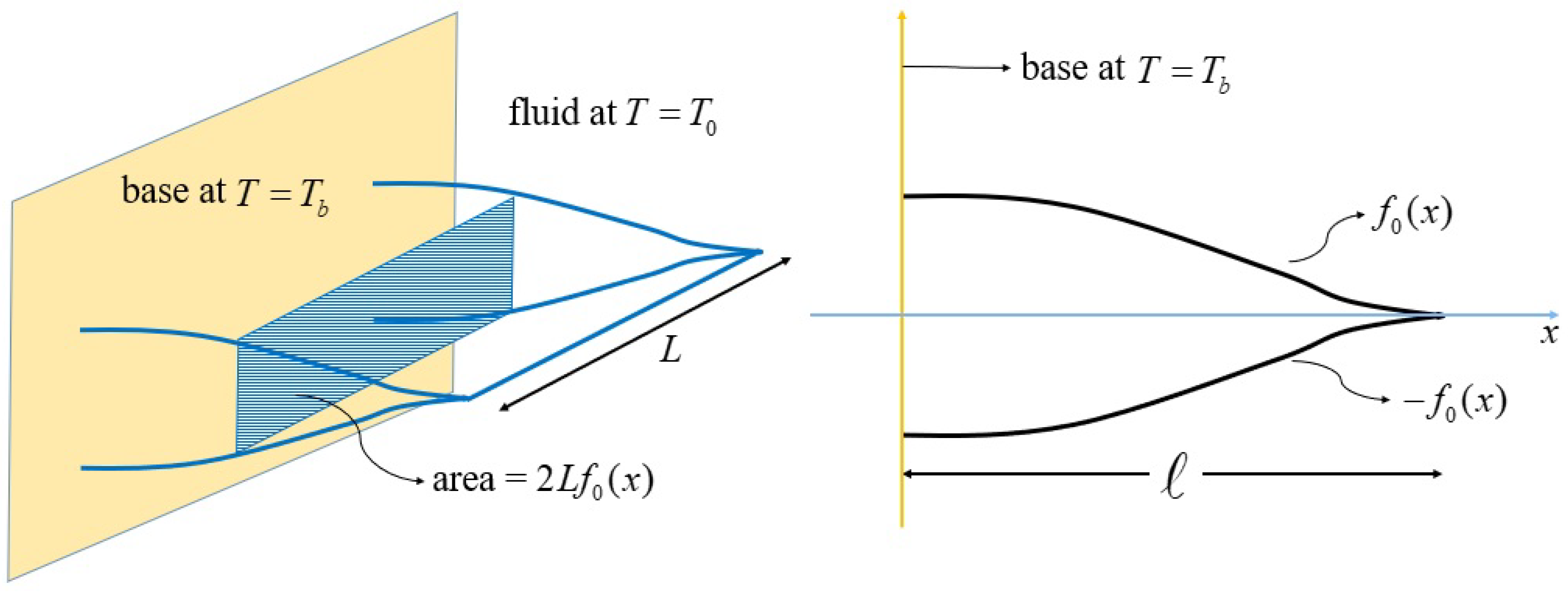
We consider a longitudinal fin of arbitrary profile attached to a base at a temperature
. The fin length is
L, whereas the fin thickness at a distance
x from the base is
. The half thickness at the base is
, whereas at the fin tip, located at
, the half thickness is denoted by
(see
Figure 1). We assume that the Fourier law of heat conduction holds inside the fin and that the temperature varies only along the
x direction. The variation of the internal energy is assumed to be equal to the energy gains (or losses) by conduction, radiation, and convection.
If
is the density of the homogeneous material,
c its specific heat,
the thermal conductivity,
h the convective heat transfer coefficient, and
the Stefan–Boltzmann constant, the evolution of temperature
is governed by the following equation:
where
is the temperature of the fluid adjacent to the fin,
represents the temperature of the effective radiation environment (i.e., the radiant energy absorbed by the fin per unit of time and surface is
), and
is the emissivity of the fin.
If the fin thickness is small compared to its length, then the term
can be ignored, and we obtain
In the following, we assume the fin to be, in general, non-gray with
, where
k is the ratio between the absorptivity and the emissivity of the fin [
2]. For a gray fin, one has to set
[
2].
Equation (
2) must be supplied with the initial and boundary conditions; we assume the boundary conditions to be given by [
1]:
and
where
and
,
, are positive constants proportional to the Biot and radiation–conduction numbers of the ends of the fin. The initial condition is given by
.
We are interested in the entropy production due to heat exchange, so we assume that the main contribution to the entropy production comes from convection and radiation. The entropy produced by the friction of the fluid on the fin has been considered elsewhere (see, e.g., [
3]). For a process starting from a temperature distribution at
given by
up to the temperature
at some time
, the contribution at
x to the entropy production due to the convection is given by
Hence, for the entire fin, we obtain
The contribution to the entropy production due to the radiation can be explicitly calculated under suitable assumptions. For completeness, we report the main formulae in the next lines; for more details, the reader can see, for example, [
4,
5,
6,
7,
8,
9,
10]. We assume that the surface of the fin is diffuse gray [
2], i.e., it absorbs a fixed fraction of incident radiation for any direction and at any frequency, and emits a fixed fraction of the blackbody radiation. For a blackbody radiation, the mean occupation number for the photon gas is given by
where
h is the Planck constant and
the Boltzmann constant. The density of states per unit volume and per unit solid angle is given by
where
c is the speed of light and
g is the degeneracy factor, which takes into account the two possible polarizations of the photons: It is equal to 2 for unpolarized photons (like in our case) and equal to 1 for polarized photons. The contribution to the entropy for each given frequency
can be written as
Equation (
8), together with (
6) and (
7), gives, for the total entropy of the blackbody radiation,
In this case, the integral can be evaluated explicitly; indeed, with an integration by parts, we get
The integral on the right can be evaluated thanks to the following identity (see, e.g., [
11]):
For simplicity, we can assume
and
. By taking the derivative of
with respect to
y and evaluating it to 0, we get
giving
This result, limited to the blackbody radiation when the number of photons is in equilibrium, is well known (see, e.g., [
4]). Due to the interaction of the radiation with matter, the number of photons is no longer conserved and the mean occupation number is reduced, for example, by the processes of absorption, emission, and reflection (see, e.g., [
5]). As a consequence, the spectral energy irradiance is reduced, too. This reduction is accounted for by the emissivity
of the material, so we can write
By repeating all the steps linking Equation (
6) for
to Equation (
13) for
S for the blackbody radiation, we get, in the case of a diffuse gray material with emissivity
,
where
is a dimensionless integral giving the dependence of the radiation entropy by emissivity, explicitly given by
The entropy rate for unit surface
is obtained from (
15) as [
6,
7]:
From (
5) and (
17), it follows that the total contribution to the entropy production (in W/
K) of the fin by convection and radiation can be written as
and, using the same approximation as in Equation (
2), it follows that
For further convenience, it is appropriate to introduce dimensionless variables. In particular, let
and
denote the dimensionless coordinates. Moreover, we define
,
,
,
, and
. Equation (
2) becomes
with initial conditions
and boundary conditions
where the Biot numbers
,
, and the radiation–conduction numbers
,
, were introduced.
3. The Role of Entropy in Assessing Efficiency of the Steady State
A common indicator of the capability of a fin to dissipate heat is given by the efficiency [
2,
12,
13]. To define this efficiency, it was necessary to introduce a reference state given by the fin at constant temperature equal to the base temperature
(
). Accordingly, the efficiency
of the fin is defined as the ratio of the actual heat transfer to the ideal heat transfer for a fin of infinite thermal conductivity in the reference state. It can be shown that, for the steady state solution of Equation (
20), the efficiency can be calculated as [
1]:
In order to make a comparison with the efficiency as above defined, the calculation of the entropy production
is performed by taking the same reference state. Hence,
is given by
and, applying (
19), it follows that
In order to get clearer formulae, we introduce the reference entropy production due to convection,
, and the reference entropy production due to radiation,
, as follows:
so that the expression of the total entropy production is reduced to
Notice that the entropy rate corresponds to the entropy produced by a fin at (i.e., ), whereas the entropy rate corresponds to the entropy produced by a fin at (i.e., ).
As pointed out in [
1], a large class of steady-state solutions of Equation (
20) with the boundary conditions (
21) are such that the dimensionless temperature
is bounded from below by the (dimensionless) fluid temperature,
, and from above by the (dimensionless) base temperature,
, i.e.,
.
We are now able to define an entropy-based indicator for the effectiveness of the fin to dissipate heat by convection and radiation. This can be done by defining
If
, then
, whereas
when
. We notice that the ratio of the reference entropies
and
is related to the ratio of the dimensionless convective and radiative coefficients
and
(see the definitions before Equation (
20)) through the formula
so Equation (
27) can also be written in the following form:
In the next section, we will investigate the reliability of this definition by analyzing the purely convective case and making a comparison with the classical definition of efficiency in (
22).
4. Analysis of the Pure Convective Case
In this section, we take into account a fin dissipating heat solely through the convective mechanism. In this case, Formula (
27) reduces to
The simplest case is that of a rectangular longitudinal profile, meaning that
for the dimensionless profile. The steady-state temperature
, solution of the Equation (
20) with the boundary conditions (
21), has been given in [
1] as
From the previous formula, it is possible to get the temperature distribution along a fin with an insulated tip and a base at
. When
and
are both zero, the boundary condition corresponding to an insulated tip is obtained from (
21) by taking
, whereas the boundary condition corresponding to a base at
is obtained by taking the limit
. If this is the case, Equation (
31) reduces to
By Equation (
30), the corresponding value of entropic efficiency is
where
. It is interesting to look at what happens when
is close to 1. In the limit
, it is possible to show that
For a temperature profile given by (
32), the classical efficiency (
22) (i.e., the ratio of the actual heat transfer to the ideal heat transfer for a fin of infinite thermal conductivity) is then given by [
1,
12]
so Formula (
34) can be rewritten as
From this example, it is apparent that (
30) can be seen as an extension of the classical definition of the efficiency based on the quantity of heat dissipated by the fin. In
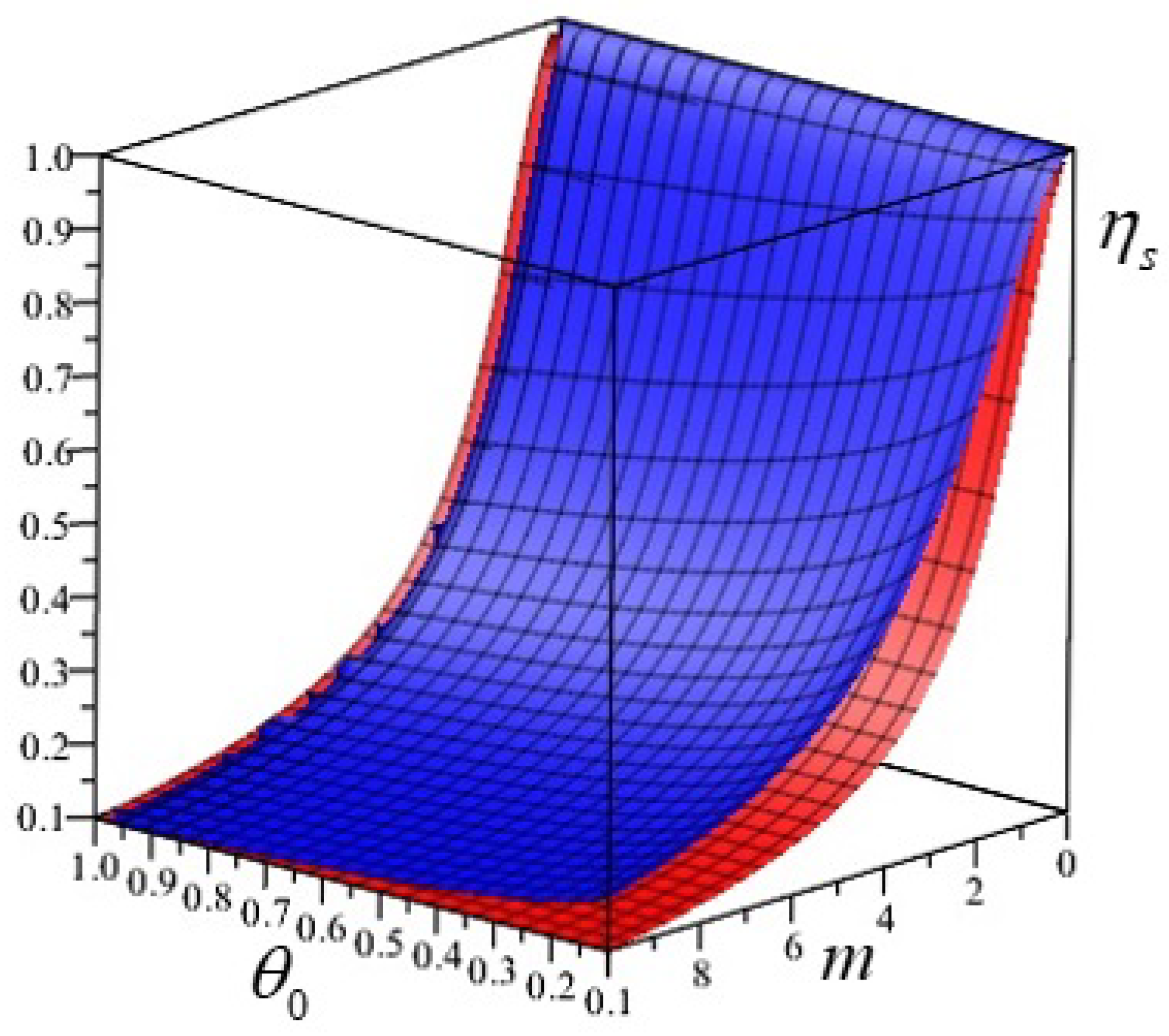
Figure 2, we plot the Formula (
33) as a function of
and
m. For comparison, Gardner’s result (
35) is also reported.
Further support for the above point of view is given by looking at the efficiency corresponding to the more general profile temperature (
31) in the same limit
. Now, from formulae (
31) and (
33), we get
Again, the first term of this expansion is exactly the efficiency obtained by applying the classical definition of efficiency (
22) (see [
1], where the classical expressions of efficiency for other different profiles have been given).
In the next section, we will look at the more general convective–radiative case.
5. Entropic Efficiency in the Convecting–Radiating Fin
The case of a fin dissipating both by convection and radiation is more challenging, since the differential equation describing the steady-state temperature along the fin is nonlinear, and the general solution of the differential equation cannot be written explicitly. In [
1], the authors were able, thanks to a change of variables, to write down (in terms of an auxiliary function
) a family of explicit solutions to Equation (
20) in the steady case with the boundary conditions (
21). For the sake of completeness, we report the main formulae and restrict the discussion to gray fins (i.e., we set
in Equations (
20) and (
21)).
If the change of variables
is inserted into the steady version of Equation (
20), and if the further constraint
is assumed, then the resulting differential equation can be integrated to give the following implicit formula for
[
1]:
where the values of
A,
,
, and
are given by:
In these expressions, the coefficients
,
, and
are explicit functions of the dimensionless fluid temperature
, the ratio
, and the parameter
w appearing in (
38). More explicitly, one has:
where the value of
b is fixed by the unique real solution of the following cubic equation:
At this point, it remains to fix the values of the constant
c, appearing in (
39), and
w, appearing in (
38). They can be fixed by exploiting the boundary condition at
. Indeed, it is possible to show (see [
1]) that the first of the two boundary conditions (
21) can be written as the following polynomial equation for
:
Furthermore, for fixed values of the parameters
,
,
, and
w, this equation always possesses one real negative solution (see [
1]), for which we use
. The initial condition for
y is then
.
For consistency with the assumed constraints
and
, it is possible to show that the value of
w must be fixed by the following equation:
whereas the value of
c is fixed by Equation (
39) evaluated at
and
. Consequently, the values of
y as a function of
z are implicitly determined by Equation (
39) for any choice of the parameters
,
a, and
b (i.e., of the parameters
,
, and
of the steady version of the differential Equation (
20)). Through Equation (
38), these functions give the corresponding values of the dimensionless temperature in the steady state
.
Now, we will apply the methodology reported above to describe the dependence of the entropic efficiency (
29) on the dimensionless convection and radiation coefficients
and
as well as on the emissivity
.
For simplicity, we analyze the case of a fin with a base at
, i.e.,
, corresponding to
and/or
. In this case, the value of
w can also be written as
To fix the ideas, we can assume the emissivity
to be equal to 0.5. The corresponding value of the integral
(
16) is given by
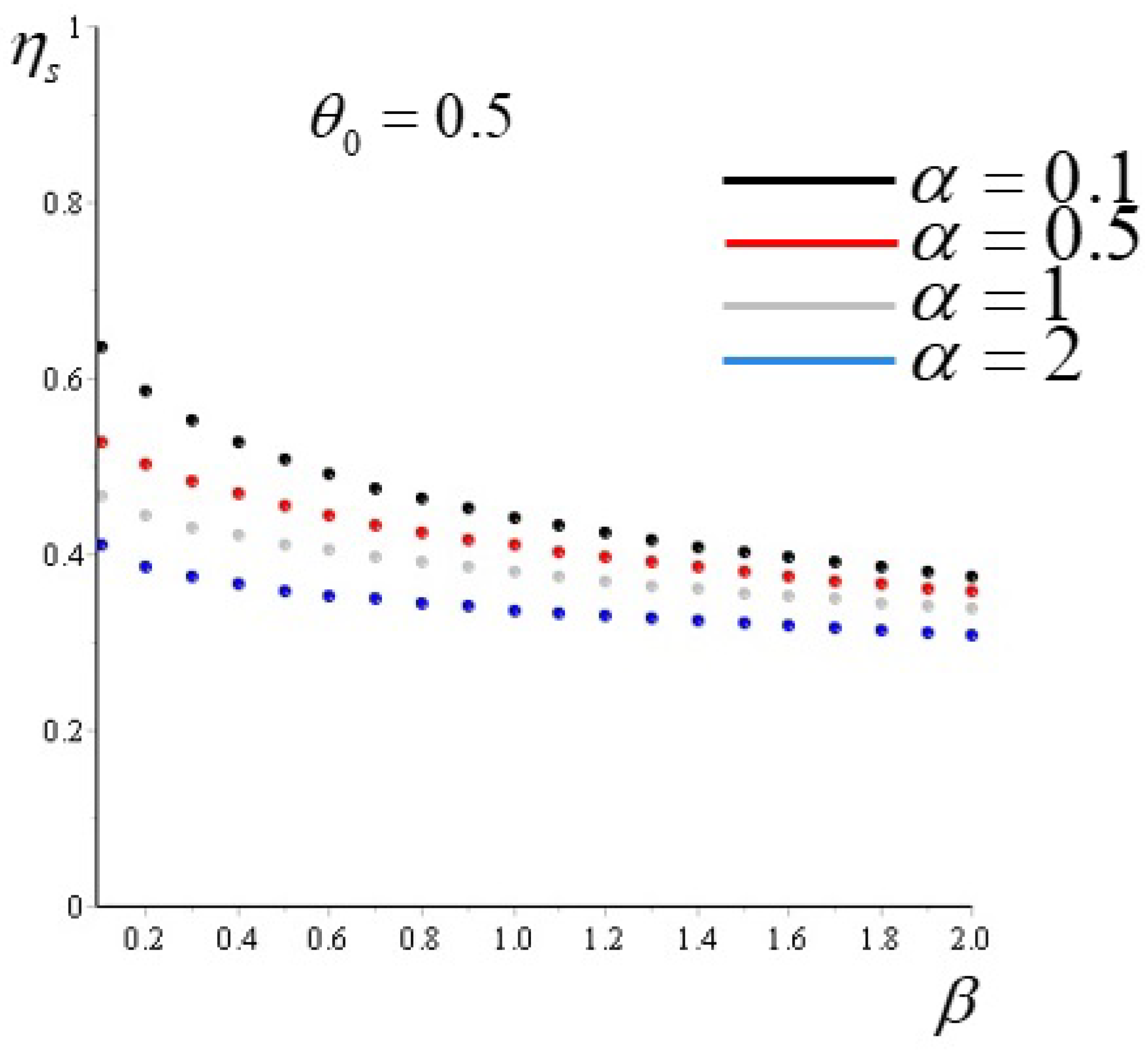
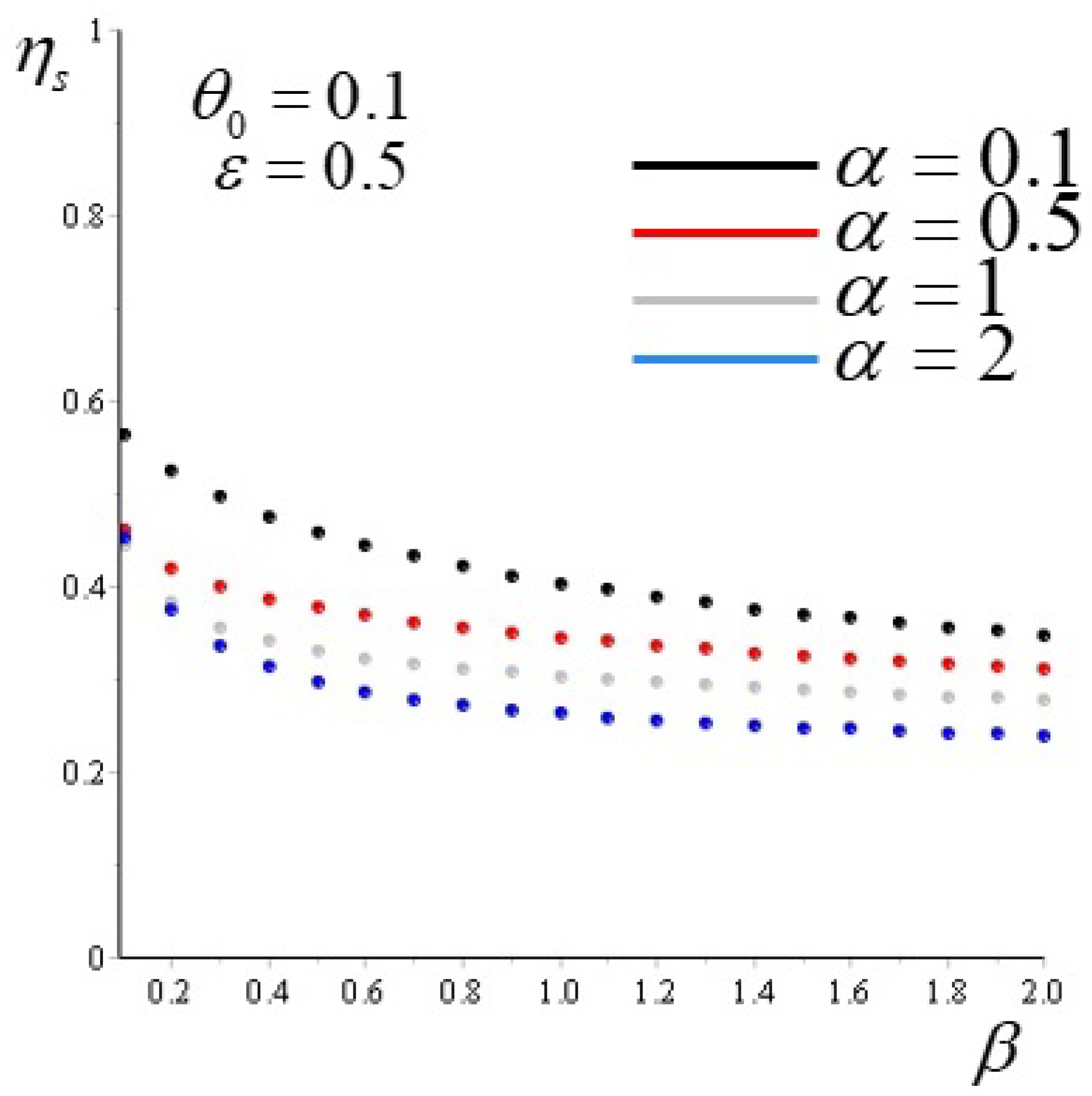
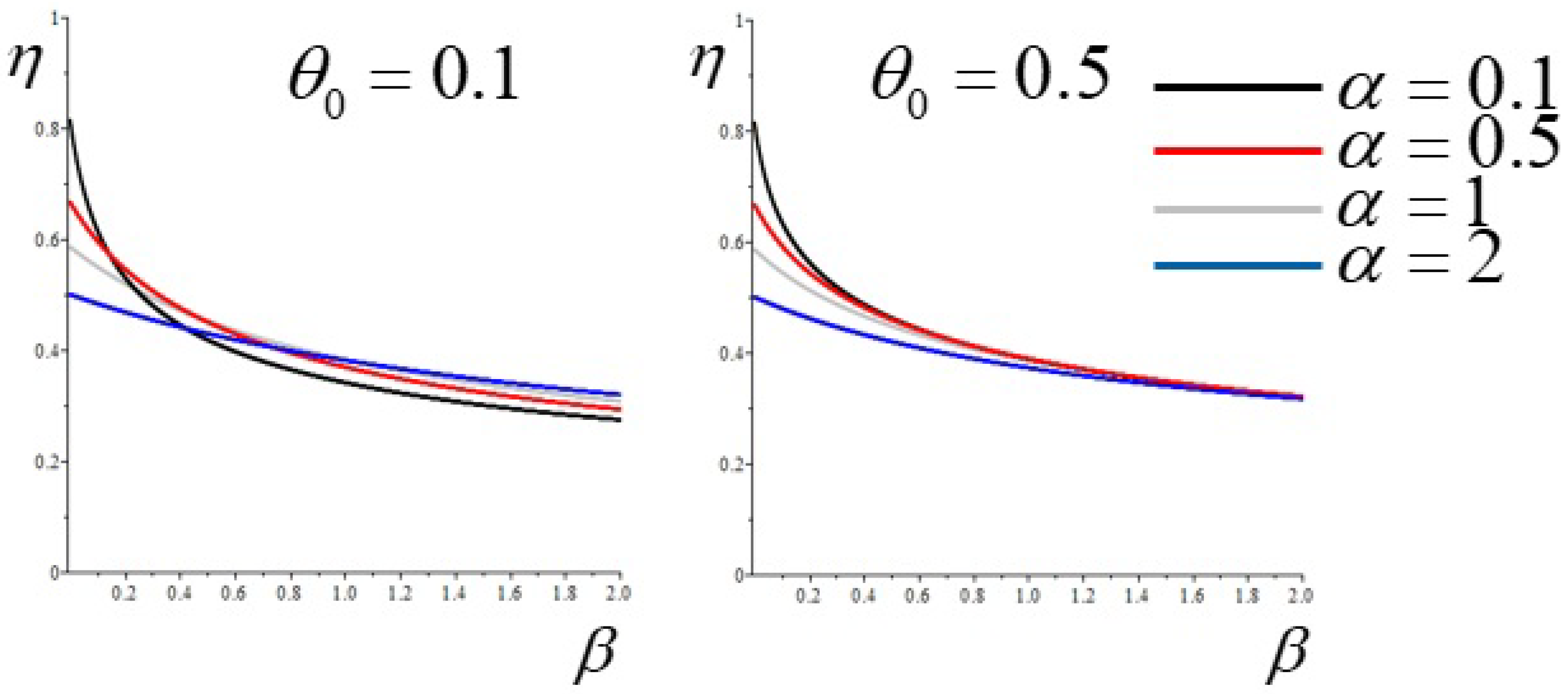
. We first choose two different values of
:
and
. For each of these choices, we consider four different values of
, namely
, and twenty different values of
, from
to
. Then, according to Equations (
38) and (
39), we calculate the distribution of temperatures along the fin, corresponding to a given set of parameters. Finally, we obtain the amount of entropic efficiency of each state by means of Equation (
29). The results are reported in
Figure 3 and
Figure 4: In all cases, the efficiency decreases with increasing
and decreases with increasing
. The resulting behavior of
is in agreement with that of the classical efficiency (
22) by performing similar variations of the parameters. For comparison, we report in
Figure 5 the values of the efficiency calculated with Formula (
22) (given in [
1]) by using the same choices of the parameters as above.