Machine Learning to Compute Implied Volatility from European/American Options Considering Dividend Yield ^†

Abstract

Computing implied volatility from observed option prices is a frequent and challenging task in finance, even more in the presence of dividends. In this work, we employ a data-driven machine learning approach to determine the Black–Scholes implied volatility, including European-style and American-style options. The inverse function of the pricing model is approximated by an artificial neural network, which decouples the offline (training) and online (prediction) phases and eliminates the need for an iterative process to solve a minimization problem. Meanwhile, two challenging issues are tackled to improve accuracy and robustness, i.e., steep gradients of the volatility with respect to the option price and irregular early-exercise domains for American options. It is shown that deep neural networks can be used as an efficient numerical technique to compute implied volatility from European/American options. An extended version of this work can be found in [1].

1. Problem Formulation

The Black–Scholes model for pricing European options reads,

$$\frac{\partial V_{eu}}{\partial t}+\frac{1}{2}{\sigma }^2{S}^2\frac{{\partial }^2{V}_{eu}}{\partial S^2}+(r-q)S\frac{\partial V_{eu}}{\partial S}-r{V}_{eu}=0,$$

(1)

where r and q are the risk-less interest rate and continuous dividend yield, respectively.

For American options, the original Black–Scholes equation becomes a variational inequality,

$$\frac{\partial V_{am}}{\partial t}+\frac{1}{2}{\sigma }^2{S}^2\frac{{\partial }^2{V}_{am}}{\partial S^2}+(r-q)S\frac{\partial V_{am}}{\partial S}-r{V}_{am}\le 0,$$

(2)

where the free boundary condition is $V_{am}(S,t)\ge H(K,S_t)$, and the terminal condition is $V_{am}(S,T)=H(K,S_T)$. We can employ a numerical method, here the COS method [2], to solve the American pricing model. In this work, we will focus on put options. The European/American Black–Scholes solution is denoted by $V_{eu/am}=B{S}_{eu/am}(\sigma ,S_0,K,\tau ,r,q,\alpha )$.

Given an observed market option price $V^{mkt}$ (European or American), the Black–Scholes implied volatility ${\sigma }^{*}$ is defined by

$$BS({\sigma }^{*};S_0,K,\tau ,r,q,\alpha )=V^{mkt}.$$

(3)

There does not exist a closed-form expression of the inverse function for neither American-style or European-style options. A popular way is to formulate the above problem into a minimization problem,

$$\underset{{\sigma }^{*}\in R^{+}}{min}BS({\sigma }^{*};S_0,K,\tau ,r,q,\alpha )-V^{mkt}$$

(4)

There are several root-finding numerical algorithms to solve (4), for example, Newton–Raphson,

$${\sigma }_{k+1}^{*}={\sigma }_k^{*}-\frac{V\left({\sigma }_k^{*}\right)-V^{mkt}}{B{S}^{\prime }\left({\sigma }_k^{*}\right)}={\sigma }_k^{*}-\frac{V\left({\sigma }_k^{*}\right)-V^{mkt}}{\mathrm{Vega}\left({\sigma }_k^{*}\right)},k=0,\dots .$$

(5)

However, some issues are likely to arise when using derivative-based algorithms, see Figure 1.

2. Methodology

In order to avoid an iterative algorithm, we provide a data-driven approach for directly approximating the inverse function of (3) via neural networks. Mathematically, an artificial neural network (ANN) can be represented as a composite function,

$$\mathrm{F}\left(\mathbf{x}\right|\mathsf{\Theta })=f^{\left(L\right)}(\cdots f^{\left(2\right)}(f^{\left(1\right)}(\mathbf{x};{\mathit{\theta }}_1);{\mathit{\theta }}_2);\cdots {\mathit{\theta }}_L),$$

(6)

where $\mathbf{x}$ stands for the input variables, $\mathsf{\Theta }$ for the hidden parameters (i.e., weights and biases), L for the number of hidden layers.

The implied volatility defined by Equation (3) can be written as an inverse function of the pricing model,

$${\sigma }^{*}=B{S}^{-1}(V^{mkt};S,K,\tau ,r,q,\alpha ),$$

(7)

where $B{S}^{-1}(·)$ denotes the inverse Black–Scholes function (European-style or American-style). Please note that the definition domain of (7) is the continuation region ${\mathsf{\Omega }}_h$ for American-style options. We use a deep neural network to approximate the inverse Black–Scholes function,

$${\sigma }^{*}=B{S}^{-1}(V^{mkt};S,K,\tau ,r,q,\alpha )\approx \mathrm{NN}(V^{mkt};S,K,\tau ,r,q,\alpha ).$$

(8)

Thus we do not need any iterative algorithm to solve (3).

2.1. ANN for European Implied Volatility

The inverse Black–Scholes function probably gives rise to steep gradients of the volatility with respect to the option price, especially for deep OTM/ITM options. It is known that the ANN has difficulties accurately representing such gradients. Here we employ the gradient-squashing technique, as in [3], to address this issue,

$${\widehat{V}}_{eu}^P=log\left(V_{eu}^P(S,t)-max(K{e}^{-r\tau }-S_t{e}^{-q\tau },0)\right).$$

(9)

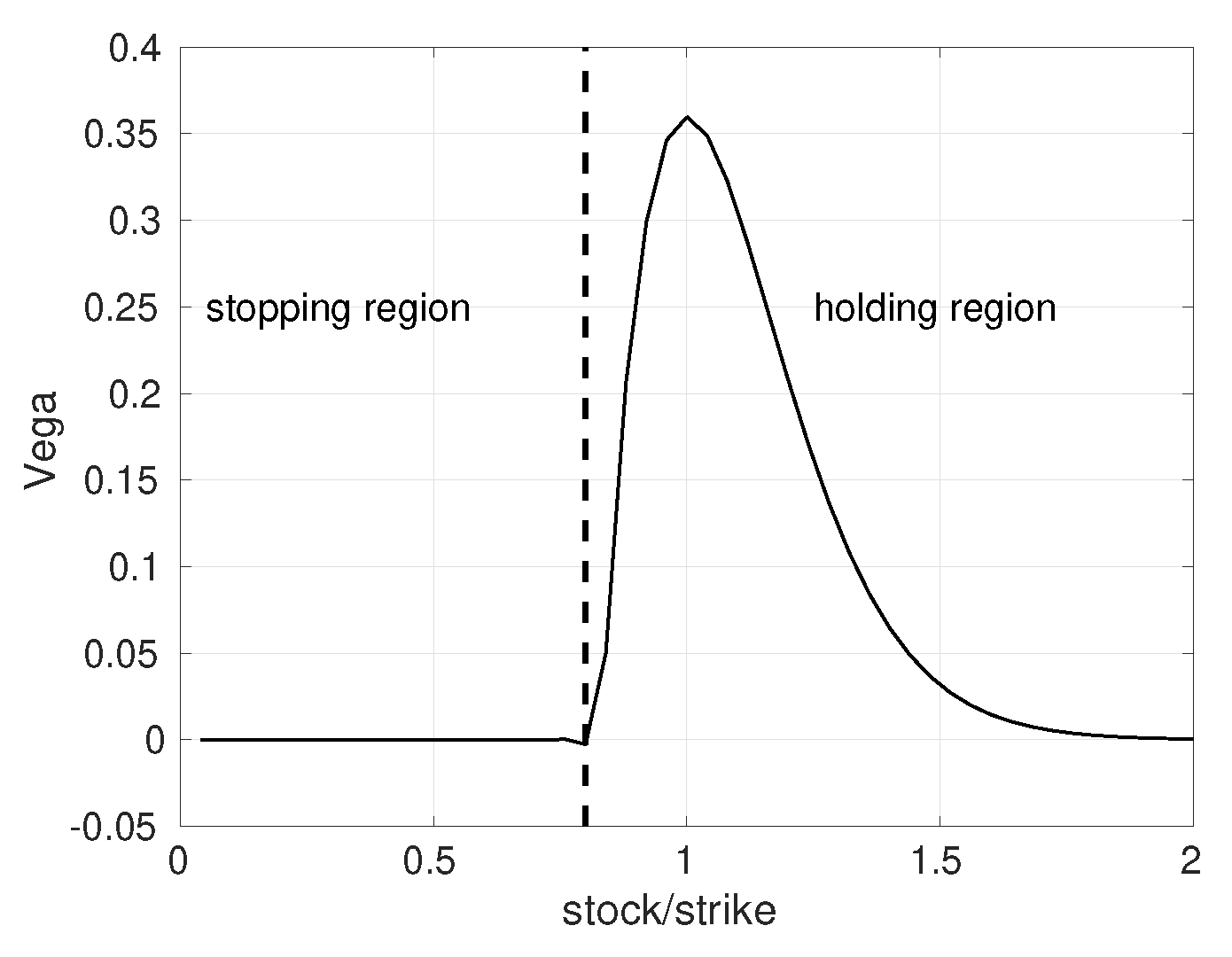
2.2. ANN for American Implied Volatility

For training the ANN to compute implied volatility from American options, there are two steps, due to the early-exercise feature. First, we need to compute again the gradient-squashed time value of an American option,

$${\widehat{V}}_{am}^P=log\left(V_{am}^P(S_t,t)-max(K-S_t,K{e}^{-r\tau }-S_t{e}^{-q\tau },0)\right).$$

(10)

Second, the effective definition domain ${\Omega }_h$ of the inverse function (8) is numerically found based on the generated samples.

3. Numerical Results

In addition to being robust, the neural network (IV-ANN) solver is much faster than an iterative numerical solver to compute implied volatility from European/American options including dividends, see

Table 1. Artificial neural network (ANN) hyper-parameters.

Parameters	Values
Hidden layers	4
Neurons(each layer)	400
Activation	ReLU
Initialization	Glorot
Optimizer	Adam
Batch size	1024

,

Table 2. Model parameter ranges.

	Parameters	Range
Inputs	Stock price ($K/S_0$)	[0.3, 1.8]
	Time to maturity ($\tau$)	[0.08, 2.5]
	Risk-free rate (r)	[0.0, 0.25]
	Dividend yield (q)	[0.0, 0.25]
	Scaled time value ($\widehat{V}$)	-
Output	Volatility ($\sigma$)	(0.01, 1.05)

,

Table 3. Performance of IV-ANN.

Phase	European Options				American Options
	MSE	MAE	MAPE	${\mathrm{R}}^{\mathbf{2}}$	MSE	MAE	MAPE	${\mathrm{R}}^{\mathbf{2}}$
Training	1.72 $\times {10}^{-7}$	3.17 $\times {10}^{-4}$	6.99 $\times {10}^{-4}$	0.9999976	7.12 $\times {10}^{-7}$	5.66 $\times {10}^{-4}$	1.42 $\times {10}^{-4}$	0.999990
Testing	1.94 $\times {10}^{-7}$	3.35 $\times {10}^{-4}$	7.39 $\times {10}^{-4}$	0.9999972	1.93 $\times {10}^{-6}$	6.52 $\times {10}^{-4}$	2.35 $\times {10}^{-3}$	0.999974

and

Table 4. Computational cost based on 20,000 option prices.

Method	GPU (s)	CPU (s)	Robustness
Newton-Raphson	19.68	23.06	No
Brent	52.08	60.67	Yes
Bi-section	337.94	390.91	Yes
IV-ANN	0.20	1.90	Yes

.