A Doubly Smoothed PD Estimator in Credit Risk ^†

Abstract

In this work a doubly smoothed probability of default (PD) estimator is proposed based on a smoothed version of the survival Beran’s estimator. The asymptotic properties of both the smoothed survival and PD estimators are proved and their behaviour is analyzed by simulation. The results allow us to conclude that the time variable smoothing reduce the error committed in the PD estimation.

1. Introduction

The debts coming from clients with unpaid credits have a important impact in the solvency of banks and other credit institutions. Therefore, one of the most crucial elements that influences the risk in credits is the probability of default (PD). For a fixed time, t, and a horizon time, b, the PD can be defined as the probability that a credit that has been paid until time t, becomes unpaid not later than time $t+b$.

The probability of default conditional on the credit scoring can be written as a transformation of the conditional survival function. Therefore, in Section 2.1 Beran’s survival estimator is used to obtain a PD estimator. A time variable smoothing for this estimator is proposed in Section 2.2. In Section 3, both estimators are applied to a real data set. Section 4 contains some concluding remarks.

2. Nonparametric PD Estimators

Let ${\left\{(X_i,Z_i,{\delta }_i)\right\}}_{i=1}^n$ be a simple random sample of $(X,Z,\delta )$ where X is the credit scoring, $Z=min\{T,C\}$ is the observed maturity, T is the time to default, C is the time until the end of the study or the time until the anticipated cancellation of the credit and $\delta =I_{\{T\le C\}}$ is the uncensoring indicator. Let x be a fixed value of the covariate X, b a horizon time and $S\left(t\right|x)$ the conditional survival function of T. Then, the probability of default in a time horizon $t+b$ from a maturity time t is defined as follows

$$\begin{array}{ccc}PD\left(t\right|x)& =& P(T\le t+b|T>t,X=x)=1-{\displaystyle \frac{S(t+b|x)}{S\left(t\right|x)}}.\hfill \end{array}$$

(1)

Replacing $S\left(t\right|x)$ with a nonparametric estimator, $\widehat{S}\left(t\right|x)$, in (1), the following estimator for $PD\left(t\right|x)$ is obtained:

$$\begin{array}{ccc}\widehat{PD}\left(t\right|x)& =& 1-{\displaystyle \frac{\widehat{S}(t+b|x)}{\widehat{S}\left(t\right|x)}}.\hfill \end{array}$$

(2)

In [5] the theoretical results that allow to obtain, under general conditions, asymptotic properties for a PD estimator are proved. They are based on these properties for the corresponding estimator of the conditional survival function.

2.1. Beran’s Estimator

Beran’s survival estimator proposed in [1] is given by

$$\begin{array}{ccc}{\widehat{S}}_h^B\left(t\right|x)& =& {\displaystyle \prod _{i=1}^n\left(1-{\displaystyle \frac{I_{\{Z_i\le t,{\delta }_i=1\}}{w}_{i,n}\left(x\right)}{1-{\sum }_{j=1}^n{I}_{\{Z_j<Z_i\}}{w}_{n,j}\left(x\right)}}\right),}\hfill \end{array}$$

(3)

where the weights are $w_{i,n}\left(x\right)={\displaystyle \frac{K\left((x-X_i)/h\right)}{{\sum }_{j=1}^{n}K\left((x-X_j)/h\right)}},$ with $i=1,\dots ,n$, K is a kernel function and $h=h_n>0$ is a smoothing parameter. Now, replacing $\widehat{S}\left(t\right|x)$ with ${\widehat{S}}_h^B\left(t\right|x)$ in (2), Beran’s estimator of the probability of default, ${\widehat{PD}}_h^B\left(t\right|x)$, is available. It was firstly used in [2].

The asymptotic properties of Beran’s estimator for the conditional survival function were proven in both [3,4] under certain assumptions. From them, the expressions of the bias and the variance of the estimator ${\widehat{PD}}_h^B\left(t\right|x)$ can be found by using Theorem 1 in [5].

A simulation study was conducted in order to analyse the performance of Beran’s estimator. Its behavior was compared with other estimators of the probability of default obtained from estimators of the survival function, including a benchmark method based on proportional hazards models. For more details about the simulation study, see [5].

The results show that the probability of default estimations obtained by means of the estimators built according to (2) are very reasonable, but they have excessive variability and they are very rough curves.

2.2. Smoothed Beran’s Estimator

Beran’s estimator is smoothed with respect to the covariate, but not with respect to the time variable. This fact along with the survival ratio structure of the PD estimator could be the cause of the instability of the estimations. Therefore, a time variable smoothing of the survival estimator is proposed.

The smoothed Beran’s survival estimator is given by

$$\begin{array}{ccc}{\tilde{S}}_{h,g}^B\left(t\right|x)& =& {\displaystyle 1-\sum _{i=1}^n{s}_{\left(i\right)}\mathbb{K}\left({\displaystyle \frac{t-Z_{\left(i\right)}}{g}}\right)}\hfill \end{array}$$

(4)

where $s_{\left(i\right)}={\widehat{S}}_h^B\left(Z_{(i-1)}\right|x)-{\widehat{S}}_h^B\left(Z_{\left(i\right)}\right|x)$ with $Z_{\left(i\right)}$ the i-th element of the sorted sample of Z, $\mathbb{K}\left(t\right)$ the distribution function of a kernel K and $g=g_n$ is the smoothing parameter for the time variable. Finally, the smoothed Beran’s PD estimator, ${\widetilde{PD}}_{h,g}^B\left(t\right|x)$, is obtained by replacing $\widehat{S}\left(t\right|x)$ with ${\tilde{S}}_{h,g}^B\left(t\right|x)$ in Equation (2).

The asymptotic expressions for the bias and the variance of the smoothed Beran’s estimator of the survival function have been recently found [6]. The results are too extensive to be shown here. By applying Theorem 1 of [5], the corresponding asymptotic properties of the smoothed Beran’s estimator of the PD are obtained.

The simulation study carried out shows that the time variable smoothing significantly reduces the error committed in the PD estimation. This technique implies a considerable increase in the computation time and the improvement is not very noticeable in the estimation of the survival function. However, in the case of the PD, the variability and roughness of the estimations is clearly reduced.

3. Application to Real Data

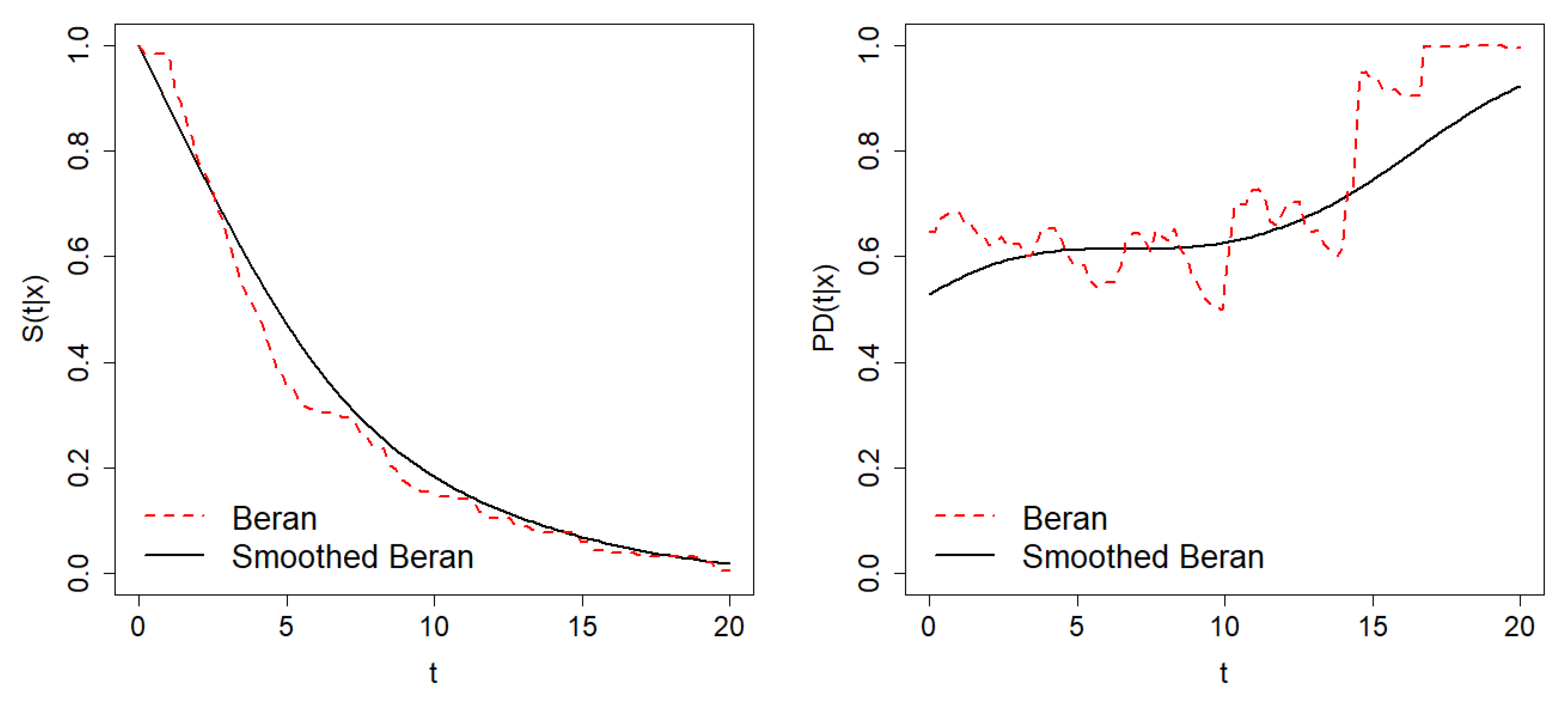
To illustrate the differences between the estimator based on Beran’s and its smoothed version, we obtain the estimation of the conditional survival function and the PD in a real data set. The data consists of a sample of 10,000 consumer credits from a Spanish bank registered between July 2004 and November 2006. The sample contains the credit scoring of each borrower, the observed lifetime and the uncensoring indicator. The sample censoring percentage is $92.8\%$. The probability of default is estimated using Beran’s and smoothed Beran’s estimators with $h=0.05$ and $g=3$. Figure 1 shows the result.

4. Conclusions

This work proposes a time variable smoothing for Beran’s estimator of the conditional survival function. General asymptotic expressions for the bias and the variance of this estimator are proven. It is used to build a doubly-smoothed PD estimator whose asymptotic properties are also proved. In view of the simulation study carried out, it can be concluded that the smoothed Beran’s estimator seems to reduce the estimation error committed when estimating the probability of default.

Work is currently underway to develop a method for choosing the smoothing parameters involved in the above-mentioned estimators. In addition, since the censoring probability is heavy in this context, nonparametric cure models are going to be considered in the study.