A Penetrometer for Quantifying the Surface Stiffness of Sport Sand Surfaces †
Abstract
:1. Introduction
- the ‘iron man competition,’ which features four main disciplines in one race: swimming, board paddling, ski paddling, and running. For the running event, flags demark a course of approximately 150 m from wet to soft sand and back;
- the beach flags event [4], which is a sand run of approximately 20 m in soft sand with competitors prone at the start;
- the beach relay [4], which has six competitors in a team running a total distance of 90 m in soft sand;
- the beach sprint [4], which has an approximate distance of 80 m;
- beach volleyball [5], which has two players on soft dry sand;
- beach soccer [6], which has five players on soft dry sand.
2. Materials and Methods
- (1)
- the penetration depth should be similar to the penetration depth of a runner’s footprint;
- (2)
- the impact force per square area during contact should be similar to that from an average-sized runner;
- (3)
- the device should be easy to deploy and operate.
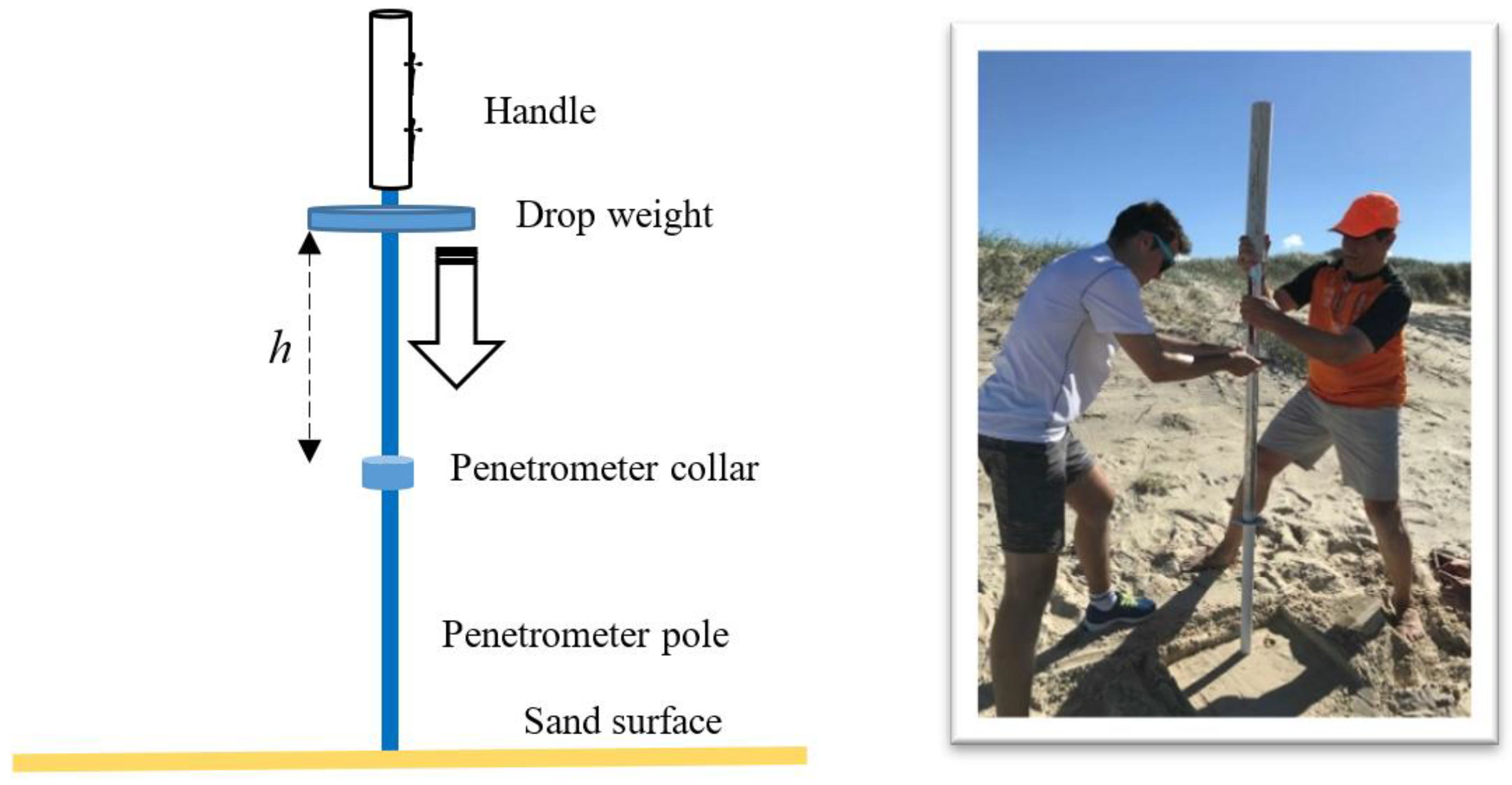
- the sand under test was smoothed on the surface to be horizontal (see Figure 1);
- the end of the penetrometer was rested on the sand’s surface;
- the penetrometer was oriented vertically;
- the weight was raised to a fixed height and released;
- the penetrometer was carefully removed from the sand and the depth of the indentation was measured.
Theory
3. Results
4. Discussion
- the measurements reported were in-situ on unconfined sand, whereas the sand box measurements [3] were constrained on five sides (only the top surface was unconfined);
- the standard deviation in the measurements was large as every measurement was on a different but adjacent sand surface;
- the in-situ, undisturbed sand could be highly layered, with the top layer consisting of very fine particles. One assumes that the sandbox measurements were conducted over a homogeneous sand sample.
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Ganderton, C.; Cook, J.; Docking, S.; Rio, E.; van Ark, M.; Gaida, J. Achilles tendinopathy: Understanding the key concepts to improve clinical management. Aust. Musculosketal Med. 2015, 19, 12–18. [Google Scholar]
- Gaudino, P.; Gaudino, C.; Alberti, G. Minetti, Biomechanics and predicted energetics of sprinting on sand: Hints for soccer training. J. Sci. Med. Sport 2013, 16, 271–275. [Google Scholar] [CrossRef] [PubMed]
- Barrett, R.; Neal, R.; Roberts, L. The dynamic loading response of surfaces encountered in beach running. J. Sci. Med. Sport 1997, 1, 1–11. [Google Scholar] [CrossRef]
- SLSQ Secondary School Surf League. Beach Flags. Available online: http://nbbsurflifesaving.com.au/wp-content/uploads/2013/05/Event-Descriptions-2013.pdf (accessed on 26 August 2019).
- Reeser, J.C.; Verhagen, E.; Briner, W.W.; Askeland, T.I.; Bahr, R. Strategies for the prevention of volleyball related injuries. Br. J. Sports Med. 2006, 40, 594–600. [Google Scholar] [CrossRef] [PubMed]
- Altman, A.; Nery, C.; Sanhudo, A.; Pinzur, M.S. Osteochondral injury of the hallux in beach soccer players. Foot Ankle Int. 2008, 29, 919–921. [Google Scholar] [CrossRef] [PubMed]
- Ferris, D.P.; Liang, K.; Farley, C.T. Runners adjust leg stiffness for their first step on a new running surface. J. Biomech. 1999, 32, 787–794. [Google Scholar] [CrossRef]
- Worsey, M.T.O.; Espinosa, H.G.; Shepherd, J.B.; Lewerenz, J.; Klodzinski, F.S.M.; Thiel, D.V. Features observed using multiple inertial sensors for athletics track and hard-soft sand running: A comparison study. MDPI Proc. accepted for publication.
- Standards Australia. Soil strength and consolidation tests—Determination of the penetration resistance of a soil—9 kg dynamic cone penetrometer tests. In Methods of Testing Spoils for Engineering Purposes; AS 1289.6.3.2-1997; Standards Australia: Sydney, Australia, 1997. [Google Scholar]
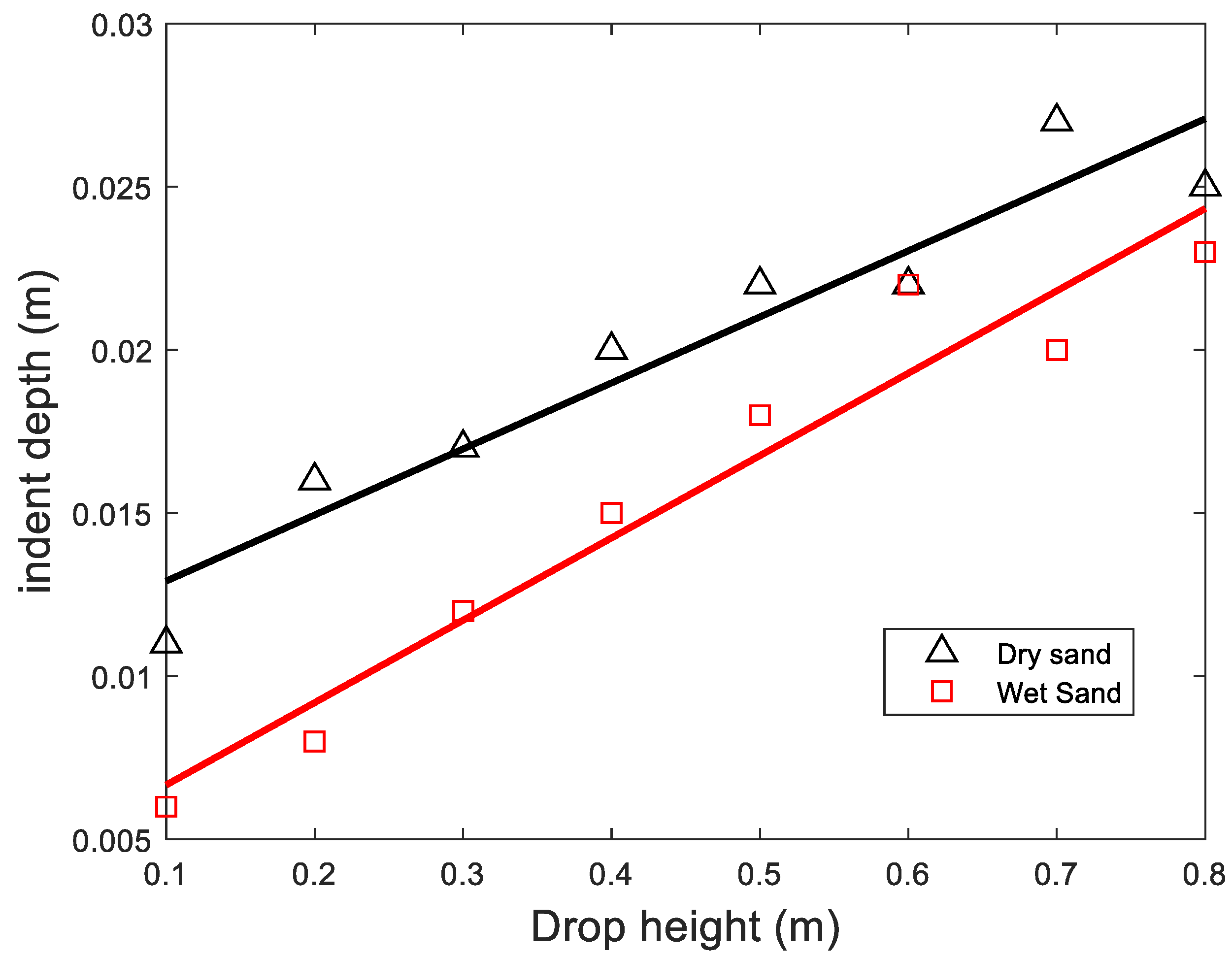
| Drop Weight | r2 | Stiffness S | S [3] | |
|---|---|---|---|---|
| Dry sand | 1.25 kg | 0.92 | 13 (2) kN/m | 59 (29) kN/m |
| Wet sand | 5.0 kg | 0.92 | 97 (32) kN/m | 380 (118) kN/m |
| Stiffness ratio | 13% | 15% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thiel, D.V.; Worsey, M.T.O.; Klodzinski, F.; Emerson, N.; Espinosa, H.G. A Penetrometer for Quantifying the Surface Stiffness of Sport Sand Surfaces. Proceedings 2020, 49, 64. https://doi.org/10.3390/proceedings2020049064
Thiel DV, Worsey MTO, Klodzinski F, Emerson N, Espinosa HG. A Penetrometer for Quantifying the Surface Stiffness of Sport Sand Surfaces. Proceedings. 2020; 49(1):64. https://doi.org/10.3390/proceedings2020049064
Chicago/Turabian StyleThiel, David V., Matthew T. O. Worsey, Florian Klodzinski, Nicholas Emerson, and Hugo G. Espinosa. 2020. "A Penetrometer for Quantifying the Surface Stiffness of Sport Sand Surfaces" Proceedings 49, no. 1: 64. https://doi.org/10.3390/proceedings2020049064
APA StyleThiel, D. V., Worsey, M. T. O., Klodzinski, F., Emerson, N., & Espinosa, H. G. (2020). A Penetrometer for Quantifying the Surface Stiffness of Sport Sand Surfaces. Proceedings, 49(1), 64. https://doi.org/10.3390/proceedings2020049064







